Quantum-chemical Ab Initio Calculations on the Donor–Acceptor Complex Pyridine–Borabenzene (C5H5N–BC5H5)
Mohammed Mbarki A , Marc Oettinghaus A and Gerhard Raabe A BA Department of Organic Chemistry, Rheinisch-Westfaelische Technische Hochschule (RWTH) Aachen University, Landoltweg 1, D-52074 Aachen, Germany.
B Corresponding author. Email: gerd.raabe@thc.rwth-aachen.de
Australian Journal of Chemistry 67(2) 266-276 https://doi.org/10.1071/CH13407
Submitted: 3 August 2013 Accepted: 2 October 2013 Published: 7 November 2013
Abstract
The adduct of borabenzene (C5H5B) and pyridine (C5H5N) was studied by means of quantum-chemical ab initio and time-dependent density functional theory calculations at different levels of theory. In the fully optimized structure (MP2/6-311++G**) of the free donor–acceptor complex (C2), the C–B–C angle amounts to 120.6°. The planes of the two aromatic rings enclose a torsion angle of ~40° with a barrier to rotation about the B–N bond of less than 3 kcal mol–1 (1 kcal mol–1 = 4.186 kJ mol–1). The highest computational level applied in this study (complete basis set limit, coupled cluster with single and double excitations (CCSD)) results in an energy associated with the reaction of borabenzene with pyridine of –52.2 kcal mol–1. Natural bond orbital analyses were performed to study the bond between the borabenzene and the pyridine unit of the adduct. The UV-vis spectrum of the adduct was calculated employing time-dependent density functional theory methods and the symmetry-adapted cluster-configuration interaction method. Our calculated electronic excitation spectrum of the pyridine adduct as well as its spectrum of the normal modes qualitatively reproduce the characteristic features of the IR and the UV-vis spectra described by experimentalists and thus allows assignment of the observed absorption bands, which in part agree with those by other authors.
Introduction
Borabenzene (C5H5B) has been the subject of some experimental[1–3] and an even higher number of theoretical[4–12] studies; however, attempts to generate the free compound have met with failure so far. At least in two experimental studies, borabenzenze apparently occurred as a transient that was trapped either by dinitrogen[1] or pyridine.[2] Although the adduct of borabenzene with N2 was not isolated as a pure compound but rather was characterized spectroscopically in a matrix of frozen dinitrogen at 10 K,[1] the adduct formed with pyridine was obtained as a yellow crystalline solid when 1-methoxy-6-(trimethylsilyl)-1-bora-2,4-cyclohexadiene was reacted with C5H5N at 60°C.[2] The crystalline compound turned out to be sufficiently stable to be subjected to single-crystal X-ray structure determination. Pyridine–borabenzene belongs to a class of compounds that are commonly called donor–acceptor complexes.[13,14] In these compounds, the electrons of the bond connecting the two components of the complex (here pyridine and borabenzene) are formally provided by one of the molecules (pyridine), which is called the donor. On bonding, the atom that donates the electron pair receives a positive formal charge while the atom of the other compound (borabenzene), which is called the acceptor and is directly bonded to the donating atom, gets a negative formal charge (see Scheme 1, limiting structure B). Compounds of this kind with different acceptors and donors have been studied in much detail using theoretical methods by Frenking and Jonas,[15,16] and our results obtained for pyridine–borabenzene are compared with the accounts of their research.

|
Using THF as a solvent, the title compound caused absorptions at λmax (ϵ) = 236 (5175), 250 (5090), 279 (3470), and 472 nm (2825 × 1000 cm2 mol–1) in the UV-vis spectrum.[2] Based on a semi-empirical Pariser–Parr–Pople (PPP) calculation, the band observed at 472 nm was assigned to a HOMO → LUMO transition involving charge transfer from the C5H5B to the C5H5N moiety.[2] The position of this band was found to strongly depend on the molecule’s environment in that it was shifted to 492 nm in benzene whereas it occurred at as long a wavelength as 596 nm in an Ar matrix. A similarly strong solvent dependence of this band was obtained by an electrostatic solvent model in combination with the semi-empirical configuration interaction including single excitations employing the spectroscopic complete neglect of differential overlap approximation (CIS CNDO/S) method.[11]
Moreover, in further characterizing the compound, Boese et al.[2] reported intense absorptions in the infrared at ~1500 and ~700 cm–1.
To get a deeper insight into the structural features and the electronic properties of the title compound, we performed quantum-chemical ab initio as well as time-dependent density functional theory (DFT) calculations at different levels of theory.
Methods
Most of the calculations that form the basis for the results presented in this paper were performed with the Gaussian09[17] suite of quantum-chemical routines using the facilities of the Computing and Communication Centre of the RWTH Aachen University. All structures under consideration were optimized at the MP2 and the CISD level employing the 6-311++G** basis set, where certain geometric constraints had to be applied in some of the calculations (structures of C2v symmetry). The nature of each optimized stationary point was determined by checking the eigenvalues of the corresponding force constant matrix for negative values. To obtain improved energies for the reaction between borabenzene and pyridine, additional single-point calculations were performed at the coupled cluster level (CC) including single (S) and double (D) (CCSD) substitutions as well as in some cases a non-iterative inclusion of triple excitations (T) (CCSD(T)).[18] Correlation-consistent basis sets (aug-cc-pTZV, aug-cc-pDZV[19]) were used in the coupled-cluster calculations. Finally, we extrapolated to a complete basis set employing the method of Truhlar et al.[20] To study the nature of the B–N bond, additional natural bond orbital (NBO) analyses were performed with the program NBO 3.0[21] as implemented in Gaussian09. Using the MP2/6-311++G**-optimized structures, UV-vis spectra were calculated within the framework of time-dependent density functional theory (TDDFT[22]) including 30 singlet states in each of the calculations. In these calculations, we used both the B3LYP and the long-range exchange-corrected CAM-B3LYP hybrid functional. This functional was reported by several authors[23a,23b,23e] to perform better for charge-transfer transitions than B3LYP. It appears, however, that the relative performance of B3LYP and CAM-B3LYP critically depends on the system under consideration,[23c,23d] and cases have been reported where the results obtained with the long-range exchange-corrected version are inferior to those from a B3LYP calculation.[23d] Both the 6-311++G(3df,3pd) and the aug-cc-pVDZ basis sets were used in the calculation of the UV-vis spectra at the TDDFT level. In addition, we also calculated electronic absorption spectra with the SAC-CI (Symmetry-Adapted Cluster-Configuration Interaction) method[24] also employing the MP2/6-311++G**-optimized geometry. Owing to the size of the system, the basis set had to be confined to 6-31G* quality in these calculations, where the corresponding restricted Hartree–Fock (RHF) wave function was used as a reference. Fifteen excited states of each of the two relevant irreducible representations (A, B) were included in the calculation for the molecules of point group C2, whereas seven states of each of the four irreducible representations (A1, A2, B1, B2) were used for species of point group C2v. The active space comprised the occupied valence molecular orbitals and all virtual molecular orbitals of the correct symmetry. The spectral curves were generated using a sum of Lorentzian curves, each of which was centred at the corresponding transition wavelength and multiplied with the associated oscillator strength. The half-bandwidth Γ was calculated using the empirical formula Γ = kλ1.5[25] with k = 0.00375 (R. W. Woody, pers. comm.).
In some TDDFT calculations, the influence of the solvent was approximated using two electrostatic solvent models, namely the polarizable continuum model (PCM)[26] and conductor-like polarizable continuum model (CPCM).[27]
Optimized structural parameters of all compounds under consideration are given in Table 1, whereas the corresponding total energies obtained at different levels of theory are collected in Table 2.

|

|
Results and Discussion
The Geometry of Pyridine–Borabenzene and the Change of Energy Associated with the Reaction Between its Molecular Fragments
The fully optimized structure of the title compound (1) in a vacuum is shown in Fig. 1 and the resulting structural parameters are listed in Table 1. For numbering of the atoms, see Fig. 2.

|

|
Optimization of the molecular structure with the 6-311++G** basis set including correlation energy at the MP2 level resulted in a structure of C2 symmetry with the two-fold axis along the B–N bond. Both aromatic rings are essentially planar and enclose a dihedral angle of 39.9°, which is not only close to the value of 39.7° obtained at the CISD/6-311++G** level but also not too different from the experimental value of 43.3° in the solid state.[2] The optimized torsion angle of pyridine–borabenzene is also slightly smaller than the dihedral angle of 44.4(1.2)° found for biphenyl in the gas phase[28] and also below the value of 46.9° obtained by an TZ2P plus thermal correction/6-311++G** geometry optimization for this compound.† All these values are significantly larger than the dihedral angle of 30.7° obtained for the pyridine–borabenzene complex by Semenow and Sigolaev at the B3LYP/6-311++G(3df,p) level of DFT.[11] The calculated N–B distances of 1.551 (TZ2P plus thermal correction/6-311++G**) and 1.566 Å (CISD/6-311++G**) are also close to that of 1.558(3) Å obtained by single-crystal X-ray diffraction.[2] Moreover, at 120.6°, the C–B–C angle is also quite similar to the experimental value of 119.1(2)° in the solid state. Like the C–B–C angle calculated at the same level of theory for the most stable C5H5B–N2 isomer (123.1°[12]), this angle is much closer to the value for an ideal hexagon than the one in free singlet borabenzene (142.2°,[12] TZ2P plus thermal correction/6-311++G**). The experimental bond lengths in both rings are slightly but consistently shorter than their calculated counterparts, and in general, the partly delocalized C=C bonds are longer in the C5H5B than in the C5H5N moiety of 1. Rotation about the B–N bond is easy because the calculated energy difference between the fully optimized structure 1 and those conformers where the two rings are either orthogonal (2, C2v) or coplanar (3, C2v) (Fig. 1) is small. Thus, 3, which has two imaginary frequencies in the spectrum of its normal modes, is only 2.60 kcal mol–1 (1 kcal mol–1 = 4.186 kJ mol–1) and 2 with one imaginary frequency only 2.85 kcal mol–1 higher in energy than minimum structure 1. At 1.572 and 1.565 Å (TZ2P plus thermal correction/6-311++G**), the B–N bonds in both 2 and 3 are longer than in the minimum structure. The small elongation of this bond in 3 relative to the value in 1 is most likely due to the repulsion between the o-hydrogen atoms between the two ring systems (distances: 2.016 in 3, 3.617 in 2, and 2.462 Å in 1, TZ2P plus thermal correction/6-311++G**). Moreover, the C1–B–C1 angles are 121.2° in 2 and 119.1° in 3 and are, therefore, very similar to the one in 1.
At the TZ2P plus thermal correction/6-311++G** level of theory, the change of energy associated with the reaction C5H5B + C5H5N → 1 is –56.3 kcal mol–1 (Table 3). This value changes to –52.3 kcal mol–1 when zero-point vibrational energy (ZPE) is included, and a somewhat more positive reaction energy of –50.4 kcal mol–1 is obtained at the ZPE+CCSD(T)/aug-cc-pVDZ//TZ2P plus thermal correction/6-311++G** level of theory. Finally, extrapolation to a basis set of infinite size at the CCSD level results in values of –52.2 kcal mol–1 without and –48.1 kcal mol–1 including the ZPE taken from the TZ2P plus thermal correction/6-311++G** normal-mode analysis. A somewhat less negative value of –46.4 kcal mol–1 was obtained in the DFT study by Semenov and Sigolaev mentioned above.[11] All these energies of reaction are similar in that the change of energy on formation of the borabenzene–pyridine complex from borabenzene and pyridine slightly exceeds three times the value of –14.9 kcal mol–1 calculated for the formation of C5H5B–N2 from borabenzene and dinitrogen (CCSD(T)aug-cc-pVTZ//TZ2P plus thermal correction/-311++G**).[12] The calculated reaction energies for the formation of 1 from its constituents are, therefore, comparable with the negative of the bond energy of Cl3Al–NMe3 (–49.3 kcal mol–1),‡ the most strongly bonded donor–acceptor complex studied by Jonas et al.[16] According to a natural population analysis, formation of 1 from borabenzene and pyridine goes in parallel with a charge transfer of 0.33 e from the C5H5N to the C5H5B unit. This is essentially identical to the charge transfer from NH3 to BH3 on formation of H3B–NH3, which, however, is associated with a change of energy of only –26.1 kcal mol–1. Thus our result is in full agreement with the conclusions drawn by Jonas et al.[16] that the charge transfer associated with the formation of the complex does not correlate with the strength of the formed B–N bond.

|
The bonding between the C5H5B and C5H5N moieties requires some further comments. The already mentioned calculated interatomic B–N distance amounts to 1.551 Å and that is closer to the value obtained for the single bond in H3B–NH3 (1.656 Å) than to the length of the B–N bond in H2B=NH2 (1.396 Å). According to an NBO analysis, the NB bond in H2B=NH2 can be considered a double bond with the π component widely located (~89 %) at the N atom. In the case of H3B–NH3, an NBO analysis gives a strongly polar covalent single bond between BH3 and NH3 (17.3 % at B, sp5.13; 82.7 % at N, sp1.68), which qualitatively agrees with the properties of this bond obtained by an analysis of the electron density by Jonas et al.[16] In the case of 1, our NBO analyses of the wave function gave two structures whose Lewis NBOs in both cases describe ~97 % of the total density. Like limiting structure A in Scheme 1, the first one has no covalent bond at all between the C5H5B and C5H5N moieties, and similar structures were also found for the orthogonal and planar structures 2 and 3. Within the framework of the NBO method, bonding between the two segments in this Lewis structure is accomplished by an energetically strongly favourable second-order interaction (–453.4 kcal mol–1) between a lone pair at nitrogen and a very weakly occupied lone pair orbital at boron (Fig. 3, both directed along the B–N axis) resulting in occupation numbers of 1.64 e at nitrogen (sp4.12) and 0.38 e at boron (sp2.88), and in a total negative charge of –0.33 e of the C5H5B unit. In the second onez,§ the boron and the nitrogen atom are connected by a single bond that is strongly polarized towards nitrogen (18.5 % at B, sp3.20; 81.5 % at N, sp1.60) and gives an ionicity parameter[21b] of 0.631 (Fig. 4). Thus within the margins of the NBO method, the strongly bonded C5H5B–NC5H5 complex might either be described by a non-bonded structure with a donor lone pair at nitrogen and an acceptor orbital at boron and predominantly stabilized by second-order interactions, or by a Lewis structure with a strongly polarized B–N single bond. Different from the perturbation theory-based approach provided by the NBO method, formation and polarity of the donor–acceptor complex can qualitatively be understood in terms of resonance†† between the two limiting structures A and B shown in Scheme 1.[13,14] The no-bond wave function[14] corresponding to A yields the sum of the total energies of borabenzene and pyridine plus the energy resulting from the interaction between the two molecules excepting the contribution due to covalency. Limiting structure B will add ionic and covalent components to the total energy of interaction and stabilization of the complex due to resonance will result from the interaction of the wave functions describing A and B. However, owing to charge separation, ionic structures like B will in many cases have significantly higher energies and, therefore, their contributions to the resonance hybrid of the ground state might be low. A quantitative treatment of the problem is given by Mulliken and will not be repeated here.[14] To estimate whether conjugative interaction between the two segments in B contributes to the energy associated with the formation of the complex, we used the isodesmic bond separation reaction‡‡ shown in Scheme 2. At the ZPE+TZ2P plus thermal correction/6-311++G** level, this reaction is endoenergetic by 147.5 kcal mol–1. Subtracting the corresponding bond separation energies of pyridine (76.0 kcal mol–1) and borabenzene (45.2 kcal mol–1) (G. Raabe, unpubl. obs.), we obtained a value of 26.3 kcal mol–1, the negative of which might be interpreted as a stabilizing contribution to the bond energy of B due to conjugative interaction between the C5H5N and the C5H5B moieties. As a result of the presumably low weight of B, the contribution of conjugation between the two rings to the total bond energy will certainly be lower.

|

|
To evaluate the quality of the employed basis set and to estimate the basis set superposition error (BSSE), we performed a counterpoise calculation employing the method of Boys and Bernardi[29] and obtained a correction to the reaction energy of 6.9 kcal mol–1 (Table 3).
The UV-vis Spectrum of Pyridine–Borabenzene
The results of two semi-empirical studies of the electronic states of the title compound have been published so far. Those calculations were performed with the PPP and the CIS CNDO/S method respectively,[2,11] and the outcome of these calculations together with the experimental data[2] are listed in Table 4. The gas-phase (vacuum) spectra resulting from our TDDFT calculations employing the B3LYP and the CAM-B3LYP functional, TZ2P plus thermal correction/6-31++G**-optimized coordinates, and the 6-311++G(3df,3pd) basis set are shown in Fig. 5a. The corresponding spectra obtained with the aug-cc-pVDZ basis set under otherwise identical conditions are given in Fig. 5b.

|

|
The calculated gas-phase spectrum (CAM-B3LYP/6-311++G(3df,3pd) shows a strong band at 499 nm caused by a single excitation (A, f = 0.1705, where A is the symmetry and f is the oscillator strength), which, in agreement with the results of the other authors, is governed by the z-polarized HOMO (Ψ41,b) → LUMO (Ψ42,b) transition. In further agreement with the results of other authors,[2,11] this transition involves significant charge transfer from the C5H5B to the C5H5N moiety in that the HOMO is predominantly located at the C5H5B part of the complex while the LUMO has its largest amplitudes at the pyridine moiety. The Kohn–Sham orbitals involved in this transition are shown in Fig. 6 and the 30 energetically lowest states from this calculation are listed in Table 5.

|
The spectral region below 300 nm is governed by two peaks at 231 and 195 and a shoulder at 257 nm. The shoulder gets most of its intensity from a state at 261 nm (B, f = 0.0833) involving mostly excitations from the HOMO to orbitals Ψ48 and higher. The band at 230 nm derives its intensity predominantly from three states at 236 (A, f = 0.1093), 230 (B, f = 0.0681), and 226 nm (A, f = 0.0601). The strongest absorption in the short-wavelength region with approximately twice the extinction coefficient of that at 499 nm has its maximum at 195 nm. Its intensity comes from three states, the most intense one at 195 nm (A, f = 0.3766), followed by two more states of A symmetry at 194 (f = 0.1447) and 192 nm (f = 0.0856). Neglecting minor differences in the calculated state energies and oscillatory strengths, essentially the same result is obtained with the correlation-consistent basis set (Fig. 5b). Surprising is the strong red shift (0.41 eV) of the energetically lowest transition to ~600 nm at the TDDFT level when using the B3LYP functional instead of CAM-B3LYP. A much smaller red shift is obtained for the absorptions below 300 nm. A similar result to the one obtained at the CAM-B3LYP level for the λmax of the long-wavelength band gave a calculation with the SAC-CI method employing the 6-31G* basis set (Fig. 7), whereas compared with the TDDFT B3LYP and CAM-B3LYP results, some of the short-wavelength transitions are shifted significantly to the blue. Thus employing the fully optimized structure, the energetically lowest transition of 1 occurs at 506 nm (A, f = 0.1241), and the spectral region below 300 nm is governed by a strong band at 168 nm, which gets its intensity predominantly from a state of A symmetry at the same wavelength (f = 1.1574).

|
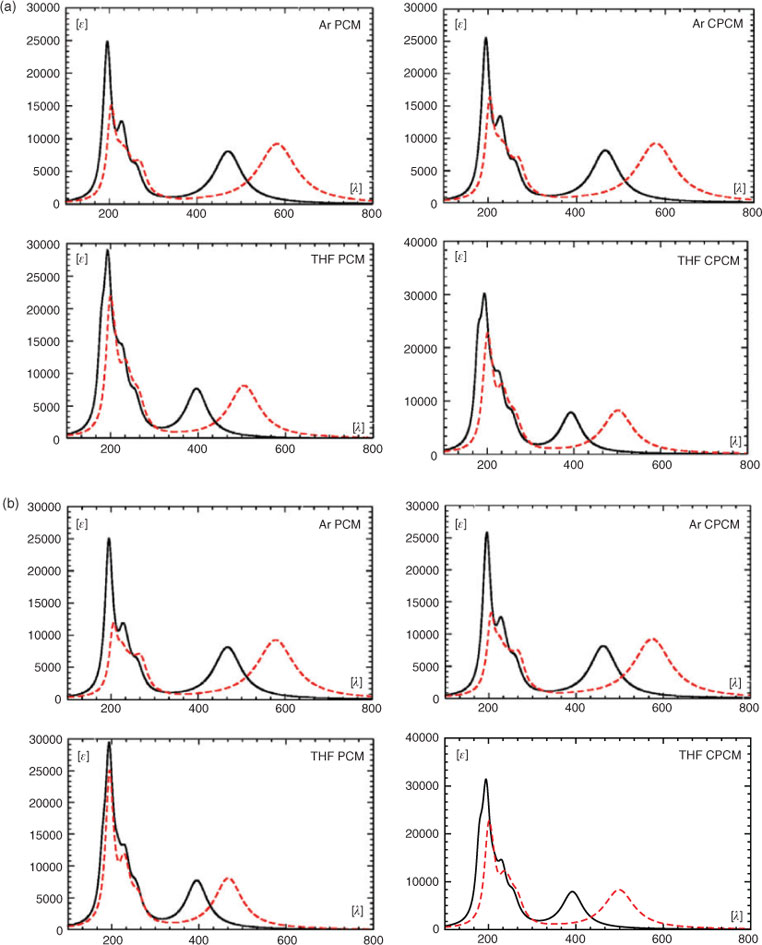
The calculations at the TDDFT and SAC-CI level discussed so far were performed in the gas phase whereas the experimental data were obtained in THF and an Ar matrix. For the spectrum obtained in THF, the most intense absorptions were reported by Boese et al.,[2] while only the λmax for the long-wavelength band was given for the matrix spectrum. We used the data for the solution spectrum to generate the approximate experimental spectrum shown in Fig. 8. We then employed two different solvent models (PCM[26] and CPCM[27]) and two different basis sets (6-311++G(3df,3pd), aug-cc-pVDZ) to model spectra in THF as a solvent and in Ar. The resulting spectra are shown in Fig. 9a and 9b. In addition, the transition wavelengths of the energetically lowest states together with the already mentioned values for the gas phase are listed in Table 6. Like in the case of the gas-phase calculations, a strong red shift of the long-wavelength band was obtained when using the B3LYP instead of the CAM-B3LYP hybrid functional (cf. Fig. 5a, b and Table 6). In a vacuum, this red shift is essentially the same with the 6-311++G(3df,3pd) (~99 nm, 0.41 eV) and the aug-cc-pVDZ basis sets (~97 nm, 0.41 eV). Somewhat higher average values for this shift were obtained with the PCM and the CPCM solvent models (~110 nm, 0.60 eV). Using the B3LYP functional together with the PCM and the CPCM method and THF as a solvent (ϵ = 7.43, ϵ∞ = 1.97), the energetically lowest states occur between 499 and 506 nm for both basis sets. They lie, therefore, much closer to the experimental value of 472 nm measured in THF than those obtained with the CAM-B3LYP functional, which results in values between 392 and 397 nm for the same dielectric constants. However, although the energy of the long-wavelength transition is reproduced in better agreement with the experimental data at the B3LYP level, more reliable relative intensities of the long-wavelength band and the most intense absorption at ~200 nm are obtained with the CAM-B3LYP functional.

|

|
As already mentioned, Boese et al.[2] reported a strong experimental bathochromic shift of the long-wavelength band of more than 120 nm (0.55 eV) on going from THF solution toan argon matrix. This shift was qualitatively reproduced by Semenov et al.[11] using single-excitation CI based on a CNDO/S wave function. As the barrier to rotation about the B–N bonds is lower than 3 kcal mol–1, deformation of the torsion angle under the influence of the matrix atoms might contribute to the observed strong red shift. We, therefore, performed additional calculations on the UV-vis spectra for 2 and 3 in a vacuum employing the 6-311++G(3df,3pd) basis set together with the B3LYP functional. Like for 1, the long-wavelength band is essentially due to the HOMO → LUMO transition in both 2 (b1 → b2) and 3 (b1 → b1). In the planar form 3, this state (z-polarized, A1) is slightly shifted to the blue and occurs with somewhat higher intensity than for 1 at 582 nm (f = 0.2286). The corresponding state of 2 would transform like A2 and will, therefore, have no non-vanishing component of the electric transition dipole moment. These results for 1, 2, and 3 are qualitatively reproduced by our SAC-CI calculations. At this level, the long-wavelength transition of the planar form 3 occurs at 509 nm although with a slightly higher oscillator strength (f = 0.1742) than in 1, and again no significant bathochromic shift is obtained relative to the corresponding transition of 1. The transition wavelength of the long-wavelength transition and the corresponding oscillator strength as a function of the torsion angle between the two rings is shown in Fig. 10. The two curves show that for angles where the red shift of the first absorption is significant, the oscillator strength is very weak. Thus, if deformation of the torsion angle plays a role for the red shift, this contribution will be low.

|
Based on our TDDFT and SAC-CI calculations, we can, therefore, exclude deformation of the molecular structure in the environment of the matrix as the main origin of the strong red shift of the long-wavelength band going from THF solution to an Ar matrix.
Compared with the transition wavelengths values of the energetically lowest state obtained with the PCM and the CPCM method using the dielectric constant of THF, the corresponding data for this shift obtained with the dielectric constant of the rare gas Ar (ϵ = 1.507§§) cover the range between 70 nm (0.32 eV) and 78 nm (0.52 eV). This is clearly less than the experimentally observed red shift of ~120 nm but covers the corresponding value obtained by Semenov and Sigolaev[11] (0.51 eV). Therefore, both the PCM and the CPCM method nevertheless qualitatively reproduce the measured shift observed going from THF solution to an Ar matrix.
Spectrum of the Normal Modes of Borabenzene–Pyridine
Using our calculated normal modes (TZ2P plus thermal correction/6-311++G**, Fig. 11) of 1, the strong absorption in the IR observed[2] with a maximum at 3005 cm–1 can easily be assigned to the symmetric and antisymmetric stretching vibrations of the C–H bonds in the heterocyclic systems, where our calculations predict those of the C5H5B moiety at lower frequencies than the corresponding vibrations of the C5H5N group. A normal mode with high intensity calculated at 1657 cm–1 (A, 39 km mol–1) is due to symmetric stretching of the C′1–C′2 bonds mixed with deformation of the C′1–N–C′1 and C′2–C′3–C′2 angles in the C5H5N part of the complex. It can be correlated with the absorption of medium intensity observed at 1618 cm–1. Its antisymmetric counterpart occurs with somewhat lower intensity (B, 24 km mol–1) at 1499 cm–1 in the calculated spectrum and is assigned to the band observed at 1455 cm–1. The corresponding normal modes of the C5H5B unit are calculated at 1574 cm–1 (symmetric) and 1449 cm–1 (antisymmetric) with much lower intensities between 1 and 2 km mol–1 and will, therefore, probably not be observed under the conditions of the experiment. The normal vibration with the highest intensity in the range around 1500 cm–1 is calculated at 1505 cm–1 (A, 49 km mol–1) and is caused by a symmetric in-plane deformation mixed with symmetric stretching of the C′1–N and C′1–C′2 bonds in the pyridine part of the compound. It is assigned to the absorption observed at 1481 cm–1 in the experimental spectrum. The most intense normal mode is calculated at 700 cm–1 (B, 119 km mol–1). It is caused by an out-of-plane deformation of the C–H bonds with larger amplitudes in the C5H5B ring. The corresponding vibration with the larger amplitudes in the C5H5N moiety is calculated with approximately half of the intensity at 744 cm–1 (B, 53 km mol–1). Those vibrations have their experimental counterparts among the three bands of very high intensity at 679, 700, and 710 cm–1. Stretching of the B–N bond mixed with symmetric in-plane deformation of the aromatic systems was calculated at 1148 cm–1 (A, 11 km mol–1). However, no experimental absorption was reported by the authors of ref. [2] in this region of the vibrational spectrum.

|
Conclusion
Our quantum-chemical ab initio calculations on the adduct of borabenzene (C5H5B) with pyridine (C5H5N) in the gas phase resulted in a structure (C2) that is quite similar to the one found by X-ray diffraction in the solid state, indicating that perturbation of the molecular structure in the crystal lattice is weak. The addition of pyridine to borabenzene results in a significant decrease of the C–B–C angle from 142.2° for the free C5H5B to 120.6° in the complex and in a transfer of 0.33 e from the C5H5N segment to the C5H5B unit. The reaction energy amounts to –52.2 kcal mol–1 and is, therefore, more than three times higher than the energy associated with the formation of C5H5B–N2 from borabenzene and dinitrogen.[12] According to NBO analyses, the complex might either be described by a Lewis structure with a strongly polar B–N bond or by a non-bonded structure with a donor lone pair at N and an acceptor orbital at B. The results of our gas-phase calculations on the UV-vis spectra are best compared with the data obtained by other authors[2] in an Ar matrix. Compared with these results, our SAC-CI calculation gives an energy for the energetically lowest transition that is 0.38 eV too high. This might be due to the small dimension of the basis set that had to be used in this calculation. Larger basis sets could be used in our TDDFT calculations using the B3LYP and the long-range-corrected CAM-B3LYP functional. The calculations with the B3LYP functional correctly predict the energetically lowest transition at ~600 nm although the relative intensities of this band and those in the short-wavelength region are significantly in error. The relative intensities of the band due to the first transition and those at ~200 nm are much better reproduced using the CAM-B3LYP functional. However, here the long-wavelength transitions are predicted at energies that are 0.41 eV too high. Additional calculations at the TDDFT level employing the PCM and the CPCM solvent models qualitatively reproduced the red shift of 0.55 eV of the energetically lowest band observed experimentally when the spectrum was recorded in an Ar matrix instead of THF solution.[2] A possible deformation of the molecule in the matrix can most likely be excluded as the major origin of this remarkable shift although it might contribute to it.
† Etot (MP2/6-311++G**): –462.005596 Hartree.
‡ MP2/TZ2P plus thermal correction;[16] –49.8 kcal mol–1 at the ZPE+MP2/6-311++G** level (present work). (Etot/ZPE) AlCl3: –1621.130147/0.004974; NMe3: –173.969271/0.121970; Cl3Al–NMe3: –1795.182550/0.130751 Hartree.
§ Defined using the keyword $CHOOSE in the NBO program.
†† Called ‘complexresonance’ by Brackman in his study of the visible absorptions that occur on mixing compounds with donor and acceptor properties.[30]
‡‡ Etot(ZPE+MP2/6-311++G**) C5H5B–NC5H5: –465.383758/0.177459; CH4: –40.379638/0.045395; NH3: –56.415523/0.034830; BH3: –26.494887/0.026701; H2C=CH2: –78.346528/0.050804; H3C–CH3: –79.571671/0.075762; H2C=NH: –94.381042/0.040265; H3C–NH2: –95.593921/0.065122; H2C=BH: –64.465957/0.033466; H3C–BH2: –65.708939/0.056480; H3B–NH3: –82.961339/0.070887 Hartree.
§§ This is the average value for the dielectric constant of liquid argon formed from the values at the melting (1.510) and the boiling point (1.504).[31]
References
[1] (a) G. Maier, H. P. Reisenauer, J. Henkelmann, C. Kliche, Angew. Chem. Int. Ed. Engl. 1988, 27, 295.(b) G. Maier, H. P. Reisenauer, J. Henkelmann, C. Kliche, Angew. Chem. 1988, 100, 303.
| Crossref | GoogleScholarGoogle Scholar |
[2] R. Boese, N. Finke, J. Henkelmann, G. Maier, P. Paetzold, H. P. Reisenauer, G. Schmid, Chem. Ber. 1985, 118, 1644.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL2MXktlOmsLw%3D&md5=6f15ff42fbd5760ee399571d54b67324CAS |
[3] G. Maier, Pure Appl. Chem. 1986, 58, 95.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL2sXosVKlug%3D%3D&md5=8c6face679e8c48dd1ea8eaca2f57ce6CAS |
[4] G. Raabe, E. Heyne, W. Schleker, J. Fleischhauer, Z. Naturforsch. A 1984, 39, 678.
[5] G. Raabe, W. Schleker, E. Heyne, J. Fleischhauer, Z. Naturforsch. A 1987, 42, 352.
| 1:CAS:528:DyaL2sXitVChsbs%3D&md5=b9200e10f56cb315189965dafa4328eaCAS |
[6] J. M. Schulman, R. L. Disch, Organometallics 1989, 8, 733.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL1MXhtFCrurk%3D&md5=29606dfdb79f735c0a623737d62aa752CAS |
[7] J. Cioslowski, P. J. Hay, J. Am. Chem. Soc. 1990, 112, 1707.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK3cXpvVGqtA%3D%3D&md5=c17a6bfe01fdfb9dfc4d35b7fbce6384CAS |
[8] P. B. Karadakov, M. Ellis, J. Gerratt, D. L. Cooper, M. Raimondi, Int. J. Quantum Chem. 1997, 63, 441.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2sXivVSitr0%3D&md5=2fc10747f6de947cc646f9774dee9c45CAS |
[9] M. C. Böhm, J. Schütt, U. Schmitt, J. Phys. Chem. 1993, 97, 11427.
| Crossref | GoogleScholarGoogle Scholar |
[10] S. G. Semenov, Yu. F. Sigolaev, Russ. J. Gen. Chem. 2006, 76, 580.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28XltVOns7c%3D&md5=1dac7531c77b4fa1a9fc97f7e6e9c25eCAS |
[11] S. G. Semenov, Yu. F. Sigolaev, Russ. J. Gen. Chem. 2006, 76, 1925.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXhsFWltLc%3D&md5=b9abde1dd398e82fc8fa5b35e59ca95cCAS |
[12] G. Raabe, M. Baldofski, Aust. J. Chem. 2011, 64, 957.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXovFyitrs%3D&md5=6bcecb996c238678a2b8fe935e59f274CAS |
[13] G. Briegleb, Elektronen-Donator–Acceptor-Komplexe 1961 (Springer Verlag: Berlin, Göttingen, Heidelberg).
[14] R. S. Mulliken, J. Am. Chem. Soc. 1952, 74, 811.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaG38Xjt1SktQ%3D%3D&md5=930389799dd1d5ff06bc7c3c80b786abCAS |
[15] V. Jonas, G. Frenking, J. Chem. Soc. Chem. Commun. 1994, 1489.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2cXkvFansL0%3D&md5=7e90bf69ab1dde00b145118c493fe3afCAS |
[16] V. Jonas, G. Frenking, M. T. Reetz, J. Am. Chem. Soc. 1994, 116, 8741.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2cXlvVOru7Y%3D&md5=1e0397a63e66e4eaa9311bc58828f62aCAS |
[17] M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez, J. A. Pople, Gaussian 03, Revision E.01 2004 (Gaussian, Inc.: Wallingford, CT).
[18] (a) J. Čížek, Adv. Chem. Phys. 1969, 14, 35.
| Crossref | GoogleScholarGoogle Scholar |
(b) G. D. Purvis, R. J. Bartlett, J. Chem. Phys. 1982, 76, 1910.
| Crossref | GoogleScholarGoogle Scholar |
(c) J. A. Pople, M. Head-Gordon, K. Raghavachari, J. Chem. Phys. 1987, 87, 5968.
| Crossref | GoogleScholarGoogle Scholar |
(d) G. E. Scuseria, C. L. Janssen, H. F. Schaefer, J. Chem. Phys. 1988, 89, 7382.
| Crossref | GoogleScholarGoogle Scholar |
(e) G. E. Scuseria, H. F. Schaefer, J. Chem. Phys. 1989, 90, 3700.
| Crossref | GoogleScholarGoogle Scholar |
[19] (a) T. H. Dunning, J. Chem. Phys. 1989, 90, 1007.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL1MXksVGmtrk%3D&md5=d4e9cc0e43c2e0f1a0ea5fbf96cf32b6CAS |
(b) R. A. Kendall, T. H. Dunning, R. J. Harrison, J. Chem. Phys. 1992, 96, 6796.
| Crossref | GoogleScholarGoogle Scholar |
(c) D. E. Woon, T. H. Dunning, J. Chem. Phys. 1993, 98, 1358.
| Crossref | GoogleScholarGoogle Scholar |
(d) K. A. Peterson, D. E. Woon, T. H. Dunning, J. Chem. Phys. 1994, 100, 7410.
| Crossref | GoogleScholarGoogle Scholar |
(e) A. K. Wilson, T. van Mourik, T. H. Dunning, J. Mol. Struct. THEOCHEM 1996, 388, 339.
[20] (a) D. G. Truhlar, Chem. Phys. Lett. 1998, 294, 45.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1cXlvVGjsbg%3D&md5=2af7c776a4de328e3f2e2aa509aff051CAS |
(b) P. L. Fast, M. L. Sánchez, D. G. Truhlar, J. Chem. Phys. 1999, 111, 2921.
| Crossref | GoogleScholarGoogle Scholar |
[21] (a) E. D. Glendening, A. E. Reed, J. E. Carpenter, F. Weinhold. NBO 3.0 Program Manual (Natural Bond Orbital/Natural Population Analysis/Natural Localized Molecular Orbital Programs) (Theoretical Chemistry Institute and Department of Chemistry, University of Wisconsin: Madison, WI). Available at ftp://ftp.ccl.net/pub/chemistry/software/NT/mopac6/nbo/NBO.HTM [accessed 14 October 2013].
(b) F. Weinhold, C. Landis, Valence and Bonding. A Natural Bond Orbital Donor–Acceptor Perspective 2005 (Cambridge University Press, Cambridge, UK).
[22] R. Bauernschmitt, R. Ahlrichs, Chem. Phys. Lett. 1996, 256, 454.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK28XksFWltrs%3D&md5=1a1b1d3d8a2afa59e592ed7ec920ac53CAS |
[23] (a) T. Yanai, D. P. Tew, N. C. Handy, Chem. Phys. Lett. 2004, 393, 51.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2cXlsFKgtbs%3D&md5=22dae8e6312df85c4fc40525d4334b54CAS |
(b) M. J. G. Peach, T. Helgaker, P. Sałek, T. W. Keal, O. B. Lutnæs, D. J. Tozer, N. C. Handy, Phys. Chem. Chem. Phys. 2006, 8, 558.
| Crossref | GoogleScholarGoogle Scholar |
(c) M. J. G. Peach, A. J. Cohen, D. J. Tozer, Phys. Chem. Chem. Phys. 2006, 8, 4543.
| Crossref | GoogleScholarGoogle Scholar |
(d) K. A. Nguyen, P. N. Day, R. Pachter, J. Chem. Phys. 2011, 135, 074109.
| Crossref | GoogleScholarGoogle Scholar |
(e) R. Kobayashi, R. D. Amos, Chem. Phys. Lett. 2006, 420, 106.
| Crossref | GoogleScholarGoogle Scholar |
[24] H. Nakatsuji, SAC-CI method: theoretical aspects and some recent topics, in Computational Chemistry–Reviews of Current Trends (Ed J. Leszczyński) 1997, Vol. 2, pp. 62–124. (World Scientific: Singapore).
[25] A. Brown, C. M. Kemp, S. F. Mason, J. Chem. Soc. A 1971, 751.
| Crossref | GoogleScholarGoogle Scholar |
[26] (a) E. Cancès, B. Mennucci, J. Tomasi, J. Chem. Phys. 1997, 107, 3032.
| Crossref | GoogleScholarGoogle Scholar |
(b) M. Cossi, V. Barone, B. Mennucci, J. Tomasi, Chem. Phys. Lett. 1998, 286, 253.
| Crossref | GoogleScholarGoogle Scholar |
(c) B. Mennucci, J. Tomasi, J. Chem. Phys. 1997, 106, 5151.
| Crossref | GoogleScholarGoogle Scholar |
(d) M. Cossi, G. Scalmani, N. Rega, V. Barone, J. Chem. Phys. 2002, 117, 43.
| Crossref | GoogleScholarGoogle Scholar |
[27] M. Cossi, N. Rega, G. Scalmani, V. Barone, J. Comput. Chem. 2003, 24, 669.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3sXivFWqsbc%3D&md5=d19c2ebd0cb476c6698187ebc7b2e885CAS | 12666158PubMed |
[28] (a) O. Bastiansen, S. Samdal, J. Mol. Struct. 1985, 128, 115.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL2MXlslOksLw%3D&md5=cde8d1e6036361caa34d3e79741d6830CAS |
(b) A. Almenningen, O. Bastiansen, L. Fernholt, B. N. Cyvin, S. J. Cyvin, S. Samdal, J. Mol. Struct. 1985, 128, 59.
| Crossref | GoogleScholarGoogle Scholar |
[29] S. F. Boys, F. Bernardi, Mol. Phys. 1970, 19, 553.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXht1alt7fM&md5=3f65c21bef3dce7b5735b3e0914cca9fCAS |
[30] W. Brackman, Recl Trav. Chim. Pays-Bas 1949, 68, 147.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaH1MXjs1Ggug%3D%3D&md5=ea3ef951f264532aafe7afcd04a247c2CAS |
[31] R. L. Amey, R. H. Cole, J. Chem. Phys. 1964, 40, 146.
| Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaF2cXhtlOhsQ%3D%3D&md5=e889332402267a5f02215cf02fa95339CAS |