Polynomial amplitude versus azimuth inversion in horizontally transverse isotropic media, as tested on fractured coal seams in the Surat Basin*
Joseph Kremor A E , Randall Taylor B and Khalid Amrouch C DA Woodside Energy Ltd., 240 St Georges Terrace, Perth, WA 6000, Australia.
B Origin Energy Ltd., 339 Coronation Drive, Milton, Qld 4064, Australia.
C Australian School of Petroleum, University of Adelaide, North Terrace, SA 5005, Australia.
D Centre for Tectonics Resources and Exploration (TRaX), Department of Physical Sciences, University of Adelaide, Adelaide, SA 5005, Australia.
E Corresponding author. Email: joseph.kremor@woodside.com.au
The APPEA Journal 57(2) 776-780 https://doi.org/10.1071/AJ16239
Accepted: 28 March 2017 Published: 29 May 2017
Abstract
A new technique of amplitude versus azimuth (AVAZ) seismic inversion in horizontally transverse isotropic (HTI) media is presented. AVAZ is an effective method of characterising anisotropic variation within individual reflectors as well as characterising fractures. The compressional wave reflectivity equation in HTI media has been reformulated into a parabolic form that allows for fast and efficient inversion. The isotropic component of the azimuthal reflectivity has been separated precisely from the anisotropic component and the anisotropic component has been decoupled exactly into its constituent elliptic and anelliptic components. The exact isotropic, elliptic and anelliptic amplitude versus offset (AVO) gradient equations in HTI media are presented herein and the amount of error associated with previous approximations is also defined under the assumption of weak anisotropy. A method of calculating Thomsen’s weak anisotropy parameters using these AVO gradient terms is then outlined. Compared with the elliptic method, there is reduced error incorporated in the new AVAZ method and the error relationships of this method are compared with the Fourier method.
Data from an open file 3D wide azimuth seismic survey in the Surat Basin were inverted to demonstrate the effectiveness of the techniques which are presented herein. Seismic amplitudes from six azimuthal stacks were extracted over two horizons and inverted around a well where full-wave sonic and density logs were acquired. For both horizons, the error between the inverted anisotropy parameters from seismic and the inverted anisotropy parameters from wire line logs were found to be less than 5% for both horizons.
Keywords: anisotropy, AVAZ, AVO, cracks, fractures, seismic, WAZ.
Introduction
Amplitude versus azimuth (AVAZ) inversion in horizontally transverse isotropic (HTI) media is an effective method of characterising anisotropic variation within individual reflectors, as well as characterising fractures. Rüger (1998) introduced the reflectivity equation in HTI media assuming weak anisotropy. Several AVAZ methods of characterising azimuthal variation in seismic exist, such as assuming ellipticity (Rüger 1998) and using azimuthal Fourier transformations (Downton and Roure 2015).
In this paper, the P-wave reflectivity equation in HTI media is reformulated to allow for the simple separation of the isotropic component from the anisotropic component of the reflectivity by recognising that the P-wave reflectivity varies parabolically with respect to the squared cosine of the azimuth, cos2 φ. Using this reformulation, the anisotropic component is then separated into the substituent elliptic and anelliptic anisotropic components that are extended to their respective AVO gradient terms. The seismic response of wet and dry crack densities is then defined (Bakulin et al. 2000). A method of AVO inversion to calculate individual Thomsen parameters is then proposed and error relationships between different techniques of characterising azimuthal anisotropy are approximated.
The inversion procedure presented herein is applied to a seismic survey from the Surat Basin and the inverted anisotropy is shown to match the anisotropy that was calculated from wire line logs to within 5%.
Calculations
The P-wave reflectivity in HTI media, RPHTI assuming weak anisotropy is
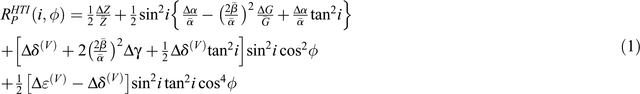
where Z is the impedance, G is the shear modulus, β is the S-wave velocity, α is the P-wave velocity, i is the incident angle, φ is the azimuth and γ, δ and ε are Thomsen (1986) parameters (Rüger 1998). Furthermore a line over a parameter indicates the average of a variable about the reflecting interface and the superscript (v) indicates that the parameter occurs in the verticle plane. Eqn 1 is in a form where the isotropic component, RPiso(i) has been separated from the anisotropic component, RPani(i, φ) of the reflectivity such that

The anisotropy has elliptic and anelliptic components (Alkhalifah and Tsvankin 1995) that can now be decoupled from the anisotropic component RPani(i, φ). For ease, the ellipticity, E(i), and anellipticity, F(i), parameters are introduced and are defined as
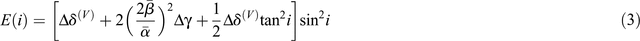

The P-wave reflectivity in HTI media in terms of cos2 φ can now be characterised by the polynomial

which is parabolic about cos2 φ. Eqn 5 is in a form where pre-stack azimuthal seismic data can be inverted to find the isotropic, RPiso(i), elliptic E(i) and anelliptic, F(i) components of the azimuthal reflectivity provided the azimuth φ is known. The azimuth φ is defined as φ = φaz – φsym (Rüger 1998) where φaz is an arbitrary azimuth and φsym is the symmetry azimuth of the anisotropy. This can be calculated using the elliptic approximation (Rüger 1998) or by using a Fourier transform (Downton and Roure 2015).
Wavelet deconvolution
To extract the parameters E(i), F(i) and RPiso(i) from seismic reflection data, the effect of the wavelet, w(t), must be removed. For zero phase data, the seismic reflection amplitude, A(tm), recorded at a time, tm is

Hence, the reflectivity over a horizon at tm for a zero-phase wavelet is

and for an arbitrary wavelet is

where  is a Fourier transform operator about time, t. Equations 7 and 8 can be extended to calculate RPiso(i), E(i) and F(i).
is a Fourier transform operator about time, t. Equations 7 and 8 can be extended to calculate RPiso(i), E(i) and F(i).
Total anisotropy inversion
To account for the total amount of azimuthal anisotropy, the anisotropic response over all azimuths can be calculated by integrating over the domain Φ where φ∈Φ = [0, π), such that
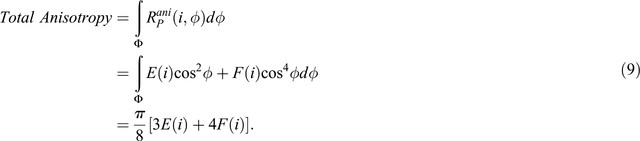
The ratio of the anisotropic to isotropic reflectivity is therefore

and will be referred to as the anisotropy ratio. The use of this term does not require the reflectivity to be decoupled from the wavelet and can therefore be used to tie inverted seismic to measurements taken from wire line logs.
AVO applications
Using the AVO approximation (Shuey 1985), three gradients can be defined from Eqn 5
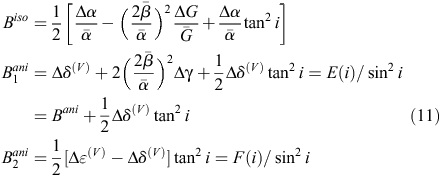
where Biso and Bani are the isotropic and anisotropic AVO gradients in HTI media, as introduced by Rüger (1998), respectively. Thus, the azimuthal AVO gradient equation in HTI media is

Parameters from Thomsen (1986), namely Δδ(V), Δε(V) and Δγ can be calculated by linearising B1ani and B2ani about tan2 i. B1ani linearised about tan2 i is defined by the gradient term

and the intercept term

which allows for the calculation of Δδ(V). Δγ can be calculated using

where  and
and  are obtained from well log data, or perhaps from an isotropic AVO inversion if the bed thickness and data quality were adequate. Δε(V) can be calculated via
are obtained from well log data, or perhaps from an isotropic AVO inversion if the bed thickness and data quality were adequate. Δε(V) can be calculated via

Crack densities
Bakulin et al. (2000) applied established fracture theory to Bani assuming weak anisotropy. This theory is applied to the parameters B1ani and B2ani assuming HTI media due to small penny-shaped cracks (Hudson 1980) which are overlain by an isotropic layer. In the case of wet cracks, the AVO gradients are approximated to
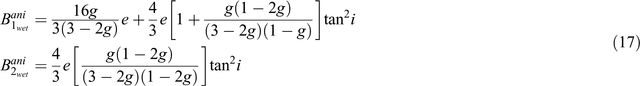
where  and e is the crack density, which is defined as the number of cracks, N, per unit volume, V, multiplied by the average radius, r, of the penny-shaped cracks (
and e is the crack density, which is defined as the number of cracks, N, per unit volume, V, multiplied by the average radius, r, of the penny-shaped cracks ( ) (Molotkov and Bakulin 1997; Tsvankin and Grechka 2011).
) (Molotkov and Bakulin 1997; Tsvankin and Grechka 2011).
In the case of dry cracks, the AVO gradients are approximated to
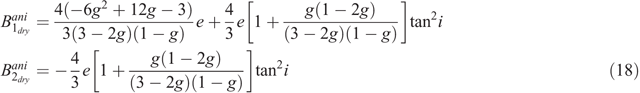
and could be used to distinguish between gas and liquid-filled cracks (Bakulin et al. 2000).
Comparison with elliptic inversion
Under the elliptic assumption, the P-wave reflectivity of HTI media is simplified to
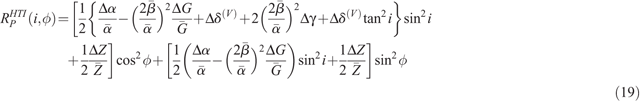
The long and short axes values of an inverted ellipse are assumed to be approximately the same as RPHTI(i, 0) and RPani(i, 0) respectively (Rüger 1998). Thus, the approximate error associated with the elliptic approach is a function of the anelliptic component of the reflectivity such that
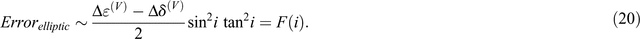
The near offset AVO gradient equation in HTI media is

and assumes that the reflectivity of an HTI interface varies elliptically with azimuth, φ, where  (Rüger 1998, 2001). Hence, the error associated with this approximation is
(Rüger 1998, 2001). Hence, the error associated with this approximation is

Comparison with Fourier coefficient inversion
The Fourier method fully models P-wave reflection in HTI media as described by Rüger (1998). If the incident angle, i, is known, then there are four independent terms in Eqn 5. However, when Eqn 1 undergoes a Fourier transform, there are six independent terms (Pšenčík and Martins 2001; Downton and Roure 2015)
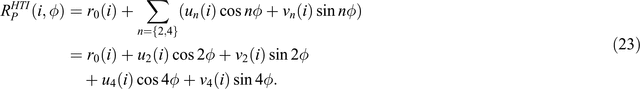
Because of this, a minimum of six azimuthal amplitude measurements are needed to define Eqn 23 and, this is therefore a more complex approach than the method presented herein.
A high-order Fourier coefficient term, r4, can be calculated from Eqn 23 (Downton and Roure 2015) that corresponds to an anelliptic term, Δη(V) /16 where  (Alkhalifah and Tsvankin 1995; Downton and Roure 2015). However, if weak anisotropy is assumed, as is the case of the parametrisation of Eqn 23 (Pšenčík and Martins 2001), then the anelliptic term in weak anisotropy is
(Alkhalifah and Tsvankin 1995; Downton and Roure 2015). However, if weak anisotropy is assumed, as is the case of the parametrisation of Eqn 23 (Pšenčík and Martins 2001), then the anelliptic term in weak anisotropy is  (Bakulin et al. 2000). This is also evident as the anelliptic component of Eqn 1 is
(Bakulin et al. 2000). This is also evident as the anelliptic component of Eqn 1 is  . Because ε(V) does not occur in the elliptic or isotropic components of Rüger’s equation, the Fourier method does not easily separate the elliptic component of the anisotropy from the anelliptic component because it is a component of all Fourier coefficients the terms r0, r2 and r4 which are introduced in (Downton and Roure 2015). In contrast, E and B1ani exactly represent elliptic components of the reflectivity and AVO gradient in HTI media respectively, making the methodology presented herein a robust technique of calculating the elliptic and anelliptic anisotropic components.
. Because ε(V) does not occur in the elliptic or isotropic components of Rüger’s equation, the Fourier method does not easily separate the elliptic component of the anisotropy from the anelliptic component because it is a component of all Fourier coefficients the terms r0, r2 and r4 which are introduced in (Downton and Roure 2015). In contrast, E and B1ani exactly represent elliptic components of the reflectivity and AVO gradient in HTI media respectively, making the methodology presented herein a robust technique of calculating the elliptic and anelliptic anisotropic components.
The r2 coefficient (which is introduced by Downton and Roure (2015)) approximates the AVO gradient, Bani, whereby, as reported by Downton and Roure (2015)

The error associated with this approximation with regard to the true elliptic component of the AVO gradient, B1ani, is of the form

This term should not be used to approximate the elliptic gradient Bani because the associated error as can be reduced from Eqn 22 is

which is the magnitude of the anelliptic term and therefore renders Eqn 24 ineffective.
Results
Data from an open file 3D seismic survey in the Surat Basin were inverted to demonstrate the effectiveness of these techniques. The equations were applied by extracting seismic amplitude measurements from six azimuth volumes along two horizons in the survey, centred around a well in which density and full-wave sonic logs were acquired. The azimuth volumes were stacked using a restricted reflection angle of incidence of 37.5°.
To compare and assess the effectiveness of the equations, Thomsen’s parameters in HTI media were also calculated from the well logs using the method described by Kremor and Amrouch (2017). A comparison of the results for the well log measurements and the equations in this paper is given in Table 1. For both horizons, the error between the two anisotropy estimates is less than 5%.

|
The authors recognise that the quality of the results are highly dependent upon the preservation of signal amplitudes of the seismic data during processing. Although these appear to have been adequate for these data at this well location, it is likely that the wider application of this technique will require considerable cooperation with processing houses and appropriate selection of seismic horizons that are free of multiple energy and other noise.
Conclusion
A method of categorising seismic anisotropy caused by HTI reflectors that can easily be separated into its isotropic, elliptic and anelliptic components is presented. This was then extended to AVO and the calculation of Thomsen (1986) parameters about an interface that were then related to penny-shaped cracks. The ratio between the anisotropic and isotropic components of the reflectivity calculated using this method has been tied to a well to within 5% error. This method affords the geoscientist more interpretable attributes than what currently available AVAZ methods for HTI media can produce and will therefore be useful in fractured and unconventional reservoirs. Furthermore, the application of this method over the elliptic method will result in a reduced amount of error incorporated into the inverted parameters and is a simpler approach than the Fourier method.
Acknowledgement
Many thanks to Andrew Aouad for interpreting the horizons upon which the inversion was applied.
References
Alkhalifah, T., and Tsvankin, I. (1995). Velocity analysis for transversely isotropic media. Geophysics 60, 1550–1566.| Velocity analysis for transversely isotropic media.Crossref | GoogleScholarGoogle Scholar |
Bakulin, A., Grechka, V., and Tsvankin, I. (2000). Estimation of fracture parameters from reflection seismic data – Part II: fractured models with orthorhombic symmetry. Geophysics 65, 1803–1817.
| Estimation of fracture parameters from reflection seismic data – Part II: fractured models with orthorhombic symmetry.Crossref | GoogleScholarGoogle Scholar |
Downton, J., and Roure, B. (2015). Interpreting azimuthal Fourier coefficients for anisotropic and fracture parameters. Interpretation (Tulsa) 3, ST9–ST27.
| Interpreting azimuthal Fourier coefficients for anisotropic and fracture parameters.Crossref | GoogleScholarGoogle Scholar |
Hudson, J. (1980). Overall properties of a cracked solid. Mathematical Proceedings of the Cambridge Philosophical Society 88, 371–384.
| Overall properties of a cracked solid.Crossref | GoogleScholarGoogle Scholar |
Kremor, J., and Amrouch, K. (2017). Anisotropy parameter inversion from sonic and density logs in horizontally transverse isotropic media. The APPEA Journal 57, .
Molotkov, L. A., and Bakulin, A. V. (1997). An effective model of a fractured medium with fractures modelled by the surfaces of discontinuity of displacements. Journal of Mathematical Sciences 86, 2735–2746.
| An effective model of a fractured medium with fractures modelled by the surfaces of discontinuity of displacements.Crossref | GoogleScholarGoogle Scholar |
Pšenčík, I., and Martins, J. (2001). Properties of weak contrast PP reflection/transmission coefficients for weakly anisotropic elastic media. Studia Geophysica et Geodaetica 45, 176–199.
| Properties of weak contrast PP reflection/transmission coefficients for weakly anisotropic elastic media.Crossref | GoogleScholarGoogle Scholar |
Rüger, A. (1998). Variation of P-wave reflectivity with offset and azimuth in anisotropic media. Geophysics 63, 935–947.
| Variation of P-wave reflectivity with offset and azimuth in anisotropic media.Crossref | GoogleScholarGoogle Scholar |
Rüger, A. (2001). ‘Reflection Coefficients and Azimuthal AVO Analysis in Anisotropic Media.’ (Society of Exploration Geophysicists: Tusla, OK.)
Shuey, R. (1985). A simplification of the Zoeppritz equations. Geophysics 50, 609–614.
| A simplification of the Zoeppritz equations.Crossref | GoogleScholarGoogle Scholar |
Thomsen, L. (1986). Weak elastic anisotropy. Geophysics 51, 1954–1966.
| Weak elastic anisotropy.Crossref | GoogleScholarGoogle Scholar |
Tsvankin I., Grechka V. (2011). ‘Seismology of Azimuthally Anisotropic Media and Seismic Fracture Characterization.’ (Society of Exploration Geophysicists: Tulsa, OK.)
* *Any views or opinions expressed in this extended abstract are solely those of the authors and do not necessarily represent those of Woodside Energy Ltd.

Joseph Kremor has been a graduate data scientist at Woodside Energy Ltd since 2016. Prior to joining Woodside, Joseph graduated first in his class from the University of Adelaide in Petroleum Geology and Geophysics and completed internships at Origin Energy. Joseph holds degrees in mathematics and geological science from the University of Queensland and is a recipient of the Geological Society of Australia’s Gold Medal. What is presented here formed part of Joseph’s undergraduate thesis. |

Randall Taylor is a seismic interpreter and QI geophysicist. As chief geophysicist for Origin Energy, Randall is responsible for the application of geophysical technology and functional assurance to Origin’s Australian and international exploration and production portfolio. Randall holds a BAppSc in geophysics from the University of Queensland (1982). Randall transferred to Origin Energy in 2000 after 6 years with Oil Co. of Australia as team leader in the Otway and Eromanga basins. Prior to this, Randall was senior geophysicist for Santos Ltd (1987–92) in their offshore group. Randall began his career in geophysics with CSR’s Oil and Gas Division. Randall is a member of several industry bodies, including ASEG, SEG and PESA. In 2001, Randall served as special editor of the ASEG journal Exploration Geophysics. |

Khalid Amrouch is a structural geologist with expertise in geomechanics. He graduated from the University of Pierre and Marie Curie (Paris) with an MSc and a PhD in structural geology. His main interest relates to brittle tectonics, fracture characterisation and 4D stress analyses. Khalid started his career in 2005 at the Institut Français du Pétrole (IFP), which sponsored his studies, followed in 2010 by a position as research engineer at Mines PariTech. In 2012, Khalid spent 1 year working for BHP as an exploration geologist in Chile, before joining the Australian School of Petroleum in February 2013. Since then, Khalid has been an active member of the S3 Research Group, one of the largest geoscience research groups at the University of Adelaide. |


