Effectiveness and costs of helicopter-based shooting of deer
Andrew J. Bengsen A , David M. Forsyth
A , David M. Forsyth  A * , Anthony Pople B , Michael Brennan B , Matt Amos B , Mal Leeson C , Tarnya E. Cox A , Bec Gray D , Ollie Orgill E , Jordan O. Hampton
A * , Anthony Pople B , Michael Brennan B , Matt Amos B , Mal Leeson C , Tarnya E. Cox A , Bec Gray D , Ollie Orgill E , Jordan O. Hampton  F H , Troy Crittle D and Kym Haebich G
F H , Troy Crittle D and Kym Haebich G
A Vertebrate Pest Research Unit, NSW Department of Primary Industries, 1447 Forest Road, Orange, NSW 2800, Australia.
B Biosecurity Queensland, Queensland Department of Agriculture and Fisheries, 41 Boggo Road, Dutton Park, Qld 4102, Australia.
C Local Land Services Regional Operations, 112 Market Street, Mudgee, NSW 2850, Australia.
D Biosecurity and Food Safety, NSW Department of Primary Industries, 4 Marsden Park Road, Calala, NSW 2340, Australia.
E Environment, Planning and Sustainable Development Directorate, ACT Government, Sanford Street, Mitchell, ACT 2911, Australia.
F Ecotone Wildlife, PO Box 76, Inverloch, Vic. 3096, Australia.
G Limestone Coast Landscape Board, 61 Anzac Terrace, Keith, SA 5267, Australia.
H Present address: Faculty of Veterinary and Agricultural Sciences, University of Melbourne, Parkville, Vic. 3052, Australia.
Wildlife Research 50(9) 617-631 https://doi.org/10.1071/WR21156
Submitted: 29 October 2021 Accepted: 14 April 2022 Published: 6 July 2022
© 2023 The Author(s) (or their employer(s)). Published by CSIRO Publishing. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)
Abstract
Context: Helicopter-based shooting has been widely used to harvest deer or control overabundant populations in Australasia, but the effectiveness and cost of this method as a deer control tool has seldom been evaluated.
Aims: We evaluated the effectiveness and costs of helicopter-based shooting of fallow deer (Dama dama) and chital deer (Axis axis) in eastern Australia by quantifying (1) reductions in density, (2) the relationship between numbers killed per hour and deer density (i.e. the functional response), (3) the costs of control and (4) the effort–outcome and cost–outcome relationships.
Methods: We evaluated the costs and effectiveness of 12 aerial shooting operations aiming to reduce fallow deer (n = 8) or chital deer (n = 4) population densities at nine sites in eastern Australia. Sites were characterised by fragmented woodland, and all but one operation aimed to reduce grazing competition with livestock. We used pre-control population density estimates and operational monitoring data to estimate the costs and outcomes of each operation. We combined data from all operations to estimate the relationship between shooting effort and population reduction, as well as costs associated with different levels of effort.
Key results: Population reductions for operations ranged from 5% to 75% for fallow deer, and from 48% to 88% for chital deer. The greatest population reductions occurred when effort per unit area was greatest, and the largest reductions in deer density occurred when shooting was conducted in consecutive years. The functional response of hourly kills to deer density was best described by a modified Ivlev model, with the asymptotic kill rate estimated to be 50 deer per hour. There was no support for the existence of a prey refuge, that is, a threshold population density below which no deer could be shot. Helicopter charter was the primary cost of helicopter-based shooting programs, followed by labour; firearm and ammunition costs were relatively minor.
Conclusions: Helicopter-based shooting can rapidly reduce deer populations over large geographic areas, but the magnitude of the reduction depends on the effort (hours of shooting) per deer per km2.
Implications: Aerial shooting operations should include a pre-control population survey so that (1) measurable objectives can be established, (2) the likely level of effort and cost required for objectives to be met can be estimated and planned for, and (3) the realised population reduction can be estimated.
Keywords: abundance, aerial gunning, aerial shooting, aerial survey, Bayesian statistics, chital deer, culling, density, effort–outcome, fallow deer, functional response, mark–recapture distance sampling.
Introduction
Deer populations are increasing in many parts of the world, sometimes causing undesirable economic, social, environmental and human health impacts (reviews in McShea et al. 1997; Côté et al. 2004; Carpio et al. 2021). There is particular concern about the impacts of deer in Australasia, where they are non-native (Forsyth et al. 2010a; Davis et al. 2016) and many populations are increasing in size and geographic range (Moriarty 2004; Moloney et al. 2021; Nugent and Forsyth 2021).
One means of reducing deer abundance (or density), and thus potentially reducing the undesirable impacts, is by helicopter-based shooting. The method was pioneered in New Zealand in the 1960s (Bennett 1979) and involves using a helicopter as a platform for finding and shooting deer. When a deer is sighted, the pilot manoeuvres the helicopter to within shooting distance and provides a stable shooting platform for the shooter, who sits either behind or adjacent to the pilot with the door removed. A semi-automatic firearm is typically used, enabling multiple shots to be fired quickly. In New Zealand, there is a commercial market for wild-shot deer and helicopters are used for shooting and recovering the deer (Bennett 1979; Challies 1985a, 1985b; Nugent and Choquenot 2004). However, carcasses are usually not removed in population control operations using helicopter-based shooting (Hampton et al. 2022). Perceived key advantages of helicopter-based shooting are that deer can be shot in remote and rugged terrain (c.f. ground-based shooting; Senate Select Committee on Animal Welfare 1991; Forsyth et al. 2013) and large numbers of deer can be shot in a short time (e.g. Challies 1985a). A perceived disadvantage is the high cost of helicopter hire. Helicopter-based shooting can be more effective than ground-based shooting in remote forest (Forsyth et al. 2013), but few studies have robustly documented the costs of such control programs (but see Warburton et al. (2018) for commercial helicopter-based shooting in New Zealand). In New Zealand, helicopter-based shooting of deer greatly reduced abundances of deer and other ungulates in the 1970s and 1980s (Challies 1977; Tustin and Challies 1978; Forsyth et al. 2011). The effectiveness and costs of helicopter-based shooting of deer in Australia have not been evaluated (Forsyth et al. 2017).
The proportion of the population killed, or population reduction, is commonly used to quantify the effectiveness of vertebrate pest control operations (Veltman and Pinder 2001; Morriss et al. 2020). A higher population reduction per unit effort or cost is desirable (Veltman and Pinder 2001), but other factors such as social acceptability (Forsyth et al. 2017) and animal welfare outcomes (Hampton et al. 2022) need to be considered. Population reduction can be usefully estimated only when the control operation occurs between the pre-control survey and the next breeding season. For ungulate control programs that span one or more breeding seasons, a useful metric is the residual density relative to the density prior to the first control. The desired population reduction or residual density will depend on the management objective (Nugent and Choquenot 2004). The proportion of a population that should be removed annually to suppress population growth (p) can be derived from its estimated maximum population growth rate (rm), as follows (Caughley 1980; Hone 1999):

p varies with the species-specific maximum annual population growth rate (Hone et al. 2010). For the nine deer species established in Australasia, the point estimate of p varies from 0.30 to 0.52 (Duncan et al. 2007; Forsyth et al. 2010b; Hone et al. 2010).
Empirical and theoretical studies of helicopter-based shooting of ungulates have indicated that population density is a key determinant of the number of animals killed per flying hour (Hone 1990; Choquenot et al. 1999; Nugent and Choquenot 2004; Warburton et al. 2018). The probability of detecting a deer (given it is present) and then killing it can also vary with topography and height and completeness of vegetation cover, and seasonally (Latham et al. 2018). The change in the number of animals killed relative to changes in animal density and the time required to find and kill an animal is described by the functional response (Hone 1990, 1994), the form of which depends on (1) a threshold animal density at which the kill rate is saturated, (2) the effect of declining animal density on the kill rate, and (3) whether or not there is a low-density ‘refuge’ in which animals are not killed. Robustly estimating the functional response requires kills-per-unit-time data to be collected over a wide range of animal densities.
A functional response can be used to predict the amount of effort required to achieve a desired outcome, expressed in terms of reduced population density (termed the effort–outcome relationship; Hone et al. 2017). If the costs of control are collated using a comprehensive framework that is applied consistently across similar operations (Iacona et al. 2018), then the cost of that amount of effort can be estimated (i.e. the cost–outcome relationship; Hone et al. 2017). To our knowledge, the effort–outcome relationship for helicopter-based shooting of deer has been parameterised only in one study (in New Zealand forests: Forsyth et al. 2013), and that relationship was characterised by large uncertainty. Hence, the effectiveness of helicopter-based deer shooting programs is poorly known. The cost–outcome relationship has not been reported for any deer control method, but Nugent and Choquenot (2004) developed hypothetical models of helicopter- and ground-based deer control operations.
Here we evaluate the effectiveness and costs of helicopter-based shooting of fallow deer, Dama dama, and chital deer, Axis axis, two species that have large and increasing distributions in eastern Australia (Moriarty 2004; van Dyck and Strahan 2008). In particular, we quantify (1) reductions in abundance and density resulting from operations conducted by management agencies, (2) the relationship between numbers killed per hour and deer density (i.e. the functional response), (3) the costs of control, and (4) the effort–outcome and cost–outcome relationships. We use the results of these analyses to make recommendations for improving the effectiveness of helicopter-based shooting of deer.
Materials and methods
Study areas
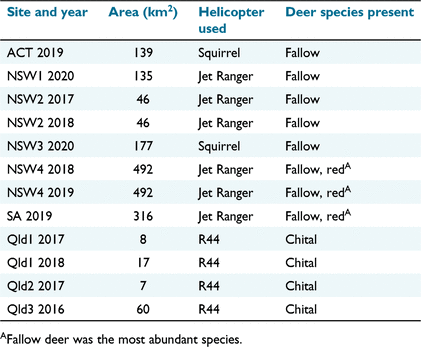
We examined 12 shooting operations at nine sites in eastern Australia (Table 1, Fig. 1). All sites except one were dominated by agricultural lands dedicated to beef cattle, sheep or, to a lesser extent, crop production. We identified sites at which local management agencies intended to use helicopter-based shooting to reduce the impacts of deer on livestock or crop production (i.e. sites were selected opportunistically). The one site in South Australia (SA) comprised a conservation park (60% of land area) within an agricultural matrix. This site was incorporated into the study after the shooting operation had been completed because a third party had estimated the pre-control abundance of deer by using aerial survey methods similar to those we used (see below).
|
The three Queensland (Qld) sites (hereafter Qld1, Qld2 and Qld3) were single beef cattle properties and chital deer were the only deer species present. Fallow deer were the dominant deer species at all other sites, with red deer (Cervus elaphus) being sometimes also present. Sites in New South Wales (NSW; NSW1, NSW2, NSW3 and NSW4) and the Australian Capital Territory (ACT) each comprised multiple adjoining properties. The terrain and vegetation at sites varied, but most contained undulating or hilly grasslands with scattered tall trees and patches of forest or woodland (Fig. 2). Hilly and riparian areas were usually more heavily wooded. For more detailed descriptions of the vegetation at each site, see Supplementary material Appendix S1. Feral pigs (Sus scrofa) were present at all sites except the one site in SA.
Population abundance estimation
Deer population density and abundance were estimated prior to each shooting operation by using a visual survey from a helicopter. Survey and analysis used distance sampling methods (Buckland et al. 2001, 2004), but details varied according to established practise in each state.
All surveys in NSW and the ACT were conducted by NSW government staff by using a Bell 206 Jet Ranger helicopter flown at approximately 46 m above the ground level at 85 km per hour. Surveys were conducted in the 2 h after sunrise or before sunset, when fallow and red deer are most active (Ensing et al. 2014; Caravaggi et al. 2018), during March–July (i.e. well outside the birth season of November–December; Bentley 1995). At the three smallest sites, parallel transects were spaced ≥1 km apart. At the two largest sites, we used an equal-spaced zigzag design to maximise survey effort while minimising variability in coverage probability and bias (Strindberg and Buckland 2004). Transects were flown either two or three times, but never on the same day, so that any deer that were disturbed on or near the transect lines by the previous survey had redistributed themselves. One observer was seated in the front of the helicopter adjacent to the pilot, and another observer was seated behind the first observer on the same side. Sighting booms with five distance classes (0–20 m; 20–40 m; 40–70 m; 70–100 m; 100–150 m) were fitted for each observer and calibrated using markers set at known distances on the ground prior to undertaking surveys (Fig. 2b). Each observer’s observations were independently geo-referenced and recorded using individual USB game controllers (Microsoft, Redmond, WA, USA) and SiRF Star IV USB GPS receivers providing input to a customised app written for Windows 10 (McLeod 2018) running on a detachable screen notebook (Hewlett-Packard x2 10-p0XX, Hewlett-Packard Inc., Palo Alto, CA, USA). The species, group size, distance class, habitat (treed or open) and geographic coordinates of the helicopter were recorded for each observation. Transects were flown at least twice to obtain sufficient observations to reliably model the detection function. For more details on this survey method, see Tracey and Fleming (2016) and Tracey et al. (2016).
Chital deer birth throughout the year (Graf and Nichols 1966; Ahrestani et al. 2012). Aerial surveys for chital deer at the three Qld sites were conducted ≤7 days prior to shooting so that recruitment from breeding was negligible. Chital deer are rarely seen beyond 4 km from homesteads in this region (Forsyth et al. 2019). Landholders also described the distribution of chital on each of the three sites. This expected distribution was used to design the aerial surveys and direct the aerial shooting. In November 2016, the Qld3 site was surveyed using parallel transects ≥500 m apart. In November 2017 and March 2018, areas on sites with higher chital deer densities were sampled more intensively, with transects approximately 300 m apart and care was taken to avoid counting the same groups of deer twice. The Qld surveys were conducted by Qld government staff by using a Robinson R44 helicopter fitted with distance-class sighting booms, flying slightly higher (approximately 61 m) and faster (approximately 93 km per hour) than in the NSW and ACT surveys (following Gentle and Pople 2013). Observers in the two rear seats used a voice recorder to record the distance class and number of individuals for each group of animals detected on either side of the helicopter. Distance classes were identical to those used in NSW and ACT surveys.
The 13 transects at the SA site were spaced 1.5 km apart on an east–west axis. They were surveyed by a private contractor between 07:30 hours and 10:30 hours on two consecutive days in March 2019, by using an AS350 B2 Squirrel helicopter flying at approximately 76 m above ground at a speed of approximately 93 km per hour. Deer were counted within a 100-m strip width on either side of the helicopter, which was delineated by sighting booms. Two observers in the rear seats and one seated next to the pilot recorded observations using an electronic keypad linked to a GPS and computer. Further details of the survey methods are provided in Lethbridge (2019).
Aerial shooting
Helicopter-based shooting was usually conducted within 8 weeks of completion of the aerial surveys, but sometimes later due to unforeseen circumstances (e.g. travel restrictions due to COVID-19 in 2020). All shooting was organised by local management agencies. The objective of shooting operations was to reduce deer densities as much as possible with the funding available, rather than to reduce densities to a pre-defined value.
The shooting at all Qld sites was conducted by the same contract pilot and shooter using a Robinson R44 helicopter (Table 1), following a national code of practise for the destruction or capture, handling and marketing of feral livestock (Standing Committee on Agriculture, Animal Health Committee 2002; Hampton et al. 2022) and in accordance with the Qld Animal Care and Protection Act 2001. In contrast to the operations at all other sites (see below), there was no requirement for repeat shooting and fly-back procedures described below (Hampton et al. 2022).
Shooting at the four NSW sites was conducted by chartered pilots and NSW Government shooters accredited by the NSW Feral Animal Aerial Shooting Team (FAAST; Feral Animal Aerial Shooting Team 2020), using Jet Ranger or Squirrel helicopters (Table 1). Helicopter-based shooting of deer is not permitted in NSW when there are dependent young (Feral Animal Aerial Shooting Team 2020), so all shooting in NSW occurred between March and October, when fallow and red deer do not have dependent young. The FAAST Manual stipulates repeat shooting, with at least one shot in the thorax or, if not possible due to the position of the animal, the head (Feral Animal Aerial Shooting Team 2020). A fly-back procedure is also prescribed to confirm that a deer that has been shot is dead; if there is any doubt, then a further shot must be placed in the heart/lung or head.
The shooting operation at the ACT site used one contract pilot and one contract shooter and followed the national feral goat (Capra hircus) aerial shooting standard operating procedure (Sharp 2012). Shots were fired at either the thorax or head, and it was required that animals be shot at least twice in total in these anatomical zones. The shooting team was required to fly back over each shot animal to apply follow-up shots to the thorax or head. The operational plan added the stipulation that all animals were to receive a minimum of two shots to the thorax prior to the shooter targeting another deer.
The one shooting operation in SA used a contract pilot and R44 helicopter with a government agency shooter. The operation was conducted following the state government standard operating procedures (Department for Environment and Water (SA) 2019).
Shooters at all sites used .308 Winchester calibre semi-automatic rifles (Springfield M1A or FN SCAR-H) fitted with non-magnified red dot scopes, firing lead-based soft- or hollow-point bullets ranging from 125 to 150 grains in mass. For further details on the shooting procedures used at the Qld, NSW and ACT sites, including an evaluation of the animal welfare outcomes of a sample of these operations, see Hampton et al. (2022).
Feral pigs and small numbers of wild dogs (Canis familiaris), red foxes (Vulpes vulpes) and feral goats were also shot during some operations. For all shooting operations, the daily numbers of hours flown and the numbers of deer (and other animals) shot were recorded by the shooting team. Deer were the dominant species targeted, comprising 94% of kills averaged across all operations.
Operational costs
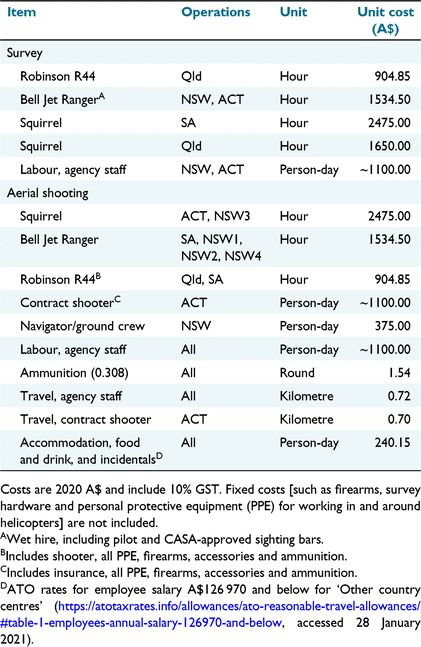
The costs of the aerial surveys and helicopter-based shooting were compiled from invoices and from conversations with staff in the agencies that conducted, or contracted, the shooting. The total cost of survey operations was estimated using hourly rates for helicopter ‘wet’ (i.e. including fuel) hire, the survey crew, data analysis and incidentals, assuming three 2.5-h visual survey flights, 2 h of helicopter ferry time and 6 h of data processing and analysis. For helicopter-based shooting operations, the overheads and deployment of support staff differed greatly among agencies, and capital assets such as firearms and vehicles were not purchased from operational budgets. Therefore, to allow consistent prediction of key costs by agencies with different fixed costs, we estimated scalable costs associated directly with operations. Ammunition consumption (shots per deer) was recorded by an independent observer in the helicopter during three operations as part of a separate investigation of animal welfare outcomes (Hampton et al. 2022). We followed the guidelines in Iacona et al. (2018) for collecting and reporting intervention-level costs. All costs are reported in 2020 Australian dollars (A$).
Statistical analyses
Population abundance estimation
Aerial survey data from NSW and ACT sites were analysed using mark–recapture distance sampling (MRDS; Amos et al. 2014; Burt et al. 2014; Peterson et al. 2020). Models included a mark–recapture submodel for estimating g(0), the probability of detecting deer on the transect line, and a multi-covariate distance sampling (MCDS) submodel for estimating the distance sampling detection function using observation-specific covariates, including habitat (open or wooded), distance class, observer position (front or rear) and deer group size. For each survey, independent deer group detections were compared between observers by using GPS location, group size and distance class to create a detection history for each group, as follows: 10 if the group was detected by the front observer only, 01 if detected by the rear observer only, or 11 if detected by both observers. We fitted independent observer models by using a two-stage process. First, we fitted a series of null models for different distance sampling detection functions (hazard rate and half-normal with cosine and simple polynomial adjustments) and selected the best-supported detection function using Akaike’s information criterion (AIC; Burnham and Anderson 2002). We then used the best-supported detection function to fit a series of MCDS submodels with different combinations of covariates and selected the best-supported model by using AIC. Goodness of fit was assessed by examining tables of observed and predicted detections. Models were fitted using the MRDS package (Laake et al. 2020) in the R statistical environment (R Core Team 2020).
Survey data from the Qld sites were analysed using MCDS in DISTANCE 7.2 (Thomas et al. 2010). Factor covariates were 3 years (2016, 2017 and 2018), three sites and three observer teams. Detection probability was modelled using a key function and up to two series adjustment terms (half normal key plus Hermite adjustment, hazard rate key plus cosine adjustment). Separate models were fitted with different combinations of the three covariates and a null model with no covariates. The models were compared using AIC. Density estimates were corrected for imperfect detection on the transect line by using the reciprocal of g(0) and its standard error estimated from an earlier MRDS survey in the same region which used the same survey team (g(0) = 0.72 ± 0.08, A. Pople, unpubl. data).
Deer density at the SA site was estimated by the contractor who performed the survey (Lethbridge 2019), using a double-count method (Edwards et al. 2004, adapted from Marsh and Sinclair 1989). Detection histories were assigned to each group of deer observed by the two left-side observers, depending on whether they were seen by one or both observers (i.e. 10, 01 or 11). These were used to calculate correction factors and variances that were applied to the counts from the single observer seated behind the pilot, and to the combined counts from the two left-side observers (following Edwards et al. 2004). Distance sampling could not be used here because no distance data were collected. For further details, see Lethbridge (2019) and Edwards et al. (2004).
Population reduction
The proportion of the population killed by each shooting operation (i.e. mortality due to shooting) was estimated using a logistic regression model in which the number of deer killed in operation i represented the number of successes out of Ni binomial trials. To account for the uncertainty in pre-control population density, Ni was drawn from a Poisson distribution described by the pre-control population abundance estimate λi:
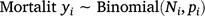
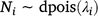
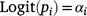
The model was fitted using JAGS (Plummer 2003) called using the runjags package (Denwood 2016) in R (R Core Team 2020), with seven chains of 10 000 draws each after discarding 5000 burn-in draws. Posterior distributions for residual population densities were derived in the model by multiplying the pre-control density by one minus the proportion of the population removed.
Functional response
The functional response for aerial shooting operations was estimated using the number of deer killed per hour of shooting (kill rate) and the estimated population density prior to each shooting operation. The kill rate was estimated for each day within each operation as the number of deer killed divided by the number of hours flown (effort). Daily effort was reduced in proportion to the number of feral pigs shot to account for time spent targeting feral pigs. The population density estimated from the pre-control survey was used as the density for the first day of shooting in each operation, with the density for subsequent days adjusted by subtracting the number of deer killed during previous days.
We used a modified Ivlev function (adapted from Choquenot et al. 1999) to estimate the functional response of helicopter shooting teams to deer density (deer per km2):
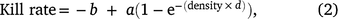
where b is the population density below which no deer can be shot, a is the asymptotic maximum kill rate achieved at a high population density, and d describes the effect of declining deer density on shooting efficiency. High values of d represent a greater impact of declining density than do lower values of d, and b > 0 implies the existence of a refuge for deer (Choquenot et al. 1999). Data from fallow and chital deer operations (n = 42 and 7 days, respectively) were used to estimate a single functional response, as there were insufficient data to sensibly estimate a functional response solely for chital deer. The model was fitted using JAGS (Plummer 2003) in R, with seven chains of 20 000 draws after discarding 5000 burn-in draws. We refitted the model using fallow deer data only to check the validity of pooling data across shooting operations for both deer species.
Hourly operational cost
The hourly cost of aerial shooting operations was estimated using a hierarchical model incorporating the hourly rates for helicopter hire and crew labour and the expected ammunition consumption for different numbers of deer shot per hour, up to the maximum observed kill rate, as follows: Hourly cost = Helicopter wet hire rate + shooter rate + navigator rate + (cost per round × deer shot per hour × shots per deer). The number of shots fired per deer was drawn from a Poisson distribution based on the observed data, and the number of deer shot per hour at different densities was drawn from the posterior distribution of the functional response.
Effort–outcome relationship
We used a Michaelis–Menten function to estimate the relationship between shooting effort and the proportion of the population removed (population reduction). The Michaelis–Menten function describes a rectangular hyperbolic curve in which the dependent variable, in this case population reduction, increases at a decelerating rate before reaching an asymptote (Rao 2000; Johnson and Goody 2011). Effort was specified as hours of deer shooting per km2, standardised by pre-control population density (Est; simplified to hours per 1000 deer available to be shot), as follows:
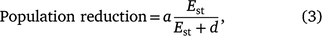
where a represents the asymptotic value of the maximum possible population reduction (i.e. 100% unless there is a refuge in which deer cannot be shot) and d represents the effort required to achieve 50% of the maximum possible population reduction. The d parameter summarises the effect of declining effort on population reduction, such that functions with higher values of d are more greatly affected by declining effort than are those with lower values of d. Each aerial shooting operation contributed one datum to this analysis (n = 12 operations at nine sites), comprising the total number of deer shot and the total effort for the entire operation. Solving for Est, the effort–outcome function was used to estimate the number of hours of shooting required to achieve a specified population reduction, given a known number of deer present prior to shooting (scaled as shooting hours required per 1000 deer present):
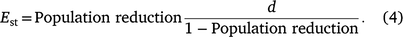
The model was fitted using JAGS via R as per the functional response model. Population reduction was bounded by zero and one and was drawn from a beta distribution. The posterior distributions of these estimates were then combined with the hourly cost of shooting operations function to estimate the total cost of shooting operations, given a range of initial population densities (0.5–40 deer per km2) and desired levels of population reduction (35–75%) over an average-sized area of operations (135 km2) by using a Jet Ranger helicopter.
Results
Deer abundance estimation
Estimated deer densities prior to aerial shooting operations ranged from 1.6 fallow deer per km2 at site SA in 2019 (Lethbridge 2019) to 39.3 fallow and red deer per km2 at site NSW4 in 2018 (Table 2). The best-supported MRDS models for estimating deer densities at sites in NSW and the ACT all included a half-normal detection function, with habitat type as a covariate on detection in the MCDS submodels. Pre-control chital deer densities at Qld sites were highest (14.2 deer per km2) at site Qld1 in 2017 and lowest (4.3 deer per km2) at the same site in 2017 (Table 2). The MCDS model including year as a covariate was the best-supported model; all other models had a ΔAIC ≥ 3.

|
Effectiveness of helicopter-based shooting
Estimated population reductions ranged from 0.05 (95% CrI: 0.03–0.07) to 0.88 (0.84–1.00; Table 2). The three sites that were surveyed and shot in consecutive years (NSW2, NSW4 and Qld1) all recorded a marked reduction in pre-control density between years, consistent with the number of deer removed, after taking into account the likely partial population recovery over the intervening birth season (Fig. 3). Examinations of 225 deer conducted during another study (Hampton et al. 2022) showed female to male sex ratios ranging from 1.07 to 1.69. Ratios of adults (including yearlings) to juveniles ranged from 1.86 to 25.20.
|
|
Functional response
The greatest number of deer shot per hour, averaged across a day’s shooting and corrected for effort expended shooting feral pigs, was 94.7 fallow and red deer (at NSW4 in 2018). The least number of deer shot per hour was 7.4 fallow deer (at the ACT site).
The Ivlev functional response model described a function in which the number of deer killed per hour increased with an underlying population density at a diminishing rate (d = 0.12, 95% CrI = 0.08, 0.19), reaching an average asymptotic kill rate (a) of 49.8 deer per hour (95% CrI = 40.9, 61.0) as deer density approached infinity (Fig. 4). There was no support for the existence of a prey refuge, i.e. a threshold population density below which no deer could be shot (b = 0.0, 95% CrI = 0.0, 0.0). There was little difference in the form of the curve or the uncertainty of the parameter estimates when the model was refitted using fallow deer data only (Fig. S1).
Operational costs
The greatest scalable cost for survey and shooting operations was helicopter hire, which ranged from A$905 per hour for an R44 to A$2475 per hour for a Squirrel (Table 3). Costs for agency staff and contractors were approximately A$1100 per day, which equated to an hourly cost of A$183 for shooters and navigators, with a maximum of 6 h flight time per day. The expected number of shots fired per deer, averaged across the three operations reported in Hampton et al. (2022), was 4.1 (s.e. = 2.2). Ammunition cost A$1.54 (Table 3), and hence the average cost of ammunition for shooting a deer, was A$6.31. Variability in the number of deer shot per hour at different population densities contributed little to the variability in the total hourly cost of aerial shooting operations compared with the cost of helicopter hire (Fig. 5). The total estimated cost for a pre-control aerial survey comprising three flights of 2.5 h each, 2 h of ferry time and 6 h for data processing and analysis was estimated at A$14 056 when using an R44, A$20 031 when using a Jet Ranger and A$28 970 when using a Squirrel.
|
Effort–outcome model
The Michaelis–Menten model described a positive relationship between deer shooting hours and population reduction, the strength of which diminished with increasing effort (Fig. 6). The function reached an asymptote (a) at 0.92 (95% CrI = 0.69, 1.00), or 92% population reduction, as effort (shooting hours per 1000 deer) approached infinity. We emphasise that a describes the shape of the curve for our observations and the estimate has large uncertainty. To better estimate a, more observations of population reductions >90% are needed. The expected level of effort required to achieve 50% of the maximum possible population reduction (d) was 18.1 h per 1000 deer (95% CrI = 7.6, 29.6 h).
|
|
The predicted level of effort needed to suppress fallow deer population growth (p ~ 0.34; Hone et al. 2010) was approximately 10.7 h, given 1000 deer present (95% prediction interval = 4.6, 17.6 h). For chital deer (p ~ 0.49; Hone et al. 2010), it was approximately 20.9 h, given 1000 deer present (95% prediction interval = 9.0, 34.3 h).
The predicted cost of shooting operations for a 135 km2 site increased with population density. The rate at which costs increased with population density scaled positively with the desired population reduction (Fig. 7). The maximum estimated cost over the range of scenarios we examined was A$1 004 110 (95% prediction interval = A$370 005, A$2 059 515) for a 75% reduction from a pre-control population density of 40 deer per km2. This equated to a cost of A$248 per deer killed over the course of the operation. The predicted costs for a 35% reduction from a pre-control density of 5 or 40 deer per km2 were A$15 882 (95% prediction interval = A$5617, A$32 467) and A$136 590 (95% prediction interval = A$49 513, A$279 539) respectively, equating to A$67 and A$72 per deer killed.
Discussion
Fallow deer and chital deer have large and expanding distributions in Australia (Moriarty 2004; Crittle and Millynn 2020; Cunningham et al. 2022), and helicopter-based shooting is increasingly being used to control some populations. Our study, which is the first to quantify the effectiveness and costs of helicopter-based shooting for deer in Australia, demonstrated that this method can quickly reduce the densities of these two species over large areas. However, the magnitude of the population reduction depends on the deer density and the shooting effort (number of helicopter hours) per unit area. Aircraft charter is the primary cost of helicopter-based shooting programs. The cost of ammunition becomes increasingly important at higher deer densities, but is small relative to aircraft charter.
The aerial surveys conducted prior to helicopter-based shooting are the first estimates of deer density in agricultural landscapes in Australia. The highest mean density (39 deer per km2) was for a mixed fallow and red deer population at the 495-km2 NSW4 site and is similar to the highest density estimate recorded in New Zealand for fallow deer (Nugent and Yockney 2004). Our study also included sites with low deer density (i.e. ≤5 deer per km2; Table 2). Given the wide range of population densities in our sample, we expect that the prediction intervals for the functional response and effort–outcomes relationships estimated in this study should hold for many Australian settings in which fallow deer or chital deer are the most abundant species.
We did not attempt to quantify spatial variation in deer density within our sites, but deer were not uniformly distributed through these agricultural landscapes. For example, fallow deer were never encountered on some transects at the NSW2 and NSW3 sites. This spatial variation in deer density contributed to uncertainty in our density and abundance estimates, and hence (through propagation in our analysis) to uncertainty in the population reduction and daily kill rates. Survey and analysis methods that account for spatial variability could provide more precise population density estimates for individual sites (Miller et al. 2013) and, therefore, less uncertainty in functional response and effort–outcome predictions. However, these results would be less generalisable to other locations with unevenly distributed populations.
Annual reductions greater than p (i.e. 0.34 for fallow deer and 0.49 for chital deer) should ensure that populations of these species are reduced (Caughley 1980; Hone et al. 2010). However, there is uncertainty in the estimates of p (Hone et al. 2010). Population reduction rates estimated in the present study did not always exceed these p estimates, suggesting that the deer populations we studied would not be greatly reduced, or could even increase, if the same helicopter-based shooting effort was sustained year-on-year. Conducting shooting in two successive years greatly reduced fallow deer and chital deer densities at NSW2 and at Qld1. The large reductions in density at these sites were due to high helicopter-based shooting effort per deer per unit area, particularly in the second year of shooting.
The three Qld sites and several of the NSW sites were in severe drought during our study (King et al. 2020). Chital deer and fallow deer persisted in these severe drought conditions, even when properties had been destocked of domestic livestock, but the year-on-year declines in density observed at NSW2 and Qld1 may have been partly due to drought-related deer mortality.
An unknown amount of ground-based shooting (recreational hunting, culling by landholders and employees, and sometimes commercial harvesting) occurred at all sites except SA; however, we consider this unlikely to have greatly affected our estimates of population reduction and daily kill rate for several reasons. First, the short period between most aerial surveys and the end of aerial shooting meant that there was little opportunity for large numbers of deer to have been removed by ground-based shooters. Second, the high densities of deer at most of the NSW sites indicates that ground shooting had historically removed only small proportions of the population, resulting in the perceived need for helicopter-based shooting. Third, most sites had high densities of deer, and hence the removal of a few animals by ground shooting would make little difference. Fourth, the sites in NSW and ACT were composed of multiple holdings (approximate range: 8 to ≥100), and the ground-based shooting was likely to vary widely among properties. Even if a few properties did have intensive ground shooting, the overall effect of this on deer density and abundance would have been small.
The number of deer killed per hour by helicopter-based shooting increased at a diminishing rate with an increasing deer density. Such a relationship was expected, because the ability of a shooter to kill more deer is increasingly limited by handling time (Hone 1990; Choquenot et al. 1999), which is the time taken to load the rifle, manoeuvre the helicopter into position such that one or more shots can be taken, and then to fly-back over the animal (if mandated for that shooting operation). A fixed handling time produces a maximum number of deer that can be shot per unit time, regardless of the number of deer available. Our functional response estimates indicated that helicopter-based shooters targeting high-density deer populations could expect to shoot approximately 50 deer per hour. However, there was substantial uncertainty in this estimate and realised outcomes will vary among shooting operations (Fig. 4). The highest observed hourly deer kill rate in our study, averaged over a day’s shooting and corrected for effort expended shooting feral pigs, was 94 (NSW4 in 2018; 39.30 ± 15.23 deer per km2). Many factors could contribute to the high variability in the number of deer killed per hour at different population densities, including differences among jurisdictions in procedural requirements for flybacks and multiple shots, spatial variability in deer density and availability, time required for the shooting team to learn the distribution of deer at a new site, helicopter ferry time to productive shooting areas, and the need to allocate effort over unproductive areas to ensure that the entire site is searched and that all properties receive some effort.
Our estimate of the maximum expected number of deer shot per hour is lower than that estimated for helicopter-based shooting of feral pigs in western NSW (76 per hour; Choquenot et al. 1999). The difference could be at least partly due to the increased difficulty of shooting deer compared with feral pigs (M. Leeson, pers. comm.; S. Boyd-Law, pers. comm.). Groups of fallow deer tend to remain together until the helicopter encroaches on their ‘flight space’, at which time they will often split up. Conversely, feral pigs tend to stay in a group running in a straight line, with usually only the larger and faster adult males breaking away on their own. Also, there was not a requirement to fly-back and repeat-shoot feral pigs when the operations evaluated by Choquenot et al. (1999) were conducted (G. Saunders and T. Korn, pers. comm.). The absence of this requirement could increase the number of feral pigs shot per hour.
In contrast to previous findings with feral pigs (Choquenot et al. 1999), our functional response estimates showed no evidence of a threshold deer population density below which no deer could be shot by helicopter-based shooters. The absence of a prey refuge in our study could be a consequence of the open agricultural landscapes that typified our sites. In New Zealand, commercial helicopter-based shooters removed nearly all red deer from alpine grassland habitats but were less able to do so in tall forest habitats (Nugent et al. 1987; Warburton et al. 2018). Trees and shrubs, under which deer could hide, were present in all our sites, and deer fled into heavily wooded areas when pursued by the helicopter. However, the extent of these refugia was low relative to those in the New Zealand forests that have been studied (e.g. see fig. 2 in Forsyth et al. 2013). Thermal imaging technologies are being used in helicopter-based shooting operations in New Zealand to reduce the value of thick and/or tall vegetation as refugia for deer and feral goats (N. Macdonald, unpubl. data), and similar methods are being trialled in Australia (T. Cox et al., unpubl. data).
Reliable estimation of the cost of wildlife management programs is important for comparing the relative costs of different management options, ensuring that costs do not outweigh benefits, and for predicting the costs of future operations. However, few wildlife management programs are reported such that the costs of management options can be usefully compared (Naidoo et al. 2006). We used standardised guidelines (Iacona et al. 2018) to report the costs of helicopter-based shooting and, wherever possible, used the actual costs incurred by the program (e.g. from invoices). If the costs of other key deer control options (e.g. ground-based shooting, fencing and trapping; Forsyth et al. 2017) are reported in the same way, the costs of various deer management options for an area of interest can be estimated, as was done for deer in New Zealand by Nugent and Choquenot (2004).
Helicopter charter was the largest cost of helicopter-based shooting, and this cost varied with helicopter type. The R44 helicopter was the cheapest of the three helicopters used to shoot deer. This helicopter has a piston engine and is considered by some state agencies as less safe than is the turbine-engined Jet Ranger and Squirrel, and during our study, NSW and ACT did not permit its use for government agency work. All chital deer shooting reported here was conducted from an R44 helicopter by contractors engaged by NQ Dry Tropics. The Squirrel helicopter is more powerful than the Jet Ranger helicopter, and in NSW/ACT the cost of the former is ~60% more per hour. However, the cost to charter a Squirrel in northern Qld was only 8% more than that for Jet Ranger. Which of these two helicopters is best suited for a given control operation will depend on state policy, local availability and price, the elevation and ruggedness of the area of operation, and budget.
After helicopter charter, labour was the next largest cost of helicopter-based shooting operations. Our labour costs were based on the NSW Government agency internal costing model. The unit cost for these staff was similar to that for the ACT contract shooter but was much greater than that for the Qld contract shooter. We emphasise that labour costs could therefore vary greatly for the same task, and these costs need to be determined when planning aerial shooting. Ammunition was a minor component of the cost of helicopter shooting and will obviously vary depending on the density of deer per unit area. If no deer are shot at, the cost of ammunition would be zero. If the asymptotic maximum number of deer is shot, on the basis of our finding of an average 4.1 shots per deer, then the cost would be approximately A$309 per hour.
The effort–outcome and cost–outcome relationships reported here can be used for planning and evaluating fallow and chital deer control operations. The effort–outcome relationship is essentially a quantitative cause-and-effect relationship (Hone et al. 2017), which for helicopter-based shooting is generated by the functional response. Thus, the effort required to achieve a desired population reduction (Eqn 4), and the costs associated with that level of effort, can be predicted for a given combination of area, pre-control population density and helicopter type. Our results suggest that aerial shooting operations aiming to suppress the growth of fallow deer populations not limited by food supply should commit approximately 11 h of shooting effort given 1000 deer present. This assumes that populations recover from shooting operations at their maximum growth rate, rm, after density-dependent constraints on population growth have been removed. For shooting operations aiming to suppress the growth of fallow deer populations over an area of 135 km2, the predicted cost of shooting operations using a Jet Ranger helicopter ranges from A$15 880 at 5 deer per km2 to A$136 590 at 40 deer per km2. Chital deer have a greater expected rm than do fallow deer (Hone et al. 2010), and effective suppression of population growth is expected to require approximately 21 h given 1000 deer present. The predicted cost of operations under the same conditions described above ranges from to A$30 870 at 5 deer per km2 to A$266 610 at 40 deer per km2. The prediction intervals arising from these functions are wide (Fig. 7) because they properly represent the underlying uncertainty in the system.
Economic modelling has shown that some of the costs of control can be offset by recovering and selling carcasses when the value of the carcass exceeds the cost of recovery (Nugent and Choquenot 2004). Wild deer carcasses can be sold legally in some states, and commercial ground-based harvesting of deer occurred on or near some properties at NSW and Qld sites. However, the Australian wild deer market is currently constrained by practical difficulties associated with harvesting, transporting, and processing carcasses and by low demand for product, resulting in low prices paid to harvesters (Australian Deer Association 2021). To our knowledge, helicopters have not been used to recover deer carcasses for sale in Australia. This is likely to be due to the lower commercial value of deer carcasses in Australia than in New Zealand (see Parkes et al. 1996; Nugent and Choquenot 2004; Warburton et al. 2018). The requirement to shoot deer in the thorax in some states, and the high probabilities of wound channels in other body regions (Hampton et al. 2022), would reduce the saleability of carcasses shot in helicopter-based shooting operations.
Given the high cost of helicopter-based shooting operations, there is a risk that the costs of control could outweigh the economic benefits accrued by producers. Diet studies have indicated that grass consumption by 100 chital deer could support 25 and 14 cattle during the wet and dry seasons respectively (Watter et al. 2020). At NSW4, the pre-control population of fallow deer was equivalent to 53 dry sheep equivalents (DSEs) per km2, resulting in a 44% reduction in DSEs in natural pasture there (N. Davis, D. Forsyth, A. Bengsen, unpubl. data). We did not have sufficient data to evaluate the relative economic benefits of helicopter-based shooting in the present study. However, most studies removed either a sufficiently large proportion of the population to be confident of suppressing population growth and future competition with livestock, or a large number of animals that could be expected to reduce current competition for food with livestock (Table 2). In addition to the data and modelling used in the present study, a robust assessment of the economic benefits of helicopter-based shooting would require estimates of realised gains in livestock production and the resulting income.
A precise estimate of deer density in an area of interest allows the amount of helicopter-based shooting needed to reduce the population by a specified level to be estimated. Aerial survey methods, as used in this study, are best suited to treeless or open woodland habitats (Forsyth et al. 2022), such as the predominantly agricultural landscapes that we studied. In more densely vegetated areas, camera trap (Ramsey et al. 2019; Bengsen et al. 2022b), faecal DNA (Brazeal et al. 2017) or thermal imaging surveys (T. Cox, E. O’Dwyer-Hall, R. Matthews, C. Wilsdon, D. Forsyth, A. Bengsen, G. Halverson, unpubl. data) could be used to estimate deer density (Forsyth et al. 2022). Knowing the deer density prior to conducting helicopter-based shooting allows the actual (rather than expected) reduction in deer density to be quantified, provided that kills are recorded by the helicopter shooting team. A pre-control survey of deer density is therefore valuable for predicting the effort and cost required to achieve a desired outcome and for evaluating the actual outcome achieved.
Conclusions
Fallow deer have been subject to control for many decades in New Zealand (Nugent and Asher 2021) and are increasing in geographic range and abundance in the eastern Australian states (Moriarty 2004; Crittle and Millynn 2020; Cunningham et al. 2022). Chital deer are increasing in range and abundance in Qld and NSW (Moriarty 2004; Crittle and Millynn 2020). Helicopter-based shooting can quickly reduce fallow and chital deer populations over large geographic areas, but the magnitude of the reduction depends on the deer density and the effort (hours of shooting) per deer per unit area. The outcomes of helicopter-based shooting of deer can be improved by conducting a pre-control survey of density, because this enables effort and costs to be predicted for a desired population reduction (e.g. 75%), and the actual reduction achieved to be estimated.
Supplementary material
Supplementary material is available online.
Data availability
The data and code used in this study are available at Zenodo (Bengsen et al. 2022a).
Conflicts of interest
David Forsyth and Anthony Pople were guest Associate Editors for this special issue. Despite this relationship, they did not at any stage have editor-level access to this manuscript while in peer review, as is the standard practise when handling manuscripts submitted by an editor to this journal. Wildlife Research encourages its editors to publish in the journal and they are kept totally separate from the decision-making process for their manuscripts. The authors have no further conflicts of interest to declare.
Declaration of funding
This study was funded by the Centre for Invasive Species Solutions project ‘Cost-effective management of wild deer’ (PO1-L-001), NSW Department of Primary Industries (Biosecurity and Food Safety and the Special Purpose Pest Management Rate), Biosecurity Queensland and Central Tablelands Local Land Services. Control operations were funded and organised by the various state management agencies. For the chital deer component: NQ Dry Tropics provided funding, Dalrymple Landcare organised landholders, and Charters Towers Regional Council helped with logistics. The South Australian control operation was funded by the SA Department for Environment and Water’s Aerial Marksman Team.
Acknowledgements
The shooting data used in this paper were collected during management programs organised by management agencies. We thank the many landholders who provided permission for shooting to be conducted on their properties, and the helicopter pilots and shooters who did the surveys and shooting. Mark Tarrant (Northern Tablelands Local Land Services) coordinated the surveys and shooting at NSW1, and Rachel Ladd and Sean Freney [both Vertebrate Pest Research Unit (VPRU), NSW Department of Primary Industries] assisted with pre-control aerial surveys at NSW sites. We thank Steve McLeod (VPRU, NSW Department of Primary Industries) for providing the customised software used to record observations in the NSW and ACT aerial surveys, and Mark Lethbridge for conducting the aerial survey at SA. We thank Aidan Laslett, Stephen Jackson, Sebastien Comte, the Associate Editor and two anonymous reviewers for comments on the manuscript.
References
Ahrestani, FS, Van Langevelde, F, Heitkönig, IMA, and Prins, HHT (2012). Contrasting timing of parturition of chital Axis axis and gaur Bos gaurus in tropical South India – the role of body mass and seasonal forage quality. Oikos 121, 1300–1310.| Contrasting timing of parturition of chital Axis axis and gaur Bos gaurus in tropical South India – the role of body mass and seasonal forage quality.Crossref | GoogleScholarGoogle Scholar |
Amos, M, Baxter, G, Finch, N, Lisle, A, and Murray, P (2014). I just want to count them! Considerations when choosing a deer population monitoring method. Wildlife Biology 20, 362–370.
| I just want to count them! Considerations when choosing a deer population monitoring method.Crossref | GoogleScholarGoogle Scholar |
(2021). A situation analysis of commercial wild deer harvesting in Australia with reference to New Zealand. Australian Deer 45, 44–47.
Bengsen AJ, Forsyth DM, Pople AR, Brennan M, Amos M, Leeson M, Cox TE, Gray B, Orgill O, Hampton JO, Haebich K (2022a) ‘AndrewBengsen/Helicopter-based-shooting-of-deer_revised.’ (Zenodo) https://doi.org/10.5281/zenodo.6070097
Bengsen, AJ, Forsyth, DM, Ramsey, DSL, Amos, M, Brennan, M, Pople, AR, Comte, S, and Crittle, T (2022b). Estimating deer density and abundance using spatial mark–resight models with camera trap data. Journal of Mammalogy , gyac016.
| Estimating deer density and abundance using spatial mark–resight models with camera trap data.Crossref | GoogleScholarGoogle Scholar |
Bennett M (1979) ‘The venison hunters.’ (A.H. & A.W. Reed: Wellington, New Zealand)
Bentley A (1995) Fallow deer. In ‘The mammals of Australia’. 2nd edn. (Ed. R Strahan) pp. 732–733. (Australian Museum/Reed New Holland: Sydney, NSW, Australia)
Brazeal, JL, Weist, T, and Sacks, BN (2017). Noninvasive genetic spatial capture-recapture for estimating deer population abundance: estimating abundance and density of mule deer. The Journal of Wildlife Management 81, 629–640.
| Noninvasive genetic spatial capture-recapture for estimating deer population abundance: estimating abundance and density of mule deer.Crossref | GoogleScholarGoogle Scholar |
Buckland ST, Anderson DR, Burnham KP, Laake JL, Borchers DL, Thomas L (2001) ‘Introduction to distance sampling.’ (Oxford University Press: London, UK)
Buckland ST, Anderson DR, Burnham KP, Laake JL, Borchers DL, Thomas L (2004) ‘Advanced distance sampling: estimating abundance of biological populations.’ (Oxford University Press: London, UK)
Burnham KP, Anderson DR (2002) ‘Model selection and multi-model inference.’ (Springer: New York City, NY, USA)
Burt, ML, Borchers, DL, Jenkins, KJ, and Marques, TA (2014). Using mark–recapture distance sampling methods on line transect surveys. Methods in Ecology and Evolution 5, 1180–1191.
| Using mark–recapture distance sampling methods on line transect surveys.Crossref | GoogleScholarGoogle Scholar |
Caravaggi, A, Gatta, M, Vallely, M-C, Hogg, K, Freeman, M, Fadaei, E, Dick, JTA, Montgomery, WI, Reid, N, and Tosh, DG (2018). Seasonal and predator–prey effects on circadian activity of free-ranging mammals revealed by camera traps. PeerJ 6, e5827.
| Seasonal and predator–prey effects on circadian activity of free-ranging mammals revealed by camera traps.Crossref | GoogleScholarGoogle Scholar | 30498626PubMed |
Carpio, AJ, Apollonio, M, and Acevedo, P (2021). Wild ungulate overabundance in Europe: contexts, causes, monitoring and management recommendations. Mammal Review 51, 95–108.
| Wild ungulate overabundance in Europe: contexts, causes, monitoring and management recommendations.Crossref | GoogleScholarGoogle Scholar |
Caughley G (1980) ‘Analysis of vertebrate populations.’ (Wiley: New York, NY, USA)
Challies, CN (1977). Effects of commercial hunting on red deer densities in the Arawata Valley, South Westland, 1972–76. New Zealand Journal of Forestry Science 7, 263–273.
Challies CN (1985a) Commercial hunting of wild red deer in New Zealand. In ‘Game harvest management’. (Eds SL Beasom, SF Robertson) pp. 279–287. (Caesar Kleberg Wildlife Research Institute: Kingsville, TX, USA)
Challies CN (1985b) Establishment, control, and commercial exploitation of wild deer in New Zealand. In ‘Biology of deer production. Vol. 22’. (Eds PF Fenessey, KR Drew) pp. 23–36. (The Royal Society of New Zealand Bulletin)
Choquenot, D, Hone, J, and Saunders, G (1999). Using aspects of predator-prey theory to evaluate helicopter shooting for feral pig control. Wildlife Research 26, 251–261.
| Using aspects of predator-prey theory to evaluate helicopter shooting for feral pig control.Crossref | GoogleScholarGoogle Scholar |
Côté, SD, Rooney, TP, Tremblay, J-P, Dussault, C, and Waller, DM (2004). Ecological impacts of deer overabundance. Annual Review of Ecology, Evolution, and Systematics 35, 113–147.
| Ecological impacts of deer overabundance.Crossref | GoogleScholarGoogle Scholar |
Crittle T, Millynn B (2020) Pest animal mapping 2020 final report. NSW Department of Primary Industries, Orange, NSW, Australia.
Cunningham, CX, Perry, GLW, Bowman, DMJS, Forsyth, DM, Driessen, MM, Appleby, M, Brook, BW, Hocking, G, Buettel, JC, French, BJ, Hamer, R, Bryant, SL, Taylor, M, Gardiner, R, Proft, K, Scoleri, VP, Chiu-Werner, A, Travers, T, Thompson, L, Guy, T, and Johnson, CN (2022). Dynamics and predicted distribution of an irrupting ‘sleeper’ population: fallow deer in Tasmania. Biological Invasions 24, 1131–1147.
| Dynamics and predicted distribution of an irrupting ‘sleeper’ population: fallow deer in Tasmania.Crossref | GoogleScholarGoogle Scholar |
Davis, NE, Bennett, A, Forsyth, DM, Bowman, DMJS, Lefroy, EC, Wood, SW, Woolnough, AP, West, P, Hampton, JO, and Johnson, CN (2016). A systematic review of the impacts and management of introduced deer (family Cervidae) in Australia. Wildlife Research 43, 515–532.
| A systematic review of the impacts and management of introduced deer (family Cervidae) in Australia.Crossref | GoogleScholarGoogle Scholar |
Denwood, MJ (2016). runjags: an R package providing interface utilities, model templates, parallel computing methods and additional distributions for MCMC models in JAGS. Journal of Statistical Software 71, 1–25.
| runjags: an R package providing interface utilities, model templates, parallel computing methods and additional distributions for MCMC models in JAGS.Crossref | GoogleScholarGoogle Scholar |
Department for Environment and Water (SA) (2019) ‘Standard operating procedure – aerial shooting of feral animals.’ (Department for Environment and Water (SA): Adelaide, SA, Australia)
Duncan, RP, Forsyth, DM, and Hone, J (2007). Testing the metabolic theory of ecology: allometric scaling exponents in mammals. Ecology 88, 324–333.
| Testing the metabolic theory of ecology: allometric scaling exponents in mammals.Crossref | GoogleScholarGoogle Scholar | 17479751PubMed |
Edwards, GP, Saalfeld, K, and Clifford, B (2004). Population trend of feral camels in the Northern Territory, Australia. Wildlife Research 31, 509–517.
| Population trend of feral camels in the Northern Territory, Australia.Crossref | GoogleScholarGoogle Scholar |
Ensing, EP, Ciuti, S, de Wijs, FALM, Lentferink, DH, ten Hoedt, A, Boyce, MS, and Hut, RA (2014). GPS based daily activity patterns in European Red Deer and North American Elk (Cervus elaphus): indication for a weak circadian clock in ungulates. PLoS ONE 9, e106997.
| GPS based daily activity patterns in European Red Deer and North American Elk (Cervus elaphus): indication for a weak circadian clock in ungulates.Crossref | GoogleScholarGoogle Scholar | 25208246PubMed |
Feral Animal Aerial Shooting Team (2020) ‘The FAAST manual. Version 2.3 (August 2020).’ (National Parks & Wildlife Service, NSW Local Land Services and NSW Department of Primary Industries, on behalf of the NSW Government: Sydney, NSW, Australia)
Forsyth, DM, Wilmshurst, JM, Allen, RB, and Coomes, DA (2010a). Impacts of introduced deer and extinct moa on New Zealand ecosystems. New Zealand Journal of Ecology 34, 48–65.
Forsyth, DM, Allen, RB, Marburg, AE, MacKenzie, DI, and Douglas, MJW (2010b). Population dynamics and resource use of red deer following release from harvesting in New Zealand. New Zealand Journal of Ecology 34, 277–287.
Forsyth, DM, Thomson, C, Hartley, L, MacKenzie, DI, Price, R, Wright, EF, Mortimer, J, Nugent, G, Wilson, L, and Livingstone, P (2011). Long-term changes in the relative abundances of introduced deer in New Zealand estimated from faecal pellet frequencies. New Zealand Journal of Zoology 38, 237–249.
| Long-term changes in the relative abundances of introduced deer in New Zealand estimated from faecal pellet frequencies.Crossref | GoogleScholarGoogle Scholar |
Forsyth, DM, Ramsey, DSL, Veltman, CJ, Allen, RB, Allen, WJ, Barker, RJ, Jacobson, CL, Nicol, SJ, Richardson, SJ, and Todd, CR (2013). When deer must die: large uncertainty surrounds changes in deer abundance achieved by helicopter- and ground-based hunting in New Zealand forests. Wildlife Research 40, 447–458.
| When deer must die: large uncertainty surrounds changes in deer abundance achieved by helicopter- and ground-based hunting in New Zealand forests.Crossref | GoogleScholarGoogle Scholar |
Forsyth DM, Pople T, Page B, Moriarty A, Ramsey D, Parkes J, Wiebkin A, Lane C (Eds) (2017) ‘2016 National wild deer management workshop proceedings’, Adelaide, SA, Australia, 17–18 November 2016. (Invasive Animals Cooperative Research Centre: Canberra, ACT, Australia) Available at https://pestsmart.org.au/wp-content/uploads/sites/3/2020/06/Proceedings-2016-National-Workshop-on-Deer-Management_FINAL.pdf
Forsyth, DM, Pople, A, Woodford, L, Brennan, M, Amos, M, Moloney, PD, Fanson, B, and Story, G (2019). Landscape-scale effects of homesteads, water, and dingoes on invading chital deer in Australia’s dry tropics. Journal of Mammalogy 100, 1954–1965.
| Landscape-scale effects of homesteads, water, and dingoes on invading chital deer in Australia’s dry tropics.Crossref | GoogleScholarGoogle Scholar |
Forsyth, DM, Comte, S, Davis, NE, Bengsen, AJ, Côté, SD, Hewitt, DG, Morellet, N, and Mysterud, A (2022). Methodology matters when estimating deer abundance: a global systematic review and recommendations for improvements. Journal of Wildlife Management 2022, e22207.
| Methodology matters when estimating deer abundance: a global systematic review and recommendations for improvements.Crossref | GoogleScholarGoogle Scholar |
Gentle, M, and Pople, A (2013). Effectiveness of commercial harvesting in controlling feral-pig populations. Wildlife Research 40, 459–469.
| Effectiveness of commercial harvesting in controlling feral-pig populations.Crossref | GoogleScholarGoogle Scholar |
Graf, W, and Nichols, L (1966). The axis deer in Hawaii. Journal of the Bombay Natural History Society 63, 630–734.
Hampton, JO, Bengsen, AJ, Pople, A, Brennan, M, Leeson, M, and Forsyth, DM (2022). Animal welfare outcomes of helicopter-based shooting of deer in Australia. Wildlife Research 49, 264–273.
| Animal welfare outcomes of helicopter-based shooting of deer in Australia.Crossref | GoogleScholarGoogle Scholar |
Hone, J (1990). Predator prey theory and feral pig control, with emphasis on evaluation of shooting from a helicopter. Australian Wildlife Research 17, 123–130.
| Predator prey theory and feral pig control, with emphasis on evaluation of shooting from a helicopter.Crossref | GoogleScholarGoogle Scholar |
Hone J (1994) ‘Analysis of vertebrate pest control.’ (Cambridge University Press: Cambridge, UK)
Hone, J (1999). On rate of increase (r): patterns of variation in Australian mammals and the implications for wildlife management. Journal of Applied Ecology 36, 709–718.
| On rate of increase (r): patterns of variation in Australian mammals and the implications for wildlife management.Crossref | GoogleScholarGoogle Scholar |
Hone, J, Duncan, RP, and Forsyth, DM (2010). Estimates of maximum annual population growth rates (rm) of mammals and their application in wildlife management. Journal of Applied Ecology 47, 507–514.
| Estimates of maximum annual population growth rates (rm) of mammals and their application in wildlife management.Crossref | GoogleScholarGoogle Scholar |
Hone, J, Drake, VA, and Krebs, CJ (2017). The effort–outcomes relationship in applied ecology: evaluation and implications. BioScience 67, 845–852.
| The effort–outcomes relationship in applied ecology: evaluation and implications.Crossref | GoogleScholarGoogle Scholar |
Iacona, GD, Sutherland, WJ, Mappin, B, Adams, VM, Armsworth, PR, Coleshaw, T, Cook, C, Craigie, I, Dicks, LV, Fitzsimons, JA, McGowan, J, Plumptre, AJ, Polak, T, Pullin, AS, Ringma, J, Rushworth, I, Santangeli, A, Strwart, A, Tulloch, A, Walsh, JC, and Possingham, HP (2018). Standardized reporting of the costs of management interventions for biodiversity conservation. Conservation Biology 32, 979–988.
| Standardized reporting of the costs of management interventions for biodiversity conservation.Crossref | GoogleScholarGoogle Scholar | 30039609PubMed |
Johnson, KA, and Goody, RS (2011). The original Michaelis constant: translation of the 1913 Michaelis–Menten paper. Biochemistry 50, 8264–8269.
| The original Michaelis constant: translation of the 1913 Michaelis–Menten paper.Crossref | GoogleScholarGoogle Scholar | 21888353PubMed |
King, AD, Pitman, AJ, Henley, BJ, Ukkola, AM, and Brown, JR (2020). The role of climate variability in Australian drought. Nature Climate Change 10, 177–179.
| The role of climate variability in Australian drought.Crossref | GoogleScholarGoogle Scholar |
Laake J, Borchers D, Thomas L, Miller D, Bishop J (2020) mrds: mark–recapture distance sampling. R package version 2.4.4. Available at https://CRAN.R-project.org/package=mrds [Verified 26 August 2021]
Latham, ADM, Cecilia Latham, M, Herries, D, Barron, M, Cruz, J, and Anderson, DP (2018). Assessing the efficacy of aerial culling of introduced wild deer in New Zealand with analytical decomposition of predation risk. Biological Invasions 20, 251–266.
| Assessing the efficacy of aerial culling of introduced wild deer in New Zealand with analytical decomposition of predation risk.Crossref | GoogleScholarGoogle Scholar |
Lethbridge MR (2019) Feral deer aerial survey of Gum Lagoon Conservation Park and Surrounds, 2019. Report to Upper South East District. Parks and Regions, Department of Environment, Water and Natural Resources, Adelaide, SA, Australia.
Marsh, H, and Sinclair, DF (1989). Correcting for visibility bias in strip transect aerial surveys of aquatic fauna. The Journal of Wildlife Management 53, 1017–1024.
| Correcting for visibility bias in strip transect aerial surveys of aquatic fauna.Crossref | GoogleScholarGoogle Scholar |
McLeod SR (2018) ‘Deer aerial survey logger. v1.0.’ (NSW Department of Primary Industries, Vertebrate Pest Research Unit: Orange, NSW, Australia)
McShea WJ, Underwood HB, Rappole JH (Eds) (1997) ‘The science of overabundance: deer ecology and population management.’ (Smithsonian Institution Press: Washington, DC, USA)
Miller, DL, Burt, ML, Rexstad, EA, and Thomas, L (2013). Spatial models for distance sampling data: recent developments and future directions. Methods in Ecology and Evolution 4, 1001–1010.
| Spatial models for distance sampling data: recent developments and future directions.Crossref | GoogleScholarGoogle Scholar |
Moloney, PD, Forsyth, DM, Ramsey, DSL, Perry, M, McKay, M, Gormley, AM, Kappers, B, and Wright, EF (2021). Occupancy and relative abundances of introduced ungulates on New Zealand’s public conservation land 2012–2018. New Zealand Journal of Ecology 45, 3437.
| Occupancy and relative abundances of introduced ungulates on New Zealand’s public conservation land 2012–2018.Crossref | GoogleScholarGoogle Scholar |
Moriarty, A (2004). The liberation, distribution, abundance and management of wild deer in Australia. Wildlife Research 31, 291–299.
| The liberation, distribution, abundance and management of wild deer in Australia.Crossref | GoogleScholarGoogle Scholar |
Morriss, GA, Parkes, JP, and Nugent, G (2020). Effects of aerial 1080 operations on deer populations in New Zealand. New Zealand Journal of Ecology 44, 3417.
| Effects of aerial 1080 operations on deer populations in New Zealand.Crossref | GoogleScholarGoogle Scholar |
Naidoo, R, Balmford, A, Ferraro, PJ, Polasky, S, Ricketts, TH, and Rouget, M (2006). Integrating economic costs into conservation planning. Trends in Ecology & Evolution 21, 681–687.
| Integrating economic costs into conservation planning.Crossref | GoogleScholarGoogle Scholar |
Nugent G, Asher GW (2021) Family Cervidae: Dama dama. In ‘The handbook of New Zealand mammals’. 3rd edn. (Eds CM King, DM Forsyth) pp. 447–527. (CSIRO: Melbourne, Vic., Australia)
Nugent, G, and Choquenot, D (2004). Comparing cost-effectiveness of commercial harvesting, state-funded culling, and recreational deer hunting in New Zealand. Wildlife Society Bulletin 32, 481–492.
| Comparing cost-effectiveness of commercial harvesting, state-funded culling, and recreational deer hunting in New Zealand.Crossref | GoogleScholarGoogle Scholar |
Nugent G, Forsyth DM (2021) Family Cervidae: Cervus elaphus. In ‘The handbook of New Zealand mammals’. 3rd edn. (Eds CM King, DM Forsyth) pp. 447–527. (CSIRO: Melbourne, Vic., Australia)
Nugent, G, and Yockney, I (2004). Fallow deer deaths during aerial-1080 poisoning of possums in the Blue Mountains, Otago, New Zealand. New Zealand Journal of Zoology 31, 185–192.
| Fallow deer deaths during aerial-1080 poisoning of possums in the Blue Mountains, Otago, New Zealand.Crossref | GoogleScholarGoogle Scholar |
Nugent, G, Parkes, JP, and Tustin, KG (1987). Changes in the density and distribution of red deer and wapiti in northern Fiordland. New Zealand Journal of Ecology 10, 11–21.
Parkes, JP, Nugent, G, and Warburton, B (1996). Commercial exploitation as a pest control tool for introduced mammals in New Zealand. Wildlife Biology 2, 171–177.
| Commercial exploitation as a pest control tool for introduced mammals in New Zealand.Crossref | GoogleScholarGoogle Scholar |
Peterson, MK, Foley, AM, Tri, AN, Hewitt, DG, DeYoung, RW, DeYoung, CA, and Campbell, TA (2020). Mark-recapture distance sampling for aerial surveys of ungulates on rangelands. Wildlife Society Bulletin 44, 713–723.
| Mark-recapture distance sampling for aerial surveys of ungulates on rangelands.Crossref | GoogleScholarGoogle Scholar |
Plummer M (2003) JAGS: a program for analysis of Bayesian graphical models using Gibbs sampling. In ‘Proceedings of the 3rd international workshop on distributed statistical computing, Vol. 124, no. 125’. (Eds K Hornik, F Leisch, A Zelleis) pp. 1–10. (Technische Universität Wien: Vienna, Austria)
Ramsey DSL, Pacioni C, Hill E (2019) Abundance and population genetics of Hog Deer (Axis porcinus) in Victoria. Technical Report Series No. 303. Arthur Rylah Institute for Environmental Research, Department of Environment, Land, Water and Planning, Melbourne, Vic., Australia.
R Core Team (2020) ‘R: a language and environment for statistical computing.’ Version 4.0.3. (R Foundation for Statistical Computing) Available at https://www.R-project.org/ [Verified 26 August 2021]
Rao, TR (2000). A curve for all reasons. Resonance 5, 85–90.
| A curve for all reasons.Crossref | GoogleScholarGoogle Scholar |
Senate Select Committee on Animal Welfare (1991) Culling of large feral animals in the northern territory. Report by the Senate Select Committee on Animal Welfare. Senate Publications Unit, Parliament House, Canberra, ACT, Australia.
Sharp T (2012) ‘Standard operating procedure GOA002: aerial shooting of feral goats.’ (Centre for Invasive Species Solutions: Canberra, ACT, Australia)
Standing Committee on Agriculture, Animal Health Committee (2002) Model code of practice for the welfare of animals. Feral Livestock Animals. Destruction or Capture, Handling and Marketing. SCARM Report 34. CSIRO, Melbourne, Vic., Australia.
Strindberg, S, and Buckland, ST (2004). Zigzag survey designs in line transect sampling. Journal of Agricultural, Biological, and Environmental Statistics 9, 443.
| Zigzag survey designs in line transect sampling.Crossref | GoogleScholarGoogle Scholar |
Thomas, L, Buckland, ST, Rexstad, EA, Laake, JL, Strindberg, S, Hedley, SL, Bishop, JRB, Marques, TA, and Burnham, KP (2010). Distance software: design and analysis of distance sampling surveys for estimating population size. Journal of Applied Ecology 47, 5–14.
| Distance software: design and analysis of distance sampling surveys for estimating population size.Crossref | GoogleScholarGoogle Scholar | 20383262PubMed |
Tracey J, Fleming PJS (2016) ‘Techniques for aerial surveys of wildlife: reference manual.’ 4th edn. (Vertebrate Pest Research Unit, NSW Department of Primary Industries: Orange, NSW, Australia)
Tracey J, Fleming PJS, McLeod S, Purcell B (2016) ‘Techniques for aerial surveys of wildlife: training manual.’ 4th edn. (Vertebrate Pest Research Unit, NSW Department of Primary Industries: Orange, NSW, Australia)
Tustin, KG, and Challies, CN (1978). The effects of hunting on the numbers and group sizes of Himalayan thar (Hemitragus jemlahicus) in Carneys Creek, Rangitata catchment. New Zealand Journal of Ecology 1, 153–157.
van Dyck S, Strahan R (2008) ‘The mammals of Australia.’ (New Holland Publishers: Sydney, NSW, Australia)
Veltman, CJ, and Pinder, DN (2001). Brushtail possum mortality and ambient temperatures following aerial poisoning using 1080. The Journal of Wildlife Management 65, 476–481.
| Brushtail possum mortality and ambient temperatures following aerial poisoning using 1080.Crossref | GoogleScholarGoogle Scholar |
Warburton B, Anderson DP, Nugent G (2018) Economic aspects of New Zealand’s wild venison recovery industry. In ‘Advances in conservation through sustainable use of wildlife. Proceedings of a conference held in Brisbane, Australia, 20 August − 1 September 2016’. (Eds G Baxter, N Finch, P Murray) pp. 265–271. (University of Queensland: Gatton, Qld, Australia)
Watter, K, Baxter, GS, Pople, A, and Murray, PJ (2020). Dietary overlap between cattle and chital in the Queensland dry tropics. The Rangeland Journal 42, 221–225.
| Dietary overlap between cattle and chital in the Queensland dry tropics.Crossref | GoogleScholarGoogle Scholar |


