Recolonisation of rabbit warrens following coordinated ripping programs in Victoria, south-eastern Australia
D. S. L. Ramsey A B G , S. R. McPhee C D , D. M. Forsyth A , I. G. Stuart E , M. P. Scroggie A , M. Lindeman A and J. Matthews FA Arthur Rylah Institute for Environmental Research, Department of Environment and Primary Industries, 123 Brown Street, Heidelberg, Vic. 3084, Australia.
B School of Earth and Environmental Sciences, University of Adelaide, Adelaide, SA 5005, Australia.
C Department of Environment and Primary Industries, 600 Sneydes Road, Werribee, Vic. 3030, Australia.
D Agricultural Technical Services P/L, 48 Warooka Road, Yorketown, SA 5576, Australia.
E Kingfisher Research P/L, 177 Progress Road, Eltham, Vic. 3095, Australia.
F Invasive Plants and Animals Operations Branch, Biosecurity Victoria, Department of Environment and Primary Industries, Hamilton Centre, Mount Napier Road, Hamilton, Vic. 3300, Australia.
G Corresponding author. Email: david.ramsey@depi.vic.gov.au
Wildlife Research 41(1) 46-55 https://doi.org/10.1071/WR13195
Submitted: 15 November 2013 Accepted: 3 March 2014 Published: 2 April 2014
Abstract
Context: Warren ripping has been demonstrated to be an effective tool for controlling rabbit populations. However, few studies have examined factors influencing the rate at which ripped warrens are likely to be recolonised (i.e. be re-opened).
Aims: To examine factors influencing the recolonisation of ripped warrens by rabbits by using data collected on 555 warrens for up to 15 years following coordinated ripping programs at 12 sites in Victoria, south-eastern Australia.
Methods: Warren-monitoring data (number of active and inactive warren entrances) were analysed using discrete-time survival analysis to determine the effects of warren-level and site-level covariates on the recolonisation of ripped warrens.
Key results: Warren recolonisation was related to the distance between the ripped warren and the nearest active warren, the number of active entrances in the nearest warren, the initial number of active entrances in the ripped warren and the rabbit spotlight abundance index at the site. The probability of warren recolonisation was highest for ripped warrens within 1 km of an active warren and negligible beyond 3 km. The probability of warren recolonisation also increased by 22% for every increase in the rabbit spotlight count at the site by 10 rabbits km–1.
Conclusions: The recolonisation of ripped warrens was highly influenced by both the distance to, and size of, neighbouring active warrens. Larger warrens also appear to be preferentially recolonised compared with smaller warrens, suggesting that recolonisation of ripped areas may be related to habitat quality. The present results are consistent with ideas from classical metapopulation theory predicting that the rates of colonisation of vacant patches are dependent on both the proximity and size of the source population as well as the quality of habitat patches.
Implications: Although coordinated warren ripping programs are effective at achieving long-term control of rabbits, their efficiency at maintaining low rabbit populations can be increased by adopting an adaptive monitoring program that incorporates warren size and the spatial relationships among warrens, and using this information to better target maintenance-control activities.
Additional keywords: Bayesian model averaging, Bayesian variable selection, discrete survival analysis, European rabbit, JAGS, Oryctolagus cuniculus, rabbit management, warren ripping.
Introduction
The introduced European rabbit (Oryctolagus cuniculus) is one of Australia’s most destructive vertebrate pests, causing major environmental and economic damage (Myers et al. 1994; Cooke 2012; Cooke et al. 2013). The destruction of rabbit warrens has been shown to be one of the most effective methods of control, resulting in dramatic reductions in rabbit numbers in arid, semiarid and temperate areas of Australia (Mutze 1991; Williams et al. 1995; McPhee and Butler 2010; Berman et al. 2011). To be effective, warren-ripping programs must be conducted over large areas to reduce the chances of re-invasion and use heavy machinery to avoid only partial destruction of warrens (Martin and Eveleigh 1976; Parer and Milkovits 1994; McPhee and Butler 2010).
Although many studies have examined the effectiveness of warren ripping for reducing rabbit densities, few studies have examined the rate at which warrens are recolonised in ripped areas (i.e. warren re-opening) and fewer still have examined the relationship between warren recolonisation and potential explanatory variables. Although surface-dwelling rabbits can reach moderately high abundances in areas with extensive surface cover, rabbits usually reach much higher densities when they are associated with a warren system (Myers et al. 1994; Williams et al. 1995). Therefore, understanding the factors that may influence the rate of warren recolonisation in ripped areas could be useful for predicting when (and where) rabbits re-establish following ripping operations; this information would be useful for improving the cost-effectiveness of maintenance control. Knowledge of spatial factors influencing warren re-establishment could also be incorporated into a decision support tool to aid the efficient planning of control programs across landscapes.
Little is known about some of the spatial effects and other factors potentially affecting rates of warren recolonisation following ripping operations. Classical metapopulation theory predicts that colonisation of vacant patches in a heterogeneous environment is dependent on their proximity to source populations (isolation effect) as well as the size of those source populations (propagule pressure; Hanski 1991). The quality of habitat patches has also been shown to have a significant influence on patch colonisation (Franken and Hik 2004; Franzén and Nilsson 2010). Parer and Milkovits (1994) found that the rate of warren recolonisation and the establishment of new warrens was positively correlated with an index of rabbit abundance in adjacent uncontrolled habitat and negatively correlated with the distance to the adjacent habitat, providing some support for these ideas. However, the sizes of their study sites were relatively small (50–80 ha) and, hence, recolonisation occurred relatively rapidly because of the short distances (<300 m) between ripped warrens and uncontrolled rabbit populations. Other studies examining the efficacy of warren ripping over larger areas and longer time periods have found that recolonisation rates of ripped areas were low up to 10 years post-ripping (Mutze 1991; McPhee and Butler 2010; Berman et al. 2011). With the exception of Mutze (1991), warrens in these studies were ripped using heavy machinery (>100 kW) to depths of at least 70 cm. McPhee and Butler (2010) examined the effect of different categories of machinery (heavy, medium and light) on the effectiveness of warren-ripping programs over a 10-year period. They found that larger reductions in rabbit numbers occurred at those sites that were ripped with heavy machinery than at sites ripped with medium and light machinery. However, there was no analysis of the rates of warren recolonisation in that study. Although the studies of Berman et al. (2011) and Mutze (1991) did examine warren recolonisation rates over a longer time interval, neither attempted to explain warren recolonisation with environmental variables.
In Victoria, the effect of coordinated ripping programs on rabbit densities was evaluated at 14 study sites (8–142 km2) over a 10-year period between 1998 and 2008, in areas where rabbits were having significant economic and/or environmental impacts (McPhee and Butler 2010). These ripping programs resulted in reductions in rabbit numbers between 36% and 98%, compared with rabbit densities recorded before the spread of rabbit haemorrhagic disease virus (RHDV). Although several environmental variables were collected at each site and examined for their influence on the efficacy of the ripping programs, the only variables with significant influence were the percentage of the warrens ripped at each site and the category of machinery used (including a ‘no ripping’ category at three non-treatment sites; McPhee and Butler 2010).
Although the coordinated ripping program was successful at reducing rabbit numbers, there was no analysis of warren recolonisation on the ripped sites and its possible relationship with warren-level and site-level environmental variables. Here, we conduct an analysis of the recolonisation rates of ripped warrens by using the same data and sites as used in McPhee and Butler (2010), but over a longer time interval (15 years). In particular, we were interested in predicting the effects of several warren-level and site-level variables as well as spatial effects on the rate that ripped warrens were recolonised. Finally, we discuss the management implications of our findings.
Methods
Study sites
The study sites were the same as those presented in McPhee and Butler (2010; Fig. 1, Table 1), with the exception that we excluded the three sites that were not subject to coordinated warren ripping (i.e. Ballan, Dunluce and Sutton Grange). We provide a brief overview of the study sites and warren-ripping programs here; however, for a detailed description, see McPhee and Butler (2010). Fourteen sites were established in 1998 across Victoria on farmland (livestock grazing or cereal cropping), with each site subject to a coordinated program of warren ripping from 1998 to 2002 designed to take advantage of the prior spread of RHDV. A range of earth-moving machinery was used to rip warrens and remove surface harbour and was categorised as either heavy (e.g. 150–225-kW machinery), moderate (e.g. 60–70-kW machinery) or light (e.g. backhoes). Sites were subject to varying intensities of follow-up control, including re-ripping and fumigation, and rabbit numbers were monitored using replicated spotlight counts between two and four times per year, usually during spring and autumn.

|
Warren activity
At each site, warrens selected for monitoring were located primarily within several subareas (1–3 ha) that had a high density of warrens. Hence, not all warrens at a site were subject to routine monitoring. The location of each warren in each of the subareas was recorded with GPS before ripping, to enable follow-up monitoring of warren activity. The activity of individual warrens was monitored both before and after the ripping programs over a 15-year period from 1998 to 2013, with most warrens being visited 2–4 times per year. At each visit, warren activity was indexed by counting the number of active and inactive entrances (e.g. Berman et al. 2011). However, at two sites (Harcourt and Cowangie), only a few warrens were surveyed before ripping operations. Because we were interested in using the number of active entrances before ripping as a potential covariate, these sites were excluded, leaving data from warrens at 12 sites available for analysis (Table 1). The response variable for our analysis was the status of the warren in the period after it was ripped. Only warrens with an active and inactive entrance count of zero immediately following ripping were considered for analyses. Here, we wish to analyse the failure rate of warrens following ripping, with the warren failure defined as the first observation of an active entrance at the warren. The times to first observed recolonised active entrance for each warren were subject to survival analysis, to estimate the recolonisation rate of warrens and its relationship with environmental variables.
Nine variables were used in the survival analysis to potentially explain the rate of warren recolonisation (Table 1). The distance to the nearest active warren (NW) was calculated for each warren at each site, by calculating the Euclidean distance from each ripped warren to the next nearest warren that had at least one active entrance. For each nearest active warren, we also recorded the number of active entrances (AE) and used this in the analysis. For each warren, we also recorded the mean number of active entrances before the warren was ripped, as a measure of the initial extent of the warren (IE). In addition, we also had measures of airborne radiometrics for each warren. The radiometric data are measures of the concentrations (particle counts) of the radioactive elements potassium (K), thorium (TH) and uranium (U) detected in soils from airborne radiometric surveys collected at a resolution of 1 ha. Concentrations of these elements provide an indication of soil- and parent-material characteristics (Slater and De Plater 1997). We used the particle counts from each channel (K, TH and U) recorded from the locations for each individual warren in the analysis. Other variables potentially related to warren recolonisation included ripping-machinery type (MT; i.e. heavy, medium, light), previously found to be an important predictor of reductions to rabbit abundance resulting from warren ripping (McPhee and Butler 2010), as well as the level of follow-up maintenance control (MC) applied at the site following ripping operations. The level of maintenance control at each site was classified as either ‘high’, ‘moderate’ or ‘light or none’. Additionally, we also considered that residual rabbit abundance following ripping treatments could potentially influence the rate of warren recolonisation. Hence, we included an index of rabbit abundance (RA) at each site collected after warren ripping during 2005–13. The rabbit-abundance index at each site was estimated from spotlight surveys of rabbit numbers (rabbits km–1) along a fixed transect and used the same data as presented in McPhee and Butler (2010), but with an additional 5 years of spotlight monitoring data. All continuous variables were standardised by subtracting the mean and dividing by the standard deviation before analysis.
Survival analysis
We fitted discrete-time survival models (Allison 1982; Congdon 2010) to the time elapsed between the warren being ripped and the first observed recolonised active entrance, to estimate the probability of warren recolonisation and its relationship to environmental variables (also called the hazard function or hazard probability). Discrete-time models were considered more appropriate than continuous-time models because the total observation period was long (~10–15 years); however, there were few observations for individual warrens with a mean time between observations of 6 months.
Let the time period between initial warren ripping and first observed recolonised active entrance be grouped into M 6-monthly intervals Tk = (tk–1, tk), k = 1,.., M, with T being a discrete random variable. We denote the discrete-time of failure or censoring occurring in a particular interval (tk–1, tk) as k, and hence, the discrete-time hazard function is given by
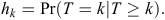
Here, the hazard function is the conditional probability that at least one active entrance was observed at a warren in time interval k (T = k), given that no active entrances were observed at any earlier time interval (T ≥ k). Hence, the survivor function S is given by
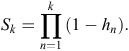
At each time interval, each warren (indexed by i) either experiences an event (active entrance found) or survives the interval (i.e. is censored). If dik is the event indicator for Warren i in time interval k, the hazard for warren i has a likelihood contribution of
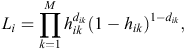
and, hence, the likelihood involves binary responses. Commonly used link functions for the probabilities hik include the logit, probit and complementary log-log. The complementary log-log model assumes an underlying proportional-hazards model in continuous time and is given by
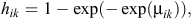
where μik represents the model for the baseline hazard and the effects of explanatory variables (Aitkin et al. 2009; Congdon 2010). We specified two competing models for the baseline hazard probabilities. Model 1 assumed a constant baseline hazard, which was given by

where α is the intercept (constant baseline hazard), β is the regression coefficients and Xik is the explanatory variables (possibly time-varying). Equation 1 thus represents a discrete-time equivalent to the exponential survival model in continuous time. Model 2 assumed a non-constant baseline hazard and is given by

where the term κ log(k) allows the baseline hazard to increase or decrease with time according to the Parameter κ. Equation 2 is thus the discrete-time equivalent to the Weibull survival model in continuous time (Allison 1982).
The variables for individual warrens (NW, AE, IE, K, TH, U) were used as explanatory variables for the regressions in Eqns 1 and 2. The other variables, namely RA, MT and MC, were known only at the site level. These were incorporated into the models by considering hierarchical versions of Eqns 1 and 2. Hierarchical models were constructed by expressing the intercept (α) as a function of site-level variables, as follows

where the fixed term α in Eqns 1 and 2 is replaced by the random equivalent αj indexed by site j. This term was drawn from a normal distribution with mean ηj and standard deviation σα. The hierarchical site-level models express the ηj as a function of the site-level variables Zj, RA, MC and MT, with ν and ρ being the regression coefficients. Hence, Eqns 1–3 represent hierarchical random-effects models and explicitly account for the nested structure of the data (warrens nested within sites). Because the number of sites ripped by both medium and light machinery (MT) was only five, we combined these levels and, hence, collapsed MT into a two-level factor (‘heavy’ vs ‘medium or light’). Similarly, MC was also collapsed into a two-level factor (‘high’ vs ‘moderate or light or none’).
Because we had a total of nine explanatory variables for the analysis, a total of 29 = 512 unique models (excluding interactions) could potentially be fitted to the data. Rather than contrive a set of fewer models to examine, we conducted Bayesian variable selection (BVS) to efficiently search the parameter and model space to determine the set of plausible models that could potentially explain the data (O’Hara and Sillanpää 2009). We used the Gibbs-based method of Kuo and Mallick (1998) to conduct variable selection and model averaging. This method uses a set of binary indicators γ ∈ {0, 1}p, with dimension p being equal to the number of variables to be considered. The binary variables γ are used to indicate which of the p variables are present in the model during the current iteration of the Markov chain. Hence, the linear predictor for the models in Eqns 1 and 2 now becomes
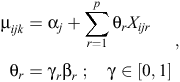
where θr and Xijr are the coefficient and values respectively for the rth covariate (r = 1, …, p). Therefore, when γr = 1, the coefficient βr is included in the model and when γr = 0, the coefficient βr is excluded. A similar modification was also made to the hierarchical site-level linear predictor (Eqn 3).
The Bayesian variable-selection algorithm was fitted using Markov Chain Monte Carlo (MCMC) sampling in JAGS version 3.3.0 (Plummer 2003). Prior distributions were placed on βr and γr, assuming conditional independence (Kuo and Mallick 1998; O’Hara and Sillanpää 2009), as follows:
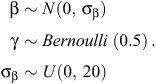
Specifying γr to have a Bernoulli prior of 0.5 for each covariate assumes that each model is given equal weight in the selection process (Dellaportas et al. 2002). A vague normal prior N(0, 100) was also placed on the hierarchical site-level intercept ν, which was included in every model, and a vague uniform prior U(0, 100) was placed on the random effects standard deviation parameter σα. For both the exponential and Weibull models (Models 1 and 2, respectively), three MCMC chains were run with diffuse initial values and checked for convergence by using the Brooks–Gelman–Rubin convergence statistic  (Brooks and Gelman 1998). Thereafter, sampling continued for 10 000 samples for each chain, giving 30 000 samples for posterior summaries. We also calculated the deviance information criterion (DIC) for both models for use as a model-selection criterion (Spiegelhalter et al. 2002). The JAGS code used to fit the Bayesian variable selection algorithm is provided in Appendix S1 (available as Supplementary Material for this paper).
(Brooks and Gelman 1998). Thereafter, sampling continued for 10 000 samples for each chain, giving 30 000 samples for posterior summaries. We also calculated the deviance information criterion (DIC) for both models for use as a model-selection criterion (Spiegelhalter et al. 2002). The JAGS code used to fit the Bayesian variable selection algorithm is provided in Appendix S1 (available as Supplementary Material for this paper).
There are multiple flavours of BVS and we tried two other approaches, namely, Gibbs variable selection with informative pseudopriors (Dellaportas et al. 2002) and the stochastic search algorithm (O’Hara and Sillanpää 2009). Both gave similar results to the algorithm used here (Kuo and Mallick 1998). We also fitted the full model containing all predictors but without the variable selection approach, and examined the posterior mass of the coefficients, with those identified by BVS all being significantly removed from zero, in contrast to those identified as unimportant, which all included zero within their 95% intervals. Hence, we have no reason to believe that the BVS algorithm used here produced spurious results.
Results
In total, 555 warrens at 12 sites were considered in the analysis (Table 1). Overall, the warren-ripping programs achieved long-term reductions in both warren activity and rabbit densities (Table 2). Reductions in warren density (warrens ha–1) over the period 2005–13 averaged 76% (range 38–95%), whereas reductions in the number of entrances per warren averaged 61% (range 15–95%). Ultimately, the reductions in the warren density and entrance count resulted in reduced numbers of rabbits, with an 84% reduction in rabbit abundance (rabbits km–1) achieved on average (range 38–99%) over the 9-year period since ripping operations ceased at all sites (2005–13; Table 2).
For both Models 1 and 2, the variable-selection algorithm was judged to have converged following 20 000 iterations of the three MCMC chains (i.e.  < 1.01 for all parameters). The DIC values for Models 1 and 2 were 1895 and 1814, respectively, indicating that Model 2 was much more supported by the data than was Model 1, based on having a difference in DIC of >10 (Lunn et al. 2013). Hence, we used the results of Model 2 (Weibull model) for all further inferences. The posterior inclusion probabilities for each of the covariates for Model 2 (Table 3) were high (>0.9) for three covariates; hence, the distance to the nearest active warren (NW), which had a inclusion probability of 1.0 was included in every model, as well as was the number of active entrances in the nearest active warren (AE), and the initial number of active entrances (IE). The RA also had a fairly high inclusion probability of 0.69 and, hence, appeared in about two-thirds of the visited models. The other four covariates had inclusion probabilities <0.50 and, hence, had relatively little support (Table 3). The posterior model probabilities of the 10 most supported models subsequently included NW, AE and IE in every model and RA was included in 7 of the 10 models (Table 4). The relative lack of support for the three soil radiometrics (K, TH, U), MT and MC was further illustrated by the model-averaged parameter estimates, which showed that mean coefficient values for K, TH, U, MT and MC shrunk toward zero and median parameter estimates equal to zero (Table 5).
< 1.01 for all parameters). The DIC values for Models 1 and 2 were 1895 and 1814, respectively, indicating that Model 2 was much more supported by the data than was Model 1, based on having a difference in DIC of >10 (Lunn et al. 2013). Hence, we used the results of Model 2 (Weibull model) for all further inferences. The posterior inclusion probabilities for each of the covariates for Model 2 (Table 3) were high (>0.9) for three covariates; hence, the distance to the nearest active warren (NW), which had a inclusion probability of 1.0 was included in every model, as well as was the number of active entrances in the nearest active warren (AE), and the initial number of active entrances (IE). The RA also had a fairly high inclusion probability of 0.69 and, hence, appeared in about two-thirds of the visited models. The other four covariates had inclusion probabilities <0.50 and, hence, had relatively little support (Table 3). The posterior model probabilities of the 10 most supported models subsequently included NW, AE and IE in every model and RA was included in 7 of the 10 models (Table 4). The relative lack of support for the three soil radiometrics (K, TH, U), MT and MC was further illustrated by the model-averaged parameter estimates, which showed that mean coefficient values for K, TH, U, MT and MC shrunk toward zero and median parameter estimates equal to zero (Table 5).

|

|

|
The predicted probabilities of warren recolonisation for Model 2 showed a relatively close fit to the data and indicated that the recolonisation probability increased more rapidly in the initial 2–3 years post-ripping, before increasing more steadily (Fig. 1). Estimates of the probability of recolonisation within 10 years post-ripping showed a strong relationship with the distance to the nearest active warren, the number of active entrances in the nearest warren and the number of initial active entrances in the ripped warren, as well as with the rabbit abundance index (Table 5). The probability of warren recolonisation decreased by 51% (e(–0.71) – 1) for every 433-m distance (1 standard deviation) between the ripped warren and the nearest active warren. Similarly, the probability of recolonisation increased by 28% for every increase in the initial active entrance count (IE) by 7 and increased by 18% for every increase in the active entrance count in the nearest warren (AE) by 15. The probability of warren recolonisation also increased by 22% for every increase in the rabbit spotlight count (RA) at the site by 10 rabbits km–1.
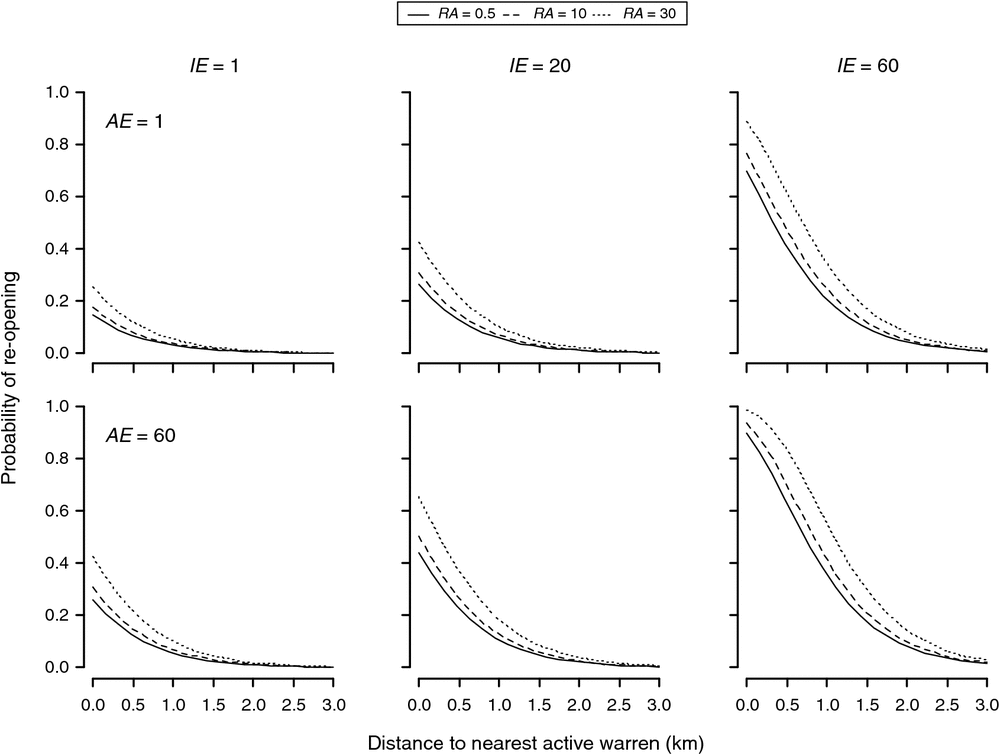
Ripped warrens having a nearest active warren at least 3 km away had negligible probabilities of reopening within 10 years, regardless of their initial size or the size of the nearest active warren. For ripped warrens, having a nearest active warren within 2 km or less, the probability of recolonisation was dependent on initial warren size as well as the size of the nearest active warren, and to a lesser extent, the background rabbit abundance (Fig. 2). For ripped warrens with small and medium initial sizes (i.e. of 1–20), recolonisation probabilities were low (<10%) if active neighbours were at least 1.5 km away and only increased substantially (>20%) for warrens with a large initial size (i.e. = 60) and with a large number of active entrances in the nearest warren (AE = 60). Ripped warrens having a nearest active warren within 1 km or less had highly variable probabilities of recolonisation with 10 years, varying from <20% for warrens of small and moderate initial size (i.e. ≤20) to ~98% for warrens of a large initial size (i.e. = 60), with a large nearby warren (<100 m) with many active entrances (AE = 60) and a high background rabbit abundance index (RA > 30) (Fig. 2).
Discussion
As was outlined in McPhee and Butler (2010), the rabbit-control operations based on coordinated ripping programs successfully reduced rabbit abundance at the 12 sites used in the present analysis, by an average of 84% over a 9-year period (2005–13) since the cessation of ripping operations. However, ripping operations in the present study occurred following the escape and controlled release of RHDV in 1995–96, when rabbit numbers were supressed by the initial epizootic (Mutze et al. 2010). Consequently, the capacity of populations to recover following the ripping operations was likely to have been impaired compared with a pre-RHD environment. Samples collected systematically to measure the impact of RHD (S. McPhee, unpubl. data) suggested that the prevalence of RHD antibodies did not differ greatly among the study sites. Hence, we conclude that differing dynamics of RHD among sites had minimal impact on the results presented here. Although the coordinated warren-ripping program was successful at most sites, at one site (Pentland Hills) the ripping program was much less successful, with rabbit abundance being reduced only by 37%. Understanding the risk factors that can lead to warren and rabbit recovery at a site will enable managers to better target resources that should lead to more cost-effective rabbit management.
Previous studies of warren ripping for rabbit control have all examined effects of ripping on rabbit abundance (usually an index derived from spotlight surveys) and warren activity. However, with the exception of Parer and Milkovits (1994), no previous studies have examined recolonisation rates of ripped warrens by rabbits and how they may be influenced by environmental variables. By far the strongest influence on the probability of warren recolonisation was the distance to the nearest warren with an active entrance. In addition, the risk of recolonisation was also positively related to the number of active entrances in the nearest warren and the initial number of active entrances present before ripping as well as the rabbit abundance at the site. These findings concur with results from metapopulation theory that relate the colonisation of habitat patches to both the distance from the source population (isolation effects) as well as the size of the source population (propagule pressure; Hanski 1991). Our findings also concur with those of Parer and Milkovits (1994) who found similar relationships between recolonisation of warrens and distance to neighbours and initial warren size. However, the present study, conducted over a longer time frame and using larger study sites, was able to make inferences about the spatial extent of recolonisation from adjacent active warrens. Ripped warrens that were at least 3 km from an active warren had a <5% chance of recolonisation within 10 years. Although long-distance dispersal of rabbits (>1.5 km) does occur, average dispersal distances are usually <1 km, with more males than females undertaking dispersal (Parer 1982). Dispersing rabbits tend to move from areas of high to low rabbit abundance and will settle in vacant warrens if they exist or will otherwise tend to shelter in surface harbour rather than construct a new warren (Williams et al. 1995).
Construction of warrens is undertaken principally by female rabbits and represents a large energetic investment over a considerable period of time. Usually, warrens are not readily replaced if destroyed (Myers et al. 1994). Hence, dispersing rabbits are likely to preferentially seek out existing warrens at the settlement site if they exist and may not re-open warrens in ripped areas. This effect would be exacerbated at larger distances, which would receive fewer dispersers from the source population and would be predominantly male-biased (Myers et al. 1994). This was illustrated in studies of warren ripping undertaken in the arid zone in Queensland and South Australia where ripped warrens were not re-established, even when rabbits had ready access to the ripped areas (Mutze 1991; Berman et al. 2011). Mutze (1991) suggested that ripping had changed the soil texture such that burrow establishment was no longer suitable for rabbits. Hence, Berman et al. (2011) suggested that ripping of warrens within 1 km of permanent water (a drought refuge for rabbits) would be sufficient to suppress rabbit numbers over a much larger area because rabbits rarely travel further than this in search of water. Thus, the results of this and other studies suggest that the effective neighbourhood from where ripped warrens could be subject to rapid recolonisation from neighbours extends out to a radius of ~1 km from the ripped areas. Similar spatial effects were also found in a study by Barrio et al. (2011) on wild-rabbit populations in Spain, where the probability of a warren being occupied was significantly negatively correlated with the distance to the nearest active warren.
In contrast, other studies have suggested that recolonisation of ripped areas may occur over much larger areas. Parer and Parker (1986) showed that recolonisation of ripped warrens occurred within 3 years on a 23 000-ha property in western New South Wales. The cause of this rapid recolonisation was thought to be the proximity of active warrens on adjacent properties ~5 km away. However, the 3 years in question also had above-average rainfall and it is unclear whether the increase in warrens on the ripped property was due to recolonisation from adjacent warrens or recovery of residual populations in situ, because not all warrens on the property were destroyed (Parer and Parker 1986). Other studies have also shown a fairly rapid recovery (1–2 years) of ripped areas if the ripping treatment was only partially effective either by not ripping all warrens (Wood 1985) or only partially destroying large warrens (Martin and Eveleigh 1976).
Larger warrens were more likely to be recolonised than smaller warrens. One explanation for this result is that rabbits were more likely to colonise areas where larger warrens were originally situated. Patch size is often used as a surrogate for habitat quality (Franzén and Nilsson 2010) and this finding suggests that colonisation of vacant patches is influenced not only by propagule pressure and isolation but also by habitat quality of the vacant patch. Hence, these results are in agreement with results from other metapopulation studies linking colonisation with habitat quality (Franken and Hik 2004; Jaquiéry et al. 2008; Franzén and Nilsson 2010). If habitat quality does indeed influence colonisation of ripped warrens, then it is perhaps surprising that there was no discernible relationship between warren recolonisation and the three soil radiometric variables used here. However, it is possible that soil radiometrics do not capture the soil properties favoured by rabbits for warren construction. An alternative explanation is that larger warrens are more likely to not be completely destroyed by ripping, and recolonisation is then driven largely by in situ recovery. The Weibull survival model fitted here suggests that the probability of recolonisation increased more rapidly in the first few years following ripping of the warren, which may suggest that some warrens were not being completely destroyed. Alternatively, the initial increase in the recolonisation probability could have also been due to the nature of the ripping programs, which were conducted in a phased manner at each site and sometimes took several years to complete. Hence, recently ripped warrens at some sites would have had active neighbours until such time as the ripping program was completed at that site. Regardless of the underlying process, because large warrens are more likely to be recolonised than are small warrens, monitoring and maintenance-control programs should be prioritised at locations where large warrens originally existed.
Contrary to the results of McPhee and Butler (2010), we did not find an effect of machinery type on the probability of warren recolonisation. Although the risk of recolonisation did increase if light or medium machinery were used, compared with heavy machinery, the difference was small (<5% increase in risk) and not statistically significant. The significant effect found in McPhee and Butler (2010) was due mainly to that study including ‘no-ripping’ as an additional level, which was in contrast to the present study where we contrasted only ‘heavy’ vs ‘medium or light’ machinery. In general, the results presented here assume that ripping operations are performed by machinery that is sufficiently heavy to completely destroy warrens, such that recolonisation of a warren is the result of movement of rabbits from adjacent occupied warrens rather than in situ recovery of rabbits.
The probability of warren recolonisation was also related to an index of rabbit abundance at the site. This spotlight index of rabbit abundance was collected from transects covering each site following the cessation of ripping activities and therefore represents the ‘background’ post-ripping recovery rate of rabbit abundance at the sites (McPhee and Butler 2010). Hence, this risk is not specific to a warren type but applies equally to all warrens at the site. For an average warren, it was found that an increase in the rabbit spotlight count of 10 rabbits km–1 equated to a 22% increase in the risk of warren recolonisation. For an average warren, this translated to an increase in the probability of recolonisation from 0.14 at 0.5 rabbits km–1 to 0.17 at 10 rabbits km–1, whereas at 40 rabbits km–1 the risk of recolonisation within 10 years was 0.29. Estimates of rabbit abundance at the site provide another measure of the general level of propagule pressure at a site that further increases the risk of recolonisation, and periodic monitoring of the background rabbit abundance should be undertaken to assess this risk.
Management implications
The recommended practice for successfully managing rabbit populations involves substantially reducing rabbit numbers to low levels and then, in the long term, maintaining a low residual population with low effort and low costs (Williams et al. 1995). Within most of the rabbit-prone areas of Victoria, rabbit warrens are crucial for the survival and maintenance of high-density rabbit populations. The present study has demonstrated that, following the spread of RHDV, coordinated ripping programs conducted over large (8–142 km2) regions were effective in achieving the long-term management of rabbit populations (McPhee and Butler 2010). However, knowledge of the rates at which ripped warrens are likely to be recolonised has important implications for the long-term management of rabbits using this technique. Although results for individual warrens can be variable, several general conclusions can be drawn from the present study. The major factor affecting the long-term efficacy of warren-ripping programs appears to be spatial effects of the proximity to neighbouring active warrens and their size. Larger active warren neighbours pose a greater risk because they would presumably provide a greater source of dispersing rabbits. The results from the present study suggest that the risk from dispersing colonisers decreases to almost negligible levels if the nearest source population is more than 3 km from the ripped warren. Hence, coordinated ripping programs conducted over a sufficiently large area and incorporating 3-km buffer zones would ensure that ripped areas are unlikely to be recolonised in the medium term (10–15 years) because of ripped areas being sufficiently remote from a potential source of dispersing propagules.
Due to their higher risk of recolonisation, areas with large warrens (>20 active entrances) should be prioritised for follow-up monitoring, to ensure that in situ recovery has not occurred as a result of the warren not being completely destroyed. Monitoring and maintenance control should occur at least annually in the first 5 years post-ripping, because the risk of recolonisation is highest in these initial years. Subsequent to this, monitoring can then occur periodically (e.g. every 2–3 years), again prioritising high-risk areas. In addition, ripped warrens that are found to have recolonised also pose a heightened risk to neighbouring ripped warrens. Hence, a warren-monitoring strategy for a region may initially prioritise larger warrens and then adaptively incorporate areas within a 1-km radius of those warrens that were found to have recolonised. Annual or biannual spotlight monitoring of rabbits should also be undertaken as a general measure of risk of warren re-establishment in the region, with a rabbit abundance index of <10 rabbits km–1 generally indicating a ‘low’ risk of warren re-establishment (average probability of warren recolonisation in 10 years of <0.2).
Warren ripping has been shown to be one of the most successful methods for controlling rabbits. Although the method is undoubtedly effective if performed proficiently, its effectiveness can be further enhanced by combining it with follow-up monitoring and maintenance control of the treated area. The results from the present study have identified some of the risk factors influencing the rates at which ripped warrens are recolonised over the medium to long term (10–15 years). Adopting an adaptive monitoring strategy of the managed areas with those key risks in mind, such as suggested above, would further enhance the effectiveness of warren ripping for sustaining long-term reductions in rabbit populations and, hence, would contribute to enhanced environmental and economic outcomes.
Acknowledgements
Funding for this study was provided by the Biosecurity Division, Department of Environment and Primary Industries. We thank the Invasive Plants and Animals Operations group, Biosecurity Victoria, Catchment Management officers and landholders involved with the management of the sites and conducting ongoing monitoring. We also thank Matt White, Arthur Rylah Institute, for providing the radiometric soil layer for Victoria used in the analysis and Alan Robley for comments on a draft version of this paper. Comments by an anonymous reviewer also greatly improved the paper.
References
Aitkin, M., Francis, B., Hinde, J., and Darnell, R. (2009). ‘Statistical Modelling in R.’ 1st edn. (Oxford University Press: New York, NY.)Allison, P. D. (1982). Discrete-time methods for the analysis of event histories. Sociological Methodology 13, 61–98.
| Discrete-time methods for the analysis of event histories.Crossref | GoogleScholarGoogle Scholar |
Barrio, I. C., Villafuerte, R., and Tortosa, F. S. (2011). Harbouring pests: rabbit warrens in agricultural landscapes. Wildlife Research 38, 756–761.
| Harbouring pests: rabbit warrens in agricultural landscapes.Crossref | GoogleScholarGoogle Scholar |
Berman, D., Brennan, M., and Elsworth, P. (2011). How can warren destruction by ripping control European wild rabbits (Oryctolagus cuniculus) on large properties in the Australian arid zone? Wildlife Research 38, 77–88.
| How can warren destruction by ripping control European wild rabbits (Oryctolagus cuniculus) on large properties in the Australian arid zone?Crossref | GoogleScholarGoogle Scholar |
Brooks, S., and Gelman, A. (1998). General methods for monitoring convergence of iterative simulations. Journal of Computational and Graphical Statistics 7, 434–455.
Congdon, P. D. (2010). ‘Applied Bayesian Hierarchical Methods.’ (Chapman and Hall/CRC Press: Boca Raton, FL.)
Cooke, B. D. (2012). Rabbits: manageable environmental pests or participants in new Australian ecosystems? Wildlife Research 39, 279–289.
| Rabbits: manageable environmental pests or participants in new Australian ecosystems?Crossref | GoogleScholarGoogle Scholar |
Cooke, B., Chudleigh, P., Simpson, S., and Saunders, G. (2013). The economic benefits of the biological control of rabbits in Australia, 1950–2011. Australian Economic History Review 53, 91–107.
| The economic benefits of the biological control of rabbits in Australia, 1950–2011.Crossref | GoogleScholarGoogle Scholar |
Dellaportas, P., Forster, J. J., and Ntzoufras, I. (2002). On Bayesian model and variable selection using MCMC. Statistics and Computing 12, 27–36.
| On Bayesian model and variable selection using MCMC.Crossref | GoogleScholarGoogle Scholar |
Franken, R. J., and Hik, D. S. (2004). Influence of habitat quality, patch size and connectivity on colonization and extinction dynamics of collared pikas Ochotona collaris. Journal of Animal Ecology 73, 889–896.
| Influence of habitat quality, patch size and connectivity on colonization and extinction dynamics of collared pikas Ochotona collaris.Crossref | GoogleScholarGoogle Scholar |
Franzén, M., and Nilsson, S. G. (2010). Both population size and patch quality affect local extinctions and colonizations. Proceedings. Biological Sciences 277, 79–85.
| Both population size and patch quality affect local extinctions and colonizations.Crossref | GoogleScholarGoogle Scholar |
Hanski, I. (1991). Single-species metapopulation dynamics: concepts, models and observations. Biological Journal of the Linnean Society. Linnean Society of London 42, 17–38.
| Single-species metapopulation dynamics: concepts, models and observations.Crossref | GoogleScholarGoogle Scholar |
Jaquiéry, J., Guélat, J., Broquet, T., Berset-Brändli, L., Pellegrini, E., Moresi, R., Hirzel, A. H., and Perrin, N. (2008). Habitat-quality effects on metapopulation dynamics in greater white-toothed shrews, Crocidura russula. Ecology 89, 2777–2785.
| Habitat-quality effects on metapopulation dynamics in greater white-toothed shrews, Crocidura russula.Crossref | GoogleScholarGoogle Scholar | 18959315PubMed |
Kuo, L., and Mallick, B. (1998). Variable selection for regression models. Sankhya B 60, 65–81.
Lunn, D., Jackson, C., Best, N., Thomas, A. and Spiegelhalter, D.J. (2013). ‘The BUGS Book: a Practical Introduction to Bayesian Analysis.’ (CRC Press: Boca Raton, FL.)
Martin, J., and Eveleigh, J. (1976). Observations on the effectiveness of warren destruction as a method of rabbit control in a semi-arid environment. The Rangeland Journal 1, 232–238.
| Observations on the effectiveness of warren destruction as a method of rabbit control in a semi-arid environment.Crossref | GoogleScholarGoogle Scholar |
McPhee, S. R., and Butler, K. L. (2010). Long-term impact of coordinated warren ripping programmes on rabbit populations. Wildlife Research 37, 68–75.
| Long-term impact of coordinated warren ripping programmes on rabbit populations.Crossref | GoogleScholarGoogle Scholar |
Mutze, G. (1991). Long-term effects of warren ripping for rabbit control in semi-arid South Australia. The Rangeland Journal 13, 96–106.
| Long-term effects of warren ripping for rabbit control in semi-arid South Australia.Crossref | GoogleScholarGoogle Scholar |
Mutze, G., Kovaliski, J., Butler, K., Capucci, L., and McPhee, S. (2010). The effect of rabbit population control programmes on the impact of rabbit haemorrhagic disease in south-eastern Australia. Journal of Applied Ecology 47, 1137–1146.
| The effect of rabbit population control programmes on the impact of rabbit haemorrhagic disease in south-eastern Australia.Crossref | GoogleScholarGoogle Scholar |
Myers, K., Parer, I., Wood, D., and Cooke, B. D. (1994). The rabbit in Australia. In ‘The European Rabbit: the History and Biology of a Successful Coloniser’. (Eds H. V. Thompson and C. M. King.) pp. 108–157. (Oxford University Press: New York.)
O’Hara, R. B., and Sillanpää, M. J. (2009). A review of Bayesian variable selection methods: what, how and which. Bayesian Analysis 4, 85–117.
| A review of Bayesian variable selection methods: what, how and which.Crossref | GoogleScholarGoogle Scholar |
Parer, I. (1982). Dispersal of the wild rabbit, Oryctolagus cuniculus, at Urana in New South Wales. Wildlife Research 9, 427–441.
| Dispersal of the wild rabbit, Oryctolagus cuniculus, at Urana in New South Wales.Crossref | GoogleScholarGoogle Scholar |
Parer, I., and Milkovits, G. (1994). Recolonisation by rabbits (Oryctolagus cuniculus) after warren ripping or warren fumigation. The Rangeland Journal 16, 51–63.
| Recolonisation by rabbits (Oryctolagus cuniculus) after warren ripping or warren fumigation.Crossref | GoogleScholarGoogle Scholar |
Parer, I., and Parker, B. (1986). Recolonisation by rabbits (Oryctolagus cuniculus) after warren destruction in western New South Wales. The Rangeland Journal 8, 150–152.
| Recolonisation by rabbits (Oryctolagus cuniculus) after warren destruction in western New South Wales.Crossref | GoogleScholarGoogle Scholar |
Plummer, M. (2003). JAGS: a program for analysis of Bayesian graphical models using Gibbs sampling. In ‘Proceedings of the 3rd International Workshop on Distributed Statistical Computing (DSC 2003) (Eds K. Hornik, F. Leisch and A. Zeileis) pp. 1–10. Vienna, Austria’.
Slater, K. R., and De Plater, K. (1997). The application of radiometric data for soil mapping - Nagambie 1 : 100,000 map. Department of Natural Resources and Environment, Victoria.
Spiegelhalter, D. J., Best, N. G., Carlin, B. P., and Van Der Linde, A. (2002). Bayesian measures of model complexity and fit. Journal of the Royal Statistical Society. Series B, Statistical Methodology 64, 583–639.
| Bayesian measures of model complexity and fit.Crossref | GoogleScholarGoogle Scholar |
Williams, K., Parer, I., Coman, B., Burley, J., and Braysher, M. (1995). ‘Managing Vertebrate Pests: Rabbits.’ (Australian Government Publishing Service: Canberra.)
Wood, D. (1985). Effectiveness and economics of destruction of rabbit warrens in sandy soils by ripping. The Rangeland Journal 7, 122–129.
| Effectiveness and economics of destruction of rabbit warrens in sandy soils by ripping.Crossref | GoogleScholarGoogle Scholar |