Comparing modeled soil temperature and moisture dynamics during prescribed fires, slash-pile burns and wildfires

Peter R. Robichaud; William J. Massman; Anthony Bova; Antonio Girona-García; Andoni Alfaro-Leranoz; Nancy E. Gibson

doi:10.1071/WF22082

RESEARCH ARTICLE (Open Access)

Previous Next Contents Vol 34(4)

Comparing modeled soil temperature and moisture dynamics during prescribed fires, slash-pile burns and wildfires

Peter R. Robichaud

^A ^* , William J. Massman ^B , Anthony Bova ^C ^D , Antonio Girona-García

^E , Andoni Alfaro-Leranoz

^F and Nancy E. Gibson ^A

+ Author Affiliations

- Author Affiliations

^A US Department of Agriculture, Forest Service, Rocky Mountain Research Station, 1221 South Main Street, Moscow, ID 83843, USA. Email: nancy.gibson@usda.gov

^B US Department of Agriculture, Forest Service, Rocky Mountain Research Station, Fort Collins, CO, USA. Email: william.massman@usda.gov

^C US Department of Agriculture, Forest Service, Pacific Northwest Research Station, Seattle, WA, USA.

^D Formerly with CPP Inc., Wind Engineering Consultants, Fort Collins, CO, USA. Email: anthony.bova@usda.gov

^E Biodiversity Research Institute (IMIB), CSIC–University of Oviedo–Principality of Asturias, Mieres, Spain. Email: a.girona@csic.es

^F GEOFOREST, Departamento de Ciencias Agrarias y del Medio Natural, Escuela Politécnica Superior de Huesca, Instituto de Investigación en Ciencias Ambientales (IUCA), Universidad de Zaragoza, 22071 Huesca, Spain. Email: a.alfaroler@unizar.es

^* Correspondence to: peter.robichaud@usda.gov

International Journal of Wildland Fire 34, WF22082 https://doi.org/10.1071/WF22082

Submitted: 8 July 2022 Accepted: 11 March 2025 Published: 27 March 2025

© 2025 The Author(s) (or their employer(s)). Published by CSIRO Publishing on behalf of IAWF. This is an open access article distributed under the Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC)

Abstract

Background

Wildfires, prescribed fires and slash-pile burns are disturbances that occur in many terrestrial ecosystems. Such fires produce variable surface heat fluxes causing a spectrum of effects on soil, such as seed mortality, nutrient loss, changes in microbial activity and water repellency. Accurately modeling soil heating is vital to predicting these second-order fire effects. The process-based Massman HMV (Heat–Moisture–Vapor) model incorporates soil water evaporation, heat transport and water vapor movement, and captures the observed rapid evaporation of soil moisture.

Aims

Improve the Massman HMV model and compare it with Campbell soil heating model using four independent soil temperature datasets collected during burning.

Methods

The models were evaluated using similar BFD curves against observed temperature and soil moisture using standard statistical methods.

Key results

Results suggest reasonable agreement between the Massman HMV model and field soil temperature data under various burn scenarios and it was consistently more accurate than the Campbell model.

Conclusions

The Massman HMV model improved soil heating predictions and provided soil moisture predictions.

Implications

The Massman HMV model was incorporated in the First Order Fire Effects Model (FOFEM ver. 6.7) with a user-friendly interface that allows managers to assess the heating impacts of fire on soil temperature and moisture.

Keywords: duff, fire intensity, First Order Fire Effects Model, FOFEM, Heat–Moisture–Vapor (HMV) model, moisture dynamics, soil heating, soil temperature, surface fire, validation.

Introduction

Soil heating during wildfires, broadcast prescribed fires, or slash-pile burns can produce a spectrum of effects in soil that, depending on fire intensity and duration, may be permanent. These near-term (first-order) fire effects often result in significant, long-term (secondary) biological, chemical, physical and hydrological fire effects (Neary et al. 2005). When using broadcast prescribed fires, slash-pile burns or managed wildfires as management tools, it is particularly important to understand and predict the potential first- and second-order effects of soil heating.

The magnitude and duration of soil heating determine the depth and duration of heat penetration, and therefore the extent of secondary effects caused by a fire (Girona-García et al. 2019; Brady et al. 2022). In a modeling context, the depth and duration of heating depend on the soil properties, the thermal boundary conditions at the soil surface and the initial distribution of soil moisture (Badía et al. 2017).

There are generally accepted temperature thresholds for specific indirect fire effects on soil (Santín and Doerr 2016). Martin and Cushwa (1966) first measured soil heating and duration in a laboratory study (e.g. heating in an oven) of effects of fire on germination of legume seeds. In addition to providing threshold temperatures for the lethal effect of vascular cambium or root tissue, Brady et al. (2022) elaborate that the duration of the heating is also important as slow heating of the soils likely results in lower thresholds. In general, soil temperatures in the range of 60–80°C for short periods of time are lethal to plant seeds, plant roots and plant tissue. At temperatures approaching the range of 120–160°C, microbial life is extinguished (Choczynska and Johnson 2009; Armas-Herrera et al. 2016). At even higher temperatures, irreversible physical, chemical, mineral and hydrologic changes may occur in the soil (DeBano et al. 1998; Neary et al. 2005; Massman et al. 2010). Temperature thresholds have been identified for numerous physical, chemical and biological properties (Certini 2005; Santín and Doerr 2016; Alcañiz et al. 2018; Agbeshie et al. 2022). For example, temperatures between 175 and 280°C can cause soils to become water-repellent, reducing infiltration potential, whereas temperatures above 300°C can break down repellency (DeBano et al. 1976; Robichaud and Hungerford 2000; Dlapa et al. 2008; Badía et al. 2017).

The energy generated by combustion of wildland fuels may be transferred to underlying soil by means of thermal radiation, conduction and convection, which in turn drive mass transport, vaporization and condensation in soils (Neary et al. 2005). Most studies employing models of coupled heat and moisture transport in soils have concentrated primarily on typical ambient environmental conditions, i.e. those involving daily and seasonal variations in solar radiation, temperature, precipitation, etc. (Novak 2010; Smits et al. 2011). A few studies have examined these processes under more extreme conditions, such as those occurring during wildfires and prescribed burns (Aston and Gill 1976; Campbell et al. 1995; Durany et al. 2010; Brady et al. 2022). Broadly speaking, the same physical principles and the basic equations are employed in these models, but the impacts of various model components vary by modeling regimes (i.e. ambient vs extreme conditions). Models developed for soil heating under ambient conditions tend to focus on the movement of soil moisture and evaporation (Novak 2010; Smits et al. 2011), whereas models developed to describe the extreme conditions of fire emphasize soil temperatures and the duration of the soil heating (Aston and Gill 1976; Campbell et al. 1995; Durany et al. 2010; Brady et al. 2022).

Numerical models (Aston and Gill 1976; Campbell et al. 1995; Durany et al. 2010; Massman 2012) have had some success estimating soil temperatures during severe heating events, but they have yielded quite poor simulations of the coupled soil heating and soil moisture dynamics owing to the model’s inability to properly represent the relationship between soil water potential and soil moisture at extremely low soil moisture contents (Massman 2012). Additionally, Albini et al. (1996) reviewed the models of Aston and Gill (1976) and Campbell et al. (1995) and found that the earlier model was prone to instabilities and that the later model did not provide an adequate simulation of soil moisture content changes with high temperatures (i.e. evaporation of the soil water), similarly to the conclusion reached by Campbell et al. (1995). Likewise, the model of Durany et al. (2010) provided reasonable model performance when simulating soil temperatures, but estimated soil volumetric moisture contents as high as 15% despite heating the soils to over 225°C, which should be sufficient to dry the soil.

Massman (2012), using Campbell et al. (1995) as a modeling template, found that all evaporated soil moisture simply recondensed and accumulated ahead of the dry zone and that no moisture escaped the soil. Therefore, the state of the science in 2012 suggested two possibilities: (1) the microphysical processes governing soil moisture evaporation and condensation were not fully understood, or (2) horizontal gradients in temperature and moisture during a fire are strong enough to give rise to diffusive horizontal heat and moisture flows. Massman et al. (2010) further suggested that advective, rather than diffusive lateral flows are induced by differential pressure fields beneath and surrounding a burning slash-pile; therefore, any possible 3D effects cannot be fully captured by a 1D model. Massman (2015, 2021) investigated the likelihood of possibility no. 1 through the development and refinement of the vapor source or sink term required for a non-equilibrium model. Simply put, an equilibrium model can not describe evaporation below a volumetric soil moisture level of ~0.02 m³ m⁻³ even though this is likely to occur with fires in dry environments. Possibility no. 2 was first noted in Massman et al. (2010) and was subsequently confirmed by Bao et al. (2020) with their model, which includes diffusive lateral transport of heat and soil moisture.

The goal of the present work is to improve the predictive ability of soil heating models that can be incorporated into larger fire behavior models and used for predicting the indirect, long-term, biological, chemical, physical and hydrological secondary fire effects of soil heating. To achieve this goal, we had two objectives: (1) incorporate Massman (2015, 2021) Heat–Moisture–Vapor (HMV) soil heating into the First Order Fire Effects Model (FOFEM), and (2) evaluate the Massman HMV model (2015, 2021) by comparing it with the Campbell model (1995) with Massman’s (2021) adaptation of the BFD curve (Barnett 2002) to a soil heating function. The performance of each model was tested and evaluated against existing field-collected independent datasets from various burn scenarios (slash-pile burn, broadcast prescribed fire, burn box study and wildfire). FOFEM is a computer model that predicts the direct (immediate) or indirect consequences of fire such as consumption of fuels, smoke emissions, tree mortality and soil heating. This is achieved by using regional databases combined with initial fuel loads, fuel moistures and soil moistures at the time of burning (Lutes 2020). The modeled soil heating uses either the Massman HMV or Campbell model to predict soil temperatures (and moisture in the case of Massman HMV) at various depths in the soil profile over time. FOFEM is actively used by fire managers and is the predominant model of first order fire effects.

Materials and methods

Massman HMV soil heating model

The Massman HMV model (Massman 2015, 2021) has three model variables – soil temperature, soil water potential and soil water vapor – and several supporting relationships that describe soil thermal conductivity, the soil water retention curve and hydraulic conductivity functions for water transport and the non-equilibrium evaporative source term. There are 35 input parameters to this model, including boundary conditions and soil physical properties. In contrast, the early Massman HMV model (Massman 2012) model has only two model variables, soil temperature and soil water potential, and approximately half as many input parameters. The Massman HMV model (Massman 2021) further improves on the 2015 version by incorporating a more physically realistic parameterization of soil thermal conductivity and the evaporation of soil moisture as the soil completely dries out (i.e. as soil moisture → 0 during a fire). These changes improved the stability and performance of the Massman HMV model (Massman 2021) over previous versions. The three conservation equations used in the physically based model are provided in the Appendix along with descriptions of surface and lower boundary conditions.

The Massman HMV model (Massman 2021) accommodates a new heat flux boundary condition. The input of radiant energy at the upper boundary of the soil is based on the BFD curve, a term coined by Barnett (2002) without explanation. The curve was originally used to empirically fit the growth and decay of structural element temperatures in fire engineering applications (Barnett 2002) but has been adapted to other fire effects applications (Bova et al. 2011). It requires only three parameters to model growth and decay: maximum temperature (or, as used herein, maximum heat flux), the time at which the maximum occurs and a shape constant that determines the profile of the curve.

The equation that describes the surface energy input is:

(1)

Q_{F} (t) = Q_{fin} + (Q_{\max} - Q_{fin}) {e^{- α (\ln (t / t_{\max}))}}^{2}

where Q_fin(t) (W m⁻²) is the surface energy input (i.e. fire intensity at soil surface; see Fig. 1) as a function of burn time, t (h) (Massman 2021). The key input parameters of this equation are: Q_max, which is the maximum fire intensity impinging on the soil surface; α, which is a dimensionless parameter determined by the duration of the fire, and t_max (h), the time to Q_max.

Fig. 1.

Graphical user interface developed for running the soil temperature and moisture content simulation with the Massman HMV Soil Heating Model. This interface is accessed through FOFEM ver. 6.7 or greater. In bold red numbers and boxes: (1) soil depths; (2) graph type (temperature or moisture); (3) graph axes limits; (4) heating curve parameters (Fire Intensity at Soil Surface Max (kW m²) is that amount of energy associated with a fire that impinges on the soil surface, Time to Max (h) is the time delay expressed in hours between when the fire begins and when the soil heating reaches its maximum value, and Fire Duration (h) gives the length of time that the fire heats the soil surface); (5) fire type (wildfire, prescribed burn, slash-pile burn and burn-up model, which uses inputs from FOFEM) and simulation time (model run time (h)); (6) soil parameters; (7) start and stop buttons; (8) output soil temperature profile; (9) output fire intensity at soil surface.

Q_F is related to the surface energy balance as:

(2)

\in_{0} (θ_{0}) Q_{F} (t) = \in_{0} (θ_{0}) σ [T_{K0}^{4} - \in_{a} (ρ_{va}) T_{ka}^{4}] + ρ_{a} c_{pa} C_{H0} [T_{0} - T_{a}] + L_{v0}^{⁎} E_{0} + G_{0}

where the subscript 0 refers to the soil surface, and the term on the left-hand side of the equation is the energy absorbed by the soil (assuming that absorptivity and emissivity of the soil are the same). From left to right, the four terms on the right-hand side of Eqn 2 represent net infrared heat loss, convective heat loss, evaporation and soil conductive heat, respectively. ∈₀(θ₀) is the soil emissivity and is a function of the soil moisture, θ₀; σ is the Stefan–Boltzmann constant; ∈_a(ρ_va) is the emissivity of the ambient atmosphere exposed to the soil surface during the fire and is a function of the ambient vapor density ρ_va according to the ‘clear sky’ parameterization of Brutsaert (1984, eqn 6.18): ρ_a = ρ_a(T_K0) = 1.29(ρ_a/ρ_ST)(T_ST/T_K0)(kg m⁻³), where ρ_a is the mass density of the ambient air at the soil surface temperature, T_K0; P_a (Pa) is the ambient pressure, and P_ST = 101 325 Pa and T_ST = 273.15° K are standard atmospheric pressure and temperature; C_H = 0.032 (m s⁻¹) is the transfer coefficient for convective heat from the surface (see Massman 2012, 2015). T_a = T_a(t) (°C), or equivalently T_Ka = T_Ka(t) (K), is the ambient temperature somewhere above the soil surface; $L_{v0}^{⁎} E_{0}$ (W m⁻²) is the rate of soil water evaporation; E₀ (kg m⁻² s⁻¹) is the evaporative mass flux at the surface; and G₀ (W m⁻²) is the soil conductive heat flux and the upper boundary condition for the modeled soil temperatures. E₀ is parameterized as the sum of a diffusional component and an advective component (Massman 2012) as follows:

(3)

E_{0} = C_{E} h_{s0} [ρ_{v0} - ρ_{va} (t)] + C_{U} u_{vl0} ρ_{v0}

where C_E (m s⁻¹) and C_U (dimensionless) are adjustable model transfer coefficients, which were determined empirically to maximize E₀ without destabilizing the model. C_U = 0.125 is associated with the air emanating from the soil with velocity u_vl0 and C_E = 10⁻⁴ m s⁻¹. The surface humidity, h_s0 (dimensionless) is determined from the soil surface temperature and moisture.

A constant heat flux function was used to test the sensitivity of the model to various parameters and to the heating exponential curve (Q_F(t) = Q_final(1 − e^−1t/t_m) W m⁻²) developed by Campbell et al. (1995) and used for the Massman HMV model (2015 version). However, during testing with constant heat flux boundary conditions, an instability was discovered that created a sensitivity of the volumetric moisture content to short time steps (<0.9 s). When a constant heat flux was applied, a sensitivity to time step became apparent, causing an increase in soil moisture. The time step issue led, in turn, to the discovery of an error in the soil conductivity model. The thermal conductivity model was subsequently corrected (see Massman 2021), which eliminated the instability and was an important step in stabilizing the HMV model and improving the observed temperature rise.

The final Massman HMV model was incorporated into the FOFEM with a simple graphical user interface (FOFEM version 6.7, Lutes 2020) (Fig. 1). The latest version of the FOFEM model is available at: https://research.fs.usda.gov/firelab/products/dataandtools/software/fofem/spatialfofem-fire-effects-model (accessed 11 January 2025).

Campbell soil heating model

The Campbell soil heating model (Campbell et al. 1995) has been the standard soil heating model used in FOFEM (Lutes 2020). It was tested using Massman’s (2021) adaptation of the BFD curve (Barnett 2002) to a soil heating function. The BFD curve is used in the Massman HMV model and was also used in the Campbell model to compare its performance between the models.

Description of the datasets used for model validation

Several different independent field datasets were used for model validation. These datasets were collected in field experiments during logging slash-pile burns (residual logging slash-piled with a dozer and subsequently burned), outdoor burn box measurements (controlled experiment with fuel bed built to desired prescription on soil; see the footnote of Table 1 for detailed description), broadcast prescribed fires (drip-torch ignited fire to reduce fuel loadings) and wildfires (lightning-ignited fire) in the western US. Each dataset consists of pre-fire fuel loads, fuel moisture conditions, forest floor characteristics (loading, compositions and moisture) and soil characteristics (texture, moisture). These studied datasets (Table 1) are provided here, and associated metadata are archived and publicly available (Robichaud et al. 2018; USDA Forest Service Rocky Mountain Research Station website: https://research.fs.usda.gov/rmrs/projects/high-soil-temperature-data-archive; accessed 11 January 2025).

Table 1.Description of the independent field datasets used for model parameterization.

Dataset, dates, publication	Location (lat., long.)	Vegetation type	Soil parent material	Thermocouple depths (cm)	Number of thermocouple locations per fire	Pre-fire fuel loads (kg m⁻²)	Fuel moisture conditions	Forest floor or environmental characteristics	Soil characteristics (texture)
Massman 2001–2004	Manitou Experimental Forest, Colorado (39.04°, −105.04°)	Ponderosa pine	Granitic, Pikes Peak Batholith	Surface, duff, 1, 2, 3, 4, 5, 6, 8	2–5	250–300, 450–600	8–10%	Pine slash	Coarse loam
Massman et al. (2010)	Manitou Experimental Forest, Colorado (39.04°, −105.04°)	Ponderosa pine	Granitic, Pikes Peak Batholith	Surface, duff, 1, 2, 3, 4, 5, 6, 8	2–5	250–300, 450–600	8–10%	Pine slash	Coarse loam
Sackett and Haase 1980–2006	Various, Arizona and California (32–41°, −109 to 123°)	Chaparral, pinyon– juniper, various pines	Various	Surface, duff, 2, 4, 10, 20, 30	2–5	14.4	Litter 14.4%, fermented, humus 19.6%	Intact patchy litter	Loam
Sackett and Haase (1992)	Various, Arizona and California (32–41°, −109 to 123°)	Chaparral, pinyon– juniper, various pines	Various	Surface, duff, 2, 4, 10, 20, 30	2–5	14.4	Litter 14.4%, fermented, humus 19.6%	Intact patchy litter	Loam
Busse et al. (2005)	Various ^A, California (38.8–39.2°, −119.9 to 120.2°)	Mixed chaparral and forests, mastication	Granitic	0, 2.5, 5.1, 10.2, 15.2	1–3	1–17	5–9%	Masticated whiteleaf manzanita, 10 cm depth	Clay loam,
Robichaud et al. (2018)	Idaho Panhandle National Forest, Idaho (48.16°, −116.06°)	Grand fir–Douglas fir forest	Metamorphic	1, 2, 3, 4, 6, 8	4	1.1	Duff 4%, litter 7–8.7%	Intact forest floor duff layer, average 7.7 cm depth	Gravelly silt loam

All data are available at https://www.fs.usda.gov/research/rmrs/projects/high-soil-temperature-data-archive; accessed 23 January 2024.

^A Materials for Busse burn box experiments were collected from Whitmore and Challenge, CA. A burn box is a metal frame (1 by 1 m) that contains forest soil, duff (forest floor material) and fuel (loaded at various amounts). Understory vegetation (fuel) was masticated and brought to the Redding Silviculture Laboratory for the experiment. Mineral soil and surface mulch were collected from the Whitmore site.

Selection of the input parameters

The input parameters needed to run the model were obtained, when possible, from the metadata collected during various pile burns, broadcast burns, burn box experiments and wildfires (Robichaud et al. 2018). The Manitou 2004 pile burn data, referred to as Manitou Center, was selected to model soil heating at the center of a slash-pile burn. Burn box measurements were from fuel added to a clay loam soil, Repetition 1, 10% moisture content, in the Busse BB1 file. Broadcast burn measurements were used from Sackett and Haase soil temperature ID #5103_YP, Sackett and Haase2. Of the four datasets collected from Cougar Wildfire, only Transect 1 was suitable for this analysis. The other three were discarded owing to anomalous conditions (preheating of the soil and low soil temperatures).

The field-collected inputs of ambient air temperature, volumetric soil moisture, soil particle density and soil bulk density were used for model parameterization (Table 2). The maximum fire intensity at the soil surface (Q_max, kW m⁻²), the time to maximum intensity (t_max, h) and the burn duration (h) were adjusted at the shallowest field-measured depth to get the best match between the modeled and observed temperatures for each of the models separately and can be found in Table 3. First, the Q_max and t_max were adjusted to match the peak temperature of the field. Afterwards, the burn duration was adjusted to best match the cooling phase. Lastly, all three parameters were slightly adjusted repeatedly to achieve the highest NSE values at the shallowest field-measured depth.

Table 2.Model parameters for each fire type and scenario.

Dataset and scenario	Soil bulk density (g cm⁻³)	Soil particle density (g cm⁻³)	Soil moisture (0–1 cm)	Soil texture	Cover type	Time interval of the recorded temperatures
Manitou Center slash-pile burn	1.3	2.65	0.16	Coarse – loamy	Ponderosa pine savanna	15 s, 2, 30 min
Busse 1 burn box ^A	0.92	2.65	0.05	Coarse – loamy	Douglas fir–sugar pine–tanoak forest	1 min
Sacket and Haase 2 broadcast prescribed burn	1.3	2.65	0.11	Loamy – skeletal	Douglas fir–sugar pine–tanoak forest	37 s
Cougar T1 wildfire	1.25	2.65	0.1	Loamy – skeletal	Grand fir–Douglas fir forest	1 min

^A Busse 1 was modeled using a custom soil model.

Table 3.Heating curve parameters: maximum fire intensity (Q_max), time to maximum intensity (t_max) and duration of the fire (burn duration) for each type of fire and modeled scenario.

Dataset and scenario	Model	Q_max (kW m⁻²)	t_max (h)	Burn duration (h)
Manitou Center slash-pile burn	Massman HMV	16	9.5	39.5
Manitou Center slash-pile burn	Campbell	18	9.5	39.5
Busse 1 burn box	Massman HMV	14	0.6	6.0
Busse 1 burn box	Campbell	16	0.6	7.0
Sacket and Haase 2 broadcast prescribed burn	Massman HMV	6.7	3.1	18.0
Sacket and Haase 2 broadcast prescribed burn	Campbell	8.2	3.8	23.0
Cougar T1 wildfire	Massman HMV	8.0	0.3	12.0
Cougar T1 wildfire	Campbell	9.0	0.6	10.0

Validation simulations were conducted for comparison with soil temperature data from each scenario (Table 2). Owing to a lack of site-specific information about the soils at the Busse burn box experiment, simulations for comparison with the Busse 1 data were run using custom soil models (WesternUS01 coarse loamy) based on Massman’s pile burn dataset from Manitou Experimental Forest. Although several measurements in these datasets are below soil depths of 12 cm, the Campbell model was limited to results at depths above 12 cm owing to constraints in the C++ code. Comparisons with the Campbell model are omitted in those cases. Further simulations were conducted for comparisons with only temperature data because no moisture data were recorded in Sackett and Haase’s broadcast prescribed fire, Busse’s burn box and Cougar Wildfire.

Data analysis and model evaluation

The accuracy of the Massman HMV model was assessed by comparing modeled soil temperatures with field measurements of soil temperature for four scenarios: a slash-pile burn, burn box, broadcast prescribed fire and wildfire. We also compared the Campbell model with field data to determine if the Massman HMV model provided improved prediction of soil heating. Statistics used in the comparison include: the Nash–Sutcliffe Efficiency (NSE) (Eqn 4), the Root Mean Squared Deviation (RMSD) (Eqn 5), the Mean Absolute Error (MAE) (Eqn 6), the Centered pattern RMS (CRMS) (Eqn 7) and the Correlation among the data (Corr) (Eqn 8), where M is the modeled value, M̅ is the mean of the modeled values, O is the observed data, O̅ is the mean of the observed data, and N is the total number of observations.

(4)

NSE = 1 - \frac{\sum_{n = 1}^{N} {(M_{n} - O_{n})}^{2}}{\sum_{n - 1}^{N} {(O_{n} - {\bar{O}}_{n})}^{2}}

(5)

RMSD = \sqrt{\frac{\sum_{n = 1}^{N} {(M_{n} - O_{n})}^{2}}{N}}

(6)

MAE = \frac{\sum_{n = 1}^{N} | M_{n} - O_{n} |}{N}

(7)

CRMS = {(\frac{1}{n} {\sum_{n = 1}^{N} [(M_{n} - \bar{M}) - (O_{n} - \bar{O})]}^{2})}^{1 / 2}

(8)

Corr = \frac{{\sum (M - \bar{M}) (O - \bar{O})}^{}}{\sqrt{\sum {(M - \bar{M})}^{2} {(O - \bar{O})}^{2}}}

The NSE values range from −∞ to 1 (Nash and Sutcliffe 1970). A NSE of 1 indicates a perfect match of the modeled data to the field observation data. However, an NSE of 0 indicates that the model is no better than using the mean to predict the data. When NSE values are below 0, they indicate that the model is not producing accurate data compared with the measured values. The RMSD, which is the square root of the average of squared errors, was used to measure the differences between the modeled and observed data. RMSD values close to 0 indicate a better fit to the data.

The MAE indicates the difference between two continuous variables, which in this case are the modeled and observed soil temperature data at various depths. The correlation coefficient alone does not allow determination of the amplitude of variation of two patterns, so the CRMS is used to accurately quantify the differences. The use of the correlation coefficient and the CRMS together provides complementary information regarding the correspondence between two patterns (Taylor 2001).

The complete statistical results for the soil temperature model comparisons are provided in the Appendix in Tables A1–A5. Important statistics such as NSE and RMSD are provided within selected figures.

Results

Comparisons with slash-pile burn data

Model results from Manitou slash-pile burns were compared using soil temperature measurements at the pile center (Fig. 2). Adjusted heating parameters for this pile burn indicated a maximum fire intensity (Q_max) of only 16–18 kW m⁻² even with the high fuel load (Table 3). This is likely due to fuel arrangement, and to soil incorporated in the pile by the dozer. Results from the Massman HMV and Campbell models compared well with field measurements of soil temperature at 0, 2 and 5 cm depths (Fig. 2), though the Massman HMV model showed lower errors and greater NSE than the Campbell model (Table A1). When comparing the predicted soil temperatures, the higher NSE values obtained for the Massman HMV model (NSE = 0.94 at 0 cm) indicate that it better predicts the soil temperature profile at the center of the pile than does the Campbell model (NSE = 0.91) at the soil surface (Fig. 2). The lower RMSD value (38.33) of the Massman HMV model at the soil surface also indicates a higher accuracy compared with the Campbell model (RMSD = 46.6) (Table A1).

Fig. 2.

Comparison of (a) Massman HMV model and (b) Campbell model with observed data from the Manitou Center slash-pile burn at 0, 2, 5 and 10 cm depth, with dashed lines representing the observed data and solid lines representing the modeled data. NSE is Nash–Sutcliffe Efficiency and RMSD is Root Mean Squared Deviation.

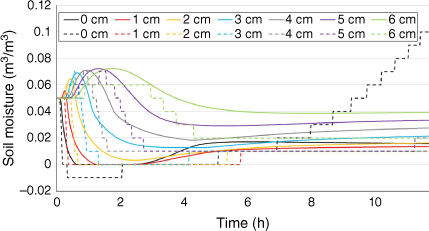
Both the Massman HMV and Campbell models simulated soil moistures below the center of the pile better at shallow (5 cm) depths than they did at greater (12–15 cm) depths, with NSEs of 0.83 and 0.76, respectively (Fig. 3, Table A2). Neither model performed well when simulating soil moisture at greater soil depths (Fig. 3). The Massman HMV model showed an increase in soil moisture at 15–19 h as a heat pulse greater than 100°C occurred at ~14 h, driving evaporated moisture downward before it dissipated over time. The statistical analysis indicates a better prediction of soil moisture data at 5 cm by the Massman HMV model, although Campbell model soil moisture did reasonably well at 5 cm but had poor correlations at greater depths (Table A2).

Fig. 3.

Comparison of the measured soil moisture from Manitou Center slash-pile burn (dashed lines) with the soil moisture values modeled by Massman HMV model (solid lines) and Campbell model (dots) at 5 and 15 cm depth.

Comparisons with burn box and broadcast prescribed burn data

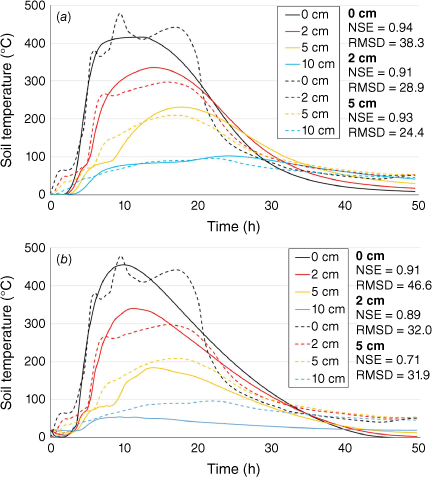
Comparison of model output with the Busse (burn box) and Sackett and Haase (broadcast prescribed burn) experiments demonstrates a better model accuracy for broadcast prescribed fires than for controlled experiments. In comparison with measured surface temperatures in the Busse 1 burn box data, the Massman HMV model shows better accuracy (NSE of 0.92) than the Campbell model (NSE of 0.87) (Table A3 and Fig. 4). Although at 2.5 and 5.1 cm both models predicted higher temperatures than observed (Fig. 4), the Massman HMV model performed well at 10.2 cm (NSE of 0.76, Corr of 0.94) (Table A3). Using the Sackett and Haase 2 prescribed fire dataset, and similarly to previous cases, the Massman HMV model data showed higher NSE than the Campbell model (Fig. 5). Although the accuracy of the Massman HMV model slightly decreased with depth, it performed better than the Campbell model for 1.9 and 2.5 cm depths (Table A4). The Massman HMV model provides more plausible estimates of soil moisture content than does the Campbell model, in comparison with both the Busse 1 burn box dataset and the Sackett and Haase 2 prescribed fire dataset (Figs 6 and 7).

Fig. 4.

Comparison of (a) Massman HMV model and (b) Campbell model temperatures with the observed soil temperatures from the Busse 1 burn box data at 0, 2.5, 5.1, 10.2 cm depth, with dashed lines representing the observed data and solid lines representing the modeled data. NSE is Nash–Sutcliffe Efficiency and RMSD is Root Mean Squared Deviation.

Fig. 5.

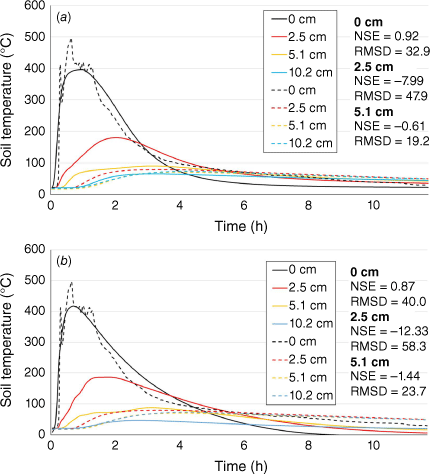
Comparison of (a) Massman HMV model and (b) Campbell model temperatures with the observed soil temperatures from the Sackett and Haase 2 broadcast prescribed burn data at 1.9 and 2.5 cm depth, with dashed lines representing the observed data and solid lines representing the modeled data. NSE is Nash–Sutcliffe Efficiency and RMSD is Root Mean Squared Deviation.

Fig. 6.

Comparison of simulated soil moistures with the Busse 1 burn box conditions: Massman HMV model (solid lines) and Campbell model (dashed lines).

Fig. 7.

Comparison of simulated soil moistures with the Sackett and Haase 2 broadcast prescribed burn conditions: Massman HMV model (solid lines) and Campbell model (dashed lines).

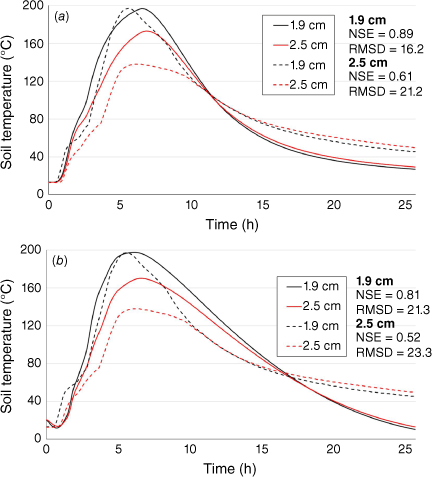
Comparisons with wildfire data

The Massman HMV model produced temperatures with better correspondence to the Cougar 1 Wildfire dataset than did the Campbell model (Table A5) for all the studied depths, specially at a depth of 1 cm (NSE of 0.97). At 1 cm, the accuracy of Campbell model was high (NSE of 0.85), denoting the quality of its prediction, but it gradually decreased with depth. However, the NSE of the Massman HMV model remained above 0.6 for all the studied depths, except for 4 cm (NSE of 0.42), where the modeled temperature reached its maximum value much before the observed data (Fig. 8). The correlation values between modeled and observed data remained high for both models (Corr >0.9), with the Massman HMV model producing slightly higher values for all the studied depths except 4 cm (Table A5).

Fig. 8.

Comparison of (a) Massman HMV model and (b) Campbell model temperatures with the observed soil temperatures from the Cougar Fire Transect 1 dataset at 1, 2, 3, 4, 5, 6 and 8 cm depth, with dashed lines representing the observed data and solid lines representing the modeled data. NSE is Nash–Sutcliffe Efficiency and RMSD is Root Mean Squared Deviation.

Discussion

The Massman HMV model was consistently more accurate than the Campbell model. The soil temperature profiles predicted by the Massman HMV model were most accurate for center pile burns (NSE of 0.94 at 0 cm, 0.91 at 2 cm), burn box burns (NSE of 0.92 at 0 cm), broadcast prescribed burns (NSE of 0.89 at 1.9 cm) and wildfires (NSE of 0.97 at 1 cm). The Massman HMV and Campbell models were also reasonable accurate when modeling 5 cm depth moisture at the center of pile burns (NSE of 0.83 and 0.76, respectively). The higher accuracy of the Massman HMV results is likely because of improvements in soil water movement (hydraulic conductivity function driven by a gradient in soil moisture potential) and better parameterizations of thermophysical properties of water and water vapor in the vertical profile with uniform heat (Massman 2021).

The Massman HMV model was able to predict near-surface temperatures owing to its ability to model time lag in actual soil heating in burn boxes and prescribed fires, but the mid-depth temperatures were not as accurate. The prescribed burn and burn box datasets were modeled with custom soil data (WesternUS01) and performed better near the soil surface than at lower depths. Predicting the time lag of the heat pulse in the soil at greater depths is challenging as the thermal conductivity of each soil texture can vary even over micro-scale measurements (Horton and Ochsner 2011).

The NSE values for the Massman HMV model were lower for the Busse 1 burn box than for other burn types (NSE of 0.92 at the surface and −7.99 at 2.5 cm). This decrease in the accuracy of the Massman HMV model is probably due to the particular conditions of the experimental burning; with a small burn box, the slash fuel load was rapidly consumed, generating a peak of heat at the surface that was barely transmitted to deeper layers owing to the low bulk density of the soil, which was hand-packed, making it porous with air voids, thus reducing heat transmission downwards. Neither of the models was able to predict this characteristic.

In comparison with the Campbell model, the Massman HMV model provides improved modeling of soil moisture flux driven by heating. The model improvement is likely due to the incorporation of liquid water transport via the hydraulic conductivity function and its dynamic representation of the physics describing moisture changes (Massman 2021). Instead of the stair-step changes in soil moisture produced by the Campbell model (Fig. 3), the Massman HMV model generates Weibull-shaped soil moisture curves that mimic observed soil moisture changes.

Although we were able to test the Massman HMV model against only one dataset with soil moisture (Manitou slash-pile burn), it showed promising results, with an NSE of 0.83 at 5 cm (Fig. 3, Table A2). This also encourages further research into the dynamics of soil moisture phase change during extreme heating events. The Massman HMV model performs better than the Campbell model, although the statistics related to soil moisture (Table A2) are not as compelling as those for soil temperature (Table A1). Both models predicted soil moisture reasonably well, with a slight increase at 6–7 h into the burn as temperatures at 5 cm approached 100°C (Fig. 3). Both models performed better at 5 cm depths than at 15 cm. Accuracy in the prediction of temperatures near the soil surface is particularly important because higher temperatures in this region could cause the formation of a water-repellent layer that affects runoff and nutrient concentrations and availability (Mataix-Solera and Doerr 2004). Higher temperatures (>400°C) near the soil surface could also cause water-repellent layers to disappear (Robichaud and Hungerford 2000; Badía et al. 2017). Additionally, accurate modeling of soil moisture near the surface is informative because the near-surface soil contains seed sources and hosts high microbial activity (Girona-García et al. 2019) that is important for long-term soil health.

The soil moisture outputs from the Massman HMV and Campbell models were directly compared from the Busse 1 burn box model and the Sackett and Haase 2 prescribed fire model (Figs 6 and 7). The Massman HMV model produces Weibull-shaped moisture curves in contrast to the stair-stepped curves produced by the Campbell model. In both cases, the Massman HMV model produced a transient pulse of increased moisture as water was evaporated at the front of the downward-propagating heat wave (Figs 6 and 7).

The enhancements described in this study were found to significantly increase the accuracy of both the Massman HMV and Campbell models of soil heating, providing better predictions of soil temperature peaks and durations above key threshold temperatures. In the case of the Massman HMV model, this is likely related to parameterization of the soil moisture evaporation and condensation, and soil moisture movement in response to extreme temperature gradients. The methods of Blagojević and Pešić (2011) were used to define a new time–temperature curve that describes smoldering fire conditions, rather than flash or peak temperature conditions, and were similar to the methods used to create BFD curves. The Blagojević and Pešić (2011) methods were created to evaluate compartment fire situations, not wildfires, but the similarity of their approach reinforces the observed heat pulse phenomena observed.

Predicting elevated soil temperatures and duration of these temperatures may be of great utility to managers who need to assess the potential for damage to soils through second-order effects after the application of common forest management treatments such as prescribed burning or slash-pile burns. The timing of ignition of slash-pile burns, for example spring versus fall (autumn) burns (high vs low soil moistures), can now be considered and provide guidance on expected maximum and duration of high temperatures using the Massman HMV model.

Conclusions

Accurate modeling of soil temperatures is essential for predicting first- and second-order effects of soil heating in wildland fires. Using previously collected field datasets, this evaluation suggests that the Massman HMV model performs better than the Campbell model in simulating soil temperatures and soil moisture transport for a variety of fuel and initial moisture conditions in slash-pile burns, burn boxes, prescribed fires and wildfires. The model estimates for all four near-surface temperatures datasets were more accurate than those for deeper soil layers owing soil moisture evaporation and condensation processes at greater depth. However, the Campbell model performs satisfactorily for shallow soil depths. In addition, it is less computationally expensive than the more sophisticated Massman HMV model. The Massman HMV model has been incorporated into FOFEM (ver. >6.7) for modeling fire effects and is applicable under broader-scale situations such as wildfires, prescribed fires and pile burns. This tool allows managers to compare soil heating effects for various forest management activities.

The scarcity of combined soil temperature and moisture measurements during fires prevents further evaluation of the soil moisture modeling component of this study. Soil moisture may be important in modeling the formation of water-repellent layers as well as seed source viability and microbial activity. Future work should include improving measurements of soil moisture concurrent with soil heating.

Data availability

The data that support this study are available in the Forest Service Rocky Mountain Research Station web site at https://research.fs.usda.gov/rmrs/projects/high-soil-temperature-data-archive (accessed 11 January 2025).

Conflicts of interest

The authors declare they have no conflicts of interest.

Declaration of funding

Funding for this project was provided in part by USDA Forest Service Rocky Mountain Research Station, and the US Department of Interior USDA Forest Service Joint Fire Science Program (15-1-05-11). A G-G is funded by a ‘Ramón y Cajal’ fellowship (RYC2021-031262-I) and the EROS INK project (PID2023-146991NA-100) from the Ministry of Science, Innovation and Universities (Spanish Government). A A-L is funded by a DGA predoctoral research grant (BOA20200713012) financed by the Government of Aragón, Spain.

References

Agbeshie AA, Abugre S, Atta-Darkwa T, Awuah R (2022) A review of the effects of forest fire on soil properties. Journal of Forestry Research 33, 1419-1441.
| Crossref | Google Scholar |

Albini F, Amin MR, Hungerford RD, Frandsen WH, Ryan KC (1996) Models for fire-driven heat and moisture transport in soils. General Technical Report INT GTR-335. (USDA Forest Service, Intermountain Research Station: Ogden, UT)

Alcañiz M, Outeiro L, Francos M, Úbeda X (2018) Effects of prescribed fires on soil properties: a review. Science of The Total Environment 613–614, 944-957.
| Crossref | Google Scholar | PubMed |

Armas-Herrera CM, Martí C, Badía D, Ortiz-Perpiñá O, Girona-García A, Porta J (2016) Immediate effects of prescribed burning in the Central Pyrenees on the amount and stability of topsoil organic matter. Catena 147, 238-244.
| Crossref | Google Scholar |

Aston AR, Gill AM (1976) Coupled soil moisture, heat and water vapor transfers under simulated fire conditions. Australian Journal of Soil Research 14, 55-66.
| Crossref | Google Scholar |

Badía D, López-García S, Martí C, Ortíz-Perpiñá O, Girona-García A, Casanova-Gascón J (2017) Burn effects on soil properties associated to heat transfer under contrasting moisture content. Science of The Total Environment 601–602, 1119-1128.
| Crossref | Google Scholar | PubMed |

Bao T, Lui S, Qin Y, Liu ZL (2020) 3D modeling of coupled soil heat and moisture transport beneath a surface fire. International Journal of Heat and Mass Transfer 149, 119163.
| Crossref | Google Scholar |

Barnett CR (2002) BFD curve: a new empirical model for fire compartment temperatures. Fire Safety Journal 37, 437-463.
| Crossref | Google Scholar |

Blagojević MD, Pešić DJ (2011) A new curve for temperature–time relationship in compartment fire. Thermal Science 15(2), 339-352.
| Crossref | Google Scholar |

Bova AS, Bohrer G, Dickinson MB (2011) A model of gas mixing into single-entrance tree cavities during wildland fires. Canadian Journal of Forest Research 41, 1659-1670.
| Google Scholar |

Brady MK, Dickinson MB, Miesel JR, Wonkka CL, Kavanagh KL, Lodge AG, Rogers WE, Starns HD, Tolleson DR, Treadwell ML, Twidwell D, Hanan EJ (2022) Soil Heating in Fire (SheFire): a model and measurement method for estimating soil heating and effects during wildland fires. Ecological Applications 32, e2627.
| Crossref | Google Scholar | PubMed |

Brutsaert W (1984) ‘Evaporation into the atmosphere: Theory, history and applications.’ (D. Reidel Publishing Co., Dordrecht: Netherlands) 10.1007/978-94-017-1497-6

Busse MD, Hubbert KR, Fiddler GO, Shestak CJ, Powers RF (2005) Lethal soil temperatures during burning of masticated forest residues. International Journal of Wildland Fire 14, 267-276.
| Crossref | Google Scholar |

Campbell GS, Jungbauer JD, Jr, Bidlake WR, Hungerford RD (1994) Predicting the effect of temperature on soil thermal conductivity. Soil Science 158(5), 307-313.
| Crossref | Google Scholar |

Campbell GS, Jungbauer JD, Jr, Bristow KL, Hungerford RD (1995) Soil temperature and water content beneath a surface fire. Soil Science 159(6), 363-374.
| Crossref | Google Scholar |

Certini G (2005) Effects of fire on properties of forest soils: a review. Oecologia 143, 1-10.
| Crossref | Google Scholar | PubMed |

Choczynska J, Johnson EA (2009) A soil heat and water transfer model to predict belowground grass rhizome bud death in a grass fire. Journal of Vegetation Science 20, 277-287.
| Crossref | Google Scholar |

DeBano LF, Savage SM, Hamilton DA (1976) The transfer of heat and hydrophobic substances during burning. Soil Science Society of America Journal 40, 779-782.
| Crossref | Google Scholar |

DeBano LF, Neary DG, Ffolliott PF (1998) ‘Fire’s effects on ecosystems.’ 331 p. (John Wiley & Sons: New York, NY, USA)

Dlapa P, Simkovic I, Jr, Doerr SH, Simkovic I, Kanka R, Mataix-Solera J (2008) Application of thermal analysis to elucidate water-repellency changes in heated soils. Soil Science Society of America Journal 72, 1-10.
| Crossref | Google Scholar |

Durany J, Fraga B, Vargas F (2010) Physical modelling and numerical simulation of soil heating under forest fire conditions. In ‘Forest Fire Research, edited by DX Viegas, ADAI/CEIF’, Coimbra, Portugal, paper no. 263 CD. (Forest Fire Research Center, University of Coimbra, Coimbra, Portugal)

Girona-García A, Ortiz-Perpiñá O, Badía-Villas D (2019) Dynamics of topsoil carbon stocks after prescribed burning for pasture restoration in shrublands of the Central Pyrenees (NE Spain). Journal of Environmental Management 233, 695-705.
| Crossref | Google Scholar | PubMed |

Horton R, Ochsner TE (2011) Soil thermal regime. In ‘Handbook of soil sciences: properties and processes’, 2nd edn. Ch. 9. (Eds PM Huang, Y Li, ME Sumner) pp. 9–1 to 9–23. (CRC Press: Boca Raton, FL, USA)

Lutes DC (2020) FOFEM 6.7 First Order Fire Effects Model Ver. 6.7. (USDA Forest Service, Rocky Mountain Research Station, Fire Modeling Institute: Missoula, MT) Available at https://www.firelab.org/project/fofem-fire-effects-model

Martin, RE, Cushwa, CT (1966) Effects of heat and moisture on leguminous seed. In ‘Proceedings, 5th Tall Timbers Fire Ecology Conference’. pp. 159–175. (Tall Timbers: Tallahassee, FL, USA)

Massman WJ (2012) Modelling soil heating and moisture transport under extreme conditions: forest fires and slash pile burns. Water Resources Research 48, W10548.
| Crossref | Google Scholar |

Massman WJ (2015) A non-equilibrium model for soil heating and moisture transport during extreme surface heating: the soil (heat–moisture–vapor) HMV-Model Version 1. Geoscience Model Development 8, 3659-3680.
| Crossref | Google Scholar |

Massman WJ (2021) The challenges of an in situ validation of a non-equilibrium model of heat and moisture dynamics during fires. Hydrology and Earth System Sciences 25, 685-709.
| Crossref | Google Scholar |

Massman WJ, Frank JM, Mooney SJ (2010) Advancing investigation and physical modelling of First-Order Fire Effects on soils. Fire Ecology 6(1), 36-54.
| Crossref | Google Scholar |

Mataix-Solera J, Doerr SH (2004) Hydrophobicity and aggregate stability in calcareous topsoils from fire-affected pine forests in southeastern Spain. Geoderma 118, 77-88.
| Crossref | Google Scholar |

Nash JE, Sutcliffe JV (1970) River flow forecasting through conceptual models. Part I—a discussion of principles. Journal of Hydrology 10, 282-290.
| Crossref | Google Scholar |

Neary DG, Ryan KC, DeBano LF (2005) Wildland fire in ecosystems, effects of fire on soil and water. General Technical Report RMRS-GTR042-Vol.4. (USDA Forest Service, Rocky Mountain Research Station: Ogden UT) 10.2737/RMRS-GTR-42-V4

Novak MD (2010) Dynamics of the near-surface evaporation zone and corresponding effects on the surface energy balance of a drying bare soil. Agricultural and Forest Meteorology 150, 1358-1365.
| Crossref | Google Scholar |

Robichaud PR, Hungerford RD (2000) Water repellency by laboratory burning of four northern Rocky Mountain forest soils. Journal of Hydrology 231–232, 207-219.
| Crossref | Google Scholar |

Robichaud PR, Massman WJ, Lesiecki ML (2018) ‘High soil temperature data archive from prescribed fires and wildfires database.’ (USDA Forest Service, Rocky Mountain Research Station: Ft. Collins, CO) Available at https://research.fs.usda.gov/rmrs/projects/high-soil-temperature-data-archive

Sackett SS, Haase SM (1992) Measuring soil and tree temperatures during prescribed fires with thermocouple probes. General Technical Report PSW-GTR-131. 15 p. (USDA Forest Service, Pacific Southwest Research Station: Berkeley, CA)

Santín C, Doerr SH (2016) Fire effects on soils: the human dimension. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences 371, 20150171.
| Crossref | Google Scholar | PubMed |

Smits KM, Cihan A, Soshihiro T, Illangasekare TH (2011) Evaporation from soils under thermal boundary conditions: experimental and modelling investigation to compare equilibrium- and non-equilibrium-based approaches. Water Resources Research 47, W05540.
| Crossref | Google Scholar |

Taylor KE (2001) Summarizing multiple aspects of model performance in a single diagram. Journal of Geophysical Research 106, 7183-719.
| Crossref | Google Scholar |

Appendix

The Massman HMV soil heating model is fully incorporated into FOFEM (ver. 6.7 or greater; Lutes 2020). This appendix provides a short description of the basic physical principles used to develop the model; however, for complete details, the reader is directed to Massman (2021). The Massman HMV model is composed of the three coupled partial differential conservation equations, namely the conservation of energy, soil liquid water and soil water vapor.

The conservation of energy is (Massman 2021, eqn 1):

C_{s} \frac{\partial T}{\partial t} - \frac{\partial}{\partial z} [λ s \frac{\partial T}{\partial z}] = - L_{v} S_{v} + W S_{w} \equiv - L_{v} \times S_{v}

where C_s (J m⁻³ K⁻¹) is the volumetric specific heat of the soil, such that C_s = C_s (T, θ) is a function of both temperature T (°C) and volumetric soil moisture, θ (m³ m⁻³), t (s) is time, z (m) is soil depth and λ_s (W m⁻¹ K⁻¹) is soil thermal conductivity, such that λ_s = λ_s (T, θ, ρ_v); L_v = L_v(T_K) (J kg⁻¹) is the enthalpy of vaporization and – L_vS_v represents the change in enthalpy associated with evaporation or condensation. S_v = S_v(T_K, θ, ψ, ρ_v) is the source term for water vapor and is discussed in more detail in Massman (2021). W S_w is the change in enthalpy associated with the heat of wetting (also termed the heat of immersion), where W (J kg⁻¹) is the heat of wetting and S_w (kg m⁻³ s⁻¹) is the source term for water liquid, or equivalently the sink term for water vapor, i.e. S_w ≡ −S_v. W can be interpreted as the additional enthalpy of vaporization that is required to break the electrostatic bonds between molecular water and the soil mineral surfaces and for modeling purposes, W = ψ.

The conservation of liquid water is as follows (Massman 2021, eqn 2):

ρ_{w} \frac{\partial θ}{\partial t} - ρ_{w} \frac{\partial}{\partial z} [K_{n} \frac{\partial ψ_{n}}{\partial_{z}} + K_{H} - V_{θ, surf}] = - S_{v}

where ρ_w = ρ_w(T_K) (kg m⁻³) is the density of liquid water, and ψ_n (dimensionless) is the non-dimensional form of ψ, i.e. ψ_n = ψ/ψ_*, where ψ_* = −10⁶ J kg⁻¹ is the nominal soil water potential of oven-dried soil (Campbell et al. 1995). K_n = K_n(T_K, ψ_n, θ) (m² s⁻¹) is the hydraulic diffusivity, K_H = K_H(T_K, ψ_n, θ) (m s⁻¹) is the hydraulic conductivity, and V_θ,surf = V_θ,surf (T_K, θ) (m s⁻¹) is the velocity of liquid water associated with surface diffusion of water. The hydraulic conductivity functions (Massman 2021, eqn 3), K_n (T_K, ψ_n, θ) and K_H (T_K, ψ_n, θ), are given as follows:

K_{n} = \frac{K_{I} K_{R} ρ_{w}}{μ_{w}} ψ_{⁎} and K_{H} = \frac{K_{I} K_{R} ρ_{w}}{μ_{w}} g

where µ_w = µ_w(T_K) (P_a s) is the viscosity of water, and g = 9.81 m s⁻² is the acceleration due to gravity. K_I (m²) is the intrinsic permeability of the soil – here assumed to be constant and uniform throughout the soil profile. K_R = K_R (θ, ψ_n, T_K) (dimensionless) is the relative hydraulic conductivity (used to describe capillary flow in soils). The model for intrinsic permeability is K_I = (6.17 ×10⁻⁴)d_g², where d_g (m) is the mean soil particle diameter.

The conservation of water vapor is given as follows (Massman 2021, eqn 4):

\frac{\partial (η - θ) ρ_{v}}{\partial t} - \frac{\partial}{\partial z} [D_{ve} \frac{\partial ρ_{v}}{\partial z} - (η - θ) u_{vl} ρ_{v}] = S_{v}

where η (m³ m⁻³) is the total soil porosity, assumed to be temporally constant and spatially uniform, and (η − θ) (m³ m⁻³) is the soil’s air-filled porosity. D_ve = D_ve(T_K, ψ, ρ_v) (m s⁻¹) is the (equivalent) molecular diffusivity associated with the diffusive transport of water vapor in the soil’s air-filled pore space, where D_ve includes the enhancement factor developed by Campbell et al. (1995).

The model includes improvements to the non-equilibrium vapor source term from Massman (2015, eqn 10), who adapted the Hertz–Knudsen equation to develop a new version of the non-equilibrium model parameter, S_v (dimensionless):

S_{v} = S_{⁎} \sqrt{\frac{R T_{K}}{M_{w}}} (A_{wa} (θ) K_{e} ρ_{v, eq} - A_{wa, dr y} K_{c} ρ_{v})

where K_e ≡ 1 has been retained – as has the original formulation for A_wa (Massman 2015), as follows:

A_{wa} (θ) = S_{w} {(1 - S_{w})}^{a 1} + a_{2} {[S_{w} (1 - S_{w})]}^{a 3}

where S_w = θ/η is the soil water saturation and dimensionless parameters a₁ = 50 (rather than the original value of 40), a₂ = 0.003 and a₃ = 1/8. This value for the parameter a₁ was chosen so that the maximum value of A_wa occurs at S_w ≈ 0.02 (=1/a₁) and is assumed to be where the soil surfaces are covered by a monolayer of water. A_{wa, dry} ≡ A_wa(θ), as long as S_w ≤ 1/a₁, and A_{wa, dry} ≡ max(A_wa) whenever S_w 1/a₁. In other words, A_wa,dry differs from A_wa whenever the soil moisture is so low that the soil particle surfaces are covered by, at most, a monolayer of water. Empirical tuning of S_* and E_av, after implementing the other changes, yielded 0.01 ≤ S_* ≤ 0.1 and E_av = 10 kJ mol⁻¹. Together, these changes in S_v improved the model’s stability and robustness.

Other improvements were to the thermal conductivity (λ_s, W m⁻¹ K⁻¹) and high-temperature thermal (infrared) radiant energy transfer within soil pore space, and are described in detail in Massman (2021, section 2.3). Basically, the vapor ‘distillation’ term (λ_v∗), which accounts for the influence of evaporation, transport and condensation of water vapor, was simplified. An explicit temperature-dependent thermal conductivity for mineral soil (quartz) and an approximation for the soil particle density were also included.

The forcing function that drives the model is the energy that is input to the soil at its surface, denoted by Q_F(t) (W m⁻²). How that energy is divided between net infrared heat loss, convective heat loss, evaporation and soil conductive heating is expressed by the surface energy balance and the upper boundary conditions. For example, beneath a burning slash-pile, surface heating may be combination of radiation and conduction; it may change over time as the pile burns and as the ash accumulates and, at later stages of the burn, as the pile collapses. In the case of a moving fire front, radiant energy is clearly a major driver, but thermal instabilities drive circulations ahead and behind the fire that input energy into the soil when these circulations force hot air into contact with the soil, which may cause direct ignition of soil biomass ahead of the flame front as well as vaporizing water. As the fire front passes, the forcing is likely to be a combination of conduction and radiation and possibly convection, whereas, after the fire front, conduction is the major forcing in areas covered with burning biomass, and radiant energy and convection in areas free of burning biomass. The lower boundary condition is the same pass-through or extrapolative boundary condition that was used in Massman (2012, 2015), i.e. the second derivative, ∂²/∂z². The lower boundary is 0.60 m below the surface. This pass-through boundary condition is used because, for field-based applications, the lower boundary condition will never be known, so it must be placed at a depth where it will not influence the model predictions within the upper few centimeters of the soil.

Table A1.Temperature statistical tests results obtained when comparing Massman HMV model and Campbell model with Manitou Center slash-pile dataset for selected soil depths.

	Massman HMV model				Campbell model
Soil depth	0 cm	2 cm	5 cm	10 cm	0 cm	2 cm	5 cm	10 cm
NSE	0.94	0.91	0.74	0.74	0.91	0.89	0.71	−1.40
RMSD	38.33	28.85	24.39	11.72	46.61	31.93	31.93	35.26
MAE	32.17	26.03	20.52	9.04	39.77	27.10	29.77	32.17
Corr	0.98	0.99	0.96	0.93	0.96	0.98	0.97	0.66
CRMS	33.97	28.85	24.38	10.96	45.61	31.14	13.39	17.25

Nash–Sutcliffe Efficiency (NSE), Root Mean Squared Difference (RMSD), Mean Absolute Error (MAE), Correlation (Corr) and Centered Pattern RMS (CRMS).

Table A2.Moisture statistical results obtained when comparing Massman HMV model and Campbell model with Manitou Center slash-pile dataset for selected soil depths.

	Manitou Center
	Massman HMV model		Campbell model
Soil depth	5 cm	15 cm	5 cm	12 cm
NSE	0.83	−31.77	0.76	−39.67
RMSD	0.02	0.08	0.03	0.09
MAE	0.01	0.07	0.02	0.08
Corr	0.93	−0.54	0.91	−0.74
CRMS	0.02	0.03	0.02	0.03

Nash–Sutcliffe Efficiency (NSE), Root Mean Squared Difference (RMSD), Mean Absolute Error (MAE), Correlation (Corr) and Centered Pattern RMS (CRMS). The lowest modeled depth of the Campbell model, 12 cm, was used for this comparison. The Campbell model results at 12 cm would not be expected to differ greatly from those at 15 cm.

Table A3.Temperature statistical test results obtained when comparing Massman HMV model and Campbell model with field-measured data for selected soil depths for Busse 1 burn box dataset.

	Busse 1
	Massman HMV model
Soil depth	0 cm	2.5 cm	5.1 cm	10.2 cm	15.2 cm
NSE	0.92	−7.99	−0.61	0.76	0.65
RMSD	32.89	47.92	19.23	7.65	3.0
MAE	26.73	34.25	13.50	7.05	2.2
Corr	0.97	0.37	0.48	0.94	0.99
CRMS	29.52	44.09	17.01	5.94	3.0

	Campbell model
Soil depth	0 cm	2.5 cm	5.1 cm	10.2 cm
NSE	0.87	−12.33	−1.44	−2.30
RMSD	40.04	58.34	23.69	28.09
MAE	35.52	47.24	20.74	25.42
Corr	0.96	0.33	0.34	0.56
CRMS	36.27	56.87	23.301	12.83

Nash–Sutcliffe Efficiency (NSE), Root Mean Squared Difference (RMSD), Mean Absolute Error (MAE), Correlation (Corr) and Centered Pattern RMS (CRMS).

Table A4.Temperature statistics test results obtained when comparing Massman HMV model and Campbell model with field-measured data for selected soil depths for Sackett and Haase 2 broadcast prescribed fire dataset using the Western US01 soil parameters.

	Sackett and Haase 2
	Massman HMV model		Campbell model
Soil depth	1.9 cm	2.5 cm	1.9 cm	2.5 cm
NSE	0.89	0.61	0.81	0.52
RMSD	16.23	21.17	21.34	23.32
MAE	14.65	18.87	18.52	20.72
Corr	0.98	0.94	0.96	0.96
CRMS	15.33	21.17	21.19	22.98

Nash–Sutcliffe Efficiency (NSE), Root Mean Squared Difference (RMSD), Mean Absolute Error (MAE), Correlation (Corr) and Centered RMS (CRMS).

Table A5.Temperature statistics obtained when comparing Massman HMV model and Campbell model for the Cougar 1 Wildfire.

	Cougar Transect 1
	Massman HMV model
Soil depth	1 cm	2 cm	3 cm	4 cm	6 cm	8 cm
NSE	0.97	0.90	0.61	0.42	0.66	0.78
RMSD	8.3	9.8008	14.67	14.73	9.04	6.86
MAE	7.47	9.17	12.97	13.07	8.34	6.06
Corr	0.99	0.98	0.96	0.944	0.97	0.99
CRMS	7.8	6.23	9.04	8.71	5.09	3.73

	Cougar Transect 1
	Campbell model
Soil depth	1 cm	2 cm	3 cm	4 cm	6 cm	8 cm
NSE	0.85	0.80	0.40	−0.25	−0.55	−0.93
RMSD	17.22	13.60	18.08	21.65	19.18	20.26
MAE	14.72	11.1	17.26	20.89	18.78	19.61
Corr	0.98	0.98	0.97	0.97	0.96	0.95
CRMS	17.19	8.37	5.79	6.31	5.12	6.42

Nash–Sutcliffe Efficiency (NSE), Root Mean Squared Difference (RMSD), Mean Absolute Error (MAE), Correlation (Corr) and Centered RMS (CRMS) for the Cougar Fire Transect 1 dataset.

The Massman HMV model (imbedded in FOFEM version >6.7, https://research.fs.usda.gov/firelab/products/dataandtools/software/fofem/spatialfofem-fire-effects-model) is publicly available. The actual code (MALAB 2017) is also publicly available via the Fort Collins, CO, Forest Service Research Data Archive at https://www.fs.usda.gov/rds/archive/Catalog/RDS-2020-0077 (Accessed: January 2025; Massman 2021).