Assessing the predictive efficacy of six machine learning algorithms for the susceptibility of Indian forests to fire
Laxmi Kant Sharma A , Rajit Gupta
A , Rajit Gupta  A * and Naureen Fatima A
A * and Naureen Fatima A
A Remote Sensing & GIS Lab, Department of Environmental Science, School of Earth Sciences, Central University of Rajasthan, N.H.-8, Bandarsindri-305817, Ajmer, Rajasthan, India.
International Journal of Wildland Fire 31(8) 735-758 https://doi.org/10.1071/WF22016
Submitted: 21 February 2022 Accepted: 30 May 2022 Published: 20 July 2022
© 2022 The Author(s) (or their employer(s)). Published by CSIRO Publishing on behalf of IAWF. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)
Abstract
Increasing numbers and intensity of forest fires indicate that forests have become susceptible to fires in the tropics. We assessed the susceptibility of forests to fire in India by comparing six machine learning (ML) algorithms. We identified the best-suited ML algorithms for triggering a fire prediction model, using minimal parameters related to forests, climate and topography. Specifically, we used Moderate Resolution Imaging Spectroradiometer (MODIS) fire hotspots from 2001 to 2020 as training data. The Area Under the Receiver Operating Characteristics Curve (ROC/AUC) for the prediction rate showed that the Support Vector Machine (SVM) (ROC/AUC = 0.908) and Artificial Neural Network (ANN) (ROC/AUC = 0.903) show excellent performance. By and large, our results showed that north-east and central India and the lower Himalayan regions were highly susceptible to forest fires. Importantly, the significance of this study lies in the fact that it is possibly among the first to predict forest fire susceptibility in the Indian context, using an integrated approach comprising ML, Google Earth Engine (GEE) and Climate Engine (CE).
Keywords: artificial neural networks, boosted logistic regression, classification and regression trees, forest fire, k-nearest neighbours, machine learning, MODIS, support vector machine, susceptibility mapping.
Introduction
Fires in tropical and temperate deciduous forests are detrimental, as these forest landscapes are not adapted to regular or intense burning, this therefore adversely impacting their ecological and commercial value (Juárez-Orozco et al. 2017; Harrison et al. 2021). Large-scale and intense fires have not been part of natural disturbances of tropical rainforests. However, their intensity and severity in recent decades (Herawati and Santoso 2011), mainly owing to warm and dry conditions associated with changing climate have significantly increased (Harrison et al. 2021). According to the FAO (2020), forest fires are one of the leading drivers of forest degradation each year. Hansen et al. (2013) reported ~4.2 million km2 of gross global forest loss from 2001 to 2018. In 2015 alone, ~98 Mha of forested area was burned, especially in the tropics (FAO 2020). In fact, fire-induced tropical forest loss accounts for 69% of total carbon addition to the atmosphere (Baccini et al. 2017; Armenteras et al. 2021). Large-scale forest loss due to fire hazards can considerably decrease the terrestrial carbon sink, and thereby alter regional weather and global climate at large (Bonan 2008; Swann et al. 2018; van Wees et al. 2021).
There is evidence to show that forest fires may become more severe and intense in the future owing to climate change (USGCRP 2017; Artés et al. 2019; Brown et al. 2021). Jolly et al. (2015) reported that the length of the fire season increased by 18.7% from 1979 to 2013; moreover, 25.3% (29.6 million km2) of the global vegetated surface was exposed to fire seasons. Forest fires are complex; their events and behaviour are determined by complex and non-linear factors, including human activities, weather and climate conditions, vegetation types, and the greater topography (Jain et al. 2020; Zhang et al. 2021). Human activities, for instance, rapidly change the land use of forest landscapes, which in turn increases the vulnerability of forests to fire incidents. Climate change, however, causes longer, more frequent and stronger dry and warmer spells (Mozny et al. 2021; Gannon and Steinberg 2021). It also creates an increased El Niño–Southern Oscillation (ENSO) and sea surface temperature anomalies (Chen et al. 2011; Cai et al. 2017), which are directly associated with increasing fire-prone areas worldwide (Burton et al. 2020). Drought leads to fuel accumulation, and a rise in surface temperature, which increases forests’ flammability (Brando et al. 2019; Ma et al. 2020), thereby triggering frequent and severe fires (De Faria et al. 2017). Additionally, the interactions of climate factors with the natural topography and wind speed direction result in severe and extended forest fire events (Buma 2015; De Faria et al. 2017; Brando et al. 2019; French 2020; Armenteras et al. 2021).
Earth observation satellites provide timely and repetitive information on active and archived fires at regional and global scales (Chuvieco et al. 2019). Remote sensing datasets have widely been used to map active fires and burned areas (Chuvieco et al. 2019). Remote sensing satellite data of MODIS (Moderate Resolution Imaging Spectroradiometer) (Pourtaghi et al. 2016; Chuvieco et al. 2019), Landsat (Syifa et al. 2020) and Sentinel-2 (Navarro et al. 2017; Lang et al. 2019; Roteta et al. 2019) provide information on the extent of fire-affected areas, burn severity and fire susceptibility. Over the last two decades, many researchers have also used MODIS fire hotspot data to integrate it with different predictive modelling approaches for mapping the susceptibility of forests to fires (Ma et al. 2020; Mohajane et al. 2021; Sulova and Joker Arsanjani 2021).
Machine learning (ML) algorithms are popular and emerging predictive approaches in wildfire science and management (Jain et al. 2020). Forest fire susceptibility prediction can be made using ML prediction models (Pourghasemi et al. 2016; de Bem et al. 2018), which define vulnerable areas based on the correlation between wildfire occurrence and sets of predictors. ML algorithms are unique owing to their efficiency, powerful computation, noise handling and ability to capture non-linear and dynamic relationships among variables (Bianco et al. 2019). A review by Jain et al. (2020) found 300 publications on ML applications in wildfire science and management up to 2019. Table 1 shows some of the recent studies that have used different ML algorithms for mapping forest fire susceptibility in some of the other fire-prone areas globally.

|
Kale et al. (2017) stated that mainly anthropogenic activities initiate forest fires in India. However, climate change and ENSO events create favourable conditions for spreading severe and intense fire. ENSO and Indian monsoon rainfall have an inverse relationship. It is well documented that ENSO events are associated with rainfall deficits, which cause warmer and dry spells (Azad and Rajeevan 2016). According to the Forest Survey of India-published Indian State of Forest Report (ISFR 2021), 35.46 % of forest cover in India is fire-prone. Extremely prone area is 2.81%, very highly prone is 7.85% and highly prone is 11.51%. Further, 45–64% of forests in India may face the effects of climate change by 2030. According to World Bank (2018), out of the 647 districts in India, 380–445 districts had fire events every year from 2003 to 2016. Among the major forest types in India, the dry deciduous broadleaved forests are found to be highly susceptible to forest fires. Sannigrahi et al. (2020) reported highly concentrated MODIS active fire alerts in India’s central and east-central states (Odisha, Chhattisgarh and Madhya Pradesh). These regions are mainly covered by deciduous forests, which are highly susceptible to seasonal forest fires. According to the World Bank Group (2021), climate extremes would be intense in the future in India, with increased drought risk and rainfall uncertainties. Northern India would witness a significant temperature increase, whereby annual minimum and maximum temperatures would be expected to increase to a larger degree than the country’s mean temperatures.
Although numerous wildfire prediction models are available worldwide, they are not yet sufficiently efficient to be adopted at different scales and for different geographical conditions. In India, both burned area and the number of fires show increasing trends. Previously, no study has explored the different ML algorithms and predictors that are used in this study to create fire prediction models. Therefore, we attempted to assess the forest fire susceptibility mapping of Indian forests of six ML algorithms, and compared their predictive efficacy, using artificial neural network (ANN), boosted logistic regression (BLR), classification and regression trees (CART), k-nearest neighbours (KNNs), penalised logistic regression (PLR) and support vector machine (SVM). In addition, we assessed the key driving factors for forest fires in the study region. Twenty years (2001–2020) of annual average data of forest, climatic and topography predictors were analysed and used in ML algorithms for fire susceptibility prediction based on 20 years of MODIS fires hotspots training data. This research suggests the best-suited algorithm for creating a fire prediction ML model, using minimal parameters related to forests, climate and topography. This study should help decision and policymakers with effective forest fire management.
Materials and methods
Study area
This study was conducted in India, a South Asian and the seventh-largest country in the world. India lies between 8°4′ and 37°6′ N latitude and 68°7′ and 97°25′ E longitude (Fig. 1). The geographical area of India is 2.4% of the world’s land area and it holds 1.7% of the global forest area (FAO 2010; Rajashekar et al. 2018). Currently, India’s forest cover is 713 789 km2, constituting 21.71% of its geographical area (ISFR 2021). The mean annual temperature is 24.83°C. India receives 1170 mm of rainfall annually, 80% of it during monsoon months (Praveen et al. 2020). Broadly, India can be categorised into four climatic regions: North-west, North-east, Central and Peninsular India (Champion and Seth 1968; Guhathakurta and Rajeevan 2008). Vegetation varies from the Himalayas in the north to the Western Ghats in the south, moist and dry deciduous in the Central, sparse and thorny in the North-west and wet evergreen forest in the North-east of India (Reddy et al. 2015). India displays nearly all types of climates owing to its physiographic position (Martínez-Austria et al. 2016). The four seasons include winter (January–February), summer (March–May), monsoon (June–September) and post-monsoon (October–December) (Das et al. 2015). Elevation varies from coastal zones to the world’s highest mountain ranges (Reddy et al. 2015).

|
Methodology design
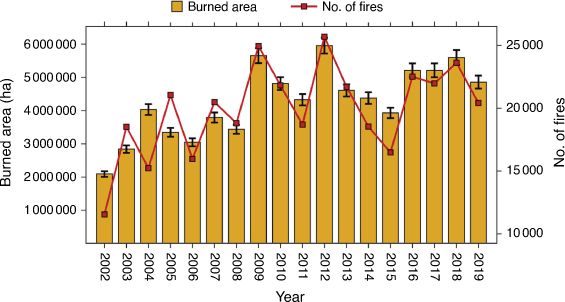
The first step in the methodology includes the data collection and analysis, including MODIS fire hotspots, forest, climatic and topographic data parameters. Fig. 2 shows an year wise variations in the number of fires and burned area. These datasets had an inconsistent spatial resolution (Table 2), so were resampled to a spatial resolution of 1 km (same as MODIS fire hotspot), followed by data filtering. All extracted data were split into train and test with a 70 and 30% ratio, respectively, followed by data normalisation. The normalisation process ranges the data between 0 and 1, which reduces data inconsistencies (Murtaza et al. 2020). A scatterplot matrix was generated to obtain the scatterplots, Pearson correlation and distribution of predictors with fire and non-fire data class. The over–under sampling method was used to remove the class imbalance problem. We trained six ML models, namely ANN, BLR, CART, KNN, PLR and SVM. A 5-fold cross-validation was performed to avoid the model’s overfitting and underfitting problem, followed by hyperparameter tuning. The relative importance was assessed to know the predictor’s importance in fire probability prediction. ML models evaluation was performed using the Area Under the Receiver Operating Characteristics Curve (ROC/AUC) (Bradley 1997). The optimal ML models were selected based on the largest ROC/AUC metrics value, followed by prediction on test data. Finally, forest fire susceptibility maps were generated and analysed for class-wise fire probability (Fig. 3).
|

|
Data collection
Fire data
MODIS Terra Collection 6.1 fire hotspots from 2001 to 2020 were downloaded from the Fire Information for Resource Management System (FIRMS) (https://earthdata.nasa.gov/firms). These data files contain the latitude, longitude, acquisition date and time, and confidence (C) (range 0–100%). The confidence class range between 0 and 30% has low, 30–80% has nominal and 80–100% has high fire detectability (Giglio et al. 2018).
Forest data
Forest fuel type, health and canopy height are the important deciding factors in forest fires. Forest types in the study region are fuel types (dry or moist vegetation or grasslands). Forest type land cover (LC) was used from the MODIS International Geosphere-Biosphere Programme (IGBP) Land Cover Type Product (MCD12Q1), having a spatial resolution of 500 m. Normalized Difference Vegetation Index (NDVI) is an effective indicator of vegetation health status (Huang et al. 2021), which can be correlated with fires. MODIS monthly mean NDVI from 2001 to 2020 was downloaded from Climate Engine (CE) (Huntington et al. 2017). The annual mean composite of NDVI was averaged to obtain a single NDVI raster. NDVI ranges from −1 to 1, which represents vegetation health status. Forest gridded mean canopy relative height (RH100) metrics with a spatial resolution of 1000 m were derived from Global Ecosystem Dynamics Investigation (GEDI) and available from the Oak Ridge National Laboratory Distributed Active Archive Center (ORNL DAAC) (Table 2).
Climatic data
We used the mean values of eight climatic data parameters from 2001 to 2020 (Table 2). These climatic parameters are actual evapotranspiration (AET), climate water deficit (CWD), maximum temperature (Tmax), minimum temperature (Tmin), precipitation (PPT), land surface temperature (LST), wind speed (WS) and Keetch–Byram drought index (KBDI). AET, CWD, Tmax, Tmin, PPT and WS data from TerraClimate (Abatzoglou et al. 2018) and LST data from MODIS were downloaded using CE, whereas KBDI (2007–2020) was obtained from the Google Earth Engine (GEE) (Gorelick et al. 2017) cloud computing platform. KBDI, derived from daily meteorological data, is widely used in wildfire prevention and forecasting. Its scale ranges from 0 to 800, with lower values indicating no moisture deficit and low fire potential and higher values indicating the opposite (Takeuchi et al. 2015).
Topographic data
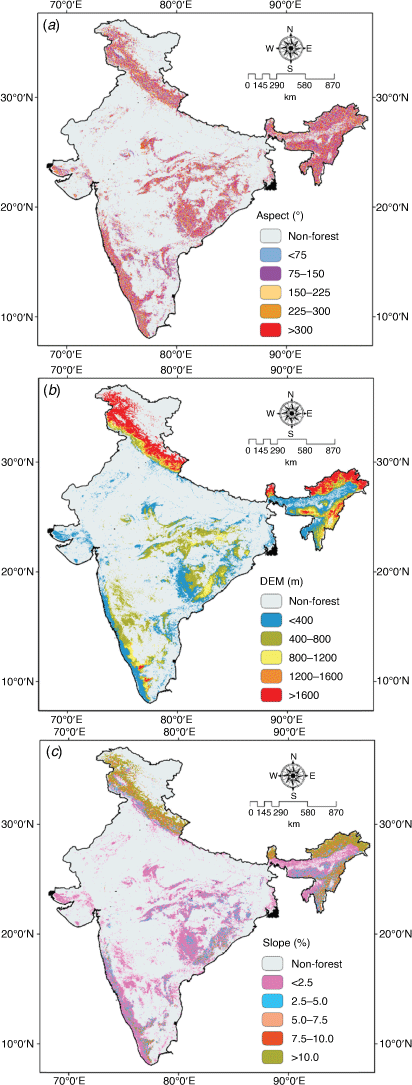
Topographic data parameters, including digital elevation model (DEM), were obtained from the National Aeronautics and Space Administration (NASA) Shuttle Radar Topography Mission (SRTM) 30 m data using GEE. The slope and aspect map was derived from DEM in ArcGIS Desktop 10.5.
Data processing
Fire data processing
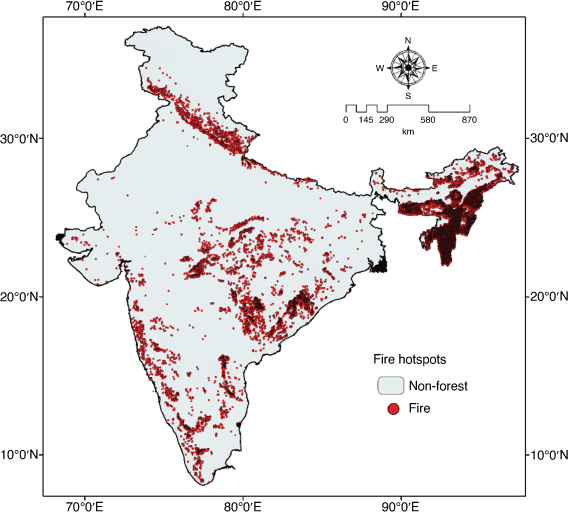
For 20 years (2001–2020), the downloaded fire hotspots were merged, cleaned and filtered. We used eight LC forest classes of MODIS data as a mask to remove fire hotspots from non-forest areas such as croplands, water bodies, barren land and settlements. Further, fire hotspots from January to June were used to avoid the inclusion of crop stubble burn pixels from September to November, and cloud-covered pixels from the monsoon period. Only confidence values greater than 85% were used as high-intensity true fire hotspots or pixels alarms. Finally, we obtained the 20-yeardistribution of 95 999 fire hotspots and pixels shown in Fig. 4.
|
Forest data processing
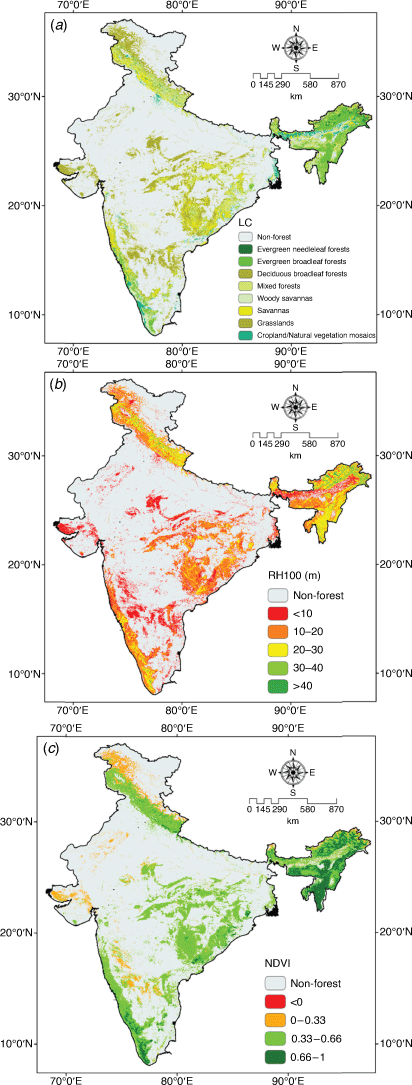
Out of 17 MODIS LC classes, 8 LC classes were selected for our analysis, as shown in Fig. 5a. Canopy height (RH100) data are sparsely distributed over the study area. Therefore, the Bayesian Empirical Kriging approach was used to interpolate the missing data values using the Geostatistical Analyst tool in ArcGIS Desktop 10.5. RH100 data was classified into five classes (<10, 10–20, 20–30, 30–40 and >40 m) (Fig. 5b). NDVI range was classified into four classes, namely dead vegetation or objects (<0), unhealthy vegetation (0–0.33), moderately healthy vegetation (0.33–0.66) and very healthy vegetation (0.66–1) (Fig. 5c).
|
Climatic data processing
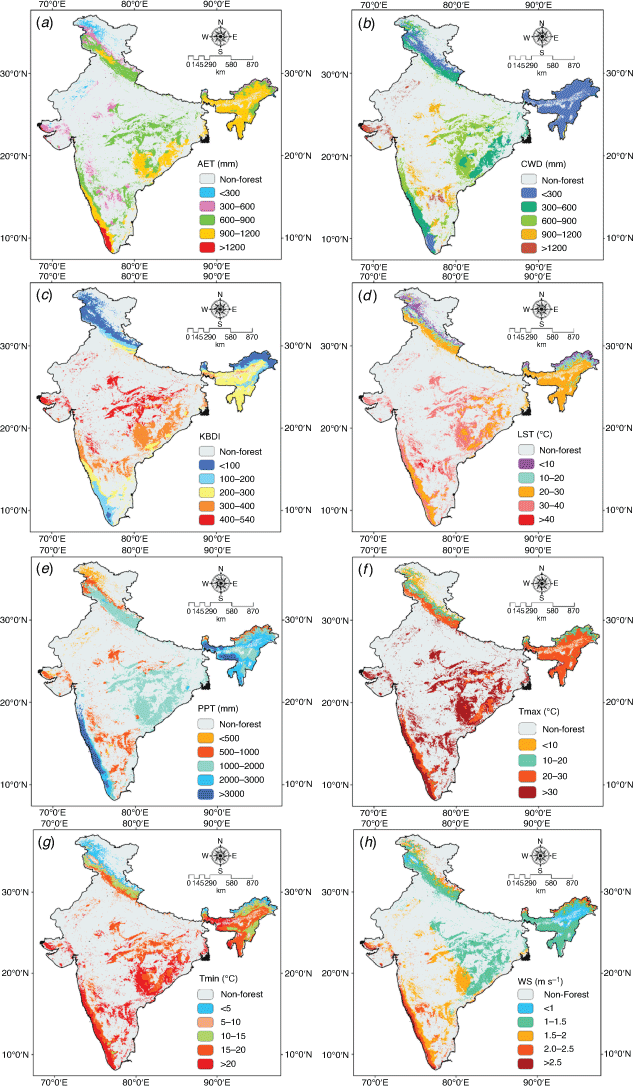
All the climatic raster maps were arranged into different classes as shown in Fig. 6a–g. Both AET (Fig. 6a) and CWD (Fig. 6b) were categorised into five classes, namely very low (<300 mm), low (300–600 mm), moderate (600–900 mm), high (900–1200 mm) and very high (>1200 mm). The five categories of KBDI represent no fire risk (<100), low fire risk (100–200), medium fire risk (200–300), high fire risk (300–400) and very high fire risk (400–540) (Fig. 6c). LST was classified into very low (<10°C), low (10–20°C), moderate (20–30°C), high (30–40°C) and very high (>40°C) (Fig. 6d). PPT was classified into very low (<500 mm), low (500–1000 mm), moderate (1000–2000 mm), high (2000–3000 mm) and very high (>3000 mm) (Fig. 6e). Tmax was classified into low (<10°C), moderate (10–20°C), high (20–30°C) and very high (>30°C) (Fig. 6f). Tmin was classified into very low (<5°C), low (5–10°C), moderate (10–15°C), high (15–20°C) and very high (>20°C) (Fig. 6g). WS was classified into very low (<1 m s–1), low (1–1.5 m s–1), moderate (1.5–2.0 m s–1), high (2.0–2.5 m s–1) and very high (>2.5 m s–1) (Fig. 6h).
|
Topographic data processing
Topographic parameters maps of aspect, DEM and slope were also categorised into different classes (Fig. 7). Aspect was classified into five classes (<75, 75–50, 150–225, 225–300 and >300°) (Fig. 7a). DEM was categorised into <400, 400–800, 800–1200, 1200–1600 and >1600 m (Fig. 7b), and slope into <2.5, 2.5–5.0, 5.0–7.5, 7.5–10.0 and >10.0% (Fig. 7c).
|
Machine learning models buildings
Data preparation
We obtained 75 577 MODIS fire hotspots or pixels over the Indian forests. Also, 24 024 non-fire points were randomly generated manually from non-fire point zones of India. We had a total of 99 601 data points containing fire and non-fire points. However, 6453 data points had null values and were excluded. Subsequently, we had 93 148 data points, split into train and test (70:30%). Therefore, 65 204 points were used as training data, and 27 944 points were the test data. Of 65 204 training data points, 49 566 were fire points, and 15 638 were non-fire points. Therefore, there is a class imbalance situation, as there are fewer non-fire points than fire points. We used the Random Over-Sampling Examples (ROSE) library (Lunardon et al. 2014) ‘ovun.sample’ function in RStudio (RStudio Team 2021) on training data to avoid class imbalance. We obtained 32 733 as non-fire points and 32 471 as fire points using the over–under class sampling approach using the ROSE library.
Machine learning models
After creating training and testing datasets, six ML algorithms were trained using only training datasets, and test data were used for models performance evaluation for unseen conditions. A 5-fold cross-validation technique was used to avoid overfitting or underfitting problems. We used the caret package (Kuhn 2008) in RStudio for models buildings. From the caret package, we used ‘nnet (ANN)’, ‘LogitBoost (BLR)’, ‘rpart (CART)’, ‘knn (KNN)’, ‘plr (PLR)’ and ‘svmRadial (SVM)’ ML models libraries.
ANN is a mathematical model designed to mimic a biological neural network (Zhang et al. 1998), with neurons as the basic building blocks. Firstly, all input values are multiplied by individual weights. Then, all weighted inputs and biases are summated and then passed through the activation function, also known as the transfer function. Neural networks consist of input, output and hidden layers. The input and output are visible, and the hidden layer is non-observable (Maeda et al. 2009). Training neural networks (nnet) using the caret package needs size and decay hyper-parameters. Size is the number of units in the hidden layer (‘nnet’ fits a single hidden layer), and decay is the regularisation parameter to avoid overfitting.
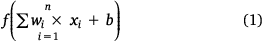
Eqn 1, show the mathematical expressions for ANN, where xi is the input, wi is the weight, f is the activation function and b is the bais.
BLR ‘LogitBoost’ is a boosting classification algorithm that performs an additive logistic regression and minimises the logistic loss (Friedman et al. 2000). LogitBoost was designed as an alternative solution to address the downsides of Adaboost in holding noise and outliers in data (Kamarudin et al. 2017). In LogitBoost, the dependent variable was a binary value representing the presence (1) or absence (0) of forest fires. The tuning parameter in BLR is ‘nIter’ (number of boosting iterations). In BLR, the input data set is N = {(x1, y1),……, (xi, yi),… (xn, yn)}, where xi ∈ X and yi ∈ Y = {−1, +1}. The model can be expressed as Eqn 2
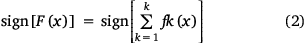
sign[F(x)] is a function that has two possible output classes; k is the number of input iterations
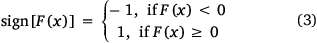
CART does not develop a prediction equation. The data are segregated along the predictor axes into subsets with the homogeneous dependent variable (Krzywinksi and Altman 2017). CART involves identifying and constructing a binary decision tree using a training data sample for which the correct classification is known (Breiman et al. 2017). The CART algorithm’s hyperparameter ‘complexity parameter' (cp) determines how deep the tree will grow. Here, it is assigned a small value, which will allow a decision on further pruning. We want a cp value for pruning the tree, minimising the xerror (cross-validation error).
KNN is a supervised machine learning algorithm that uses previously memorised data to classify new data points into the target class depending on the nearest available points (Wu et al. 2018). The performance of KNN in computing the prediction areas depends on D, the distance between similarities; k, the number of nearest neighbours to be used when calculating predictions, and the scheme to weight individual neighbours when computing predictions (Chirici et al. 2016). The model can be expressed by Eqn 4
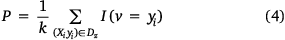
The PLR generalises the standard logistic regression (LR) with a penalty term on the coefficients (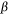 ). PLR can be fitted in the regularisation framework with loss + penalty (Wahba 1999; Gao et al. 2000; Park and Liu 2011). The loss function controls the model’s goodness of fit, and the penalisation term helps to minimise overfitting so that generalisation can be obtained. The PLR uses the unbounded logistic loss, making the classifier sensitive to outliers (Park and Liu 2011). Wahba (1999) showed that the linear PLR is equivalent to Eqn 5:
). PLR can be fitted in the regularisation framework with loss + penalty (Wahba 1999; Gao et al. 2000; Park and Liu 2011). The loss function controls the model’s goodness of fit, and the penalisation term helps to minimise overfitting so that generalisation can be obtained. The PLR uses the unbounded logistic loss, making the classifier sensitive to outliers (Park and Liu 2011). Wahba (1999) showed that the linear PLR is equivalent to Eqn 5:
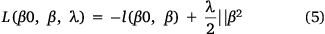
where l is the binomial log-likelihood, and lambda (λ) is a positive constant. As a result of the quadratic penalisation, the norm of the coefficient estimates is smaller than regular LR; however, none of the coefficients is zero. The penalty term measures the smoothness to avoid overfitting, and the tuning parameter λ decides how smooth the PLR model will be. Therefore, the hyperparameter λ choice significantly affects the resulting model (Park and Liu 2011).
SVM is one of the most robust and accurate machine learning techniques, which separate the classes present in the data by identifying the optimal hyperplane of separation (Wu et al. 2008; Rodrigues and De la Riva 2014). SVM was introduced by Vapnik (1995) and followed the statistical learning theory and structural risk minimisation principal methods. Bui et al. (2012), Naghibi et al. (2018) and Jaafari and Pourghasemi (2019) also trained the SVM algorithm to create a hyperplane that segregates the classes into fire and non-fire data. SVM’s tuning parameter ‘cost' (C) defines the possible misclassifications. This hyperparameter imposes a penalty to the SVM model for making an error. The higher the value of C, the fewer chances that the SVM algorithm will misclassify the data point. The SVM radial kernel also requires setting a smoothing hyperparameter ‘sigma’ to give the curvature weight of the decision boundary. Eqn 6 represents the general operation of the SVM model for computing the prediction for a binary-class dataset. Here, 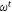 is weight vector,
is weight vector, 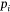 is an input vector, b = Intercept and bias term of the hyperplane equation
is an input vector, b = Intercept and bias term of the hyperplane equation

Hyperparameter tuning gives an optimal value of tuning parameters to build an accurate model from a dataset. A tunelength of 10 was used for each model’s hyperparameter tuning. We tuned ‘size and decay for ANN’, ‘nIter for BLR’, ‘cp for CART’, ‘k for KNN’, ‘λ for PLR’ and ‘Cost (C) and sigma for SVM’. Further, pre-processing steps, including centre and scaling, were applied for data normalisation. We used classProbs = TRUE in ‘trainControl’ function of the caret package for predicted outcomes as a probability (0–1).
Models evaluation
Most ML models using binary variables are evaluated using ROC/AUC (Grau et al. 2015), which measures the model’s performance. The graph of sensitivity and specificity provides a visual and statistical extent of ML algorithms prediction accuracy (Kalantar et al. 2020). ROC/AUC can be used to validate the prediction of various ML models against an original training dataset. Therefore, the ROC/AUC technique is a productive method for portraying the efficiency of a probability map predicted by a particular ML model (Satir et al. 2016). Here, true positive (TP) and true negative (TN) are sample datasets that are correctly classified, and false positive (FP) and false negative (FN) are samples that are misclassified (Bui et al. 2017). The ROC/AUC calculated using the sensitivity (TP rate) (7) and specificity (FN rate) (8) quantifies the performance of the models. ROC/AUC values below 0.6 indicate poor performance, values of 0.7–0.8 denote good performance, values of 0.80–0.90 represent very good performance and greater than 0.90 shows an excellent performance of the model (Bui et al. 2017; Jaafari and Pourghasemi 2019).
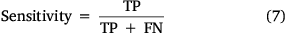
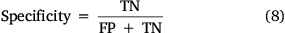
Forest fire susceptibility mapping
After evaluating the model’s performance and desired accuracy using the ROC/AUC method, forest fire susceptibility mapping was performed on a raster stack over the study region. Finally, the computed probability was displayed as a map, which shows the forest fire susceptible zones, and parameters class-wise mean fire probability was calculated using the zonal statistics tool in ArcGIS Desktop 10.5.
Results
Parameters analysis
Fig. 8a–h shows the variations in the annual mean of climatic parameters and the number of fires. Fig. 8a shows that the number of fires was at a maximum in 2012 when AET was 823.37 mm. In high AET years, such as 2006, 2010, 2011, 2013, 2014 and 2015, fires decreased. The number of fires and CWD in 2009, 2016 and 2016 was higher than in other years. In 2015, CWD was lowest at 391.54 mm, and the number of fires sharply declined (Fig. 8b). Drought index KBDI had a higher value in 2009 and 2012 as did the number of fires, while in 2019, the KBDI was less than 200, and the number of fires also declined. In 2015, the reverse trend was observed as the KBDI was high; however, the number of fires sharply declined (Fig. 8c). The number of fires also shows high peaks in 2009, 2012 and 2018 when LST was 26.04, 25.35 and 25.06°C respectively (Fig. 8d). Maximum fire incidents were observed in 2012 when NDVI was low at 0.543. In 2013, 2014 and 2015, NDVI showed increasing trends, decreasing the number of fires. The maximum NDVI of 0.581 was in 2015, and the number of fires was also lowest between 2009 and 2019.

|
Further, in 2019, the NDVI was high at 0.573, and the number of fires declined (Fig. 8e). Fig. 8f shows that fires rose with PPT decline in 2009, 2012 and 2018. Also, the years 2010, 2011, 2013 and 2019 recorded higher PPT and a lower number of fires. In 2015, the number of fires was the lowest between 2009 and 2019 as this year received precipitation of >1700 mm annually (Fig. 8f). Likewise, between 2009 and 2019, fire incidents peaked in 2009, 2012, 2016 and 2018 when Tmax was 27.27, 26.41, 26.98 and 26.34°C respectively. The lowest number of fire incidents was observed in 2011, 2015 and 2019 when Tmax was 26.51, 26.42 and 26.86°C respectively (Fig. 8h). As Tmax sharply rose from 2015 (26.42°C) to 2016 (26.98°C), the number of fires from 2015 to 2016 also sharply increased (Fig. 8h).
Pearson correlation
The Pearson correlation (r) among parameters during the fire and non-fire events was computed and plotted into a scatterplot matrix structure, as shown in Fig. 9. A high correlation between LST and KBDI (r = 0.766) was observed, and both of these parameters were inversely related to NDVI (r = −0.339, −0.291). Also, a correlation (r = 0.413) between PPT and NDVI was observed for fire class; however, they showed an inverse relation with CWD (r = −0.458, −0.698). Tmax and NDVI showed an inverse correlation (r = −0.291) with fire class. Tmax and LST strongly correlate (r = 0.849) with fire class. Also, RH100 and slope are positively correlated (r = 0.382) with fire class. AET and NDVI correlate (r = 0.687) with fire class.

|
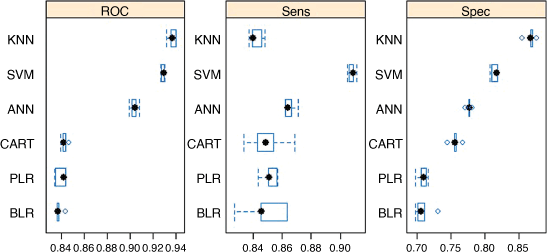
Training accuracy of ML models
Fig. 10 shows the variations in ROC/AUC across tuning parameters of the ML models, and Fig. 11 compares ROC/AUC, sensitivity (Sens) and specificity (Spec) of the optimal ML models. The optimal model was selected based on the largest ROC/AUC value. ROC/AUC variations across tuning parameters show that the optimal ANN model has a final ROC/AUC value of 0.903 at size = 19 (Fig. 10a), while sensitivity and specificity were 0.860 and 0.778 respectively. The final ROC/AUC value of 0.838 was used for the optimal BLR model at nIter = 81(Fig. 10b), while sensitivity and specificity were 0.849 and 0.710 respectively. For optimal CART, the final value ROC/AUC was 0.842 at cp = 0.001817006 (Fig. 10c), while sensitivity and specificity were 0.849 and 0.756 respectively. The optimal KNN was obtained at k = 5, for which ROC/AUC is 0.937 (Fig. 10d), while sensitivity and specificity were 0.842 and 0.867 respectively. The final values ROC/AUC of 0.839 used for the PLR model were λ = 0.001333521 (Fig. 10e), while sensitivity and specificity were 0.852 and 0.708 respectively. For SVM training, the tuning parameter sigma was held constant at 0.1278743. The final ROC/AUC value of 0.927 was used for the SVM model at σ = 0.1278743 and C = 128 (Fig. 10f), while sensitivity and specificity were 0.907 and 0.813, respectively (Fig. 11).

|
|
Predictors’ overall importance
Fig. 12a–f shows the overall importance (scaled from 0 to 100) of the predictors in the ML models for fire prediction. All climatic parameters such as Tmax, CWD, LST, Tmin, PPT and AET have a high importance score (>50) for fire probability prediction by the ANN model. Forest parameter RH100 is the least important predictor (Fig. 12a). NDVI is the most important predictor in the CART model, whereas climatic parameters WS, Tmax and CWD have a high overall importance score in the CART model. The slope is the least important predictor in the CART model (Fig. 12c). The KNN, BLR, PLR and SVM models have the same importance for their respective predictors in fire probability prediction. Fig. 12b, d, e, f shows that forest parameter NDVI is the most important predictor, and LC and RH100 have a high overall importance score for fire prediction.

|
Models evaluation
The ROC/AUC curves in Fig. 13a compare the ML models for prediction rate, while ROC/AUC curves in Fig. 13b compare the ML models for success rate. Fig. 13a shows that SVM and ANN are the best-performing models and have the highest prediction rate with ROC/AUC of 0.908 and 903 respectively, and BLR has an ROC/AUC of 0.802, which is the lowest (Table 3). The success rate ROC/AUC curve shows that KNN is the best-performing (Fig. 13b) with the highest ROC/AUC of 0.945, SVM has 0.930, and ANN has 0.904, whereas BLR has 0.808, which is the lowest.
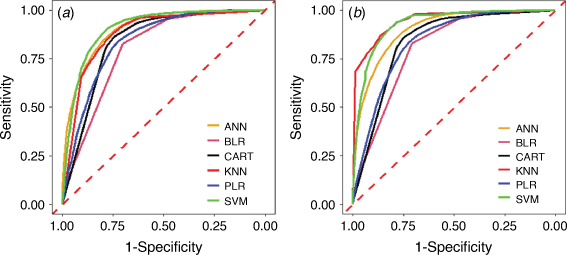
|
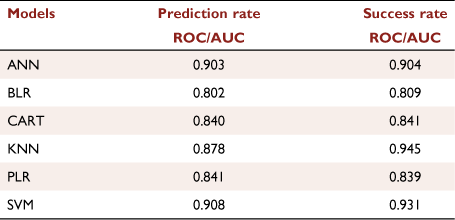
|
Forest fire susceptibility mapping
Fig. 14a–f shows the forest fire susceptibility maps of the Indian forest regions predicted using the six ML models. Models slightly vary in their outcomes of fire probability prediction maps in different parts of India; however, all six ML models predicted a high to a very high probability of forest fire in the North-east regions of India. The Central Indian forest regions are also susceptible, as the probability of forest fire is moderate to high. The Himalayan forests in Uttarakhand and Himachal Pradesh states (parts of the lower Himalayas) have moderate to very high susceptibility to fires. The Western Ghats of India have low to moderate susceptibility, while the Eastern Ghats and Peninsular Indian forest regions have moderate to high susceptibility to forest fires. North-western parts of India have very low to low susceptibility. Coastal zones and the upper Himalayan region of India have very low to low forest fires susceptibility.

|
Table 4 shows the class-wise mean of forest fire probability predictors in the ML models. Models predicted that Evergreen broadleaf forests have maximum fire probability (0.55–0.64) among other LC classes. The best-performing SVM model predicts that precipitation class 2000–3000 mm has a maximum mean fire probability of 0.44. Tmax in the range of 20–30°C has a maximum mean fire probability of 0.45. NDVI with moderately healthy vegetation (0.33–0.66) and very healthy vegetation (0.66–1) has a fire probability of 0.25 and 0.54, respectively. RH100 in the range of 20–30 m has a maximum mean fire probability of 0.44, while RH100 >40 m has the lowest mean fire probability of 0.11. KBDI in the range of 200–300 has the maximum mean fire probability of 0.43.

|
Discussion
As in several parts of the world, forest fires and burned area have dramatically increased in Indian forests. Although numerous wildfire prediction models are available worldwide, they are not yet efficient enough to be adopted on a large scale and in different geographical conditions. Our findings suggest the best-suited algorithm for creating a fire prediction ML model, using minimal important parameters related to forests, climate and topography. We noted that climate parameters, such as PPT, CWD, Tmax, LST and KBDI are associated with the number of forest fires. Specifically, we noted that the forest parameter NDVI has an inverse link to number of fires; for instance, when NDVI increases, the incidence of forest fires decreases; this was specifically observed in 2011, 2015 and 2019. Additionally, it can be seen that all forests, climatic and topographic parameters have a complex and mutual relationship in increasing the intensity and number of forest fires. Therefore, efficient models that determine complex, non-linear and dynamic relationships between parameters are helpful for accurate fire susceptibility prediction.
Of the six ML models that we used, SVM and ANN models outperformed the others, and yielded an excellent performance (>0.90) in terms of the prediction rate. The other four models, namely KNN, PLR, CART and BLR, had an ROC/AUC in the range of 0.80–0.87. The high predictive efficacy of SVM is possibly due to its ability to deal with dynamic relationships, handling complexity in data, and be least affected by noisy data, and less prone to overfitting (Ballabio and Sterlacchini 2012; Pham et al. 2016). It may also be noted that SVM is an advantageous algorithm for binary classification problems, such as non-fire and fire class. Similarly, the excellent performance of ANN was due to its capacity to recognise hidden relationships between complex and non-linear datasets. The performance obtained from SVM and ANN also supports extant literature, which showed similar performance of the SVM model in different fields, including flooding and landslide susceptibility mapping (Sakr et al. 2010; Li et al. 2011; Ballabio and Sterlacchini 2012; Pham et al. 2016; Bui et al. 2017; Wu et al. 2018). ANN showed similar predictive performance to that observed in the current study in various wildfire modelling studies (Lee et al. 2012a, 2012b; Satir et al. 2016). De Vasconcelos et al. (2001), Bisquert et al. (2012), Jafari Goldarag et al. (2016), Adab (2017) also obtained an improved performance of the ANN model in binary classification. Kumar and Kumar (2020) generated fire detection and classification models using MLP and KNN algorithms and compared them, and their findings showed that the MLP algorithm had a higher accuracy (99.96%) than the KNN algorithm. Even if KNN had a better success rate ROC/AUC value (0.945), it was considered biased, and could fail, especially if there were no nearest values (Magnussen et al. 2010). Compared with both SVM and ANN, the KNN, BLR, PLR and CART models have been slightly less accurate in our study. However, these require only one hyperparameter tuning, and less time in training. The advantage of ML techniques over traditional methods is that the former (i.e. ML techniques) can be handy with noisy data, and thereby overcome uncertainties even with limited observations. However, to increase the accuracy of the ML models, the quality of the input data in ML models is also important to consider (Pourghasemi et al. 2020).
Analysis of parameters shows a mutual, complex and interconnected relationship between the predictors and the number of fires. The climatic parameters Tmax, CWD, LST, Tmin, PPT and AET had high overall importance for fire prediction by the ANN model. Generally, these parameters also have an inverse correlation with forest parameter NDVI. Notably, NDVI is the most important parameter for fire prediction in SVM, BLR, KNN, PLR and CART, while forest parameters such as LC and RH100 also have high importance. Previous studies found that these climatic and forest parameters are important for predicting forest fire susceptibility. For instance, Bui et al. (2019) found that NDVI is the main factor that influences forest fire mapping. Pourtaghi et al. (2015) also found the most important factors were NDVI, land use, soil and annual temperature for forest fire susceptibility mapping in the Minudasht forests of Iran. WS is the second-most important predictor after NDVI in SVM, BLR, KNN, PLR and CART. Achu et al. (2021) found that WS is important in forest fire prediction, as our study suggested. Williams et al. (2019) revealed that wind events and delayed onset of winter precipitation are the dominant wildfire triggers.
Although some parameters were considered in the context of their effects and forest fire susceptibility mapping, all the algorithms used effectively operated efficiently in the study region. Satir et al. (2016) considered the role of anthropogenic factors insignificant in fire susceptibility prediction. However, Achu et al. (2021) demonstrated that anthropogenic factors, such as land use and distance to roads, are important in forest fire modelling. In addition, some studies found that human-related variables have a stronger influence than climate-related variables for fire ignition (Pham et al. 2020; Mohajane et al. 2021). However, in tropical countries like India, where forests are generally non-adapted to fire and climate change has a large impact on forests, the role of climate-related variables in forest fires is very important to investigate. Human activities largely act as fire ignition sources; however, fire intensity and severity depend on the climatic, forest, topographic and weather conditions of the area. Initiation of forest fires in India is generally anthropogenic; however, intensity and severity largely depend on forests, climatic and topographic factors. The present study ignored factors like distance to roads, rivers and settlements, because data on these factors are hard to obtain at a local scale, especially for a country-level study. However, we did consider factors such as NDVI, forest canopy height and land cover that are directly or indirectly impacted by anthropogenic activities.
Forest fire susceptibility maps show that large areas of North-east India’s forests have a very high susceptibility to forest fires. The North-east regions of India do face a huge human burden from activities like shifting cultivation and deforestation. The lower Himalayan region, Eastern Ghats, and Peninsular regions also are highly susceptible to forest fires, specifically because these regions are vulnerable to climate change and experience large variations in climatic factors. The Western Ghats, however, have low to moderate susceptibility, while coastal zones and the upper Himalayan region have very low to low susceptibility. Additionally, North-western India also has a very low to low fire probability due to the presence of sparsely vegetated areas. Our fire susceptibility maps also support FSI ISFR reports on the biannual Indian forest cover assessment, indicating that these regions are prone to forest fires. Therefore, our prediction models based on MODIS data and two decades of mean climatic parameters represent accurate outcomes. It should also be noted that many researchers in the past have stated that climate change will also have an impact in terms of the intensity of wildfires in the future, as evidenced by increased mean temperature, drying conditions and weather patterns. Based on these findings, and observations from extant literature, this study does support climate change linked to wildfires and forest fires in India, and expresses its apprehensions for the future, when conditions are expected to be more severe.
Dutta et al. (2016), Mayr et al. (2018), Jain et al. (2020) suggested that the ensemble ML approaches perform better than a single classifier. Ensemble ML models like RF and boosting algorithms (XGBoost) have offered improved accuracy in some previous studies (Milanović et al. 2021; Mohajane et al. 2021); however, we believe that these ensemble models take more time to run than our ML models. In fact, recently, some studies have also highlighted the improved results of deep learning over other methods. For instance, Zhao et al. (2018) and Zhang et al. (2019, 2021) found that CNN was better in classification than SVM. However, more testing on model comparisons, situations criteria and well-established accuracy measurements are needed in order to take care of overfitting and underfitting, using suitable validation approaches.
Conclusion
The current study is possibly among the first attempts to map the forest fire susceptibility of Indian forests, using six ML algorithms and comparing them. This study suggests that SVM and ANN are the best-suited ML algorithms for creating a model to assess the probability of the area being susceptible to fire using minimal parameters. Importantly, both these models showed an excellent accuracy (AUC/ROC > 0.9) in the prediction rate. Further, this study also identified the most to least important forest, climatic and topographic parameters useful in forest fire susceptibility mapping. Climate parameters are uncertain owing to the changing climate; however, they are strongly linked to increased fires and burned area. Forest fire susceptibility maps are helpful in identifying the most to least fire-prone forest regions in India. The ensemble ML and deep learning models possibly improve accuracy; however, they are complex, and training takes considerable computational time. Therefore, we recommend that the inclusion of other fire-related factors and anthropogenic parameters in the best-performing algorithms (SVM and ANN) could improve the accuracy of outcomes. Moreover, seasonal variations in ENSO-related parameters, such as sea surface temperature anomalies, do play an important role in triggering forest fires, and must be identified and used in the modelling process. Furthermore, using ML algorithms for fire susceptibility, prediction should be enhanced, using all available information and data related to fire events before implementation, possibly by using cloud computing platforms like GEE and CE.
Data availability
The data supporting this study will be shared on reasonable request to the corresponding author.
Conflicts of interest
The authors declare no conflict of interest.
Declaration of funding
This research did not receive any specific funding.
Author contributions
Laxmi Kant Sharma: conceptualisation, methodology design, formal analysis, reviewing, writing and editing. Rajit Gupta: data curation, methodology design, coding, model run, formal analysis, reviewing writing, visualisation. Naureen Fatima: data curation, formal analysis, writing.
Acknowledgements
We are highly thankful to the Central University of Rajasthan for research facilities in the DST-FIST funded Remote sensing and GIS Lab in the Department of Environmental Science. The corresponding author wishes to acknowledge the support from the University Grants Commission (UGC) for providing the UGC NET-JRF fellowship (Ref no. 3551/(NET-JAN2017)). Finally, we are thankful to the anonymous reviewers and editors for their valuable suggestions and comments.
References
Abatzoglou JT, Dobrowski SZ, Parks SA, Hegewisch KC (2018) TerraClimate, a high-resolution global dataset of monthly climate and climatic water balance from 1958-2015 Scientific Data 5, 170191| TerraClimate, a high-resolution global dataset of monthly climate and climatic water balance from 1958-2015Crossref | GoogleScholarGoogle Scholar |
Achu AL, Thomas J, Aju CD, Gopinath G, Kumar S, Reghunath R (2021) Machine-learning modelling of fire susceptibility in a forest–agriculture mosaic landscape of southern India. Ecological Informatics 64, 101348
| Machine-learning modelling of fire susceptibility in a forest–agriculture mosaic landscape of southern India.Crossref | GoogleScholarGoogle Scholar |
Adab H (2017) Landfire hazard assessment in the Caspian Hyrcanian forest ecoregion with the long-term MODIS active fire data. Natural Hazards 87, 1807–1825.
| Landfire hazard assessment in the Caspian Hyrcanian forest ecoregion with the long-term MODIS active fire data.Crossref | GoogleScholarGoogle Scholar |
Armenteras D, Dávalos LM, Barreto JS, Miranda A, Hernández-Moreno A, Zamorano-Elgueta C, González-Delgado TM, Meza-Elizalde MC, Retana J (2021) Fire-induced loss of the world’s most biodiverse forests in Latin America. Science Advances 7, eabd3357
| Fire-induced loss of the world’s most biodiverse forests in Latin America.Crossref | GoogleScholarGoogle Scholar |
Artés T, Oom D, De Rigo D, Durrant TH, Maianti P, Libertà G, San-Miguel-Ayanz J (2019) A global wildfire dataset for the analysis of fire regimes and fire behaviour. Scientific Data 6, 296
| A global wildfire dataset for the analysis of fire regimes and fire behaviour.Crossref | GoogleScholarGoogle Scholar |
Azad S, Rajeevan M (2016) Possible shift in the ENSO–Indian monsoon rainfall relationship under future global warming. Scientific Reports 6, 20145
| Possible shift in the ENSO–Indian monsoon rainfall relationship under future global warming.Crossref | GoogleScholarGoogle Scholar |
Baccini A, Walker W, Carvalho L, Farina M, Sulla-Menashe D, Houghton RA (2017) Tropical forests are a net carbon source based on aboveground measurements of gain and loss. Science 358, 230–234.
| Tropical forests are a net carbon source based on aboveground measurements of gain and loss.Crossref | GoogleScholarGoogle Scholar |
Ballabio C, Sterlacchini S (2012) Support vector machines for landslide susceptibility mapping: the Staffora River Basin Case Study, Italy. Mathematical Geosciences 44, 47–70.
| Support vector machines for landslide susceptibility mapping: the Staffora River Basin Case Study, Italy.Crossref | GoogleScholarGoogle Scholar |
Banerjee P (2021) Maximum entropy-based forest fire likelihood mapping: analysing the trends, distribution, and drivers of forest fires in Sikkim Himalaya. Scandinavian Journal of Forest Research 36, 275–288.
| Maximum entropy-based forest fire likelihood mapping: analysing the trends, distribution, and drivers of forest fires in Sikkim Himalaya.Crossref | GoogleScholarGoogle Scholar |
Bianco MJ, Gerstoft P, Traer J, Ozanich E, Roch MA, Gannot S, Deledalle CA (2019) Machine learning in acoustics: Theory and applications. Journal of the Acoustical Society of America 146, 3590–3628.
| Machine learning in acoustics: Theory and applications.Crossref | GoogleScholarGoogle Scholar |
Bisquert M, Caselles E, Sánchez JM, Caselles V (2012) Application of artificial neural networks and logistic regression to the prediction of forest fire danger in Galicia using MODIS data. International Journal of Wildland Fire 21, 1025–1029
| Application of artificial neural networks and logistic regression to the prediction of forest fire danger in Galicia using MODIS data.Crossref | GoogleScholarGoogle Scholar |
Bonan GB (2008) Forests and climate change: forcings, feedbacks, and the climate benefits of forests. Science 320, 1444–1449.
| Forests and climate change: forcings, feedbacks, and the climate benefits of forests.Crossref | GoogleScholarGoogle Scholar |
Bradley AP (1997) The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognition 30, 1145–1159.
| The use of the area under the ROC curve in the evaluation of machine learning algorithms.Crossref | GoogleScholarGoogle Scholar |
Brando PM, Paolucci L, Ummenhofer CC, Ordway EM, Hartmann H, Cattau ME, Rattis L, Medjibe V, Coe MT, Balch J (2019) Droughts, wildfires, and forest carbon cycling: A pantropical synthesis. Annual Review of Earth and Planetary Sciences 47, 555–581.
| Droughts, wildfires, and forest carbon cycling: A pantropical synthesis.Crossref | GoogleScholarGoogle Scholar |
Breiman L, Friedman JH, Olshen RA, Stone CJ (2017) ‘Classification and regression trees.’ (Routledge)
| Crossref |
Brown EK, Wang J, Feng Y (2021) US wildfire potential: A historical view and future projection using high-resolution climate data. Environmental Research Letters 16, 034060
| US wildfire potential: A historical view and future projection using high-resolution climate data.Crossref | GoogleScholarGoogle Scholar |
Bui DT, Pradhan B, Lofman O, Revhaug I, Dick OB (2012) Application of support vector machines in landslide susceptibility assessment for the Hoa Binh province (Vietnam) with kernel functions analysis. International Congress on Environmental Modelling and Software 226, Available at https://scholarsarchive.byu.edu/iemssconference/2012/Stream-B/226
Bui DT, Le K-TT, Nguyen VC, Le HD, Revhaug I (2016) Tropical forest fire susceptibility mapping at the Cat Ba National Park Area, Hai Phong City, Vietnam, using GIS-based kernel logistic regression. Remote Sensing 8, 347
| Tropical forest fire susceptibility mapping at the Cat Ba National Park Area, Hai Phong City, Vietnam, using GIS-based kernel logistic regression.Crossref | GoogleScholarGoogle Scholar |
Bui DT, Bui QT, Nguyen QP, Pradhan B, Nampak H, Trinh PT (2017) A hybrid artificial intelligence approach using GIS-based neural-fuzzy inference system and particle swarm optimization for forest fire susceptibility modeling at a tropical area. Agricultural and Forest Meteorology 233, 32–44.
| A hybrid artificial intelligence approach using GIS-based neural-fuzzy inference system and particle swarm optimization for forest fire susceptibility modeling at a tropical area.Crossref | GoogleScholarGoogle Scholar |
Bui DT, Hoang N-D, Samui P (2019) Spatial pattern analysis and prediction of forest fire using new machine learning approach of Multivariate Adaptive Regression Splines and Differential Flower Pollination optimization: A case study at Lao Cai province (Viet Nam). Journal of Environmental Management 237, 476–487.
| Spatial pattern analysis and prediction of forest fire using new machine learning approach of Multivariate Adaptive Regression Splines and Differential Flower Pollination optimization: A case study at Lao Cai province (Viet Nam).Crossref | GoogleScholarGoogle Scholar |
Buma B (2015) Disturbance interactions: Characterization, prediction, and the potential for cascading effects. Ecosphere 6, 1–15.
| Disturbance interactions: Characterization, prediction, and the potential for cascading effects.Crossref | GoogleScholarGoogle Scholar |
Burton C, Betts RA, Jones CD, Feldpausch TR, Cardoso M, Anderson LO (2020) El Niño driven changes in global fire 2015/16. Frontiers in Earth Science 8, 199
| El Niño driven changes in global fire 2015/16.Crossref | GoogleScholarGoogle Scholar |
Cai W, Wang G, Santoso A, Lin X, Wu L (2017) Definition of extreme El Niño and its impact on projected increase in extreme El Niño frequency. Geophysical Research Letters 44, 11–184.
| Definition of extreme El Niño and its impact on projected increase in extreme El Niño frequency.Crossref | GoogleScholarGoogle Scholar |
Champion HG, Seth SK (1968) ‘A revised survey of the forest types of India.’ (Manager of Publications, Government of India)
Chen Y, Randerson JT, Morton DC, DeFries RS, Collatz GJ, Kasibhatla PS, Giglio L, Jin Y, Marlier ME (2011) Forecasting fire season severity in South America using sea surface temperature anomalies. Science 334, 787–791.
| Forecasting fire season severity in South America using sea surface temperature anomalies.Crossref | GoogleScholarGoogle Scholar |
Chirici G, Mura M, McInerney D, Py N, Tomppo EO, Waser LT, Travaglini D, McRoberts RE (2016) A meta-analysis and review of the literature on the k-Nearest Neighbors technique for forestry applications that use remotely sensed data. Remote Sensing of Environment 176, 282–294.
| A meta-analysis and review of the literature on the k-Nearest Neighbors technique for forestry applications that use remotely sensed data.Crossref | GoogleScholarGoogle Scholar |
Chuvieco E, Mouillot F, Van der Werf GR, San Miguel J, Tanase M, Koutsias N, García M, Yebra M, Padilla M, Gitas I, Heil A (2019) Historical background and current developments for mapping burned area from satellite Earth observation. Remote Sensing of Environment 225, 45–64.
| Historical background and current developments for mapping burned area from satellite Earth observation.Crossref | GoogleScholarGoogle Scholar |
Coffield SR, Graff CA, Chen Y, Smyth P, Foufoula-Georgiou E, Randerson JT (2019) Machine learning to predict final fire size at the time of ignition. International Journal of Wildland Fire 28, 861–873.
| Machine learning to predict final fire size at the time of ignition.Crossref | GoogleScholarGoogle Scholar |
Das S, Dey S, Dash SK, Giuliani G, Solmon F (2015) Dust aerosol feedback on the Indian summer monsoon: sensitivity to absorption property. Journal of Geophysical Research: Atmospheres 120, 9642–9652.
| Dust aerosol feedback on the Indian summer monsoon: sensitivity to absorption property.Crossref | GoogleScholarGoogle Scholar |
de Bem PP, de Carvalho Júnior OA, Matricardi EAT, Guimarães RF, Gomes RAT (2018) Predicting wildfire vulnerability using logistic regression and artificial neural networks: a case study in Brazil’s Federal District. International Journal of Wildland Fire 28, 35–45.
| Predicting wildfire vulnerability using logistic regression and artificial neural networks: a case study in Brazil’s Federal District.Crossref | GoogleScholarGoogle Scholar |
De Faria BL, Brando PM, Macedo MN, Panday PK, Soares-Filho BS, Coe MT (2017) Current and future patterns of fire-induced forest degradation in Amazonia. Environmental Research Letters 12, 095005
| Current and future patterns of fire-induced forest degradation in Amazonia.Crossref | GoogleScholarGoogle Scholar |
De Vasconcelos MP, Silva S, Tome M, Alvim M, Pereira JC (2001) Spatial prediction of fire ignition probabilities: comparing logistic regression and neural networks. Photogrammetric Engineering & Remote Sensing 67, 73–81.
Dubayah RO, Luthcke SB, Sabaka TJ, Nicholas JB, Preaux S, Hofton MA (2021) ‘GEDI L3 Gridded Land Surface Metrics, Version 2.’ (ORNL DAAC: Oak Ridge, Tennessee, USA)
| Crossref |
Dutta R, Das A, Aryal J (2016) Big data integration shows Australian bushfire frequency is increasing significantly. Royal Society Open Science 3, 150241
| Big data integration shows Australian bushfire frequency is increasing significantly.Crossref | GoogleScholarGoogle Scholar |
FAO (2010) ‘Global forest resources assessment 2010: Main report.’ (Food and Agriculture Organization of the United Nations)
FAO (2020) ‘Global Forest Resources Assessment 2020: Main report.’ (Food and Agriculture Organization of the United Nations: Rome)
| Crossref |
French CC (2020) America on fire: climate change, wildfires & insuring natural catastrophes. UC Davis Law Review 54, 817
Friedman J, Hastie T, Tibshirani R (2000) Additive logistic regression: a statistical view of boosting (with discussion and a rejoinder by the authors). The Annals of Statistics 28, 337–407.
| Additive logistic regression: a statistical view of boosting (with discussion and a rejoinder by the authors).Crossref | GoogleScholarGoogle Scholar |
Gannon CS, Steinberg NC (2021) A global assessment of wildfire potential under climate change utilizing Keetch–Byram Drought Index and land cover classifications. Environmental Research Communications 3, 035002
| A global assessment of wildfire potential under climate change utilizing Keetch–Byram Drought Index and land cover classifications.Crossref | GoogleScholarGoogle Scholar |
Gao F, Klein R, Klein B, Lin X, Wahba G, Xiang D (2000) Smoothing spline ANOVA models for large data sets with Bernoulli observations and the randomized GACV. The Annals of Statistics 28, 1570–1600.
| Smoothing spline ANOVA models for large data sets with Bernoulli observations and the randomized GACV.Crossref | GoogleScholarGoogle Scholar |
Giglio L, Schroeder W, Hall JV, Justice CO (2018) MODIS Collection 6 Active Fire Product User’s Guide Revision B. Available at http://modis-fire.umd.edu/files/MODIS_C6_Fire_User_Guide_B.pdf
Gorelick N, Hancher M, Dixon M, Ilyushchenko S, Thau D, Moore R (2017) Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sensing of Environment 202, 18–27.
| Google Earth Engine: Planetary-scale geospatial analysis for everyone.Crossref | GoogleScholarGoogle Scholar |
Grau J, Grosse I, Keilwagen J (2015) PRROC: Computing and visualizing precision-recall and receiver operating characteristic curves in R. Bioinformatics 31, 2595–2597.
| PRROC: Computing and visualizing precision-recall and receiver operating characteristic curves in R.Crossref | GoogleScholarGoogle Scholar |
Guhathakurta P, Rajeevan M (2008) Trends in the rainfall pattern over India. International Journal of Climatology: A Journal of the Royal Meteorological Society 28, 1453–1469.
| Trends in the rainfall pattern over India.Crossref | GoogleScholarGoogle Scholar |
Hansen MC, Potapov PV, Moore R, Hancher M, Turubanova SA, Tyukavina A, Thau D, Stehman SV, Goetz SJ, Loveland TR, Kommareddy A, Egorov A, Chini L, Justice CO, Townshend JRG (2013) High‐resolution global maps of 21st‐century forest cover change. Science 342, 850–853.
| High‐resolution global maps of 21st‐century forest cover change.Crossref | GoogleScholarGoogle Scholar |
Harrison SP, Prentice IC, Bloomfield KJ, Dong N, Forkel M, Forrest M, Ningthoujam RK, Pellegrini A, Shen Y, Baudena M, Cardoso AW (2021) Understanding and modelling wildfire regimes: an ecological perspective. Environmental Research Letters 16, 125008
| Understanding and modelling wildfire regimes: an ecological perspective.Crossref | GoogleScholarGoogle Scholar |
Herawati H, Santoso H (2011) Tropical forest susceptibility to and risk of fire under changing climate: A review of fire nature, policy and institutions in Indonesia. Forest Policy and Economics 13, 227–233.
| Tropical forest susceptibility to and risk of fire under changing climate: A review of fire nature, policy and institutions in Indonesia.Crossref | GoogleScholarGoogle Scholar |
Huang S, Tang L, Hupy JP, Wang Y, Shao G (2021) A commentary review on the use of Normalized Difference Vegetation Index (NDVI) in the era of popular remote sensing. Journal of Forestry Research 32, 1–6.
| A commentary review on the use of Normalized Difference Vegetation Index (NDVI) in the era of popular remote sensing.Crossref | GoogleScholarGoogle Scholar |
Huntington JL, Hegewisch KC, Daudert B, Morton CG, Abatzoglou JT, McEvoy DJ, Erickson T (2017) Climate Engine: cloud computing and visualization of climate and remote sensing data for advanced natural resource monitoring and process understanding. Bulletin of the American Meteorological Society 98, 2397–2410.
| Climate Engine: cloud computing and visualization of climate and remote sensing data for advanced natural resource monitoring and process understanding.Crossref | GoogleScholarGoogle Scholar |
ISFR (2021) India State of Forest Report. Forest Survey of India, Ministry of Environment, Forest & Climate Change, Government of India, Dehradun.
Jaafari A, Pourghasemi HR (2019) Factors influencing regional-scale wildfire probability in Iran: an application of random forest and support vector machine. In ‘Spatial modeling in GIS and R for Earth and Environmental sciences’. (Eds HR Pourghasemi, C Gokceoglu). pp. 607–619.
| Crossref |
Jafari Goldarag Y, Mohammadzadeh A, Ardakani AS (2016) Fire risk assessment using neural network and logistic regression. Journal of the Indian Society of Remote Sensing 44, 885–894.
| Fire risk assessment using neural network and logistic regression.Crossref | GoogleScholarGoogle Scholar |
Jain P, Coogan SCP, Subramanian SG, Crowley M, Taylor S, Flannigan MD (2020) A review of machine learning applications in wildfire science and management. Environmental Reviews 28, 478–505.
| A review of machine learning applications in wildfire science and management.Crossref | GoogleScholarGoogle Scholar |
Jolly WM, Cochrane MA, Freeborn PH, Holden ZA, Brown TJ, Williamson GJ, Bowman DM (2015) Climate-induced variations in global wildfire danger from 1979 to 2013. Nature Communications 6, 7537
| Climate-induced variations in global wildfire danger from 1979 to 2013.Crossref | GoogleScholarGoogle Scholar |
Juárez-Orozco SM, Siebe C, Fernández y Fernández D (2017) Causes and effects of forest fires in tropical rainforests: a bibliometric approach. Tropical Conservation Science 10, 1940082917737207
| Causes and effects of forest fires in tropical rainforests: a bibliometric approach.Crossref | GoogleScholarGoogle Scholar |
Kalantar B, Ueda N, Idrees MO, Janizadeh S, Ahmadi K, Shabani F (2020) Forest fire susceptibility prediction based on machine learning models with resampling algorithms on remote sensing data. Remote Sensing 12, 3682
| Forest fire susceptibility prediction based on machine learning models with resampling algorithms on remote sensing data.Crossref | GoogleScholarGoogle Scholar |
Kale MP, Ramachandran RM, Pardeshi SN, Chavan M, Joshi PK, Pai DS, et al. (2017) Are climate extremities changing forest fire regimes in India? An analysis using MODIS fire locations during 2003–2013 and gridded climate data of India meteorological department. Proceedings of the National Academy of Sciences, India – Section A: Physical Sciences 87, 827–843.
| Are climate extremities changing forest fire regimes in India? An analysis using MODIS fire locations during 2003–2013 and gridded climate data of India meteorological department.Crossref | GoogleScholarGoogle Scholar |
Kamarudin MH, Maple C, Watson T, Safa NS (2017) A logitboost-based algorithm for detecting known and unknown web attacks. IEEE Access 5, 26190–26200.
| A logitboost-based algorithm for detecting known and unknown web attacks.Crossref | GoogleScholarGoogle Scholar |
Krzywinksi M, Altman N (2017) Correction: Corrigendum: Classification and regression trees. Nature Methods 14, 928
| Correction: Corrigendum: Classification and regression trees.Crossref | GoogleScholarGoogle Scholar |
Kuhn M (2008) Building predictive models in R using the caret package. Journal of Statistical Software 28, 1–26.
| Building predictive models in R using the caret package.Crossref | GoogleScholarGoogle Scholar |
Kumar N, Kumar A (2020) Australian bushfire detection using machine learning and neural networks. In ‘2020 7th International Conference on Smart Structures and Systems (ICSSS)’. pp. 1–7. (IEEE)
| Crossref |
Lang N, Schindler K, Wegner JD (2019) Country-wide high-resolution vegetation height mapping with Sentinel-2. Remote Sensing of Environment 233, 111347
| Country-wide high-resolution vegetation height mapping with Sentinel-2.Crossref | GoogleScholarGoogle Scholar |
Lee S, Park I, Choi JK (2012a) Spatial prediction of ground subsidence susceptibility using an artificial neural network. Environmental Management 49, 347–358.
| Spatial prediction of ground subsidence susceptibility using an artificial neural network.Crossref | GoogleScholarGoogle Scholar |
Lee S, Song KY, Kim Y, Park I (2012b) Cartographie régionale du potentiel de productivité des aquifères à partir d’un système d’information géographique base sur un modèle de réseau de neurones artificiels. Hydrogeology Journal 20, 1511–1527.
| Cartographie régionale du potentiel de productivité des aquifères à partir d’un système d’information géographique base sur un modèle de réseau de neurones artificiels.Crossref | GoogleScholarGoogle Scholar |
Li J, Heap AD, Potter A, Daniell JJ (2011) Application of machine learning methods to spatial interpolation of environmental variables. Environmental Modelling and Software 26, 1647–1659.
| Application of machine learning methods to spatial interpolation of environmental variables.Crossref | GoogleScholarGoogle Scholar |
Lunardon N, Menardi G, Torelli N (2014) ROSE: a package for binary imbalanced learning. The R Journal 6, 79–89.
| ROSE: a package for binary imbalanced learning.Crossref | GoogleScholarGoogle Scholar |
Ma W, Feng Z, Cheng Z, Chen S, Wang F (2020) Identifying forest fire driving factors and related impacts in China using random forest algorithm. Forests 11, 507
| Identifying forest fire driving factors and related impacts in China using random forest algorithm.Crossref | GoogleScholarGoogle Scholar |
Maeda EE, Formaggio AR, Shimabukuro YE, Arcoverde GFB, Hansen MC (2009) Predicting forest fire in the Brazilian Amazon using MODIS imagery and artificial neural networks. International Journal of Applied Earth Observation and Geoinformation 11, 265–272.
| Predicting forest fire in the Brazilian Amazon using MODIS imagery and artificial neural networks.Crossref | GoogleScholarGoogle Scholar |
Magnussen S, Tomppo E, McRoberts RE (2010) A model-assisted k-nearest neighbour approach to remove extrapolation bias. Scandinavian Journal of Forest Research 25, 174–184.
| A model-assisted k-nearest neighbour approach to remove extrapolation bias.Crossref | GoogleScholarGoogle Scholar |
Martínez-Austria PF, Bandala ER, Patiño-Gómez C (2016) Temperature and heat wave trends in northwest Mexico. Physics and Chemistry of the Earth, Parts A/B/C 91, 20–26.
| Temperature and heat wave trends in northwest Mexico.Crossref | GoogleScholarGoogle Scholar |
Mayr MJ, Vanselow KA, Samimi C (2018) Fire regimes at the arid fringe: A 16-year remote sensing perspective (2000–2016) on the controls of fire activity in Namibia from spatial predictive models. Ecological Indicators 91, 324–337.
| Fire regimes at the arid fringe: A 16-year remote sensing perspective (2000–2016) on the controls of fire activity in Namibia from spatial predictive models.Crossref | GoogleScholarGoogle Scholar |
Milanović S, Marković N, Pamučar D, Gigović L, Kostić P, Milanović SD (2021) Forest fire probability mapping in eastern Serbia: Logistic regression versus random forest method. Forests 12, 5
| Forest fire probability mapping in eastern Serbia: Logistic regression versus random forest method.Crossref | GoogleScholarGoogle Scholar |
Mohajane M, Costache R, Karimi F, Pham QB, Essahlaoui A, Nguyen H, Laneve G, Oudija F (2021) Application of remote sensing and machine learning algorithms for forest fire mapping in a Mediterranean area. Ecological Indicators 129, 107869
| Application of remote sensing and machine learning algorithms for forest fire mapping in a Mediterranean area.Crossref | GoogleScholarGoogle Scholar |
Mozny M, Trnka M, Brázdil R (2021) Climate change driven changes of vegetation fires in the Czech Republic. Theoretical and Applied Climatology 143, 691–699.
| Climate change driven changes of vegetation fires in the Czech Republic.Crossref | GoogleScholarGoogle Scholar |
Murtaza G, Shuib L, Abdul Wahab AW, Mujtaba G, Nweke HF, Al-garadi MA, Zulfiqar F, Raza G, Azmi NA (2020) Deep learning-based breast cancer classification through medical imaging modalities: state of the art and research challenges. Artificial Intelligence Review 53, 1655–1720.
| Deep learning-based breast cancer classification through medical imaging modalities: state of the art and research challenges.Crossref | GoogleScholarGoogle Scholar |
Naderpour M, Rizeei HM, Ramezani F (2021) Forest fire risk prediction: a spatial deep neural network-based framework. Remote Sensing 13, 2513
| Forest fire risk prediction: a spatial deep neural network-based framework.Crossref | GoogleScholarGoogle Scholar |
Naghibi SA, Pourghasemi HR, Abbaspour K (2018) A comparison between ten advanced and soft computing models for groundwater qanat potential assessment in Iran using R and GIS. Theoretical and Applied Climatology 131, 967–984.
| A comparison between ten advanced and soft computing models for groundwater qanat potential assessment in Iran using R and GIS.Crossref | GoogleScholarGoogle Scholar |
Navarro G, Caballero I, Silva G, Parra PC, Vázquez Á, Caldeira R (2017) Evaluation of forest fire on Madeira Island using Sentinel-2A MSI imagery. International Journal of Applied Earth Observation and Geoinformation 58, 97–106.
| Evaluation of forest fire on Madeira Island using Sentinel-2A MSI imagery.Crossref | GoogleScholarGoogle Scholar |
Negara BS, Kurniawan R, Nazri MZA, Abdullah SNHS, Saputra RW, Ismanto A (2020) Riau forest fire prediction using supervised machine learning. Journal of Physics: Conference Series 1566, 012002
| Riau forest fire prediction using supervised machine learning.Crossref | GoogleScholarGoogle Scholar |
Park SY, Liu Y (2011) Robust penalized logistic regression with truncated loss functions. Canadian Journal of Statistics 39, 300–323.
| Robust penalized logistic regression with truncated loss functions.Crossref | GoogleScholarGoogle Scholar |
Pham BT, Pradhan B, Tien Bui D, Prakash I, Dholakia MB (2016) A comparative study of different machine learning methods for landslide susceptibility assessment: A case study of Uttarakhand area (India). Environmental Modelling & Software 84, 240–250.
| A comparative study of different machine learning methods for landslide susceptibility assessment: A case study of Uttarakhand area (India).Crossref | GoogleScholarGoogle Scholar |
Pham BT, Jaafari A, Avand M, Al-Ansari N, Dinh Du T, Yen HPH, Phong TV, Nguyen DH, Le HV, Mafi-Gholami D, Prakash I (2020) Performance evaluation of machine learning methods for forest fire modeling and prediction. Symmetry 12, 1022
| Performance evaluation of machine learning methods for forest fire modeling and prediction.Crossref | GoogleScholarGoogle Scholar |
Pourghasemi HR, Beheshtirad M, Pradhan B (2016) A comparative assessment of prediction capabilities of modified analytical hierarchy process (M-AHP) and Mamdani fuzzy logic models using Netcad-GIS for forest fire susceptibility mapping. Geomatics, Natural Hazards and Risk 7, 861–885.
| A comparative assessment of prediction capabilities of modified analytical hierarchy process (M-AHP) and Mamdani fuzzy logic models using Netcad-GIS for forest fire susceptibility mapping.Crossref | GoogleScholarGoogle Scholar |
Pourghasemi HR, Kariminejad N, Amiri M, Edalat M, Zarafshar M, Blaschke T, Cerda A (2020) Assessing and mapping multi-hazard risk susceptibility using a machine learning technique. Sci Rep 10, 3203
| Assessing and mapping multi-hazard risk susceptibility using a machine learning technique.Crossref | GoogleScholarGoogle Scholar |
Pourtaghi ZS, Pourghasemi HR, Rossi M (2015) Forest fire susceptibility mapping in the Minudasht forests, Golestan province, Iran. Environmental Earth Sciences 73, 1515–1533.
| Forest fire susceptibility mapping in the Minudasht forests, Golestan province, Iran.Crossref | GoogleScholarGoogle Scholar |
Pourtaghi ZS, Pourghasemi HR, Aretano R, Semeraro T (2016) Investigation of general indicators influencing on forest fire and its susceptibility modeling using different data mining techniques. Ecological Indicators 64, 72–84.
| Investigation of general indicators influencing on forest fire and its susceptibility modeling using different data mining techniques.Crossref | GoogleScholarGoogle Scholar |
Praveen B, Talukdar S, S, Mahato S, Mondal J, Sharma P, Islam ARMT, Rahman A, et al. (2020) Analyzing trend and forecasting of rainfall changes in India using non-parametrical and machine learning approaches. Sci Rep 10, 10342–10342.
| Analyzing trend and forecasting of rainfall changes in India using non-parametrical and machine learning approaches.Crossref | GoogleScholarGoogle Scholar |
Rajashekar G, Fararoda R, Reddy RS, Jha CS, Ganeshaiah KN, Singh JS, Dadhwal VK (2018) Spatial distribution of forest biomass carbon (above and below ground) in Indian forests. Ecological Indicators 85, 742–752.
| Spatial distribution of forest biomass carbon (above and below ground) in Indian forests.Crossref | GoogleScholarGoogle Scholar |
Reddy CS, Jha CS, Diwakar PG, Dadhwal VK (2015) Nationwide classification of forest types of India using remote sensing and GIS. Environmental Monitoring and Assessment 187, 777
| Nationwide classification of forest types of India using remote sensing and GIS.Crossref | GoogleScholarGoogle Scholar |
Rodrigues M, De la Riva J (2014) An insight into machine-learning algorithms to model human-caused wildfire occurrence. Environmental Modelling and Software 57, 192–201.
| An insight into machine-learning algorithms to model human-caused wildfire occurrence.Crossref | GoogleScholarGoogle Scholar |
Roteta E, Bastarrika A, Padilla M, Storm T, Chuvieco E (2019) Development of a Sentinel-2 burned area algorithm: Generation of a small fire database for sub-Saharan Africa. Remote Sensing of Environment 222, 1–17.
| Development of a Sentinel-2 burned area algorithm: Generation of a small fire database for sub-Saharan Africa.Crossref | GoogleScholarGoogle Scholar |
RStudio Team (2021) ‘RStudio: Integrated Development for R.’ (RStudio, PBC: Boston, MA) Available at http://www.rstudio.com/
Sachdeva S, Bhatia T, Verma AK (2018) GIS-based evolutionary optimized Gradient Boosted Decision Trees for forest fire susceptibility mapping. Natural Hazards 92, 1399–1418.
| GIS-based evolutionary optimized Gradient Boosted Decision Trees for forest fire susceptibility mapping.Crossref | GoogleScholarGoogle Scholar |
Sakr GE, Elhajj IH, Mitri G, Wejinya UC (2010) Artificial intelligence for forest fire prediction. In ‘2010 IEEE/ASME International Conference on Advanced Intelligent Mechatronics’, Montreal, QC, Canada. pp. 1311–1316. (IEEE)
| Crossref |
Sannigrahi S, Pilla F, Basu B, Basu AS, Sarkar K, Chakraborti S, Joshi PK, Zhang Q, Wang Y, Bhatt S, Bhatt A (2020) Examining the effects of forest fire on terrestrial carbon emission and ecosystem production in India using remote sensing approaches. Science of the Total Environment 725, 138331
| Examining the effects of forest fire on terrestrial carbon emission and ecosystem production in India using remote sensing approaches.Crossref | GoogleScholarGoogle Scholar |
Satir O, Berberoglu S, Donmez C (2016) Mapping regional forest fire probability using artificial neural network model in a Mediterranean forest ecosystem. Geomatics, Natural Hazards and Risk 7, 1645–1658.
| Mapping regional forest fire probability using artificial neural network model in a Mediterranean forest ecosystem.Crossref | GoogleScholarGoogle Scholar |
Sulova A, Joker Arsanjani J (2021) Exploratory analysis of driving force of wildfires in Australia: An application of machine learning within Google Earth Engine. Remote Sensing 13, 10
| Exploratory analysis of driving force of wildfires in Australia: An application of machine learning within Google Earth Engine.Crossref | GoogleScholarGoogle Scholar |
Swann ALS, Laguë MM, Garcia ES, Field JP, Breshears DD, Moore DJP, Saleska SR, Stark SC, Villegas JC, Law DJ, Minor DM (2018) Continental‐scale consequences of tree die‐offs in North America: Identifying where forest loss matters most. Environmental Research Letters 13, 055014
| Continental‐scale consequences of tree die‐offs in North America: Identifying where forest loss matters most.Crossref | GoogleScholarGoogle Scholar |
Syifa M, Panahi M, Lee CW (2020) Mapping of post-wildfire burned area using a hybrid algorithm and satellite data: the case of the Camp Fire wildfire in California, USA. Remote Sensing 12, 623
| Mapping of post-wildfire burned area using a hybrid algorithm and satellite data: the case of the Camp Fire wildfire in California, USA.Crossref | GoogleScholarGoogle Scholar |
Takeuchi W, Darmawan S, Shofiyati R, Khiem MV, Oo KS, Pimple U, Heng S (2015) Near-real time meteorological drought monitoring and early warning system for croplands in Asia. In ‘Asian Conference on Remote Sensing 2015: Fostering Resilient Growth in Asia’. Vol. 1, pp. 171–178.
USGCRP (2017) Climate Science Special Report: Fourth National Climate Assessment, Volume I. (Eds Wuebbles DJ, Fahey DW, Hibbard KA, Dokken DJ, Stewart C, Maycock TK) (US Global Change Research Program: Washington DC, USA) Available at https://www.nrc.gov/docs/ML1900/ML19008A410.pdf
van Wees D, van Der Werf GR, Randerson JT, Andela N, Chen Y, Morton DC (2021) The role of fire in global forest loss dynamics. Global Change Biology 27, 2377
| The role of fire in global forest loss dynamics.Crossref | GoogleScholarGoogle Scholar |
Vapnik V (1995) ‘The nature of statistical learning theory.’ (Springer Science & Business Media)
| Crossref |
Wahba G (1999) Support vector machines, reproducing kernel hilbert spaces and the randomized GACV. In ‘Advances in Kernel Methods Support Vector Learning’. (Eds S Bernhard, CJS Burges, AJ Smola) pp. 69–88. (MIT Press: Cambridge, MA)
Williams AP, Abatzoglou JT, Gershunov A, Guzman‐Morales J, Bishop DA, Balch JK, Lettenmaier DP (2019) Observed impacts of anthropogenic climate change on wildfire in California. Earth’s Future 7, 892–910.
| Observed impacts of anthropogenic climate change on wildfire in California.Crossref | GoogleScholarGoogle Scholar |
World Bank (2018) ‘Strengthening forest fire management in India.’ (World Bank: Washington DC)
World Bank Group (2021) ‘Climate risk country profile: India.’ (The World Bank Group)
Wu N, Zhang C, Bai X, Du X, He Y (2018) Discrimination of chrysanthemum varieties using hyperspectral imaging combined with a deep Convolutional Neural Network. Molecules 23, 2831
| Discrimination of chrysanthemum varieties using hyperspectral imaging combined with a deep Convolutional Neural Network.Crossref | GoogleScholarGoogle Scholar |
Wu X, Kumar V, Ross QJ, Ghosh J, Yang Q, Motoda H, McLachlan GJ, Ng A, Liu B, Yu PS, Zhou ZH, Steinbach M, Hand DJ, Steinberg D (2008) Top 10 algorithms in data mining. Knowledge and Information Systems 14, 1–37.
| Top 10 algorithms in data mining.Crossref | GoogleScholarGoogle Scholar |
Zhang G, Eddy Patuwo B, Hu MY (1998) Forecasting with artificial neural networks: The state of the art. International Journal of Forecasting 14, 35–62.
| Forecasting with artificial neural networks: The state of the art.Crossref | GoogleScholarGoogle Scholar |
Zhang G, Wang M, Liu K (2019) Forest fire susceptibility modeling using a convolutional neural network for Yunnan Province of China. International Journal of Disaster Risk Science 10, 386–403.
| Forest fire susceptibility modeling using a convolutional neural network for Yunnan Province of China.Crossref | GoogleScholarGoogle Scholar |
Zhang G, Wang M, Liu K (2021) Deep neural networks for global wildfire susceptibility modelling. Ecological Indicators 127, 107735
| Deep neural networks for global wildfire susceptibility modelling.Crossref | GoogleScholarGoogle Scholar |
Zhao Y, Ma J, Li X, Zhang J (2018) Saliency detection and deep learning based wildfire identification in UAV imagery. Sensors 18, 712
| Saliency detection and deep learning based wildfire identification in UAV imagery.Crossref | GoogleScholarGoogle Scholar |



