Monte Carlo-based ensemble method for prediction of grassland fire spread
Miguel G. CruzA Bushfire Dynamics and Applications, Climate Adaptation Flagship – CSIRO Sustainable Ecosystems, GPO Box 284, Canberra, ACT 2601, Australia. Email: miguel.cruz@csiro.au
B Bushfire Cooperative Research Centre, East Melbourne, VIC 3002, Australia.
International Journal of Wildland Fire 19(4) 521-530 https://doi.org/10.1071/WF08195
Submitted: 2 December 2008 Accepted: 25 September 2009 Published: 24 June 2010
Abstract
The operational prediction of fire spread to support fire management operations relies on a deterministic approach where a single ‘best-guess’ forecast is produced from the best estimate of the environmental conditions driving the fire. Although fire can be considered a phenomenon of low predictability and the estimation of input conditions for fire behaviour models is fraught with uncertainty, no error component is associated with these forecasts. At best, users will derive an uncertainty bound to the model outputs based on their own personal experience. A simple ensemble method that considers the uncertainty in the estimation of model input values and Monte Carlo sampling was applied with a grassland fire-spread model to produce a probability density function of rate of spread. This probability density function was then used to describe the uncertainty in the fire behaviour prediction and to produce probability-based outputs. The method was applied to a grassland wildfire case study dataset. The ensemble method did not improve the general statistics describing model fit but provided complementary information describing the uncertainty associated with the predictions and a probabilistic output for the occurrence of threshold levels of fire behaviour.
Acknowledgments
The author acknowledges the reviews and constructive suggestions provided by Stuart Mathews, Wendy Anderson and four anonymous reviewers, which strengthened the paper. Wendy Anderson’s contribution to the Appendix is also recognised.
Alexander ME , Cruz MG (2006) Evaluating a model for predicting active crown fire rate of spread using wildfire observations. Canadian Journal of Forest Research 36, 3015–3028.
| Crossref | GoogleScholarGoogle Scholar |
Araújo MB , New M (2007) Ensemble forecasting of species distributions. Trends in Ecology & Evolution 22, 42–47.
| Crossref | GoogleScholarGoogle Scholar |
Cheney NP , Gould JS (1995) Fire growth in grassland fuels. International Journal of Wildland Fire 5, 237–247.
| Crossref | GoogleScholarGoogle Scholar |
Cruz MG , Fernandes PM (2008) Development of fuel models for fire behaviour prediction in maritime pine (Pinus pinaster Ait.) stands. International Journal of Wildland Fire 17, 194–204.
| Crossref | GoogleScholarGoogle Scholar |
Gill AM , Zylstra P (2005) Flammability of Australian forests. Australian Forestry 68, 87–93.
Justus CG, Hargraves WR, Mikhail A , Graber D (1978) Methods for estimating wind speed frequency distributions. Journal of Applied Meteorology 17, 350–353.
| Crossref | GoogleScholarGoogle Scholar |
Keeves A , Douglas DR (1983) Forest fires in South Australia on 16 February 1983 and consequent future forest management aims. Australian Forestry 46, 148–162.
McNees SK (1992) The uses and abuses of ‘consensus’ forecasts. Journal of Forecasting 11, 703–710.
| Crossref |
Noble IK, Bary GAV , Gill AM (1980) McArthur’s fire-danger meters expressed as equations. Australian Journal of Ecology 5, 201–203.
| Crossref | GoogleScholarGoogle Scholar |
Sullivan AL , Knight IK (2001) Estimating error in wind speed measurements for experimental fires. Canadian Journal of Forest Research 31, 401–409.
| Crossref | GoogleScholarGoogle Scholar |
Taylor SW, Wotton BM, Alexander ME , Dalrymple GN (2004) Variation in wind and crown fire behaviour in a northern jack pine–black spruce forest. Canadian Journal of Forest Research 34, 1561–1576.
| Crossref | GoogleScholarGoogle Scholar |
Zhu Y (2005) Ensemble forecast: a new approach to uncertainty and predictability. Advances in Atmospheric Sciences 22, 781–788.
| Crossref |
A This appendix is the result of a collaboration of Wendy Anderson (UNSW@ADFA) and Miguel Cruz.
Appendix
In this appendixA, it is demonstrated through a Taylor series expansion that for the model of Cheney et al. (1997), or others with similar formulation, the predicted rate of spread by the deterministic method is essentially equal to the average rate of spread from the ensemble method. This is to say that a model of the form:
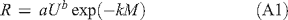
where a and b are constants, requires:
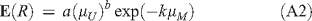
where E(R) is the expected (or mean) value of the random variable R, and μU and μM are the means of U and M respectively from the ensemble method.
Mathematically, we need to decide under what conditions
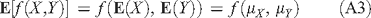
where X and Y are two random variables with means μX and μY and variances σX2 and σY2. Consider the Taylor series expansion of f(X, Y) around (μX, μY)
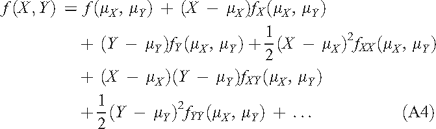
where fX(μX, μY) and fXX(μX, μY) are the first and second partial derivatives respectively of f with respect to X, fY(μX, μY) and fYY(μX, μY) are the first and second partial derivatives respectively of f with respect to Y, and fXX(μX, μY) is the partial derivative of f with respect to X and Y, all evaluated at (μX, μY).
Terms in higher-order derivatives have been omitted and should be relatively small.
Taking mathematical expectations, and remembering that E(X) = μX, E(Y) = μY, E(X – μX)2 = σX2, E(Y – μY)2 = σY2 and E(X – μX)(Y – μY) = σXY (where σXY2 is the covariance of X and Y) results in the following equation:
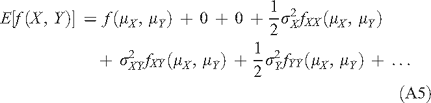
If X and Y are independent, σXY2 = 0. The approximate equity of A3 requires:
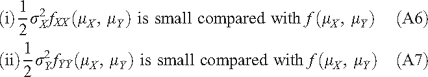
In the example above:
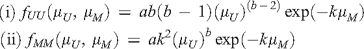
In case (i), the ratio of 
and 
.
It was assumed that σU ≅ 0.2μU, resulting in (σU)2 ≅ 0.04(μU)2. From this, the ratio becomes approximately (0.5)(0.04)b(b – 1). In Cheney et al. (1997), b = 0.844 for U10 > 5 km h–1, so the ratio of the terms is approximately –0.003. (Note that even with b = 2, the ratio would be 0.04, which is quite small.)
In case (ii), the ratio of 
and f(μU, μM) is 
.
The standard deviations of the temperature and vapour pressure distributions were set at 0.1 of their corresponding means. For the wildfire case study distribution in Fig. 2, this resulted in a moisture distribution with standard deviation σM = 0.44, and a mean of μM = 2.97. Thus σM ≅ 0.15μM, resulting in (σM)2 ≅ 0.0225(μM)2. The ratio becomes approximately (0.5)(0.0225)(μM)2k2. In Cheney et al. (1997), k = 0.108 for M < 20%, so the ratio of the terms is ∼0.001.
The small ratios indicate that 
is small compared with f(μX, μY), and 
is small compared with f(μX, μY), validating the approximate equity of Eqn A3, i.e. the predicted rate of spread by the deterministic method is essentially equal to the average rate of spread from the ensemble method.
