An examination of flame shape related to convection heat transfer in deep-fuel beds
Kara M. Yedinak A B D , Jack D. Cohen A C D , Jason M. Forthofer A and Mark A. Finney AA USDA Forest Service, Rocky Mountain Research Station, Missoula, MT 59808, USA.
B Laboratory of Atmospheric Research, Washington State University, Pullman, WA 99163, USA.
C Corresponding author. Email: jcohen@fs.fed.us
D Authors have contributed equally to this paper.
International Journal of Wildland Fire 19(2) 171-178 https://doi.org/10.1071/WF07143
Submitted: 29 September 2007 Accepted: 15 August 2008 Published: 31 March 2010
Abstract
Fire spread through a fuel bed produces an observable curved combustion interface. This shape has been schematically represented largely without consideration for fire spread processes. The shape and dynamics of the flame profile within the fuel bed likely reflect the mechanisms of heat transfer necessary for the pre-heating and ignition of the fuel during fire spread. We developed a simple laminar flame model for examining convection heat transfer as a potentially significant fire spread process. The flame model produced a flame profile qualitatively comparable to experimental flames and similar to the combustion interface of spreading fires. The model comparison to flame experiments revealed that at increasing fuel depths (>0.7 m), lateral flame extension was increased through transition and turbulent flame behaviour. Given previous research indicating that radiation is not sufficient for fire spread, this research suggests that flame turbulence can produce the convection heat transfer (i.e. flame contact) necessary for fire spread particularly in vertically arranged, discontinuous fuels such as shrub and tree canopies.
Additional keywords: crown fires, discontinuous fuels, laminar flame model, wildfire convection heat transfer.
Acknowledgements
We thank Ian Grob, Anita Hershman, Danielle Paige, Isaac Grenfell, Kyle Shannon and James Riser for their technical support in the development of this research.
Albini FA (1982) Response of free-burning fires to non-steady wind. Combustion Science and Technology 29, 225–241.
| Crossref | GoogleScholarGoogle Scholar |
Beer T (1995) Fire propagation in vertical stick arrays: the effects of wind. International Journal of Wildland Fire 5, 43–49.
| Crossref | GoogleScholarGoogle Scholar |
Fons WL (1946) Analysis of fire spread in light forest fuels. Journal of Agricultural Research 72, 93–120.
McCarter RJ , Broido A (1965) Radiative and convective energy from wood crib fires. Pyrodynamics 2, 65–85.
Van Wagner CE (1977) Conditions for the start and spread of crown fire. Canadian Journal of Forest Research 7, 23–34.
| Crossref | GoogleScholarGoogle Scholar |

Vogel M , Williams FA (1970) Flame propagation along matchstick arrays. Combustion Science and Technology 1, 429–436.
| Crossref | GoogleScholarGoogle Scholar |

Weber RO (1990) A model for fire propagation in arrays. Mathematical and Computer Modelling 13, 95–102.
| Crossref | GoogleScholarGoogle Scholar |

Weber RO (1991) Modelling fire spread through fuel beds. Progress in Energy and Combustion Science 17, 67–82.
| Crossref | GoogleScholarGoogle Scholar |

Appendix
Eqn A1 represents the Grashof number.
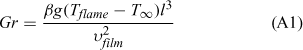
A Grashof number value of Gr ≥ 109 indicates turbulent natural convection (Quintiere 2006). By setting Gr = 109 and solving for the flow length, l we can estimate the flame height at which turbulent flow is expected:
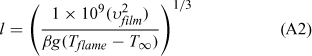
where Tflame = 1000 K; T∞ = 294 K; Tfilm = (Tflame + T∞)/2 = 647 K; g = 9.81 m s–2; β, fluid expansion coefficient; for an ideal gas, β ≈ 1/Tfilm = 1.48 × 10–3 K–1; νfilm, kinematic viscosity; νfilm(Tfilm) = 59.76 × 10–6 m2 s–1 (A4; Incopera and DeWitt 2002); l = 0.694 m (flow length).
The Grashof number analysis indicates that we should expect turbulent flame convection at lengths of 0.7 m and greater.


