Numerical study of a crown fire spreading toward a fuel break using a multiphase physical model

Baines PG (1990) Physical mechanisms for the propagation of surface fires. Mathematical and Computer Modelling  13, 83–94.
| Crossref | GoogleScholarGoogle Scholar | Cohen M, Rigolot E, Valette JC (2003) From the vegetation to the inputs of a fire model: fuel modelling for WUI Management. In ‘Proceedings of the international workshop “Forest fires in the Wildland–urban interface and rural areas in Europe: an integral planning and management challenge”, May 15 and 16 2003, Athens, Greece’. pp. 113–120. (Ed. G Xanthopoulos)

Di Blasi C (1993) Modeling and simulation of combustion processes of charring and non-charring solid fuels. Progress in Energy and Combustion Science  19, 71–104.
| Crossref | GoogleScholarGoogle Scholar | Dureau R (coord.) (2003) ‘Gestion des garrigues à chêne kermés sur coupures de combustible.’ Réseau Coupures de combustible RCC no. 8. (Editions de la Cardère: Morières, France)

Grishin AM (1997) ‘Mathematical modelling of forest fires and new methods of fighting them’. (Ed. FA Albini) (Publishing House of the Tomsk State University: Tomsk)

Haines DH (1982) Horizontal roll vortices and crown fires. Journal of Climate and Applied Meteorology  21, 751–763.
| Crossref | GoogleScholarGoogle Scholar | Klose W, Damm S, Wiest W (2000) Pyrolysis and activation of different woods: thermal analysis (TG/EGA) and formal kinetics. In ‘Proceedings of the fourth international symposium of catalytic and thermochemical conversions of natural organic polymers’, June 2000, Krasnoyarsk.

Larini M, Giroud F, Porterie B , Loraud J-C (1998) A multiphase formulation for fire propagation in heterogeneous combustible media. International Journal of Heat and Mass Transfer  41, 881–897.
| Crossref | GoogleScholarGoogle Scholar | Linn R, Winterkamp J, Edminster C, Colman J, Steinzig M (2003) Modeling interactions between fire and atmosphere in discrete element fuel beds. In ‘Proceedings of the fifth symposium on fire and forest meteorology’, November 2003, Orlando, FL.

Magnussen BF, Hjertager H (1976) On mathematical modeling of turbulent combustion with special emphasis on soot formation and combustion. In ‘Proceedings of the 16th symposium (international) on combustion’, pp. 719–729. (The Combustion Institute: Pittsburgh)

Morvan D , Dupuy JL (2001) Modeling of fire spread through a forest fuel bed using a multiphase formulation. Combustion and Flame  127, 1981–1994.
| Crossref | GoogleScholarGoogle Scholar | Morvan D, Tauleigne V, Dupuy JL (2002) Wind effects on wildfire propagation through a Mediterranean shrub. In ‘Proceedings of the fourth international conference on forest fire research’. (Ed. DX Viegas) (Millpress: Rotterdam)

Pagni PJ, Peterson TG (1973) Flame spread through porous fuels. In ‘Proceedings of the 14th symposium (international) on combustion’. pp. 1099–1107. (The Combustion Institute: Pittsburgh)

Pitts WM (1991) Wind effects on fires. Progress in Energy and Combustion Science  17, 83–134.
| Crossref | GoogleScholarGoogle Scholar | Rigolot E (2002) Fuel-break assessment with an expert appraisement approach. In ‘Proceedings of the fourth international conference on forest fire research’. (Ed. DX Viegas) (Millpress: Rotterdam)

Rigolot E, Costa M (Coord.) (2000) ‘Conception des coupures de combustible.’ Réseau Coupures de combustible RCC no. 4. (Editions de la Cardère: Morières, France)

Scott JH, Reinhardt ED (2001) ‘Assessing crown fire potential by linking models of surface and crown fire behavior.’ USDA-Forest Service, Rocky Mountain Research Station Research Paper RMRS-RP-29. (Fort Collins, CO)

Siegel R, Howell JR (1992) ‘Thermal radiation heat transfer.’ 3rd edn. (Taylor & Francis: Washington, DC)

Stocks BJ, Alexander ME , Lanoville RA (2004) Overview of the international crown fire modelling experiment (ICFME). Canadian Journal of Forest Research  34, 1543–1547.
| Crossref | GoogleScholarGoogle Scholar |

Tien CL , Lee SC (1982) Flame radiation. Progress in Energy and Combustion Science  8, 41–59.
| Crossref | GoogleScholarGoogle Scholar |

Van Wagner CE (1977) Conditions for the start and spread of crown fire. Canadian Journal of Forest Research  7, 23–34.


Weber RO (1991) Modelling fire spread through fuel beds. Progress in Energy and Combustion Science  17, 67–82.
| Crossref | GoogleScholarGoogle Scholar |

Yakhot V , Orszag SA (1986) Renormalization group analysis of turbulence. Journal of Scientific Computing  1, 3–51.
| Crossref | GoogleScholarGoogle Scholar |

Latin symbols

a_p radiation absorption coefficient of the gas–soot mixture (m⁻¹)

B Stefan-Boltzman constant (W m⁻² K⁻⁴)

C_p,s,k specific heat of the solid phase k (J kg⁻¹ K⁻¹)

D mass diffusivity (kg m⁻¹ s⁻¹)

F_i,s drag forces due to interactions between the solid phases and the gaseous phase (component in the i-direction) (kg m⁻² s⁻²)

g_i gravity acceleration (component in the i-direction) (m s⁻²)

h enthalpy (J m⁻³)

h_conv heat transfer coefficient (convection between a solid phase k and the gaseous phase) (W m⁻² K⁻¹)

I radiative intensity (W sr⁻¹ m⁻²)

J irradiance (W m⁻²)

k turbulent kinetic energy (m² s⁻²)

M_s,k,α production of the α chemical species due to thermal degradation of the solid phase k (kg m⁻³ s⁻¹)

t time (s)

T temperature (K)

u_i gas velocity (component in the i-direction) (m s⁻¹)

x_i cartesian coordinate in the i-direction (m)

Y mass fraction

Greek symbols

α volume fraction

ϵ dissipation rate (m² s⁻³)

ρ density (kg m⁻³)

σ_i,j stress tensor (kg m⁻¹ s⁻²)

σ_s,k surface area-to-volume ratio of the solid phase k (m⁻¹)

ω reaction rate (kg m⁻³ s⁻¹)

Subscripts

α chemical species

g gaseous phase

k solid phase

The following set of balance equations governs the evolution of each solid phase (or fuel family) k:

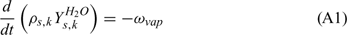
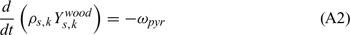
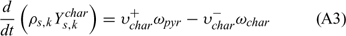
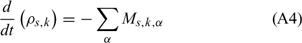
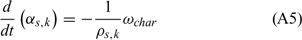
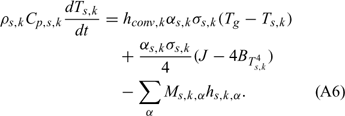
Equations (A1), (A2) and (A3) govern the evolution of the mass fractions of water, dry material and char respectively, resulting from drying, pyrolysis and char combustion processes. The terms on the right hand side of equation (A3) are written assuming that the rate of production of char is a known fraction (υ_char) of the pyrolysis reaction rate and that a part of char is lost in the plume to form soot particles (υ_char⁺ = υ_char − υ_soot · ω_char represents the rate of char combustion. Equation (A4) represents the mass balance of the solid phase. Equation (A5) governs the evolution of the volume fraction, assuming that the reduction of the volume of solid fuel particles results only from char combustion (when the particle undergoes drying and pyrolysis processes, its volume remains constant). The first and second terms on the right hand side of the energy balance equation (A6) represent the contributions resulting from convective exchanges with the surrounding gas and from radiation heat transfer respectively. The third term represents energy transfers due to mass transfers between the solid phase and the gaseous phase.

Basically, the transport equations of the gaseous phase are the Navier-Stokes equations generalised to a compressible, reactive and multiphase flow:

Mass:

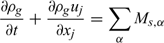
Momentum:

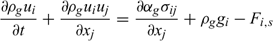
Energy:

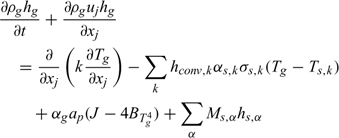
Chemical species:

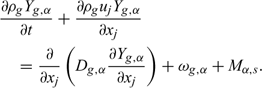
To take into account the turbulence effects, these basic transport equations are time-averaged using the Favre formalism and a turbulent diffusion model (RNG k–ϵ) is introduced.

The radiation intensity I is calculated solving the following radiation transfer equation:

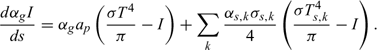
The irradiance J, which appears in the equations of energy balance, is formally calculated at each point through an integration of the radiation intensity over the space solid angle: