Investigating the Haines Index using parcel model theory
Mary Ann JenkinsDepartment of Earth and Space Science and Engineering, Faculty of Pure and Applied Science, York University, 4700 Keele Street, Toronto, ON, M3J 1P3, Canada. Email: maj@yorku.ca
International Journal of Wildland Fire 13(3) 297-309 https://doi.org/10.1071/WF03055
Submitted: 22 July 2003 Accepted: 22 March 2004 Published: 16 November 2004
Abstract
By using parcel model theory to construct a two-dimensional parameter space formed by low-level atmospheric stability and moisture, a simple framework on which to examine certain fire parcel properties associated with vertical column development is established. This framework is used to investigate if the Haines Index has some skill at predicting wildfire severity, where wildfire severity is assumed to be directly connected to vertical column development and the result of significant fire parcel ascent. By modeling the ascent of a moist, entraining fire parcel in four different background states—a 3 km deep boundary layer, a 2 km deep boundary layer, a 3 km deep boundary layer topped by an inversion layer, and a 2 km deep boundary layer topped by an inversion layer—the study shows that parcel properties that describe ascent and vertical column development are most significant when the boundary layer temperature lapse rate is near adiabatic and lower-level atmospheric humidity is relatively high. A shallower instead of a deeper boundary layer lowers parcel ascent, and an upper-level inversion lowers parcel ascent even further. This study shows that entraining fire parcel properties and magnitudes associated with significant ascent do not necessarily correspond to a Haines Index for a potential for high fire severity. The results suggest that the Haines Index may need to be refined or reformed depending on the stability and humidity in the boundary layer and vertical structure of the atmosphere. This study is a start to understanding the influence of the background state on fire parcel convection and an attempt to explain how the Haines Index works from an elementary but physical point of view.
Brotak EA (1993) Low-level weather conditions preceding major wildfires. US Department of Agriculture Forest Service. Fire Management Notes 53–54, 23–26.
do not indicate supersaturated air; whether real fire parcels become and remain supersaturated are not known. It is also assumed that cloud droplets evaporate immediately when the relative humidity falls below 100%. These conditions imply that, when the air is saturated, qv = qs, where qs = qs(T, p) is the saturation mixing ratio, and when unsaturated, qc = 0.
During the saturation adjustment,



The net condensation rate C is unknown, and is eliminated from this set of equations by forming the following set of equations,
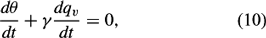

which imply that
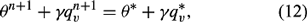
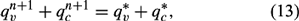
where
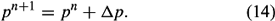
Here n is the previous time level, n + 1 the current time level, and Δp the change in the parcel’s pressure. The pn+1 is found by integrating the hydrostatic pressure equation, pn+1 = pn−
It is now assumed that the air is saturated so that qvn+1 = qs(T*, pn+1). Although this closes the set, it must be solved iteratively since qs is a non-linear function of T. Instead, to obtain a direct solution, qs is expanded in a Taylor series about qs(T*, pn+1) and all terms of second and higher order are neglected. The result is
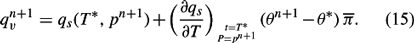
Equations (12), (13), (14), and (15) constitute a closed set of equations. To solve this set, A, B, C, and D are substituted for known terms or expressions at time level n and pressure pn + 1:


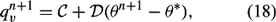
where
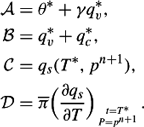
The saturation water vapor mixing ratio qs is determined by
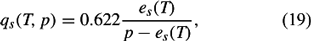
where es is the saturation vapor pressure. The saturation vapor pressure es is found by
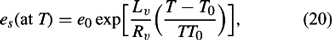
the integrated Clausius–Clapeyron equation, where Rv = 4.615 J kg−1 K−1 is the gas constant for moist air, T0 = 273.15 K, and e0 (es at T0) = 0.611 kPa. The Clausius–Clapeyron equation,

is used to determine des/dT. Equations (16) and (18) are combined to eliminate qvn+1 and to solve for θn+1:
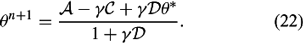
Then θn+1 is substituted into equation (18) to solve for qvn+1, and qvn+1 is substituted into equation (17) to solve for qcn+1. If qcn+1 ≠ 0 then θn+1, qvn+1, and qcn+1 are the values for a saturated air parcel. If qcn+1 = 0, then the ascending parcel is not saturated and



The horizontal momentum carried by rising thermals differs from the environmental momentum, and the differences in horizontal momentum create horizontal shears. The turbulence generated by the shear at the parcel’s surface causes mixing or entrainment across the convective cell or parcel boundary. To model entrainment, represented by Di in equations (3) to (6), where entrainment is considered to take place during the first stage of ascent, the following assumptions are made: air is mixed instantaneously (continuous) and completely (homogeneous) across the parcel, and entrainment is lateral. Let β represent the value of any (arbitrary) conservable variable per unit mass of air. The change of β due to entrainment of environmental air of value
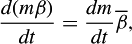
which can be written
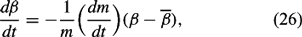
where m is the mass of the entraining air parcel. Equation (26) can determine the change of β due to entrainment when the entrainment rate 1/m(dm/dt) is available. Conservation of mass for a spherical parcel of radius r implies that the entrainment rate is
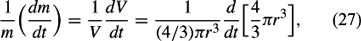
where V is volume, and it is assumed that density is not changed by lateral entrainment. For dr/dt = (dz/dt)ϵ = wϵ, where wϵ is the entrainment velocity normal to the parcel’s surface, and z is the height of the center of the thermal, equation (27) becomes
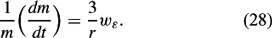
Laboratory thermals in a neutral environment are observed to expand along a cone, where the radius is proportional to z:
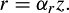
If dz = w dt and dr/dt = αrw, then equation (28) becomes
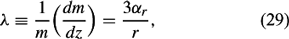
where λ, the fractional rate of entrainment, depends only on r. Observations indicate that r is approximately constant for a given thermal, but varies widely among different thermals. Laboratory experiments suggest that αr ~0.2. Substituting dz = w, dt and λ into equation (26) gives
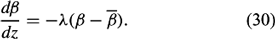
Equation (30) forms the basis for incorporating entrainment effects into the parcel model. The fractional rate of entrainment λ is a specified input parameter. For cloud studies, values for λ can range from 0.05 km−1 to 0.20 km−1. Entrainment rates are large for fire convection and, in this study, λ = 0.20 km−1, an entrainment rate that is valid for active cloud convection. Although not entirely realistic, equation (30) represents another way that the air parcel interacts with its surroundings. Therefore, for entrainment during the first stage of ascent (or descent), θ, qv*, qc*, and w* are modified using
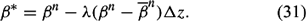
Note that there is no dependence on the time interval. Turbulent mixing comes before the saturation adjustment process.
Up to now −gqc, the drag force due to cloud water, has been neglected when calculating w in equation (6) and Ar has been set to zero when calculating qc in equation (5). Following Lord and Arakawa (1980), dqc/dz = 1/w dqc/dt, where Ar/w ≡ c0, and c0 is known as the autoconversion parameter. The c0 is simply specified as c0 = 0.002 m−1, the empirical value used by Lord and Arakawa (1980) in the Arakawa–Schubert cumulus parameterization. Lord and Arakawa (1980) assume that any rain water formed immediately falls out of the parcel and, after the first stage of ascent, the cloud water mixing ratio is calculated using
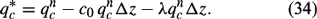
This calculation takes place before the second stage of saturation adjustment.
By introducing w = dz/dt, equation (32) can be written
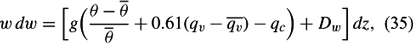
which when integrated over height z0 to z becomes
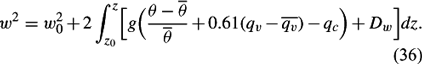
To compute parcel vertical velocity, equation (36) is used and written in the form
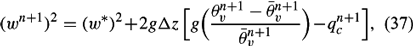
with no dependence on the time interval. For each Δz, the parcel undergoes adiabatic ascent, during which entrainment or turbulent mixing occurs. Parcel then undergoes saturation adjustment. Some of the condensation in the parcel gets converted into rain, which drops immediately out of the parcel. While the condensation remaining in the parcel acts as a drag force in equation (37).


