KAPAS II: simulation of peatland wildfires with daily variations of peat moisture content
Dwi M. J. Purnomo A , Sebastian Apers B , Michel Bechtold
B , Michel Bechtold  B , Parwati Sofan
B , Parwati Sofan  C and Guillermo Rein
C and Guillermo Rein  A *
A *
A Department of Mechanical Engineering, Leverhulme Centre for Wildfires, Environment and Society, Imperial College London, London, SW7 2AZ, UK.
B Department of Earth and Environmental Sciences, KU Leuven, Heverlee, Belgium.
C Research Center for Remote Sensing, National Research and Innovation Agency of Indonesia (BRIN), Jakarta, Indonesia.
International Journal of Wildland Fire 32(6) 823-835 https://doi.org/10.1071/WF22109
Submitted: 29 June 2022 Accepted: 10 March 2023 Published: 21 April 2023
© 2023 The Author(s) (or their employer(s)). Published by CSIRO Publishing on behalf of IAWF. This is an open access article distributed under the Creative Commons Attribution 4.0 International License (CC BY).
Abstract
Background: Peatland wildfires involve flaming vegetation and smouldering peat. The smouldering behaviour strongly depends on peat moisture, which can change significantly and quickly due to weather or human activities.
Aims: We simulated wildfire in peatlands at the field scale and, for the first time, included daily variations of peat moisture.
Methods: We developed KAPAS II, a cellular automaton that includes flaming and smouldering, and coupled it with PEATCLSM (Catchment Land Surface Model) for peatland hydrology.
Key results: Compared with the satellite observations over 90 days of a 2018 wildfire in Borneo, KAPAS II predictions provide good agreement for burn scars (79% accuracy) and for the number of smouldering hotspots (85% accuracy). For the same burn scar, the model predicts that 54 ha of peat would smoulder when considering daily moisture variations, but only 12 ha if moisture was constant. Simulations at the same Borneo location, but in different years from 2000 to 2019, show the importance of seasons and climate events like El Niño.
Conclusion: Temporal variations in peat moisture, which are strongly influenced by weather and climate, are important to predict the behaviour and severity of peatland wildfires.
Implications: This model improves our understanding of wildfire behaviour in peatlands and can contribute to its mitigation.
Keywords: cellular automaton, fire, KAPAS, modelling, moisture, peat, smouldering, soil, wildfire.
Introduction
Peatland wildfires release carbon stored in peat, thus resulting in a positive feedback that contributes to climate change (Rein 2013). These wildfires involve both flaming and smouldering, with flames mainly burning surface vegetation (such as trees, shrubs, crops and grasses) and smouldering mainly burning peat, the organic soil underneath the vegetation. Smouldering wildfires can be sustained for weeks to months (Rein 2013; Turetsky et al. 2015; Lin et al. 2019; Rein and Huang 2021). Compared with flaming, smouldering spreads more slowly and at a lower temperature but releases a higher yield of pollutants, both gas and particulate matter (Rein 2013; Hu et al. 2018). An example where the importance of smouldering is clear is the 1997 peatland wildfires in southeast Asia. These wildfires emitted 0.8–2.56 Gt C (gigatonnes of Carbon) to the atmosphere, which is equivalent to 13–40% of global anthropogenic carbon emissions in that year, but only ~0.1 Gt C of these emissions resulted from flaming (Page et al. 2002).
The peat moisture content (MC), which in this paper is referred to as the gravimetric MC if not stated otherwise, plays a prominent role in the behaviour of smouldering wildfires (Rein 2013; Christensen et al. 2020; Lin et al. 2021). In natural peatlands, the peat MC changes temporally owing to weather and seasonal variations that can be increased by anthropogenic activities (Waddington et al. 2015; Bechtold et al. 2020; Goldstein et al. 2020). Because these temporal variations can be large within a short time span (daily, even hourly, Waddington et al. 2015; Bechtold et al. 2020; Goldstein et al. 2020) and because smouldering wildfires can sustain themselves for weeks to months (Rein 2013; Scholten et al. 2021), understanding the effects of temporal peat MC variations on smouldering behaviours is important.
Research on smouldering wildfires at the field scale is limited (Purnomo et al. 2021; Widyastuti et al. 2021; Yuan et al. 2021). The complexity and spatiotemporal extents of peatland wildfires prevent state-of-the-art wildfire models from properly simulating these phenomena. While physics-based computational models (e.g. computational fluid dynamics models) are too computationally expensive for field-scale scenarios (Purnomo et al. 2021), semiphysical and empirical models (e.g. the Fire Area Simulator model; Finney 1998) lack the ability to couple flaming and smouldering (Purnomo et al. 2021).
Here, we used cellular automata (CA), which use simple rules rather than complex physics-based equations (von Neumann 1967; Wolfram 1984), to simulate peatland wildfires that involve both flaming and smouldering. Despite being simpler than other models and thus requiring fewer equations and fewer resources, sufficiently accurate results can be achieved with CA (Alexandridis et al. 2008; Fernandez-Anez et al. 2019). CA consider a grid of cells that can be in different states (e.g. unburned, burning, or burned). The state of each grid cell is updated at discrete time steps by following a set of simple rules.
Purnomo et al. (2021) successfully simulated both flaming and smouldering in peatland wildfires at the field scale over a 3-month period; however, they did not consider temporal variations in peat MC. Owing to the long lifespan of smouldering wildfires and the significant changes in peat MC that can occur within a short time span, the model produced in Purnomo et al. (2021), KAPAS,1 insufficiently captured realistic peatland conditions and thus led to inaccurate simulations. In addition, KAPAS can be used with only one set of spatial and temporal resolutions in the computational domain, which must be equal to the resolutions used in the model calibration. Each time the simulation requires a different spatial or temporal resolution, KAPAS must be recalibrated with this new resolution; otherwise, its predictions could become unrealistic (e.g. resulting in smouldering that spreads a few orders of magnitude faster than the expected spread rate). This problem occurs in most CA fire models (Purnomo 2022).
Here, we further developed KAPAS to simulate field-scale peatland wildfires by integrating temporally varying peat MC and allowing simulations at any spatiotemporal resolution. We used remote sensing data to derive the model input parameters (e.g. the vegetation type and density) and a peat-specific land surface model to estimate the temporal peat MC variations. We validated our CA model against satellite observations of burn scars, which in this paper are referred to as flaming burn scars if not stated otherwise, and smouldering hotspots. We then used our model to investigate the effects of daily and seasonal peat moisture variations on smouldering wildfires over contrasting climatic conditions.
Materials and methods
Cellular automata
CA are discrete computational models that use simple rules to simulate physical phenomena (von Neumann 1967; Wolfram 1984). In these models, the domain is a matrix of cells in which each grid cell can be in one of n discrete states that is updated at discrete time steps. The updating process of these states follows a set of rules (e.g. stochastic, empirical and physical rules) that affects both the cell and its nearby cells (called a neighbourhood). The set of rules and the neighbourhood are selected based on the phenomenon being simulated (Karafyllidis and Thanailakis 1997; Belcher et al. 2010; Collin et al. 2011; Fernandez-Anez et al. 2019).
In the initial work on modelling peatland wildfires with CA, the KAPAS model developed in Purnomo et al. (2021) employed stochastic rules called bond percolation. In the bond percolation concept, the flow of information from one entity to adjacent entities occurs with a certain probability (Favier 2004; Purnomo 2022). In the context of wildfire modelling, the bond percolation concept allows a fire to spread from one cell to adjacent cells with a certain probability representing the flammability of the fuel, where higher probabilities correspond to higher fuel flammability levels, thus facilitating a faster spread rate (Purnomo 2022). Owing to the probabilistic rules in the bond percolation CA model, when this model is run repeatedly with identical input parameters, the simulation results reflect stochastic uncertainty, and the results obtained from multiple repetitions (of simulations with identical input parameters) differ. This trait can mimic the uncertainty observed in nature, for example the uncertainty caused by landscape heterogeneity.
In this work, we used the bond percolation rules with a Moore neighbourhood (in which the eight cells directly surrounding a considered cell are included in the neighbourhood, forming a 3 × 3 square grid), similar to that used in KAPAS (Purnomo et al. 2021). However, we implemented significant modifications to these rules to improve the accuracy and applicability of KAPAS. We refer to the updated model as KAPAS II, as this new model has a similar approach and is used for the same purpose as the initial KAPAS model (to model flaming and smouldering wildfires) developed in Purnomo et al. (2021).
States and rules of the KAPAS II model
KAPAS II considers the same five possible states as the model developed in Purnomo et al. (2021) for each cell: surface vegetation (SV), flaming vegetation (FV), exposed peat (EP), smouldering peat (SP) and burned peat (BP) (Fig. 1). EP represents a state in which the cell has lost its surface vegetation owing to flaming but has intact peat soil because smouldering peat fails to ignite.

|
At the initial time step (t = 0), the fire is ignited at a specific location to initiate the FV state. The FV cells then ignite the neighbouring vegetation with a probability of Pf and may ignite the underlying peat (SP) with a probability of Pt (see Fig. 1). A higher Pf value corresponds to a faster flaming spread rate, whereas a higher Pt value corresponds to nucleation (i.e. multiple ignitions of hotspots that arise at randomly distributed locations) of more smouldering hotspots. If the FV fails to ignite the peat, the cell adopts the EP state. An SP cell spreads at a rate dependent on the Ps value (smouldering spread probability) and eventually extinguishes with a probability of Pe, thus becoming BP.
Following Fernandez-Anez et al. (2019) and Purnomo et al. (2021), in the KAPAS II model, we use separate surface and soil layers in the cells (see Fig. 1) to enable the simulation of smouldering spread underneath unburned vegetation or firebreaks (if a flammable peat layer is present between a firebreak and the water table or mineral soil). By applying two separate layers, the cells in the soil layer can become smouldering peat, although in the surface layer, neither unburned vegetation nor firebreaks change state. The transition of flaming vegetation on the surface resulting from underlying smouldering is not considered in KAPAS II, as this would require the inclusion of additional rules involving the transition from smouldering to flaming, which misses the objective of KAPAS II. The flaming of peat is unlikely (Huang and Rein 2015; Lin et al. 2019); thus, it is not considered in KAPAS II.
Input parameters and validation datasets
We simulated a peatland wildfire in Borneo (located at 3.087°S, 113.991°E) that started on 21 September 2018 and was fully extinguished on 10 October 2018, which was selected owing to the availability of the data. Fig. 2 shows the progression of the flaming wildfire captured by the Sentinel-2 satellite (Copernicus 2022). These satellite images were obtained by using false-colour urban composites that clearly distinguish among surface vegetation, burn scars and flames (Stavrakoudis et al. 2020). The black colour in Fig. 2 represents the burn scar, whereas the red areas represent regions of flames. The light green colour represents a non-combustible region such as a firebreak or burned area that resulted from previous wildfires that were not considered in this research.

|
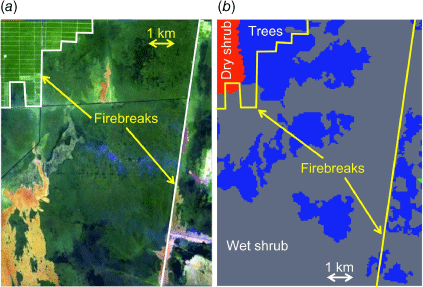
The data obtained from Sentinel-2 were used to estimate the burn scar in the validation process. In the model, the shape formed by EP cells corresponded to the burn scar. We used the seed-fill algorithm (Khayal et al. 2011) to detect burn scar pixels (black colour) from the satellite images shown in Fig. 2. The burn scar also shows the locations of firebreaks, which serve to stop flames from spreading. Firebreaks are indicated by the abrupt stop of a flaming wildfire, thus causing the burn scar to exhibit smooth edges (see Day 20 in Fig. 2). Fig. 3a shows the landscape distribution, including the estimated locations of firebreaks before the flames began (on 8 September 2018).
|
KAPAS II considers three different surface vegetation types: dry shrubs, wet shrubs and trees (shown in Fig. 3b), following Ferraz et al. (2019), who used field sampling and satellite observations to estimate vegetation types. KAPAS II also considers the rain and wind conditions to simulate flaming wildfires. We used meteorological data from a local weather station to obtain daily precipitation, wind speed and wind direction data (measured 6 m above the surface). This weather station is located at 2.220°S, 113.951°E, ~93 km north of the landscape under study (BMKG 2018). For the wind direction, we used the convention of direction of origin; thus, for instance, a south-eastern wind describes wind coming from the southeast and moving northwest. These meteorological phenomena significantly change over short time spans (hourly or even shorter); however, these daily data are the only locally available data. KAPAS II can be run with higher temporal resolution of meteorological data (e.g. hourly) if available.
We considered the vegetation density in KAPAS II (see Fig. 4). We classified the vegetation density based on Normalized Difference Vegetation Index data (NDVI, a surface vegetation greenness index) as shown in Fig. 4a, which are commonly used to estimate vegetation density (Camps-Valls et al. 2021), obtained from Sentinel-2 (Copernicus 2022). However, we considered only three classes of vegetation density, recently burned, regrown or intact vegetation, corresponding to the methods of Alexandridis et al. (2008). Therefore, the values shown in Fig. 4a were reclassified into three classes: values ranging from 0 to 0.2 corresponded to recently burned vegetation, 0.2–0.4 indicated regrown vegetation, and 0.4–0.65 indicated intact vegetation (as shown in Fig. 4b). Recently burned vegetation corresponds to vegetation that was burned in recent previous wildfires; regrown vegetation corresponds to previously burned vegetation that has started to regrow; and intact vegetation refers to fuel that has not been affected by recent wildfires (see Fig. 3a, in which the green colour in the landscape consists of dark and light greens). Fig. 4c shows the vegetation density classification used in the model. Although the entire region in the landscape under study consists of peatlands, the black region in Fig. 4c was not considered in the model because it is completely separated by firebreaks (see Fig. 3a), inhibiting flame spread into the black region. We selected NDVI data collected at the start of the wildfire (on 21 September 2018), and therefore, the data represented the actual ground conditions.

|
The peat MC data were obtained from simulations conducted with the peat-specific land surface model in Apers et al. (2022), using the tropical version of the peat-specific land surface model developed by Bechtold et al. (2019). The model in Apers et al. (2022) was specifically developed and extensively evaluated for tropical peatland conditions and was shown to perform best over southeast Asian peatlands. This model was based on the Catchment Land Surface Model (CLSM) of the NASA GEOS (Goddard Earth Observing System) Earth System Modelling framework and has two modules, one for drained tropical peatlands (PEATCLSMTrop,Drain) and one for natural tropical peatlands (PEATCLSMTrop,Nat); these different peatland types have distinct hydrological conditions and thus have different peat MC characteristics (Apers et al. 2022). Canal construction had been under way in central Kalimantan since the 1990s (Ritzema et al. 2014), and we found a number of canals inside our study area based on the canal map produced by Dadap (2020); therefore, we assumed that the peatland under the study area was drained. From this assumption, the PEATCLSMTrop,Drain model in Apers et al. (2022) was used to obtain the peat MC data for KAPAS II. We used the soil surface MC (0–5 cm depth) instead of a deeper MC, because the ignition of smouldering wildfires most of the time occurs at the surface.
The MC information obtained from the model in Apers et al. (2022) was volumetric (volume-based), whereas that used in KAPAS II is gravimetric (mass-based). Thus, to obtain gravimetric MC data, we divided the volumetric MC by the peat bulk density (in g/cm3). The peat bulk density is a function of the peat solid density and porosity. We assumed the peat solid density to be 1.5 g/cm3, adopting the value reported by Huang and Rein (2017). The porosity of peat in natural peatlands varies significantly with depth; at the surface, porosity can exceed 0.8, whereas at deeper points (~50 cm), it can be less than 0.5 (Rezanezhad et al. 2016). Although the peat porosity described in Rezanezhad et al. (2016) corresponds to non-tropical peat, a study in Indonesian tropical peatlands revealed that the peat porosity at a 50 cm depth was approximately 0.41 (Islami et al. 2018). In KAPAS II, we selected the average of surface (0.8) and deep (0.41) peat porosity values; thus, a porosity of 0.61. This value is lower than 0.9 (Huang and Rein 2015), the commonly used value in smouldering models that focus on the porosity of surface peat. However, the peat porosity used in KAPAS II is similar to that used in Apers et al. (2022) (0.68). From these selected values, the peat bulk density in KAPAS II is 0.585 g/cm3; thus, the obtained volumetric MC was divided by 0.585 to convert to gravimetric MC.
Whereas we used satellite burn scar data to validate the flaming component in the KAPAS II model, we used a remote sensing algorithm developed by Sofan et al. (2020), called Tropical Peatland Combustion ALgorithm (ToPeCAL), to detect smouldering hotspots to validate the smouldering model component. ToPeCAL performs arithmetic and logic operations on short-wave infrared (SWIR) data from Sentinel-2 to detect smouldering wildfires that are separated from flaming wildfires. Fig. 5 shows the smouldering hotspots that were detected using ToPeCAL and used to validate the smouldering component of the KAPAS II model. However, we consider only the number of smouldering hotspots, rather than the shape of the smouldering burn scar (which is the output of ToPeCAL) when validating our model. This indicates that we validated the model based only on the ignition of smouldering without considering smouldering spread. We did not validate the spread because it can occur undetected and even in the subsurface, thus invalidating detection results obtained via satellite remote sensing.

|
Model calibration
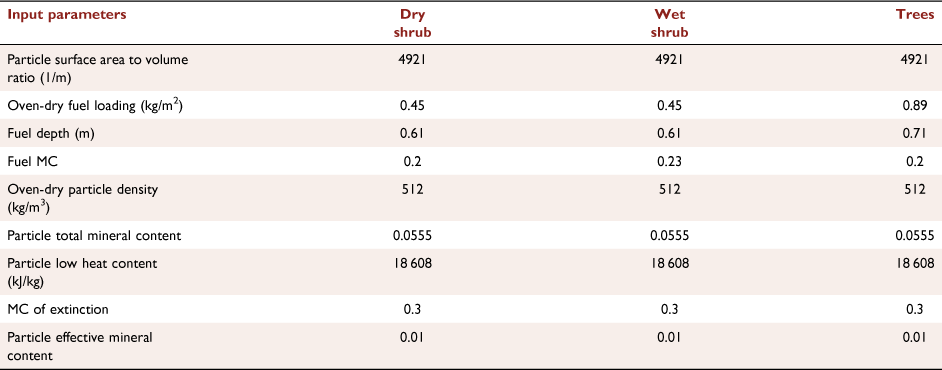
KAPAS II predictions are dependent on the values of the main probabilities (Pf, Pt, Ps and Pe). Pf (Eqn 1) is a function of the flaming spread rate (R), spatiotemporal resolution (λ), vegetation density factor (αd) and wind factor (αw). The λ term contains the information of the cell size (Δx) and time step (Δt) and is formulated in Eqn 2. R is formulated based on the Rothermel model for flame spread (Rothermel 1972) under no-wind conditions. Table A1 in the appendix lists the values of input parameters used to calculate R. R is translated into a probability value depending on λ, which then becomes the base value of Pf (i.e. if αd and αw are equal to 1). This translation was performed by optimising the probability value to have KAPAS II predict flaming spread rate of R given the cell size and time step. Fig. 6a clearly shows that R and the base Pf value reflect a log–log relationship with slopes independent of λ. With this method, any cell size and time step can be used in the model with a less than 15% relative absolute error, thus significantly improving the previous model (KAPAS) developed in Purnomo et al. (2021).
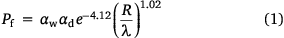

KAPAS II considers the effect of wind (αw) as formulated in Eqn 3. αw is based on the wind factor formulation by Rothermel for the maximum downwind spread rate and on the 2D propagation behaviour (Rothermel 1972; Alexander 1985; Finney 1998). αw is a function of the wind coefficient (Φw), the direction of flame spread relative to the wind direction (θ), the ellipse parameters: semiminor axis (a), semimajor axis (b), and linear eccentricity (c), and the correction factor (φ). Φw is determined based on the Rothermel model, whereas the ellipse parameters are formulated using Eqns A1–A3 in the appendix and depend on the wind speed (U) following Finney (1998). These formulation represent an improved version of the wind effect in KAPAS (Purnomo et al. 2021), because KAPAS did not maintain an elliptical shape under high wind speeds.
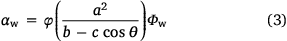
The correction factor of the wind effect (φ) is required to maintain agreement in the downwind spread rate with Rothermel. Without this correction factor, the spread rate differs significantly, up to 90%. From the calibration, we found that φ is linearly correlated with U, as shown in Eqn 4, and the variations that arise owing to different λ values remain within 10% (see Fig. 6b).
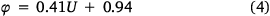
The effect of the vegetation density (αd), which was not considered in KAPAS, is determined by calibrating the model against satellite-derived burn scar data. KAPAS II considers three different vegetation density classes (intact, regrown and recently burned), and the αd value for regrown vegetation was calibrated. The αd value for intact vegetation was set to 1, and that for recently burned vegetation was set to 0 for the sake of simplicity. From the calibration process, we found that for αd = 0.01 for the regrown vegetation, flame spread predictions provide good agreement with the satellite-derived burn scar data (<25% relative absolute error).

|
The flaming to smouldering transition probability (Pt) and smouldering extinction probability (Pe) values in KAPAS II were set following KAPAS. Pt is a function of peat MC, as in Eqn 5, using the ignition probability formulated in Frandsen (1997) (see Fig. 6c), and Pe is selected to be 5 × 10−10, sustaining a smouldering fire for approximately 3 months (the typical duration of the wildfire season in Indonesia; Huijnen et al. 2016). The formulation of smouldering spread probability (Ps) in KAPAS II was also adapted from KAPAS and the values fit the experiments of Huang et al. (2016) and Prat-Guitart et al. (2016); however, different spatiotemporal resolution values (λ) were input into KAPA1S II to enable modelling at any spatial or temporal resolution of the computational domain (thus improving the KAPAS model). We found that Ps is linearly correlated in log–log axis with MC (R2 = 0.89) and has a slope independent of λ (see Fig. 6d); Ps is formulated in Eqn 6. The MC values used in Eqns 5, 6 change daily based on the model in Apers et al. (2022); thus, Pt and Ps also change daily. KAPAS II considers temporal variations in peat MC but assumes it is spatially uniform across the entire landscape. Peat MC also varies spatially (Prat-Guitart et al. 2017); however, whereas the spatial peat MC variations can be considered in KAPAS II, there are currently no reliable peat moisture data at fine spatial resolution and the resolution of the model in Apers et al. (2022) was too coarse for the landscape under study (5-km resolution).
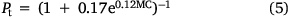
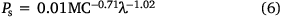
In this work, we used a domain with a 45-m cell size and a 1200-s time step (λ = 135 m/h). To limit computational costs, we selected the coarsest cell size that still gave a higher than 80% accuracy on flaming and smouldering spread rate predictions, resulting in the domain having ~200 000 cells. The time step was determined based on the stability criteria of Courant–Friedrichs–Lewy to avoid the diffusion of any entity exceeding one cell at one time step (Lautenberger 2013).
We verified the KAPAS II predictions in a simpler domain of uniform fuel with constant wind. We compared KAPAS II spread rate predictions of the flames for different wind speed with the Rothermel model (Fig. A1a) and of the smouldering at different moisture content with the experiments of Huang et al. (2016) and Prat-Guitart et al. (2016) (Fig. A1b). We found that for both flaming and smouldering spread, KAPAS II predictions are within 20% relative absolute error of the benchmarks.
Results and discussions
Fig. 7 shows snapshots of KAPAS II predictions at four different times from Day 3 to Day 90. Fig. 7a–c corresponds to the spread of flames, whereas Fig. 7d corresponds to the spread of smouldering. On Day 3 after the start of the wildfire (Fig. 7a), flames had burned a relatively small area of surface vegetation, and the shape of the burn scar was quite circular, with non-smoothness at the perimeter caused by the stochastic approach of KAPAS II. The south-eastern wind of 7 km/h had only a slight effect on the burn scar. On Day 8 (Fig. 7b), the western wind (see Fig. 4) caused eastward spread of the flames. The low vegetation density caused the formation of an unburned patch in the north of the burn scar. Smouldering hotspots began to form at this stage. We refer to the smouldering hotspots formation by flames as nucleation, and smouldering spread grows these hotspots. On Day 20 (Fig. 7c), all flames had become extinguished, and the nucleation of smouldering hotspots stopped. KAPAS II predicted that the flames were extinguished on Day 15. For comparison purposes, Fig. 7c shows a snapshot of Day 20, a day for which a clear satellite image was available (on the other days, satellite images were either unavailable or significantly cloud-covered). The extinction of the flames corresponded with 14.7 mm of precipitation on Day 15. This precipitation continued for 3 days. Therefore, we argue that the flames and hotspot nucleation lasted for 16 days (Day 0–15). From Day 16, hotspots started to spread and grew larger, and at the end of the simulation on Day 90, the hotspots had significantly enlarged, and some had merged (Fig. 7d).

|
Fig. 8a–c shows a comparison between the satellite-based burn scars in Fig. 2 and those predicted by KAPAS II (Fig. 7a–c) at three different times (Days 3, 8 and 20). In the figure, the red lines represent the perimeter of the actual burn scar observed by the satellite. The true positive and true negative terms represent accurate predictions in which the burn scars observed by the satellite and predictions both indicated burned or unburned conditions, respectively. False positives correspond to an area that was predicted to be burned but was not burned in the satellite observation, and false negatives indicate regions that were not predicted to be burned but were observed to be burned by the satellite; both of these were considered inaccurate predictions. The flames burned approximately 8734 ha of vegetation in the 25 700-ha study area. KAPAS II simulated the flame spread that resulted in burn scars with a 29.8% share of true positives, 49.2% true negatives, 16.9% false positives and 4.1% false negatives compared with the burn scar observed by the satellite at the end of the wildfire (Fig. 8c). Therefore, a Cohen’s kappa value (a shape similarity indicator) of 0.57 was achieved, corresponding to reasonable agreement between KAPAS II predictions and observations (Sun et al. 2021). The main reason for the errors is the effect of wind. This can clearly be seen in Fig. 8a, b, where the burn scars observed by the satellite were elongated, whereas the simulated burn scars were significantly less elongated. We argue that this discrepancy resulted from KAPAS II considering the daily average wind speed and direction, whereas in reality, both the wind speed and direction vary significantly over the course of a day, especially when gusty winds occur. The flame spread predictions from KAPAS II were of similarly accuracy to the predictions from FARSITE (see Fig. 8d); FARSITE achieved a 32.9% share of true positives, 47.5% true negatives, 17.3% false positives and 2.3% false negatives, thus a Cohen’s kappa value of 0.61.
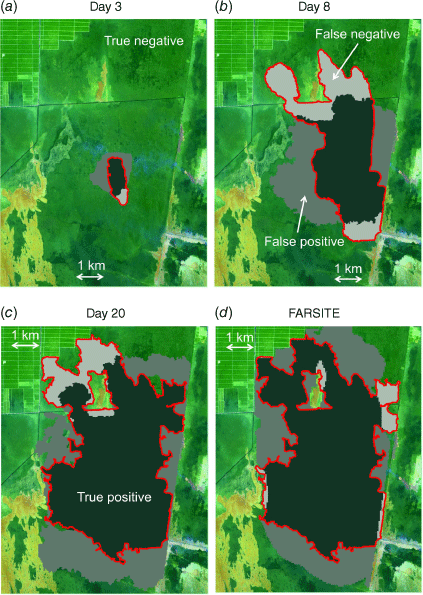
|
We found that KAPAS II overestimated the burn scars by 30%, as KAPAS II predicted that flames burned 11 143 ha of vegetation (see Fig. 9a). After 16 days, the area burned by flames did not change; thus, it is not presented in Fig. 9a. We considered that the flames only lasted for 16 days (owing to precipitation); thus, both predictions and observations were compared based on Day 16 of flaming instead of Day 20 (Day 20 corresponds to the day clear satellite images were available). While flames spread, smouldering hotspots were nucleated, as shown in Fig. 9b. We validated the smouldering component of KAPAS II by comparing the number of smouldering hotspots at different times against satellite observations (see Fig. 5). The 61 predicted hotspots agreed well with the observed 53 hotspots, which means a relative error of 15%. KAPAS II is the only model that can predict nucleation accurately against satellite observations.

|
The discrepancies in the locations of hotspots between the predictions and observations may have stemmed from the actual spatial non-uniformity of peat MC, which is not considered in KAPAS II. This is supported by the number of new smouldering hotspots observed on Day 8 (42 new hotspots), which decreased over 75% on Day 16 (11 new hotspots), as shown in Fig. 5, although the burn scar from flames was similar, indicating that the region where flames spread during Day 8 had drier peat compared with the region within the burn scar on Day 16. Day 20 in Fig. 5 corresponds to Day 16 in this comparison because we argue that the flames stopped on Day 16. Meanwhile, KAPAS II predicted that the numbers of hotspots nucleated on Day 8 (27 hotspots) and Day 16 (34 hotspots) only differed by 25%.
Fig. 10a shows the evolution of the smouldering burned area. The magenta shade indicates the area under the smouldering nucleation regime (during flame spread), whereas the cyan shade indicates the area under the smouldering growth regime (after the flames were extinguished). Because of both nucleation and growth, the smouldering burned area increased exponentially with time, but this increase was slower during the growth regime than the nucleation regime. Overall, KAPAS II predicted that smouldering had burned a total of 54 ha of peat 90 days after the start of the wildfire.

|
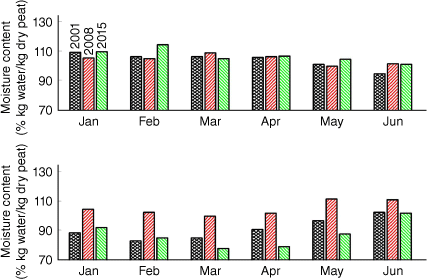
Peat MC could significantly change over short time; for instance, as shown in the error bars in Fig. 10b, which represent the range of daily peat MC variations within 1 week. We analysed the importance of temporal peat MC variations by comparing the KAPAS II predictions with daily peat MC variations, a transient MC scenario, and the predictions with constant peat MC, a constant MC scenario. In the constant MC scenario, the peat MC was assumed to be constant at 83% kg water/kg dry peat (the average peat MC calculated over 90 days; see Fig. 10b). We found that the exponential increase of smouldering burned area in nucleation and growth regimes prevailed in both transient MC and constant MC scenarios. However, the smouldering area was significantly smaller in the constant MC scenario (12 ha) than in the transient MC scenario (54 ha). This finding emphasises the importance of implementing temporal peat MC variations.
We further used KAPAS II with transient MC to predict the smouldering burned area, nucleated over the same burn scar, if it happened in different months in the years 2000–2019. Each individual case runs for 90 days. A total of 240 cases were considered; the first case goes from January 2000 to March 2000, whereas the last case is from December 2019 to February 2020. Each of the cases had different temporal peat MC variations that were estimated with the drained version of the model in Apers et al. (2022) (see Fig. A2 for examples).
Fig. 11a shows that the smouldering burned area by growth regime is linearly proportional to the burned area by nucleation regime (R2 = 0.98). However, Fig. 11b shows that the burned area by growth regime decreases exponentially with the monthly averaged peat MC during the nucleation period (R2 = 0.93), but independent of the monthly averaged peat MC during the growth period (R2 = 0.05). Therefore, the peat MC during the nucleation period is the crucial factor determining the total smouldering area. This inverse exponential correlation between peat MC during the nucleation period and smouldering burned area, which is highly dependent on the number of hotspots, agrees with the experiments of Frandsen (1997) in which the probability of a smouldering nucleation exponentially decreases with MC. The maximum difference of peat MC identified between the nucleation and growth periods shown in Fig. 11a, b is less than 20%. Thus, this finding might not apply when a very large difference of peat MC occurs.

|
Fig. 11c shows the temporal evolution patterns of the smouldering areas predicted for different months and years. The smouldering area varied significantly and ranged from 0 to 93 ha. The smouldering area is minimal if the flames spread in the wet season, between November and May, and it significantly increases in the dry season. In the wet season, owing to the relatively high peat MC, smouldering hotspots were less likely to be nucleated; thus, some cases exhibited a smouldering area of 0 ha, whereas in the dry season, the peat became drier and more vulnerable to nucleation. This temporal pattern is mainly controlled by peat MC, thus strongly indicating the importance of temporal MC variations.
When a strong La Niña event occurred, the smouldering area was smaller than 10 ha throughout the year (see 2008 in Fig. 11c). During an El Niño event, the smouldering area significantly increased (see 2015 in Fig. 11c). The maximum smouldering area predicted for the dry season of a strong El Niño year (2015) was 93 ha, whereas in a year without El Niño (e.g. 2001), it was 48 ha (see Fig. 11c). The unique findings on the effect of different seasons on smouldering area indicate that seasonal peat MC variations, which are influenced by climate, determine the severity of smouldering wildfires.
Conclusions
We integrated CA and field data to simulate flaming and smouldering wildfires in peatland at the field scale in KAPAS II, and for the first time, we considered temporal peat MC variations. We simulated a peatland wildfire that occurred in Borneo in September 2018 and found that within 90 days, 54 ha of peat was affected by smouldering. When considering a constant peat MC, the smouldering burned area was significantly underestimated (12 ha), emphasising the importance of temporal peat MC variations.
We used KAPAS II to predict smouldering burned areas for fires that began in different months and years between 2000 and 2019 (240 cases); each case simulates 90 days. The smouldering burned area varied significantly and ranged from 0 to 93.4 ha; the area was below 10 ha if the flames began during the wet season and above 40 ha if the flames began during the dry season. We found that the nucleation of smouldering hotspot by flames is crucial for determining overall damage to peatlands. Wet peat during the nucleation period prevents the formation of smouldering hotspots and greatly minimises the overall damage.
In La Niña years, the smouldering burned areas are less than 10 ha throughout the year. In strong El Niño events, the smouldering burned area during the dry season would double compared with years without El Niño. For instance, in 2015 (a strong El Niño year), the smouldering burned area was 93 ha, whereas in 2001 (a year without El Niño), it was only 48 ha. These findings show that the significant seasonal peat MC variations, which are affected by climate, greatly determine the extent of smouldering wildfires. The modelling methods presented in this study provide a tool for predicting wildfire spread in peatlands, allow faster-than-real-time simulations, inform peatland management and thus can contribute to the mitigation of carbon emissions and haze-related adversities resulting from wildfires.
Data availability
The data that support this study are available on request.
Conflicts of interests
The authors declare no conflicts of interest.
Declaration of funding
This research was sponsored by European Research Council (ERC) Consolidator Grant HAZE (682587), Indonesian Endowment Fund for Education (LPDP), and by the Research Foundation Flanders (FWO, G095720N). Computer resources and services used for PEATCLSM simulations were provided by the High Performance Computing system of the Vlaams Supercomputer Center funded by FWO and the Flemish Government.
References
Alexander ME (1985) Estimating the length-to-breadth ratio of elliptical forest fire patterns. In ‘8th Conference on Fire and Forest Meteorology’, Detroit, MI. pp. 287–304. (Society of American Foresters: Detroit, MI)Alexandridis A, Vakalis D, Siettos CI, Bafas G V (2008) A cellular automata model for forest fire spread prediction: The case of the wildfire that swept through Spetses Island in 1990. Applied Mathematics and Computation 204, 191–201.
| A cellular automata model for forest fire spread prediction: The case of the wildfire that swept through Spetses Island in 1990.Crossref | GoogleScholarGoogle Scholar |
Alexandridis A, Russo L, Vakalis D, Bafas G V, Siettos CI (2011) Wildland fire spread modelling using cellular automata: Evolution in large-scale spatially heterogeneous environments under fire suppression tactics. International Journal of Wildland Fire 20, 633–647.
| Wildland fire spread modelling using cellular automata: Evolution in large-scale spatially heterogeneous environments under fire suppression tactics.Crossref | GoogleScholarGoogle Scholar |
Apers S, De Lannoy GJM, Baird AJ, Cobb AR, Dargie GC, del Aguila Pasquel J, Gruber A, Hastie A, Hidayat H, Hirano T, Hoyt AM, Jovani‐Sancho AJ, Katimon A, Kurnain A, Koster RD, Lampela M, Mahanama SPP, Melling L, Page SE, Reichle RH, Taufik M, Vanderborght J, Bechtold M (2022) Tropical Peatland Hydrology Simulated With a Global Land Surface Model. Journal Of Advances In Modeling Earth Systems 14, e2021MS002784
| Tropical Peatland Hydrology Simulated With a Global Land Surface Model.Crossref | GoogleScholarGoogle Scholar |
Bechtold M, De Lannoy GJM, Koster RD, Reichle RH, Mahanama SP, Bleuten W, Bourgault MA, Brümmer C, Burdun I, Desai AR, Devito K, Grünwald T, Grygoruk M, Humphreys ER, Klatt J, Kurbatova J, Lohila A, Munir TM, Nilsson MB, Price JS, Röhl M, Schneider A, Tiemeyer B (2019) PEAT-CLSM: A Specific Treatment of Peatland Hydrology in the NASA Catchment Land Surface Model. Journal of Advances in Modeling Earth Systems 11, 2130–2162.
| PEAT-CLSM: A Specific Treatment of Peatland Hydrology in the NASA Catchment Land Surface Model.Crossref | GoogleScholarGoogle Scholar |
Bechtold M, De Lannoy GJM, Reichle RH, Roose D, Balliston N, Burdun I, Devito K, Kurbatova J, Strack M, Zarov EA (2020) Improved groundwater table and L-band brightness temperature estimates for Northern Hemisphere peatlands using new model physics and SMOS observations in a global data assimilation framework. Remote Sensing of Environment 246, 111805
| Improved groundwater table and L-band brightness temperature estimates for Northern Hemisphere peatlands using new model physics and SMOS observations in a global data assimilation framework.Crossref | GoogleScholarGoogle Scholar |
Belcher CM, Yearsley JM, Hadden RM, McElwain JC, Rein G (2010) Baseline intrinsic flammability of Earth’s ecosystems estimated from paleoatmospheric oxygen over the past 350 million years. Proceedings of the National Academy of Sciences 107, 22448–22453.
| Baseline intrinsic flammability of Earth’s ecosystems estimated from paleoatmospheric oxygen over the past 350 million years.Crossref | GoogleScholarGoogle Scholar |
BMKG (2018) Data Online - Pusat Database. Available at https://dataonline.bmkg.go.id/data_iklim
Camps-Valls G, Campos-Taberner M, Moreno-Martínez Á, Walther S, Duveiller G, Cescatti A, Mahecha MD, Muñoz-Marí J, García-Haro FJ, Guanter L, Jung M, Gamon JA, Reichstein M, Running SW (2021) A unified vegetation index for quantifying the terrestrial biosphere. Science Advances 7, eabc7447
| A unified vegetation index for quantifying the terrestrial biosphere.Crossref | GoogleScholarGoogle Scholar |
Christensen EG, Fernandez-Anez N, Rein G (2020) Influence of soil conditions on the multidimensional spread of smouldering combustion in shallow layers. Combustion and Flame 214, 361–370.
| Influence of soil conditions on the multidimensional spread of smouldering combustion in shallow layers.Crossref | GoogleScholarGoogle Scholar |
Collin A, Bernardin D, Séro-Guillaume O (2011) A physical-based cellular automaton model for forest-fire propagation. Combustion Science and Technology 183, 347–369.
| A physical-based cellular automaton model for forest-fire propagation.Crossref | GoogleScholarGoogle Scholar |
Copernicus (2022) Sentinel data, processed by the European Space Agency. Available at https://apps.sentinel-hub.com/eo-browser/?zoom=12&lat=-3.07853&lng=113.98528&themeId=DEFAULT-THEME&visualizationUrl=https%3A%2F%2Fservices.sentinel-hub.com%2Fogc%2Fwms%2Fbd86bcc0-f318-402b-a145-015f85b9427e&datasetId=S2L2A&fromTime=2018-09-28T00%3A00%3A00.000Z&toTime=2018-09-28T23%3A59%3A59.999Z&layerId=4-FALSE-COLOR-URBAN&demSource3D=%22MAPZEN%22
Dadap N (2020) Drainage Canals in Southeast Asian Peatland, Index Map. Stanford Digital Repository. Available at https://earthworks.stanford.edu/catalog/stanford-zy089tj2215
Favier C (2004) Percolation model of fire dynamic. Physics Letters A 330, 396–401.
| Percolation model of fire dynamic.Crossref | GoogleScholarGoogle Scholar |
Fernandez-Anez N, Christensen K, Frette V, Rein G (2019) Simulation of fingering behavior in smoldering combustion using a cellular automaton. Physical Review E 99, 023314
| Simulation of fingering behavior in smoldering combustion using a cellular automaton.Crossref | GoogleScholarGoogle Scholar |
Ferraz A, Saatchi S, Xu L, Hagen S, Chave J, Yu Y, Meyer V, Garcia M, Silva C, Roswintiarti O, Samboko A, Sist P, Walker S, Pearson T, Wijaya A, Sullivan F, Rutishauser E, Hoekman D, Ganguly S (2019) ‘Aboveground Biomass, Landcover, and Degradation, Kalimantan Forests, Indonesia, 2014.’ (Oak Ridge National Laboratory Distributed Active Archive Center: Oak Ridge, TN, USA)
| Crossref |
Finney MA (1998) FARSITE: Fire Area Simulator – Model Development and Evaluation. (USDA Forest Service: MT)
Frandsen WH (1997) Ignition probability of organic soils. Canadian Journal of Forest Research 27, 1471–1477.
| Ignition probability of organic soils.Crossref | GoogleScholarGoogle Scholar |
Goldstein JE, Graham L, Ansori S, Vetrita Y, Thomas A, Applegate G, Vayda AP, Saharjo BH, Cochrane MA (2020) Beyond slash-and-burn: The roles of human activities, altered hydrology and fuels in peat fires in Central Kalimantan, Indonesia. Singapore Journal of Tropical Geography 41, 190–208.
| Beyond slash-and-burn: The roles of human activities, altered hydrology and fuels in peat fires in Central Kalimantan, Indonesia.Crossref | GoogleScholarGoogle Scholar |
Hu Y, Fernandez-Anez N, Smith TEL, Rein G (2018) Review of emissions from smouldering peat fires and their contribution to regional haze episodes. International Journal of Wildland Fire 27, 293–312.
| Review of emissions from smouldering peat fires and their contribution to regional haze episodes.Crossref | GoogleScholarGoogle Scholar |
Huang X, Rein G (2015) Computational study of critical moisture and depth of burn in peat fires. International Journal of Wildland Fire 24, 798–808.
| Computational study of critical moisture and depth of burn in peat fires.Crossref | GoogleScholarGoogle Scholar |
Huang X, Rein G (2017) Downward spread of smouldering peat fire: The role of moisture, density and oxygen supply. International Journal of Wildland Fire 26, 907–918.
| Downward spread of smouldering peat fire: The role of moisture, density and oxygen supply.Crossref | GoogleScholarGoogle Scholar |
Huang X, Restuccia F, Gramola M, Rein G (2016) Experimental study of the formation and collapse of an overhang in the lateral spread of smouldering peat fires. Combustion and Flame 168, 393–402.
| Experimental study of the formation and collapse of an overhang in the lateral spread of smouldering peat fires.Crossref | GoogleScholarGoogle Scholar |
Huijnen V, Wooster MJ, Kaiser JW, Gaveau DLA, Flemming J, Parrington M, Inness A, Murdiyarso D, Main B, Van Weele M (2016) Fire carbon emissions over maritime southeast Asia in 2015 largest since 1997. Scientific Reports 6, 26886
| Fire carbon emissions over maritime southeast Asia in 2015 largest since 1997.Crossref | GoogleScholarGoogle Scholar |
Islami N, Irianti M, Azhar , Nor M, Fakhrudin (2018) Geophysical survey for groundwater potential investigation in peat land area, Riau, Indonesia. IOP Conference Series: Earth and Environmental Science 144, 012001
| Geophysical survey for groundwater potential investigation in peat land area, Riau, Indonesia.Crossref | GoogleScholarGoogle Scholar |
Karafyllidis I, Thanailakis A (1997) A model for predicting forest fire spreading using cellular automata. Ecological Modelling 99, 87–97.
| A model for predicting forest fire spreading using cellular automata.Crossref | GoogleScholarGoogle Scholar |
Khayal MSH, Khan A, Bashir S, Khan FH, Aslam S (2011) Modified new algorithm for seed filling. Journal of Theoretical and Applied Information Technology 26, 28–32.
Lautenberger C (2013) Wildland fire modeling with an Eulerian level set method and automated calibration. Fire Safety Journal 62, 289–298.
| Wildland fire modeling with an Eulerian level set method and automated calibration.Crossref | GoogleScholarGoogle Scholar |
Lin S, Sun P, Huang X (2019) Can peat soil support a flaming wildfire? International Journal of Wildland Fire 28, 601–613.
| Can peat soil support a flaming wildfire?Crossref | GoogleScholarGoogle Scholar |
Lin S, Liu Y, Huang X (2021) How to build a firebreak to stop smouldering peat fire: Insights from a laboratory-scale study. International Journal of Wildland Fire 30, 454–461.
| How to build a firebreak to stop smouldering peat fire: Insights from a laboratory-scale study.Crossref | GoogleScholarGoogle Scholar |
Null J (2021) ‘El Niño and La Niña Years and Intensities.’ (Golden Gate Weather Service)
Page SE, Siegert F, Rieley JO, Boehm HD V, Jaya A, Limin S (2002) The amount of carbon released from peat and forest fires in Indonesia during 1997. Nature 420, 61–65.
| The amount of carbon released from peat and forest fires in Indonesia during 1997.Crossref | GoogleScholarGoogle Scholar |
Prat-Guitart N, Rein G, Hadden RM, Belcher CM, Yearsley JM (2016) Propagation probability and spread rates of self-sustained smouldering fires under controlled moisture content and bulk density conditions. International Journal of Wildland Fire 25, 456–465.
| Propagation probability and spread rates of self-sustained smouldering fires under controlled moisture content and bulk density conditions.Crossref | GoogleScholarGoogle Scholar |
Prat-Guitart N, Belcher CM, Thompson DK, Burns P, Yearsley JM (2017) Fine-scale distribution of moisture in the surface of a degraded blanket bog and its effects on the potential spread of smouldering fire. Ecohydrology 10, e1898
| Fine-scale distribution of moisture in the surface of a degraded blanket bog and its effects on the potential spread of smouldering fire.Crossref | GoogleScholarGoogle Scholar |
Purnomo DMJ (2022) Cellular Automata Simulations of Field-Scale Flaming and Smouldering Wildfires in Peatlands. PhD thesis, Imperial College London, United Kingdom.
Purnomo DMJ, Bonner M, Moafi S, Rein G (2021) Using cellular automata to simulate field-scale flaming and smouldering wildfires in tropical peatlands. Proceedings of the Combustion Institute 38, 5119–5127.
| Using cellular automata to simulate field-scale flaming and smouldering wildfires in tropical peatlands.Crossref | GoogleScholarGoogle Scholar |
Rein G (2013) Smouldering Fires and Natural Fuels. In ‘Fire Phenomena and the Earth System’. (Ed. CM Belcher) pp. 15–33. (Wiley and Sons)
| Crossref |
Rein G, Huang X (2021) Smouldering wildfires in peatlands, forests and the arctic: Challenges and perspectives. Current Opinion in Environmental Science & Health 24, 100296
| Smouldering wildfires in peatlands, forests and the arctic: Challenges and perspectives.Crossref | GoogleScholarGoogle Scholar |
Rezanezhad F, Price JS, Quinton WL, Lennartz B, Milojevic T, Van Cappellen P (2016) Structure of peat soils and implications for water storage, flow and solute transport: A review update for geochemists. Chemical Geology 429, 75–84.
| Structure of peat soils and implications for water storage, flow and solute transport: A review update for geochemists.Crossref | GoogleScholarGoogle Scholar |
Ritzema H, Limin S, Kusin K, Jauhiainen J, Wösten H (2014) Canal blocking strategies for hydrological restoration of degraded tropical peatlands in Central Kalimantan, Indonesia. Catena 114, 11–20.
| Canal blocking strategies for hydrological restoration of degraded tropical peatlands in Central Kalimantan, Indonesia.Crossref | GoogleScholarGoogle Scholar |
Rothermel RC (1972) A mathematical model for predicting fire spread in wildland fuels. USDA Forest Service, Intermountain Forest and Range Experiment Station, Research Paper INT-RP-115. (Ogden, UT) Available at https://www.fs.usda.gov/treesearch/pubs/32533
Scholten RC, Jandt R, Miller EA, Rogers BM, Veraverbeke S (2021) Overwintering fires in boreal forests. Nature 593, 399–404.
| Overwintering fires in boreal forests.Crossref | GoogleScholarGoogle Scholar |
Sofan P, Bruce D, Jones E, Khomarudin MR, Roswintiarti O (2020) Applying the tropical peatland combustion algorithm to Landsat-8 Operational Land Imager (OLI) and Sentinel-2 Multi Spectral Instrument (MSI) imagery. Remote Sensing 12, 3958
| Applying the tropical peatland combustion algorithm to Landsat-8 Operational Land Imager (OLI) and Sentinel-2 Multi Spectral Instrument (MSI) imagery.Crossref | GoogleScholarGoogle Scholar |
Stavrakoudis D, Katagis T, Minakou C, Gitas IZ (2020) Automated Burned Scar Mapping Using Sentinel-2 Imagery. Journal of Geographic Information System 12, 221–240.
| Automated Burned Scar Mapping Using Sentinel-2 Imagery.Crossref | GoogleScholarGoogle Scholar |
Sun L, Xu C, He Y, Zhao Y, Xu Y, Rui X, Xu H (2021) Adaptive forest fire spread simulation algorithm based on cellular automata. Forests 12, 1431
| Adaptive forest fire spread simulation algorithm based on cellular automata.Crossref | GoogleScholarGoogle Scholar |
Turetsky MR, Benscoter B, Page S, Rein G, Van Der Werf GR, Watts A (2015) Global vulnerability of peatlands to fire and carbon loss. Nature Geoscience 8, 11–14.
| Global vulnerability of peatlands to fire and carbon loss.Crossref | GoogleScholarGoogle Scholar |
von Neumann J (1967) In ‘Theory of Self-Reproducing Automata’. (Ed. AW Burks) (University of Illinois Press: Urbana)
| Crossref |
Waddington JM, Morris PJ, Kettridge N, Granath G, Thompson DK, Moore PA (2015) Hydrological feedbacks in northern peatlands. Ecohydrology 8, 113–127.
| Hydrological feedbacks in northern peatlands.Crossref | GoogleScholarGoogle Scholar |
Widyastuti K, Imron MA, Pradopo ST, Suryatmojo H, Sopha BM, Spessa A, Berger U (2021) PeatFire: an agent-based model to simulate fire ignition and spreading in a tropical peatland ecosystem. International Journal of Wildland Fire 30, 71–89.
| PeatFire: an agent-based model to simulate fire ignition and spreading in a tropical peatland ecosystem.Crossref | GoogleScholarGoogle Scholar |
Wolfram S (1984) Cellular automata as models of complexity. Nature 311, 419–424.
| Cellular automata as models of complexity.Crossref | GoogleScholarGoogle Scholar |
Yuan H, Restuccia F, Rein G (2021) Spontaneous ignition of soils: A multi-step reaction scheme to simulate self-heating ignition of smouldering peat fires. International Journal of Wildland Fire 30, 440–453.
| Spontaneous ignition of soils: A multi-step reaction scheme to simulate self-heating ignition of smouldering peat fires.Crossref | GoogleScholarGoogle Scholar |
1 Modified abbreviation of CA for Flaming And Smouldering that also means ‘cotton’ in the Indonesian language, as cotton is a material that can facilitate both flaming and smouldering.
Appendix
Ellipse parameters
The formulation of the ellipse perimeter used in the model to estimate the effect of wind on flames (Eqn 3) is shown below:
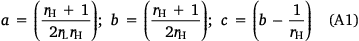
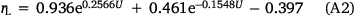
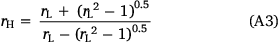
where rL is length to breadth ratio, rH is head to back ratio, and U is wind speed.
Recursive burning rule of flaming wildfires
The cells with FV states transition to become either EP or SP after several time steps. If the transition happens after too few time steps, the spread of the flaming wildfire is not sustained, whereas if the transition happens after too many time steps, the flaming wildfires are sustained for too long, which violates the observed phenomena. We found that by using a probability of FV cells changing their state between 5Pf and 25Pf, flaming wildfires were sustained but not for too long. The long-sustained flaming wildfires are indicated by a wide flaming vegetation front. We determined that this width is less than 10 cells. This value was selected based on the width that facilitated a continuous flaming vegetation layer. With less than 10 cells flaming vegetation width, the perimeter of the flaming vegetation is disconnected at several locations, which correspond to the unburned vegetation. Therefore, once the width of flaming vegetation layer exceeds 10 cells, the flaming wildfire can be considered as being sustained for too long. Between 5Pf and 25Pf, the value of φ to maintain the accuracy of the model against Rothermel model calculations does not significantly change. Therefore, we selected the middle value, in which the FV cells transition to either EP or SP at the subsequent time step with a probability of 15Pf. However, this value changes to become 15Pfexp(0.2σ) when there is rain, where σ is precipitation, as adapted from Alexandridis et al. (2011).

|
|
|


