Dynamics of standing dead wood and severe fire in north Australian savannas: implications for carbon management
Peter J. Whitehead A B , Brett P. Murphy C , Jay Evans A , Dominique Lynch D , Cameron P. Yates A * , Andrew Edwards A , Harry Mcdermott A and Jeremy Russell-Smith A BA
B
C
D
Abstract
Many fires in north Australian savannas are severe enough to cause canopy scorch, tree death and removal of stags. Better fire management may increase carbon sequestration in trees, perhaps including stags.
To describe and analyse dynamics of stags in tropical savannas (600–1000 mm annual rainfall) in relation to fire and better understand their role in biomass sequestration.
We monitored marked populations of live and dead trees over 12 years. Statistical models describing influences on stag creation and loss are applied in stag dynamics simulations.
Immediately following severe fire, stag biomass increases acutely because many more live trees are killed than stags removed. Between severe fires, stag losses exceed tree deaths, so peaks are quite short. Many ‘new’ stags are lost (fallen or consumed) quickly.
Between fires, stags comprise ~7.5–8.9% of standing above-ground biomass, more under dry conditions and during recovery from severe fire or other drivers of increased tree mortality. Fire management is unlikely to increase proportions of total woody biomass in stags unless it also reduces live biomass.
Reducing frequency of severe fires can increase total carbon sequestration in dry tropical savannas. Prediction uncertainties and management risks around sequestration present daunting challenges for policy-makers and fire management practitioners.
Keywords: biomass, carbon accounting, carbon sequestration, dead wood, fire severity, fire management, savannas, stags, tree mortality.
Introduction
Dead standing stems (stags) are conspicuous features of north Australia’s vast (1.9 million km2), highly fire-prone tropical savanna open forests and woodlands, providing important ecosystem services in carbon storage and dynamics (Harmon et al. 1986), as wildlife habitat (Woolley et al. 2018) and in nutrient cycling. Cook et al. (2020) estimated that over these mostly structurally unmodified savannas, 13.6% of standing stems >5 cm in diameter were dead. The purpose of our long-term monitoring study is to add to understanding of the factors influencing the size and dynamics of this substantial component of north Australia’s savannas.
Self-evidently, the spatial and temporal distribution and abundance of stags are determined by variation in rates of input and loss, but little is known about the importance of the many potential influences on these dynamics in north Australia’s savannas. Rates of input through tree mortality may vary with tree density and stand structure and related changes in the frequency and severity of multiple causes of tree death or damage. Chronic influences include local factors like nutrient deficiencies or moisture deficits, exacerbated by competition with other plants, and resident populations of consumers of leaves, bark and woody tissues that weaken function or structure. Episodic, often larger-scale, external pressures include outbreaks of disease or eruptions/invasions of consumer populations, drought, storm and fire, and their interactions.
The role of fire is particularly germane in Australian savannas, where annual fire frequency is 0.2 fires year−1 over the whole area and 0.5 in higher-rainfall (>1000 mm) zones (Whitehead et al. 2014; Edwards et al. 2015). Fire affects rates of input of dead wood through acute episodic as well as chronic effects on tree growth, recruitment and/or mortality (Edwards et al. 2018; Murphy et al. 2023). Most savanna fire is anthropogenic (Russell-Smith et al. 2007) and so potentially manageable.
Under unusually dry conditions, tree mortality may also increase stag populations (Fensham et al. 2009; Leitold et al. 2018). Damage from severe storms (e.g. cyclones) can have extreme effects over large areas, with many trees suffering breakage or uprooting (e.g. Hutley et al. 2013). Disease outbreaks may kill a large proportion of tree populations over large areas (Fei et al. 2019). Nonetheless, Lugo and Scatena (1996) argue that, in most environments, the low frequency of extreme events means that at most sites for most of the time, chronic background mortality remains the dominant source of dead wood.
Removal of dead wood, including stags, is mostly driven by on-site decay, consumption by invertebrates or combustion. Rates of loss vary with microbial, fungal or macro-invertebrate decomposer and consumer assemblages (Law et al. 2019), and with local micro-climate (Gora et al. 2019a, 2019b). Rates of decay increase with temperature (Pietsch et al. 2019). Fire can remove dead wood more rapidly than decomposition, in flaming combustion or more prolonged smouldering (Russell-Smith et al. 2009). For wood on the ground, some Australian studies find that fire of any severity reduces woody debris, particularly affecting more flammable (Zhao et al. 2018) highly decayed wood (Aponte et al. 2014; Threlfall et al. 2019).
Effects of fire on stags in particular is less consistently reported. Fensham (2005) found from a single site in Australia’s tropical savannas affected by drought that 27% of standing dead wood biomass was consumed by each of several low-intensity fires. In Victorian eucalypt forests, stag numbers were higher in fire-affected sites, including those burnt by severe fire, suggesting that fire exposure produced more stags than it removed (Bassett et al. 2015). Cook et al. (2020) proposed that stag biomass (above-ground biomass, AGB) relative to live biomass in north Australian savannas would be increased by lowering fire frequencies, which, if advanced as an option for increasing total carbon storage, requires that prevailing fire regimes remove stags faster than they are created.
In the present study, we seek to quantify, from observations of individual stems (~6000) in Australia’s lower rainfall zone (LRZ: 600–1000 mm year–1) tropical savannas, effects of fire on both inputs to and removals of standing dead stems in areas subject to little other anthropogenic disturbance, by tracking the fate of standing dead stems in permanent plots monitored regularly over periods of up to 12 years. We discuss implications for active fire management to influence spatial and temporal variation of carbon stores and other ecological benefits (Franklin et al. 1987). We connect these observations to Australia’s existing programs to reduce fire-generated greenhouse gas emissions through incentives to generate saleable carbon credits, available to landholders who act to improve fire management (Commonwealth of Australia 2018).
Methods
Methods have been described in other reports (Murphy et al. 2023) that cover a larger area and are not repeated in full detail here. Lower rainfall zone (LRZ) sites covered by the present study are in Fig. 1 and a description of variables used previously and in this study in Supplementary Table S1. At each site, permanent plots were established and individual stems marked and monitored at each visit between 2006 and 2018. Stems included live trees and stags with diameter at breast height (DBH) >5.0 cm. On each visit, all marked stems were re-measured, stem status recorded and incidence and severity of fire between visits assigned. Fire severity classes were as defined by Russell-Smith and Edwards (2006) as: mild (scorch height <2 m, patchy); moderate (scorch height to mid-canopy); and severe (scorch to upper canopy). Assignment of fire severity to a plot, although based on physical site visits and on-site photographs, often occurred some time after fire and it was not verified that all monitored stems were exposed to fire to an equivalent extent. Fire assessments were also validated against remotely sensed imagery, usually Landsat.
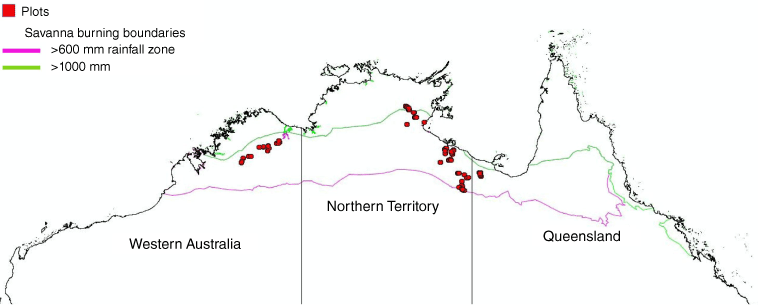
North Australian locations of long-term monitoring plots in relation to the rainfall-based boundaries for savanna fire management methods. The area north of the 1000 mm line is the high rainfall zone (HRZ) and between 600 and 1000 mm the low rainfall zone (LRZ), which is the focus of this study.
Data from long-term monitoring of stags were addressed most systematically in the LRZ and have not been reported previously. In reporting these new stag observations, we also analyse tree mortality for the same plots in relation to fire and rainfall, explicitly matched to treatment of stag loss to facilitate joint use in simulations of biomass dynamics. Stem growth (DBH increment) and recruitment are also re-examined in sufficient detail to permit inclusion in LRZ-specific simulations. We also examine in detail delayed or cumulative effects of environmental variation on living stems and stags including a stronger focus on rainfalls preceding monitoring visits and more comprehensive treatment of time since fire. To facilitate comparisons among statistical models for different responses over different time frames, annual plot rainfalls were normalised to the long-term mean as a rainfall index (ri for actual rainfalls within observation intervals, ry0 for full rain-year ending immediately prior to observation and ryi for all rain-years ending before observation and overlapping with observation interval).
Our treatment of fire of different severity (as used in Russell-Smith and Edwards 2006) also differs from earlier work. Because a fire of any severity usually precludes additional fires in the same year, plots with high frequencies of (say) mild fire are less likely to record high frequencies of other severities. Ideally, inherently correlated vectors would not be considered within the same model because they inflate variance and produce less reliable parameter values. Nonetheless, we included frequencies and timing of fires of different severity in some sets of candidate models to assess the lability of parameter values in different combinations. We found both mild and moderate fire parameters to vary substantially when more than one was included in the same model. We therefore selected models with a single fire vector as viable candidates and then used the best model on Akaike Information Criterion (AICc) rankings (Burnham and Anderson 2002), preferring the simplest model when candidates were ranked equivalently (ΔAICc <2).
Stem dbh was considered as a fixed effect in all candidate models. Because previous analyses showed non-linearity in relationships of DBH to mortality, we used generalised additive mixed models (gamms) that use splines for non-linear fits. Default settings were used to optimise fit by penalising overfitting (see Wood 2017). The penalised component of the DBH smoothing function was treated by default as a random effect. Other random effects were: tree species (sp) and unique identifiers for stem (stemID), plus vectors that took a single value for each plot: (plotID), slope (slo), aspect (asp), elevation (ele), topography (top), soil index (si), long-term mean rainfall (mar) and plot basal area (ba). All were added individually and in combination to models including dbh. Random effects vectors were dropped if they were found to offer near zero variance and/or their inclusion generated singular fits.
A set of candidate models adding fixed effects on fire and rainfall to dbh (and random effects) was assembled. Covariates examined in all analyses were: within-interval rainfall index relative to long-term mean rainfall ri (annualised ari), ry0 and ryi; numbers of mild, moderate and severe fires during each observation interval (fmi, fmo and fse annualised as afmi, afmo and afse in fires year−1); and years from last fire of each severity class to year of visit (tsfmi, tsfmo, tsfse). Given uncertainty regarding fire severities prior to the study period, years since last fire was set up as an ordered factor with levels for known exposures at annual increments from 0 years (y0 = fire in the visit/record year) to an additional 2 years or more (y2+). A ‘no record’ level where fire of the given severity was not observed during the study was considered as the longest fire-free interval and treated as reference level to generate contrasts.
We did not fit smoothing functions to vectors other than dbh. Selection of models to be used in simple simulations was informed by AICc rankings, using package MuMIn to retrieve summaries. At ΔAICc <2, we always preferred the simpler (fewer degrees of freedom) model and did not attempt model averaging. Graphics present fixed effects over their full range, with covariates usually set at the 10%, 50% (median) or 90% quantiles if continuous, and factors at the most common level (defaults used in package visreg; Breheny and Burchett 2017). Predicted values for individual predictors set other covariates to their medians unless otherwise stated. Random effects were set to zero when generating predicted values and related graphics.
Stem mortality – stag creation
Monitored stems were recorded as alive or dead at each visit. Death or survival of monitored stems between visits was analysed as a binary response using a gamm. We used the package gamm4 (Wood and Scheipl 2020), which uses the fitting functions of lme4 (Bates et al. 2015). We also adopted a modified logit link function as described by Shaffer (2004) and Bolker (2019) that transforms the response by taking account of variation in length of exposure in the intervals between visits. Exposure times (expo in years) invariably included at least one whole wet season (December to April) and usually exceeded a year.
Rates of stag loss
We also modelled rates of stag loss as a binary response: standing (1) versus fallen from below breast height, or lost entirely (0). We excluded observations (n = 583) for small stems for which there was no information on time of death. These were of two types: stems observed once as alive as they entered the study population (DBH >5 cm) but that were never recorded again on subsequent visits, and stems that were dead at the first observation. Given their small size and rapid turnover, we considered these stems of limited relevance to our principal interest in the biomass of standing dead wood. These observations were, however, included in analyses of mortality and recruitment where appropriate.
To fire and rainfall covariates, we added stag origin (or: two-level factor) distinguishing stags from trees dying during the study (dd, approximately known ‘age’ since death) from the longer-exposed stags present when the study began (doa, unknown age). Years-observed-as-stag (yas) was estimated as the interval between first observation of a stem as dead and first observation as collapsed or lost entirely. Although not equivalent to stag ‘age’ because the times of stem death of stags present at the start of the study were unknown, in conjunction with stag origin, it was useful for summarising patterns of loss through time. Rationale for including rainfall vectors as affecting dead trees was that during wetter periods, stags may more likely fail through accelerated decay, rain and surface flows disturbing or softening soils, and more frequent wind-storms associated with higher rainfalls.
Stem increment
The primary purpose of this study was to better understand influences on standing dead woody biomass in savannas. Given demonstration of delayed responses to effects of fire and rainfall on mortality rates, we also chose to consider continuing suppression of stem growth after exposure to adverse conditions (Murphy et al. 2023) because DBH influences both mortality and stag loss. Stem DBH increments were estimated from measures of DBH of live stems taken between visits and annualised. Increments estimated from the visit interval when stems were first recorded as dead were excluded from generalisations of growth rates. We retained negative increments in the dataset but discarded the most extreme observations falling above the 99.9 percentile (positive) and below the 0.1 percentile (negative). These extreme observations appear to result most often from measurement (including transcription) error or – less often – structural change unrelated to underlying patterns of stem growth or shrinkage. Fire and rainfall covariates (fixed effects) and stem or plot-related random effects were as considered elsewhere in this paper.
Recruitment
New stems found during plot visits entered the monitored population at DBH of ~5 cm. We compared Poisson, negative binomial and zero-inflated models of counts of stems added to plots between visits, using package glmmTMB (Brooks et al. 2017) with number of recruits appearing between visits as the response and rainfall and fire exposure as predictors. Plot-related variables including plotID were treated as random effects, together with the same fire and rainfall fixed effect covariates as elsewhere.
Above-ground biomass
We used allometric equations in Paul et al. (2016) to estimate live stem AGB from DBH and species. All references to biomass or biomass density are dry AGB. Estimates of dead AGB for stems dying during the study assumed that all leaves and half of the branch biomass fell to the ground prior to first record as dead and that remaining branch biomass was retained until stag loss was reported. Proportions of biomass in tree components (leaves, branches, stem, etc.) were estimated using coefficients in table 1 of Cook et al. (2005), using the mean of four named eucalypts for other eucalypts in our samples and coefficients for Terminalia ferdinandiana for other non-eucalypts. When stags were not identifiable to genus, we used the equation generating a lower estimate (non-eucalypts of lower wood density). For simulated populations, we generalised assuming a break up into allometric categories mimicking the distribution across the whole of the initial LRZ sample.
We assumed C-content (carbon content) of dry wood as 50% (Gifford 2000) to estimate CO2-e (carbon dioxide equivalents). We made no adjustments for hollows, assuming these were captured in allometric equations for live trees, or decay, which may substantially reduce the density of standing dead trees (Cousins et al. 2015).
Simulation of live stem and stag dynamics
For an overview of the implications of fire effects on stags over periods longer than the study duration, the various relationships established in this study were integrated with related information in simple simulations. In brief, simulations used a starting configuration of 10,000 live stems with DBH distributions similar at the beginning of the study, generated (package fitdistplus) assuming a log-normal distribution. Simulated stems and stags were then exposed to different severe fire frequencies (other fire treated as background incorporated in no-severe-fire parameters) and variable rainfall over 150 years. Relevant predictions (of mortality, stag loss and growth) were generated from model objects using the predict function. Stems of the same DBH and hence mortality risk were selected randomly until the number of deaths indicated by mean DBH-weighted mortality for that time step had been reached. The number of new stems added at each annual time-step was determined from the recruitment model. Full details are in Table 1.
| Component | Description | Statistical models | Source(s) | |
|---|---|---|---|---|
| Parameter values | ||||
| Starting configuration | ||||
| Live stems | 10,000 stems at DBHs drawn randomly from a log-normal distribution fitted to observed size distributions | Mean(log(DBH [cm])) = 2.54 | Present study: all LRZ plots pooled | |
| s.d.(log(DBH [cm])) = 0.54 | ||||
| Stags | None: generated from statistical model for DBH-specific mortality (below) in 50-year run-up | Analyses indicate less than 1% of original stags remain after ~20 years | Present study | |
| Simulation length | ||||
| 100 years (150 with run-up) | In annual time-steps with 50-year run-up before outputs used | |||
| Vital rates | ||||
| Stem increment rate (mm year−1) | Predicted annual stem increment in LRZ plots (all tree species): rainfall index and severe fire exposure predictors | lme4:lmer model Table 6. Maximum DBH set at 80 cm | Murphy et al. (2023); present study | |
| Recruitment rate (stems ha–1 year−1) | Number of stems added annually at 5 cm DBH: rainfall index as predictor | glmmTMB (negative binomial) model Table 7 | Murphy et al. (2023); present study | |
| Mortality | DBH-weighted mortality rates. Rainfall index and time since severe fire as additional predictors | gamm4 (binomial): Table 3 | Murphy et al. (2023); present study | |
| Stag creation | ||||
| Stems designated as dying during simulations | Annual rates of creation equal to mortality rates applied to the number and size of lives stems present at each time step | As for mortality above | Present study | |
| Stag loss | ||||
| Stags from trees dying during simulation | DBH-specific probability of loss (no longer standing) with rainfall and severe fire exposure as predictors | gamm4 model: Table 4 | Present study | |
| Increase in rates of loss on exposure to single severe fire | As above; see Fig. 6 | Present study | ||
| Above-ground biomass (AGB) | ||||
| Live trees | Allometry based on DBH by taxonomic/wood density groupings | Estimates of total tree AGB weighted to relative abundance of density groups in LRZ sample | Paul et al. (2016); present study | |
| Stags | AGB for trunk and half of branches | Estimates for tree components weighted to relative abundance of density groups in LRZ plots | Cook et al. (2005) for tree components applied to allometric estimates | |
| Losses (to ground) | Annual sum of AGB lost from dying trees (leaves, twigs and half branches) plus full AGB of stags lost (fallen or consumed) | Cook et al. (2005) for tree components applied to allometric estimates | ||
| Process | ||||
| Live stem deaths | Total deaths at each time step | Number to die specified as DBH-weighted mean mortality applied to all remaining live stems, including recruits | ||
| Death assigned randomly to individual stems | Selections weighted to relative mortalities at individual stem DBH | |||
| Stag creation | Mortalities at each time step added to existing standing deads | Starting at 0 stags in 50-year run-in | ||
| Stag loss | Loss assigned randomly to individual stags | Selections weighted to relative vulnerability at individual stag DBH | ||
| Fire regimes | Mild and moderate fires not explicitly modelled but treated as influences on background rates of stem vital rates and stag loss | Choice of models based on best fit (AICc as criterion) | ||
| Severe fire applied or not at each time step, to specified schedules or randomly | Schedules for annual severe fire frequencies of 0, 0.05, 0.10, varied in timing | Present study: within observed range mean ~0.062, maximum 0.333 | ||
| All live stems and stags in simulated populations at same risk of exposure to severe fire in each severe fire year | ||||
| Rainfall | Ratio of annual (rain-year) falls to long-term averages selected randomly in the range observed during the study and over the long term (1972–2018) | Aggregated (to periods based on mean between-visit intervals) or by individual rain-years to match relevant statistical models | Present study | |
| Outputs | ||||
| Standing live AGB | AGB density (Mg ha−1) of live stems summed at each annual time-step | Taking account of mortality, recruitment and growth of present live stems and recruits | ||
| Standing stag AGB | AGB density of dead standing dead stems | Assuming all leaves and twigs and half of branches shed immediately after mortality and remainder retained until collapse or consumption | ||
| Stag AGB lost | Summed AGB of collapsed stems at each time-step | Heavy debris only | ||
| Dying tree AGB | Summed AGB of stems dying at each time step less AGB of portions of stems (stags) remaining standing | This measure of lost AGB may include both heavy and fine debris | ||
| Model uncertainty | ||||
| 100 sets of each 100 (150) year simulation | Model uncertainty for all statistical models applied to all simulation runs in conjunction with random variation in rainfalls at each annual timestep: in most summaries, means of 100 simulations are presented | Effects of model uncertainty based on standard error of predictions for each output (mortality, recruitment, growth, stag loss) applied to every individual (simulated) stem | Present study | |
All simulations are based on the same initial live stem populations.
We treated the first 50 years as run-in. Analyses of stag loss rates indicate that this was sufficient to establish a simulated stag assemblage ‘old’ enough to mimic the observed doa (study commencement) stag assemblage. At each time step, statistical model uncertainty was incorporated in projections by random picks from a normal distribution defined by the predicted value and its standard deviation retrieved using the predict function. This was done for every stem at every time step. Results (predicted AGB in Mg ha−1) are generally presented as the mean at each time step from 100 separate runs.
We varied frequency and timing of severe fires under two rainfall regimes: long term (average) and recent (above average). For a few simulation sets, rainfalls were switched between the long-term (lower) and recent (higher) rainfall regimes. Simulated severe fire frequencies fell within the range observed in the study (Fig. 2, Supplementary Table S2) at 0.02 (severe fire event specified at years 2 and 22), 0.05 (timing evenly spaced at 10, 30, 50, 70 and 90 years, and separate runs of five fires at randomly selected intervals), and 0.10 (timing of 10 severe fires randomly selected). Every stem was treated as exposed equally to simulated fires and variations in moisture availability associated with variable rainfall, as necessarily assumed in the derivation of the contributing statistical models from the relatively small homogeneous plots. At larger spatial scales and in more topographically or otherwise diverse sites, greater diversity in exposure and response will be expected but are not explicitly incorporated in the simulations presented here.
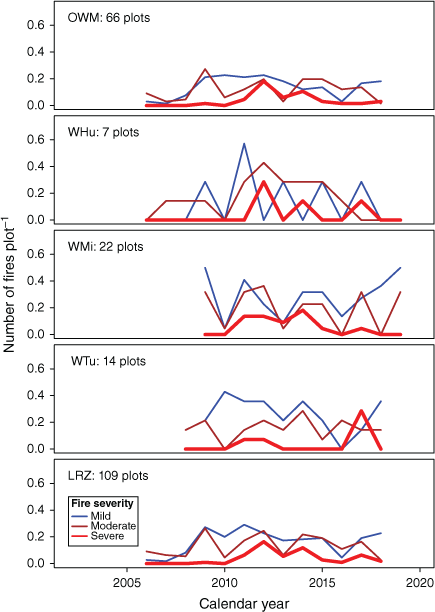
Time series of fire in study plots by vegetation-fuel class (VFT) and fire severity. OWM, Open woodland, mixed grasses; WHu, Woodland, hummock grasses; WMi, Woodland, mixed grasses; WTu, Woodland, tussock grasses; LRZ, All plots in 600-100 mm zone. A single Sandstone heath, hummock grasses (SHH) plot that was omitted from most statistical analyses is not included.
Results
A snapshot of the stem and biomass density of LRZ plots monitored from 2006 to 2018 that provided the stem and stag data is in Table 2. Time series of rainfalls and fires are in Figs 2 and 3. A numerical summary of these details is in Supplementary Table S2.
| Stem density (stems ha−1) | AGB density (Mg ha−1) | ||||||
|---|---|---|---|---|---|---|---|
| VFT class (plots) | Dead ± s.d. | Living ± s.d. | % dead | Dead ± s.d. | Living ± s.d. | % dead | |
| Open woodland/mixed grasses understorey (66/59) | 19.0 ± 5.5 | 119.2 ± 15.9 | 13.7 | 1.2 ± 1.1 | 13.5 ± 3.7 | 8.2 | |
| Sandstone heath hummock grass (1) | 3.6 ± 0 | 21.4 ± 0 | 14.4 | 0.0 ± 0 | 1.0 ± 1.0 | 0.0 | |
| Woodland hummock grasses (7) | 56.4 ± 35.8 | 298.3 ± 1.0 | 15.9 | 1.7 ± 1.3 | 30.1 ± 5.5 | 5.3 | |
| Woodland mixed grasses (22/20) | 36.7 ± 6.1 | 259.8 ± 7.2 | 12.4 | 2.1 ± 1.5 | 36.7 ± 6.1 | 5.4 | |
| Woodland tussock grasses (14) | 39.8 ± 14.8 | 241.2 ± 10.3 | 14.2 | 2.9 ± 1.7 | 39.8 ± 6.3 | 6.8 | |
| All VFT(110) | 27.4 ± 11.8 | 173.4 ± 71.3 | 13.7 | 1.6 ± 0.6 | 22.4 ± 11.7 | 7.2 | |
Stag AGB is estimated as trunk and half branches. The All VFTs mean is weighted by numbers of plots.
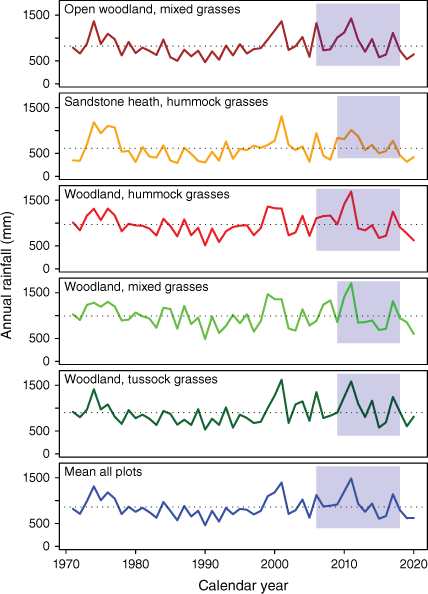
Time series of rainfall in study plots by vegetation fuel class (VFT). The blue rectangles indicate the study period and the dotted horizontal line the long term mean.
Stem mortality
Models including beyond-interval vectors for years since fire and rainfall as predictors offered considerably better fits to the data than predictors based only on within-interval observations (Supplementary Tables S3 and S5). The highest-ranked on AICc included, additional to smoothed DBH (s-dbh), time since severe fire (tsfse) and the averaged rainfall index for full rain-years ending immediately before and falling within the observation interval (ryi) (Table 3). The highest-ranked models examining fixed effects within visit intervals included s-dbh, afse, afmo and ri (see Supplementary Table S4), but for the reasons given earlier, we rejected models that accommodated the possibility of multiple fires in the same year.
| (a) Parametric coefficients | Estimate | s.e. | t-value | P-value | |
|---|---|---|---|---|---|
| (Intercept) | 2.663 | 0.262 | 10.16 | <0.0001 | |
| tsfse-y0 | −0.855 | 0.140 | −6.11 | <0.0001 | |
| tsfse-y1 | −1.620 | 0.129 | −12.58 | <0.0001 | |
| tsfse-y2+ | −0.543 | 0.126 | −4.32 | <0.0001 | |
| ryi | 0.933 | 0.153 | 6.10 | <0.0001 |
| (b) Smooth terms | edf | Ref. df | F-value | P-value | |
|---|---|---|---|---|---|
| s(dbh) | 5.67 | 5.67 | 215.0 | <0.0001 |
Coefficients for time since severe fire (tsfse) factor levels use contrasts with the ‘no severe fire record’ category.
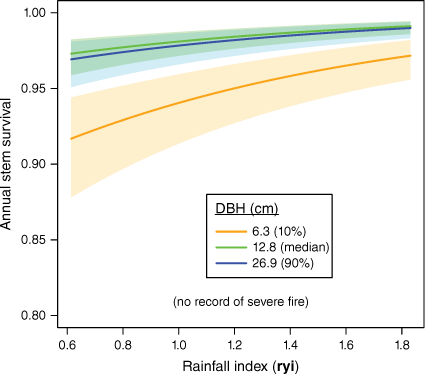
The relationship between tree DBH and annual survival rates was non-linear (Fig. 4: P for splined fit ≪0.0001) with smaller stems most likely to die. At median rainfalls and with no recorded exposure to severe fire, predicted annual survival was 0.916 at 5.0 cm, increasing substantially with DBH up to ~10 cm (to 0.977 or 2.3% annual mortality) and then rising gradually to a peak predicted annual survival of 0.995 in the largest stems (57.4 cm) included in analyses. However, at larger DBH (>40 cm) where observations are sparse, prediction uncertainty increased, with the lower bound of 95% confidence intervals for predictions in the largest stems being similar to the smallest (Fig. 4).
Predicted annual stem survival with DBH (cm) and years since most recent fire, at median values of the rainfall (rain-year) variation index. The blue line is the relationship with DBH in the absence of severe fire. For clarity, predictions for y2+ have been omitted and confidence intervals for predictions are shown only for no recorded fire exposure (blue shading) and the severe fire y1 effect (red shading). See Supplementary Fig. S1 for additional visualisations. Prediction uncertainties are large for very large stems.
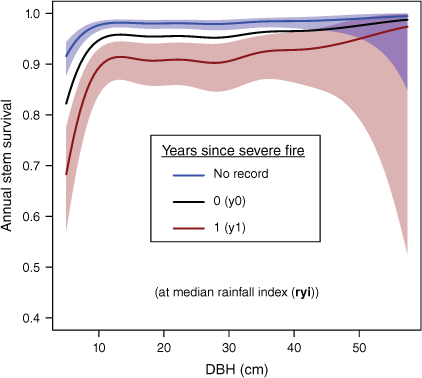
Exposure to severe fire increased mortality substantially (Fig. 4), with lowest annual survival being recorded in visits 1 year after severe fire exposure (y1 in Fig. 4). At median rainfalls, predicted survival 1 year after a severe fire is 0.914, or mortality ~4.8 times that without severe fire (Fig. 4). Elevated mortality for some years after exposure to severe fire increases total tree deaths beyond the year of exposure.
Observation of highest predicted mortality 1 year after severe fire rather than in the fire year may be in part a methodological artefact. Stems were most confidently recorded as dead when there was evidence of loss of structural integrity. Canopy scorch and associated loss of all leaves was not in itself treated as evidence of stem death, so it is unsurprising that fewer stems were recorded as dying immediately (even if death had occurred) rather than later when physical deterioration of dead stems was pronounced.
Other analyses – setting the number of levels (yearly increments) of fire timing at the maximum observed for severe fire exposure – show predicted values lower (although not always significantly lower, hence the pooling after 2 years) than the ‘no record’ level for up to 7 years (e.g. Supplementary Fig. S2). Delayed fire-related mortality of trees continuing for several years after fire exposure has been observed in other settings (e.g. Angers et al. 2011; Kwon et al. 2021).
Variation in rainfall most affected survival of smaller stems, below the median DBH (Fig. 5). At the lowest average rainfall index in the years encompassing and preceding the observation interval (ryi), stem survival for median-DBH stems was 0.973 (mortality 2.7%), ~0.9% above mortality rate in periods of median falls. At 5 cm DBH, the mortality differential was much greater at 3.6% (0.880 vs 0.916 annual survival). At the observed rainfall maximum, predicted survival at median DBH was 0.991 (mortality <1%).
Predicted annual stem survival at three DBH sizes with variation in rainfall index (ryi, full rain-years ending in calendar years encompassed by an observation interval relative to long-term plot mean). Effects are most pronounced for small stems.
All of these observations relate to net effects on the array of species present in plots, with random effects for species set to zero in model predictions. Species variation in mortality rates is, however, substantial, and this issue is revisited later in the context of stag dynamics.
Stag loss
The highest-ranked statistical model for the probability of a stag remaining standing for a year – from here on termed resilience – includes s-dbh, stag origin (or), years observed as stag (yas), annualised frequency of severe fire in the observation interval (afse) and rainfall index for the full rain-year ending immediately before observation of stag status (ry0) (Table 4; see also model selection in Supplementary Table S5). There were statistically strong interactions between or and yas indicating differences in the rate of loss of doa and dd stags, and between ry0 (rainfall) and yas indicating differences in ‘age’-related responses to rainfall variation (Table 4).
| (a) Parametric coefficients | Estimate | s.e. | t-value | P-value | |
|---|---|---|---|---|---|
| (Intercept) | 0.4640 | 0.4191 | 1.1072 | 0.2682 | |
| or-doa | 0.7770 | 0.2254 | 3.4475 | 0.0006 | |
| yas | 0.2084 | 0.0884 | 2.3564 | 0.0185 | |
| ry0 | 1.4301 | 0.3296 | 4.3392 | <0.0001 | |
| afse | −0.7929 | 0.2183 | −3.6320 | 0.0003 | |
| or-doa:yas | −0.1135 | 0.0554 | −2.0496 | 0.0404 | |
| yas:ry0 | −0.2765 | 0.0731 | −3.7849 | 0.0002 |
| (b) Smooth terms | edf | Ref. df | F-value | P-value | |
|---|---|---|---|---|---|
| s(dbh) | 3.7664 | 3.7664 | 33.6164 | <0.0001 |
Interaction between years observed as stag (yas) and stag origin (or; as ‘dd’ (died during study) or ‘doa’ (dead at study commencement)) is strong, indicating substantially earlier and faster loss of stags from recent tree deaths.
Larger stags persisted longer. As yas increased, resilience of doa stags declined monotonically (Fig. 6). We had hypothesised that ‘newer’ dd stags would initially be more resilient because they are ‘younger’. However, soon after death, the rate of loss of dd stags was actually higher and remained so over several years (Fig. 6). We have probably underestimated early dd vulnerability by excluding stems that were lost too quickly to enable time as stag to be determined. Later resilience of dd stags increased relative to doa, presumably as the most vulnerable stags were lost.
Predicted variation in annual probability of stag retention with years of observation as stag (yas) using the statistical model summarised in Table 4 and illustrating the interaction between stag origin (or) and yas and effects of severe fire (afse, annualised fire frequency). Dead trees present at plot establishment (doa) are of unknown age and an approximate stag age is known for trees dying during the study (dd). Effects of exposure to fire (afse = 1) are shown by additional lines with red dashed overlay.
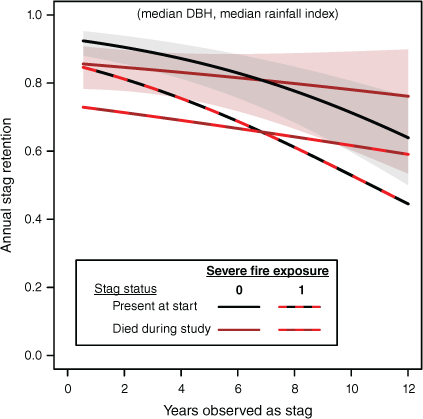
Contrasting with stem mortality, variables relating stag resilience to time since last severe fire (tsfse) performed poorly compared with annualised frequency of severe fire (afse) occurring between visits (Supplementary Table S6: ΔAICc >25.5). Effects of recent exposure to severe fire were substantial (Fig. 6), with predicted resilience of doa stags at median values of other predictors decreasing by 0.092 (from 0.907 to 0.814) and dd stags by 0.107 (0.887–0.780). For the ‘newest’ dd stags (yas = 0), the corresponding figures are a reduction of 0.107 (0.886–0.779).
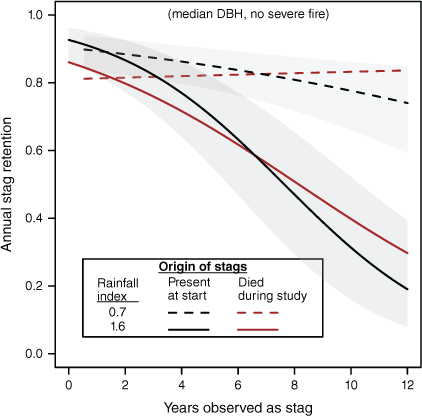
But given the fairly low frequency of severe fires (6.2% of years), in most years, resilience is more likely to be affected by rainfall, with losses accelerated in wetter periods (Fig. 7). That effect was most pronounced for longer-observed (older) doa stags, which were several times more likely to fail under the wettest conditions observed during the study. For example, between the 10% and 90% quantiles for ry0, predicted resilience of doa stags observed over 4 years (~median for doa) was little changed (0.863 and 0.893 respectively). For stags observed over 10 years within the same rainfall range, resilience fell acutely from 0.775 to 0.522 (−0.253). Newer dd stags were somewhat less affected by variation in rainfall over this range, falling from 0.831 to 0.610 (−0.221).
Predicted annual probability of stag retention with variation in rainfall index for full rain-year immediately preceding observations (ry0) and its interaction with stag ‘aging’ (yas). Model parameters are in Table 4. Stags are lost more quickly under wetter conditions, and rates of loss accelerate with age.
It is difficult to infer from the patterns summarised in Fig. 6 when rates of loss of dd stems might converge with doa trends, or to infer the age of doa stems. Demonstration that the annual probability of stag loss changes substantially through time means that it is untenable to apply simple models to predict trajectories of stag loss that assume loss of the same proportion of the ‘population’ in equal time steps. Nonetheless, we have used the empirical relationships described here to derive figures for stag ‘half-lives’ (Table 5) under fairly benign conditions (ry0 = 1 and no severe fire exposure) to permit crude comparisons with other reports.
| DBH (cm) (quantile) | Years for probability of stag standing to decrease below 50 and 1% | ||||
|---|---|---|---|---|---|
| doa – stags initially present | dd – stags of ~known age | ||||
| <50% | <1% | <50% | <1% | ||
| 5.8 (0.10) | 3.9 | 12.9 | 2.2 | 13.8 | |
| 10.0 (0.50) | 5.2 | 14.8 | 3.4 | 17.3 | |
| 22.4 (0.90) | 6.5 | 16.5 | 4.7 | 20.7 | |
Projections for 0.50 loss are not directly comparable with stag half-lives reported in other studies that assume constant proportional (negative exponential) losses, because our estimates include changes in annual probabilities of loss with age. Estimates of 99% loss extrapolation beyond the longest period of direct observation.
Over all stag sizes and sources, stag loss rates are considerably higher than the rates of stem mortalities that create them. To illustrate, predicted stem mortalities at median DBH and median rainfalls are 1.8% year–1 in the absence of recent severe fire. Stag losses under the same conditions are 11.4% year–1. More or less stable stag numbers require inputs from tree deaths in a much larger population of live stems. The dynamics of this relationship are further examined in simulations.
Stem increment
Mean annual stem increment in live trees was 1.41 ± 0.02 (s.e., n = 5816) mm year−1, somewhat lower than the savanna-wide rate of 2.0 mm year−1 used, for example, by Cook et al. (2020) for analyses of biomass production in the savannas encompassing our study areas. Annual increments from stems that died during the study were lower (0.994 ± 0.093 (s.e.), n = 777) than from those alive at its end (1.474 ± 0.023, n = 5039) (t = −5.0, P < 0.0001). Chronically low growth is often associated with future mortality of affected stems (Gillner et al. 2013; Verschuren et al. 2023). Annualised stem increment for the interval in which stems were first recorded as dead showed mean net reduction of −3.4 ± 0.03 (s.e., n = 437) mm year−1 from the immediately preceding interval when they were last reported as live. Mean increment for that preceding interval (0.9–4.0 years) was also slightly negative (−0.12 ± 0.02 (s.e.) mm year−1), suggesting arrested growth before mortality was recognised (see also Supplementary Fig. S3).
Statistical models of stem increment indicate that, in addition to the differences between dying stems and survivors to study end (fate), preceding rainfall and fire affected growth. Better-fitting models included rainfall index in the interval between visits (ri) and time since severe fire (tsfse) (Supplementary Table S7). Introducing a quadratic term for rainfall (ri2) substantially improved fit. Growth was lowest when rainfalls were unusually low, and peaked at approximately double average annual falls (Supplementary Fig. S4). For stems exposed to severe fire that nonetheless survived to the end of the study, growth was suppressed in the year of fire and in the following year (Table 6; Supplementary Fig. S5).
| Parameter | Coefficient | s.e. | t-value | |
|---|---|---|---|---|
| (Intercept) | 0.991 | 0.212 | 4.66 | |
| dbh | 0.010 | 0.003 | 3.69 | |
| fate-lived | 0.654 | 0.066 | 9.92 | |
| poly(ri, 2)1 | 85.923 | 3.212 | 26.75 | |
| poly(ri, 2)2 | −38.778 | 3.259 | −11.90 | |
| tsfse-y0 | −0.492 | 0.097 | −5.08 | |
| tsfse-y1 | −0.979 | 0.107 | −9.17 | |
| tsfse-y2+ | 0.098 | 0.082 | 1.20 |
Random effects were as used in mortality and stag loss models, except for stemID and soi (soil index) that returned near-zero variance or singular fits.
Recruitment
Over the whole study, 809 new saplings (>5 cm BDH) apparently independent of existing stems were added to plots, at a median of five per plot (from 0 to 44). Numbers of stems appearing between visits was most frequently 0 (55.2% of plot intervals). When recruitment occurred, a median of two stems (range 1−37) was added (mean 2.90 ± 0.253 (s.e.)). Median DBH at entry to the monitored population was 5.5 cm. Additional new stems (234) were first recorded as dead, apparently having reached 5 cm DBH and then died between visits, and 164 secondary stems associated with a monitored primary stem survived after the primary stem had died. We treated these ‘ghosts’ and primary stem replacements as recruits when ˃5 cm DBH. Negative binomial models offered substantially better fits than Poisson; zero-inflation models did not improve fits.
There was consistent evidence of strong responses to rainfall, but fire vectors produced inferior fits or more complex models with no useful improvement (Supplementary Table S8). We chose the simplest model from equivalently ranked fits, with ryi as fixed effect (Table 7, Supplementary Fig. S6).
| Coefficients | Estimate | s.e. | z-value | P-value | |
|---|---|---|---|---|---|
| (Intercept) | 0.07785 | 0.33813 | 0.2302 | 0.8179 | |
| ryi | 1.10787 | 0.23473 | 4.7197 | <0.0001 |
Response is in units of recruits ha−1 year−1.
Simulations of AGB change in standing live stems and stags
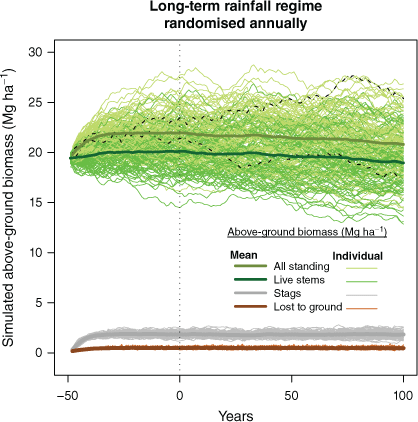
Initial simulations indicated that a 50-year run-up generated a relevant sample of simulated stags (Fig. 8). Randomised rainfalls and inclusion of prediction uncertainty generated great variation in individual trajectories (the fine lines for individual simulations). These simulations make no explicit provisions for topographic or other large-scale variation in fire or rainfall effects, and should not be used to make predictions for individual sites. Rather, they indicate the direction and potential scale of AGB variation under contrasting rainfall and fire exposures. (Additional summaries of simulation outputs are in Supplementary Figs S7–S23.)
Mean and individual plots for 100 simulations in absence of severe fire and randomised annual rainfall index taken from pooled observation of ratio of rain-year falls to long-term mean for the same plot. Mean simulated index for the 100-year simulations (post 50-year run-up) was 1.02 (range 0.94–1.09 over individual simulations). Simulated mean standing AGB was 21.2 Mg ha−1 (22.0 at start and 20.8 at end). Mean stag AGB was 1.83 Mg ha−1, ~8.6% of standing AGB. Dashed and dotted black lines are for two haphazardly chosen individual simulations, illustrating potential for temporal variation driven primarily by randomised annual rainfalls but also including uncertainty in statistical model predictions.
The variable trajectories of individual simulations illustrate sensitivity to rainfall, which is also evident from mean outputs where simulated rainfalls were drawn from different pools. Fig. 9 compares mean outputs from: 3 sets of 100 simulations for (i) long-term rainfall regime (1971–2018), (ii) draws from the long-term to which ~10% was added in alternating decades, and (iii) random draws from the pool of recent (study period) observations (2006–2018).
Simulated trajectories for standing AGB from mean of 100 simulations for each of three rainfall regimes. Mean sampled annual rainfall index for the long-term regime was 1.02, for the decadal cycles 1.06 and for recent 1.11. Green segments in cyclical simulations are higher rainfall. Increase in simulated live AGB at sustained higher rainfalls sees proportions of AGB in stags lower than in drier conditions. Increased rates of stag loss in periods of higher rainfall are particularly apparent in the ‘cyclical’ simulation (panels b, c).
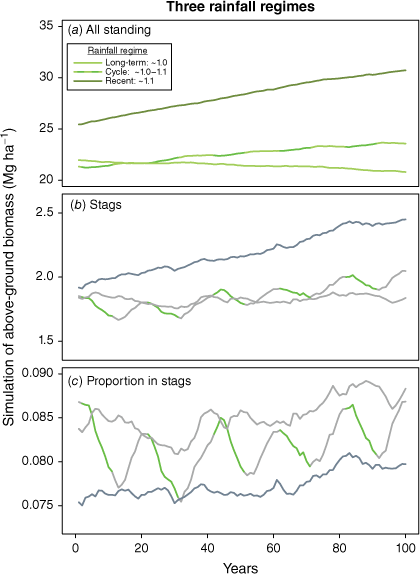
Fairly minor changes (<10%) in average annual rainfall, if sustained, drive substantial changes in simulated biomass in both living and dead standing stems over time frames relevant to carbon storage.
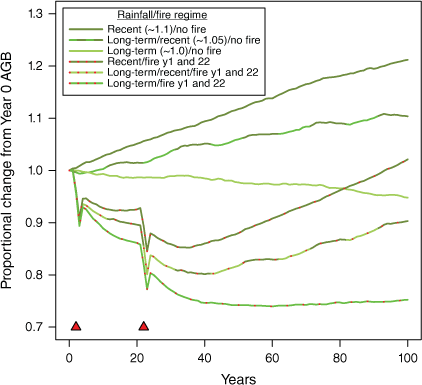
In one set of simulations, severe fires were specified at 2 and 22 years to simulate early losses to fire and illustrate the pattern of recovery in the subsequent absence of severe fire (Fig. 10). Stag biomass showed a rapid and substantial increase as a proportion of standing AGB in the few years after fire as live stems died (Fig. 11), and might require more than a decade to return to pre-fire proportions. The slow rate of return to background levels is not primarily due to the resilience of stags but because live biomass takes so long to recover (Fig. 10).
Simulation of long-term effects of two severe fires (red triangles) on standing woody biomass (live trees and stags) under different rainfall regimes, set to a comparable origin as proportion of AGB at Year 0 (after the 50-year run-up) to facilitate comparisons. At annual rainfalls sampled randomly from long-term records, recovery 80 years after the last fire appears limited, but early fire-related losses are recovered over the long term at higher rainfalls. AGB recovery from severe fire requires more than 10 years and often much longer.
Simulations of the proportion of standing AGB in stags in relation to rainfall and severe fire. Relative abundance peaks at ~19% after two consecutive severe fires, but relaxes to fire-free levels of 7–9% in 10–20 years, varying with timing of subsequent severe fires and with rainfall. Stags are a smaller component of AGB at higher rainfalls because live AGB increases and mortalities are slightly lower but stags are lost more quickly.
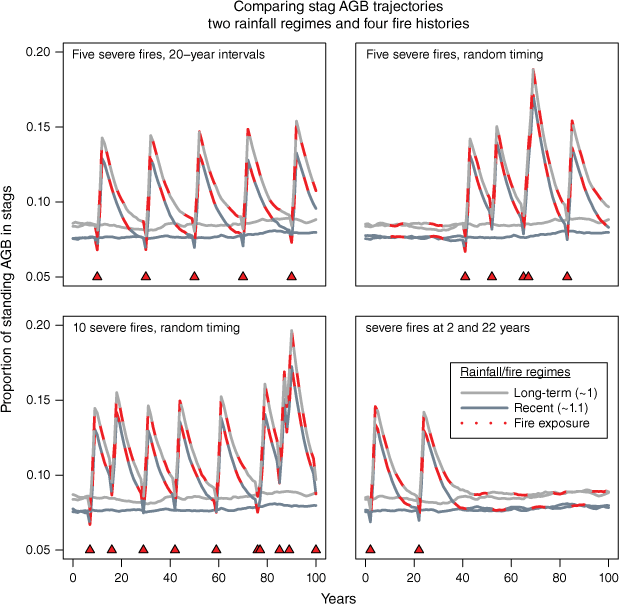
At higher severe fire frequencies, simulated AGB is strongly suppressed despite favourable rainfalls (Fig. 11). Increased stag AGB associated with fire-driven mortality is relatively short term and every fire necessarily results in an immediate net decrease in total standing biomass as live trees shed biomass on death and stags are lost to increased rates of collapse or combustion in the year of fire.
Differences in the area under the no-fire and with-fire lines offer an index of sequestration performance (in Mg ha−1 year−1; e.g. Fig. 12a). In simulations with five evenly spaced fires in a 100-year period, the net reduction is 22.3% of the estimate in the absence of fire. There is no accumulated gain in stag AGB to offset losses from live stems (Fig. 12). Different temporal fire patterns show a strong influence of fire timing on patterns of variation in standing AGB (Fig. 12). A randomly chosen sequence that saw the first fire delayed until 42 years into the simulation resulted in lower standing AGB at simulation end but a substantially better biomass sequestration outcome over the whole of the simulation period. Assessments of sequestration performance may vary markedly with choice of assessment intervals and metrics.
Simulation of sequestration performance with severe fire at a frequency of 0.05 comparing evenly spaced intervals with randomly selected timing with later onset of severe fire. Green hatching in panel (c) shows the gain in sequestration performance with a delay in exposure to severe fires. Peaks of stag AGB after fire are reduced as their source of live trees declines in abundance and biomass with repeated fire.
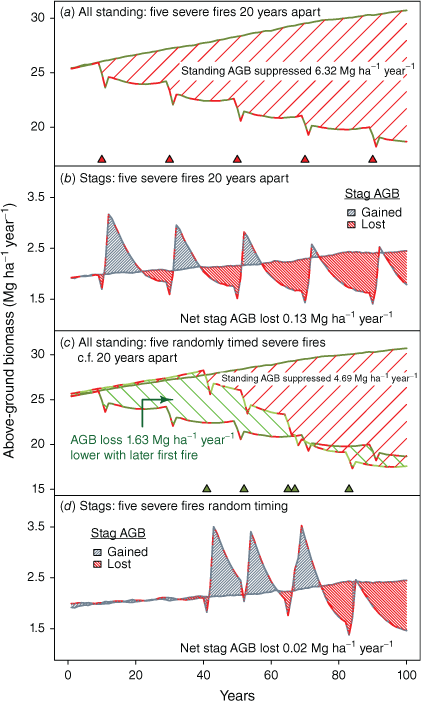
Growth of live stems makes the largest input to simulated stand AGB, several times higher than recruitment (Supplementary Fig. S11). Severe fire slows recovery from mortality-driven AGB losses by also suppressing subsequent growth-dependent additions to AGB. Mid- to long-term effects derive from: reduced numbers of growing live stems, smaller stem diameter increments in surviving stems, and lower average stem size given an increased proportion of recent recruits. The scale of these effects can be illustrated by extracting details from the simulated AGB trajectories in Fig. 10.
Under the study period rainfall regime, in the 3 post-fire years during which mortality most increases, ~1200 additional stems died, reducing the live (growing) population by ~11%. The AGB density of these lost stems is ~1.5 Mg ha−1. After taking account of recurring background mortality and all else being equal, replacement would require 6–7 years’ growth in a fire-free stand. But all else is not equal: growth rates of the remaining smaller population of smaller stems are also suppressed, increasing the live AGB replacement period to ~13 years.
To summarise, simulations indicate that severe fire drives losses of biomass that are recovered slowly. Stag turnover is too high to provide more than a modest and short-term buffer in dead wood against both acute and sustained suppression of living AGB.
Discussion
Management of fire in wooded environments is controversial: intense debate around objectives and practice is likely to continue (Pyne et al. 1996; Hanson 2021; Lindenmayer and Zylstra 2024). All fire management decisions involve trade-offs that are rarely simply reconciled. Important improvements in fire management performance in Australia’s tropical savannas – quintessential fire-prone environments – have attracted related dispute. Despite demonstrable success in reducing the severity of fires (Price et al. 2012), mobilising an effective fire-control workforce and enhancing the lives of fire management practitioners (Ansell et al. 2020), savanna burning projects supported by Australian carbon farming law and sale of related credits are questioned on conservation (Corey et al. 2019) and socio-cultural grounds (Wohling 2009; Perry et al. 2018). A recent inquiry into the credibility of some of Australia’s land management offsets dependent on recovery of damaged natural systems to reduction of anthropogenic disturbance identified the need for changes in process to ‘enhance confidence in … integrity and effectiveness’ (see Butler et al. 2022; Chubb et al. 2022).
Against this background, technical and policy development of new savanna burning methods involving carbon sequestration, built on the long-standing and fundamental emissions avoidance approach substituting early cooler burns for later hotter and more emissions-intensive burns, have proceeded cautiously. A method for recognising sequestration in coarse woody debris has been approved (Commonwealth of Australia 2018) but so far failed to engage many practitioners. In a continuation of research related to the method development process, Cook et al. (2020) concluded, following a study of dead standing wood (stags) in Australian savannas, that because ‘the proportion of total biomass comprising dead wood increased with decreasing fire frequency’ there exists ‘scope for increasing the carbon stock in the woody debris pool with improved fire management’.
Our study calls into question the conclusion of Cook et al. (2020) about opportunity and a key assumption required by that conclusion: that fire, as a creator of stags through increased mortality, removes existing stags faster than it creates new ones.
Stag creation
As described by Edwards et al. (2018), we found that exposure to a single severe fire was associated with substantial increase in tree mortality over background levels, several times higher at median stem sizes. Fire-related mortalities were highest 1 calendar year after severe fire and recovered towards background levels over several years (Fig. 4 and Supplementary Fig. S2). Over the 3 years post-fire during which survival is most compromised, mortalities for exposed stems of median DBH and related stag production almost tripled, from 5.4 to 15.2%.
Fensham et al. (2009) describe pulses of tree death during drought in dry savannas in Queensland, where interannual rainfall variability tends to be much higher than in our study region. Acute increases in stag numbers have also been reported in dry conditions in temperate (Gray et al. 2012) and tropical forests (Leitold et al. 2018). There were no prolonged periods of unusually dry conditions during our study (Fig. 3): aggregate rainfall averaged across all sites was slightly above average. Nonetheless, rainfall variation had measurable impact on tree survival and growth, both improving when rainfalls were higher. Simulations indicate that proportions of standing AGB in stags are ~12% higher under slightly lower (long-term average) rainfalls because more trees die and fewer stags fall. Rainfall variation and severe fire exposure drive substantial shifts in annual stem mortality and hence relative stag density and biomass, over time-scales ranging from the short to very long term.
Stag loss
Stags already present at the beginning of the study were lost at progressively accelerating rates. Predicted ‘half life’ for doa stags at median DBH was 5.2 years. Oberle et al. (2018) reported average stag half life of 7.2 years in eastern North America, and substantially lower at higher temperatures. Dunn et al. (2019) estimated half-lives from 8 to 11 years in 20 cm fire-killed stags in colder environments. Hilger et al. (2012) reviewed stag annual ‘fall rates’ to arrive at a US estimate of 8.75%, or a half-life of approximately 9 years assuming a constant rate. Our approximations of stag half-life from 4.7 to 6.5 years for stems of appoximately similar DBH do not diverge aberrantly from these observations, given our study sites’ relatively high ambient temperatures.
Early losses of dd stags often comprised fast-growing taxa like Acacia and Grevillea. As new stags age, those that remain standing increasingly comprise the more resilient taxa such as Erythrophleum, Callitris and larger eucalypts that dominate the original stag cohort (see in Supplementary Fig. S24). We did not attempt a detailed analysis, but note that Erythrophleum and Callitris timbers are regarded as particularly durable in northern Australian (wet–dry tropical) conditions.
Arguably our most surprising result is accelerated loss of stags at higher rainfalls. Among older stags, effects of rainfall variation within the observed range may exceed impacts of a single severe fire (Figs 5 and 6). We assume that accelerated decay or increased invertebrate (e.g. termite) consumption under wetter conditions contributes to higher rates of stag fall, perhaps exacerbated by wind-throw during rainstorms. During periods of above average rainfalls, tree mortalities are somewhat reduced (Fig. 5), with the net effect that in the absence of other acute disturbance such as severe fire, relative stag biomass (in relation to live stems) is lower under wetter conditions (Fig. 9).
Stag creation versus stag loss
Under benign conditions – average rainfalls and no severe fire – existing stags of median DBH are lost at approximately 6 times the rate that live stems die to replace them. Severe fire increases stag creation ~three-fold over 3 years of elevated mortality but promotes stag loss much less, by ~1.25 times. And fire affects many more live stems than stags, creating approximately three times as many new stags as are lost to the fire over the same period. Simulations show the resultant acute increase in proportions of AGB in standing dead wood (e.g. Fig. 11) and its fairly rapid post-fire decline. Nonetheless, proportionally elevated levels of stag AGB persist for some time, because the greater reductions in live AGB take much longer to fully restore (Fig. 9).
Fensham (2005) estimated losses of 27% of stag biomass per low-intensity fire. In the present study, stag losses (at median DBH and rainfall) in the year of severe fire exposure were increased to 25.4%, approximately double the annual background rate. These figures are not directly comparable because, inter alia, we have effectively included the effects of less severe fire in the ‘background’ rate. More generally, the extent to which fire accelerates loss of stags appears to vary widely. In southern Australian temperate eucalypt forests, dead trees have been reported to collapse predominantly following severe wildfire (Collins et al. 2012). Effects of fire on stags varies with topographic position (Bassett et al. 2015). Lloyd et al. (2012) found no consistent effect of fire season or frequency on the density of stags in a Florida pine forest, suggesting these features of the fire regime were relatively unimportant. Polo et al. (2013) rejected the notion that fire suppression had led to increased dead woody material in north America, reporting no effects of prescribed burns in dry oak forests. Although there is no ambiguity about the potential for severe fire to create more stags than it removes in these Australian savannas, more work is required in a wider range of settings to deal with the full array of issues raised by Fensham (2005) for improved accounting of stag dynamics and their significance.
The argument of Cook et al. (2020) that an observation of increased proportion of dead wood biomass at lower fire frequencies offers ‘scope for increasing the carbon stock in the woody debris pool with improved fire management’ requires qualification. Conclusions about carbon storage benefits cannot reasonably be based on observations of higher than average proportions of biomass in stags alone, and must start from recognition that stags were live stems that, given their quite short persistence times died in larger than usual numbers in the fairly recent past. The scale and source of prior deaths must be considered in any analysis of the meaning and value of increased stag presence (Gray et al. 2012). It is difficult to see how management of standing dead wood for increased dead biomass can be uncoupled from concurrent trends in live biomass.
Simulations and implications for carbon management
Our individual-based statistical models and their additive summaries in simulations are consistent with recent broad-scale analyses of tree cover and savanna AGB pools (Barber et al. 2023; Paul and Roxburgh 2024) in indicating substantial long-term carbon storage benefits from exclusion of severe fire from lower rainfall savanna landscapes, mostly in live trees and, to a much lesser extent, in stags. Our focus on severe fires and other differences in approach prevent detailed comparisons with Paul and Roxburgh’s (2024) calibration of Australia’s national carbon accounting model (FullCAM) to incorporate savanna fire of all intensities. However, we identified no direct incompatibilities. For example, their ‘no-fire’ mortality analogue (proportion of live AGB pools lost annually) at 1.1% for low rainfall savanna woodland is, as expected, lower than our (AGB-weighted) mean for ‘no-severe-fire’ mortality of 1.8% for stems exposed to mild and moderate fires. Our estimate of mean long-term proportions of standing AGB in stags under fairly benign conditions (no severe fire and long-term average rainfalls) at 8.6% is comparable with their 8.1% for lower rainfall savannas.
Our simulations were designed to reveal recurring patterns in mean responses to quite infrequent but high-disturbance events (severe fires) rather than single estimates of sequestration consequences at individual sites. Local estimates are challenged by model uncertainty, numerous simplifying assumptions, prospects of change in rainfall quanta and temporal patterns (NESP ESCC Hub 2020), unaccounted additional variation in topographic, edaphic and floristic features, and environmental history. Arguably, because derived from comparatively small and internally homogeneous plots, they may exaggerate fire impacts by failing to incorporate larger-scale diversity in both exposure and response. However, because they do not directly incorporate extreme wildfire events like those documented by Edwards et al. (2018) for the region, they may understate risk.
Despite such limitations, we consider that our focus on severe fires’ acute and enduring impact offers an important new perspective on risks for biomass sequestration projects in the Australian savannas. In particular, they illustrate potential for striking variations in trajectories of standing live and dead AGB – over periods directly relevant to time-bounded assessments of projects – determined by idiosyncracies of timing of severe fire events (and sequences of rainfalls during subsequent recovery), independently of any underlying variation in operational performance. Simulations indicate that sequestration outcomes estimated from pre- and post-project comparisons will often be difficult to interpret if the timing of those fires is random, despite success in reducing severe fire frequency in managed landscapes (see examples in Supplementary Tables S9 and S10 and Fig. S25).
In fire management, operational and policy uncertainties interact with the biophysical. What resources will be required to exclude severe fire over large areas for extended periods? How will a relevant baseline be identified and assessed? Should calculations of benefits include only (presumably more vulnerable) sites that have experienced severe fire in the recent past? Will climate change also alter fire regimes? Will institutional failure to control the spread of fire-promoting invasive grasses (e.g. gamba, Andropogon gayanus; Setterfield et al. 2010) continue to drive severe fire frequencies beyond levels simulated here, suppressing live AGB even further? If topographically or otherwise apparently protected sites are excluded from assessment of baselines, how will they be treated if a severe fire does in fact occur in more challenging future conditions?
In such an environment, risks arising from a single or repeated failure to exclude severe fire indefinitely are too serious for current generations to commit their communities to potentially large carbon debts. Another option to nonetheless encourage additional effort for better savanna fire management, in the short term at least, may be to supplement credits currently available through emission avoidance with an area-based, non-repayable sequestration bonus, paid for each year in which all or part of the eligible area excludes severe fire through both programmed preventive burning and energetic ad hoc control of non-prescribed burns. If restricted, as in existing approved methods, by consideration of dead wood alone, the quantum should take account of much larger benefits of success in simultaneously enhanced live storage.
Even if assessment and operational uncertainties are reduced, sequestration through fire management will still require facilitation by arrangements to share risk equitably. Effective risk-sharing requires that government explicitly accept and operationalise a role as overarching risk manager (Beck 1992) for activities that in aggregate produce national-scale public benefits. Methods must discourage speculative projects of limited prospects of success, while ‘insuring’ competent and committed participants against effectively random damage to finances or credibility.
It is in Australia’s interest to foster credible land-management offsets that realise real opportunities in savanna fire management, while avoiding overoptimistic project-level assessments that foster speculative involvement and ultimate failure. For broad-scale validation of collective benefits from multiple projects, further development of direct monitoring methods based on integrated systems of LiDAR and other satellite-based remote sensing (J Calvert, G Davidson, T Peter, E Taylor, L Taylor, et al., unpubl.) may offer plausible options. Local fine-resolution studies contributing to those methods can improve parameterisation of models applicable at all relevant scales. This study indicates that improved estimates of mortality in larger stems (e.g. Fig 4) and rates of loss of larger stags will be particularly valuable.
Data availability
Data have been lodged with the Dryad data repository as a component of a more comprehensive dataset including higher rainfall regions. Available at https://datadryad.org/stash/dataset/doi:10.5061/dryad.b8gtht7gq. Data are also held by the National Greenhouse Gas Inventory group at Department of Climate Change, Energy, the Environment and Water, Commonwealth of Australia.
Conflicts of interest
Jeremy Russell-Smith and Andrew Edwards are guest editors for the Savanna burning Special Issue of the International Journal of Wildland Fire. To mitigate this potential conflict of interest, they didn’t have any editor-level access to this manuscript during peer review. The authors have no other conflicts of interest to declare.
Declaration of funding
The study was supported by the Indigenous Land and Sea Corporation, The Nature Conservancy and Meat and Livestock Australia. BPM was supported by a grant from the Australian Research Council (FT170100004).
Acknowledgements
Jon Schatz, Felicity Watt and Mark Desailly assisted with data collection and entry. Many other individuals assisted with the fieldwork over the years, especially protected area staff and Indigenous rangers, including the Balanggarra Rangers and Wunggurr Rangers in the Kimberley; Mimal Rangers and Yugul Mangi Rangers in Central Arnhem Land; and Waanyi Garawa Rangers and Gangalidda Garawa Rangers in the Gulf of Carpentaria.
References
Angers V, Gauthier S, Drapeau P, Jayen K, Bergeron Y (2011) Tree mortality and snag dynamics in North American boreal tree species after a wildfire: a long-term study. International Journal of Wildland Fire 20, 751-763.
| Crossref | Google Scholar |
Ansell J, Evans J, Adjumarllarl Rangers, Arafura Swamp Rangers, Djelk Rangers, Jawoyn Rangers, Mimal Rangers, Numbulwar Numburindi Rangers, Warddeken Rangers, Yirralka Rangers, Yugul Mangi Rangers (2020) Contemporary Aboriginal savanna burning projects in Arnhem Land: a regional description and analysis of the fire management aspirations of Traditional Owners. International Journal of Wildland Fire 29, 371-385.
| Crossref | Google Scholar |
Aponte C, Tolhurst KG, Bennett LT (2014) Repeated prescribed fires decrease stocks and change attributes of coarse woody debris in a temperate eucalypt forest. Ecological Applications 24, 976-989.
| Crossref | Google Scholar | PubMed |
Barber G, Edwards A, Zander KK (2023) Fire, rain and CO2: potential drivers of tropical savanna vegetation change, with implications for carbon crediting. Fire 6, 465.
| Crossref | Google Scholar |
Bassett M, Chia EK, Leonard SW, Nimmo DG, Holland GJ, Ritchie EG, Clarke MF, Bennett AF (2015) The effects of topographic variation and the fire regime on coarse woody debris: insights from a large wildfire. Forest Ecology and Management 340, 126-134.
| Crossref | Google Scholar |
Bates D, Mächler M, Bolker B, Walker S (2015) Fitting linear mixed-effects models using lme4. Journal of Statistical Software 67, 1-48.
| Crossref | Google Scholar |
Bolker B (2019) Logistic regression, accounting for differences in exposure: 29 Sep 2019. RPubs by RStudio. Available at https://rpubs.com/bbolker/logregexp
Breheny P, Burchett W (2017) Visualization of regression models using visreg. The R Journal 9, 56-71.
| Crossref | Google Scholar |
Brooks ME, Kristensen K, van Benthem KJ, Magnusson A, Berg CW, Nielsen A, Skaug HJ, Mächler M, Bolker BM (2017) glmmTMB balances speed and flexibility among packages for zero-inflated generalized linear mixed modeling. The R Journal 9(2), 378-400.
| Crossref | Google Scholar |
Collins L, Bradstock RA, Tasker EM, Whelan RJ (2012) Can gullies preserve complex forest structure in frequently burnt landscapes? Biological Conservation 153, 177-186.
| Crossref | Google Scholar |
Cook G, Liedloff A, Eager R, Chen X, Williams R, O’Grady A, Hutley L (2005) The estimation of carbon budgets of frequently burnt tree stands in savannas of northern Australia, using allometric analysis and isotopic discrimination. Australian Journal of Botany 53, 621-630.
| Crossref | Google Scholar |
Cook GD, Liedloff AC, Meyer CP, Richards AE, Bray SG (2020) Standing dead trees contribute significantly to carbon budgets in Australian savannas. International Journal of Wildland Fire 29, 215-228.
| Crossref | Google Scholar |
Corey B, Andersen A, Legge S, Woinarski JC, Radford IJ, Perry JJ (2019) Better biodiversity accounting is needed to prevent bioperversity and maximize co-benefits from savanna burning. Conservation Letters 13, e12685.
| Crossref | Google Scholar |
Cousins S, Battles J, Sanders JE, York R (2015) Decay patterns and carbon density of standing dead trees in California mixed conifer forests. Forest Ecology and Management 353, 136-147.
| Crossref | Google Scholar |
Dunn CJ, O’Connor CD, Reilly MJ, Calkin DE, Thompson MP (2019) Spatial and temporal assessment of responder exposure to snag hazards in post-fire environments. Forest Ecology and Management 441, 202-214.
| Crossref | Google Scholar |
Edwards A, Russell-Smith J, Meyer M (2015) Contemporary fire regime risks to key ecological assets and processes in north Australian savannas. International Journal of Wildland Fire 24, 857-870.
| Crossref | Google Scholar |
Edwards AC, Russell-Smith J, Maier SW (2018) A comparison and validation of satellite-derived fire severity mapping techniques in fire prone north Australian savannas: extreme fires and tree stem mortality. Remote Sensing of Environment 206, 287-299.
| Crossref | Google Scholar |
Fei S, Morin RS, Oswalt CM, Liebhold AM (2019) Biomass losses resulting from insect and disease invasions in US forests. Proceedings of the National Academy of Sciences 116, 17371-17376.
| Crossref | Google Scholar | PubMed |
Fensham RJ (2005) Monitoring standing dead wood for carbon accounting in tropical savanna. Australian Journal of Botany 53, 631-638.
| Crossref | Google Scholar |
Fensham RJ, Fairfax RJ, Ward DP (2009) Drought-induced tree death in savanna. Global Change Biology 15, 380-387.
| Crossref | Google Scholar |
Franklin JF, Shugart HH, Harmon ME (1987) Tree death as an ecological process. BioScience 37, 550-556.
| Crossref | Google Scholar |
Gillner S, Rüger N, Roloff A, Berger U (2013) Low relative growth rates predict future mortality of common beech (Fagus sylvatica L.). Forest Ecology and Management 302, 372-378.
| Crossref | Google Scholar |
Gora EM, Lucas JM, Yanoviak SP (2019a) Microbial composition and wood decomposition rates vary with microclimate from the ground to the canopy in a tropical forest. Ecosystems 22, 1206-1219.
| Crossref | Google Scholar |
Gora EM, Kneale RC, Larjavaara M, Muller-Landau HC (2019b) Dead wood necromass in a moist tropical forest: stocks, fluxes, and spatiotemporal variability. Ecosystems 22, 1189-1205.
| Crossref | Google Scholar |
Gray A, Ganey JL, Vojta SC (2012) Trends in snag populations in drought-stressed mixed-conifer and ponderosa pine forests (1997-2007). International Journal of Forestry Research 2012, 529197.
| Crossref | Google Scholar |
Harmon ME, Franklin JF, Swanson FJ, Solkins PJ, Gregory SV, Lattin JP, Andersen NH, Cline SP, Aumen N, Sedell JR, Lienkaemper GW, Cromack K, Cummins KW (1986) Ecology of coarse woody debris in temperate ecosystems. Advances in Ecological Research 15, 133-302.
| Crossref | Google Scholar |
Hilger AB, Shaw CH, Metsaranta JM, Kurz WA (2012) Estimation of snag carbon transfer rates by ecozone and lead species for forests in Canada. Ecological Applications 22, 2078-2090.
| Crossref | Google Scholar | PubMed |
Hutley LB, Evans BJ, Beringer J, Cook GD, Maier SW, Razon E (2013) Impacts of an extreme cyclone event on landscape-scale savanna fire, productivity and greenhouse gas emissions. Environmental Research Letters 8, 045023.
| Crossref | Google Scholar |
Kwon S, Kim S, Kim J, Kang W, Park K-H, Kim C-B, Girona MM (2021) Predicting post-fire tree mortality in a temperate pine forest, Korea. Sustainability 13, 569.
| Crossref | Google Scholar |
Law S, Eggleton P, Griffiths H, Ashton L, Parr C (2019) Suspended dead wood decomposes slowly in the tropics, with microbial decay greater than termite decay. Ecosystems 22, 1176-1188.
| Crossref | Google Scholar |
Leitold V, Morton DC, Longo M, dos-Santos MN, Keller M, Scaranello M (2018) El Niño drought increased canopy turnover in Amazon forests. New Phytologist 219, 959-971.
| Crossref | Google Scholar | PubMed |
Lindenmayer D, Zylstra P (2024) Identifying and managing disturbance-stimulated flammability in woody ecosystems. Biological Reviews 99, 699-714.
| Crossref | Google Scholar | PubMed |
Lloyd JD, Slater GL, Snyder JR (2012) The role of fire-return interval and season of burn in snag dynamics in a south Florida slash pine forest. Fire Ecology 8, 18-31.
| Crossref | Google Scholar |
Lugo AE, Scatena FN (1996) Background and catastrophic tree mortality in tropical moist, wet, and rain forests. Biotropica 28, 585-599.
| Crossref | Google Scholar |
Murphy BP, Whitehead PJ, Evans J, Yates CP, Edwards AC, MacDermott HJ, Lynch DC, Russell-Smith J (2023) Using a demographic model to project the long-term effects of fire management on tree biomass in Australian savannas. Ecological Monographs 93, e1564.
| Crossref | Google Scholar |
Oberle B, Ogle K, Zanne AE, Woodall CW (2018) When a tree falls: controls on wood decay predict standing dead tree fall and new risks in changing forests. PLoS One 13, e0196712.
| Crossref | Google Scholar | PubMed |
Paul KI, Roxburgh SH (2024) A national accounting framework for fire and carbon dynamics in Australian savannas. International Journal of Wildland Fire 33, WF23104.
| Crossref | Google Scholar |
Paul KI, Roxburgh SH, Chave J, England JR, Zerihun A, Specht A, Lewis T, Bennett LT, Baker TG, Adams MA, Huxtable D, Montagu KD, Falster DS, Feller M, Sochacki S, Ritson P, Bastin G, Bartle J, Wildy D, Hobbs T, Larmour J, Waterworth R, Stewart HT, Jonson J, Forrester DI, Applegate G, Mendham D, Bradford M, O’Grady A, Green D, Sudmeyer R, Rance SJ, Turner J, Barton C, Wenk EH, Grove T, Attiwill PM, Pinkard E, Butler D, Brooksbank K, Spencer B, Snowdon P, O’Brien N, Battaglia M, Cameron DM, Hamilton S, McAuthur G, Sinclair J (2016) Testing the generality of above-ground biomass allometry across plant functional types at the continent scale. Global Change Biology 22, 2106-2124.
| Crossref | Google Scholar | PubMed |
Perry JJ, Sinclair M, Wikmunea H, Wolmby S, Martin D, Martin B (2018) The divergence of traditional Aboriginal and contemporary fire management practices on Wik traditional lands, Cape York Peninsula, Northern Australia. Ecological Management & Restoration 19, 24-31.
| Crossref | Google Scholar |
Pietsch KA, Eichenberg D, Nadrowski K, Bauhus J, Buscot F, Purahong W, Wipfler B, Wubet T, Yu MJ, Wirth C (2019) Wood decomposition is more strongly controlled by temperature than by tree species and decomposer diversity in highly species rich subtropical forests. Oikos 128, 701-715.
| Crossref | Google Scholar |
Polo JA, Hallgren SW, Leslie DM (2013) Effect of long-term understory prescribed burning on standing and down dead woody material in dry upland oak forests. Forest Ecology and Management 291, 128-135.
| Crossref | Google Scholar |
Price OF, Russell-Smith J, Watt F (2012) The influence of prescribed fire on the extent of wildfire in savanna landscapes of western Arnhem Land, Australia. International Journal of Wildland Fire 21, 297-305.
| Crossref | Google Scholar |
Russell-Smith J, Edwards AC (2006) Seasonality and fire severity in savanna landscapes of monsoonal northern Australia. International Journal of Wildland Fire 15, 541-550.
| Crossref | Google Scholar |
Russell-Smith J, Yates C, Whitehead P, Smith R, Craig R, Allan G, Thackway R, Frakes I, Cridland S, Meyer C, Gill M (2007) Bushfires ‘Down Under’: patterns and implications of contemporary Australian landscape burning. International Journal of Wildland Fire 16, 361-377.
| Crossref | Google Scholar |
Russell-Smith J, Murphy BP, Meyer CP, Cook GD, Maier S, Edwards AC, Schatz J, Brocklehurst P (2009) Improving estimates of savanna burning emissions for greenhouse accounting in northern Australia: limitations, challenges, applications. International Journal of Wildland Fire 18, 1-18.
| Crossref | Google Scholar |
Setterfield S, Rossiter-Rachor N, Hutley L, Douglas M, Williams R (2010) Turning up the heat: the impacts of Andropogon gayanus (gamba grass) invasion on fire behaviour in northern Australian savannas. Diversity and Distributions 16, 854-861.
| Crossref | Google Scholar |
Shaffer TL (2004) A unified approach to analyzing nest success. The Auk 121, 526-540.
| Crossref | Google Scholar |
Threlfall CG, Law BS, Peacock RJ (2019) Benchmarks and predictors of coarse woody debris in native forests of eastern Australia. Austral Ecology 44, 138-150.
| Crossref | Google Scholar |
Verschuren L, De Mil T, De Frenne P, Haneca K, Van Acker J, Vandekerkhove K, Van den Bulcke J (2023) Heading for a fall: the fate of old wind-thrown beech trees (Fagus sylvatica) is detectable in their growth pattern. Science of The Total Environment 903, 166148.
| Crossref | Google Scholar | PubMed |
Whitehead PJ, Russell-Smith J, Yates C (2014) Fire patterns in north Australian savannas: extending the reach of incentives for savanna fire emissions abatement. The Rangelands Journal 36, 371-388.
| Crossref | Google Scholar |
Wohling M (2009) The problem of scale in indigenous knowledge: a perspective from northern Australia. Ecology and Society 14(1),.
| Crossref | Google Scholar |
Wood S, Scheipl F (2020) gamm4: generalized additive mixed models using ‘mgcv’ and ‘lme4’. Available at https://rdrr.io/cran/gamm4/
Woolley L-A, Murphy BP, Radford IJ, Westaway J, Woinarski JC (2018) Cyclones, fire, and termites: the drivers of tree hollow abundance in northern Australia’s mesic tropical savanna. Forest Ecology and Management 419–420, 146-159.
| Crossref | Google Scholar |
Zhao WW, van Logtestijn RSP, van der Werf GR, van Hal JR, Cornelissen JHC (2018) Disentangling effects of key coarse woody debris fuel properties on its combustion, consumption and carbon gas emissions during experimental laboratory fire. Forest Ecology and Management 427, 275-288.
| Crossref | Google Scholar |


