Wildfire aerial thermal image segmentation using unsupervised methods: a multilayer level set approach
Tiago Garcia A * , Ricardo Ribeiro A and Alexandre Bernardino A
A * , Ricardo Ribeiro A and Alexandre Bernardino A
A Institute for Systems and Robotics, Instituto Superior Tecnico, Lisbon, Portugal.
International Journal of Wildland Fire 32(3) 435-447 https://doi.org/10.1071/WF22136
Submitted: 1 July 2022 Accepted: 17 February 2023 Published: 17 March 2023
© 2023 The Author(s) (or their employer(s)). Published by CSIRO Publishing on behalf of IAWF. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)
Abstract
Background and aims: Infrared thermal images of a propagating wildfire taken by manned or unmanned aerial vehicles can help firefighting authorities with combat planning. Segmenting these images into regions of different fire temperatures is a necessary step to measure the fire perimeter and determine the location of the fire front.
Methods: This work proposes a multilayer segmentation method based on level sets, which have the property of handling topology, making them suitable to segment images that contain scattered fire areas. The experimental results were compared using hand-drawn labels over a set of images provided by the Portuguese Air Force as ground truth. These labels were carefully drawn by the authors to ensure that they complied with the requirements indicated by the Portuguese National Authority for Emergency and Civil Protection. The proposed method was optimised to ensure contour smoothness and reliability, as well as reduce computation time.
Key results: The proposed method can surpass other common unsupervised methods in terms of intersection over union, although it has not yet been able to perform real-time segmentation.
Conclusions: Although falling out of use in relation to supervised and deep learning methods, unsupervised segmentation can still be very useful when annotated datasets are unavailable.
Keywords: airborne sensors, firefront tracking, image segmentation, level set segmentation, thermal images, thermal mapping, unsupervised segmentation, wildfire monitoring.
Introduction
Motivation and objectives
Forest fires are an important ecological process and are responsible for the shaping of ecosystems (Bowman et al. 2020; Tymstra et al. 2020). They are responsible for clearing forest soil of debris and foliage and for enriching the soil with nutrients, allowing new plants to grow and receive sunlight (Zavala et al. 2014). Additionally, the frequent occurrence of controlled fires renovates forest flora by consuming vegetation that otherwise can overgrow and result in a potential catastrophic fire (Butz 2009).
However, wildfires that burn in an uncontrolled way become devastating events, destroying infrastructure, damaging the economy and endangering human lives. Heavy rains that follow an intensive fire result in flooding and landslides (Lourenço et al. 2012). Furthermore, wildfires release greenhouse gases into the atmosphere that promote the effects of climate change. In turn, climate change creates longer and more extreme fire weather seasons that along with human activity may result in an increase in the risk of fire occurrence (Dupuy et al. 2020; Jones et al. 2022).
The Portuguese hot and dry summers make the landscape very prone to fire (Verde and Zêzere 2010; Turco et al. 2019), which along with arson and negligence cases (Parente et al. 2018) may explain the increase in the number and intensity of wildfires in Portugal. In the last 10 years, there were an average of 15 553 wildfires that consumed an average area of 125 831 ha, which is ~1.4% of the Portuguese continental territory.
After the catastrophic summer of 2017, in which there were multiple human casualties in the fires of Pedrógão Grande and the infamous day of 15 October 2017, when there were almost 500 occurrences of wildfires in Portugal on the same day, the FIREFRONT (www.firefront.pt) and VOAMAIS (www.voamais.pt) projects were born. These projects aim at developing solutions to support firefighting action in forest fires, using data obtained from manned and unmanned aerial vehicles (UAVs) equipped with a combination of different visible colour (red, green, blue (RGB)) and infrared thermal (IR) cameras and using reliable communication and navigation systems. This constitutes a powerful tool in the observation of forest areas and can be relevant in every stage of emergency management (Bailon-Ruiz and Lacroix 2020). For early detection, it is important to accurately identify images containing wildfires while avoiding false positives, for example, with similar colour patterns such as sunsets or dry foliage as they have the same shades of yellow and red (Perrolas et al. 2022; Harkat et al. 2023). During the response stage, UAVs can help geolocalise the fire front (Santana et al. 2022; Sargento et al. 2022), measure the fire extent, and discern any sudden changes in the smoke plume indicating variations in the speed and direction of the wind that may induce a change in the wildfire rate of spread (Cruz et al. 2012; Pinto et al. 2022). When a wildfire is eventually declared controlled, it is still worth detecting if and where reburns occur to quickly extinguish them, preventing a new critical situation.
Thermal cameras can prove extremely useful when smoke and vegetation obscure the field of vision of aircraft, allowing better characterisation of the fire and identification of active fire pockets. This work aims at developing methods for segmentation of aerial wildfire thermal images into different regions of similar characteristics. This goal, however, poses some challenges. Firstly, there is a lack of databases with annotated thermal images of wildfires, which restricts our approach to unsupervised methods that only use information contained in the images themselves, such as pixel intensity. Secondly, we need to account for image noise and the fact that the images may contain multiple fire patches spread across the image. Finally, it is not clear at the data collection stage which regions are the most relevant for decision making by fire management agencies.
The implemented fire detection algorithms should be able to systematically receive thermal images and output contours that sort the image into relevant regions with similar intensities. The contour lines will resemble level curves, allowing users to eventually construct a thermal map of the image and obtain the perimeter of the wildfire and the extent of the fire front, which are two key parameters of interest to the ANEPC (Portuguese National Authority for Emergency and Civil Protection). As the ANEPC requires one set of contours to encircle the entire fire area and another set to identify just the active pockets, we address this problem as a division of the images in three classes:
Class 1 (outer): outside the fire
Class 2 (middle): region inside the fire that does not belong to the propagating front
Class 3 (inner): the hottest (brightest) regions, which represent the propagating front.
The contours should be smooth for later calculation of the perimeter of the burning areas. Additionally, small high-intensity dots within the fire should be classified as Class 2, given that they most likely correspond to trees or other objects that are still burning actively but do not represent the fire front that it is desired to track.
Related work
Segmentation of IR images has been done mainly in the field of medical imaging, using watershed (Grau et al. 2004), K-means (Ng et al. 2006) and level set methods (Banerjee and Bhattacharya 2010). The segmentation of aerial IR wildfire images for tracking of the active front was attempted using, for example, a combination of Otsu and optical flow (Yuan et al. 2017) and Canny edge detectors (Valero et al. 2018). However, these methods only present a division of the image into two classes. Extensive research on automated wildfire monitoring techniques was compiled by Yuan et al. (2015).
Multilayer level set methods allow detection of multiple classes. Examples of past applications of these methods include temperature analyses in concrete structures (Huang and Wu 2010; Huang et al. 2013), in medical imaging (Moreno et al. 2014) and in plant leaves (Wen et al. 2020), all of which make use of two level set functions. The present work is the first to apply the multilayer level set technique to the segmentation of thermal images of wildfires. It differs from the methods previously referred to by using only one level set function, which makes the algorithm faster, by adding an edge stopping local term and by using multi-class segmentation with further selection of the relevant contours.
Theoretical background on level set segmentation, active contours and the Chan–Vese model
The concept of active contour models is to derive a contour, depending on the gradient of an image, such that it is attracted towards the boundary of the object to detect while minimising its internal energy, therefore maximising the smoothness of the curve. In our approach, this minimisation is obtained by taking the contour of the zero-level set of a level set function Φ.
Oscher and Sethian (1988) introduced the concept of implicitly representing a contour C (or propagating front) using the evolution of an implicit higher-dimensional Lipschitz function Φ. Let us define a two-dimensional image  where Ω is a given image domain, constituting a bounded open subset of the real number set R. Let ω be a subset of Ω, consisting of an open region with smooth boundary that corresponds to the object that is to be detected. The implicit function Φ(x, y, t) is time-dependent (the time corresponding to the iterative process of finding the contours in a single image), but for simplicity of notation, let us ignore for now the time dependency, that is, considering the function Φ(x, y) as defined by
where Ω is a given image domain, constituting a bounded open subset of the real number set R. Let ω be a subset of Ω, consisting of an open region with smooth boundary that corresponds to the object that is to be detected. The implicit function Φ(x, y, t) is time-dependent (the time corresponding to the iterative process of finding the contours in a single image), but for simplicity of notation, let us ignore for now the time dependency, that is, considering the function Φ(x, y) as defined by 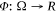 . This function satisfies
. This function satisfies
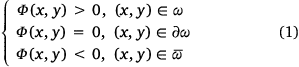
where x and y represent the two dimensions of an image, ∂ω is the boundary of ω and 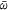 represents the complement of ω. As such, the implicit function Φ is positive inside the region ω, negative outside it and the contour C that corresponds to the boundary ∂ω is obtained by taking the zero level set of Φ.
represents the complement of ω. As such, the implicit function Φ is positive inside the region ω, negative outside it and the contour C that corresponds to the boundary ∂ω is obtained by taking the zero level set of Φ.
To ensure a smooth evolution of the contour C, it is made to depend on the contour curvature k along its normal direction N, as shown in Fig. 1. Remember that the curvature is given by the inverse of the respective circle radius, 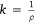 .
.

|
The normal unit vector N and the curvature k of the contour C are given as a function of Φ, respectively, by


where ∇Φ = [Φx; Φy] is the space gradient of Φ and |∇Φ| is its absolute value. The evolution of the level set function is given by
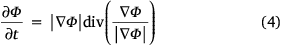
as explained by Osher and Sethian (1988), Malladi and Sethian (1996) and Zhao et al. (1996). The divergence of the gradient of a function, also called the Laplacian operator, is a smoothing term, therefore making Eqn 4 a regularising term that allows smooth contours to be obtained even on noisy images.
The main advantage of level set methods for image segmentation is that all derivatives are taken on a fixed rectangular grid representing an image, instead of being taken on a curve. In the latter case, such derivatives would be very difficult to implement, especially when change of topology occurs, for example with merging (two contours that become one) and breaking (one contour becomes two). Note that this effect happens during the iterative process of contour evolution in the same image and is not to be confused with the temporal evolution of the wildfire, when fire fronts coalescence and spotting occurs.
Edge-based active contour models use gradient information to stop the contour evolution near strong edges. This can be achieved through the use of an edge-stopping function g that has the property of being positive and decreasing with gradient magnitude, so that g becomes near zero at the edges and near one when the gradient is null. An example chosen in Caselles et al. (1993) is

where the image I is convoluted with a two-dimensional Gaussian filter 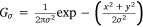 with standard deviation σ.
with standard deviation σ.
Edge-based methods, such as the Geodesic Active Contour (GAC) model (Caselles et al. 1997), are sensitive to the placement of the initial contour. If it is initialised away from the object, it may never reach it and instead detect another strong edge, because it has no information about the whole image. This is especially concerning if the image is very noisy, as then the smoothing Gaussian will have to be strong and will also smooth the edges.
Area-based active contour models use global image information, attempting to divide an image into regions by associating the pixels that share common properties, such as similar intensities. One of the most famous examples is the method introduced in Chan and Vese (2001), which is based on the functional in Mumford and Shah (1989). The Mumford–Shah formulation for image segmentation comprises the decomposition of an image into n regions, such that the intensities vary slowly within each region and briskly across the borders between them.
The original Chan–Vese model is a particular case of the Mumford–Shah minimal partition problem, in which an image is only divided into two regions. It aims at approximating an image I by an image I0 that takes only two values, the average of I inside C denominated c1 and the average of I outside C denominated c2.
The approximation I0 is then defined by

where  is the Heaviside function,
is the Heaviside function,

while c1 and c2 are the averages of the intensities inside and outside the image, respectively. They can be calculated as a function of Φ with

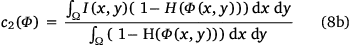
Adding regularising terms like the length of the contour and the area of the detected region, and using the length and area measures from Chan and Vese (2001) and Zhao et al. (1996) and finally replacing the Heaviside and Dirac functions for their regularised versions (which are defined later in the Methods section), the Chan–Vese energy functional Ecv to be minimised is
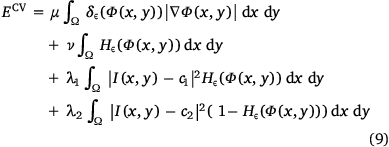
where I is the image in the domain Ω, Hε is the regularised Heaviside function, δε is the regularised Dirac function and µ, v, λ1 and λ2 are weight parameters. The minimisation of Ecv results in the original Chan–Vese model

where v is typically set to zero. The model implies that differences of the intensities within each area are as low as possible while the contour stays smooth. This will effectively result in correct signalling of the burning areas if they have clearly distinct intensities from the rest of the image.
The Chan–Vese method, initially developed for a two-class segmentation that was achieved by cutting the level set function at level set zero, was generalised to multiclass segmentation (Vese and Chan 2002; Chung and Vese 2005, 2009; He and Osher 2007). For m contours and n = m + 1 regions, the multi-layer Chan–Vese model determines the evolution of Φ as
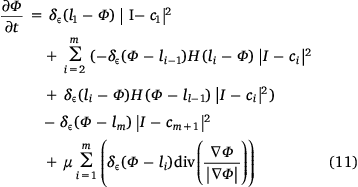
which is given by the sum of an area term and a length term. The Dirac and Heaviside functions are used for the length and area terms, respectively. Multiplying a term by the Dirac function evaluates the term at the respective level set (border). Multiplying a term by a Heaviside function (or by a product of Heaviside functions) evaluates that term at one of the regions. The area term evaluates the influence, on each level curve, of the sum of differences between the mean intensities of each region and each pixel within the region. If the difference is high, that difference will be evaluated by the Dirac function at the respective level set and thus it will have a high weight at that level. The contour will then shrink or expand to minimise this weight. This effect is referred to as ‘balloon force’. The length regularisation term guarantees that the curve follows a smooth evolution according to its curvature. Smoother contours are shorter, and so they will be favoured by having a lower weight in the overall term. The balance between the two terms is controlled by the parameter µ.
The mean intensities c1, …ci, …cm+1 (i = {2, …, m}) of each region are given by
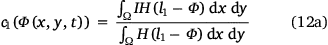
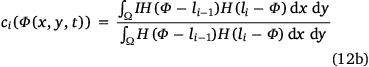
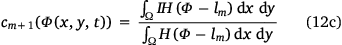
Methods
Datasets
The datasets used for segmentation were provided by the Portuguese Air Force and consisted of images and videos taken during real wildfire occurrences. The data were collected using drones manufactured by UAVISION, model Ogassa OGS42 VN. The drones were equipped with a USG 400 UAVISION gyro-stabilised gimbal that included a full High-Definition (HD) long-range visible camera (RGB) and a 640 pixel × 480 pixel LWIR (long-wave infrared) infrared camera. The infrared camera has a 25 mm lens with an HFOV (horizontal field of view) of 24.6° capturing IR bands from 8 to 14 µm at a frame rate of 30 Hz. The power and voltage specifications are 50 W and 24 V, respectively.
The videos used for this work were exclusively obtained with the LWIR camera and the information used to perform segmentation consists only of the resulting pixel intensities, represented as an 8-bit unsigned integer value ranging between 0 and 255. In these cameras, the pixel intensities are associated with higher temperatures but owing to the presence of auto-gain that is influenced by lighting and atmospheric conditions, the same pixel intensity may correspond to different temperatures in separate frames.
The main video is dubbed FOGO_1. It consists of different points of view of a wildfire with nearly 1 min of IR footage in total between RGB segments. The fire occurred on 16 August 2019 near Vilã Chã, Pombal, Portugal, and the footage was taken ~5:30 pm. To quantitatively evaluate the segmentation, 55 images were selected, 1 s apart from each other, from the total 1342 frames. The frames of FOGO_1 were supplied with a resolution of 768 × 576 as they were resized after acquisition. The ground-truth masks were created by hand using the MATLAB® R2020a Image Labeler app, following the indications given by the ANEPC, described in the Introduction Motivation and Objectives section.
The remaining images that were provided had erratic calibration of the cameras and the image resolution was sometimes very low, which resulted in images with low contrasts, overall more challenging to process. Despite their provenance from different locations, namely Lousã, Mirandela and Monchique, these images were catalogued in dataset FOGO_2. They were taken in September 2020 and have the original 640 × 480 resolution of the IR sensor.
Proposed model
Our approach addresses the problem of fire perimeter and fire front delimitation using a multi-class segmentation formulation. Considering the challenges described in the Introduction section, we decided to use level sets; they are able to obtain smooth contours and are insensitive to initialisation. The proposed method is based on the multilayer active contour model that originated in the Chan–Vese method, although with some modifications. These are presented in this section along with the general proposed solution.
For practical purposes, the Heaviside and Dirac functions need to be approximated by a continuous smooth function. The regularised version of the Heaviside and Dirac functions are given respectively, by

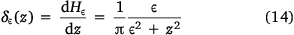
where ε is a regulating term that controls the level of regularisation; ε = 0 corresponds to no regularisation and typical values range from 1 to 1.5 (Chan and Vese 2001; Huang and Wu 2010). A higher value of ε corresponds to a softer function.
Because the Chan–Vese energy is not convex (Chan and Vese 2001), it allows the existence of many local minima. As the regularisation functions presented in Eqns 13, 14 never truly reach zero, they allow for the search of a global energy minimiser, therefore making the model non-sensitive to the initialisation of the level set function.
The numerical computation of the equation that translates the level set function evolution is achieved by converting the curvature term to the discrete form using the discretisation model in Chan and Vese (2001). The method used for solving the discrete partial differential equation starts by computing the values of gradient terms C1, C1, C3 and C4, according to Chung and Vese (2009).

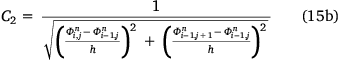
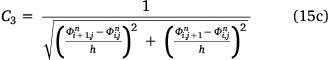
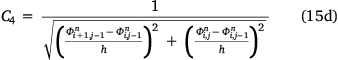
where h is a step constant typically set to 1. Next, compute the value of m1, given by
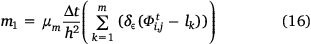
where lk is the kth level set, 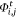 is the current level set function, Δt is the time step and μm = μ × 256 × 256 (256 being the total number of grey level intensities). Then, compute the value of C, given by C = 1 + m(C1 + C2 + C3 + C4).
is the current level set function, Δt is the time step and μm = μ × 256 × 256 (256 being the total number of grey level intensities). Then, compute the value of C, given by C = 1 + m(C1 + C2 + C3 + C4).
The evolution of the discrete level set function (Chung and Vese 2005, 2009; Huang and Wu 2010) is given by
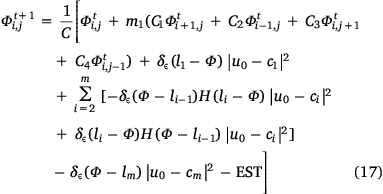
where EST (edge-stopping term) is the term that will be introduced in Eqn 18 and Φ is equal to 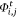 (for simplicity of notation).
(for simplicity of notation).
Inclusion of edge stopping term
As the segmentations were experimented with, it was verified that with the inclusion of more contours, the outer contours were detecting non-relevant edges or no edges at all, and inner contours were not sticking with the borders of the innermost areas. To correct this issue, it was decided to add an edge stopping term directly to the evolution rule, as was done by Li et al. (2010). This term is given by

where α is a weight term, g(∇I) is given by Eqn 5 and δε(Φ − li) allows for the selective application of this term to the ith level set, which is performed as the inclusion of this term has a destabilising effect on Φ. The term in Eqn 18 approximates the inner contour, given by the level set lm to the boundary of the brightest areas and keeps the outermost contour (corresponding to l1) from propagating outside the wildfire area. Fig. 2 demonstrates this effect, where the colour map used for the contours (yellow to red) represents contours encircling progressively brighter (hotter) areas. The legend of Fig. 2 represents the mean intensities ci that the respective coloured contour encircles (so the outermost region is not shown). For simplicity reasons, we will no longer include this type of legend as it is no longer relevant for presenting our work and may overlap with important regions of the images. However, the colour map logic still holds.

|
Multigrid implementation
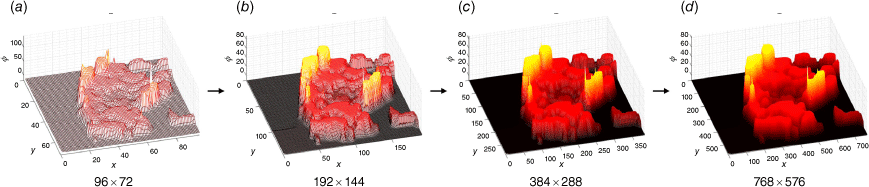
The calculations required to apply the law in Eqn 17 may have an extremely high computational cost if the input image has a high resolution. Even at a resolution of 768 × 576, which is the most common resolution of the IR images supplied by the Portuguese Air Force, the time needed to achieve convergence on the level set function can be over 1 min. To address this issue, we compute several K lower-resolution images from the input image I, as shown in Fig. 3, each one with half the pixels of the previous one in each direction. Let κ be the current resolution. The level set function is initialised on the coarser grid (κ = K), evolved until convergence, and extrapolated to the next-finer grid (κ = κ − 1). This process is repeated until convergence is reached on the grid with the original image resolution (κ = 0).
Stabilisation of the level set function
The evolution of the level set function relies on the computation of discrete differences, along with other high volatility calculations associated with solving a partial differential equation. This generates fluctuations in the resulting level set function in that iteration that if not stabilised will eventually produce inaccurate results.
This problem can be solved in one of two ways, either decrease the time step Δt, ensuring a smoother evolution of the level set function, but at a cost of more iterations, or keep the same inverse gradient terms C1, C2, C3 and C4 and re-calculate the other terms for a smaller number of relaxation iterations. The latter solution was chosen, as it skipped the calculation of the inverse gradient terms. As these terms are extremely sensitive to small variations in the function, we evolve the level set function for a fixed number of iterations, so it can converge. This strategy for numerically solving partial differential equations is described in Briggs et al. (2000).
Definition of initial level set function and level set positions
The initialisation of Φ should be done in a way that allows its evolution to smoothly reach all of the level sets, which were empirically selected to be multiples of 10, L = {0, 10, …, 10n}, n being the number of classes. Also, it needs to contain (or be near) at least one of the level sets, because it will otherwise evolve in the opposite direction and fall into a local minimum.
The regularisation term μ plays a very important role in the evolution of Φ. If this parameter is too high, the function will never reach the more distant level sets. If this parameter is too low, then the method becomes a simple pixel clustering algorithm based on intensities of the whole image, which will lead to over-segmentation.
For the initial mask, it was decided to start with small circles scattered evenly across the entire image. This allowed not only a smoother evolution, as a circle has no sharp edges, but also a faster and more uniform convergence because the evolution starts at multiple points simultaneously. The transformation from the initial mask to the initial level set function used the Euclidean distance to the centre of every circle.
Truncation of the level set function
The computation of the edge-stopping term disrupts the evolution of the overall level set function. Near the borders of the regions, the gradients are the highest, and thus the edge stopping function will have a value of approximately 1. As the EST is subtracted when evolving Φ, this causes it to reach very low instantaneous values near the contours. These low spikes have such high absolute values that the level set function cannot recover and stabilise again in the affected points. In the end, this effect causes the respective pixels to be incorrectly classified as belonging to the outermost region because they are below zero (Fig. 4a). To avoid this, a simple truncation of the level set function is performed at each iteration. If the value of Φ reaches a value below vmax at a certain point, it gets the value of vmax = −10 (Fig. 4b). This effectively assures that the function can recover from this sudden drop in the next iterations.

|
Results
The frames of the FOGO_1 dataset were subjected to a segmentation ranging from two to seven classes using the level set method in Eqn 17. The purpose was to evaluate the ability of the algorithm to construct thermal maps of the wildfire. Fig 5, Table 1 show the influence of the number of contours on the segmentations obtained and the segmentation time, respectively.

|

|
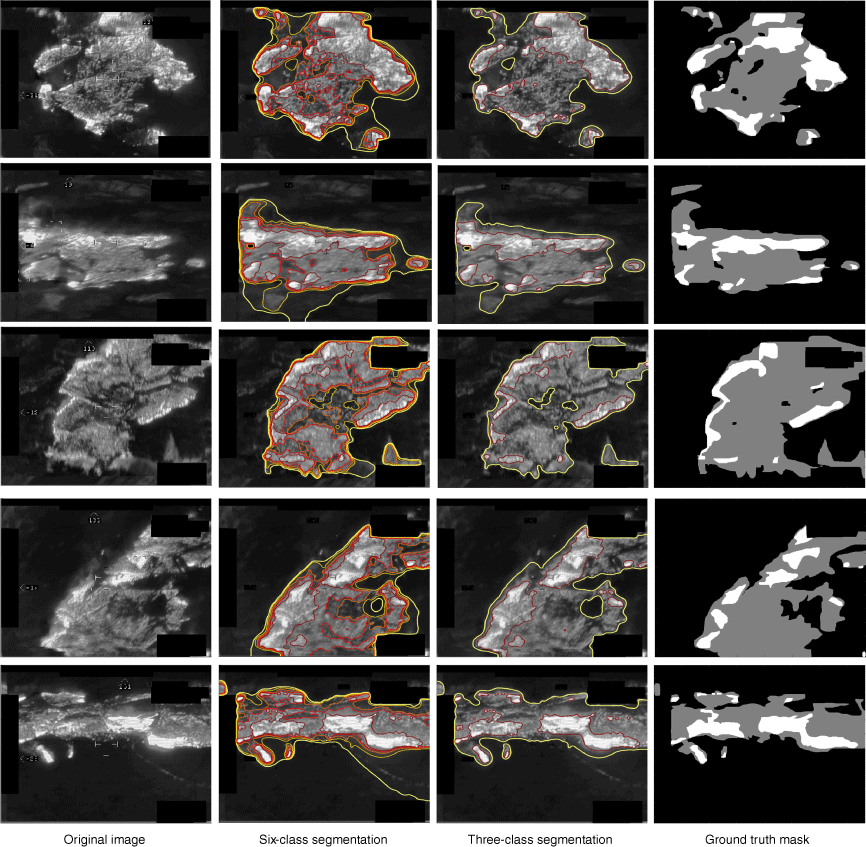
Ordinarily, and as stated in the objectives, we would desire a three-class segmentation, but realising how sometimes a two-contour segmentation would result in bad identification of the fire front, we tested the possibility of performing a segmentation with more contours and then selecting the two relevant ones that corresponded to the fire perimeter and the fire front. For this purpose, we compiled a series of images with three, four, five and six-class segmentations and different combinations of selected contours and presented them to the ANEPC staff. We reached the conclusion that for the images presented, the best overall combination was an initial six-class segmentation from which only contours 2 and 5 were retained and used to generate the three-class classification map. The numbering of contours is presented in Fig. 6. This technique resulted in an improvement of IoU (intersection over union) from 0.653 (with direct three-class segmentation) to 0.775. Fig. 7 presents the results of both approaches to an image.

|

|
Fig. 8 shows some of the results obtained for the FOGO_1 dataset with the optimal tuning parameters found through a grid search that are described in Table 2.

|
To test the algorithm over the whole video sequence, all the frames in FOGO_1 were segmented and compiled in a video that is available in the following link: https://youtu.be/kD9TEFOaHxw.
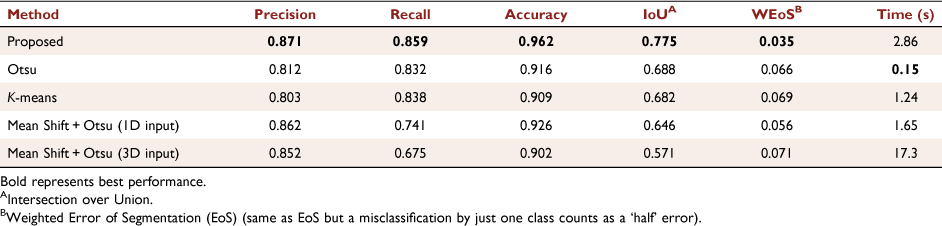
To further compare the performance of the proposed method against other common unsupervised methods, the 55 selected frames were also subjected to the application of the multi-layer Otsu (Otsu 1979; Liu and Yu 2009), K-means (Liu and Yu 2009; Sinaga and Yang 2020) and Mean Shift (Fukunaga and Hostetler 1975; Comaniciu and Meer 1999) algorithms. The class grouping technique described earlier, with six-class initial segmentation and same choice of relevant contours, was also tested when using these methods, resulting in an improvement in IoU in every case.
The best experimental results for each method presented in Table 3 were obtained with MATLAB 2020a, using a computer running in Windows 10 64-bit with an Intel® Core™ i7-6700HQ microprocessor and 8 GB of RAM. All the metric values displayed correspond to the average of the values for the three classes referred to. For Mean Shift, the three-dimensional input contained the pixel intensity (i) and position (x, y), with respective weights 0.8 and 0.2, while the 1-D input contained only the pixel intensity. As Mean Shift calculates the number of classes automatically, we combine it with Otsu thresholding to aggregate classes. It is important to state that the ground truths have compromised reliability, because they were not determined by the authorities.
|
In the process of exploring and tuning parameters for this approach, a MATLAB standalone application was developed, allowing for user-friendly tuning of parameters. We also developed a C++ implementation, which made our method ready to be implemented in a ground station that receives the images and allowed us to reduce the segmentation time to approximately 2.1 s (0.8 s improvement).
Discussion
In terms of computational time, Otsu vastly outperforms all the other methods, allowing real-time segmentation. However, to obtain curve regularisation, Otsu needs to increase the intensity of pre-process blurring, which leads to less reliable contours. As the results obtained using Otsu and K-means are almost identical, confirming what was stated in Liu and Yu (2009), and Otsu has a greatly reduced computational time in relation to K-means, it is thus concluded that there is no advantage in using K-means. In general, the combination of the Mean Shift method with the Otsu method does not bring better results in comparison with simple Otsu, although it can more accurately detect the brightest regions.
The method presented based on level sets allows for a highly customisable contour regularisation; therefore, it has the best segmentation results. Nevertheless, they tend to be less reliable on images where the burned area is small and where there is intensity inhomogeneity between regions, like the ones from dataset FOGO_2, as exemplified in Fig. 9. This is most likely because the piece-wise constant Mumford–Shah functional, which constitutes the basis for this model, assumes the input image can be approximated by regions with constant intensities. However, the inner contour correctly detects the burning region in all the examples.

|
Directly comparing the performance of our approach with other approaches for mapping fire fronts and perimeters is not possible because for that, the algorithms would need to be applied to the same dataset. However, our method has some advantages because it is able to classify different kinds of fire areas, namely burnt, unburnt and active fire areas. Regarding optical flow approaches, we consider that these are very interesting ways to recognise burning active regions of a fire, but only when there is movement present (high flames for example). Our method can be a viable alternative because it does not require the presence of movement in the image as it only uses the pixel intensities in a thermal image.
Conclusions and future work
This work presented a study on the implementation of various unsupervised segmentation methods to the problem of segmentation of aerial thermal images of wildfires, which was outlined in the FIREFRONT project. To address the described problem, we proposed a method based on a multilayer level set formulation that uses both global and local information. Globally, it attempts to minimise an energy functional based on the Chan–Vese method. Locally, the method makes use of an edge stopping term that further guides the innermost and outermost contours to the desired frontier of the active fire front. The main reasons that motivated the choice of this method for the segmentation of these types of images are its ability to perform multiple detections of objects scattered around an image and its ability to handle topology, which is a characteristic of the level set methods. The method was compared against other common unsupervised segmentation methods, being deemed the most appropriate.
The automation of the segmentation process of aerial thermal images of wildfires allows the acquisition of contours that can be used in future work to calculate the fire perimeter and extent of the fire front. This can be obtained by using a video similar to FOGO_1 and combining the segmentations performed over sequential images to obtain a general model of the whole wildfire.
The lack of a labelled database dictated the non-use of supervised machine Learning. The hand labels created throughout the development of this thesis can be used to start such a database. It would be interesting to apply state-of-the-art supervised and deep-learning models to these images and compare the results with the ones obtained in this research, in terms of the computational time and quality of the segmentations.
In a future application, the information retrieved from IR imagery can be combined with other remote sensing data from other FIREFRONT research works, providing valuable details about geolocation (Santana et al. 2022; Sargento et al. 2022), weather and terrain to the ANEPC. Future applications will also allow users to select the number of contours for the initial segmentation, as well as select the ones relevant to determine the perimeter and fire front. Moreover, observed data may be used to adjust fire spread simulators in real time, such as the one described in Viegas et al. (2021) (also outlined in the FIREFRONT project) so that they can produce accurate forecasts about fire evolution. These developments can make important contributions towards achieving reliable operational decision support systems that can be deployed during an emergency.
This application is currently in development, supported by the VOAMAIS project. The images and metadata (geographical coordinates, camera angles, etc.) obtained by the aircraft are transmitted in real time to a ground station using a Transmission Control Protocol/Internet Protocol (TCP/IP). The data are published in ROS (Robot Operating System) topics that the RGB and IR nodes subscribe to. Each node corresponds to a graphical user interface that applies the algorithms created in the FIREFRONT project and displays the results. The IR node will attempt to stitch multiple infrared images to construct a local thermal map of the fire and at the same time apply the level set segmentation algorithm proposed in this work to display the contours to the authorities and the geo-location of the fire front to improve their response capabilities.
Data availability
The MATLAB app functions referred to can be found at https://github.com/TiagoElGringo/MLSSegmApp and the C++ application files can be found at https://github.com/TiagoElGringo/MLSSegm. Unfortunately, we are not authorised to distribute the original images used in this work.
Conflicts of interest
The authors declare no conflicts of interest.
Declaration of funding
This work was supported by FCT projects FIREFRONT (PCIF/SSI/0096/2017) and VOAMAIS (PTDC/EEI-AUT/31172/2017, 02/SAICT/2017/31172).
Acknowledgements
The authors would like to thank everyone involved in the FIREFRONT and VOAMAIS projects for fruitful discussions and collaborations. Furthermore, we express our gratitude to the Portuguese Air Force for providing the surveillance images and videos used throughout this work and to the ANEPC for support in defining the segmentation requirements and their many suggestions. Finally, we thank the editor and the reviewers for their comments, which helped us improve this paper.
References
Bailon-Ruiz R, Lacroix S (2020) Wildfire remote sensing with UAVs: A review from the autonomy point of view. In ‘2020 International Conference on Unmanned Aircraft Systems (ICUAS)’, September 2020. pp. 412–420. (IEEE)Banerjee S, Bhattacharya M (2010) Segmentation of medical images using Selective Binary and Gaussian Filtering regularized level set (SBGFRLS) method. In ‘2010 3rd International Conference on Biomedical Engineering and Informatics’, October 2010. Vol. 2. pp. 541–545. (IEEE)
Bowman DMJS, Kolden CA, Abatzoglou JT, Johnston FH, van der Werf GR, Flannigan M (2020) Vegetation fires in the Anthropocene. Nature Reviews Earth & Environment 1, 500–515.
| Vegetation fires in the Anthropocene.Crossref | GoogleScholarGoogle Scholar |
Briggs WL, Henson VE, McCormick SF (2000) ‘A multigrid tutorial.’ (Society for Industrial and Applied Mathematics)
Butz RJ (2009) Traditional fire management: historical fire regimes and land use change in pastoral East Africa. International Journal of Wildland Fire 18, 442–450.
| Traditional fire management: historical fire regimes and land use change in pastoral East Africa.Crossref | GoogleScholarGoogle Scholar |
Caselles V, Catté F, Coll T, Dibos F (1993) A geometric model for active contours in image processing. Numerische Mathematik 66, 1–31.
| A geometric model for active contours in image processing.Crossref | GoogleScholarGoogle Scholar |
Caselles V, Kimmel R, Sapiro G (1997) Geodesic active contours. International Journal of Computer Vision 22, 61–79.
| Geodesic active contours.Crossref | GoogleScholarGoogle Scholar |
Chan TF, Vese LA (2001) Active contours without edges. IEEE Transactions on Image Processing 10, 266–277.
| Active contours without edges.Crossref | GoogleScholarGoogle Scholar |
Chung G, Vese LA (2005) Energy minimization based segmentation and denoising using a multilayer level set approach. In ‘Energy Minimization Methods in Computer Vision and Pattern Recognition’. Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 3757 LNCS. (Eds A Rangarajan, B Vemuri, AL Yuille) pp. 439–455. (Springer Berlin Heidelberg)
Chung G, Vese LA (2009) Image segmentation using a multilayer level-set approach. Computing and Visualization in Science 12, 267–285.
| Image segmentation using a multilayer level-set approach.Crossref | GoogleScholarGoogle Scholar |
Comaniciu D, Meer P (1999) Mean shift analysis and applications. In ‘Proceedings of the seventh IEEE international conference on computer vision’, September 1999. Vol. 2. pp. 1197–1203. (IEEE)
Cruz MG, Sullivan AL, Gould JS, Sims NC, Bannister AJ, Hollis JJ, Hurley RJ (2012) Anatomy of a catastrophic wildfire: the Black Saturday Kilmore East fire in Victoria, Australia. Forest Ecology and Management 284, 269–285.
| Anatomy of a catastrophic wildfire: the Black Saturday Kilmore East fire in Victoria, Australia.Crossref | GoogleScholarGoogle Scholar |
Dupuy J-l, Fargeon H, Martin-StPaul N, Pimont F, Ruffault J, Guijarro M, Hernando C, Madrigal J, Fernandes P (2020) Climate change impact on future wildfire danger and activity in southern Europe: a review. Annals of Forest Science 77, 35
| Climate change impact on future wildfire danger and activity in southern Europe: a review.Crossref | GoogleScholarGoogle Scholar |
Fukunaga K, Hostetler L (1975) The estimation of the gradient of a density function, with applications in pattern recognition. IEEE Transactions on Information Theory 21, 32–40.
| The estimation of the gradient of a density function, with applications in pattern recognition.Crossref | GoogleScholarGoogle Scholar |
Grau V, Mewes AUJ, Alcañiz M, Kikinis R, Warfield SK (2004) Improved watershed transform for medical image segmentation using prior information. IEEE Transactions on Medical Imaging 23, 447–458.
| Improved watershed transform for medical image segmentation using prior information.Crossref | GoogleScholarGoogle Scholar |
Harkat H, Nascimento JMP, Bernardino A, Ahmed HFT (2023) Fire images classification based on a handcraft approach. Expert Systems with Applications 212, 118594
| Fire images classification based on a handcraft approach.Crossref | GoogleScholarGoogle Scholar |
He L, Osher S (2007) Solving the Chan–Vese Model by a Multiphase Level Set Algorithm Based on the Topological Derivative. In ‘Scale Space and Variational Methods in Computer Vision’. (Eds F Sgallari, A Murli, N Paragios) pp. 777–788. (Springer: Berlin Heidelberg)
Huang Y, Wu JW (2010) Infrared thermal image segmentations employing the multilayer level set method for non-destructive evaluation of layered structures. NDT & E International 43, 34–44.
| Infrared thermal image segmentations employing the multilayer level set method for non-destructive evaluation of layered structures.Crossref | GoogleScholarGoogle Scholar |
Huang Y, Lee M-G, Lin S-Y, Xiaoyu Y-I (2013) Segmenting thermal images of pervious concrete pavement temperature with employing the multilayer level set approach. In ‘Proceedings of the International Conference on Sustainable Design, Engineering, and Construction 2012, November 7–9, 2012, Fort Worth, Texas, United States’. (Eds WKO Chong, J Gong, J Chang, MK Siddiqui) ISBN (print): 9780784412688. pp. 757–764.
| Crossref |
Jones MW, Abatzoglou JT, Veraverbeke S, Andela N, Lasslop G, Forkel M, et al. (2022) Global and regional trends and drivers of fire under climate change. Reviews of Geophysics 60, e2020RG000726
| Global and regional trends and drivers of fire under climate change.Crossref | GoogleScholarGoogle Scholar |
Li C, Xu C, Gui C, Fox MD (2010) Distance regularized level set evolution and its application to image segmentation. IEEE Transactions on Image Processing 19, 3243–3254.
| Distance regularized level set evolution and its application to image segmentation.Crossref | GoogleScholarGoogle Scholar |
Liu D, Yu J (2009) Otsu method and K-means. In ‘2009 Ninth International Conference on Hybrid Intelligent Systems’, August 2009. Vol. 1. pp. 344–349. (IEEE)
Lourenço L, Nunes A, Bento-Gonçalves A, Vieira A (2012) Soil erosion after wildfires in Portugal: What happens when heavy rainfall events occur. In ‘Research on Soil Erosion’. (Eds D Godone, S Stanchi) pp. 65–88. (InTech)
Malladi R, Sethian JA (1996) Level Set and Fast Marching Methods in Image Processing and Computer Vision. In ‘Proceedings of 3rd IEEE International Conference on Image Processing, Lausanne, Switzerland’. Vol. 1, Issue 4. pp. 489–492. (IEEE)
Moreno JC, Surya Prasath VB, Proença H, Palaniappan K (2014) Fast and globally convex multiphase active contours for brain MRI segmentation. Computer Vision and Image Understanding 125, 237–250.
| Fast and globally convex multiphase active contours for brain MRI segmentation.Crossref | GoogleScholarGoogle Scholar |
Mumford D, Shah J (1989) Optimal approximations by piecewise smooth functions and associated variational problems. Communications on Pure and Applied Mathematics 42, 577–685.
| Optimal approximations by piecewise smooth functions and associated variational problems.Crossref | GoogleScholarGoogle Scholar |
Ng HP, Ong SH, Foong KWC, Goh PS, Nowinski WL (2006) Medical image segmentation using k-means clustering and improved watershed algorithm. In ‘Proceedings of the IEEE Southwest Symposium on Image Analysis and Interpretation’, 2006. pp. 61–65. (IEEE)
Oscher S, Sethian JA (1988) Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton–Jacobi formulations. Journal of Computational Physics 79, 12–49.
| Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton–Jacobi formulations.Crossref | GoogleScholarGoogle Scholar |
Otsu N (1979) A threshold selection method from gray-level histograms. IEEE Transactions on Systems, Man, and Cybernetics 9, 62–66.
| A threshold selection method from gray-level histograms.Crossref | GoogleScholarGoogle Scholar |
Parente J, Pereira MG, Amraoui M, Tedim F (2018) Negligent and intentional fires in Portugal: Spatial distribution characterization. Science of the Total Environment 624, 424–437.
| Negligent and intentional fires in Portugal: Spatial distribution characterization.Crossref | GoogleScholarGoogle Scholar |
Perrolas G, Niknejad M, Ribeiro R, Bernardino A (2022) Scalable Fire and Smoke Segmentation from Aerial Images Using Convolutional Neural Networks and Quad-Tree Search. Sensors 22, 1701
| Scalable Fire and Smoke Segmentation from Aerial Images Using Convolutional Neural Networks and Quad-Tree Search.Crossref | GoogleScholarGoogle Scholar |
Pinto P, Silva ÁP, Viegas DX, Almeida M, Raposo J, Ribeiro LM (2022) Influence of Convectively Driven Flows in the Course of a Large Fire in Portugal: The Case of Pedrógão Grande. Atmosphere 13, 414
| Influence of Convectively Driven Flows in the Course of a Large Fire in Portugal: The Case of Pedrógão Grande.Crossref | GoogleScholarGoogle Scholar |
Santana B, Cherif EK, Bernardino A, Ribeiro R (2022) Real-Time Georeferencing of Fire Front Aerial Images Using Iterative Ray-Tracing and the Bearings-Range Extended Kalman Filter. Sensors 22, 1150
| Real-Time Georeferencing of Fire Front Aerial Images Using Iterative Ray-Tracing and the Bearings-Range Extended Kalman Filter.Crossref | GoogleScholarGoogle Scholar |
Sargento F, Ribeiro R, Cherif EK, Bernardino A (2022) Real-time Georeferencing of Fire Front Aerial Images using Structure from motion and Iterative Closest Point. In ‘Workshop on Image Analysis for Forest Environmental Monitoring’, ICPR, 2022.
Sinaga KP, Yang MS (2020) Unsupervised K-means clustering algorithm. IEEE Access 8, 80716–80727.
| Unsupervised K-means clustering algorithm.Crossref | GoogleScholarGoogle Scholar |
Turco M, Jerez S, Augusto S, Tarín-Carrasco P, Ratola N, Jiménez-Guerrero P, Trigo RM (2019) Climate drivers of the 2017 devastating fires in Portugal. Scientific Reports 9, 13886
| Climate drivers of the 2017 devastating fires in Portugal.Crossref | GoogleScholarGoogle Scholar |
Tymstra C, Stocks BJ, Cai X, Flannigan MD (2020) Wildfire management in Canada: Review, challenges and opportunities. Progress in Disaster Science 5, 100045
| Wildfire management in Canada: Review, challenges and opportunities.Crossref | GoogleScholarGoogle Scholar |
Valero MM, Rios O, Pastor E, Planas E (2018) Automated location of active fire perimeters in aerial infrared imaging using unsupervised edge detectors. International Journal of Wildland Fire 27, 241–256.
| Automated location of active fire perimeters in aerial infrared imaging using unsupervised edge detectors.Crossref | GoogleScholarGoogle Scholar |
Verde JC, Zêzere JL (2010) Assessment and validation of wildfire susceptibility and hazard in Portugal. Natural Hazards and Earth System Sciences 10, 485–497.
| Assessment and validation of wildfire susceptibility and hazard in Portugal.Crossref | GoogleScholarGoogle Scholar |
Vese LA, Chan TF (2002) A multiphase level set framework for image segmentation using the Mumford and Shah model. International Journal of Computer Vision 50, 271–293.
| A multiphase level set framework for image segmentation using the Mumford and Shah model.Crossref | GoogleScholarGoogle Scholar |
Viegas DXFC, Raposo JRN, Ribeiro CFM, Reis LCD, Abouali A, Viegas CXP (2021) On the non-monotonic behaviour of fire spread. International Journal of Wildland Fire 30, 702–719.
| On the non-monotonic behaviour of fire spread.Crossref | GoogleScholarGoogle Scholar |
Wen D, Ren A, Ji T, Flores-Parra IM, Yang X, Li M (2020) Segmentation of thermal infrared images of cucumber leaves using K-means clustering for estimating leaf wetness duration. International Journal of Agricultural and Biological Engineering 13, 161–167.
| Segmentation of thermal infrared images of cucumber leaves using K-means clustering for estimating leaf wetness duration.Crossref | GoogleScholarGoogle Scholar |
Yuan C, Zhang Y, Liu Z (2015) A survey on technologies for automatic forest fire monitoring, detection, and fighting using unmanned aerial vehicles and remote sensing techniques. Canadian Journal of Forest Research 45, 783–792.
| A survey on technologies for automatic forest fire monitoring, detection, and fighting using unmanned aerial vehicles and remote sensing techniques.Crossref | GoogleScholarGoogle Scholar |
Yuan C, Liu Z, Zhang Y (2017) Fire detection using infrared images for UAV-based forest fire surveillance. In ‘2017 International Conference on Unmanned Aircraft Systems’, ICUAS, 2017. pp. 567–572. (IEEE)
Zavala LM, de Celis R, Jordán A (2014) How wildfires affect soil properties. A brief review. Cuadernos de Investigación Geográfica 40, 311–331.
| How wildfires affect soil properties. A brief review.Crossref | GoogleScholarGoogle Scholar |
Zhao HK, Chan T, Merriman B, Osher S (1996) A variational level set approach to multiphase motion. Journal of Computational Physics 127, 179–195.
| A variational level set approach to multiphase motion.Crossref | GoogleScholarGoogle Scholar |