A comparative study of the combustion dynamics and flame properties of dead Mediterranean plants
A. Sahila A , H. Boutchiche A , D. X. Viegas B , L. Reis B and N. Zekri
A , H. Boutchiche A , D. X. Viegas B , L. Reis B and N. Zekri  A *
A *
A Faculty of Physics, LEPM (Laboratoire d'Etude Physique des Matériaux), Université des Sciences et de la Technologie d’Oran Mohamed Boudiaf, BP 1505 El Mnaouer, 31000, Oran, Algeria.
B Department of Mechanical Engineering, ADAI (Associação para o Desenvolvimento da Aerodinâmica Industrial), University of Coimbra, Rua Luís Reis Santos, Pólo II, 3030-788 Coimbra, Portugal.
International Journal of Wildland Fire 32(6) 979-988 https://doi.org/10.1071/WF22130
Submitted: 1 July 2022 Accepted: 9 April 2023 Published: 15 May 2023
© 2023 The Author(s) (or their employer(s)). Published by CSIRO Publishing on behalf of IAWF. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)
Abstract
Background: The physical processes governing flame behaviour are key elements for a better understanding of forest fires.
Aims: To study the combustion properties of several dead Mediterranean forest fuels.
Method: Samples of straw, eucalyptus, shrubs and Pinus Pinaster with the same load were placed in circular containers of the same size, and ignited in the absence of wind.
Key results: The combustion parameters (burning rate, flame height, temperature and gas velocity) evolved according to the same trend regardless of the fuel type. A new law is proposed to account for the anomalous relaxation processes occurring in the growth and decay phases of the flame. The dynamic exponent depends on the vegetation type only in the growth phase (highest for Pinus Pinaster and lowest for straw). The relaxation times are shortest for shrubs and largest for straw. The maximum flame height and burning rate are largest for shrubs and lowest for straw. Froude modelling suggests that the scaling behaviour of the flame may depend on the fuel type.
Conclusions: The observed relaxation parameters driving fire dynamics and the combustion characteristics depend on the nature of the fuel.
Implications: Further investigation of the vegetation region’s influence on these properties is necessary.
Keywords: air velocity and temperature profiles, anomalous diffusion, anomalous relaxation, flame height, flaming combustion, forest fires, heat release rate, Mediterranean plants, turbulent diffusion flame.
Introduction
The increasing intensity and severity of forest fires around the globe represent a major concern because they seriously endanger the ecosystem by affecting flora and fauna and the environment (Pausas et al. 2008; Vilén and Fernandes 2011). Therefore, a deeper understanding of the combustion dynamics of forest fuels and a better estimation of their combustion characteristics and their correlations are necessary. Forest fire is a very complex phenomenon involving physical processes that occur at different spatial scales ranging from the microscopic (smallest) scale, where the three phases of the fuel can be distinguished (solid, liquid and gas), to the gigascopic (largest) scale, where a fractal analysis of its pattern becomes feasible (Séro-Guillaume and Margerit 2002; Sahila et al. 2021). At intermediate scales, many works have already been devoted to examining the behaviour of these parameters in the case of pool fires (Zabetakis and Burgess 1961; Tarifa 1967; Kung and Stavrianidis 1982; Babrauskas 1983; Koseki and Yumoto 1988; Koseki 1989; Klassen and Gore 1994; Chatris et al. 2001), fire whirls (Martin et al. 1976; Lei et al. 2011; Pinto et al. 2017) and natural fires (Thomas 1963; Dupuy et al. 2003; Sun et al. 2006; Sahila et al. 2023). In the present work, an experimental study of the burning characteristics of several Mediterranean forest fuels was carried out where the turbulent diffusion flame was subjected only to buoyancy forces. Samples of dead shrubs (mix of heather (Erica australis) and gorse (Pterospartum tridentatum)), Pinus Pinaster needles, Eucalyptus globulus leaves and Avena sativa straw were placed in cylindrical baskets of the same size and ignited to study the fuel type’s effect on fire behaviour. These containers can represent single fuel bed items (e.g. trees) in fire spread modelling. For instance, using the so-called small-world-network model, the fuel bed items were considered cylindrical to simulate wildfire spread (Adou et al. 2010). However, in this model, as well as in many other semi-physical models (e.g. Rothermel’s model (1972)), the heat released by the burning items is assumed to be independent of time, which does not account for the different burning phases of these items (growth, fully developed and decay; see Manzello 2020). Only computational fluid dynamics (CFD) models estimate the time-dependent burning rate by using a set of physical equations. Indeed, the dynamics of a fluid flow can be described by a set of differential equations expressing the conservation of mass, momentum, energy and chemical species (see table 1 of Williams (1969)). When considering a multi-component fluid with various chemical species that interact, the mass conservation of a particular species i (i ∈ F, F being the set of all the chemical species constituting the fluid) is given by the advection–diffusion equation (de Groot and Mazur 1984; Rosner 1986; Kee et al. 2003; Manzello 2020):
where ci = ρixi is the concentration of species i and xi its mass fraction, D is the diffusion coefficient and ωi the production rate of the species by chemical reactions. By summing all the species’ mass conservation equations, we recover the fluid’s mass conservation equation (the well-known continuity equation), where the sum of all the mass production and destruction rates and diffusion fluxes is null (Kuwana 2019). From a statistical physics point of view, this advection–diffusion equation corresponds to the Fokker–Planck equation, describing the time evolution of the particle velocity probability density function under the influence of drag forces, which can be deduced from a generalised/anisotropic random walk model. The diffusion term in the right side of Eqn 1 is provided by Fick’s law, which is valid only when the gas particles exhibit normal (Brownian) diffusion. In this case, their Mean Square Displacement (MSD) is given by <Δx2> ∝ Dt, where D = RT/6πηrNA with R, T, η, r and NA being the universal gas constant (8.314 J/mol*K), temperature (in Kelvin), dynamic viscosity, radius of the particle and Avogadro’s number respectively. A normal diffusion was found to be related to an exponential relaxation (Metzler and Klafter 2000; Bouchaud 2008). Relaxation means that the system moves irreversibly towards an equilibrium state under the application of an external force (Kremer and Schonhals 2003). In the case of forest fires, it is induced by the existence of storing (heating of the fuels) and dissipative (heat release/particle emission from the burning vegetation) processes. The relaxation process obeys the following differential equation (Stanislavski and Weron 2010):
where ϕ(t) is the relaxation function with the boundary conditions ϕ(t = 0) = 1 and ϕ(t = ∞) = 0. ϕ(t) is usually given, in its general form, by the empirical Kohlrausch–Williams–Watts equation (Kohlrausch 1854; Williams and Watts 1970):
Here, τ is the relaxation time. The exponential relaxation, associated with Brownian diffusion, occurs only when a(t) = 1/τ is constant in Eqn 2, corresponding to β = 1, where β is the stretching exponent. In most cases, heterogeneous complex systems exhibit a non-exponential relaxation process (β ≠ 1), corresponding to a broad distribution of exponential-like relaxation times (Bouchaud and Georges 1990; Metzler and Klafter 2000; Morgado et al. 2002; Bouchaud 2008). If β < 1, the system exhibits a stretched exponential relaxation that is associated with a ‘sub-diffusion’ process (Metzler and Klafter 2000). In the case of forest fire spread, sub-diffusion may correspond to an anomalously slow propagation of fire induced by the existence of a broad distribution of ignition times (trapping times) (Sahila et al. 2021). If β > 1, there is a compressed exponential relaxation related to a ‘super-diffusion’ process (Bouchaud 2008) that may be induced by the existence of long-range physical effects beyond the primary combustion zone during fire spread (Porterie et al. 2008). These anomalous diffusion processes do not follow Fick’s law, and the linear relationship between the MSD of the particles and time occuring for normal diffusion (Oliveira et al. 2019) can be affected significantly by disorder in a real medium (e.g. porous fuel), which renders the temporal evolution of these particles’ MSD non-linear, Δx2 ~ tα, with α a real positive number (Metzler and Klafter 2000; Morgado et al. 2002) discriminating between sub-diffusion (α < 1), Brownian/normal diffusion (α = 1) and superdiffusion (α > 1) regimes. However, the first four equations listed in table 1 of Williams (1969) used by CFD models consider only normal diffusion processes, and do not account for the trapping effect of flammable volatiles by fuel particles (in the condensed phase) and buoyant gases (in the gas phase) or their jump caused by the coherent flow leading to anomalous diffusion. Anomalous diffusion and relaxation processes have been observed in various systems (Richardson 1926; Scher and Montroll 1975; Koch and Brady 1988; Bunde and Havlin 1996; Küntz and Lavallée 2001; Bennett et al. 2003; Dobrovolskis et al. 2007; Matthäus et al. 2009; Llievski et al. 2018). Sahila et al. (2023) found recently that these anomalous processes drive the burning dynamics of dead straw, and they introduced a Kohlrausch–Williams–Watts (KWW) equation to accurately describe the time evolution of the source’s heat flux.
These processes are examined in the present work for the above-mentioned Mediterranean plants to characterise their burning dynamics through their relaxation properties, and to check the universality of these dynamics for their use in spread modelling. Indeed, it is well known that pyrolysis gas particles move from a region of higher concentration to a region of lower one, but what is the nature of this diffusion, and is it dependent on the vegetation type? Do they diffuse in the same way during the growth and decay phases of the flame? These questions are of fundamental importance for an accurate understanding of turbulent diffusion flame dynamics and will be addressed in this work. Moreover, the time evolution of the mass-loss rate, flame height and temperature, and upward gas velocity are examined during all the phases of fire development. A systematic comparison between the combustion characteristics and relaxation properties of these fuels is carried out to study their correlations and their role in flaming combustion.
Experimental setup
Samples of dead shrubs (mix of heather (Erica australis) and gorse (Pterospartum tridentatum)), Pinus Pinaster needles, Eucalyptus globulus leaves and Avena sativa straw with the same initial fuel mass (Mf 1.56 kg), height (0.34 m) and bulk density (ρf 23.4 kg/m3) were placed in cylindrical containers (with a fixed diameter dc 0.5 m) made of a metallic grid and open at the top. Before each burning experiment, the fuel moisture content was estimated using a moisture analyser A&D MX-50 with a resolution of 0.01%. The relative humidity of the air and ambient temperature were measured by a thermo-hygrometer. The flame is subdivided into three regions (McCaffrey 1979): (i) a continuous zone that begins at the fuel surface and where the velocity v of gas particles increases with height z and the temperature is constant (T ∝ z0); (ii) the intermittent region (the pulsating part of the flame) where v is approximately invariant and the flame temperature decreases inversely with height (T ∝ z−1); (iii) the thermal plume (situated above the flame tip) where the gas velocity begins to decrease with height (v ∝ z−1/3) and the smoke temperature continues falling at a faster rate (T ∝ z−5/3). A K-type thermocouple (nickel–chromium/nickel aluminium, metallic shielded, with a diameter of 0.5 mm) and a S-Pitot tube were placed 1 m above the fuel surface to determine the flame temperature and air velocity at this height respectively (see Fig. 1). It is difficult to perform corrections for the thermocouple measurements owing to radiation losses because for certain periods of time, the thermocouple was surrounded by the flames – in which case there are no radiative losses – whereas in other periods, it was intermittently inside the flames, and in others it was placed at variable distances from the flame. Owing to these errors, we assume that the absolute values of the measured temperatures are not accurate. Nevertheless, the relative temporal variation of the temperature indicates a pattern that is consistent with the expected trend (higher values for lower relative positions and vice versa).
At the beginning of each test, the lowest region of the basket was ignited by a gas burner, and three experiments were carried out for each fuel to ensure the repeatability of the tests. Note that each test corresponds to a different configuration of the porous fuel bed, which induces statistical fluctuations in the measured parameters (mass-loss rate and flame height). The three replicates allowed relative fluctuations smaller than 20% to be obtained (see the Results section below), which are estimated as the tolerance of the measurement due to statistical errors (not only to the limited precision of the apparatus). Each experiment was recorded by an optical video camera (Sony FDR-AX53) and a digital camera (Canon EOS 550D). The videos were segmented into images using video to gif converter software, allowing the flame heights during the entire duration of flaming combustion to be estimated. The flame height was measured manually as the distance from the flame bottom to its visual tip. Hence, a vertical scale was placed near the container to allow proper scaling of the flame height values (the rubbers are equidistant by 0.2 m). A digital balance A&D HW-100KGL (10 g resolution) with a frequency of 1 Hz was used to measure the mass loss of the fuels during their combustion, and values were recorded on computer by RSKey v.1.40 software.
Results and discussion
The time evolution of the normalised fuel mass (Mf/M0, M0 being the initial mass of the fuel) is shown in Fig. 2a for all the fuels considered. The fuel mass decreases towards an asymptotic minimal value Mfmin, and this tendency to equilibrium seems to depend on the fuel type: it is faster for shrubs than for Pinus Pinaster needles (PP), straw and Eucalyptus leaves (Euc). These curves can be described by the following equation (Drysdale 2011):
where K(T) obeys the Arrhenius law K(T) ∝ exp(−EA/RT). EA is the activation energy (J/mol) and R the universal gas constant (8.314 J/K mol). This formula is very simple because it takes into consideration only water evaporation accompanied by volatiles emission during the combustion of the fuel. It does not take into consideration other mechanisms such as the decomposition and formation of molecules (David 1975). In earlier work, Sahila et al. (2023) studied the combustion characteristics of dead straw for different container sizes, and demonstrated that Eqn 4 can also describe a relaxation process where Mf is replaced by a relaxation function ϕ(t) = (Mf(t) − Mfmin/(M0(t) − Mfmin)) obeying Eqn 2 with K = 1/τ, τ being a relaxation time that measures the rate of decrease of the relaxation function (see Eqn 3), i.e. the rate of consumption of the fuel during a characteristic period (growth or decay). If K (hence, the temperature) is constant, ϕ(t) decreases exponentially over time, describing normal relaxation (β = 1). However, as temperature varies with time, one expects that heterogeneous porous fuels exhibit non-exponential relaxation processes described by Eqn 3. To verify the existence of such anomalous dynamic physical processes for all the Mediterranean vegetation species studied, it is more suitable to use −ln(ϕ(t)):
Hence, by plotting −ln(ϕ(t)) in logarithmic scales, the dynamic exponent β and the relaxation time τ can be deducted directly from the linear fit, as shown in Fig. 2b for dead shrubs.
(a) Temporal evolution of the normalised fuel mass for several dead forest fuels; (b) −lnϕ as a function of time in a double logarithmic scale (shrubs).
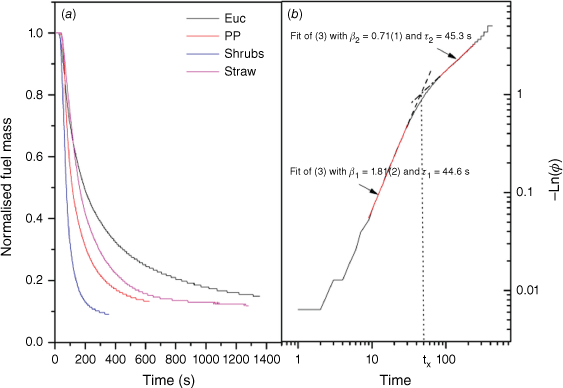
For short times, the burning fuel’s mass exhibits super-relaxation through time (the first slope β1 is greater than unity), characterising the growth phase of the turbulent diffusion flame. Then, a transition zone characterising a crossover time tx appears, corresponding to the fully developed phase of the flame. Finally, during the decay phase of the flame (long times), the relaxation process becomes anomalously slow (the second slope β2 is smaller than unity). The curves for all the vegetation types studied exhibit the same trend.
The dynamic exponents (β1 and β2) and the relaxation times (τ1 and τ2) obtained for each vegetation type in the two regimes are summarised in Table 1. The results show that the growth phase is characterised by a super-relaxation process (β1 > 1) of the burning fuel’s mass, while the decay phase is characterised by an anomalously slow relaxation process (β1 < 1) regardless of the vegetation type for all experiments. Hence, it seems that these anomalous processes are universal, and inherently characterise the various phases of flaming combustion. β1 varies from one vegetation type to another; it is highest for Pinus Pinaster and lowest for straw. However, β2 seems to be independent of the vegetation type. The relaxation times (τ1 and τ2) are shorter for shrubs than for Pinus Pinaster needles, eucalyptus leaves and straw.
| Fuel | Test | β1 | τ1 | β2 | τ2 | ||
| Shrubs | N01 | 44.6 | 0.99 | 45.3 | 0.99 | ||
| N02 | 53.2 | 0.99 | 50.5 | 0.99 | |||
| N03 | 41.7 | 0.99 | 37.9 | 0.99 | |||
| Pinus Pinaster | N01 | 57.7 | 0.99 | 76.8 | 0.99 | ||
| N02 | 55.2 | 0.99 | 89.8 | 0.99 | |||
| N03 | 61.3 | 0.99 | 93.6 | 0.99 | |||
| Eucalyptus | N01 | 90.7 | 0.99 | 146.9 | 0.99 | ||
| N02 | 109.9 | 0.99 | 200.1 | 0.99 | |||
| N03 | 90.8 | 0.99 | 129.7 | 0.99 | |||
| Straw | N01 | 136.1 | 0.99 | 144.2 | 0.99 | ||
| N02 | 131.4 | 0.99 | 147.8 | 0.99 | |||
| N03 | 183.9 | 0.99 | 201.6 | 0.99 |
The mass-loss rate Mf is a measure of the rate at which the fuel is consumed, and is a key element to understanding the combustion dynamics. It was deducted from the balance data and its averaged values were estimated at regular intervals (5 s). The results illustrated in Fig. 3 show the same temporal trend as for the flame height, mass loss rate, temperature at thermocouple position and gas velocity at Pitot tube position. Fire development is as follows: after ignition, the growth phase begins, where the flame spreads vertically very rapidly along the lateral fuel bed surface; then, a consistent flame is formed, accompanied by horizontal spread of the flame through the upper surface of the fuel. In this phase, the flame height, mass loss rate, temperature and upward gas velocity increase continuously until they attain their peak. The above observed super-relaxation (see Fig. 2b and Table 1) corresponds to super-diffusion of the emitted gas particles (α > 1). Gas particles are mainly emitted from the fuel surface in the growth phase, and the absence of obstacles to their motion in addition to the fact that they are coherently convected along the streamlines (gas molecule jumps) may explain this anomalously fast diffusion. At the end of this stage, the flame becomes fully developed and its height reaches the maximum lmax. This phase is followed by a decrease of flame height, mass-loss rate, temperature and gas velocity over a relatively long period, characterising the decay phase. As combustion occurs mainly in the bulk of the fuel bed in this phase, the anomalously slow relaxation of the burning vegetation (see Fig. 2b and Table 1) corresponds to sub-diffusion (α < 1) of gas particles that may be due to the slowing down of their propagation through the porous fuel (they are ‘trapped’ by upper layers of the fuel bed for a finite time), and through the dense air/flammable gas mixture owing to the buoyant gases. Once there is no longer sufficient chemical energy to sustain the flame, it extinguishes and only smouldering combustion propagating slowly in the condensed phase subsists (Ohlemiller 2002; Rein 2009). The transition from flaming to smouldering combustion begins already in the decay phase, when there is an unsufficient amount of oxygen in the bulk to allow the initiation of a flame.
Temporal evolution of: (a) flame height (m), (b) mass loss rate (g/s), (c) flame temperature (°C), (d) air velocity (m/s).
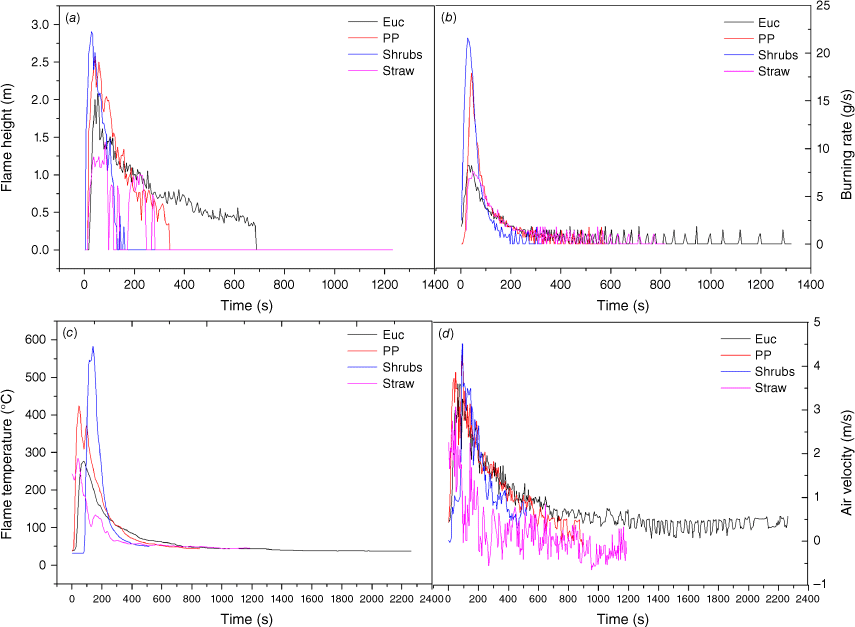
As the thermocouple and Pitot tube are placed at the same position with respect to the initial fuel bed surface, the temperature and the vertical motion of gas particles are measured at different relative positions of the flame structure during its temporal evolution. Hence, the flame temperature and gas velocity reach their maximum values when the flame is fully developed because they are measured at the closest position to the continuous zone (see Fig. 3a where lmax > 1 m is much higher than the thermocouple position for all the fuels studied). As l < 1 m in the begining of the growth phase and the last period of the decay phase, the temperatures and velocities measured in these periods are those of the thermal plume and not the flame itself. Therefore, the convection coefficient, which is related to air velocity, varies with the vertical position in the flame.
There is a time delay Δt between the time at which the burning rate is maximum (tmax) and that at which the flame height is maximum (lmax), and it has been found to depend linearly on the fuel moisture content (Sun et al. 2006). The moisture content may not be the only cause of this delay because even for completely dried fuels, Δt is not expected to vanish because a time delay is required for the emitted gas molecules to diffuse and advect through the porous fuel bed before contributing to the flame. An experimental investigation of moisture content effect on this time shift is necessary. In the current work, the moisture content of the samples was ~8–10% for all experiments, Δt seems to not change significantly (within statistical errors) for the dead fuels considered (apart from a slight increase for straw), as shown in Table 2 where the maximal values of the flame geometrical and physical characteristics are summarised. The maximum flame height and mass-loss rate are largest for shrubs and lowest for straw. The mass-loss rate of the fuel bed is related to its heat release rate and its effective heat of combustion ΔHc as . These parameters, given in Table 2, depend on the geometrical and physico-chemical properties of the fuel particles and also on the experimental conditions. On one hand, the gross heat of combustion depends only on the vegetation species (Rivera et al. 2012), i.e. on their organic components involved in combustion reactions (volatiles and heavy organic compounds). On the other hand, the mass-loss rate corresponds to the rate of gas emission from the fuel particles, and thus depends on their surface-to-volume ratio (SVR) and density ρp (see Table 3 where their values as well as those of packing ratios are summarised). Assuming that the flammable volatiles are emitted through the whole particle surface, the rate of their emission is higher for plants with higher SVR. Moreover, for the same volume, larger particle densities imply larger volatiles mass emission. Therefore, at first look, one can suggest the following linear relation . From Fig. 4, it is clear that the maximum mass-loss rate increases with (SVR × ρp), but the linear trend seems to be observed only for stick-like fuels (Eucalyptus leaves deviate from this trend). Among the various reasons for this deviation, the following seem important: (i) the strong variations in the experimental data of SVR and ρp; (ii) Eucalyptus leaves seem more closely packed than the other fuels. The packing ratio may also influence the mass-loss rate, because it contributes to trapping of the gases emitted from the bulk; (iii) not all the fuel particles components are combustible because they are also composed of minerals, for instance; (iv) the pore distribution in leaves is different from that in needles (see Sabi et al. (2021) and references therein).
| Fuel type | ΔHc (kJ/g) (Pinto et al. 2017) | lmax (m) | (g/s) | Tmax (°C) | vmax (m/s) | tres (s) | Δt (s) | |
| Eucalyptus | 22.5 | 1.9(3) | 10(2) | 1.1(1) | 292(30) | 3.9(4) | 845(260) | 7(6) |
| Pinus Pinaster | 13.5 | 2.5(3) | 18(1) | 1.2(1) | 397(19) | 4.2(2) | 242(83) | 8(8) |
| Shrubs | 16.9 | 2.9(1) | 24(2) | 2.0(2) | 488(78) | 4.9(4) | 148(35) | 13(8) |
| Straw | 11.7 | 1.5(3) | 7(1) | 0.4(1) | 334(34) | 3.3(4) | 296(67) | 25(7) |
| Fuel | Particle density (kg/m3) | SVR (m−1) | Packing ratio (%) |
| Shrubs (Fernandes and Rego 1998) | 780 | 6330–7950 | 3 |
| Pinus Pinaster (Lamorlette et al. 2015) | 660–927 | 4820–5500 | 2.5–3.5 |
| Eucalyptus (Fernandes and Rego 1998) | 650 | 5690–6180 | 3.6 |
| Straw (Adapa et al. 2009) | 268–286 | 2342 | 8.1–8.7 |
Mass-loss rate vs ρ × SVR for the fuels considered in this work (the data are taken from Tables 2 and 3).
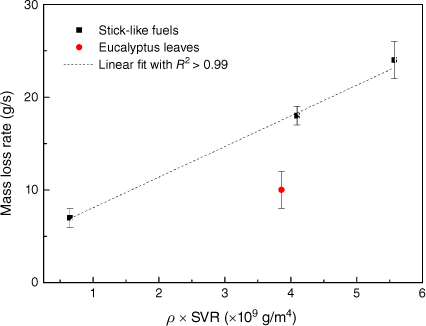
The mass-loss rate at ignition (for cone calorimeter tests) was found by Boutchiche et al. (2022) to be independent of the packing ratio (defined as the ratio of the bulk and particle densities). However, an optimum packing ratio for the rate of spread has been observed (Rothermel 1972). Hence, the packing ratio is expected to influence particularly the combustion dynamics of the fuel bed (time evolution of the mass-loss rate) because the diffusion of flammable gases through the porous fuel depends on the mean free path between the fuel particles. Therefore, the dynamic exponent β2 is expected to vary with the fuel bed’s porosity because combustion occurs mainly in the bulk during the decay phase of the flame, as mentioned above. Therefore, it is interesting to investigate the effect of the packing ratio on the burning rate dynamics for each vegetation species separately.
The time-dependent heat release rate (mass-loss rate) can be deduced directly from the time derivative of KWW Eqn 3:
with a constant that depends on the relaxation properties of the fuel. This law taking into account the different phases of flaming combustion can render the semi-physical models more realistic by replacing the constant heat release rate used in these models. It also improves the existing physical (CFD) models that use equations accounting only for normal diffusion/relaxation processes as discussed above.
Zukoski (1975) introduced a dimensionless heat release rate defined as the square root of the Froude number:
where dc is the container diameter, and g, ρa, Ta and cpa are the gravitational acceleration, density, temperature and specific heat of ambient air respectively. The variation of the maximum normalised flame height (lmax/dc) as a function of allows the identification of three regions of the scaling behaviour of the flame: the buoyancy-driven diffusion flames (), the momentum-controlled jet fires () and a transition zone between these (Thomas 1963; Zukoski 1986; Quintiere and Grove 1998; Drysdale 2011; Finney and McAllister 2011). In the case of buoyancy-controlled diffusion flames, the normalised maximum flame height increases as a power-law with , the power exponent being: 2 for , 2/3 for , and 2/5 for , where the flame height becomes independent of dc.
A two-fifth power law was observed for Pinus Pinaster needles and excelsior (Dupuy et al. 2003), chaparral fuels (Sun et al. 2006) and shrubs (Pinto et al. 2017). The results presented in Table 2 suggest that, on one hand, the dimensionless heat release rate is in the range for shrubs (in agreement with the results of Pinto et al. 2017), Pinus Pinaster (in agreement with the results of Dupuy et al. 2003) and Eucalyptus. On the other hand, for straw, which is consistent with the results found by Sahila et al. (2023) where . This suggests that, for the same load and bulk density, the fuel type affects the scaling behaviour of the buoyancy-driven turbulent diffusion flames. A complete scaling analysis of the burning behaviour of these species is then necessary for the same load and bulk density to check this scaling exponent.
The flaming combustion duration defines the residence time of the flame tres. In Table 2, the maximum flame height (and maximum mass-loss rate) decreases as the residence time tres increases for the fuels considered with a saturation tendency for Eucalyptus and straw. This is in qualitative agreement with the experimental results found in the case of fire whirls (Pinto et al. 2017). Note the very large residence time of Eucalyptus, which is also characterised by a large heat of combustion.
Conclusion
An experimental study of the burning characteristics of several dead forest fuels was carried out. Samples of dead Eucalyptus, Pinus Pinaster, straw and shrubs with the same fuel load and bulk density were placed in cylindrical baskets and ignited from the bottom. The time evolution of the combustion parameters was found to follow the same trend for all the fuels considered. In the growth phase of the flame, the fuel mass-loss rate, flame height, temperature and upward gas velocity increase rapidly. This phase is characterised by an anomalously fast relaxation of the fuel mass (β1 > 1) and corresponds to a super-diffusion of gas particles through the fuel bed surface caused by advection-induced particle jumps. Afterwards, a crossover (transition zone) appears when the flame is fully developed, and the burning rate attains its maximal value after a time that was found to be the same for all the fuels considered. Finally, these parameters decrease over a relatively long period (decay phase) characterised by an anomalously slow relaxation of the fuel mass (β2 < 1) corresponding to a sub-diffusion of gas particles due to the trapping effect of the fuel bed. The first relaxation exponent β1 is highest for Pinus Pinaster and lowest for straw, whereas the second (β2) seems to be independent of the vegetation type. The relaxation times (τ1 and τ2) are shorter for shrubs than for Pinus Pinaster needles, Eucalyptus leaves and straw. The maximum flame height and mass loss rate are largest for shrubs and lowest for straw, which is due to their linear increase with particle density and surface volume ratio, as observed for stick-like fuels. The comparison between the Froude numbers (estimated from the maximum burning rate) of all the fuels considered suggests that the scaling behaviour of straw may be different from that of the other species. It will be interesting to investigate the scaling behaviour of the maximum burning characteristics of these species by varying the basket diameter, and to analyse the influence of their bulk and particle densities as well as their SVR on their combustion and relaxation properties.
Conflicts of interest
D. X. Viegas is an Associate Editor of International Journal of Wildland Fire. To mitigate this potential conflict of interest, he was blinded from the review process and was not involved at any stage in the editing of this manuscript.
Declaration of funding
The work reported in this article was carried out under the scope of projects IMfire (PCIF/SSI/0151/2018) and SmokeStorm (PCIF/MPG/0147/2019) supported by the Portuguese National Science Foundation, and European Union’s Horizon 2020 research and innovation programme under grant agreement No. 101003890, FirEUrisk – Developing A Holistic, Risk-Wise Strategy For European Wildfire Management.
Author contributions
Conceptualisation: A. Sahila, N. Zekri and D. X. Viegas; data curation: A. Sahila, H. Boutchiche, L. Reis; dormal analysis: A. Sahila, N. Zekri and D. X. Viegas; methodology: A. Sahila, N. Zekri, H. Boutchiche and D. X. Viegas; experimental test: A. Sahila, H. Boutchiche, L. Reis; supervision: N. Zekri and D. X. Viegas; writing original draft: A. Sahila and N. Zekri; writing – review and editing – A. Sahila, N. Zekri, D. X. Viegas, H. Boutchiche, L. Reis.
Acknowledgements
A. Sahila and H. Boutchiche are thankful to the European Community for supporting their visit to Coimbra University under the Erasmus framework, where a part of this work was carried out. This work was supported by the Directorate-General for Scientific Research and Technological Development (DGRSDT) Algeria under the number W1030400.
References
Adapa P, Tabila L, Schoenau G (2009) Compaction characteristics of barley, canola, oat and wheat straw. Biosystems Engineering 104, 335-344.
| Crossref | Google Scholar |
Adou JK, Billaud Y, Brou DA, Clerc JP, Consalvi JL, Fuentes A, Kaiss A, Nmira F, Porterie B, Zekri L, Zekri N (2010) Simulating wildfire patterns using a small-world network model. Ecological Modelling 221, 1463-1471.
| Crossref | Google Scholar |
Babrauskas V (1983) Estimating large pool fire burning rates. Fire Technology 19, 251-261.
| Crossref | Google Scholar |
Bennett KM, Schmainda KM, Bennett (Tong) R, Rowe DB, Lu H, Hyde JS (2003) Characterization of continuously distributed water diffusion rates in the cerebral cortex with a stretched exponential model. Magnetic Resonance in Medicine 50, 727-734.
| Crossref | Google Scholar |
Bouchaud JP (2008) Anomalous relaxation in complex systems: from stretched to compressed exponentials. In ‘Anomalous transport: Foundations and applications’. (Eds HR Klages, G Radons, IM Sokolov) pp. 327–345. (Wiley-VCH: Berlin) 10.1002/9783527622979.ch11
Bouchaud JP, Georges A (1990) Anomalous diffusion in disordered media: statistical mechanisms, models and physical applications. Physics Reports 195, 127-293.
| Crossref | Google Scholar |
Boutchiche H, Mosbah O, Sahila A, Raposo J, Reis L, Viegas DX, Zekri N (2022) Influence of compactness upon flammability properties of forest fuels. SSRN
| Crossref | Google Scholar |
Bunde A, Havlin S (Eds) (1996) ‘Fractals and Disordered Systems.’ (Springer Verlag Berlin: Heidelberg) 10.1007/978-3-642-84868-1
Chatris JM, Quintela J, Folch J, Planas E, Arnaldos J, Casal J (2001) Experimental study of burning rate in hydrocarbon pool fires. Combustion and Flame 126, 1373-1383.
| Crossref | Google Scholar |
David C (1975) Thermal degradation of polymers. In ‘Comprehensive Chemical Kinetics’. (Eds CH Bamford, FH Tipper) pp. 1–173. (Elsevier: Amsterdam) 10.1016/S0069-8040(08)70333-9
Dobrovolskis AR, Alvarellos JL, Lissauer JJ (2007) Lifetimes of small bodies in planetocentric (or heliocentric) orbits. Icarus 188, 481-505.
| Crossref | Google Scholar |
Dupuy JL, Maréchal J, Morvan D (2003) Fires from a cylindrical forest fuel burner: combustion dynamics and flame properties. Combustion and Flame 135, 65-76.
| Crossref | Google Scholar |
Fernandes PM, Rego FC (1998) A new method to estimate fuel surface area-to-volume ratio using water immersion. International Journal of Wildland Fire 8(2), 59-66.
| Crossref | Google Scholar |
Finney MA, McAllister SS (2011) A review of fire interactions and mass fires. Journal of Combustion 2011, 1-14.
| Crossref | Google Scholar |
Koch DL, Brady JF (1988) Anomalous diffusion in heterogeneous porous media. The Physics of Fluids 31, 965.
| Crossref | Google Scholar |
Kohlrausch R (1854[In German]) Theorie des elektrischen Rückstandes in der Leidener Flasche. Annalen der Physik 167, 179-214.
| Crossref | Google Scholar |
Koseki H (1989) Combustion properties of large liquid pool fires. Fire Technology 25, 241-255.
| Crossref | Google Scholar |
Koseki H, Yumoto T (1988) Air entrainment and thermal radiation from heptane pool fires. Fire Technology 24, 33-47.
| Crossref | Google Scholar |
Kung HC, Stavrianidis P (1982) Buoyant plumes of large-scale pool fires. Symposium (International) on Combustion 19, 905-912.
| Crossref | Google Scholar |
Küntz M, Lavallée P (2001) Experimental evidence and theoretical analysis of anomalous diffusion during water infiltration in porous building materials. Journal of Physics D: Applied Physics 34(16), 2547.
| Crossref | Google Scholar |
Kuwana K (2019) Fluid Mechanics. In ‘Encyclopedia of Wildfires and Wildland–Urban Interface (WUI) Fires’. (Ed. S Manzello) pp. 483–490. (Springer: Cham) 10.1007/978-3-319-51727-8_149-1
Lamorlette A, El Houssami M, Thomas JC, Simeoni A, Morvan D (2015) A dimensional analysis of forest fuel layer ignition model: Application to the ignition of pine needle litters. Journal of Fire Sciences 33, 320-335.
| Crossref | Google Scholar |
Lei J, Liu N, Zhang L, Chen H, Shu L, Chen P, Deng Z, Zhu J, Satoh K, De Ris JL (2011) Experimental research on combustion dynamics of medium-scale fire whirl. Proceedings of the Combustion Institute 33, 2407-2415.
| Crossref | Google Scholar |
Llievski E, de Nardis J, Medenjak M, Prosen T (2018) Superdiffusion in one-dimensional quantum lattice models. Physics Review Letters 121, 230602.
| Google Scholar |
Manzello SL (Ed) (2020) ‘Encyclopedia of Wildfires and Wildland–Urban interface (WUI) Fires.’ (Springer Cham: USA) 10.1007/978-3-319-51727-8
Martin RE, Pendleton DW, Burgess W (1976) Effect of fire whirlwind formation on solid fuel burning rates. Fire Technology 12, 33-40.
| Crossref | Google Scholar |
Matthäus F, Jagodič M, Dobnikar J (2009) E. coli superdiffusion and chemotaxis – search strategy, precision, and motility. Biophysical Journal 97(4), 946-957.
| Crossref | Google Scholar |
Metzler R, Klafter J (2000) The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Physics Reports 339, 1-77.
| Crossref | Google Scholar |
Morgado R, Oliveira FA, Batrouni GG, Hansen A (2002) Relation between anomalous and normal diffusion in systems with memory. Physics Review Letters 89, 100601.
| Crossref | Google Scholar |
Oliveira FA, Ferreira RMS, Lapas LC, Vainstein MH (2019) Anomalous diffusion: a basic mechanism for the evolution of inhomogeneous systems. Frontiers in Physics 7, 18.
| Crossref | Google Scholar |
Pausas JG, Llovet J, Rodrigo A, Vallejo R (2008) Are wildfires a disaster in the Mediterranean basin? - A review. International Journal of Wildland Fire 17, 713-723.
| Crossref | Google Scholar |
Pinto C, Viegas D, Almeida M, Raposo J (2017) Fire whirls in forest fires: An experimental analysis. Fire Safety Journal 87, 37-48.
| Crossref | Google Scholar |
Porterie B, Kaiss A, Clerc JP, Zekri L, Zekri N (2008) Universal scaling in wildfire fractal propagation. Applied Physics Letters 93, 204101.
| Crossref | Google Scholar |
Quintiere JG, Grove BS (1998) A unified analysis for fire plumes. Symposium (International) on Combustion 27(2), 2757-2766.
| Crossref | Google Scholar |
Rein G (2009) Smouldering combustion phenomena in science and technology. International Review of Chemical Engineering 1, 3-18.
| Google Scholar |
Richardson LF (1926) Atmospheric diffusion shown on a distance-neighbour graph. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 110, 709-737.
| Crossref | Google Scholar |
Rivera JdD, Davies GM, Jahn W (2012) Flammability and the heat of combustion of natural fuels: a review. Combustion Science and Technology 184, 224-242.
| Crossref | Google Scholar |
Sabi FZ, Terrah SM, Mosbah O, Dilem A, Hamamousse N, Sahila A, Harrouz O, Boutchiche H, Chaib F, Zekri N, Kaiss A, Clerc JP, Giroud F, Viegas DX (2021) Ignition/non-ignition phase transition: A new critical heat flux estimation method. Fire Safety Journal 119, 103257.
| Crossref | Google Scholar |
Sahila A, Zekri N, Clerc JP, Kaiss A, Sahraoui S (2021) Fractal analysis of wildfire pattern dynamics using a Small World Network model. Physica A: Statistical Mechanics and its Applications 583, 126300.
| Crossref | Google Scholar |
Sahila A, Boutchiche H, Viegas DX, Reis L, Pinto C, Zekri N (2023) Experimental study of the burning characteristics of dead forest fuels. International Journal of Wildland Fire 32, 593-609.
| Crossref | Google Scholar |
Scher H, Montroll EW (1975) Anomalous transit-time dispersion in amorphous solids. Physical Review B 12, 2455.
| Crossref | Google Scholar |
Séro-Guillaume O, Margerit J (2002) Modelling forest fires. Part I: a complete set of equations derived by extended irreversible thermodynamics. International Journal of Heat Mass Transfer 45, 1705-1722.
| Crossref | Google Scholar |
Sun L, Zhou X, Mahalingam S, Weise DR (2006) Comparison of burning characteristics of live and dead chaparral fuels. Combustion and Flame 144, 349-359.
| Crossref | Google Scholar |
Thomas PH (1963) The size of flames from natural fires. Symposium (International) on Combustion 9, 844-859.
| Crossref | Google Scholar |
Vilén T, Fernandes PM (2011) Forest fires in Mediterranean countries: CO2 emissions and mitigation possibilities through prescribed burning. Environmental Management 48, 558-567.
| Crossref | Google Scholar |
Williams FA (1969) Scaling mass fires. In ‘Research Abstracts and Reviews. Vol. 11’. (Eds National Academy of Sciences and National Research Council) pp. 1–23. (The National Academies Press: Washington) 10.17226/18860
Williams G, Watts DC (1970) Non-symmetrical dielectric relaxation behaviour arising from a simple empirical decay function. Transactions of the Faraday Society 66, 80.
| Crossref | Google Scholar |
Zabetakis MG, Burgess DS (1961) Research on the hazards associated with the production and handling of liquid hydrogen. BM-RI-5707. (Bureau of Mines) 10.2172/5206437
Zukoski EE (1985) Fluid Dynamic Aspects of Room Fires. Fire Safety Science 1, 1-30.
| Crossref | Google Scholar |



