Assessing wildfire risk to critical infrastructure in central Chile: application to an electrical substation
Gonzalo Severino A * , Andrés Fuentes
A * , Andrés Fuentes  A , Alejandro Valdivia B , Fernando Auat-Cheein
A , Alejandro Valdivia B , Fernando Auat-Cheein  C and Pedro Reszka
C and Pedro Reszka  D
D
A
B
C
D
Abstract
Wildfires have caused significant damage in Chile, with critical infrastructure being vulnerable to extreme wildfires.
This work describes a methodology for estimating wildfire risk that was applied to an electrical substation in the wildland–urban interface (WUI) of Valparaíso, Chile.
Wildfire risk is defined as the product between the probability of a wildfire reaching infrastructure at the WUI and its consequences or impacts. The former is determined with event trees combined with modelled burn probability. Wildfire consequence is considered as the ignition probability of a proxy fuel within the substation, as a function of the incident heat flux using a probit expression derived from experimental data. The heat flux is estimated using modelled fire intensity and geometry and a corresponding view factor from an assumed solid flame.
The probability of normal and extreme fires reaching the WUI is of the order of 10−4 and 10−6 events/year, respectively. Total wildfire risk is of the order of 10−5 to 10−4 events/year
This methodology offers a comprehensive interpretation of wildfire risk that considers both wildfire likelihood and consequences.
The methodology is an interesting tool for quantitatively assessing wildfire risk of critical infrastructure and risk mitigation measures.
Keywords: burn probability, consequence analysis, critical infrastructure, event tree, ignition probability, probit, risk, wildland–urban interface.
Introduction
In the last decade, wildfires in Chile have caused significant human, ecological and economic damage to cities, protected areas and economic sectors such as forestry and electricity distribution. In 2014, the Great Valparaíso Fire caused the death of 15 people, destroyed 2900 structures and caused losses of over USD 110 million (Reszka and Fuentes 2014), while the fires that occurred in the central zone of Chile in 2017 caused 11 deaths, burned more than 550 000 ha and destroyed more than 1000 structures (Bowman et al. 2019). Climate change is expected to increase the occurrence and severity of these events (McWethy et al. 2018; Pausas and Keeley 2021; United Nations Environment Programme 2022). Interactions between climate–weather, vegetation and people are not fully understood and are still subject to scientific scrutiny (Flannigan et al. 2009); hence, the potential impact of wildfires on communities and assets in the wildland–urban interface (WUI) may be assessed by estimating wildfire risk for as many climate scenarios as possible (Liu et al. 2021). Incorporating wildfire risk into fire management and land use planning would help to achieve this goal (Moritz et al. 2014; United Nations Environment Programme 2022). In this context, a need to address wildfire risk with quantitative tools has been recognised to support decision-making in the management of assets located in the WUI (Lautenberger 2017; Papakosta et al. 2017; Alcasena et al. 2022), an approach aligned with modern paradigms of wildfire management focused on avoiding socio-ecological damages and losses via mitigation, adaptation and preparation instead of relying solely on fire suppression and exclusion (Calkin et al. 2014; Moreira et al. 2020). In this sense, wildfire management in Chile has been historically focused on defining qualitative indices and rankings for evaluating fire danger, a framework that rests on a set of qualitative indicators of ignition potential, wildfire spread and consequences (Castillo Soto et al. 2015).
Wildfire risk is conventionally considered by the wildfire research community as an expectation of loss or benefit, defined as the product between the potential impacts of the wildfire (a net value change) and the likelihood of those impacts occurring (Finney 2005; Miller and Ager 2013; Johnston et al. 2020). Several frameworks for assessing wildfire risk have been proposed in the past decade. Scott et al. (2013) presented a framework based on modelling approaches to characterise wildfire likelihood and intensity, fire effects, and the relative importance of highly valued resources and assets that could be impacted by a wildfire. Johnston et al. (2020) synthesised wildland fire risk research in Canada to establish a formal quantitative risk framework, where fire occurrence, fire behaviour and values are defined as inputs to assess wildfire likelihood, the exposure experienced by such values and wildfire impacts, thus giving wildfire risk as an output. Recently, the first pan-European prototype of a wildfire risk assessment framework was published by the European Commission’s Joint Research Centre, whose main components are fire danger or hazard (ignition and fire behaviour) and vulnerability (of people, ecological values and socioeconomical values) (Oom et al. 2022). These and other wildfire risk models consider different but interconnected components that can be analysed separately, with standardisation of model outputs being one among several challenges in this matter (Oliveira et al. 2021).
Although these frameworks are intended to be applicable to local, regional and global scales (Oom et al. 2022), they are typically used to provide tools and information to fire managers and decision makers by assessing risk at national or regional levels only. Wildfire risk frameworks for analysis at parcel levels have been developed recently (Khakzad et al. 2018; Maranghides et al. 2022), but simple methods applicable for specific structures, such as industrial buildings and infrastructure, are still uncommon in the wildfire literature, which represents one among several challenges related to this problem (Planas et al. 2023). However, the state of the art in quantitative risk assessments considers risk as a probability of sustaining a loss (for example, in nuclear and chemical process industries, aeronautics, and finances). Exploring how risk is assessed in other areas may thus be fruitful for developing wildfire risk analysis methods at parcel levels. For example, in the chemical process industry (CPI), risk is defined as a measure of human injury, environmental damage or economic loss in terms of both the incident likelihood and the magnitude of the loss or injury (Center for Chemical Process Safety 2000). In the CPI, risk is the result of a quantitative assessment that depends on the identified scenario, the probability of that scenario and the consequence (damage probability) of that scenario. Incident frequencies from historical records and event tree analyses are used jointly to estimate the distribution of incident outcomes and their likelihoods, while physical and effect models are used to describe the incident consequences on the object of study (Center for Chemical Process Safety 2000). This approach reduces the inherent uncertainty associated with estimating incident likelihood and consequences, enabling risk to be compared with a tolerable threshold and subsequently mitigated to a level as low as is reasonably practicable (Pike et al. 2020).
In this context, critical infrastructure such as electrical substations and power lines can be particularly vulnerable to fires. For example, wildfire-induced temperatures can lead to oil-immersed transformer explosions (Waseem and Manshadi 2020), power line tripping and failure can occur because of annealing processes in overhead conductors (Jazebi et al. 2020) and changes in dielectric properties (Waseem and Manshadi 2020), leakage currents can be induced by soot accumulation in insulators (Fonseca et al. 1990), and transmission and distribution operations can be negatively impacted by aerial discharges of fire retardant and preventive shutdowns (Sathaye et al. 2013).
The goal of this work is to estimate the risk posed by wildfires to an electrical substation operated by Chilquinta Distribución S.A. (henceforth Chilquinta) in Valparaíso, central Chile, using a quantitative methodology. To the authors’ knowledge, this is the first time that a quantitative approach is applied on a Chilean landscape at the parcel level to assess wildfire risk. For this purpose, the definitions of wildfire likelihood and exposure provided by Johnston et al. (2020) are adopted in the present work. An event tree analysis is included to provide more details on the outcomes from the ignition of a wildland fuel. The definition given by Miller and Ager (2013) for vulnerability is also adopted here, whose modelling via empirical response functions in terms of fire intensity and distance is available in the literature (Abo El Ezz et al. 2022). However, a vulnerability model based on analysing physically how the object of study responds to thermal attack from a wildfire would improve the quantitative nature of the methodology. Therefore, wildfire consequences are operationally defined here as the probability that a target will experience an ignition due to an incident heat flux. With these techniques for estimating wildfire likelihood and consequences, it is expected that this work will contribute to bridging the gap between the approaches employed by the wildfire research community and the CPI to assess fire risk.
Methodology
Modern views on the WUI fire problem suggest focusing management practices on addressing the susceptibility of structures to the inevitability of wildfire exposure, given that keeping wildfires out of the WUI is an unattainable goal (Calkin et al. 2014). Considering that fire risk mitigation achieved by reducing vulnerability and increasing defensibility of developed property is more attractive than decreasing exposure to fires (Finney 2021), the methodology presented in the present work is developed and implemented to assess risk at the property scale (parcel level), being more focused on physically modelling the consequences of a fire on infrastructure rather than on the likelihood of fire arrival at that infrastructure.
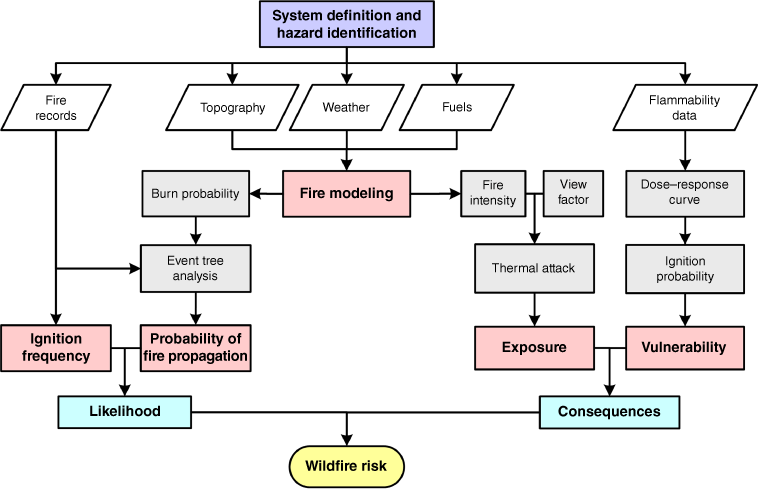
This methodology is illustrated in Fig. 1. First, the system to be studied must be defined by establishing the physical boundaries of the infrastructure of interest and a portion of land where an ignition could take place and develop into a wildfire propagating to the infrastructure. These two items (infrastructure and land) represent the study area. The following step is hazard identification. A hazard is defined here as a condition that has the potential for causing damage to people, property, or the environment (Center for Chemical Process Safety 2000), and can be regarded as stored energy that can cause damage on being released, i.e. a fuel. Thus, hazards are wildland fuels spatially distributed in the study area in this methodology. Vegetation is the most relevant fuel, but other fuels such as trash that has accumulated in empty lots may represent additional hazards (Reszka and Fuentes 2014). Once the system and hazards are identified, the following inputs are required: fire historical records, terrain features, weather and fuel properties. With these inputs, a fire modelling tool is used to calculate burn probability (BP), fireline intensity and flame length at the perimeter of the infrastructure.
Flowchart illustrating the methodology implemented in this work to analyse the risk posed by wildfires to critical infrastructure. The first step is system definition and hazard identification. The inputs are represented by white blocks. The main components of the methodology and the intermediate calculations are represented by violet and grey blocks, respectively. The risk components are the likelihood of a fire reaching the infrastructure and the consequences of a fire that has already reached it. The output is wildfire risk.
Fire modelling
Fire modelling aims to reproduce and anticipate properties of wildfire behaviour and its effects. From an operational standpoint, these models are usually classified as physics-based, empirical and quasi-empirical, and mathematical analogues (Sullivan 2009). Nowadays, many wildfire modelling tools developed either for operational or research purposes are available for predictive and planning activities (Pacheco et al. 2015), with FARSITE and FlamMap being the most widely used by the wildfire research community (Radočaj et al. 2022). Note that FARSITE was included into FlamMap in 2008; henceforth, they are treated as only one piece of software.
FlamMap is a computational tool developed to model potential fire behaviour characteristics under static conditions of weather and fuel distribution (Finney 2006). Fireline intensity and flame length are among these characteristics. The version used in the present work (v. 6.1) also includes a module to estimate conditional BP using the Minimum Travel Time method (Finney 2002) to a large number of fires ignited at random locations in the study area. The number of fires, their duration and the ignition locations can be controlled by the user. BP is thus computed as the number of times fires reached each point in the study area out of the total number of fires simulated (Parisien et al. 2019). Firebrand production is an important mechanism for wildfire propagation via spot fires (Fernandez-Pello 2017), typically acting in parallel to continuous propagation through surface and crown fires (Pastor et al. 2003). This phenomenon is addressed with FlamMap by simulating lofted embers that are tracked to determine maximum spotting distance and direction. To reduce computational costs, FlamMap allows control of the number of crown fires able to launch embers. These features justify selecting this tool for the present methodology, because it represents a good compromise between a reasonable physical representation of fire behaviour and spread, and the computational time required to carry out the simulations. It must be noted that this wildfire risk methodology is independent of the selected tool; hence, any computational tool that provides fire intensity, flame length and BP would be equally useful depending on the user requirements.
Likelihood of a fire reaching the infrastructure analysed
According to Scott et al. (2013), ‘annual BP is the probability that a wildfire will burn a given pixel during a single calendar year’, while ‘conditional BP is the probability that a wildfire occurring during a specified weather condition will burn a given pixel, given that a fire does occur in that weather condition somewhere in the landscape’. The second BP definition applies here, because in this methodology, wildfire likelihood is considered as the probability that a fire propagates to the infrastructure studied, under the condition that an ignition occurred somewhere in the study area, i.e. the ignition frequency estimated from a historical database multiplied by the conditional BP. Considering that the conditional BP is estimated under fixed weather conditions, an event tree is proposed in this methodology to refine the calculation of wildfire likelihood. Event trees are used in risk analyses to identify the consequences of a potentially hazardous initiating event by examining all possible responses to that event (Andrews and Dunnett 2000). In the CPI, event trees provide coverage of the time sequence of an initiating event propagation, and identify incident outcomes in post-incident applications by tracing the temporal sequences of occurrence of relevant safety functions or events, with each branch representing a separate outcome (Center for Chemical Process Safety 2000).
In the current work, the initiating event is the ignition of a wildland fuel, and the outcome of interest is the propagation of a wildland fire from that ignition point to the infrastructure analysed. This outcome can be the propagation of a normal or an extreme wildfire. The other outcome is fire propagation to other points, which is of no interest for the purpose of this methodology. A succession of intermediate events is assumed between the ignition of a wildland fuel and the propagation of a fire to the infrastructure. The first intermediate event is having a burned area above some threshold. Historically, most of the fires in Chilean landscapes cover small areas, of the order of 1 ha or less, with a small fraction of ignitions leading to larger wildfires. The following intermediate events are related to having weather conducive to fire propagation. In this work, these events are temperature and wind velocity surpassing some thresholds estimated from historic fire records, which represent conditions that have been present in historic fires. Therefore, fire propagation to the structure analysed under these weather conditions should be more likely than under other conditions. To discriminate between the probability of normal and extreme wildfires, two wind thresholds are defined: one is the most frequent wind speed when ignitions took place, whereas the other is representative of the more intense winds recorded when ignitions occurred in the study area. The final intermediate event is the conditional BP, as defined in the paragraph above. The likelihood of a fire reaching the infrastructure of interest (Pp) is then estimated as:
where fig is the historic ignition frequency, Pp|ig is the conditional probability of a fire reaching the point of interest, Pp|ig,j is the probability of an intermediate event after the jth node in the event tree, and N is the number of nodes in the branch leading to the outcome of interest. Note that with this technique, the calculation of conditional BP is refined by multiplying it with a historic ignition frequency and with several additional probabilities representing conditions that were historically present when actual ignitions took place in the study area.
Consequences of a fire reaching the infrastructure analysed
Wildfire consequences depend on the exposure of the asset studied to thermal attacks, and asset vulnerability to these attacks. These two items are evaluated separately as follows.
Exposure
A configuration consisting of a rectangular solid flaming front at some distance from the target of interest (Fig. 2) has been deemed acceptable for wildfire applications (Sullivan et al. 2003; Cohen 2004; Zárate et al. 2008). This approach is proposed here to translate the results of modelling at landscape level to a scale comparable with that of a structure in the WUI. To estimate incident heat flux from a flaming front, it is thus necessary to compute a view factor between the front and the target. Thermally excited soot particles represent the major source of thermal radiation from wildfire flames; hence, emissivity should be estimated with correlations found in the literature in terms of a mean absorption coefficient for soot (Lautenberger et al. 2016). If the flaming front is sufficiently thick, i.e. with a flame depth of the order of 4 m or more (Àgueda et al. 2010; Johnston et al. 2014), it is reasonable to consider it as a black body. As it is likely that flame depths in actual wildfires will be less than 4 m, the emissive power from the flaming front would be overestimated under this assumption. Nevertheless, given the limitations of the fire models used in this study, particularly applied to Chilean wildland fuels, this assumption is applied here to simplify the analysis. Thus, assuming the flame front as a rectangular black body and neglecting atmospheric transmissivity, radiant heat flux on the target is:
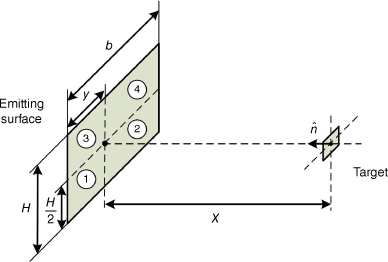
where F is the view factor between the flaming front and the target, r is radiant fraction, Af is the flaming front surface (Af = b × H, where b is the rectangular front width, H is flame length) and If is fireline intensity. The methodology described by Morandini et al. (2013) is used here to estimate view factor, which consists of dividing the emitting surface into four smaller rectangles and aligning the normal vector of the target to the common vertex of the smaller rectangles (Fig. 2); hence, the sum of the view factors between the rectangles and the target is the view factor for the entire surface. Two parameters required for this model are the horizontal distance at which the target is located with respect to the emitting surface (y = b/2) and the distance between the target and the surface (x). The radiant fraction (i.e. the fraction of the heat released by combustion that is given off as thermal radiation) is assumed as equal to 0.3, a value commonly used in fire safety engineering (Mudan 1984). Note that firebrands may represent a parallel mechanism for target damage owing to their impact on some components of the infrastructure analysed, which would increase wildfire risk. However, characterising the effects of a firebrand attack quantitatively requires extensive data and fundamental knowledge related to processes that are not fully understood (Manzello et al. 2020). Therefore, exposure is considered in the present work as due to thermal radiation from the flames only. Also, note that the existence of a wall or a fence between the flaming front and the target is omitted to simplify the problem.
Flaming front modelled as four rectangular emitting surfaces (numbered 1 to 4 in the figure) to determine its view factor with respect to a target of small size within the infrastructure analysed. The target unit normal vector points perpendicularly to the common vertex of the rectangles. The parameters required are flame length (H), flame width (b), the horizontal distance where the target is located with respect to the emitting surface (y = b/2) and the distance between the target and the surface (x).
Vulnerability
In fires, for damage to occur, the target must experience some physical or chemical alteration that leads to a disruption in the continuity of services provided by the infrastructure analysed. As there is a range of damage severity that the target could experience, ignition is considered in this work as the criterion to quantify vulnerability as a function of thermal exposure. Note that the failure of a component could occur before it ignites; therefore, other criteria based on thermal or structural properties (such as melting temperature or loss of tensile strength) may be also used to assess vulnerability. However, a criterion based on ignition allows failure to be discerned more directly (because it is modelled as a binary response). Additionally, the relationship between ignition and incident heat flux has been thoroughly studied via experimental and theoretical work; hence, extensive flammability data are available for modelling ignition probability. Thus, a way of evaluating asset vulnerability is to express it in terms of an ignition probability Pd for different radiant incident heat fluxes, resulting in a dose–response curve.
A dose–response curve generally takes a sigmoidal form that can be converted to a linear function with a probit analysis (Center for Chemical Process Safety 2000). The probit function Y is the inverse of the cumulative distribution function (CDF) of the standard normal distribution. As the normal CDF and its inverse are not available in closed form, computing the probit function requires approximations, e.g.
By converting probabilities into probit variables with this equation, the dose–response curve in terms of the probit variable becomes linearly related to the logarithm of the dose :
where k1 and k2 are constants from a linear regression. This method is commonly used to evaluate the vulnerability of people (Center for Chemical Process Safety 2000) and vessels (Cozzani et al. 2005) to thermal exposure, and is implemented in the present work to develop a vulnerability model from piloted ignition data available in the literature.
The criterion for piloted ignition is typically defined using the thermal ignition theory (Parot et al. 2022), which requires measuring the time to ignition as a function of the heat flux in standardised experimental configurations. A critical heat flux is obtained by linearly extrapolating these data when time to ignition tends to infinity, but non-linearities emerge when this extrapolation is performed. An alternative approach considering ignition as a phase transition has been proposed to tackle some of these issues (Sabi et al. 2021). This approach suggests a probabilistic instead of a deterministic process in the critical region, which is well suited to understanding the sigmoid nature of the dose–response curve for flammability data in terms of an ignition probability.
Wildfire risk
The initiating event of any wildfire is a wildland fuel ignition that develops into sustained combustion of the surrounding fuels, and its relevant outcome is the arrival of a flaming front at the point of interest. Risk is thus estimated as:
where Pp is the probability of a wildfire propagating to point (x, y), and Pd is the probability of a target sustaining damage, defined here as ignition of the most vulnerable material in the infrastructure analysed. Therefore, the fire risk for the infrastructure analysed has units of events/year because it is the product of likelihood of a fire reaching the point of interest (events/year) and damage probability, which has no units but represents a share of the events per year that may end in actual damage according to this definition.
Case study
The methodology described above can be used to estimate risk at any point of a study area but is applied in this work to analyse an electrical substation in Valparaíso, central Chile (Fig. 3). This substation reduces voltage from 110 to 12 kV and belongs to a grid constituted of ~17 000 km of power lines operated by Chilquinta to supply electricity to more than 600 000 clients. Therefore, a fire reaching this infrastructure could result not only in material damage or asset losses, but also potentially in power cuts, leading to negative consequences to a significant fraction of the population served by Chilquinta and penalty fees imposed by Chilean authorities on the company. Potential targets within the substation include transformers, structures, cables, lightning rods, isolators and switches, which are manufactured with metallic alloys, polymers and ceramics. Therefore, polymeric components are expected to be the most vulnerable to thermal exposure.
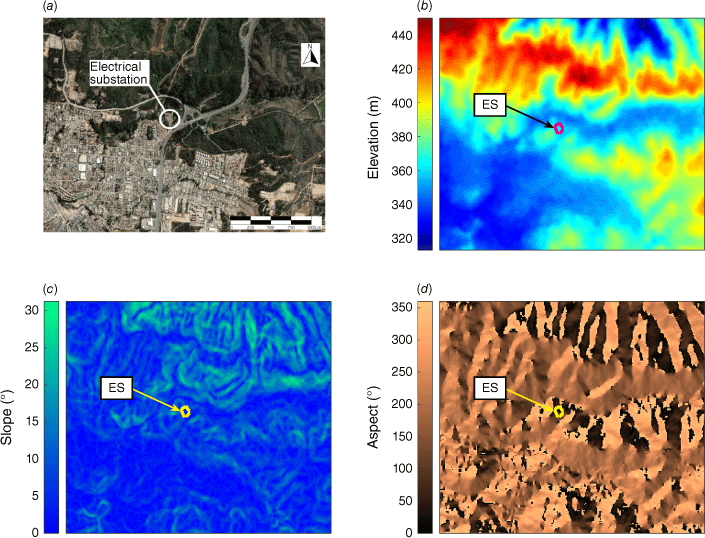
Satellite image of the study area, showing the location of the electrical substation (ES) analysed (a), along with a Digital Elevation Model (DEM) acquired by the ALOS satellite with a resolution of 12.5 m per pixel (b). Slope (c) and aspect (d) maps were produced with this DEM. The orientation and scale shown in Fig. 3a are the same as for all the images showing the study area in this document.
Study area
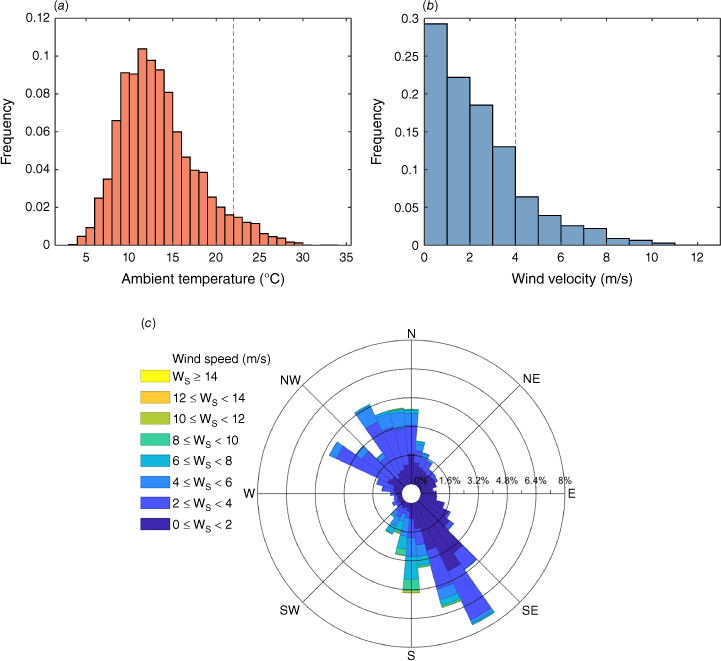
A satellite image of the study area, whose surface is ~996 ha, is shown in Fig. 3. The dimensions of the study area are selected to consider only a strip of wildland beyond the WUI of ~500 m, where it is assumed that ignitions could lead to fires propagating to the substation before brigades could arrive to prevent this. This assumption is justified by the existence of a fire station in the urban area, 3 km from the electrical substation. Considering fire brigades moving from this station at 20 km/h through the urban area, they would arrive at the substation 9 min after an alarm was raised. This time is in line with those recommended in the UK and other countries for urban fire stations (Yang et al. 2007; Shahparvari et al. 2020). If the fire has a rate of spread (ROS) of 50 m/min, which was proposed as the maximum ROS for a normal forest fire by Tedim et al. (2018), the distance that a fire front would advance in 9 min would be 450 m. Although ignitions occurring farther than 500 m from the WUI may also lead to wildfires escaping control and propagating to the infrastructure analysed, the likelihood of these propagations is assumed as negligible, because in Chile, almost 100% of ignitions are of human origin near urban areas and roads (Castillo Soto et al. 2015). This assessment will influence the size of the study area, and consequently, more remote parts of the WUI (i.e. further away from fire stations) should consider larger regions of interest. The topography of the study area (Fig. 3) is characterised by hills to the north, with a peak elevation of ~450 m, and a lower area to the south, where the urban infrastructure is located. The elevation in the lower area is ~340 m, thus generating slopes between 10 and 25° in the vicinity of the electrical substation. Weather data for the year 2020 were obtained from a meteorological station near the study area. Temperature and wind velocity are presented as histograms, whereas wind direction is presented in a wind rose (Fig. 4). The most frequent temperatures and wind velocities are 11–12°C and 0–1 m/s. The wind rose shown in Fig. 4 indicates that wind comes predominently from the southeast (150°). Fig. 5 shows the distribution of fuel types in the study area, according to a land classification made by the Chilean Forest Service (CONAF). This classification indicates that Eucalyptus globulus plantations cover most of the study area (~59%); therefore, two fuel distributions are considered. One distribution is a simplified landscape consisting only of an urban and a wildland area (Fig. 5a), with fuel models 91 (urban/developed) and 163 (moderate load, humid climate timber–grass–shrub) from the Scott and Burgan classification (Scott and Burgan 2005) assigned to model the urban area and eucalyptus plantations, respectively. The other corresponds to a more detailed landscape (Fig. 5b), with fuel models 91, 93 (agricultural), 98 (water), 122 (moderate load, dry climate grass–shrub), 149 (very high load, humid climate shrub) and 163 assigned to each patch of land in the CONAF classification. Note that a highway running in the north–south direction crosses the study area, which is considered in the second fuel distribution (Fig. 5b) as an urban area. CONAF also reports canopy cover classes for each land division: urban area, wide open, open, semi-dense and dense. The following canopy cover percentages are assigned to these classes: 0, 10, 35, 65 and 90%, respectively. These two fuel distributions are used along with the topography and wind direction described before as inputs to fire modelling. Additionally, canopy cover information is useful for crown fire modelling.
Histograms of temperature (a) and wind velocity (Ws) (b), along with a wind rose (c), produced from hourly data recorded by a weather station (WMO code: 85560) located near the study area for the entire year 2020.
Spatial fuel distribution in the study area. Two distributions are considered: a simplified one consisting only of an urban area and wildland (a), and a more detailed distribution determined from a subdivision made by the Chilean Forest Service, CONAF (b). Colours represent the fuel models assigned: urban/developed (light grey), agricultural (dark grey), water (blue), moderate load, dry climate grass–shrub (brown), very high load, humid climate shrub (dark red), and moderate load, humid climate timber–grass–shrub (green) (Scott and Burgan 2005). The electrical substation (ES) is in the urban area in both figures.
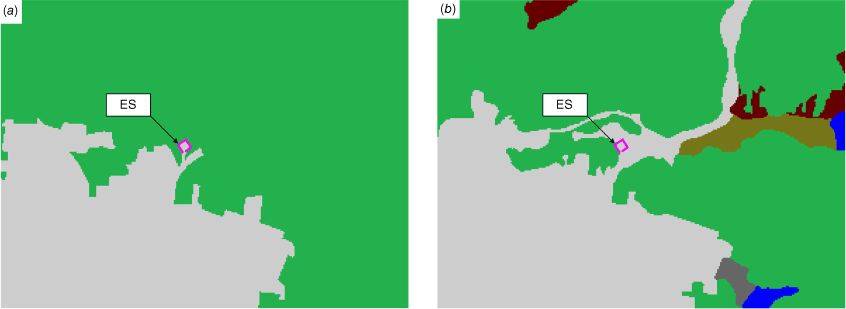
Fire modelling
FlamMap is selected in this work to provide estimations of conditional BP and fireline intensity in the vicinity of the infrastructure analysed using the topography, fuel distributions and wind direction shown in Fig. 3. Crown fire is modelled with constant values for stand height (15 m) and canopy base height (1 m), which were validated with field observations of the substation surroundings. Canopy bulk density is set at 0.2 kg/m3 (Keane et al. 2005). Fuel moistures of 6, 7, 8, 60 and 90% are assumed for 1, 10, 100 h, live herbaceous and live woody fuels, respectively, for all the fuel models in the study area. No weather stream is specified; hence, these initial fuel moistures are assumed as constant. A uniform wind field coming from the southeast (at 150° from the north) is considered in the simulations. Two wind velocities are imposed, one representative of average conditions (5 m/s) and the other of extreme conditions (25 m/s).
BP was estimated by simulating 1000 fires ignited at random locations in the study area. The number of simulated fires was increased until no relevant difference in the results was observed. Resolution for BP calculations was the same as the Digital Elevation Model of the study area (12.5 m per pixel, Fig. 3). The maximum simulation time was defined as 180 min per ignition, as it was assumed that by that time, fires were already detected and brigades had intervened. The justification for this analysis time frame is detailed in the study area section concerning urban firefighters. Additionally, records kept by CONAF for the Valparaíso and Viña del Mar municipalities indicate that, between July 2018 and June 2019, the response time of wildland fire brigades (defined as the time elapsed between fire detection and the first attack by CONAF brigades) was on average 21 min, with 97% of the responses between 0 and 60 min, while the average time between the first attack and fire control was 164 min, with 59% of these actions taking between 0 and 60 min. As the substation is next to a highway, and predicted fire intensities can be handled by firefighters as discussed further in this section, these response and fire control times may be lower. Considering these aspects, for the purpose of this case study, the simulation time was set at 180 min. Note that both the simulation time and the size of the study area have an effect on the calculated BP. Spot probability was set at 0.5 to reduce the computational time that would be required if this probability was set to 1.0.
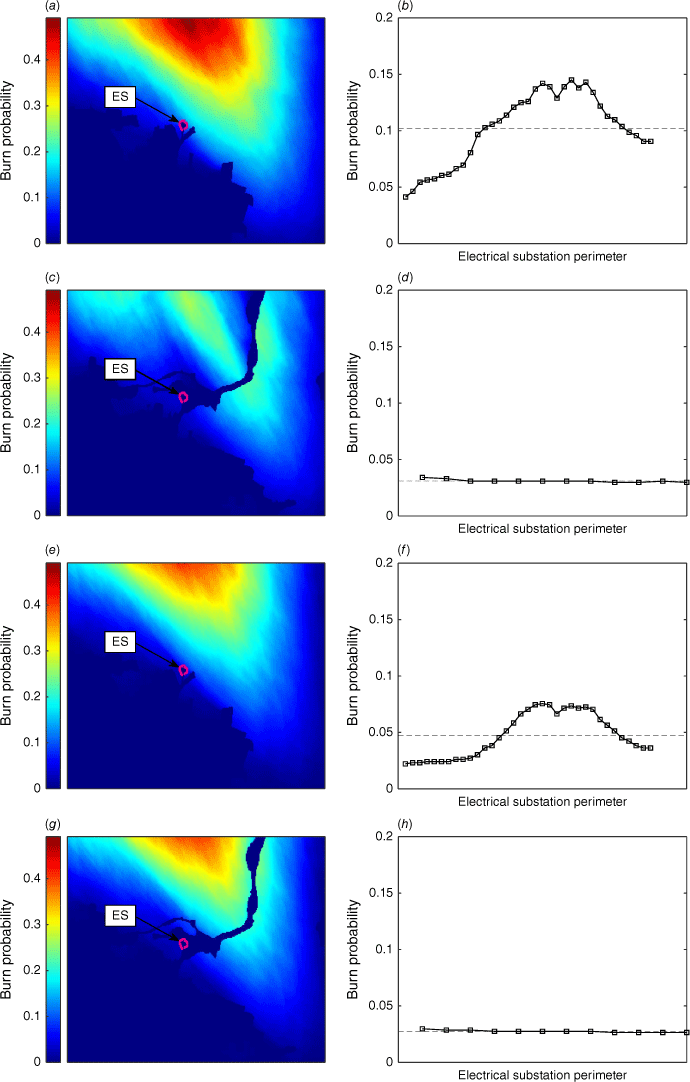
Fig. 6 shows the BP results. In general, similar BP patterns concerning magnitude and alignment with wind direction are observed for the two wind speeds imposed and the two simulated landscapes. In all figures, the highest BP magnitudes are observed downstream of the wind, to the north of the study area, where the maximum BP is ~0.5. However, the substation is in a zone with relative low BP; average BPs between 0.028 and 0.102 are estimated on the electrical substation perimeter. Note that by considering the highway as an urban area in the detailed fuel distribution, the study area becomes separated into two areas in terms of BP distribution (Fig. 6c, g). This effect is more pronounced for lower winds (Fig. 6a vs c) than for a more intense wind, where the highway does not significantly affect the BP distribution (Fig. 6e vs g). Also, imposing a stronger wind produces a decrease in the BP around the substation, an effect that is more significant in the simplified landscape (Fig. 6b vs f) than in the detailed one (Fig. 6d vs h).
Burn probability (BP) estimated with FlamMap for the study area, considering uniform wind velocities of 5 m/s (a–d), and 25 m/s (e–h). Results with a simplified fuel distribution (a, b, e, f), and a more detailed distribution (c, d, g, h) are shown. Representative BPs in the electrical substation vicinity are calculated by taking the average of the BP curves (b, d, f, h) corresponding to the substation perimeter, giving 0.102 (b), 0.031 (d), 0.047 (f) and 0.028 (h).
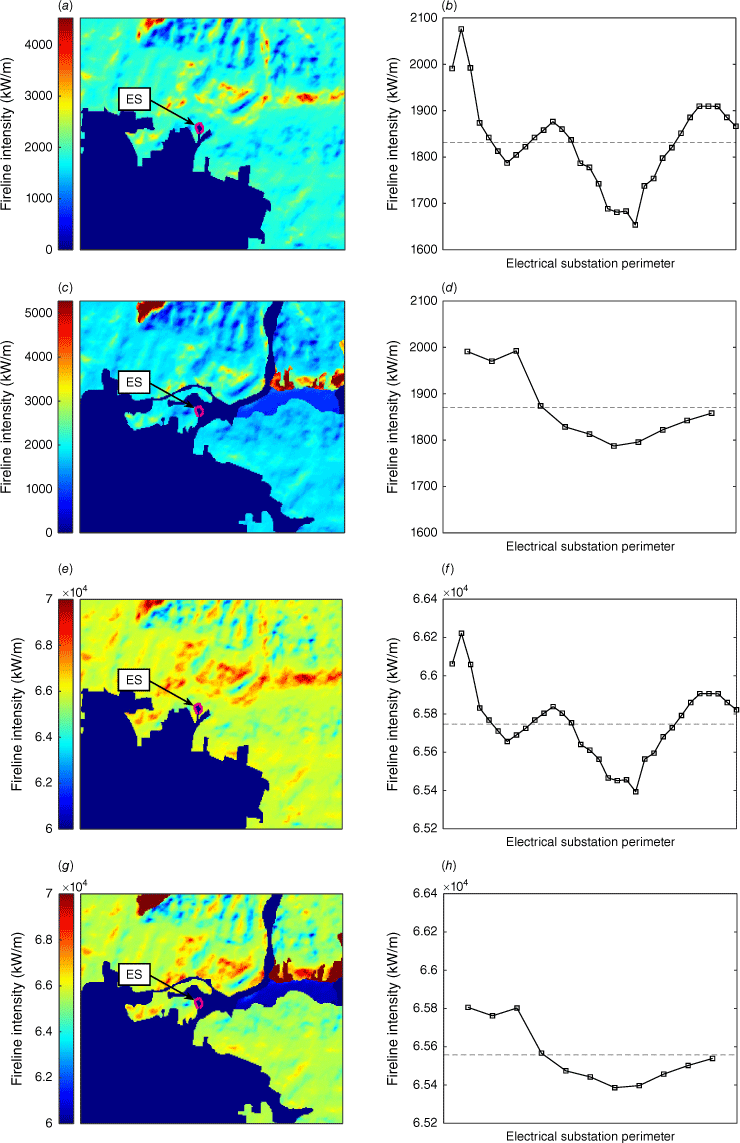
Fireline intensity of a potential wildfire surrounding the substation is estimated from fire behaviour simulations (Fig. 7). The patterns observed for the two simulated landscapes are rather similar, with the zones of relative highest intensity being far from the substation, to the north and east of the study area. For low winds (Fig. 7a–d), average fireline intensity at the substation perimeter is between 1800 and 1900 kW/m, while average flame length is of the order of 4 m. These differences between average fireline intensity and flame length estimated for the two simulated landscapes are very small; hence, the impact of these differences on further results should not be significant. However, for a stronger wind (Fig. 7e–h), average fireline intensity and flame length are of the order of 65 000 kW/m and 43 m. These fire behaviour results are summarised in Table 1. Clearly, the imposed wind plays a more significant role on these outputs than the modelled fuel distribution in the study area. Therefore, varying the wind speed is a convenient way of producing fire behaviours representative of normal fires (500–2000 kW/m) and extreme fires (30 000–100 000 kW/m), according to the classification proposed by Tedim et al. (2018).
Fireline intensity estimated with FlamMap for the study area, considering uniform wind velocities of 5 m/s (a–d), and 25 m/s (e–h). Results with a simplified fuel distribution (a, b, e, f), and a more detailed distribution (c, d, g, h) are shown. Representative fireline intensities in the electrical substation vicinity are calculated by taking the average of the fireline intensity curves (b, d, f, h) corresponding to the substation perimeter, giving 1832 kW/m (b), 1870 kW/m (d), 65 747 kW/m (f) and 65 558 kW/m (h).
| Scenario | A | B | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Simulated landscape | Simplified | Detailed | Simplified | Detailed | |||||
| Wind conditions | Average | Extreme | Average | Extreme | Average | Extreme | Average | Extreme | |
| Wind (m/s) | 5 | 25 | 5 | 25 | 5 | 25 | 5 | 25 | |
| If (kW/m) | 1832 | 65 747 | 1 870 | 65 558 | 1 832 | 65 747 | 1870 | 65 558 | |
| H (m) | 4 | 43 | 4 | 43 | 4 | 43 | 4 | 43 | |
| 6.20 | 172 | 6.23 | 171 | 8.31 | 215 | 8.36 | 214 | ||
Likelihood of a fire reaching the infrastructure analysed
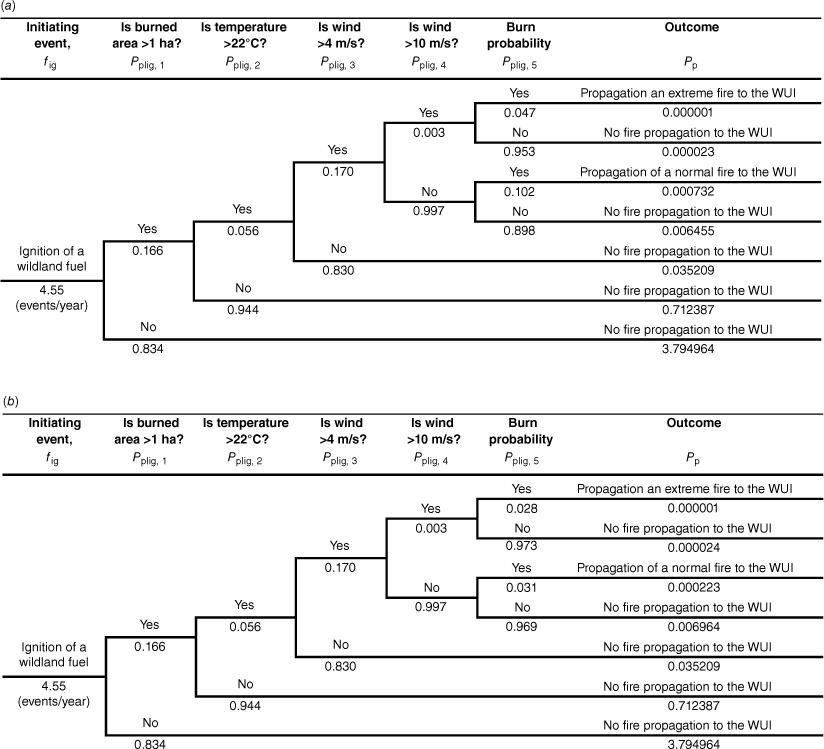
Fig. 8 shows event trees developed to estimate the probability of a wildfire reaching the substation. Using Eqn 1, the combination of ignition frequency and the conditional probability of a fire reaching the substation are Pp = 7.34 × 10−4 events/year and Pp = 2.24 × 10−4 events/year for the simplified and detailed simulated landscapes, respectively. For estimating ignition frequency, CONAF records for the Valparaíso and Viña del Mar municipalities between 2002 and 2019 (Fig. 9a) are analysed. Ignition data encompassing this larger area are selected to minimise spatial variability that could arise owing to the smallness of the study area compared with that of the territory where the study area is located. Ignition frequency is thus estimated more robustly at 239 events per year, and because this frequency corresponds to the total area of the two municipalities (52 320 ha), it is scaled down to the study area (996 ha), giving events per year. Additionally, CONAF has recorded the resulting burned areas from these fires, along with ambient temperature and wind velocity when they started (Fig. 9b–d). These historic conditions are used to estimate the probabilities of intermediate outcomes in the event tree as follows.
Event trees developed to estimate the likelihood of a wildfire reaching the infrastructure of interest, for the simplified (a) and the detailed (b) simulated landscapes. In both cases, the initiating event is the ignition of a wildland fuel, and the first four intermediate events are having burned area, temperature and wind above historic thresholds. The fifth intermediate event is BP. Finally, the probabilities of the outcomes of interest (propagation of a normal or extreme fire to the WUI) result from multiplying the ignition frequency and the five intermediate probabilities. In these event trees, BPs are the averages in the substation perimeter, estimated in the simplified (a) and the detailed (b) simulated landscapes for the two wind conditions (average and extreme wind).
Fire records analysed in this work to estimate ignition frequency and the subsequent conditional probability of a fire reaching the point of interest. These records correspond to fires in the Valparaíso and Viña del Mar municipalities in the 2002–2019 period: number of ignitions per year (a), histogram of burned area that resulted from these fires (b), and histograms of ambient temperature (c), and wind velocity (d) when ignitions leading to burned areas larger than 1 ha occurred.
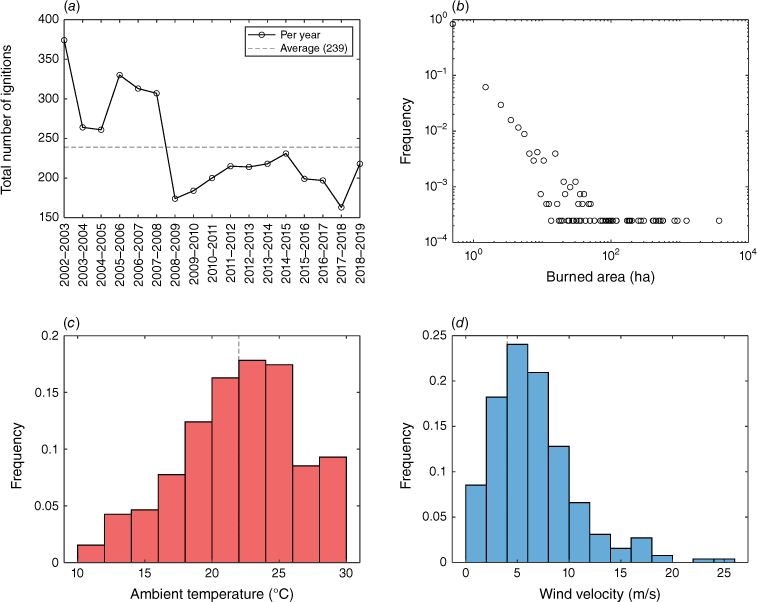
The first intermediate event is having a burned area larger than 1 ha, because ignitions leading to burned areas smaller than 1 ha are much less likely to represent an actual threat to the infrastructure analysed. This probability is calculated as 0.166 (1–0.834, where 0.834 is the frequency corresponding to range 0–1 ha in Fig. 9b). The second and third intermediate events are having temperature and wind velocities representative of weather conditions that occur concurrently with actual wildfires, whose probabilities are estimated as follows. Temperature and wind velocity recorded when actual fires having burned areas >1 ha took place in the 2002–2019 period are plotted as histograms (Fig. 9c, d), where the most frequent ranges are identified (22–24°C and 4–6 m/s). These magnitudes represent past weather conditions under which fire ignition and propagation are most likely. To predict the probability of having these conditions in the future, the hourly data recorded in 2020 by the weather station mentioned in the study area section is analysed as a proxy for future weather conditions (Fig. 4a, b). Only the most recent year is considered because risk is quantified on an annual basis, and its analysis requires addressing the likelihood of a fire reaching the infrastructure in terms of current weather, leaving aside potential variability in these data induced by climate change in past years. The cumulative frequencies corresponding to temperatures and wind velocities higher than 22°C and 4 m/s are determined from Fig. 4a and b, giving 0.056 and 0.170, respectively. These frequencies represent the probabilities of having future weather conditions conducive to the propagation of normal fires. Note that the data used for these estimations includes those recorded at night-time and in months that do not belong to the fire season, as the goal of this analysis is to predict probabilities at any time of a future year. To discriminate between the propagation of normal and extreme wildfires, the event trees are expanded with a fourth intermediate event: the probability of having a stronger wind leading to the propagation of an extreme fire. Historically, in the study area, the most intense winds were of the order of 25 m/s (Fig. 9d), but the maximum wind speed recorded in 2020 was ∼12 m/s (Fig. 4b). Thus, this event was defined as having a wind speed higher than 10 m/s, and its probability assigned in the event trees was the summed frequency of the two deciles corresponding to the highest velocities in Fig. 4b, giving 0.003. Finally, the fifth intermediate event is the conditional BP, which was considered as the average BP in the substation perimeter determined in the fire modelling section for the two simulated landscapes and the two wind conditions considered (average wind of 5 m/s and an extreme wind of 25 m/s). In the simplified landscape, these BPs are 0.102 and 0.047 for the average and extreme winds, respectively, while these BPs are 0.031 and 0.028 in the detailed landscape for the same wind conditions. Therefore, the event trees shown in Fig. 8 provide the likelihood of normal and extreme fires propagating to the infrastructure of interest.
Consequences of a fire reaching the infrastructure analysed
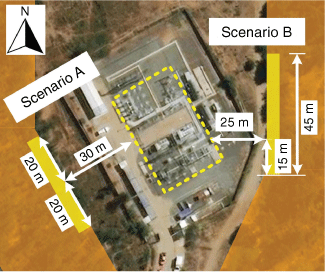
The fireline intensity and flame length results described in the previous section represent fire behaviour in all pixels of the study area. This is equivalent to a wildfire engulfing the entire substation perimeter; therefore, a more realistic scenario would be a flaming front arriving at one side of the substation perimeter at a time. Two scenarios are considered (Fig. 10). In scenario A, a fire coming from the left is assumed as a rectangle of 40 m width at 30 m from a small target within the substation; hence, the view factor is 0.045. Scenario B is a fire on the right side of the substation, 25 m from the target and whose width and view factor are 45 m and 0.060, respectively. As the distance between the flaming front and the target may have a noticeable effect on the view factor, this distance is assumed in a worst-case scenario with the flaming front at the vegetation perimeter. Using Eqn 2 with these calculated view factors, the resulting heat fluxes are summarised in Table 1. It is observed that the most relevant factor in these results is the wind condition assumed in the study area. With an average wind of 5 m/s, heat fluxes are of the order of 6–8 kW/m2, but with a stronger wind (25 m/s), these fluxes increase to values between 171 and 214 kW/m2. The different geometric configurations between the flaming front and the target (scenario A vs. B) induce a difference of ~2 kW/m2 under average wind, but for extreme wind conditions, this difference rises to ~40 kW/m2. Therefore, scenario geometry plays a more prominent role as the wildfire increases in intensity owing to stronger winds. Finally, the simulated landscape (simplified vs detailed fuel distribution) does not represent a relevant factor in the results for a given scenario.
Scenarios for estimating the heat flux on a target within the electrical substation analysed. Orange indicates a wildfire engulfing the substation from all sides, whereas yellow rectangles represent two flaming fronts coming from the sides of the substation. The scale of the image is larger than that in Fig. 3.
The dose–response method described by Eqns 3 and 4 is used in this work to develop a vulnerability model, assuming a binary response for the material (ignition/no ignition). Considering that polymer is the most fire-vulnerable material among those present within the substation, polymethylmethacrylate (PMMA) is selected as a proxy fuel to develop this model from flammability data. A probit equation is determined from the experimental data compiled by Bal and Rein (2011), which is shown in Fig. 11a. In this graph, no unique value of critical heat flux is observed. Instead, a transition from a very low (~1%) to a very high ignition probability (~99%) takes place. To estimate the incident heat fluxes that give ignition probabilities of 1% and 99%, these data are assumed to be bounded by two curves of the kind that tend to two limiting heat fluxes as time to ignition increases, with γ being a common exponent determined with a linear fit to the data plotted in logarithmic scales (Fig. 11b). By adjusting two curves to bound the data in this plot and obtaining the corresponding intersections with the y axis, the resulting curves are and . To determine a critical heat flux, the ignition time should tend to infinity. Therefore, by further setting a high ignition time (tig = 900 s), the critical heat flux is found to range from 5.0 to 16.6 kW/m2 (dashed lines in Fig. 11a).
Flammability data for PMMA, compiled by Bal and Rein (2011) from several sources and analysed here for developing a vulnerability model, presented as time to ignition (in seconds) as a function of heat flux (in kW/m2) in linear (a), and log–log scales (b). From these data, a probit function is proposed (c), which serves to estimate an ignition probability curve in the critical heat flux region (d).
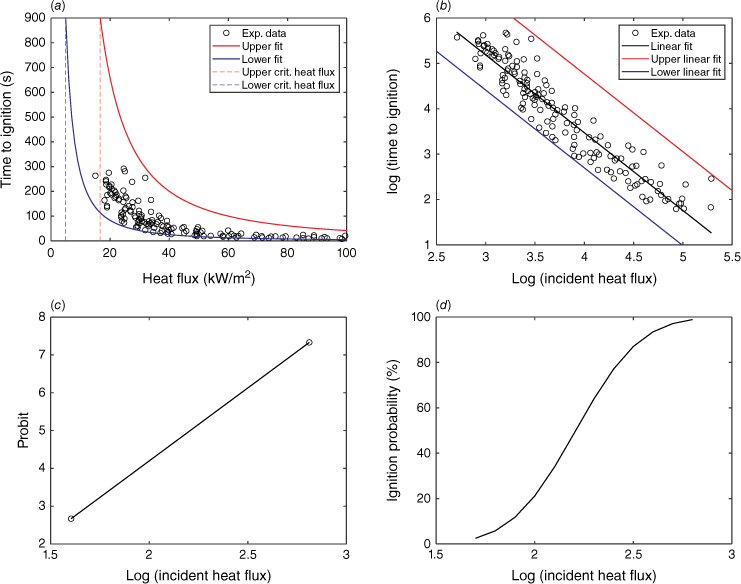
As probit values corresponding to probabilities of 1 and 99% are 2.67 and 7.33, respectively, a probit equation is obtained by applying a linear fit to these probit values as a function of the logarithm of critical heat fluxes (log(5.0) = 1.61 and log(16.6) = 2.81, Fig. 11c). The resulting probit equation is:
Using Eqn 3 to estimate ignition probability from probit variables, Fig. 11d shows ignition probability in terms of the logarithm of critical heat flux. This curve effectively models the transition between the no-ignition and 100% ignition conditions and provides a sound model for estimating vulnerabilities of polymeric targets to thermal exposure.
Wildfire risk
Wildfire risk is calculated with Eqn 5, using the probabilities of a normal and an extreme fire reaching the electrical substation (Fig. 8). With respect to damage probability, the vulnerability model developed for PMMA (Eqn 6) is applied to calculate the probit variables corresponding to the heat fluxes determined in the exposure analysis (Table 1). For average wind conditions, these heat fluxes are between 6.20 and 8.36 kW/m2, thus being in the critical heat flux region for PMMA and representing a thermal exposure capable of inducing ignition in this proxy fuel. The calculated probits are then converted to ignition probabilities with Eqn 3. However, the estimated heat fluxes under extreme wind are between 171 and 215 kW/m2. The corresponding probits thus exceed 7.33, which in practice means an ignition probability of 100% for PMMA. These results are shown in Table 2, along with the risk estimates determined with Eqn 5. It is seen that, for a given scenario (A or B) and simulated landscape (simplified or detailed), there are two risk estimates, one for regular fires and another for extreme ones. They are directly added to estimate the total wildfire risk on the asset, resulting in four wildfire risk magnitudes for the two scenarios and simulated landscapes. Although they are slightly different, it is seen that wildfire risk ranges approximately from 10−5 to 10−4 events/year (i.e. one event every 10 000 to 100 000 years), with the scenario considered for the exposure analysis inducing a change of one order of magnitude in wildfire risk and the detail level of the simulated landscape being less relevant in these results.
| Scenario | A | B | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Simulated landscape | Simplified | Detailed | Simplified | Detailed | |||||
| Wind conditions | Average | Extreme | Average | Extreme | Average | Extreme | Average | Extreme | |
| Wind (m/s) | 5 | 25 | 5 | 25 | 5 | 25 | 5 | 25 | |
| Pp (events/year) | 7.32 × 10−4 | 1.16 × 10−6 | 2.23 × 10−4 | 6.74 × 10−7 | 7.32 × 10−4 | 1.16 × 10−6 | 2.23 × 10−4 | 6.74 × 10−7 | |
| 1.82 | 5.14 | 1.83 | 5.14 | 2.12 | 5.37 | 2.12 | 5.37 | ||
| Y | 3.52 | 16.33 | 3.54 | 16.32 | 4.65 | 17.20 | 4.67 | 17.19 | |
| Pd | 0.069 | 1 | 0.072 | 1 | 0.364 | 1 | 0.373 | 1 | |
| R x,y (events/year) | 5.1 × 10−5 | 1.2 × 10−6 | 1.6 × 10−5 | 6.7 × 10−7 | 2.7 × 10−4 | 1.2 × 10−6 | 8.3 × 10−5 | 6.7 × 10−7 | |
| Total risk (events/year) | 5.2 × 10−5 | 1.7 × 10−5 | 2.7 × 10−4 | 8.4 × 10−5 | |||||
The likelihood of a fire reaching the point of interest is estimated with event trees (Fig. 8). Ignition probabilities are converted from the probits estimated with the probit equation developed for the proxy fuel (Eqn 6), using the heat fluxes calculated in the exposure analysis (Table 1). For a given scenario and simulated landscape, the risk of normal and extreme fires is summed, giving the total risk on the asset.
Discussion
A quantitative methodology for estimating the risk posed by wildfires to critical infrastructure at the parcel level is presented. To demonstrate its utilisation, it was applied to assess wildfire risk at an electrical substation located in central Chile. This is the first time that a methodology of this kind is applied in a Chilean landscape. Three aspects of this methodology are novel. First, event trees are proposed to discriminate the outcomes from the ignition of a wildland fuel and estimate the probability of a fire reaching the point of interest. Second, a vulnerability model based on the response of a target to thermal attack from a flaming front is developed for a proxy fuel representative of the infrastructure analysed, giving its ignition probability. Third, risk is calculated as the product between the probability of a fire reaching the infrastructure and its ignition probability, interpreted as the probability of sustaining a loss. This methodology is focused on critical infrastructure, but could be also applicable to other structures, such as dwellings and public utilities, by developing and applying appropriate probit equations for the specific materials encountered in each case. Very few equations of this kind can be found in the literature currently, which highlights a significant research need on this matter (Planas et al. 2023).
Considerations on data and modelling
This methodology requires defining a period and spatial delimitation for historical ignition data. Data availability can be an issue because historical records are imperative to estimate ignition frequency. As climate and weather impact on the propensity of wildland fuels to ignite, an extended period of analysis should be clearly defined so that the estimated ignition frequency is representative of current climatic conditions. In Chile, CONAF has kept data since the 1980s, but additional data from other public and private institutions, focused on specific areas or assets, would be ideal. The CONAF wildfire database provides an overview of the historical weather conditions under which ignitions took place in the study area. To predict if current weather conditions are conducive to new ignitions, information from weather stations in the study area needs to be retrieved. In this case study, one station was deemed representative of the study area, but if no weather measurements are available, predictive tools such as WindNinja (Wagenbrenner et al. 2016) may be useful. The spatial delimitation of the study area is also relevant: because its ignition pattern could be different to that of the territory in which it is located, varying its boundaries may also impact on ignition frequency. Fuel mapping of the study area is another challenging aspect, as it needs territorial division in terms of plant species, forest type (native or plantation), canopy cover, stand height, fuel load, etc. In Chile, CONAF has formulated a land classification in terms of these variables, but if this information is unavailable, satellite imagery can help to match actual vegetation with standard fuel models (Aragoneses and Chuvieco 2021), a procedure that can be assisted by relating vegetation spectral indices to wildland fuel properties (Villacrés et al. 2019; Arevalo-Ramirez et al. 2021). Simplifying the fuel distribution as done in this case study is also recommended, as it does not produce significant variation in the results. Therefore, this methodology requires reporting clearly the period and spatial distribution of data used to estimate ignition frequency, along with the fuel distribution in the study area, but at the same time, it provides enough flexibility to be adapted to the site conditions, as demonstrated with this case study.
In this case study, fire modelling was carried out with FlamMap, but the proposed methodology is independent of the fire modelling software employed. In these tools, flame length is usually correlated with fireline intensity by power-law relationships that require two empirical parameters (Egorova et al. 2022). This uncertainty may be circumvented by employing simulators based on Computational Fluid Dynamics (CFD), which may be more suitable to estimate incident heat fluxes at specific points within the infrastructure analysed by increasing the spatial resolution of the analysis and considering the geometry between the flaming front and the target in more detail, as proposed by some authors for housing vulnerability (Vacca et al. 2020). This approach would also allow one to estimate flame depth and to verify the black body assumption for the flaming front, thus providing a more precise estimation of heat flux on the target.
Risk mitigation
Wildfire risk management requires information from risk analyses to evaluate strategic options affecting risk factors, so that cost-effective investments in risk mitigation can be implemented (Calkin et al. 2014) and assessed in terms of the risk remaining after their implementation, i.e. the residual risk, as defined by Thompson et al. (2016). Some mitigation measures can be suggested by inspecting the main components of risk considered in the methodology presented here. The probability of a fire reaching the infrastructure analysed depends on the historic ignition frequency, which could be reduced by educational campaigns, law enforcement or other measures of this kind. This likelihood also depends on burn probability: because a patchy landscape typically hinders wildfire propagation, BP could be lowered by treating the wildland fuels and reducing the fuel load near the infrastructure analysed (i.e. increasing the non-fuel buffer zone around it). The probability of a wildfire in the study area reaching the infrastructure analysed is of the order of 10−4 events/year, but this result cannot be considered as a full risk metric, because it does not consider the potential consequences on the substation, which include potential exposure to the wildfire and how the asset responds to this exposure (ignition in this work). In this case study, it was observed that the incident heat flux on the target analysed is sensitive to the scenario considered regarding the idealised flaming front; hence, wildland configuration in the infrastructure perimeter plays a relevant role in this calculation. Asset ignition probability, which depends on the heat flux received by the target, was between 0.07 and 0.37 for average wind, and practically 1.00 for extreme wind. These probabilities could be decreased by establishing fuel breaks, fire walls and other active and passive fire protection measures. But this probability alone is also insufficient to quantify risk because it does not consider the likelihood of a wildfire producing such thermal exposures. It is therefore necessary for these two components (wildfire likelihood and consequences) to be considered when analysing wildfire risk in a more comprehensive manner than frameworks relying only on ignition occurrence (KC et al. 2022), exposure (Haas et al. 2013), burn probability (Meier et al. 2023) or other risk components, as noted by Johnston et al. (2020).
Limitations
The essence of a risk analysis is to use existing knowledge (normally gained through experience) to estimate the safety and environmental threat of a particular hazardous event (Wilson and Crouch 1987), wildland fuel ignition in this case. But because this analysis requires projecting past data into the future, uncertainty in risk estimates depends on the assumptions made in the analysis, which also serve to indicate the limitations of the methodology. This is particularly significant when estimating ignition frequency in Chilean landscapes, because in Chile, most fires are human-related, and predicting ignition trends would thus require modelling human behaviour. However, these human-related ignitions are located near urban areas and roads in Chile, which justifies neglecting the likelihood of wildfires starting outside the study area boundaries and propagating to the infrastructure analysed. Estimating this likelihood would help improve the study area delimitation and the fire modelling process.
In this study, spotting is considered in fire spread modelling, but when a wildfire front arrives at the infrastructure of interest, spotting due to firebrand action becomes a crucial ignition mechanism. It should be noted that, in actual wildfires, thermal radiation and spotting work in parallel; hence, the risk they pose to a target should be addressed separately, and then summed. A vulnerability model considering firebrand attack requires experimental data on ignition probability due to firebrand landing. Some data on ignition probability in terms of incident heat flux can be found in the literature (Fang et al. 2021), but incorporating spotting into this methodology needs a more extensive database, which is as yet not compiled, considering the complex ignition characteristics of structural fuels (Manzello et al. 2020; Abo El Ezz et al. 2022). Promising results have been obtained using experimental apparatuses where variables such as heat flux and wildland fuel properties are fully controlled (Rivera et al. 2021). Ignition probability due to firebrands could thus be quantified in bench-scale configurations and incorporated into this wildfire risk methodology.
Conclusion
The risk posed by wildfires to an electrical substation in central Chile was quantified with a novel methodology developed for assessing risk at the parcel level. FlamMap was used for fire modelling, but the methodology is independent of the fire modelling tool. Two fuel distributions were assumed for the study area to estimate BP and fire behaviour with FlamMap, while two wind conditions (5 and 25 m/s) were imposed in the fire modelling to simulate average and extreme wind conditions. The historic ignition frequency along with probabilities of having burned area, temperature and wind speed larger than historic thresholds were incorporated into event trees to refine the conditional BP calculation, giving the probabilities of normal and extreme fires reaching the infrastructure analysed. The consequences of the wildfire on a proxy fuel for the electrical substation were estimated by considering the modelled fireline intensities and two idealised flaming fronts to estimate the heat flux on the substation. Asset vulnerability was modelled by linking these incident heat fluxes with ignition probability via dose–response curves determined with a probit analysis. Wildfire risk was computed as the product between wildfire likelihood and ignition probability, and the risk of normal and extreme fires was summed for each scenario and simulated landscape considered, and found to be between 10−5 and 10−4 events/year.
Risk analyses are not formulated to make a judgment: this falls to society, by way of a criterion of risk acceptance or tolerance (Wilson and Crouch 1987). An interesting criterion is reducing risk to a level both technically and economically feasible known ‘As Low As Reasonably Practicable’ (ALARP, Pike et al. 2020). In the absence of a current ALARP criterion for wildfires, risk estimates for other activities may serve as comparison. For example, the maximum tolerable risks posed by industrial activities to the public are between 10−4 and 10−6, as established by several national authorities (Muhlbauer 2004). Therefore, the results obtained with the methodology described in the present work are reasonable, beause they are of the same order of magnitude as industrial risks. This comprehensive methodology considers both wildfire occurrence probability and asset vulnerability, thus enabling a systematic analysis of wildfire risk evolution in time (particularly under climate change scenarios) and of risk mitigation measures.
Data availability
The data that support this study will be shared upon reasonable request to the corresponding author.
Declaration of funding
This research was jointly funded by grant ANID SCIA/ANILLO ACT210052, UTFSM through the ‘Programa de Incentivo a la Iniciación Científica’ (PIIC) initiative, and Chilquinta Distribución S.A. Neither supporting source was involved in preparing the data or the manuscript, or the decision to submit for publication. The only role of Chilquinta Distribución S.A. was identifying the electrical substation to be studied owing to its relevance to the company’s operation.
Acknowledgements
The support provided by Mr Jorge Valdivia in producing the input maps for FlamMap simulations is gratefully acknowledged.
References
Abo El Ezz A, Boucher J, Cotton-Gagnon A, Godbout A (2022) Framework for spatial incident-level wildfire risk modelling to residential structures at the wildland–urban interface. Fire Safety Journal 131, 103625.
| Crossref | Google Scholar |
Àgueda A, Pastor E, Pérez Y, Planas E (2010) Experimental study of the emissivity of flames resulting from the combustion of forest fuels. International Journal of Thermal Sciences 49, 543-554.
| Crossref | Google Scholar |
Andrews JD, Dunnett SJ (2000) Event-tree analysis using binary decision diagrams. IEEE Transactions on Reliability 49, 230-238.
| Crossref | Google Scholar |
Alcasena F, Ager AA, Belavenutti P, Krawchuk M, Day MA (2022) Contrasting the efficiency of landscape versus community protection fuel treatment strategies to reduce wildfire exposure and risk. Journal of Environmental Management 309, 114650.
| Crossref | Google Scholar | PubMed |
Aragoneses E, Chuvieco E (2021) Generation and mapping of fuel types for fire risk assessment. Fire 4, 59.
| Crossref | Google Scholar |
Arevalo-Ramirez TA, Fuentes Castillo AH, Reszka Cabello PS, Auat Cheein FA (2021) Single bands leaf reflectance prediction based on fuel moisture content for forestry applications. Biosystems Engineering 202, 79-95.
| Crossref | Google Scholar |
Bal N, Rein G (2011) Numerical investigation of the ignition delay time of a translucent solid at high radiant heat fluxes. Combustion and Flame 158, 1109-1116.
| Crossref | Google Scholar |
Bowman DMJS, Moreira-Muñoz A, Kolden CA, Chávez RO, Muñoz AA, Salinas F, González-Reyes Á, Rocco R, de la Barrera F, Williamson GJ, Borchers N, Cifuentes LA, Abatzoglou JT, Johnston FH (2019) Human–environmental drivers and impacts of the globally extreme 2017 Chilean fires. Ambio 48, 350-362.
| Crossref | Google Scholar | PubMed |
Calkin DE, Cohen JD, Finney MA, Thompson MP (2014) How risk management can prevent future wildfire disasters in the wildland-urban interface. Proceedings of the National Academy of Sciences 111, 746-751.
| Crossref | Google Scholar | PubMed |
Cohen JD (2004) Relating flame radiation to home ignition using modeling and experimental crown fires. Canadian Journal of Forest Research 34, 1616-1626.
| Crossref | Google Scholar |
Cozzani V, Gubinelli G, Antonioni G, Spadoni G, Zanelli S (2005) The assessment of risk caused by domino effect in quantitative area risk analysis. Journal of Hazardous Materials 127, 14-30.
| Crossref | Google Scholar | PubMed |
Egorova VN, Trucchia A, Pagnini G (2022) Fire-spotting generated fires. Part II: The role of flame geometry and slope. Applied Mathematical Modelling 104, 1-20.
| Crossref | Google Scholar |
Fang W, Peng Z, Chen H (2021) Ignition of pine needle fuel bed by the coupled effects of a hot metal particle and thermal radiation. Proceedings of the Combustion Institute 38, 5101-5108.
| Crossref | Google Scholar |
Fernandez-Pello AC (2017) Wildland fire spot ignition by sparks and firebrands. Fire Safety Journal 91, 2-10.
| Crossref | Google Scholar |
Finney MA (2002) Fire growth using minimum travel time methods. Canadian Journal of Forest Research 32, 1420-1424.
| Crossref | Google Scholar |
Finney MA (2005) The challenge of quantitative risk analysis for wildland fire. Forest Ecology and Management 211, 97-108.
| Crossref | Google Scholar |
Finney MA (2006) An overview of FlamMap fire modeling capabilities. In ‘Fuels management – how to measure success: conference proceedings’, 28–30 March 2006, Portland, OR. Proceedings RMRS-P-41. (Eds PL Andrews, BW Butler) pp. 213–220. (USDA Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA)
Finney MA (2021) The wildland fire system and challenges for engineering. Fire Safety Journal 120, 103085.
| Crossref | Google Scholar |
Flannigan MD, Krawchuk MA, De Groot WJ, Wotton BM, Gowman LM (2009) Implications of changing climate for global wildland fire. International Journal of Wildland Fire 18, 483-507.
| Crossref | Google Scholar |
Fonseca J, Tan A, Silva R, Monassi V, Assuncao L, Junqueira W, Mel M (1990) Effects of agricultural fires on the performance of overhead transmission lines. IEEE Transactions on Power Delivery 5, 687-694.
| Crossref | Google Scholar |
Haas JR, Calkin DE, Thompson MP (2013) A national approach for integrating wildfire simulation modeling into wildland–urban interface risk assessments within the United States. Landscape and Urban Planning 119, 44-53.
| Crossref | Google Scholar |
Jazebi S, de León F, Nelson A (2020) Review of wildfire management techniques – Part I: Causes, prevention, detection, suppression, and data analytics. IEEE Transactions on Power Delivery 35, 430-439.
| Crossref | Google Scholar |
Johnston JM, Wooster MJ, Lynham TJ (2014) Experimental confirmation of the MWIR and LWIR grey body assumption for vegetation fire flame emissivity. International Journal of Wildland Fire 23, 463-479.
| Crossref | Google Scholar |
Johnston LM, Wang X, Erni S, Taylor SW, McFayden CB, Oliver JA, Stockdale C, Christianson A, Boulanger Y, Gauthier S, Arseneault D, Wotton BM, Parisien MA, Flannigan MD (2020) Wildland fire risk research in Canada. Environmental Reviews 28, 164-186.
| Crossref | Google Scholar |
KC Ujjwal, Hilton J, Garg S, Aryal J (2022) A probability-based risk metric for operational wildfire risk management. Environmental Modelling and Software 148, 105286.
| Crossref | Google Scholar |
Khakzad N, Dadashzadeh M, Reniers G (2018) Quantitative assessment of wildfire risk in oil facilities. Journal of Environmental Management 223, 433-443.
| Crossref | Google Scholar | PubMed |
Keane RE, Reinhardt ED, Scott J, Gray K, Reardon J (2005) Estimating forest canopy bulk density using six indirect methods. Canadian Journal of Forestry Research 35, 724-739.
| Crossref | Google Scholar |
Lautenberger C (2017) Mapping areas at elevated risk of large-scale structure loss using Monte Carlo simulation and wildland fire modeling. Fire Safety Journal 91, 768-775.
| Crossref | Google Scholar |
Liu Y, Liu Y, Fu J, Yang CE, Dong X, Tian H, Tao B, Yang J, Wang Y, Zou Y, Ke Z (2021) Projection of future wildfire emissions in western USA under climate change: contributions from changes in wildfire, fuel loading and fuel moisture. International Journal of Wildland Fire 31, 1-13.
| Crossref | Google Scholar |
Manzello SL, Suzuki S, Gollner MJ, Fernandez-Pello AC (2020) Role of firebrand combustion in large outdoor fire spread. Progress in Energy and Combustion Science 76, 100801.
| Crossref | Google Scholar | PubMed |
Maranghides A, Link E, Nazare S, Hawks S, McDougald J, Quarles S, Gorham D (2022) WUI Structure/parcel/community fire hazard mitigation methodology. NIST Technical Note 2205. (National Institute of Standards and Technology: Gaithersburg, MD, USA) 10.6028/NIST.TN.2205
McWethy DB, Pauchard A, García RA, Holz A, González ME, Veblen TT, Stahl J, Currey B (2018) Landscape drivers of recent fire activity (2001-2017) in south-central Chile. PLoS One 13(8), e0201195.
| Crossref | Google Scholar | PubMed |
Meier S, Strobl E, Elliott RJR, Kettridge N (2023) Cross-country risk quantification of extreme wildfires in Mediterranean Europe. Risk Analysis 43, 1745-1762.
| Crossref | Google Scholar | PubMed |
Miller C, Ager AA (2013) A review of recent advances in risk analysis for wildfire management. International Journal of Wildland Fire 22, 1-14.
| Crossref | Google Scholar |
Morandini F, Perez-Ramirez Y, Tihay V, Santoni PA, Barboni T (2013) Radiant, convective and heat release characterization of vegetation fire. International Journal of Thermal Sciences 70, 83-91.
| Crossref | Google Scholar |
Moreira F, Ascoli D, Safford H, Adams MA, Moreno JM, Pereira JMC, Catry FX, Armesto J, Bond W, González ME, Curt T, Koutsias N, McCaw L, Price O, Pausas JG, Rigolot E, Stephens S, Tavsanoglu C, Vallejo VR, Van Wilgen BW, Xanthopoulos G, Fernandes PM (2020) Wildfire management in Mediterranean-type regions: paradigm change needed. Environmental Research Letters 15, 011001.
| Crossref | Google Scholar |
Moritz MA, Batllori E, Bradstock RA, Gill AM, Handmer J, Hessburg PF, Leonard J, McCaffrey S, Odion DC, Schoennagel T, Syphard AD (2014) Learning to coexist with wildfire. Nature 515, 58-66.
| Crossref | Google Scholar | PubMed |
Mudan KS (1984) Thermal radiation hazards from hydrocarbon pool fires. Progress in Energy and Combustion Science 10, 59-80.
| Crossref | Google Scholar |
Oliveira S, Rocha J, Sá A (2021) Wildfire risk modeling. Current Opinion in Environmental Science & Health 23, 100274.
| Crossref | Google Scholar |
Oom D, de Rigo D, Pfeiffer H, Branco A, Ferrari D, Grecchi R, Artés-Vivancos T, Houston Durrant T, Boca R, Maianti P, Libertá G San-Miguel-Ayanz J, et al. (2022) ‘Pan-European wildfire risk assessment.’ (Publications Office of the European Union, EUR 31160 EN: Luxembourg) 10.2760/9429
Papakosta P, Xanthopoulos G, Straub D (2017) Probabilistic prediction of wildfire economic losses to housing in Cyprus using Bayesian network analysis. International Journal of Wildland Fire 26, 10-23.
| Crossref | Google Scholar |
Parisien MA, Dawe DA, Miller C, Stockdale CA, Armitage BO (2019) Applications of simulation-based burn probability modelling: a review. International Journal of Wildland Fire 28, 913-926.
| Crossref | Google Scholar |
Parot R, Rivera JI, Reszka P, Torero JL, Fuentes A (2022) A simplified analytical model for radiation dominated ignition of solid fuels exposed to multiple non-steady heat fluxes. Combustion and Flame 237, 111866.
| Crossref | Google Scholar |
Pastor E, Zárate L, Planas E, Arnaldos J (2003) Mathematical models and calculation systems for the study of wildland fire behaviour. Progress in Energy and Combustion Science 29, 139-153.
| Crossref | Google Scholar |
Pausas JG, Keeley JE (2021) Wildfires and global change. Frontiers in Ecology and the Environment 19, 387-395.
| Crossref | Google Scholar |
Pacheco AP, Claro J, Fernandes PM, de Neufville R, Oliveira TM, Borges JG, Rodrigues JC (2015) Cohesive fire management within an uncertain environment: a review of risk handling and decision support systems. Forest Ecology and Management 347, 1-17.
| Crossref | Google Scholar |
Pike H, Khan F, Amyotte P (2020) Precautionary Principle (PP) versus As Low As Reasonably Practicable (ALARP): which one to use and when. Process Safety and Environmental Protection 137, 158-168.
| Crossref | Google Scholar |
Planas E, Paugam R, Àgueda A, Vacca P, Pastor E (2023) Fires at the wildland–industrial interface. Is there an emerging problem? Fire Safety Journal 141, 103906.
| Crossref | Google Scholar |
Radočaj D, Jurišić M, Gašparović M (2022) A wildfire growth prediction and evaluation approach using Landsat and MODIS data. Journal of Environmental Management 304, 114351.
| Crossref | Google Scholar | PubMed |
Reszka P, Fuentes A (2014) The Great Valparaiso Fire and fire safety management in Chile. Fire Technology 51, 753-758.
| Crossref | Google Scholar |
Rivera J, Hernández N, Consalvi JL, Reszka P, Contreras J, Fuentes A (2021) Ignition of wildland fuels by idealized firebrands. Fire Safety Journal 120, 103036.
| Crossref | Google Scholar |
Sabi FZ, Terrah SM, Mosbah O, Dilem A, Hamamousse N, Sahila A, Harrouz O, Boutchiche H, Chaib F, Zekri N, Kaiss A, Clerc J, Giroud F, Viegas DX (2021) Ignition/non-ignition phase transition: a new critical heat flux estimation method. Fire Safety Journal 119, 103257.
| Crossref | Google Scholar |
Sathaye JA, Dale LL, Larsen PH, Fitts GA, Koy K, Lewis SM, de Lucena AFP (2013) Rising temps, tides, and wildfires: assessing the risk to California’s energy infrastructure from projected climate change. IEEE Power and Energy Magazine 11, 32-45.
| Crossref | Google Scholar |
Scott JH, Burgan RE (2005) Standard fire behavior fuel models: a comprehensive set for use with Rothermel’s surface fire spread model. General Technical Report RMRS-GTR-153. (USDA Forest Service, Rocky Mountain Research Station) 10.2737/RMRS-GTR-153
Scott JH, Thompson MP, Calkin DE (2013) A wildfire risk assessment framework for land and resource management. General Technical Report RMRS-GTR-315. (USDA Forest Service, Rocky Mountain Research Station) 10.2737/RMRS-GTR-315
Shahparvari S, Fadaki M, Chhetri P (2020) Spatial accessibility of fire stations for enhancing operational response in Melbourne. Fire Safety Journal 117, 103149.
| Crossref | Google Scholar |
Sullivan AL (2009) Wildland surface fire spread modelling, 1990-2007. 1: Physical and quasi-physical models. International Journal of Wildland Fire 18, 349-368.
| Crossref | Google Scholar |
Sullivan AL, Ellis PF, Knight IK (2003) A review of radiant heat flux models used in bushfire applications. International Journal of Wildland Fire 12, 101-110.
| Crossref | Google Scholar |
Thompson MP, Zimmerman T, Mindar D, Taber M (2016) Risk terminology primer: basic principles and a glossary for the wildland fire management community. General Technical Report RMRS-GTR-349. (USDA Forest Service, Rocky Mountain Research Station: Fort Collins, CO) 10.2737/RMRS-GTR-349
Tedim F, Leone V, Amraoui M, Bouillon C, Coughlan MR, Delogu GM, Fernandes PM, Ferreira C, McCaffrey S, McGee TK, Parente J, Paton D, Pereira MG, Ribeiro LM, Viegas DX, Xanthopoulos G (2018) Defining extreme wildfire events: difficulties, challenges, and impacts. Fire 1, 9.
| Crossref | Google Scholar |
Vacca P, Caballero D, Pastor E, Planas E (2020) WUI fire risk mitigation in Europe: a performance-based design approach at home-owner level. Journal of Safety Science and Resilience 1, 97-105.
| Crossref | Google Scholar |
Villacrés J, Arevalo-Ramirez T, Fuentes A, Reszka P, Auat Cheein F (2019) Foliar moisture content from the spectral signature for wildfire risk assessments in Valparaíso–Chile. Sensors 19, 5475.
| Crossref | Google Scholar | PubMed |
Wagenbrenner NS, Forthofer JM, Lamb BK, Shannon KS, Butler BW (2016) Downscaling surface wind predictions from numerical weather prediction models in complex terrain with WindNinja. Atmospheric Chemistry and Physics 16, 5229-5241.
| Crossref | Google Scholar |
Waseem M, Manshadi SD (2020) Electricity grid resilience amid various natural disasters: challenges and solutions. The Electricity Journal 33, 106864.
| Crossref | Google Scholar |
Wilson R, Crouch EAC (1987) Risk assessment and comparisons: an introduction. Science 236, 267-270.
| Crossref | Google Scholar | PubMed |
Yang L, Jones BF, Yang SH (2007) A fuzzy multi-objective programming for optimization of fire station locations through genetic algorithms. European Journal of Operational Research 181, 903-915.
| Crossref | Google Scholar |
Zárate L, Arnaldos J, Casal J (2008) Establishing safety distances for wildland fires. Fire Safety Journal 43, 565-575.
| Crossref | Google Scholar |


