Sand and fire: applying the sandpile model of self-organised criticality to wildfire mitigation†
Joshua E. Gang A # , Wanqi Jia B # and Ira A. Herniter C *
C *
A Google LLC, Mountain View, CA 94043, USA.
B University High School, Irvine, CA 92612, USA.
C Department of Plant Biology, Rutgers University, 59 Dudley Road, Room 379, New Brunswick, NJ 08901, USA.
International Journal of Wildland Fire 31(9) 847-856 https://doi.org/10.1071/WF22017
Submitted: 5 May 2021 Accepted: 20 July 2022 Published: 30 August 2022
© 2022 The Author(s) (or their employer(s)). Published by CSIRO Publishing on behalf of IAWF. This is an open access article distributed under the Creative Commons Attribution 4.0 International License (CC BY)
Abstract
Background: Prescribed burns have been increasingly utilised in forest management in the past few decades. However, their effectiveness in reducing the risk of destructive wildfires has been debated. The sandpile model of self-organised criticality, first proposed to model natural hazards, has been recently applied to wildfire research for describing a negative linear relationship between the logarithm of fire size, in area burned, and the logarithm of fire incidence number of that size.
Aims: We demonstrate the applicability of the sandpile model to an understanding of wildfire incidence and its trend with interested factors, such as prescribed burns.
Methods: We leverage the sandpile model to perform a series of simulations, along with comparisons to historical wildfire data in three American states: Florida, California, and Georgia.
Key results: Both simulated and historical data indicate that increased prescribed burning is associated with lowered incidence of large wildfires.
Conclusions: Our study justifies the application of the sandpile model to wildfire research and establishes a novel method for facilitating the investigation of potential risk factors of wildfires.
Implications: The sandpile model may be utilised for the development of optimal strategies for prescribed burning. An R-script for sandpile model simulation is available for further wildfire investigation.
Keywords: California, fire management, Florida, Georgia, prescribed burn, sandpile model, self-organised criticality, United States of America, wildfire.
Introduction
Wildfire is of increasing risk to people and landscapes as anthropogenic climate change progresses (IPCC 2018). The 2018 Camp Fire in Northern California was the largest and most destructive fire in California history, burning 153 336 acres (620.5 km2) and responsible for 85 fatalities (Cal Fire 2019). Even if global warming can be limited to just 1.5°C above preindustrial levels, the incidence and intensity of wildfires is expected to increase dramatically (Settele et al. 2015).
While wildfires can be deadly and destructive, fire also plays a major role in promoting ecological diversity and maintaining sustainability in bio-systems. For example, regular fires result in increased diversity of bat species (Steel et al. 2019), and some plant species require fire treatment of their seeds for germination (Keeley 1987). Efforts to prevent as many fires as possible over the past century by federal and state agencies in the United States have resulted in unhealthy buildups of brush and dead wood littering forest floors, promoting more intense and destructive fires (Minnich and Chou 1997; Haugo et al. 2019; Roos et al. 2020). Prescribed fires, as defined by the National Park Service (2020), are intentionally set, low intensity fires, which are used to manage land. The main hypothetical function of prescribed burning is to reduce the ground litter, which serves as fuel driving the most destructive wildfires. There is evidence to show that regularly prescribed burning of forests may be highly beneficial by, among other effects, maintaining critical species habitat (Russell et al. 1999). Other research, however, has claimed that the association between previous fires and reduction of the area of wildfire does not generally hold in global case-studies from a range of biomes (Bradstock et al. 2012; Price et al. 2012, 2015). The hypothesis that prescribed burns can significantly reduce the risk of destructive wildfires needs to be further tested using properly selected models, in which other covariates are well controlled.
The sandpile model of self-organised criticality was introduced by Bak et al. (1987). In this model, the main ingredients include (1) slow driving towards some instability and (2) a mechanism to relax tension locally and partially. The model consists of an imagined plane organised as a grid, in which a large number of individual grains of sand are dropped onto the plane in a random fashion. In each site of the grid, grains of sand can be placed. Fig. 1 contains an example of such a grid. Once the number of grains reaches a predefined threshold, the pile in the site collapses, transferring its collected grains to neighbouring sites in the cardinal directions. If any of those sites then reach the threshold, the piles in the adjacent sites collapse and transfer their collected grains to their respective neighbouring sites. When placing a sand grain causes a pile collapse on a site, this collapse can propagate across the plane until the plane reaches equilibrium without affecting sites on the borders of the plane, or until the propagating collapse impacts on the border(s) to cause an avalanche – an event of interest in the process. The size of an event (avalanche) is represented by the number of hit(s) on the boundaries, i.e. a propagating collapse that reaches the borders of the plane. Testing this model has shown that the size of avalanches and the frequency of avalanches of that size follows a power-law, which takes the following form:

where Ac is the size of collapse (the number of hit(s) on the plane boundaries) and f(Ac) is the corresponding frequency (Bak et al. 1987; Cajueiro and Andrade 2010). In examining this effect, it has been found that numerous real-world phenomena follow this same pattern, including earthquake power (Bak and Tang 1989), solar X-ray flares (Crosby et al. 1993), and even evolutionary rates (Sneppen et al. 1995). Of particular relevance, the sandpile model has been successfully applied to natural wildfire systems to demonstrate the relationship between wildfire sizes and their frequencies (Ricotta et al. 1999; Malamud et al. 1998; Yoder et al. 2011). The analysis of historical wildfire data from ‘natural experiments’ using the sandpile model showed that small early season fires, left to burn to natural extinction, contribute to a region’s natural fire resistance (Yoder et al. 2011). This conclusion suggests that prescribed burning likely provides additional resistance.

|
Ishii et al. (2002) showed that agent choice, or anthropogenic intervention, had a significant impact on the size of the avalanches in counterintuitive ways. When the agent’s intention is to create a large avalanche, the average avalanche size is decreased relative to the random deposition. However, if the agent’s intention is to cause the smallest possible avalanche, the result is a major increase in the chances of triggering exceptionally large avalanches. The relevance between the sandpile model and forest fires is that the buildup of fuel functions like the buildup of sand, releasing in critical events. The agent’s intention effect in the sandpile experiment is in agreement with the observation in anthropogenic wildfire management, where aggressively suppressing small early season fires can facilitate conditions that significantly increase the rate of large and destructive events (Yoder et al. 2011). To expand the conceptual model, the setting of prescribed fires can be considered analogous to an agent’s intention to cause a collapse of the sandpile. Here, for the first time, we leverage this powerful model to quantify the effect of prescribed fire, a major intervention of forest management, on the incidence of wildfires. A series of simulations and a comprehensive analysis of historical data of forest fires from multiple states in the United States demonstrate that prescribed burns can significantly reduce the incidence of especially destructive wildfires.
Materials and methods
Simulation
Basic sandpile model
The basic sandpile model for describing natural wildfires without anthropogenic effects is defined as follows:
A sand grain drops onto a random position on a L × L square grid, for example, a 20 × 20 grid.
Each position can hold up to three sand grains. If a position has more than three sand grains, the sandpile will collapse and these sand grains will be evenly distributed to cardinally adjacent sites.
A collapse of a sand pile at one site can cause collapse at adjacent sites, leading to a propagation across the plane until the grid reaches equilibrium.
A border hit, referred to as an ‘avalanche’ or ‘event of interest,’ is when a propagating collapse causes a sand pile at any edge site to collapse. The number of border hits is recorded as the size of the event. Any sand grains which would fall off the edge are lost.
Simulation process: repeat steps (i) through (iv) for a large number of times, for example, 64 000 sequentially dropped sand grains onto the grid.
The observed event sizes and their corresponding frequencies during the simulation process are summarised for further analysis.
The random drops of sand grains represent net fuel deposition, including both biomass accumulation through plant growth and removal through decomposition, whereas local collapses may be regarded as small-scale natural wildfires in the areas where too much fuel has been piled up. When the tension due to fuel accumulation keeps being built up, a local collapse (wildfire) may be propagated very quickly, yielding an avalanche (destructive wildfire). A simple example of implementing the basic sandpile model (dropping a single sand grain) on a 5 × 5 square grid is depicted in Fig. 1. In this case, dropping a sand grain to the centre position of a loaded grid causes a series of collapses, which eventually leads to an event of size 1.
Sandpile model with intervention
We incorporated the periodic prescribed fires (anthropogenic wildfire intervention) into the basic sandpile model by simply emptying the positions with three sand grains (risky pileup) at different time intervals, i.e. between dropping every 2, 4, 5, 8, 10, 16, 20, 25, 50, 100, 200, 400, 800, 1600, 3200, 6400, and 12 800 sand grains, as well as a system with no interventions or no burning (NB). These numbers were chosen to make the total number of sand grains, 64 000, divisible by each. This setting in the simulation can be considered analogous to a planned prescribed burn in a region with various frequencies, from high to low.
Historical fire data
We used fire data from Florida, California, and Georgia. Wildfire data from Florida were available from the Florida Forest Service (Florida Fire Service 2020; http://fireinfo.fdacs.gov/fmis.publicreports), with additional data provided by the Prescribed Fire Manager of the Florida Forest Service, John Saddler (pers. comm., 18 December 2020). Wildfire data from California were available from CalFire (https://www.fire.ca.gov/stats-events/) as were prescribed fire data (https://gis.data.cnra.ca.gov/). Wildfire and prescribed fire data from Georgia were provided by Fire Chief Frank Sorrells of the Georgia Forestry Commission (pers. comm., 21 October 2020). The fire incidence data from each state were divided for each year into seven class sizes, A–G, as defined by the federal government. We did not use Class A fires (<0.25 acres [<0.001 km2]) in the analysis as they are likely heavily underreported (Ricotta et al. 1999) and so the numbers associated with this class in the data severely underestimate their true incidence. The maximum fire size in each class was used to represent that class for the subsequent analysis. Classes B, C, D, E, and F were considered to be 9.9, 99, 299, 999, and 4999 acres, respectively (0.04. 0.40, 1.21, 4.04, and 20.2 km2, respectively). Class G, which included wildfires at least 5000 acres (>20.2 km2), was set to be 10 000 acres (40.47 km2) for ease of analysis. Prescribed and wildfire data were available for Florida for 1993–2019, for California for 1963–2019, and for Georgia for 1995–2020, all inclusive. Additional wildfire data, but no prescribed fire data, were available for Florida for 1981–1992, inclusive. Complete data can be found in Supplementary Table S1.
Log10 transformation based on sandpile model of self-organised criticality
For each state (Florida, California, and Georgia), we divided yearly data into quintiles based on the number of acres subject to prescribed burning that year. The breakdown of the data from all three states is shown in Table 1. Based on the theorem described in the sandpile model of self-organised criticality by Bak et al. (1987), we took the log10 of the average number of fires in each fire size class for each category and plotted them against the log10 of the maximum fire size in acres in that class for that category. For each plot we calculated the slope of the fitted linear regression line as determined by the sum of least squares, which represents the relative risk for destructive fires. The estimated values and standard errors of these slopes were analysed for model comparisons and for hypothesis testing.

|
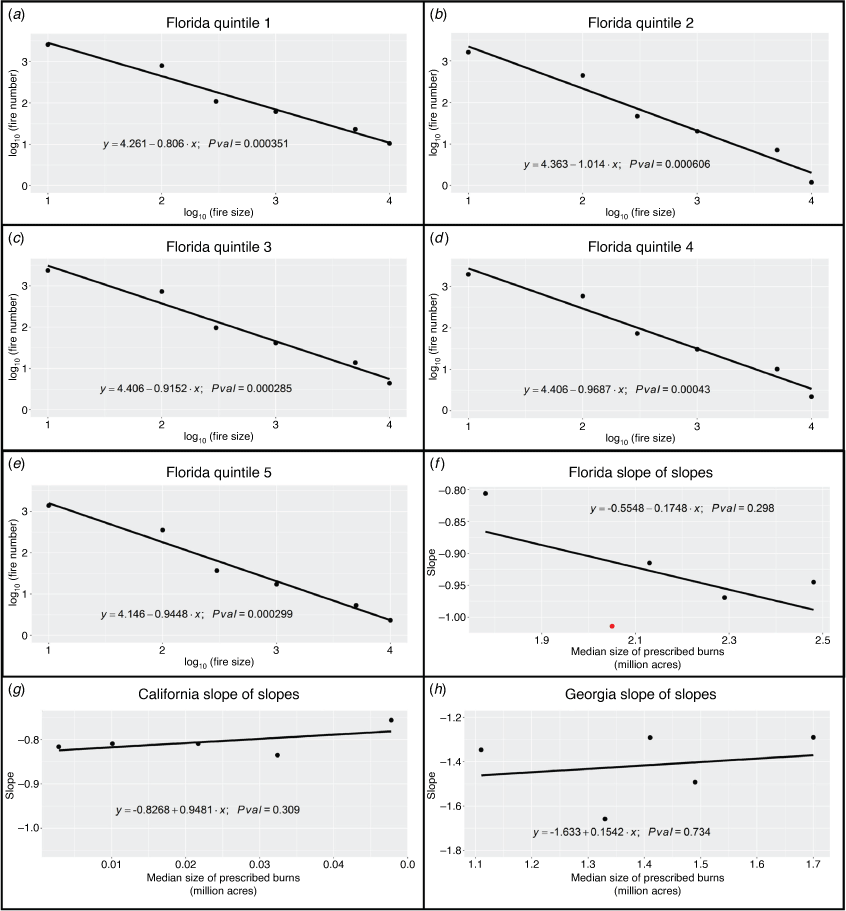
As an example, we demonstrate the method using the first quintile of the data from Florida (Table 1). As noted above, we do not make use of the Class A fires. For Classes B–G, we take the average number of fires in that class size and determine the log10 of the value. For Class B fires in the first quintile of Florida data, that would be an average of 2572.67 fires per year, the log10 of which is 3.41. For Class C fires in the first quintile of Florida data, that would be an average of 795.83 fires per year, the log10 of which is 2.90, and so on, for the remaining fire classes. To obtain the slope, the log10 of the number of fires in a class is plotted against the log10 of the maximum fire size of the class. For Class B fires, that would be log10 (9.9), or 0.99957; for Class C fires, that would be log10 (99.9), or 1.99957, and so on. The slope taken from this graph (Fig. 2a) is −0.806. Once completed for each quintile, the slope of slopes was determined (Fig. 2f).
Comparison of data with and without prescribed fires
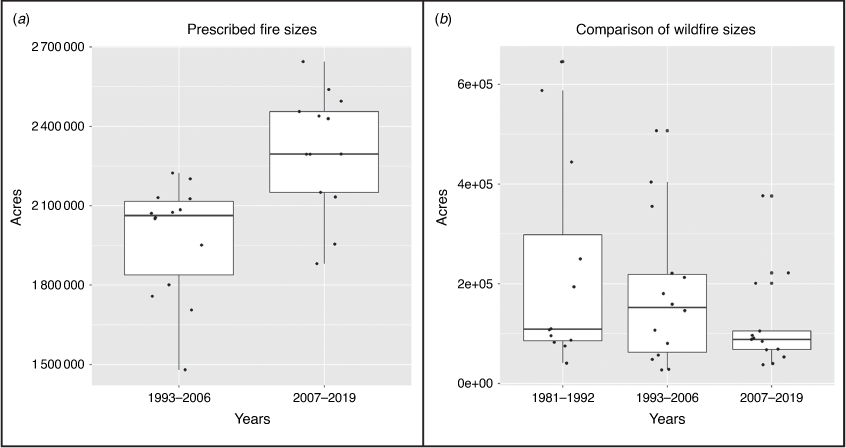
The Florida data consist of data without the record of prescribed fires (1981–1992) and data with the record of prescribed fires (1993–2019). To compare subsets of fire incidence data in Florida, we split the data with the record of prescribed fires into first (1993–2005) and second (2006–2019) halves, yielding three consecutive periods for comparisons: period I (1981–1992), period II (1993–2005), and period III (2006–2019). We then plotted the data from each subset in a box plot for visual examination (Fig. 3).
We used a two-sample t-test of analysis of variance (ANOVA) to compare the Florida data with and without the record of prescribed fires. The nominal P < 0.05 was used to claim a significant difference between any comparison.
Analysis of slopes
We conducted the pairwise comparison of slopes of the fitted regression lines for various categories using the pooled t-test. Suppose we would like to test whether two slopes are identical, i.e. Ho: b1 = b2 vs Ha: b1 ≠ b2, where b1 and b2 are slopes estimated from two linear regression models, respectively. Under the null hypothesis, the t-test statistic

follows a t distribution with degree of freedom n1 + n2 − 4, where  and
and  represent the standard errors for two slopes and n1 and n2 are the sample sizes for two models, respectively. The R script, named ‘TwoSlope.ttest’, for implementing the comparison of two slopes of fitted regression lines, is available in Supplementary File S1.
represent the standard errors for two slopes and n1 and n2 are the sample sizes for two models, respectively. The R script, named ‘TwoSlope.ttest’, for implementing the comparison of two slopes of fitted regression lines, is available in Supplementary File S1.
We used simple linear regression to analyse the association between the estimated slopes (risk of destructive wildfire) and the average acres per year that were subject to prescribed burn in various categories.
Results
Simulated study
Following the simulation strategy described in Materials and Methods, we randomly dropped a total of 64 000 sand grains onto a 20 × 20 grid in each simulation scenario and monitored the fire sizes (number of border hits) and their frequencies (numbers of occurrence) for subsequent analysis and comparison. Graphs showing the relationship between fire sizes and the logarithm of their frequencies based on a single simulation when prescribed burns (or interventions) were administered at various intervals can be found in Supplementary Fig. S1. This simulation scheme was repeated three times and the mean and standard deviation of slopes for each scenario are summarised in Fig. 4. When prescribed fires were sparsely administered, i.e. for every 12 800, 6400, 3200, 1600, or 800 sand drops, the estimated values for their slopes did not differ from the slope when no prescribed fire was applied (NB). While passing a threshold of every 800 sand drops, the slope values decreased in an approximately linear fashion as the frequency of prescribed fires increased. This indicated that the chance of destructive wildfires can be substantially reduced if prescribed burns are administered more often. When prescribed fires were used more often than every 50 sand drops, there were not consistently at least three differently sized events, so slopes could not be confidently determined, and the slopes for those data points were not used. Only when prescribed burns were administered every 200 sand drops or more sparsely did events of at least size 5 (at least five sand grains hitting the borders) occur consistently.

|
Comparison of data with and without record of prescribed fires
The Florida data consist of data without the record of prescribed fires (period I, 1981–1992) and data with the record of prescribed fires (1993–2019). We split the data with the record of prescribed fires into first (period II, 1993–2006) and second (period III, 2007–2019) halves, yielding three consecutive periods for comparison. Fig. 3a indicates that there was a significant increase in the total size of prescribed burns between periods II and III. We assume that the undocumented prescribed fires in period I (1981–1992) were significantly less than in periods II or III. The comparisons of the total areas burnt yearly between these three periods are shown by boxplot (Fig. 3b). Although no significant difference in means was detected among these three periods, there is a clear trend in the reduction of giant wildfires as the prescribed burns have been progressively introduced to forest management.
Analysis of slopes calculated from sandpile model
For the log10 transformed Florida data, the scatter plots with the best fitted linear regression lines for the five quintiles are shown in Fig. 2a–e, with the slope of slopes shown in Fig. 2f. The intersects, estimated slopes, standard errors, and P-values are shown in Table 2. We carried out a pairwise comparison among slopes of the fitted regression lines for various categories using the log10 transformed Florida data, the results of which are shown in Table 3. Due to the limited sample size (n = 6) in each category, only marginally significant differences (0.05 < P < 0.1) have been detected between quintiles 1 and 2 and between quintiles 1 and 4. Similarly, due to the limited sample size, the regression of these slopes on the median land areas that were subject to prescribed burn in five categories only showed a trend of negative association (slope of −0.17 with P = 0.298, Fig. 2), suggesting that increased prescribed burning tended to reduce the risk of destructive wildfires. Note that the magnitude of the slope for quintile 2, coloured red in Fig. 2, appeared to be much lower than expected. Possible explanations for this outlier slope associated with the data in quintile 2 are proposed in the Discussion.

|

|
For the log10 transformed California data, the slope of slopes for the five quintiles is shown in Fig. 2g. The intercepts, the slopes estimated for these five categories, their standard errors, and P-values are shown in Table 4. We did not carry out a pairwise comparison among slopes for California data since these slope values were close to one another with a slope of slopes that was nearly flat. The slope of the line of best fit in all quintiles ranged from −0.84 to −0.75, with an average P-value of 0.00023. Similar results were obtained when investigating the Georgia data, the slope of slopes of which is shown in Fig. 2h, in which the slopes of the line of best fit in all quintiles ranged from −1.66 to −1.29 with an average P-value of 0.0066. The intercepts, the slopes estimated for these five categories, their standard errors, and P-values are shown in Table 5. The differences between the results from analysing Florida data and those from California or Georgia data are likely due to greatly varied overall size of prescribed burns in these states (Table 6). Scatter plots with the best fitted linear regression lines for the five categories in both California and Georgia can be found in Supplementary Figs S2 and S3.

|

|

|
Discussion
The analysis of our simulated data (Fig. 4, Supplementary Fig. S2) as well as the historical data for Florida (Figs 3 and 2a–f), California (Fig. 2g, Supplementary Fig. S3), and Georgia (Fig. 2h, Supplementary Fig. S3), supports the previous claim that the behaviour of natural wildfires can be well described using the sandpile model (Ricotta et al. 1999; Malamud et al. 1998; Yoder et al. 2011). For the first time, we used both simulated data (Fig. 4) and historical forest wildfire data (Fig. 2) to demonstrate that the sandpile model may also be used to test whether prescribed fires reduce the risk of destructive wildfires. These results suggested that the application of this model may be expanded to investigate the influence of other wildfire drivers, such as temperature, rainfall, atmospheric circulation patterns, and socioeconomic factors (Pereira et al. 2005; Costa et al. 2011). To facilitate such research, we developed an R program, which researchers can use to study the association between wildfire outcome and any factor of interest using simulations. Outcomes of natural wildfires are often the results of influences from multiple factors. For this reason, the current version of the simulation program is not sufficiently powerful to handle the complexity due to the potential interactions between factors, for example, temperature and rainfall in a specific landform. Since prescribed burns are an anthropogenic intervention rather than a natural condition, this may be regarded as a factor independent of other drivers. Therefore, the current simulation program is suitable for studying the relatedness between prescribed fires and outcomes of wildfires. In future studies, we intend to develop advanced simulation schemes to extend the sandpile model for analysing data with interacting factors for wildfires or other complications, such as fuel decomposition, which would reduce the fuel load in a cell, but could not be represented as a collapse.
Previous studies applied mathematical models to temporal and spatial data of local fires (microenvironment) and identified a strong association between past and current fires, indicating that recently burned areas may be less flammable than those not recently burned (Malamud et al. 2005; Bradstock et al. 2012; Price et al. 2012, 2015). However, it is challenging to expand this strategy to estimate the general effect of recent fires on future fires at a much larger scale, such as statewide or nationwide levels, for two reasons: (1) various regions are highly heterogeneous in many aspects, including landscape, climate, fire history, and anthropogenic effects; and (2) existing wildfire database statistics often have low spatial and/or temporal resolution of their data sets. Therefore, a model that may be overfitted to local data likely has limited predictive ability when applied to other regions with different microfeatures. In contrast, the sandpile model is intentionally at a broader scale, so as to mitigate potential issues due to overfitting to local conditions.
In our study, we adapted the sandpile model to study wildfires at statewide scale, in which the connection between past and current fires, and the gradual buildup of fuel between, are well represented by local collapses of sand piles, redistribution of the collapsed sand grains, and rebuilding of sand piles at these loci. One major advantage of using the power-law represented by the sandpile model to describe natural hazards, including earthquakes, asteroid impacts, volcanic eruptions, and wildfire (the subject of this manuscript), is leveraging a simple model to account for complex systems which are determined by many interacting factors. Note the rate of fuel build-up varies geographically and is likely to be different in, for example, Florida and California, reflecting their respective natural resistances to wildfire. Our simulation suggests that such baseline features of Florida and California would likely be reflected by the slopes of fire categories when no prescribed fires (NB) were applied in the two states. Indeed, given the wide range of environments in each state there are differences in areas within the states in terms of resistance to wildfire. Further research is required to develop the model to account for ecological differences in different locations.
The simulation shows a correlation between an increase in prescribed burning and a decrease in the slope value, i.e. a more negative slope (Fig. 4), given that prescribed fires are administered within a certain range. Only when prescribed burns were administered following every 200 grains of sand dropped, or less often, did events of at least size 5 (at least five sand grains hitting the borders) occur regularly. This result indicates that (1) insufficient intervention fires are not effective in reducing the risk of gigantic wildfires and additionally that (2) excessive burns cannot further increase such an effect, resulting in wasted cost and effort. These conclusions are supported by the analysis of wildfire data in multiple states: Florida, California, and Georgia. The slope of the Florida first quintile is −0.81, the second −1.01, the third −0.92, the fourth −0.97, and the fifth −0.94. The negative slope of slopes observed in Florida data demonstrates that increasing the number of acres subject to prescribed burning has substantially reduced the incidence of destructive wildfires. This tracks with the increasing use of prescribed burning in Florida over the past 27 years, while use has remained essentially static in California and Georgia at low and high levels, respectively. From 1993 to 2002, an average of about 1.9 million acres (7689 km2) in Florida were subject to prescribed burning, while from 2010 to 2019 an average of about 2.3 million acres (9308 km2) were subject, an increase of ~20%. Compared to Florida, the intervention fires appeared to be far from enough in California to be effective in preventing gigantic wildfires. As shown in Table 6, the median prescribed burn in California was dramatically less than that in Florida, while the Georgia prescribed fire data for the fifth quintile were comparable to the first quintile in Florida. It may be that California is in the ‘low burn’ section of Fig. 4, while Georgia is in the ‘high burn’ section. These statistics of historical prescribed fires may explain why, unlike the result from Florida data, the slopes for five quintiles were invariant when California or Georgia data were analysed.
Interestingly, the slope of the log10 of fire incidence of the second quintile in Florida is far lower than would be expected based on the trend present in the other data (Fig. 2f). The slope of the second quintile is −1.01, lower even than the fifth quintile, which had a slope of −0.94. It may be that the major dip indicates the presence of an optimal level of prescribed burning. The possible presence of optima requires further study to determine if judicious application of prescribed burning can be more effective, both in terms of cost and effort, than generally increasing the use of prescribed burning. Our data and conclusions warrant future research involving the use of this model to develop the optimal strategy, with both geographic and temporal considerations, for prescribing fires which can achieve the maximum efficacy of suppressing giant wildfires with minimum possible human efforts and operative costs.
In all examined fire incidence data, Class A fires (<0.25 acres [0.001 km2]) were greatly underrepresented relative to expectations based on the modelling. This is likely because many, if not most, small fires are not reported to statewide agencies and may be put out by landowners or simply run out of fuel and sputter out without intervention. The national fire policy in the United States from the late 1800s has been fire suppression, leading to significant fire deficits in the 20th century. This fire suppression policy has been demonstrably linked to major increases in fire intensity, especially in the 21st century (Haugo et al. 2019; Roos et al. 2020). The increased incidence of especially destructive fires could be due to buildup of debris on the forest floor. It should be noted that not all the blame for increased fire intensity is due to fire suppression; indeed, global climate change has greatly stressed forests by shifting rainfall patterns, causing prolonged droughts (Stephens et al. 2018) and opportunistic infestations, such as by bark beetles (Preisler et al. 2017), leading to large stands of dead trees, which fuel the more intense fires. The fire regime in California can be compared to the fire regime in Florida, which has made aggressive use of prescribed burns. The results show that not only does the fire incidence track the expected negative linear log10 line, but that in years in which more acreage was subject to prescribed burns the slope of the line of best fit of the log10 line is more negative, indicating across the board reductions in larger and more destructive fires.
Data availability
Complete wildfire and prescribed fire data can be found in Supplementary Table S1. The R script, named ‘TwoSlope.ttest’, for implementing the comparison of two slopes of fitted regression lines, is available in Supplementary File S1. The R script, named ‘Sandpile_wildfire’, for implementing the simulations of wildfire model with an impacting factor, is available in Supplementary File S2.
Conflicts of interest
The authors declare no conflicts of interest.
Declaration of funding
This research did not receive any specific funding.
Supplementary material
Supplementary material is available online.
Acknowledgements
We would like to thank Dr. Zhenyu Jia at University of California Riverside for his insightful comments and suggestions during our discussion on this project, John Saddler of the Florida Forest Service and Frank Sorrells of the Georgia Forestry Commission for providing fire data, and John H. Miller for bringing the phenomenon of self-organised criticality to our attention.
References
Bak P, Tang C (1989) Earthquakes as a Self-Organized Critical Phenomenon. Journal of Geophysical Research: Solid Earth 94, 15635–15637.| Earthquakes as a Self-Organized Critical Phenomenon.Crossref | GoogleScholarGoogle Scholar |
Bak P, Tang C, Wiesenfeld K (1987) Self-Organized Criticality: An Explanation of the 1/f Noise. Physical Review Letters 59, 381–384.
| Self-Organized Criticality: An Explanation of the 1/f Noise.Crossref | GoogleScholarGoogle Scholar |
Bradstock RA, Cary GJ, Davies I, Lindenmayer DB, Price OF, Williams RJ (2012) Wildfires, fuel treatment and risk mitigation in Australian eucalypt forests: Insights from landscape-scale simulation. Journal of Environmental Management 105, 66–75.
Cajueiro DO, Andrade RFS (2010) Controlling Self-Organized Criticality in Sandpile Models. Physical Review E 81, 015102
| Controlling Self-Organized Criticality in Sandpile Models.Crossref | GoogleScholarGoogle Scholar |
Cal Fire (2019) Camp Fire. Available at https://www.fire.ca.gov/incidents/2018/11/8/camp-fire [Verified 29 December 2020]
Costa P, Castellnou M, Larrañaga A, Miralles M, Kraus D (2011). Prevention of Large Wildfires using the Fire Types Concept. (Generalitat de Catalunya: Barcelona, Spain).
Crosby NB, Aschwanden MJ, Dennis BR (1993) Frequency Distributions and Correlations of Solar X-Ray Flare Parameters. Solar Physics 143, 275–299.
| Frequency Distributions and Correlations of Solar X-Ray Flare Parameters.Crossref | GoogleScholarGoogle Scholar |
Florida Fire Service (2020) Florida Forest Service reporting system. Available at http://fireinfo.fdacs.gov/fmis.publicreports/ [Verified 29 December 2020]
Haugo RD, Kellogg BS, Cansler CA, Kolden CA, Kemp KB, Robertson JC, Metlen KL, Vaillant NM, Restaino CM (2019) The Missing Fire: Quantifying Human Exclusion of Wildfire in Pacific Northwest Forests, USA. Ecosphere 10, e02702
| The Missing Fire: Quantifying Human Exclusion of Wildfire in Pacific Northwest Forests, USA.Crossref | GoogleScholarGoogle Scholar |
IPCC (2018) Global Warming of 1.5°C: An IPCC Special Report on the Impacts of Global Warming of 1.5°C above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, sustainable development, and efforts to eradicate poverty. (Eds V Masson-Delmotte, P Zhai, HO Pörtner, D Roberts, J Skea, PR Shukla, A Pirani, W Moufouma-Okia, C Péan, R Pidcock, S Connors, JBR Matthews, Y Chen, X Zhou, MI Gomis, E Lonnoy, T Maycock, M Tignor, T Waterfield) (Cambridge University Press, Cambridge, UK and New York, NY, USA). Available at
| Crossref |
Ishii H, Wang N, Page SE (2002) A Day at the Beach: Human Agents Self Organizing on the Sand Pile. In ‘Modeling Complexity in Economic and Social Systems’. (Ed. F Schweitzer) pp. 371–391. (World Scientific: Singapore)
| Crossref |
Keeley JE (1987) Role of Fire in Seed Germination of Woody Taxa in California Chaparral. Ecology 68, 434–443.
| Role of Fire in Seed Germination of Woody Taxa in California Chaparral.Crossref | GoogleScholarGoogle Scholar |
Malamud BD, Morein G, Turcotte DL (1998) Forest Fires: An Example of Self-Organized Critical Behavior. Science 281, 1840–1842.
| Forest Fires: An Example of Self-Organized Critical Behavior.Crossref | GoogleScholarGoogle Scholar |
Malamud BD, Millington JDA, Perry GLW (2005) Characterizing wildfire regimes in the United States. Proceedings of the National Academy of Sciences 102, 4694–4699.
| Characterizing wildfire regimes in the United States.Crossref | GoogleScholarGoogle Scholar |
Minnich RA, Chou YH (1997) Wildland Fire Patch Dynamics in the Chaparral of Southern California and Northern Baja California. International Journal of Wildland Fire 7, 221–248.
| Wildland Fire Patch Dynamics in the Chaparral of Southern California and Northern Baja California.Crossref | GoogleScholarGoogle Scholar |
National Park Service (2020) Wildland Fire: What Is a Prescribed Fire? Available at https://www.nps.gov/articles/what-is-a-prescribed-fire.htm [Verified 29 December 2020]
Pereira MG, Trigo RM, da Camara CC, Pereira JMC, Leite SM (2005) Synoptic patterns associated with large summer forest fires in Portugal. Agricultural and Forest Meteorology 129, 11–25.
| Synoptic patterns associated with large summer forest fires in Portugal.Crossref | GoogleScholarGoogle Scholar |
Preisler HK, Grulke NE, Heath Z, Smith SL (2017) Analysis and out-year forecast of beetle, borer, and drought-induced tree mortality in California. Forest Ecology and Management 399, 166–178.
| Analysis and out-year forecast of beetle, borer, and drought-induced tree mortality in California.Crossref | GoogleScholarGoogle Scholar |
Price OF, Bradstock RA, Keeley JE, Syphard AD (2012) The impact of antecedent fire area on burned area in southern California coastal ecosystems. Journal of Environmental Management 113, 301–307.
| The impact of antecedent fire area on burned area in southern California coastal ecosystems.Crossref | GoogleScholarGoogle Scholar |
Price OF, Pausas JG, Govender N, Flannigan M, Fernandes PM, Brooks ML, Bird RB (2015) Global patterns in fire leverage: the response of annual area burnt to previous fire. International Journal of Wildland Fire 24, 297–306.
| Global patterns in fire leverage: the response of annual area burnt to previous fire.Crossref | GoogleScholarGoogle Scholar |
Ricotta C, Avena G, Marchetti M (1999) The flaming sandpile: self-organized criticality and wildfires. Ecological Modelling 119, 73–77.
| The flaming sandpile: self-organized criticality and wildfires.Crossref | GoogleScholarGoogle Scholar |
Roos CI, Rittenour TM, Swetnam TW, Loehman RA, Hollenback KL, Liebmann MJ, Rosenstein DD (2020) Fire suppression impacts on fuels and fire intensity in the western U.S.: insights from archaeological luminescence dating in northern New Mexico. Fire 3, 32
| Fire suppression impacts on fuels and fire intensity in the western U.S.: insights from archaeological luminescence dating in northern New Mexico.Crossref | GoogleScholarGoogle Scholar |
Russell KR, Van Lear DH, Guynn DC (1999) Prescribed fire effects on herpetofauna: review and management implications. Wildlife Society Bulletin 27, 374–384. Available at https://www.jstor.org/stable/3783904 [Verified 29 October 2020]
Settele J, Scholes R, Betts RA, Bunn S, Leadley P, Nepstad D, Overpeck JT, Taboada MA, Fischlin A, Moreno JM, Root T, Musche M, Winter M (2015) Terrestrial and inland water Systems. In ‘Climate Change 2014 Impacts, Adaptation and Vulnerability: Part A: Global and Sectoral Aspects’. pp. 271–360 (Cambridge University Press)
| Crossref |
Sneppen K, Bak P, Flyvbjerg H, Jensen MH (1995) Evolution as a self-organized critical phenomenon. Proceedings of the National Academy of Sciences 92, 5209–5213.
| Evolution as a self-organized critical phenomenon.Crossref | GoogleScholarGoogle Scholar |
Steel ZL, Campos B, Frick WF, Burnett R, Safford HD (2019) The effects of wildfire severity and pyrodiversity on bat occupancy and diversity in fire-suppressed forests. Scientific Reports 9, 16300
| The effects of wildfire severity and pyrodiversity on bat occupancy and diversity in fire-suppressed forests.Crossref | GoogleScholarGoogle Scholar |
Stephens SL, Collins BM, Fettig CJ, Finney MA, Hoffman CM, Knapp EE, North MP, Safford H, Wayman RB (2018) Drought, tree mortality, and wildfire in forests adapted to frequent fire. BioScience 68, 77–88.
| Drought, tree mortality, and wildfire in forests adapted to frequent fire.Crossref | GoogleScholarGoogle Scholar |
Yoder MR, Turcotte DL, Rundle JB (2011) Forest-fire model with natural fire resistance. Physical Review E 83, 046118
| Forest-fire model with natural fire resistance.Crossref | GoogleScholarGoogle Scholar |
† Preprint available at https://doi.org/10.48550/arXiv.2106.06591.