Comparing calibrated statistical and machine learning methods for wildland fire occurrence prediction: a case study of human-caused fires in Lac La Biche, Alberta, Canada
Nathan Phelps A B and Douglas G. Woolford A CA Department of Statistical and Actuarial Sciences, University of Western Ontario, London N6A 3K7, Canada.
B Department of Computer Science, University of Western Ontario, London N6A 3K7, Canada.
C Corresponding author. Email: dwoolfor@uwo.ca
International Journal of Wildland Fire 30(11) 850-870 https://doi.org/10.1071/WF20139
Submitted: 1 September 2020 Accepted: 24 August 2021 Published: 29 September 2021
Journal Compilation © IAWF 2021 Open Access CC BY-NC-ND
Abstract
Wildland fire occurrence prediction (FOP) modelling supports fire management decisions, such as suppression resource pre-positioning and the routeing of detection patrols. Common empirical modelling methods for FOP include both model-based (statistical modelling) and algorithmic-based (machine learning) approaches. However, it was recently shown that many machine learning models in FOP literature are not suitable for fire management operations because of overprediction if not properly calibrated to output true probabilities. We present methods for properly calibrating statistical and machine learning models for fine-scale, spatially explicit daily FOP followed by a case-study comparison of human-caused FOP modelling in the Lac La Biche region of Alberta, Canada, using data from 1996 to 2016. Calibrated bagged classification trees, random forests, neural networks, logistic regression models and logistic generalised additive models (GAMs) are compared in order to assess the pros and cons of these approaches when properly calibrated. Results suggest that logistic GAMs can have similar performance to machine learning models for FOP. Hence, we advocate that the pros and cons of different modelling approaches should be discussed with fire management practitioners when determining which models to use operationally because statistical methods are commonly viewed as more interpretable than machine learning methods.
Keywords: artificial intelligence, classification, ensemble, forest fire occurrence prediction, generalised additive model, human-caused, supervised learning.
Introduction
Human-caused wildland fires have caused growing levels of concern across the globe (e.g. Costafreda-Aumedes et al. 2017). In Canada, the threat of wildland fires to life, property and natural resources has increased over the last several years (Canadian Council of Forest Ministers Wildland Fire Management Working Group 2016). In the province of Alberta alone, over 7000 wildland fires occurred from 2011 to 2016, burning over 1.5 million ha of land (Government of Alberta 2018). Hundreds of millions of dollars are spent on efforts to mitigate the negative impacts associated with wildland fires. For example, the average annual expenditure on fire management in the province of Alberta, Canada exceeds CA$200 million (Stocks 2013). In order to increase the effectiveness of wildland fire management without increasing its costs, statisticians, operations research specialists and other researchers have studied a variety of wildland fire-related problems, including attempting to optimise wildland fire detection strategies, initial attack strategies and wildland fire occurrence prediction (FOP) (Martell 2007).
More and more, wildland fire management is being regarded as a type of natural hazards risk management, where ‘risk’ in this context considers the likelihood of fire and its potential impacts (Xi et al. 2019; Johnston et al. 2020). Fine-scale, spatially explicit daily FOP plays a crucial role in wildland fire risk modelling since it quantifies likelihood (namely probability) of fire occurrence, a necessary component for any risk computation. Fire occurrences can be thought of as following a spatio-temporal point process (e.g. Turner 2009), but a binary approximation to this process is typically used in FOP literature (e.g. Woolford et al. 2011; Magnussen and Taylor 2012). Wildland fires are very rare events when modelled on a fine space–time scale (e.g. 10 × 10 km daily cells). Thus, the number of cells with more than one fire occurrence is negligible, so observations are represented as either a fire occurrence or a non-fire occurrence, generating what is referred to as a highly imbalanced binary classification problem.
There are many different methods that have been used to model wildland fire occurrences. Recent summaries, reviews and discussions appear in Plucinski (2012), Taylor et al. (2013), Costafreda-Aumedes et al. (2017), Nadeem et al. (2020) and Woolford et al. (2021). These methods can be broadly viewed as coming from one of the following two dominant data modelling cultures: model-based (i.e. statistical modelling/learning) or algorithmic-based (i.e. machine learning) (e.g. Breiman 2001b). Statistical modelling techniques assume the response data are generated by a specified stochastic model that involves other predictors/covariates. Examples of this approach include regression-type models, such as logistic regression (LR) and logistic generalised additive models (GAMs) (e.g. Wood 2017). Machine learning approaches employ an algorithm to make predictions of a response given a set of predictors.
Early FOP models used LR (e.g. Martell et al. 1987, 1989; Vega-Garcia et al. 1995). More recently, extensions of that method that allow for non-linear relationships and automatic variable selection have been used. Non-linear relationships between the response and covariates are commonly modelled using spline-smoothers in logistic GAMs (e.g. Brillinger et al. 2003; Preisler et al. 2004; Vilar et al. 2010; Woolford et al. 2011, 2021; Magnussen and Taylor 2012). Automatic variable selection methods are based on regularisation approaches, such as lasso LR (Tibshirani 1996), that modify the likelihood function used to fit the models so that coefficients for non-important predictors are ‘shrunk’ towards zero (e.g. Nadeem et al. 2020). Several other studies have employed machine learning methods (e.g. Vega-Garcia et al. 1996; Alonso-Betanzos et al. 2003; Stojanova et al. 2006, 2012; Sakr et al. 2010, 2011; Van Beusekom et al. 2018). For a thorough review of machine learning applications in wildland fire, see Jain et al. (2020).
Recently, Phelps and Woolford (2021) demonstrated that the machine learning methods developed thus far for FOP are not well suited for operational use. This was done through a case study that included the comparison of uncalibrated models using the same data and study region we consider herein. They showed that if one does not account for any undersampling (also called downsampling) to create balanced datasets required for training machine learning-based FOP models, the resulting fitted models ‘systematically overpredicted the number of fire occurrences’ when applied to testing data that represented what would be used in operational practice for fine-scale, spatially explicit human-caused FOP.
A balanced dataset in this context is one where the number of fire and non-fire observations are equal. This is not representative of fire occurrence in space–time. Wildland fires are extremely rare on a fine spatio-temporal scale. When anything other than the complete dataset or a simple random sample of the complete dataset is used to create a dataset for training a model, the resulting data do not represent what happens in practice and the fitted model will overpredict unless it is properly calibrated. For example, generating a balanced dataset for model training leads to models whose systematic overprediction of fire occurrence can be orders of magnitude higher than what is actually observed (e.g. see Phelps and Woolford 2021, figs 3 and 4). Consequently, it is crucial to properly fit or calibrate an FOP model to account for how the training data were generated so that it will output true probabilities when making predictions in practice.
In this work, we introduce calibration methods for machine learning-based FOP modelling that are new to FOP modelling literature. These facilitate the development of well-calibrated machine learning models for fine-scale, spatially explicit FOP in the sense that the calibrated models output predictions that are true probabilities. Employing these methods, we develop models for human-caused FOP in the Lac La Biche region in Alberta. We use and calibrate three machine learning approaches: bagged classification trees (BCTs), random forests (RFs) and neural networks (NNs). Those models are compared with both the historically dominant and state-of-the-art statistical modelling approaches, LR and logistic GAMs, respectively.
Machine learning models for FOP have been compared with LR previously (e.g. Vega-Garcia et al. 1996; Stojanova et al. 2006, 2012), but to our knowledge, this is the first comparison of machine learning models with logistic GAMs for FOP. In particular, we believe that our work may be the first to use calibrated machine learning models and the first to compare machine learning models with a state-of-the-art statistical model. Thus, the two contributions of this work are introducing calibration methods for machine learning models to FOP literature and comparing calibrated machine learning and state-of-the-art statistical models for a case study of the Lac La Biche region of Alberta.
Materials and methods
Study region and data
Our study region and period are the Lac La Biche area of the province of Alberta, Canada (Fig. 1) over the 1996–2016 fire seasons, which are defined operationally to be March through October of each year. This region was chosen in collaboration with fire management practitioners at Alberta Agriculture and Forestry because it is an area that commonly experiences many human-caused wildland fires each year.
To develop spatially and temporally explicit models, we partitioned our region and period into a set of spatio-temporal voxels (space–time cells). Excluding cells on the boundary, each grid cell is ~10 km2 in size. The temporal resolution used for the modelling is 1 day. For each day, a count of the number of wildland fires in each grid cell was recorded, stratified based on the ignition cause of the fire (e.g. lightning or human, where the latter can take a variety of sub-categories such as being caused by recreation, by residents, or by industrial logging operations). Since lightning-caused fires may require a different modelling framework because they can smoulder for many days before being detected and reported (see Wotton and Martell 2005), we focused our analysis on human-caused fire occurrences. Our response was whether or not a given voxel had at least one human-caused fire occurrence (i.e. ignition), recorded as a dichotomous response with 1 denoting that voxel experiencing a fire day and 0 indicating that no human-caused fires occurred in that grid cell on that given day. The spatial resolution was set in collaboration with fire management practitioners at Alberta Agriculture and Forestry and was chosen to be fine enough so that counts of human-caused fires were mapped essentially to a dichotomous (i.e. 0 or 1) process. This permits the use of binary classification methods to develop fine-scale, spatially explicit models representing individual fire occurrences.
Alberta Agriculture and Forestry provided several datasets that were used to create the voxel-based data for training and testing our models. Voxel-specific covariates available for FOP modelling are shown in Table 1 and can be viewed as either static or dynamic in space–time. Static variables include land use characteristics such as the length of highways, railways and powerlines in the cell, as well as the percentage of each cell that is classified as being in the wildland–urban interface (WUI), the wildland–industrial interface (WUI-Ind) and the wildland–infrastructure interface (WUI-Inf) areas as defined by Johnston and Flannigan (2018). Other static variables are ecological characteristics such as fuel type inventories (e.g. vegetation, water and non-fuel proportions) and nature region. Dynamic variables include weather (e.g. precipitation, temperature, wind speed) as well as fire-weather variables (e.g. the Fine Fuel Moisture Code (FFMC), Initial Spread Index (ISI) and Fire Weather Index (FWI); see Wotton 2009). The fire-weather variables were computed using the cffdrs package (Wang et al. 2017) in R (R Core Team 2017), with the default FFMC, Duff Moisture Code (DMC) and Drought Code (DC) values used for initialisation at the start of each year. The fire-weather data consist of observations recorded daily at 1300 hours local daylight time at a network of weather stations within the province of Alberta as well as stations that were within (but not in) 200 km of its provincial boundary in order to avoid boundary effects when the weather variables at those points are then interpolated (Flannigan and Wotton 1989) to the centroid of each daily grid cell (i.e. voxel) used in our analysis. For October 31, 2016, the dynamic weather variables were not measured, so observations from this day were discarded.

|
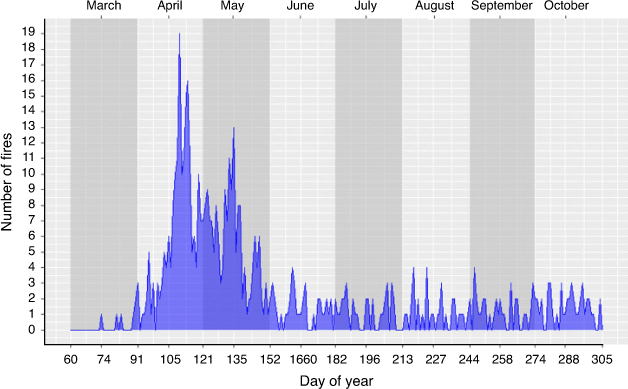
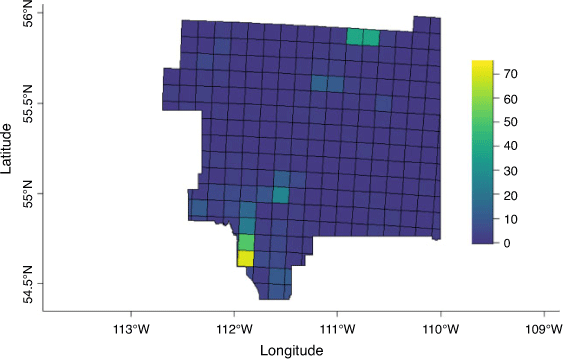
In order to both fit our models as well as examine their predictive performance, we split our study period into training and testing datasets. The training dataset, used for fitting the models, was composed of data from 1996 to 2011. Data from the last 5 years (2012–2016) were reserved for model testing, namely making predictions on data that were not used in the model-fitting process. Wildland fire occurrences are rare at the fine space–time scale of our modelling. Our training dataset contained only 550 ~10 km2 × daily voxels in which a fire occurred, which corresponds to less than 0.06% of the voxels. Fire occurrences exhibit seasonal and spatial patterns in this region. Fig. 2 illustrates that the majority of fires in the study region occurred in the spring, while Fig. 3 shows the number of fires for each sector of the study region in the training dataset (1996–2011).
|
|
Statistical and machine learning modelling methods
In what follows, we present overviews of each of the statistical and machine learning modelling techniques used for our FOP models, as well as methods for calibrating such models so that they predict true probabilities. For a detailed technical discussion of LR and GAMs, see Wood (2017). James et al. (2013) also provide an excellent overview of statistical and machine learning methods including logistic models, smoothing with GAMs, BCTs and RFs. A thorough treatment of NNs appears in Goodfellow et al. (2016).
Logistic regression (LR)
LR is a modelling technique that is part of the family of generalised linear models. It is used to model a dichotomous response based on relationships between the predictors and the response, which are assumed to be linear on the log odds scale. The model for the probability of a human-caused wildland fire in a specific region on a particular day is summarised by the following equation, with p representing the probability of a wildland fire in a specific region on a particular day as a function of predictors xj representing the value of the jth predictor and βj representing the coefficient associated with the jth predictor:
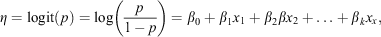
which can be mapped back to the probability scale by inverting the logit-transformation as follows:
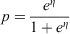
Logistic generalised additive models (GAMs)
Logistic GAMs extend the LR framework by using smoothing functions to model the effect of each predictor, facilitating non-linear relationships between the predictors and the response on the log odds scale. With sj(xj) representing a smoothing function for the jth predictor, the equation for logistic GAMs using only univariate smoothing functions is as follows:
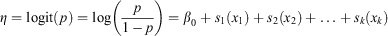
Multivariate smoothing functions can also be used. We implemented the logistic GAMs using the mgcv package (Wood 2011), which uses thin plate regression splines as its default smoothing basis. For more technical details on LR and how it can be extended using penalised spline smoothing in GAMs, see Wood (2017). Like an LR model, probabilities can be obtained using the inverse logit function.
Calibration of logistic-based statistical models
A common strategy when modelling rare events given a large volume of highly imbalanced data is to use a response-dependent sampling design to augment the dataset used for model fitting. In FOP literature, one typically keeps all of the fire observations and only some proportion,  , of the non-fire observations. This sampling procedure is commonly referred to as undersampling or downsampling (e.g. He and Garcia 2009). It was first employed for FOP by Vega-Garcia et al. (1995) and has been employed successfully in several fine-scale, spatio-temporal FOP studies (e.g. Brillinger et al. 2003, 2006; Preisler et al. 2004; Vilar et al. 2010; Woolford et al. 2011; Nadeem et al. 2020). Undersampling induces a bias because the distribution of the training data is not a simple random sample from the population and therefore its distribution differs from that of the testing data. In other words, the models are not well calibrated; they predict event probabilities that systematically deviate from the true probability of the event. For LRs and logistic GAMs, this bias is accounted for by adding a deterministic offset (i.e. an adjustment to the intercept term) of –log(π) to the model (e.g. Brillinger et al. 2003; Taylor et al. 2013). As illustrated by Woolford et al. (2011), enough non-fire voxels must be retained when undersampling in order to ensure the relationships with the predictors are estimated accurately. As in Woolford et al. (2011), we sampled 10% of the non-fire voxels (i.e. π = 0.1) when augmenting our training data for model fitting.
, of the non-fire observations. This sampling procedure is commonly referred to as undersampling or downsampling (e.g. He and Garcia 2009). It was first employed for FOP by Vega-Garcia et al. (1995) and has been employed successfully in several fine-scale, spatio-temporal FOP studies (e.g. Brillinger et al. 2003, 2006; Preisler et al. 2004; Vilar et al. 2010; Woolford et al. 2011; Nadeem et al. 2020). Undersampling induces a bias because the distribution of the training data is not a simple random sample from the population and therefore its distribution differs from that of the testing data. In other words, the models are not well calibrated; they predict event probabilities that systematically deviate from the true probability of the event. For LRs and logistic GAMs, this bias is accounted for by adding a deterministic offset (i.e. an adjustment to the intercept term) of –log(π) to the model (e.g. Brillinger et al. 2003; Taylor et al. 2013). As illustrated by Woolford et al. (2011), enough non-fire voxels must be retained when undersampling in order to ensure the relationships with the predictors are estimated accurately. As in Woolford et al. (2011), we sampled 10% of the non-fire voxels (i.e. π = 0.1) when augmenting our training data for model fitting.
Tree-based methods
Two of the machine learning methods we employed are based on classification trees (Breiman et al. 1984), which use recursive binary splitting of the data in order to create groups, called nodes, within the data. Splits are selected greedily by choosing the split that provides the greatest improvement in node purity, which in our context with a binary response corresponds to a node that contains either only 0s or only 1s being viewed as pure. Here, greedy selection means that the best split at that time in the algorithm is selected; in other words, possible splits further down the tree are not considered. The splitting continues until some criterion is reached. For example, the splitting may continue until all terminal nodes, or leaves, of the tree are pure.
Classification trees are high-variance models and are susceptible to overfitting, which is when a model fits its training data well but performs relatively poorly on new data. In an attempt to avoid overfitting, classification trees are often pruned. Pruning involves removing some of the splits that are lower in the tree near the terminal nodes. Alternatively, ensemble techniques that use multiple individual models can be used to build models that are based on classification trees but have lower variance. We employed the latter approach in this study.
Bagged classification trees (BCTs)
Bagging (Breiman 1996) is an ensemble technique commonly used with classification trees (e.g. Stojanova et al. 2006, 2012). The bagging process involves creating many training datasets using bootstrapping (resampling with replacement from the training dataset), then fitting a classification tree to each of these training datasets. When using bagging, each tree is typically fitted perfectly to its training data so that all terminal nodes are pure, and pruning is not used. In order to make a prediction, each tree votes on how to classify an observation and the predicted probability of the event is based on the fraction of trees that predicted that the event will occur. We implemented the BCTs using the randomForest package (Liaw and Wiener 2002) using their default number of trees, 500.
Random forests (RFs)
RFs (Breiman 2001a) are very similar to bagged trees. They use one additional step in order to reduce the correlation between the trees, helping to ensure that the variance of the model is much less than the variance of an individual tree. When making a split, rather than considering all possible predictors, only a randomly chosen subset of the predictors is considered. BCTs are a specific case of RF, where the number of predictors considered at each split is equal to the actual number of predictors. As with the BCTs, we used the randomForest package (Liaw and Wiener 2002) to implement the RFs. We used 500 trees and the default number of predictors given consideration at each split of the tree.
Calibration of tree-based methods
When fitting BCTs and RFs for problems with imbalanced data, it is recommended to balance the training dataset. We opted to use the ‘balanced random forest’ algorithm proposed by Chen et al. (2004). They suggested generating the training dataset for each tree using a stratified random sample with replacement of n1 observations from each class, where n1 is the number of observations from the minority class. Like the stratified sampling technique used for the statistical modelling methods, this technique induces a bias in the models.
Platt’s scaling (PS) (Platt 1999) is a method that can be used to adjust the predictions of a model in order to improve the model’s calibration. Traditionally, PS is implemented by fitting an LR model to the predictions of a model. However, the LR model used for rescaling will be biased if it uses the same dataset that was used to train the tree-based model (e.g. Niculescu-Mizil and Caruana 2005). We used four-fold cross-validation to avoid this bias. The training dataset was split into four folds of data such that each fold contained data from four randomly selected years. The BCT and RF models were repeatedly fitted to three of the folds and predictions were made on the fourth fold, eventually creating a training dataset for calibration equal in size to the original training dataset. We then fitted two types of logistic-based models to this data: we used LR in accordance with the traditional PS methodology and we also considered a logistic GAM in order to allow for the possibility of a non-linear relationship on the log odds scale. The BCTs and RFs were fitted to all 16 years of training data and their predictions on the testing data were calibrated using these logistic models. Separate scaling models were constructed for the BCT and RF models.
Neural networks (NNs)
NNs are models that were originally developed based on the brains of animals (McCulloch and Pitts 1943). Data are given to an input layer of neurons, or nodes, and signals are passed from the neurons of one layer to the neurons of the next layer, with weights applied to each connection between the neurons. Inputs are summed within each neuron, and an activation function is applied to that sum. For more background on NNs, see Goodfellow et al. (2016).
Backpropagation (Rumelhart et al. 1985) was the first successful algorithm proposed for training the weights between the neurons and is still widely used (e.g. Mason et al. 2018; Alkronz et al. 2019), but genetic algorithms have also been used (e.g. Vasconcelos et al. 2001). As NNs have evolved over the last several decades, they have increasingly deviated from their biological inspiration. The family of NN models has grown to include models such as convolutional NNs (e.g. Lawrence et al. 1997; Krizhevsky et al. 2012) and recurrent NNs (e.g. Mikolov et al. 2010; Sak et al. 2014), and model architectures are much more extensive (e.g. new activation functions, more hidden layers) than in early NNs. Techniques such as early stopping (e.g. Prechelt 1998) and dropout (Srivastava et al. 2014) have been introduced to prevent overfitting. However, while there is a sense of which type of NN may be most suitable for certain types of problems (e.g. convolutional NNs for classification of images), to our knowledge there is no well-defined process for choosing a model architecture.
Ensemble of NNs
When training an NN, it is recommended to use a balanced training dataset (e.g. Vega-Garcia et al. 1996; Jain and Nag 1997). As our dataset is extraordinarily imbalanced, balancing the training dataset requires removing over 99.9% of the non-fire occurrences. In order to facilitate using more of the non-fire occurrence observations for training, we opted to create an ensemble of 100 NNs, where each network was fitted to a different set of balanced training data and the predictions of the models were averaged. All of the fire occurrences were used in each training dataset, but the non-fire occurrences were uniformly randomly sampled each time.
As noted in the review of LeCun et al. (2015), deep learning methods, namely NNs with many hidden layers, have been successful in many studies. However, several other studies have found that using only one hidden layer in an NN is sufficient for their problem (e.g. Dutta and Shekhar 1988; Collins et al. 1988; Salchenberger et al. 1992; Jain and Nag 1997). Given that our approach involves fitting many NNs, we chose to use networks with only one hidden layer to reduce training time relative to models with several layers. As recommended by Klimasauskas (1988) and used by Jain and Nag (1997), we used the following heuristic guideline for choosing the number of neurons in the hidden layer:
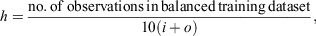
where 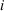 , o and h (which is rounded to the nearest whole number) are the number of neurons in the input, output and hidden layers respectively.
, o and h (which is rounded to the nearest whole number) are the number of neurons in the input, output and hidden layers respectively.
We used the keras package (Allaire and Chollet 2020) to create an ensemble of 100 multilayer perceptrons. Each perceptron was an NN that consisted of three layers: the input layer, which performed batch normalisation (Ioffe and Szegedy 2015), the hidden layer, which used the rectified linear unit (ReLU) activation function (Nair and Hinton 2010), and the output layer, which used the sigmoid activation function. Models were created using binary cross entropy loss with the Adam optimiser (Kingma and Ba 2015) and trained using 300 epochs. Like with BCTs and RFs, we were not concerned with each individual NN overfitting its training dataset because the individual predictions were averaged, so we did not use early stopping or dropout.
Calibration of NN-based methods
As with the other modelling methods, the ensemble of NNs is impacted by the bias induced by undersampling. We did not use PS to calibrate the ensemble of NNs because the time needed to train the ensemble was much larger than all of the other modelling methods and using PS in the same way it was implemented for the BCTs and RFs would have required fitting this ensemble several times. Instead, we used the following equation (Dal Pozzolo et al. 2015), which relates the distribution of the data before sampling to the distribution of the data after sampling:
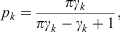
where pk is the modelled probability of a fire for the original distribution, γk is the modelled probability of a fire for the sampled distribution, and π is the proportion of non-fire observations sampled. The transformation applied through this equation is analogous to the offset applied to the data modelling methods. As discussed by Preisler et al. (2004), this equation and the offset are equivalent for LR and logistic GAMs.
Model building and variable selection
For the statistical models (LR and logistic GAM), variable selection was performed using domain knowledge, exploratory data analysis and standard statistical model building procedures. Since our focus was on human-caused FOP, we used the FFMC as our measure for fuel moisture because fine surface fuel moisture is an important factor for FOP. FFMC is used by Canadian wildland fire management agencies as a measure of the receptivity of surface fuels to ignition (Wotton 2009) and has been found to be a significant predictor for human-caused FOP in other regions in Canada (e.g. Cunningham and Martell 1973; Woolford et al. 2011; Magnussen and Taylor 2012; McFayden et al. 2020). Weather variables that are used to calculate fuel moisture, namely relative humidity, temperature and precipitation, were excluded to avoid possible multicollinearity effects with FFMC, which is calculated as a function of those variables (Van Wagner 1987). Other fire-weather variables were excluded as well given that FFMC has been well established as the key fuel moisture-based driver of human-caused fire occurrence.
Additional exploratory data analyses were used to identify other possible important predictors as well as the shape of their relationship with the probability of fire occurrence. Likelihood ratio tests were used to determine when the addition of a variable led to a significant improvement in the fit of the model. For comparative purposes, the predictors that were used in the selected logistic GAM were also used in the LR model. However, an additive spatial effect was also included in the GAM using a bivariate smoother. To account for spatial effects in the LR model, we followed the method suggested by Nadeem et al. (2020) where a baseline risk was computed and used as a predictor in the LR model. Here, the baseline risk at each location was calculated as the historical proportion of fire occurrences within each grid cell. We chose to use the logit baseline because the LR model assumes a linear relationship between the response and the predictors on the log odds scale. However, some cells did not have a fire in our study period, so the smallest non-zero baseline was added to each baseline (including non-zero baselines) before performing the logit-transformation in order to avoid obtaining undefined values when calculating the logit baseline.
For the machine learning approaches, we opted to fit multiple models for each technique. We fitted one model that used all of the predictors and another with the predictors used in the selected statistical models, essentially using the statistical models as variable selection ‘experts’ as was done in Vega-Garcia et al. (1996). For each of these models, we created one model with the (untransformed) baseline predictor and one without, in case modelling the spatial patterns in this way offers some advantage. Thus, a model was created for each machine learning approach using four different sets of predictors. The selected model for each technique was chosen using the methods outlined in the next section.
Evaluating and comparing model performance
As suggested by Phelps and Woolford (2021), we used area under the precision-recall curve (AUC-PR), negative logarithmic score (NLS) and temporal and spatial visualisations to evaluate and compare the models. AUC-PR was computed using the integration approach (Boyd et al. 2013; Keilwagen et al. 2014) from the PRROC package (Grau et al. 2015), while the temporal plots with corresponding root-mean-squared error (RMSE) values were computed using aggregated daily totals across the entire study region. Phelps and Woolford also suggest the use of customised metrics from the Beta family of scoring rules (Merkle and Steyvers 2013). The two parameters of this family, α and β, can be set such that the fraction α/(α + β) reflects a fire management agency’s relative cost of false positives to false negatives. Setting α = 1, we used three different values of β (9, 99 and 999) to produce customised metrics that place more and more importance on identifying fire occurrences. Smaller values of the Beta family score are preferred when comparing candidate models using a given parameterisation of that scoring rule. For the methods used to assess calibration, we used paired t-tests to determine if models’ performances were statistically significantly different from one another.
Results
Summary of selected models
The selected statistical models used FFMC, length of road within the cell, day of year, percentage of cell covered in water and percentage of cell covered by aspen trees, as well as the percentages of each cell that are in the WUI, the WUI-Ind and the WUI-Inf areas as defined by Johnston and Flannigan (2018). In addition, both models included a spatial component as described previously: a bivariate smoother of longitude and latitude was used for the logistic GAM and a logit baseline calculated for each grid cell was used as a predictor for the LR model. The best BCT model used all predictors except the baseline, while the best RF and ensemble of NNs used the baseline and the predictors used in the logistic GAM. The BCT and RF models were each calibrated using PS with a logistic GAM, as this was found to be more effective than rescaling with LR. It should be noted that the model selection process was subjective and there were other reasonable choices for the selected model from each technique.
Comparing the predictive performance of the selected models using metrics
Table 2 shows several measures for the selected models from each modelling technique. Results for other candidate models are shown in Appendix 1. For comparison, the null model has also been included in Table 2. The null model is an LR model that only has an intercept term. For all observations, the null model predicts a probability of wildland fire equal to the percentage of observations in the training dataset where a wildland fire occurred.
We first consider the models’ ability to rank observations by assessing their AUC-PR. Although the scores were small for all of the models, it must be noted that the AUC-PR of the null model was 6.625 × 10−4 and that the more sophisticated models had AUC-PR scores that were orders of magnitude larger. The logistic GAM performed best, with the tree-based models ranking second and third, followed by the ensemble of NNs and finally LR. The logistic GAM’s AUC-PR was more than 10% greater than the AUC-PR for any other selected model, but the precision-recall curves for the logistic GAM and the tree-based approaches (shown in Fig. 4) suggest that such a large difference may be misleading. For such heavily imbalanced data, a model’s AUC-PR is very dependent on the outcomes of the observations deemed most likely to be a fire occurrence; see Phelps and Woolford (2021) for more details. The two largest predictions of the logistic GAM were both fire occurrences, contributing to the spike seen in its precision-recall curve. By simulating fire seasons under the assumption that the probability of a fire occurrence was exactly as predicted by the logistic GAM, we determined that even if the logistic GAM perfectly modelled the probability of fire occurrence, an AUC-PR as large as the one observed is unlikely. Prior to the spike in the logistic GAM’s precision-recall curve, it appears that the tree-based models both had a better AUC-PR than the logistic GAM. For these models, such a spike is even less likely because their predicted probabilities were not unique owing to the structure of the models; the number of distinct probabilities for these models was 501 (the number of trees plus one). Thus, for such a spike to occur, all of the observations in the highest probability group must be fire observations.
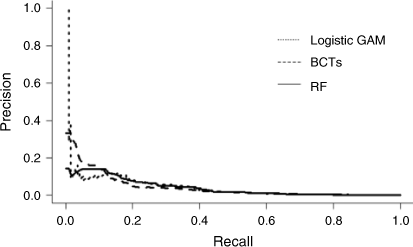
|
In terms of calibration, it again appears that the logistic GAM was the best-performing model overall. In addition to having the best NLS, it also had the second smallest score for all three customised metrics, just falling behind the best tree-based models (see Table 2). However, using paired t-tests with a significance level of 0.05, no model’s performance was significantly different from all the other selected models in terms of any of the calibration metrics.
Comparing the temporal and spatial predictive performance of the selected models
The temporal plots in Fig. 5 compare time series of the predicted and observed total of daily fires for the 2013 fire season for the LR, logistic GAM, BCTs, RF and ensemble of NNs. Plots for the other years in the testing dataset are shown in Appendix 2. Clearly, the LR and NN models did not capture the daily fluctuation in fire occurrences as successfully as the other models. Both models consistently predicted too many fires in the early spring. This phenomenon is especially noticeable for the LR model, likely due to the linear restriction on its seasonality component. The logistic GAM and the tree-based methods appear to have performed similarly. The most notable differences occurred in 2013, when the GAM had a much sharper peak than the other models, in 2014, when the GAM predicted more fire occurrences in late April to the start of May than the other models, and in 2016, when the GAM predicted more fire occurrences in April than the other models.
The spatial maps in Fig. 6 show the predicted probabilities of a human-caused wildland fire for 3 days from the testing data using the same models as in Fig. 5. The LR model created prediction maps that were fairly uniform relative to the other models, limiting its usefulness in practice. The map from the NN model is not as uniform as the map from the LR model, but aside from highlighting a few sectors, it also seems to offer limited spatial discrimination relative to the other more complicated models. In general, the logistic GAM and tree-based methods generated fairly similar prediction maps, but with differing magnitudes of output. The 3 days shown have been chosen to illustrate some of the differences between the models. One noticeable difference is that the tree-based models were generally more aggressive than the logistic GAM when predicting fire occurrences in cells in the central portion of the study region. However, the logistic GAM made more extreme predictions than the tree-based models, as shown in Fig. 6b. An interesting observation (illustrated in Fig. 6b) is that the BCT model sometimes estimated very little chance of a fire in the south-west part of the study region while both the logistic GAM and RF predicted relatively high probabilities.
Discussion
Recent work has shown that the machine learning models used for FOP in past studies systematically overpredict the probability of wildland fires, and thus are unsuitable for operational use (Phelps and Woolford 2021). We presented methods for fitting properly calibrated FOP models using both statistical and machine learning approaches, and then compared a set of well-calibrated models for human-caused FOP in Lac La Biche, Alberta. All such models predict true probabilities resulting from their calibration. There are several advantages to developing FOP models that predict true probabilities. As discussed and illustrated in Woolford et al. (2021), such predictions can be summed to predict the expected number of fires in a given region (such as a region or sector used by fire management) on a given day; they can be used to create spatially explicit colour-coded fire occurrence maps that are interpretable; and they can be used to produce prediction intervals that reflect the uncertainty in such predictions. Spatially explicit FOP output can also be incorporated into risk-based frameworks to aid aerial detection routeing (e.g. McFayden et al. 2020).
Analysis of the performance metrics and visualisations clearly indicate that the LR model was not competitive with the best of the more sophisticated models, including the more state-of-the-art logistic GAM. This is not surprising given its restriction to linear relationships on the log odds scale. The best ensemble of NNs performed better than the LR model, but one of the ensembles performed worse than the LR model for four of the five metrics we considered. These results are similar to the findings of Vega-Garcia et al. (1996), who found only a slight improvement from using an NN instead of LR. The best-performing NN model was inferior to the three selected models from the other approaches, which offered similar performance to one another. Using two-sided paired t-tests with a significance level of 0.05, we found that none of the models were able to significantly outperform all of the other models in terms of the calibration metrics. Statistical significance is a prerequisite to practical significance; thus, it is reasonable to suggest that the difference in predictive performance between the logistic GAM and the best tree-based models was not practically significant.
Spatial differences in FOP were noted when comparing models. The BCT model was sometimes observed to predict very low fire probability in the south-west part of the study region while both the logistic GAM and RF predicted relatively high fire probability. This appears to be caused by the predictors used in the model rather than the modelling technique; the spatial prediction maps created by BCTs using the predictors in the selected RF very closely resemble the maps shown for the RF.
Given the similar performance of the best tree-based methods and the logistic GAM, perhaps the most striking difference between the models is in interpretability. The estimated coefficients of an LR model and the estimated partial effects curves of logistic GAMs can be used to provide a visual explanation of how the model works as well as reassurance to end users that the model captures the impact of various predictors in expected ways. The ‘black boxes’ of BCTs, RFs and NNs provide no such reassurance to an end user in a fire management organisation. Fire management agencies are much more likely to make use of a model and value its outputs if they have some understanding of how the model arrived at its output, so the poor interpretability of the machine learning models may result in underutilisation of the model in practice (Costafreda-Aumedes et al. 2017). For this reason, there may be a practical improvement to fire management from using a logistic GAM for FOP instead of a machine learning model. Since there is very limited evidence in our results to support the choice of any candidate model instead of the logistic GAM, we believe that the logistic GAM is the most well suited for operational use in the Lac La Biche region. We recognise that it is possible that this opinion could change depending on the specifications of the end users of the model. As shown in Table 2, the ranking of the models can change based on the values of the end users and such values can be incorporated through development of a custom metric, such as the customised metrics from the Beta family of scoring rules we considered. Although the selected ensemble of NNs did not seem to perform well compared with the other more complex models in general, it was better than the RF for the Beta family metric that placed the highest importance on identifying fire occurrences. However, based on the metrics that we have considered and the temporal and spatial visualisations, the logistic GAM offered the best combination of performance and interpretability.
Typically, there is a trade-off between model performance and interpretability. It is much easier to interpret an LR model than BCTs, RFs or NNs, but our results, as well as the results of other FOP studies (e.g. Stojanova et al. 2006, 2012) and studies of the related problem of wildland fire susceptibility modelling (e.g. Vasconcelos et al. 2001; Bar Massada et al. 2013; Rodrigues and de la Riva 2014), have shown that these techniques can perform better than LR. However, this is the first fine space–time FOP study that has compared machine learning techniques with logistic GAMs. Our results suggest that logistic GAMs can perform just as well as machine learning models for FOP. Although they are not as easily interpreted as LR, they are much more interpretable than machine learning models. If logistic GAMs can consistently perform on par with machine learning approaches, they should be the preferred model for FOP for fire management operations.
Conclusion
In this study, we have introduced well-calibrated machine learning models to FOP literature and compared the performance of these models with two well-calibrated statistical models, an LR model and a logistic GAM. To the best of our knowledge, all other comparative studies have focused on making comparisons with LR models. Logistic GAMs represent a much more flexible statistical modelling approach that uses data-driven smoothing methods to estimate what could be highly non-linear relationships, something that cannot adequately be represented by an LR framework. Our results show that logistic GAMs offer competitive performance. Since logistic GAMs are more interpretable than machine learning models – which are commonly viewed as a ‘black box’ approach – the similar performance of the models suggests that logistic GAMs should be the preferred modelling technique. We note, however, that our case study used only a subset of possible machine learning techniques on a single study region, and thus is not sufficient evidence that logistic GAMs are consistently competitive with machine learning models for FOP. It is possible that other machine learning approaches (e.g. boosting) or changes to the hyperparameters and/or architecture of the techniques used in this study could produce a model that outperforms the logistic GAM for our study region. For example, the BCTs and RF may have been hindered by having only 500 trees, leading to only 501 unique outputs. In addition, future studies should be performed that compare logistic GAMs with a more comprehensive selection of machine learning models across multiple wildland fire ecosystems in order to assess the generalisability of our findings.
Data availability
The datasets used for our modelling were provided by Alberta Agriculture and Forestry.
Conflicts of interest
The authors declare no conflicts.
Declaration of funding
We acknowledge the support of the Government of Alberta, the Natural Sciences and Engineering Research Council of Canada (NSERC) (RGPIN-2015–04221 and its Undergraduate Student Research Award program) and the Institute for Catastrophic Loss Reduction.
Acknowledgements
We thank the Government of Alberta for providing the data. B. Moore, A. Stacey and M. Wotton are thanked for their assistance in data preparation. C. Tymstra, B. Moore, D. Finn, M. Wotton and M. Flannigan are thanked for helpful conversations related to wildland fire occurrence in Alberta. C. Tymstra is also acknowledged for his strong advocacy for the use of FOP in Alberta. B. Bilodeau is thanked for help with restructuring the methods section. Helpful comments made by an anonymous associate editor and a set of reviewers that led to significant improvements in the manuscript are gratefully acknowledged.
References
Alkronz ES, Moghayer KA, Meimeh M, Gazzaz M, Abu-Nasser BS, Abu-Naser SS (2019) Prediction of whether mushroom is edible or poisonous using back-propagation neural network. International Journal of Academic and Applied Research 3, 1–8.Allaire JJ, Chollet F (2020) keras: R Interface to ‘Keras’. R package version 2.3.0.0. Available at https://CRAN.R-project.org/package=keras
Alonso-Betanzos A, Fontenla-Romero O, Guijarro-Berdiñas B, Hernández-Pereira E, Andrade MIP, Jiménez E, Soto JLL, Carballas T (2003) An intelligent system for forest fire risk prediction and firefighting management in Galicia. Expert Systems with Applications 25, 545–554.
| An intelligent system for forest fire risk prediction and firefighting management in Galicia.Crossref | GoogleScholarGoogle Scholar |
Bar Massada A, Syphard AD, Stewart SI, Radeloff VC (2013) Wildfire ignition-distribution modelling: a comparative study in the Huron–Manistee National Forest, Michigan, USA. International Journal of Wildland Fire 22, 174–183.
| Wildfire ignition-distribution modelling: a comparative study in the Huron–Manistee National Forest, Michigan, USA.Crossref | GoogleScholarGoogle Scholar |
Boyd K, Eng KH, Page CD (2013) Area under the precision-recall curve: point estimates and confidence intervals. In ‘Joint European conference on machine learning and knowledge discovery in databases’. (Eds H Blockeel, K Kersting, S Nijssen, F Železný) pp. 451–466. (Springer: Berlin, Heidelberg)
Breiman L (1996) Bagging predictors. Machine Learning 24, 123–140.
| Bagging predictors.Crossref | GoogleScholarGoogle Scholar |
Breiman L (2001a) Random forests. Machine Learning 45, 5–32.
| Random forests.Crossref | GoogleScholarGoogle Scholar |
Breiman L (2001b) Statistical modeling: The two cultures (with comments and a rejoinder by the author). Statistical Science 16, 199–231.
| Statistical modeling: The two cultures (with comments and a rejoinder by the author).Crossref | GoogleScholarGoogle Scholar |
Breiman L, Friedman J, Oshen R, Stone C (1984) ‘Classification and regression trees’. (Wadsworth and Brooks: Monterey, CA)
Brillinger DR, Preisler HK, Benoit JW (2003) Risk assessment: a forest fire example. Lecture Notes-Monograph Series / Institute of Mathematical Statistics 40, 177–196.
| Risk assessment: a forest fire example.Crossref | GoogleScholarGoogle Scholar |
Brillinger DR, Preisler HK, Benoit JW (2006) Probabilistic risk assessment for wildfires. Environmetrics 17, 623–633.
| Probabilistic risk assessment for wildfires.Crossref | GoogleScholarGoogle Scholar |
Canadian Council of Forest Ministers Wildland Fire Management Working Group (2016) Canadian Wildland Fire Strategy: A 10-year review and renewed call to action. Natural Resources Canada report Fo79–22/2016E-PDF.
Chen C, Liaw A, Breiman L (2004) Using random forest to learn imbalanced data. University of California, Berkeley, Department of Statistics Report 666. Available at https://statistics.berkeley.edu/sites/default/files/tech-reports/666.pdf
Collins E, Ghosh S, Scofield C (1988) An application of a multiple neural network learning system to emulation of mortgage underwriting judgments. In ‘Proceedings of the IEEE International Conference on Neural Networks’. pp. 459–466. (IEEE)
Costafreda-Aumedes S, Comas C, Vega-Garcia C (2017) Human-caused fire occurrence modelling in perspective: a review. International Journal of Wildland Fire 26, 983–998.
| Human-caused fire occurrence modelling in perspective: a review.Crossref | GoogleScholarGoogle Scholar |
Cunningham AA, Martell DL (1973) A stochastic model for the occurrence of man-caused forest fires. Canadian Journal of Forest Research 3, 282–287.
| A stochastic model for the occurrence of man-caused forest fires.Crossref | GoogleScholarGoogle Scholar |
Dal Pozzolo A, Caelen O, Johnson RA, Bontempi G (2015) Calibrating probability with undersampling for unbalanced classification. In ‘2015 IEEE symposium series on computational intelligence’. pp. 159–166. (IEEE)
Dutta S, Shekhar S (1988) Bond rating: A non-conservative application of neural networks. In ‘Proceedings of the IEEE international conference on neural networks’. pp. 443–450. (IEEE)
Flannigan MD, Wotton BM (1989) A study of interpolation methods for forest fire danger rating in Canada. Canadian Journal of Forest Research 19, 1059–1066.
| A study of interpolation methods for forest fire danger rating in Canada.Crossref | GoogleScholarGoogle Scholar |
Goodfellow I, Benjio Y, Courville A (2016) ‘Deep learning’. (MIT Press) Available at http://www.deeplearningbook.org
Government of Alberta (2018) Agriculture and Forestry Annual Report 2017–18. (Government of Alberta: Edmonton, AB, Canada)
Grau J, Grosse I, Keilwagen J (2015) PRROC: computing and visualizing precision-recall and receiver operating characteristic curves in R. Bioinformatics 31, 2595–2597.
| PRROC: computing and visualizing precision-recall and receiver operating characteristic curves in R.Crossref | GoogleScholarGoogle Scholar | 25810428PubMed |
He H, Garcia EA (2009) Learning from imbalanced data. IEEE Transactions on Knowledge and Data Engineering 21, 1263–1284.
| Learning from imbalanced data.Crossref | GoogleScholarGoogle Scholar |
Ioffe S, Szegedy C (2015) Batch normalization: Accelerating deep network training by reducing internal covariate shift. In ‘Proceedings of the 32nd international conference on machine learning’. (Eds F Bach, D Blei) Volume 37, pp. 448–456. (Proceedings of Machine Learning Research) Available at https://proceedings.mlr.press/v37/ioffe15.html
Jain BA, Nag BN (1997) Performance evaluation of neural network decision models. Journal of Management Information Systems 14, 201–216.
| Performance evaluation of neural network decision models.Crossref | GoogleScholarGoogle Scholar |
Jain P, Coogan SC, Subramanian SG, Crowley M, Taylor S, Flannigan MD (2020) A review of machine learning applications in wildfire science and management. Environmental Reviews 28, 478–505.
| A review of machine learning applications in wildfire science and management.Crossref | GoogleScholarGoogle Scholar |
James G, Witten D, Hastie T, Tibshirani R (2013) ‘An introduction to statistical learning with applications in R.’ (Springer: New York)
Johnston LM, Flannigan MD (2018) Mapping Canadian wildland fire interface areas. International Journal of Wildland Fire 27, 1–14.
| Mapping Canadian wildland fire interface areas.Crossref | GoogleScholarGoogle Scholar |
Johnston LM, Wang X, Erni S, Taylor SW, McFayden CB, Oliver JA, Stockdale C, Christianson A, Boulanger Y, Gauthier S, Arseneault D, Wotton BM, Parisien M-A, Flannigan MD (2020) Wildland fire risk research in Canada. Environmental Reviews 999, 1–23.
Keilwagen J, Grosse I, Grau J (2014) Area under precision-recall curves for weighted and unweighted data. PLoS One 9, e92209
| Area under precision-recall curves for weighted and unweighted data.Crossref | GoogleScholarGoogle Scholar | 24651729PubMed |
Kingma DP, Ba J (2015) Adam: A method for stochastic optimization. Poster presentation in ‘Proceedings of the 3rd international conference on learning representations’. (DBLP: computer science bibliography) Available at https://dblp.org/db/conf/iclr/iclr2015.html
Klimasauskas CC (1988) ‘NeuralWorks™: An introduction to neural computing’. (NeuralWare: Sewickley, PA)
Krizhevsky A, Sutskever I, Hinton GE (2012) Imagenet classification with deep convolutional neural networks. In ‘NeurIPS Proceedings: Advances in neural information processing systems 25’. (Eds F Pereira, CJC Burgess, L Bottou, KQ Weinberger) pp. 1097–1105. (Curran Associates Inc.: Red Hook, NY, USA) Available at https://papers.nips.cc/paper/2012/file/c399862d3b9d6b76c8436e924a68c45b-Paper.pdf
Lawrence S, Giles CL, Tsoi AC, Back AD (1997) Face recognition: A convolutional neural-network approach. IEEE Transactions on Neural Networks 8, 98–113.
| Face recognition: A convolutional neural-network approach.Crossref | GoogleScholarGoogle Scholar | 18255614PubMed |
LeCun Y, Bengio Y, Hinton G (2015) Deep learning. Nature 521, 436–444.
| Deep learning.Crossref | GoogleScholarGoogle Scholar | 26017442PubMed |
Liaw A, Wiener M (2002) Classification and regression by randomForest. R News 2, 18–22.
Magnussen S, Taylor SW (2012) Prediction of daily lightning- and human-caused fires in British Columbia. International Journal of Wildland Fire 21, 342–356.
| Prediction of daily lightning- and human-caused fires in British Columbia.Crossref | GoogleScholarGoogle Scholar |
Martell DL (2007) Forest fire management: current practices and new challenges for operational researchers. In ‘Handbook of operations research in natural resources’. (Eds A Weintraub, C Romero, T Bjørndal, R Epstein). pp. 489–509. (Springer)
Martell DL, Otukol S, Stocks BJ (1987) A logistic model for predicting daily people-caused forest fire occurrence in Ontario. Canadian Journal of Forest Research 17, 394–401.
| A logistic model for predicting daily people-caused forest fire occurrence in Ontario.Crossref | GoogleScholarGoogle Scholar |
Martell DL, Bevilacqua E, Stocks BJ (1989) Modelling seasonal variation in daily people-caused forest fire occurrence. Canadian Journal of Forest Research 19, 1555–1563.
| Modelling seasonal variation in daily people-caused forest fire occurrence.Crossref | GoogleScholarGoogle Scholar |
Mason C, Twomey J, Wright D, Whitman L (2018) Predicting engineering student attrition risk using a probabilistic neural network and comparing results with a backpropagation neural network and logistic regression. Research in Higher Education 59, 382–400.
| Predicting engineering student attrition risk using a probabilistic neural network and comparing results with a backpropagation neural network and logistic regression.Crossref | GoogleScholarGoogle Scholar |
McCulloch WS, Pitts W (1943) A logical calculus of the ideas immanent in nervous activity. The Bulletin of Mathematical Biophysics 5, 115–133.
| A logical calculus of the ideas immanent in nervous activity.Crossref | GoogleScholarGoogle Scholar |
McFayden CB, Woolford DG, Stacey A, Boychuk D, Johnston JM, Wheatley MJ, Martell DL (2020) Risk assessment for wildland fire aerial detection patrol route planning in Ontario, Canada. International Journal of Wildland Fire 29, 28–41.
| Risk assessment for wildland fire aerial detection patrol route planning in Ontario, Canada.Crossref | GoogleScholarGoogle Scholar |
Merkle EC, Steyvers M (2013) Choosing a strictly proper scoring rule. Decision Analysis 10, 292–304.
| Choosing a strictly proper scoring rule.Crossref | GoogleScholarGoogle Scholar |
Mikolov T, Karafiát M, Burget L, Černocký J, Khudanpur S (2010) Recurrent neural network-based language model. In ‘INTERSPEECH 2010, 11th Annual conference of the International Speech Communication Association, Makuhari, Chiba, Japan, September 26–30, 2010’. pp. 1045–1048
Nadeem K, Taylor SW, Woolford DG, Dean CB (2020) Mesoscale spatio-temporal predictive models of daily human and lightning-caused wildland fire occurrence in British Columbia. International Journal of Wildland Fire 29, 11–27.
| Mesoscale spatio-temporal predictive models of daily human and lightning-caused wildland fire occurrence in British Columbia.Crossref | GoogleScholarGoogle Scholar |
Nair V, Hinton GE (2010) Rectified linear units improve restricted Boltzmann machines. In ‘ICML’10: Proceedings of the 27th international conference on machine learning’. (Eds J Furnkranz, T Joachims) pp. 807–814. (Omnipress: Madison, WI, USA)
Niculescu-Mizil A, Caruana R (2005) Predicting good probabilities with supervised learning. In ‘ICML’05: Proceedings of the 22nd international conference on machine learning’. (Eds S Dzeroski, L De Raedt, S Wrobel) pp. 625–632. (Association for Computing Machinery: New York, NJ, USA)
Phelps N, Woolford DG (2021) Guidelines for effective evaluation and comparison of wildland fire occurrence prediction models. International Journal of Wildland Fire 30, 225–240.
| Guidelines for effective evaluation and comparison of wildland fire occurrence prediction models.Crossref | GoogleScholarGoogle Scholar |
Platt J (1999) Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods. Advances in Large Margin Classifiers 10, 61–74.
Plucinski MP (2012) A review of wildfire occurrence research. Bushfire Cooperative Research Centre. (Melbourne, Vic., Australia). Available at https://www.bushfirecrc.com/sites/default/files/managed/resource/attachment_g_fire_occurrence_literature_review_0.pdf
Prechelt L (1998) Early stopping – but when? In ‘Neural networks: Tricks of the trade’. (Eds G Montavon, GB Orr, KR Müller) pp. 55–69. (Springer: Berlin, Heidelberg) https://DOI.ORG/10.1007/978-3-642-35289-8_5
Preisler HK, Brillinger DR, Burgan RE, Benoit JW (2004) Probability based models for estimation of wildfire risk. International Journal of Wildland Fire 13, 133–142.
| Probability based models for estimation of wildfire risk.Crossref | GoogleScholarGoogle Scholar |
R Core Team (2017) R: A language and environment for statistical computing. (R Foundation for Statistical Computing: Vienna, Austria). Available at https://www.R-project.org/
Rodrigues M, de la Riva J (2014) An insight into machine-learning algorithms to model human-caused wildfire occurrence. Environmental Modelling & Software 57, 192–201.
| An insight into machine-learning algorithms to model human-caused wildfire occurrence.Crossref | GoogleScholarGoogle Scholar |
Rumelhart DE, Hinton GE, Williams RJ (1985) Learning internal representations by error propagation (no. ICS-8506). California University San Diego La Jolla Institute for Cognitive Science.
Sak H, Senior AW, Beaufays F (2014) Long short-term memory recurrent neural network architectures for large scale acoustic modeling. In ‘INTERSPEECH-2014’. pp. 338–342.
Sakr GE, Elhajj IH, Mitri G, Wejinya UC (2010) Artificial intelligence for forest fire prediction. In ‘2010 IEEE/ASME international conference on advanced intelligent mechatronics’. (Eds) pp. 1311–1316. (IEEE)
Sakr GE, Elhajj IH, Mitri G (2011) Efficient forest fire occurrence prediction for developing countries using two weather parameters. Engineering Applications of Artificial Intelligence 24, 888–894.
| Efficient forest fire occurrence prediction for developing countries using two weather parameters.Crossref | GoogleScholarGoogle Scholar |
Salchenberger LM, Cinar EM, Lash NA (1992) Neural networks: A new tool for predicting thrift failures. Decision Sciences 23, 899–916.
| Neural networks: A new tool for predicting thrift failures.Crossref | GoogleScholarGoogle Scholar |
Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R (2014) Dropout: a simple way to prevent neural networks from overfitting. Journal of Machine Learning Research 15, 1929–1958.
Stocks BJ (2013) Evaluating past, current and future fire load trends in Canada. Canadian Interagency Forest Fire Centre. (Winnipeg, MB, Canada)
Stocks BJ, Lynham TJ, Lawson BD, Alexander ME, Wagner CV, McAlpine RS, Dube DE (1989) Canadian Forest Fire Danger Rating System: An Overview. The Forestry Chronicle 65, 258–265.
Stojanova D, Panov P, Kobler A, Dzeroski S, Taskova K (2006) Learning to predict forest fires with different data mining techniques. In ‘Conference on data mining and data warehouses’. pp. 255–258. (SiKDD: Ljubljana, Slovenia)
Stojanova D, Kobler A, Ogrinc P, Ženko B, Džeroski S (2012) Estimating the risk of fire outbreaks in the natural environment. Data Mining and Knowledge Discovery 24, 411–442.
| Estimating the risk of fire outbreaks in the natural environment.Crossref | GoogleScholarGoogle Scholar |
Taylor SW, Woolford DG, Dean CB, Martell DL (2013) Wildfire prediction to inform management: Statistical science challenges. Statistical Science 28, 586–615.
| Wildfire prediction to inform management: Statistical science challenges.Crossref | GoogleScholarGoogle Scholar |
Tibshirani R (1996) Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society. Series B. Methodological 58, 267–288.
| Regression shrinkage and selection via the lasso.Crossref | GoogleScholarGoogle Scholar |
Turner R (2009) Point patterns of forest fire locations. Environmental and Ecological Statistics 16, 197–223.
| Point patterns of forest fire locations.Crossref | GoogleScholarGoogle Scholar |
Van Beusekom AE, Gould WA, Monmany AC, Khalyani AH, Quiñones M, Fain SJ, Andrade-Núñez MJ, González G (2018) Fire weather and likelihood: characterizing climate space for fire occurrence and extent in Puerto Rico. Climatic Change 146, 117–131.
| Fire weather and likelihood: characterizing climate space for fire occurrence and extent in Puerto Rico.Crossref | GoogleScholarGoogle Scholar |
Van Wagner CE (1987) Development and structure of the Canadian Forest Fire Weather Index System. Canadian Forestry Service. (Ottawa, ON, Canada)
Vasconcelos MJP, Silva S, Tome M, Alvim M, Pereira JC (2001) Spatial prediction of fire ignition probabilities: comparing logistic regression and neural networks. Photogrammetric Engineering and Remote Sensing 67, 73–81.
Vega-Garcia C, Woodard PM, Titus SJ, Adamowicz WL, Lee BS (1995) A logit model for predicting the daily occurrence of human caused forest-fires. International Journal of Wildland Fire 5, 101–111.
| A logit model for predicting the daily occurrence of human caused forest-fires.Crossref | GoogleScholarGoogle Scholar |
Vega-Garcia C, Lee BS, Woodard PM, Titus SJ (1996) Applying neural network technology to human-caused wildfire occurrence prediction. AI Applications 10, 9–18.
Vilar L, Woolford DG, Martell DL, Martín MP (2010) A model for predicting human-caused wildfire occurrence in the region of Madrid, Spain. International Journal of Wildland Fire 19, 325–337.
| A model for predicting human-caused wildfire occurrence in the region of Madrid, Spain.Crossref | GoogleScholarGoogle Scholar |
Wang X, Wotton BM, Cantin AS, Parisien MA, Anderson K, Moore B, Flannigan MD (2017) cffdrs: an R package for the Canadian forest fire danger rating system. Ecological Processes 6, 5
| cffdrs: an R package for the Canadian forest fire danger rating system.Crossref | GoogleScholarGoogle Scholar |
Wood SN (2011) Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models. Journal of the Royal Statistical Society. Series B, Statistical Methodology 73, 3–36.
| Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models.Crossref | GoogleScholarGoogle Scholar |
Wood SN (2017) ‘Generalized additive models: An introduction with R (2nd edn)’. (Chapman and Hall/CRC)
Woolford DG, Bellhouse DR, Braun WJ, Dean CB, Martell DL, Sun J (2011) A spatio-temporal model for people-caused forest fire occurrence in the Romeo Malette Forest. Journal of Environmental Statistics 2, 2–16.
Woolford DG, Martell DL, McFayden CB, Evens J, Stacey A, Wotton BM, Boychuk D (2021) The development and implementation of a human-caused wildland fire occurrence prediction system for the province of Ontario, Canada. Canadian Journal of Forest Research 51, 303–325.
| The development and implementation of a human-caused wildland fire occurrence prediction system for the province of Ontario, Canada.Crossref | GoogleScholarGoogle Scholar |
Wotton BM (2009) Interpreting and using outputs from the Canadian Forest Fire Danger Rating System in research applications. Environmental and Ecological Statistics 16, 107–131.
| Interpreting and using outputs from the Canadian Forest Fire Danger Rating System in research applications.Crossref | GoogleScholarGoogle Scholar |
Wotton BM, Martell DL (2005) A lightning fire occurrence model for Ontario. Canadian Journal of Forest Research 35, 1389–1401.
| A lightning fire occurrence model for Ontario.Crossref | GoogleScholarGoogle Scholar |
Xi DD, Taylor SW, Woolford DG, Dean CB (2019) Statistical models of key components of wildfire risk. Annual Review of Statistics and Its Application 6, 197–222.
| Statistical models of key components of wildfire risk.Crossref | GoogleScholarGoogle Scholar |
Appendix 1. Values of performance metrics on the testing dataset for models using each technique: bagged classification trees (BCTs) calibrated using Platt’s Scaling (PS) with logistic regression (LR), BCTs calibrated using PS with a logistic generalised additive model (GAM), a random forest calibrated using PS with LR, a random forest calibrated using PS with a GAM, and an ensemble of neural networks (NNs)
The metrics are area under the precision-recall curve (AUC-PR), negative logarithmic score (NLS) and customised metrics from the Beta family of scoring rules. Values are rounded to four significant figures and the selected models shown in Table 2 are in bold. ‘Same as GAM’ used the predictors from the selected logistic GAM model, namely the Fine Fuel Moisture Code, road length, day of year, percentage water, percentage aspen fuel type, percentage wildland–urban interface, percentage wildland–industrial interface and percentage wildland–infrastructure interface. ‘Baseline’ refers to the baseline risk predictor as described by Nadeem et al. (2020). ‘All predictors’ used all potential predictor variables (see Table 1)

|







