Computational study of critical moisture and depth of burn in peat fires
Xinyan Huang A and Guillermo Rein A BA Department of Mechanical Engineering, Imperial College London, London SW7 2AZ, United Kingdom.
B Corresponding author. Email: g.rein@imperial.ac.uk
International Journal of Wildland Fire 24(6) 798-808 https://doi.org/10.1071/WF14178
Submitted: 1 October 2014 Accepted: 11 March 2015 Published: 30 July 2015
Journal Compilation © IAWF 2015
Abstract
Smouldering combustion is the slow, low-temperature, flameless burning of porous fuels and the most important phenomenon of wildfires in peatlands. Smouldering fires propagate both horizontally and vertically through organic layers of the ground and can reach deep into the soil. In this work, we develop a one-dimensional computational model of reactive porous media in the open-source code Gpyro. We investigate the vertical in-depth spread of smouldering fires into peat columns 20 cm deep with heterogeneous profiles of moisture content (MC), inert content (IC) and density. The model solves the species, momentum and energy conservation equations with five-step heterogeneous chemistry, to predict the transient profiles of temperature, species concentration, reaction rates and depth of burn from ignition to spread and to extinction. Modelling results reveal that smouldering combustion can spread over peat layers with very high MC (>250%) if the layer is thin and located below a thick, drier layer. It is shown that the critical moisture for extinction can be much higher than the previously reported critical MC for ignition (e.g. extinction MC up to 256% for low-IC peat, with critical ignition MC of 117%). The predicted critical MC values and depths of burn are compared with experimental measurements for field samples in the literature, showing good agreement. This study provides the physical understanding of the role of moisture in the ignition and extinction of smouldering peat fires, and explains for the first time the phenomenon of smouldering in very wet peat layers.
Additional keywords: extinction, ignition, modelling, peatland, smouldering, soil moisture, surface fuel, wildfire.
Introduction
Smouldering combustion is the slow, low-temperature, flameless burning of porous fuels and the most persistent type of combustion – different from flaming combustion in its chemistry, transport processes and time scales (Ohlemiller 1985; Rein 2013). Smouldering is the dominant phenomenon in the burning of natural deposits of peat, which are the largest and longest burning fires on Earth (Page et al. 2002; Turetsky et al. 2015; Rein 2013). Locally, smouldering wildfires cause severe and long-term damage to the soil system (Ryan and Frandsen 1991; Stephens and Finney 2002; Rein et al. 2008). Organic soils and peat store around 25% of the planet’s terrestrial organic carbon – approximately the same mass of carbon as found in the atmosphere – despite peatlands occupying only 3% of the Earth’s surface (Gorham 1994; Turetsky et al. 2015). Globally, these fires contribute greatly to greenhouse gas emissions, and result in widespread destruction of ecosystems and regional haze events, examples being the recent megafires in Southeast Asia, North America and Northern Europe (Rein 2013). During the 1997 extreme haze event in Indonesia, peat fires released the equivalent of 13–40% of global manmade carbon emissions for the same year (Page et al. 2002). More recent figures estimate that the average annual carbon footprint is equivalent to 15% of manmade emissions (Poulter et al. 2006). Moreover, pollutants in smouldering haze substantially increase the risk of cardiopulmonary diseases in the human population (Rappold et al. 2011; Kim et al. 2014).
Peat can hold a wide range of moisture contents (MC1), from 10% under drought conditions to well in excess of 300% under flooded conditions (Benscoter et al. 2011; Watts 2013). Water represents a significant energy sink and can prevent fire in undisturbed wetlands, but natural or anthropogenic-induced droughts are the leading cause of fires (Turetsky et al. 2015). Therefore, soil moisture is the single most important property governing the ignition, spread and extinction of smouldering wildfires (Frandsen 1987; Frandsen 1997; Rein et al. 2008; Garlough and Keyes 2011; Watts 2013). During an ignition, water evaporates and then the organic content of the peat undergoes pyrolysis until the exothermic char oxidation begins, which can lead to spread of a self-sustaining fire. The critical moisture content for smouldering ignition (MC*ig) for various peat types has been reported in the range of 40–150% (Frandsen 1987, 1997; Rein et al. 2008; Garlough and Keyes 2011). When drier than this critical content, peat becomes susceptible to smouldering. Other factors affecting soil susceptibility to smouldering include inert content (IC2), bulk density, porosity and chemical composition. The pioneering experiments of Frandsen (1987, 1997) showed that there is a decreasing relationship between MC*ig and IC: a soil of high IC can only be ignited at low MC. The influence of bulk density was studied experimentally by Hartford (1989) and Garlough and Keyes (2011), who reported contrasting results with respect to smouldering. Hartford (1989) found that a higher bulk density decreases the probability of smouldering, whereas Garlough and Keyes (2011) found that bulk density has no significant effect.
If ignition of the top peat layer occurs, a self-sustaining smouldering front can spread both laterally and in depth (Rein 2013; Huang and Rein 2014). After extinction, the depth of burn (DOB) can be used to estimate the amount of carbon lost in the fire per unit area (Page et al. 2002; Rein 2013; Davies et al. 2013). According to Rein (2013), extinction happens when the vertical spread is quenched by: (i) the presence of the mineral soil layer; (ii) the presence of a thick wet layer; or (iii) the timing of flooding, heavy continuous rains or firefighting. The mechanism of extinction of interest in this work is by a wet layer (ii), which leads to the definition of the critical moisture for extinction (MC*ex).
Wade et al. (1980) reported experiments where the top layer could only be ignited at MC <65%, but once ignited, the fire continued to burn in depth through wetter layers of MC = 150%, a higher MC than the critical value reported by Frandsen (1987, 1997). More recently, Benscoter et al. (2011) conducted a series of experiments for in-depth spread in field samples with heterogeneous profiles of MC, IC and density. For most of their experiments, the smouldering front did not spread through peat layers with MC >150%, but for one particular sample, the smouldering front spread over a 3-cm thick layer of 295% MC, a much higher value than the MC*ig expected from Frandsen (1987, 1997). All these experimental studies in the literature suggest that MC*ex differs from MC*ig, and that DOB depends on both peat MC and thickness of the layers above and below (heterogeneous profile).
The number of computational studies on smouldering peat in the literature is small. Benscoter et al. (2011) modified Van Wagner’s (1972) analytical heat transfer model, and by calibrating the downward heat transfer rate, their predictions of DOB were in good agreement with the experiment measurements. In our previous work (Huang and Rein 2014; Huang et al. 2015), a multi-physics one-dimensional (1-D) model of reactive porous media was developed to investigate the ignition of smouldering peat fire using a five-step chemistry scheme combining drying, pyrolysis and oxidations reactions. The model successfully predicts the experiments of Frandsen (1987, 1997) on small and homogeneous soil samples and revealed the sensitivity of smouldering ignition (MC*ig) to IC, chemical kinetics and soil properties as well as to the ignition protocol.
In this work, we continue using the existing multi-physics model, and further improve it to consider column samples with heterogeneous profiles of MC and properties that vary with depth. The MC*ex and DOB are investigated computationally and applied to the experiment of Benscoter et al. (2011).
Computational model of peat fire
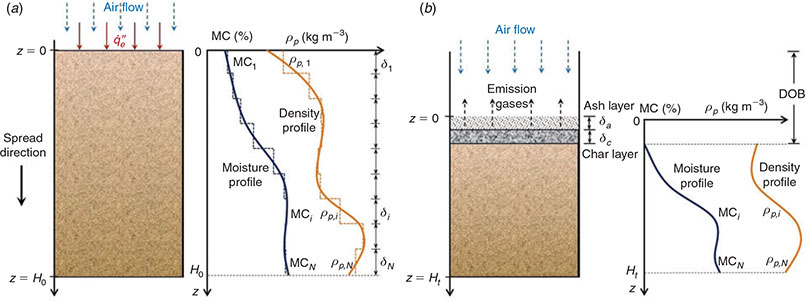
In-depth smouldering in the vertical direction is best studied in column peat samples as in the experiments of Benscoter et al. (2011), Watts (2013) and Zaccone et al. (2014), which can be approximated as 1-D along the vertical direction of in-depth spread. Fig. 1a shows the computational domain of a peat column with heterogeneous MC and density profiles. The ignition is attempted on the top surface by applying a constant heat flux for a period of time. If the ignition source is weak or MC near the top is high, the smouldering front may not propagate. Once ignited, a smouldering front spreads in depth, drying and consuming the peat below. At the same time, a char layer appears and propagates in depth, and an ash layer gradually accumulates on top, as illustrated in Fig. 1b. The depth at which the fire extinguishes gives the final DOB (Benscoter et al. 2011; Rein 2013).
1-D governing equations
The open-source code Gpyro for generalised pyrolysis simulations is used to model smouldering peat. Details of Gpyro can be found in Lautenberger and Fernandez-Pello (2009), so only the essentials are presented here. The model solves transient equations for both the condensed and gas phases. The governing equations include Eqn (1) for condensed-phase mass conservation, Eqn (2) for condensed-phase species conservation (assuming thermal equilibrium with the gas phase), Eqn (3) for condensed-phase energy conservation, Eqn (4) for gas-phase mass conservation, Eqn (5) for gas-phase species conservation and Eqn (6) for gas-phase momentum conservation (Darcy’s law):






All symbols are explained in Appendix 1. Subscripts i, j and k refer to the index of condensed-phase species, gas-phase species and reaction, respectively; d and f refer to the destruction and formation of species.
Each condensed-phase species is assumed to have constant properties (e.g. bulk density, specific heat and porosity). All gaseous species are assumed to have a unit Schmidt number and the same specific heat (set to that of nitrogen). The properties in each cell are weighted averages based on mass fraction Yi or volume fraction Xi (Lautenberger and Fernandez-Pello 2009). As an example, Eqn (7) shows the expression to average four important properties whose format is the same for the other properties (M, K, ϵ and Y):

At the free surface of the top layer (z = 0), the boundary conditions simulate natural convection and no cross-wind for heat transfer (hc,0 = 10 W m−2 K−1; radiative emissivity ϵ = 0.95) and mass transfer (hm,0 ~ hc,0/cp,g ~ 0.02 kg m−2 s−1). The initial pressure and temperature in the domain are atmospheric and 300 K. The ignition source is modelled as an external heat flux ( ) applied at z = 0 for 5 min. Whether the ignition is successful or not depends on MC, IC and properties of the peat layer near the ignition source as well as the ignition protocol, details of which are discussed in depth in Huang et al. (2015). At the bottom of the column (z = H0), the mass flux is set to be zero (sealed boundary) and heat transfer is purely convective (hc,L ≈ kwall/δwall = 3W m−2 K−1) to simulate a small heat loss through an insulating boundary. A fully implicit formulation is adopted for solution of the coupled system of Eqns (1–6). Details about the numerical solution can be found in Lautenberger and Fernandez-Pello (2009). The sample height during spread is equal to the sum of the heights of each cell,
) applied at z = 0 for 5 min. Whether the ignition is successful or not depends on MC, IC and properties of the peat layer near the ignition source as well as the ignition protocol, details of which are discussed in depth in Huang et al. (2015). At the bottom of the column (z = H0), the mass flux is set to be zero (sealed boundary) and heat transfer is purely convective (hc,L ≈ kwall/δwall = 3W m−2 K−1) to simulate a small heat loss through an insulating boundary. A fully implicit formulation is adopted for solution of the coupled system of Eqns (1–6). Details about the numerical solution can be found in Lautenberger and Fernandez-Pello (2009). The sample height during spread is equal to the sum of the heights of each cell,  , which depends on mass conservation and density. Simulations were run with an initial cell size of Δzn,0 = 0.2 mm and initial time step of 0.02 s. Reducing the cell size and time step by a factor of two results in no significant difference, so this discretisation is acceptable.
, which depends on mass conservation and density. Simulations were run with an initial cell size of Δzn,0 = 0.2 mm and initial time step of 0.02 s. Reducing the cell size and time step by a factor of two results in no significant difference, so this discretisation is acceptable.
Chemical kinetics
The heterogeneous reaction k of condensed species A in mass basis is given as:

where vB,k = 1 + (ρB/ρA – 1)χk and χk quantifies the shrinkage or expansion. The destruction rate of species A in the reaction k is expressed by the Arrhenius equation given in Eqns (9) and (10):


The formation rates of the condensed species B and all gases from reaction k are  and
and  , respectively. The corresponding condensed-phase heat of reaction is
, respectively. The corresponding condensed-phase heat of reaction is  .
.
In our previous work (Huang and Rein 2014), various chemical kinetic schemes for smouldering combustion were investigated using thermogravity data from four peat samples from Scotland (SC), Siberia (SI-A and SI-B) and China (CH). The best kinetics scheme was found to include one drying step (Eqn 11), one pyrolysis of peat (Eqn 12) and three oxidations of peat (Eqn 13), β-char (Eqn 14), and α-char (Eqn 15).





where, vw,dr = MC and the subscripts w, p, α, β and a represent the five condensed species (water, peat, α-char, β-char and ash). Four gaseous species are considered: oxygen (O2), nitrogen (N2), water vapour (H2O) and combustion products (Gas). The composition of the gaseous combustion products in peat fire was discussed further in Rein et al. (2009).
In-depth smouldering
For the model implementation, the vertical profile is discretised in N number of layers (i = 1, 2, 3, … N) of varying thickness (δi), moisture content (MCi), properties (e.g. ρi, ki, cp,i) and chemistry, as shown in Fig. 1a. This discretisation is convenient to simulate field samples that typically include heterogeneous profiles with depth for the properties. For example, in the experiment of Benscoter et al. (2011), the 20–30 cm tall peat columns were divided into multiple layers, each of 3 cm in thickness.
We first study in detail a simple and ideal column with a heterogeneous profile made of three layers: a top layer (δt), a middle wet layer (δw) and a bottom dry layer (δb). Fig. 2 shows the computational domain, with a fixed height of h0 = δt + δw + δb = 20 cm, while the thickness of each layer varies for different cases. The top layer has an MC lower than the critical value for ignition (MCt < MC*ig) so it can be ignited by external heating. The middle layer (MCw) is much wetter, and the bottom layer is air-dried peat, which is in equilibrium with the ambient MCb = 10% (Cancellieri et al. 2012; Huang and Rein 2014). The function of this dry layer is to create a consistent boundary and to minimise its influence on extinction and DOB.

|
If MCw is below a threshold, the smouldering front arriving from the top is able to propagate through it and to burn to the bottom layer, eventually consuming the whole sample (i.e. DOB = h0 = 20 cm). This threshold is the critical MC for extinction (MC*ex) and can be found by continuously increasing MC*w in different simulations until it results in DOB = h0.
Parameter selection
The thermo-physical properties of each condensed-phase species (i) are listed in Table 1. The bulk densities ρi,0 are taken from Benscoter et al. (2011) or Hadden et al. (2013). The properties of the solid (non-porous) material ρs,i, ks,i, cp,i for peat, char and ash are taken from Jacobsen et al. (2003). The porosity is calculated as:

|

The effective thermal conductivity includes the radiation across pores as:

where γi ~ 10−4 m depends on the pore sized as γi = 3dp,i (Yu et al. 2006). The average pore size relates to the particle specific surface area S as dp,j = 1/Siρi where Sp = Sc = 0.05 m2 g−1 and Sa = 0.2 m2 g−1 (de Jonge et al. 1996). The absolute permeability can be calculated from the empirical expression of Punmia and Jain (2005) as:

where Ki varies from 10–12 to 10−9 m2 and decreases with the bulk density. Because of the high porosity of peat (ψp = 0.973) and its low volumetric water content (Benscoter et al. 2011), water can be assumed to stay in the pores without causing volume expansion. The bulk density of moist peat is ρ = (1 + MC)ρp. The properties of α-char and β-char are assumed to be the same.
The smouldering chemistry corresponding to the Scotland (SC) samples of subshrub and sphagnum high-moor peat (Rein et al. 2008; Cancellieri et al. 2012; Huang and Rein 2014) is selected for all three peat layers. Table 2 lists the kinetic and stoichiometric parameters. The heat of oxidation is related to the organic content as ΔHk = Ck(1 – vB,k). The surface peat reported in Benscoter et al. (2011) has a low bulk density and a low degree of decomposition, so the heat of combustion is set to a lower value than the high-density peat with high degree of decomposition reported in Frandsen (1987) and Leroy-Cancellieri et al. (2014). By integrating the heat flow measurements for peat samples (see Bergner and Albano 1993; Chen et al. 2011), we estimate that Cpo = 7.5 MJ kg−1 and Cao = Cbo = 15 MJ kg−1. The oxygen consumption coefficients in Eqns (13–15) are related to the heat of oxidation as vO2,k = ΔHk/13.1, where ΔHk is given in MJ kg−1 (Huggett 1980).

|
Base case
We arbitrarily choose a base case to investigate the smouldering process and front structure in detail (δt = 6 cm, δw = 3 cm and δb = 11 cm). The peat sample has a uniform bulk density of 40 kg m−3 and a wet layer of MCw = 180%. Air-dried peat is chosen for both the top and bottom layers (MCt = MCb = 10%). Using the method in Huang et al. (2015), the weakest ignition protocols required to ignite the dry top layer are 8.3 kW m−2 for 5 min, or 5.0 kW m−2 for 30 min. Based on this result and to ensure a successful ignition, a strong heating source ( kW m−2, similar to a flame) for 5 min is chosen as the ignition protocol. The predicted mass evolution of each species mi and the evolution of DOB and spread rate are shown in Figs 3(a) and (b). The instantaneous DOB is calculated by the deepest location at which most peat has been consumed (i.e. Yp < 5%). The spread rate is obtained by tracking the position of the peak temperature.
kW m−2, similar to a flame) for 5 min is chosen as the ignition protocol. The predicted mass evolution of each species mi and the evolution of DOB and spread rate are shown in Figs 3(a) and (b). The instantaneous DOB is calculated by the deepest location at which most peat has been consumed (i.e. Yp < 5%). The spread rate is obtained by tracking the position of the peak temperature.

|
Four different stages can be seen during propagation across each of the three different peat layers and at burnout: (I) t < 15 min, (II) 15 < t < 60 min, (III) 60 < t < 170 min and (IV) 170 < t < 270 min. When the smouldering front propagates through the wet layer (Stage II), the drying becomes fast while the peat consumption slows down. The spread rate decreases due to the heat sink of water, increasing the residence time for the exothermic char oxidation to drive the smouldering front in depth to the bottom layer. Once the bottom dry layer is burning (Stage III), the spread rate increases rapidly and the char layer grows. The original peat is degraded into char within 170 min, and afterwards, the char oxidation dominates the spread (Stage IV).
The temperature evolution with depth and time is shown in Fig. 4, along with the regression of the top surface. The peak temperature is found at 1–2 cm below the top surface. Although the peak temperature in the dry layers (Stage I and III) is predicted to be around 850°C – higher than the peak values (500–600°C) measured by Rein et al. (2008) – the peak temperatures across the wet layer (Stage II) is 550–600°C and agrees well with measurements. Fig. 4 also qualitatively shows the size of the reaction zones. The thickness of the high-temperature (exothermic oxidation) region grows in the dry layers (Stage I & III), whereas it decreases in the wet layer (Stage II) as well as near fuel burnout (Stage IV). The thickness of the lower temperature (drying) region follows a similar trend. At ~130 min, the smouldering front reaches the bottom and the boundary affects the fire propagation; burnout takes place at 270 min.

|
Fig. 5 shows results of the predicted temperature, reaction rates, MC and species profiles at different instants of time. During Stage I and II, the smouldering front is thin – around 2 cm thick. The thickness then increases to 5 cm in Stage III due to the growth of char layer (from 1 cm to 3 cm as seen in Fig. 5e), and then decreases to a thinner zone in Stage IV. The thickness of ash layer (Fig. 5f) continues to increases from zero to δa,max ≈ 2 cm at the bottom. After burnout, the residue left is very small in mass, and made of ash at the top and char below. This is the typical composition of the residue found after smouldering wildfires in the field (Moreno et al. 2011) and experiments (Zaccone et al. 2014).
Critical moisture and depth of burn
Critical moisture content for ignition and extinction
As peat MC increases, it requires more heat to dry the fuel, thus slowing down the spread rate (see Fig. 3b) and eventually, extinction occurs. This event defines the critical MC for extinction (MC*ex). The value of MC*ex depends on the properties across the vertical heterogeneous profile. This is shown in Fig. 6 where MC*ex is predicted to vary with the thicknesses of the top layer (δt, MCt = 10%) and the wet layer (δw). Above a critical line in Fig. 6, extinction occurs in the wet layer; below the line, no extinction occurs before burnout.

|
Fig. 6 shows that a smouldering fire is able to spread across very wet layers above 250% MC as the thickness of the top dry layer increases. On the other hand, the heat sink of water increases with δw, thus reducing MC*ex. For example, with δt = 8 cm, the MC*ex decreases from 256% to 195%, as the wet layer thickness δw increases from 2 to 8 cm.
If there is no top layer (δt = 0), the case becomes an ignition problem. Frandsen (1987, 1997) conducted a series of ignition experiments on multiple small and homogeneous peat samples of 4–5 cm thick, which had been successfully predicted in the previous work (Huang et al. 2015). For the current ignition protocol and peat properties, MC*ig is found to be 117% based on the method in Huang et al. (2015). The maximum critical value for ignition MC*ig,max reported by Frandsen (1987, 1997) is 145%. This value is included for reference in Fig. 6. The predictions show that MC*ex is always higher than MC*ig and explain for the first time the experimental observation in Wade et al. (1980) where the measured MC*ig of 65% was much lower than the MC*ex of 150%.
Depth of burn
After extinction, the final DOB is obtained. Fig. 7 shows the DOB v. MCw for several possible profiles. MC*ex is indicated as a jump in DOB: below MC*ex, the whole peat column (20 cm) is burnt, whereas above it, only the top dry layer (δt) plus 1–2 cm of the wet layer are consumed.

|
Sensitivity to moisture of the top layer
The moisture of the top layer (MCt) controls the possibility of ignition, and serves as an upstream condition to control the spread in the wet layer below. Fig. 8a shows the predicted MC*ex v. MCt for several cases. The value of MC*ex slowly decreases with the increasing MCt until it is near the critical value for ignition (MC*ig). Afterwards, MC*ex quickly drops to 117%, converging to MC*ig, and the system becomes an ignition problem. In addition, as δw increases, the curve becomes flatter (i.e. MC*ex becomes less sensitive to MCt). For example, in the base case (δt = 6 cm, δw = 3 cm ), when MCt increases from 10% to 100%, MC*ex only decreases from 192% to 173%.
Fig. 8b shows the corresponding DOB v. MC*ex and MCt for the base case, where four different regions (A–D) can be seen. If the top layer is very wet (Region A: MCt > MC*ig), no ignition occurs. If the moisture anywhere in the sample is less than the ignition threshold (Region B: MCi < MC*ig), no extinction occurs before burnout. These two zones were identified in the experiments of Frandsen (1987, 1997) and in the simulations of Huang et al. (2015). However, once ignited (MCt < MC*ig), there is an additional region of wetter conditions (Region C: MC*ig < MCw < MC*ex), where the whole peat column is also burnt but this has not been identified or explained before. Moreover, in Region D (MC*ex < MCw), only the top layer and a short depth of the wet layer burn, which was observed in the experiment of Benscoter et al. (2011).
Sensitivity to peat density
Fig. 9 shows that the bulk density of peat (ρp) affects the ignition and extinction criteria. The critical moisture for extinction is shown to be much larger than that for ignition (MC*ex > MC*ig) across the whole density range. For MC*ex, it first increases with ρp until reaching a peak around ρp = 100 kg m−3, and then slowly decreases. This result agrees with the duff experiment of Garlough and Keyes (2011), who found that MC*ex and DOB for lower density samples ( kg m−3) were smaller than higher density samples in depth (
kg m−3) were smaller than higher density samples in depth ( kg m−3). The peak in MC*ex implies that the sample density affects two competing mechanisms in the extinction of smouldering: heat transfer (via energy conservation in Eqn (3)) and oxygen supply (via energy conservation in Eqn (3) and permeability in Eqn (18)). On the other hand, the marked decrease in MC*ig in the high-density range is caused by the increase in thermal inertia (via energy conservation in Eqn (3)), as previously observed in Hartford (1989) and modelled in Huang et al. (2015). In addition, for this short 5-min ignition protocol, the results for MC*ex do not change for an external heat flux level
kg m−3). The peak in MC*ex implies that the sample density affects two competing mechanisms in the extinction of smouldering: heat transfer (via energy conservation in Eqn (3)) and oxygen supply (via energy conservation in Eqn (3) and permeability in Eqn (18)). On the other hand, the marked decrease in MC*ig in the high-density range is caused by the increase in thermal inertia (via energy conservation in Eqn (3)), as previously observed in Hartford (1989) and modelled in Huang et al. (2015). In addition, for this short 5-min ignition protocol, the results for MC*ex do not change for an external heat flux level  kW m−2, whereas the curve of MC*ig significantly drops in value as the external heat flux level decreases.
kW m−2, whereas the curve of MC*ig significantly drops in value as the external heat flux level decreases.

|
Modelling of natural peat samples
Benscoter et al. (2011) extracted cores from six different peat types in the Athabasca Bog, Canada (dominated by Sphagnum fuscum and Pleurozium schreberi) and divided them into column samples. Each peat type was treated differently for drying, according to three methods: field moisture (no drying); 2-week air drying; and 2-week air drying plus 48-h oven drying at 40°C – producing a total of 18 samples. The central portion of each column was tested inside a vertical box made of 1.3-cm ceramic fibreboard with the top open to the air.
Prior to testing, the columns were sliced into 3-cm layers, and the average values of MC, IC and bulk density were measured to capture the vertical profiles (similar to Fig. 1a). The bulk density of peat samples ranged from 2 to 90 kg m−3 with an average value of ~40 kg m−3, much lower than the samples in Frandsen (1987, 1997) and Rein et al. (2008). These profiles are used as inputs to the model. Other physical parameters are shown in Table 1; these are assumed to be independent of temperature. The ignition source in Benscoter et al. (2011) was a propane-fired radiator, placed above the top surface for 5 min. This is modelled by a heat flux of 30 kW m−2 for 5 min as a boundary condition, which is high enough to accommodate the flaming ignition of the top layer observed in the experiment. It is acceptable to model a strong ignition source this way because as shown in Fig. 6, MC*ex increases only slightly for δt < 1 cm, implying the influence of ignition protocol is limited to the top 1 cm.
Case study
We choose one representative case, the oven-dried mixed-species hollow sample 2 (Oven Hol 2), to study in detail the smouldering process. This sample is 21 cm high, and Table 3 lists the measured profiles of ρp, MC, and IC for each of seven 3-cm layers. The corresponding measurements for all 18 columns are available in Benscoter et al. (2011). In general, ρp increases with depth due to soil compaction and aging. The MC also increases with depth due to the proximity of the watertable. The average IC of the column is relatively high ( ), so for simulations we use the decomposition chemistry of a Siberian scheuchzeria and sphagnum transition peat, ICSI–B ≈ 8.8% (Cancellieri et al. 2012), the kinetic parameters of which were found in Huang and Rein (2014).
), so for simulations we use the decomposition chemistry of a Siberian scheuchzeria and sphagnum transition peat, ICSI–B ≈ 8.8% (Cancellieri et al. 2012), the kinetic parameters of which were found in Huang and Rein (2014).

|
Fig. 10 shows the predicted evolutions of the temperature and moisture for the Oven Hol 2 sample. The modelled smouldering fire lasts for ~110 min, close to ~90 min observed in the experiment. The column does not burn completely due to the very high moisture at z > 9 cm and the predicted DOB is 11.5 cm, in agreement with the experimental measurement of 9±3 cm. It can be seen in Fig. 10a that the temperature trends to decrease with the depth as the peat MC increases, and it drops rapidly after 90 min when the drying front reaches the wetter layer of MC = 373% at z = 12 cm where extinction occurs. After extinction, the high-temperature front is able to continue drying the peat until the residual column cools down completely.

|
Comparison of depths of burn
All 18 samples in Benscoter et al. (2011) were simulated. For the low-mineral peat types ( ), the smouldering chemistry of a Scotland subshrub and sphagnum high-moor peat, ICSC ≈ 2% (Cancellieri et al. 2012; Huang and Rein 2014) is used (see Table 2). For the high-mineral peat type (
), the smouldering chemistry of a Scotland subshrub and sphagnum high-moor peat, ICSC ≈ 2% (Cancellieri et al. 2012; Huang and Rein 2014) is used (see Table 2). For the high-mineral peat type ( ), the same Siberia (SI–B) peat as the Oven Hol 2 sample is used. Fig. 11 compares our predicted DOB to the measurements in Benscoter et al. (2011). The degree of agreement is measured by the R2 coefficient, which is 0.87. Despite the model limitations due to the 1-D assumption and the approximation of heat and mass transfer boundary conditions at the top surface (hc and hm), and considering the complexity of the fire process and the field samples, the predictions reported here are very good and outperformed any other peat fire model in the literature, e.g. Benscoter et al. (2011).
), the same Siberia (SI–B) peat as the Oven Hol 2 sample is used. Fig. 11 compares our predicted DOB to the measurements in Benscoter et al. (2011). The degree of agreement is measured by the R2 coefficient, which is 0.87. Despite the model limitations due to the 1-D assumption and the approximation of heat and mass transfer boundary conditions at the top surface (hc and hm), and considering the complexity of the fire process and the field samples, the predictions reported here are very good and outperformed any other peat fire model in the literature, e.g. Benscoter et al. (2011).

|
In general, the chemical and physical properties of peat (e.g. the heat of smouldering ΔHsm, heat capacity cp, conductivity k) vary with the depth and from site to site, which translates to a degree of uncertainty in model predictions. We have studied this uncertainty and found that both MC* and DOB increase with ΔHsm, but decrease with cp and k. In order to quantify how these variations (uncertainties) in these properties propagate into the modelling results (in particular the predicted DOB), we investigate ranges of parameter values for these peat properties taken from the literature: ΔHsm ∈ [9.5, 15] MJ kg−1 (Bergner and Albano 1993; Leroy-Cancellieri et al. 2014), cp,p ∈ [1500, 2000] J kg−1 K−1, and ks,p ∈ [0.8, 1.2] W m−1 K−1 (Jacobsen et al. 2003). The resulting ranges of predictions are shown as vertical error bars in Fig. 11. In comparison with the effect of peat MC, these properties have a small influence on DOB. Both for very dry peat (points in upper-right corner) and very wet peat (points in lower-left corner), the vertical uncertainty bars are too small to be seen. Only for the peat layer with moderate moisture (near MC*) do these properties have a significant influence on DOB (by 5–10 cm). In short, the main mechanism driving the in-depth spread of surface peat fires over high MC layers is heat transfer to dry the peat.
Conclusions
We developed a comprehensive 1-D model of a reactive porous media to investigate the in-depth spread of smouldering fires in vertical peat columns with heterogeneous profiles of density, MC and IC. The critical MCs and DOB are predicted. It is found that the smouldering combustion can spread over peat layers of very high moisture (MC > 250%) if the top dry layer is thick and the lower wet layer is thin. The critical moisture for extinction is found to be higher than that for ignition (MC*ex > MC*ig). The model simulates the experiments of all 18 natural peat samples in Benscoter et al. (2011), and the predicted DOB agrees well with experimental measurements. The influence on key thermo-physical properties of peat is investigated and found to be less important than the peat moisture, IC and bulk density. This study provides a physical understanding of the role of moisture in ignition and extinction in smouldering peat fires, and explains for the first time the phenomenon of smouldering in very wet peat layers.

|
Acknowledgements
The authors thank Prof. B. W. Benscoter (Florida Atlantic University), Prof. M. G. Davies (Ohio State University) and N. Prat (University College Dublin) for data and valuable discussions.
References
Benscoter BW, Thompson DK, Waddington JM, Flannigan MD, Wotton BM, de Groot WJ, Turetsky MR (2011) Interactive effects of vegetation, soil moisture and bulk density on depth of burning of thick organic soils. International Journal of Wildland Fire 20, 418–429.| Interactive effects of vegetation, soil moisture and bulk density on depth of burning of thick organic soils.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXlsFGlsLo%3D&md5=bf007bb32e6daa078bd254093327a707CAS |
Bergner K, Albano C (1993) Thermal analysis of peat. Analytical Chemistry 65, 204–208.
| Thermal analysis of peat.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK3sXkt1Skuw%3D%3D&md5=3f090aba0934fc30d9f549c50c0c1113CAS |
Cancellieri D, Leroy-Cancellieri V, Leoni E, Simeoni AYa, Kuzin A, Filkov AI, Rein G (2012) Kinetic investigation on the smouldering combustion of boreal peat. Fuel 93, 479–485.
| Kinetic investigation on the smouldering combustion of boreal peat.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC38XhtVGku7o%3D&md5=9c07dd4cd4fb434e39e6512b0981f433CAS |
Chen H, Zhao W, Liu N (2011) Thermal analysis and decomposition kinetics of Chinese forest peat under nitrogen and air atmospheres. Energy & Fuels 25, 797–803.
| Thermal analysis and decomposition kinetics of Chinese forest peat under nitrogen and air atmospheres.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXmtVensw%3D%3D&md5=63fa1e23395c45f79a770040af6af957CAS |
Davies GM, Gray A, Rein G, Legg CJ (2013) Peat consumption and carbon loss due to smouldering wildfire in a temperate peatland. Forest Ecology & Management 308, 169–177.
| Peat consumption and carbon loss due to smouldering wildfire in a temperate peatland.Crossref | GoogleScholarGoogle Scholar |
de Jonge H, Mittelmeijer-Hazeleger MC (1996) Adsorption of CO2 and N2 on soil organic matter: nature of porosity, surface area, and diffusion mechanisms. Environmental Science & Technology 30, 408–413.
| Adsorption of CO2 and N2 on soil organic matter: nature of porosity, surface area, and diffusion mechanisms.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK28XhtFWitg%3D%3D&md5=95f65b47b0cbf1b7fc20b7e3be745a1fCAS |
Frandsen WH (1987) The influence of moisture and mineral soil on the combustion limits of smoldering forest duff. Canadian Journal of Forest Research 17, 1540–1544.
| The influence of moisture and mineral soil on the combustion limits of smoldering forest duff.Crossref | GoogleScholarGoogle Scholar |
Frandsen WH (1997) Ignition probability of organic soils. Canadian Journal of Forest Research 27, 1471–1477.
| Ignition probability of organic soils.Crossref | GoogleScholarGoogle Scholar |
Garlough EC, Keyes CR (2011) Influences of moisture content, mineral content and bulk density on smouldering combustion of ponderosa pine duff mounds. International Journal of Wildland Fire 20, 589–596.
| Influences of moisture content, mineral content and bulk density on smouldering combustion of ponderosa pine duff mounds.Crossref | GoogleScholarGoogle Scholar |
Gorham E (1994) The future of research in Canadian peatlands: a brief survey with particular reference to global change. Wetlands 14, 206–215.
| The future of research in Canadian peatlands: a brief survey with particular reference to global change.Crossref | GoogleScholarGoogle Scholar |
Hadden RM, Rein G, Belcher CM (2013) Study of the competing chemical reactions in the initiation and spread of smouldering combustion in peat. Proceedings of the Combustion Institute 34, 2547–2553.
| Study of the competing chemical reactions in the initiation and spread of smouldering combustion in peat.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2cXhvV2ntbY%3D&md5=a9526bd00b43e630d30206a7f7c59628CAS |
Hartford R (1989) Smoldering combustion limits in peat as influenced by moisture, mineral content, and organic bulk density. In ‘Proceedings of the 10th Conference on Fire and Forest Meteorology’, 17–21 April, Ottawa, ON (Eds DC MacIver, H Auld, R Whitewood) pp. 282–286. (Atmospheric Environment Service: Downsview, ON)
Huang X, Rein G (2014) Smouldering combustion of peat in wildfires: Inverse modelling of the drying and the thermal and oxidative decomposition kinetics. Combustion & Flame 161, 1633–1644.
| Smouldering combustion of peat in wildfires: Inverse modelling of the drying and the thermal and oxidative decomposition kinetics.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2cXht1Cjs7Y%3D&md5=6bd168f67e53436d9c9258def31e1bdaCAS |
Huang X, Rein G, Chen H (2015) Computational smoldering combustion: predicting the roles of moisture and inert contents in peat wildfires. Proceedings of the Combustion Institute
| Computational smoldering combustion: predicting the roles of moisture and inert contents in peat wildfires.Crossref | GoogleScholarGoogle Scholar | , (In press)
Huggett C (1980) Estimation of rate of heat release by means of oxygen consumption measurements. Fire & Materials 4, 61–65.
| Estimation of rate of heat release by means of oxygen consumption measurements.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL3MXhslyktw%3D%3D&md5=2d04e7c4af93dbd85c093329829b0b24CAS |
Kim YH, Tong H, Daniels M, Boykin E, Krantz QT, McGee J, Hays M, Kovalcik K, Dye AJ, Gilmour MI (2014) Cardiopulmonary toxicity of peat wildfire particulate matter and the predictive utility of precision cut lung slices. Particle & Fibre Toxicology 11, 29–45.
| Cardiopulmonary toxicity of peat wildfire particulate matter and the predictive utility of precision cut lung slices.Crossref | GoogleScholarGoogle Scholar |
Lautenberger C, Fernandez-Pello C (2009) Generalized pyrolysis model for combustible solids. Fire Safety Journal 44, 819–839.
| Generalized pyrolysis model for combustible solids.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXotlOltL4%3D&md5=5feeb730d1659fd9516bd13a95778439CAS |
Leroy-Cancellieri V, Cancellieri D, Leoni E, Simeoni A, Filkov A (2014) Energetic potential and kinetic behavior of peats. Journal of Thermal Analysis & Calorimetry 117, 1497–1508.
| Energetic potential and kinetic behavior of peats.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2cXhtFeqs7%2FJ&md5=71fcee14e682c58523cf1722eb6e5adeCAS |
Moreno L, Jimenez ME, Aguilera H, Jimenez P, Losa A (2011) The 2009 smouldering peat fire in Las Tablas de Daimiel national park (Spain). Fire Technology 47, 519–538.
| The 2009 smouldering peat fire in Las Tablas de Daimiel national park (Spain).Crossref | GoogleScholarGoogle Scholar |
Ohlemiller T (1985) Modeling of smoldering combustion propagation. Progress in Energy & Combustion Science 11, 277–310.
| Modeling of smoldering combustion propagation.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL28XhsFWrtbY%3D&md5=9d69256b669e8ac6387e29d4ac3eb248CAS |
Page SE, Siegert F, Rieley JO, Boehm HDV, Jaya A, Limin S (2002) The amount of carbon released from peat and forest fires in Indonesia during 1997. Nature 420, 61–65.
| The amount of carbon released from peat and forest fires in Indonesia during 1997.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD38XosVCmu78%3D&md5=de5be6bef53f1d6ed9bf0771239b5938CAS | 12422213PubMed |
Poulter B, Christensen J, Norman L, Halpin PN (2006) Carbon emissions from a temperate peat fire and its relevance to interannual variability of trace atmospheric greenhouse gases. Journal of Geophysical Research, D, Atmospheres 111, D06301
| Carbon emissions from a temperate peat fire and its relevance to interannual variability of trace atmospheric greenhouse gases.Crossref | GoogleScholarGoogle Scholar |
Punmia B, Jain A (2005) ‘Soil Mechanics and Foundations.’ (Laxmi Publications: New Delhi, India)
Rappold AG, Stone SL, Cascio WE, Neas LM, Kilaru VJ, Carraway MS, Szykman JJ, Ising A, Cleve WE, Meredith JT, Vaughan-Batten H, Deyneka L, Devlin RB (2011) Peat bog wildfire smoke exposure in rural North Carolina is associated with cardiopulmonary emergency department visits assessed through syndromic surveillance. Environmental Health Perspectives 119, 1415–1420.
| Peat bog wildfire smoke exposure in rural North Carolina is associated with cardiopulmonary emergency department visits assessed through syndromic surveillance.Crossref | GoogleScholarGoogle Scholar | 21705297PubMed |
Rein G (2013) Smouldering fires and natural fuels. In ‘Fire Phenomena and the Earth System.’ (Ed. C Belcher) pp. 15–33. (Wiley & Sons: Oxford, UK)
Rein G, Cleaver N, Ashton C, Pironi P, Torero JL (2008) The severity of smouldering peat fires and damage to the forest soil. Catena 74, 304–309.
| The severity of smouldering peat fires and damage to the forest soil.Crossref | GoogleScholarGoogle Scholar |
Rein G, Cohen S, Simeoni A (2009) Carbon emissions from smouldering peat in shallow and strong fronts. Proceedings of the Combustion Institute 32, 2489–2496.
| Carbon emissions from smouldering peat in shallow and strong fronts.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXjvFyqsLw%3D&md5=5535a22b5c707b2090ca2d1ef508909bCAS |
Ryan KC, Frandsen WH (1991) Basal injury from smoldering fires in mature Pinus ponderosa laws. International Journal of Wildland Fire 1, 107–118.
| Basal injury from smoldering fires in mature Pinus ponderosa laws.Crossref | GoogleScholarGoogle Scholar |
Stephens SL, Finney MA (2002) Prescribed fire mortality of Sierra Nevada mixed conifer tree species: effects of crown damage and forest floor combustion. Forest Ecology & Management 162, 261–271.
| Prescribed fire mortality of Sierra Nevada mixed conifer tree species: effects of crown damage and forest floor combustion.Crossref | GoogleScholarGoogle Scholar |
Turetsky M, Benscoter B, Page S, Rein G, van der Werf GR, Watts A (2015) Global vulnerability of peatlands to fire and carbon loss. Nature Geoscience 8, 11–14.
| Global vulnerability of peatlands to fire and carbon loss.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2cXitFKltbbE&md5=c5d2c71f592345e74da9b275eb4185deCAS |
Wade D, Ewel J, Hofstetter R (1980) Fire in south Florida ecosystems. USDA Forest Service, South-eastern Forest Experiment Station, General Technical Report SE-17. (Asheville, NC)
Wagner CEV (1972) Duff consumption by fire in eastern pine stands. Canadian Journal of Forest Research 2, 34–39.
| Duff consumption by fire in eastern pine stands.Crossref | GoogleScholarGoogle Scholar |
Watts AC (2013) Organic soil combustion in cypress swamps: moisture effects and landscape implications for carbon release. Forest Ecology & Management 294, 178–187.
| Organic soil combustion in cypress swamps: moisture effects and landscape implications for carbon release.Crossref | GoogleScholarGoogle Scholar |
Yu F, Wei G, Zhang X, Chen K (2006) Two effective thermal conductivity models for porous media with hollow spherical agglomerates. International Journal of Thermophysics 27, 293–303.
| Two effective thermal conductivity models for porous media with hollow spherical agglomerates.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28XmtVSms7Y%3D&md5=2de59259feb2df6f0a4409c12d8dfb04CAS |
Zaccone C, Rein G, D’Orazio V, Hadden RM, Belcher CM, Miano TM (2014) Smouldering fire signatures in peat and their implications for palaeoenvironmental reconstructions. Geochimica et Cosmochimica Acta 137, 134–146.
| Smouldering fire signatures in peat and their implications for palaeoenvironmental reconstructions.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC2cXps12nsrs%3D&md5=43eea975a02aa38c9f9ec16ca1966828CAS |
1 Moisture content (MC) is defined on a dry basis as the mass of water divided by the mass of a dried sample, expressed as a percentage.
2 Inert content (IC) is defined on a dry basis as the mass of inorganic matter (minerals) divided by the mass of a dried sample, expressed as a percentage.