Free Standard AU & NZ Shipping For All Book Orders Over $80!
Register      Login
Marine and Freshwater Research Marine and Freshwater Research Society
Advances in the aquatic sciences
Shopping Cart: ( empty )
You are here: Home > Journals > MF > MF05132
RESEARCH ARTICLE
Contents Vol 57(3)

Corroborating the ages of walleye pollock (Theragra chalcogramma)

Daniel K. Kimura A C , Craig R. Kastelle A , Betty J. Goetz A , Christopher M. Gburski A and Alexander V. Buslov B
+ Author Affiliations
- Author Affiliations

A Alaska Fisheries Science Center, National Marine Fisheries Service, NOAA, 7600 Sand Point Way N.E., Seattle, WA 98115-6349, USA.

B Kamchatka Research Institute of Fisheries and Oceanography, Kamchatniro, 18 Naberezhnaya, Petropavlovsk-Kamchatsky, Russia 683602.

C Corresponding author. Email: dan.kimura@noaa.gov

Marine and Freshwater Research 57(3) 323-332 https://doi.org/10.1071/MF05132
Submitted: 2 July 2005  Accepted: 17 January 2006   Published: 27 April 2006

Abstract

Fish ageing researchers have long recognised the importance of validating age-reading methodologies. The strongest age validations require the acquisition of ageing structures from fish of known-ages, or specimens whose ages are appropriate for bomb carbon validation. Often such specimens are extremely difficult or impossible to acquire so researchers have sought alternatives to validation. The alternative to age validation is age corroboration. Corroboration of a fish ageing method occurs when fish ages are found to be consistent with some ancillary information when comparisons are made in an unbiased manner. The question pursued in this study is how desirable are such comparisons from a scientific viewpoint. Information is presented that corroborates otolith ages for walleye pollock (Theragra chalcogramma), one of the largest groundfish fisheries in the world. Walleye pollock ages were corroborated using marginal increment analysis, ages following the strong 1978 year class in the eastern Bering Sea, and a comparison of ages read from otoliths with ages read from vertebrae. A new statistical method is suggested for comparing otolith and vertebra age readings. The walleye pollock example demonstrated that corroborating evidence can improve confidence in fish ages and ageing techniques.

Extra keywords: age corroboration, age determination, age validation.


Acknowledgments

We thank Dr Gregor Cailliet and Mr Allen Andrews of the Moss Landing Marine Laboratories for their thoughtful, insightful, reviews. We also thank Ms Delsa Anderl of the Alaska Fisheries Science Center for several helpful comments.


References

Bakkala R. G., and Wespestad V. G. (1983). Walleye pollock. In ‘Condition of Groundfish Resources in the Eastern Bering Sea and Aleutian Islands Region in 1982’. (Eds R. G. Bakkala and L. L. Low.) pp. 1–37. NOAA Technical Memorandum NMFS F/NWC-42.

Beamish, R. J. , and McFarlane, G. A. (1983). The forgotten requirement for age validation in fisheries biology. Transactions of the American Fisheries Society 112, 735–743.
| Crossref | GoogleScholarGoogle Scholar | Beamish R. J., and McFarlane G. A. (1995). A discussion of the importance of aging errors, and an application to walleye pollock: the world’s largest fishery. In ‘Recent Developments in Fish Otolith Research’. (Eds D. H. Secor, J. M. Dean and S. E. Campana) pp. 545–565. (University of South Carolina Press: Columbia, SC.)

Brown, A. L. , and Bailey, K. M. (1992). Otolith analysis of juvenile walleye pollock Theragra chalcogramma from the western Gulf of Alaska. Marine Biology 112, 23–30.
| Crossref | GoogleScholarGoogle Scholar | Cailliet G. M., Martin L. K., Kusher D., Wolf P., and Welden B. A. (1983). Techniques for enhancing vertebral bands in age estimation of California elasmobranchs. In ‘Proceedings of the International Workshop on Age Determination of Oceanic Pelagic Fishes: Tunas, Billfishes, and Sharks’. (Eds E. D. Prince, and L. M. Pulos.) pp. 157–165. NOAA Technical Report NMFS 8.

Campana, S. E. (2001). Accuracy, precision and quality control in age determination, including a review of the use and abuse of age validation methods. Journal of Fish Biology 59, 197–242.
| Crossref | GoogleScholarGoogle Scholar | Chilton D. E., and Beamish R. J. (1982). ‘Age Determination Methods for Fishes Studied by the Groundfish Program at the Pacific Biological Station.’ Canadian Special Publication of Fisheries and Aquatic Sciences 60.

Coggins L. G., and Quinn II, T. J. (1998). A simulation study of the effects of aging error and sample size on sustained yield estimates. In ‘Fishery Stock Assessment Models’. (Eds F. Funk II, T. J. Quinn, J. Heifetz, J. N. Ianelli, J. E. Powers, J. F. Schweigert, P. J. Sullivan, and C.-I. Zhang.) pp. 955–975. Alaska Sea Grant College Program Report No. AK-SG-98–01. (University of Alaska Fairbanks: Fairbanks, AK.)

Guralnik D. B. (Ed.) (1972). ‘Webster’s New World Dictionary.’ (The World Publishing Company: New York.)

Ianelli J. N., Barbeaux S., Honkalehto T., Walters G., and Williamson N. (2002). Eastern Bering Sea walleye pollock stock assessment. In ‘Appendix A, Stock Assessment and Fishery Evaluation Report for the Groundfish Resources of the Eastern Bering Sea/Aleutian Islands Regions’. (Compiled by The Plan Team for the Groundfish Fisheries of the Bering Sea and Aleutian Islands.) pp. 33–120. (North Pacific Fishery Management Council: Anchorage, AK.)

Kalish J. M., Beamish R. J., Brothers E. B., Casselman J. M., Francis R. I. C. C., Mosegaard H., Panfili J., Prince E. D., Thresher R. E., Wilson C. A., and Wright P. J. (1995). Glossary for otolith studies. In ‘Recent Developments in Fish Otolith Research’. (Eds D. H. Secor, J. M. Dean and S. E. Campana.) pp. 723–729. (University of South Carolina Press: Columbia, SC.)

Kimura, D. K. , and Lyons, J. J. (1991). Between-reader bias and variability in the age-determination process. Fishery Bulletin 89, 53–60.
Lee D. W., Prince E. D., and Crow M. E. (1983). Interpretation of growth bands on vertebrae and otoliths of Atlantic bluefin tuna, Thunnus thynnus. In ‘Proceedings of the International Workshop on Age Determination of Oceanic Pelagic Fishes: Tunas, Billfishes, and Sharks’. (Eds E. D. Prince and L. M. Pulos.) pp. 61–69. NOAA Technical Report NMFS 8.

Mather, III, F. J. , and Schuck, H. A. (1960). Growth of bluefin tuna of the western North Atlantic. Fishery Bulletin 61, 39–52.
Munk K. M. (2001). Walleye pollock otolith aging: comparison of the techniques used by two agencies. Regional Information Report No. 5J01–06. Alaska Department of Fish and Game, Juneau, AK.

NPFMC (2005). ‘Fishery Management Plan for Groundfish in the Bering Sea and Aleutian Islands Management Area. January, 2005.’ (North Pacific Fishery Management Council: Anchorage, AK.)

Polat, N. , and Gümüs, A. (1996). Ageing of whiting (Merlangius merlangus euxinus, Nord., 1840) based on broken and burnt otoliths. Fisheries Research 28, 231–236.
| Crossref | GoogleScholarGoogle Scholar | Prince E. D., and Pulos L. M. (Eds) (1983). ‘Proceedings of the International Workshop on Age Determination of Oceanic Pelagic Fishes: Tunas, Billfishes, and Sharks. U.S. Department of Commerce.’ NOAA Technical Report NMFS 8.

Rao C. R. (1973). ‘Linear Statistical Inference and Its Applications.’ 2nd edn. (John Wiley and Sons: New York.)

Reeves, S. A. (2003). A simulation study of the implications of age-reading errors for stock assessment and management advice. ICES Journal of Marine Science 60, 314–328.
| Crossref | GoogleScholarGoogle Scholar | Tyler A. V., Beamish R. J., and McFarlane G. A. (1989). Implications of age determination errors to yield estimates. In ‘Effects of Ocean Variability on Recruitment and an Evaluation of Parameters used in Stock Assessment Models’. (Eds R. J. Beamish and G. A. McFarlane.) pp. 27–35. Canadian Special Publication in Fisheries and Aquatic Sciences 108.

Wintner, S. P. , and Cliff, G. (1999). Age and growth determination of the white shark, Carcharodon carcharias, from the east coast of South Africa. Fishery Bulletin 97, 153–169.


Yilmaz, S. , and Polat, N. (2002). Age determination of shad (Alosa pontica Eichwald, 1838) inhabiting the Black Sea. Turkish Journal of Zoology 26, 393–398.




Appendix 1. Statistical method for comparing two different ageing methods from two different age readers

The observations from the present study are essentially the different ages read from a particular fish by two different age readers using otoliths and vertebrae. These data were analysed using the standard percentage agreement statistic [(#agree/#aged) × 100]. Also, since ages from a particular fish, using either structure, should ideally lie on the line y = x, these data can be nicely summarised in cross-tabulations or on simple plots with the line y = x. We use cross-tabulations that avoid the problem of over plotting integer data.

To quantify the differences in the fits to the line of equality, we use the simple sum of squares of residuals, SSR = Σ (yi − xi)2 ; the larger the SSR, the poorer the fit. The mean square error (MSE) is defined as MSE = Σ (yi − xi)2 / n, where n is the number of fish aged in the comparison. Let the subscripts 1 and 2 refer to the age readers and let O and V refer to otolith and vertebra ages respectively. In what follows the sum on specimen i is made implicit, and the variables x, y are replaced by variables O1, O2, V1, V2 referring to structure and reader. We can consider three types of SSR:

  1. between readers: Σ (O1 − O2)2 and Σ (V1 − V2)2;

  2. between ageing structures: Σ (O1 − V1)2 and Σ (O2 − V2)2; and

  3. between readers and ageing structures: Σ (O1 − V2)2 and Σ (O2 − V1)2.

The third SSR should have the largest values since they should include error introduced by both the age structures and the age readers.

Generally these sums of squares, scaled by the true variance, can be treated as independent chi-square random variables for the purpose of constructing F-tests and testing hypotheses (see Rao 1973). To do this, all we need under the null hypothesis is that each ageing method is unbiased and has an independent random normal error of the same magnitude. If this is true, F-tests such as 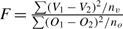MF05132_EI3.gif where n fish are aged will have d.f. = nv, no. This test can be used to test if vertebra agreement is as good as otolith agreement. If the between vertebra ages variance is greater than between otolith ages variance, then the F-test will tend to be significant.

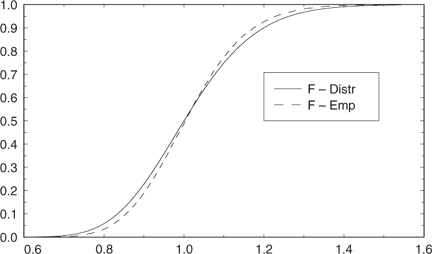
If we consider the modified F-test 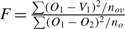MF05132_EI4.gif, this test can be used to test whether vertebra ages are significantly different to otolith ages. Because O1 occurs in the numerator and the denominator, the null distribution does not have the correct central F-distribution. However, simulation using normally distributed deviates (Appendix Fig. 1) indicated that this failure in assumption caused only a modest departure from the central F-distribution under the null hypothesis of no difference in structures. In addition, the change in distribution made the test statistic more conservative. That is, the modified statistic would be even more significant than indicated by the central F-distribution (i.e. the nominal P-values). Alternatively, the significance of the modified test statistic can be estimated from the empirical modified F-distribution (Appendix Fig. 1).

Another possibility is to read another set of independent otolith readings from either age reader so that O1 does not appear in both the numerator and denominator. In this case it would appear that the standard F-test, and not the modified F-test, could be applied. We should not lose sight that the residual SSR = Σ (yi − xi)2 provide a simple and fairly intuitive statistical way of analysing different ageing methods.


Appendix Fig. 1. The cumulative distribution function of the central F-distribution compared with an empirical distribution of a modified F-statistic calculated when the numerator and denominator contain identical age sequences, and n = 200 for each sample (see text).
FA1