Hierarchical variance decomposition of fish scale growth and age to investigate the relative contributions of readers and scales
L. Aulus-Giacosa A B , J.-C. Aymes A , P. Gaudin
A B , J.-C. Aymes A , P. Gaudin  A and M. Vignon
A and M. Vignon  A
A
A ECOBIOP, INRA, Univ. Pau and Pays Adour, E2S UPPA, F-64310 Saint-Pée-sur-Nivelle, France.
B Corresponding author. Email: lucie.aulus@inra.fr
Marine and Freshwater Research 70(12) 1828-1837 https://doi.org/10.1071/MF19059
Submitted: 18 August 2018 Accepted: 29 May 2019 Published: 29 August 2019
Journal Compilation © CSIRO 2019 Open Access CC BY-NC-ND
Abstract
Correct estimation of interindividual variability is of primary importance in models aiming to quantify population dynamics. In a fisheries context, individual information such as age and growth is often extracted using scales; however, the rationale for using a given scalimetric method (i.e. number of scales per individual and number of readers) is rarely discussed, but different sources of variance may affect the results. As a case study, we used scale growth and age of brown trout (Salmo trutta) caught in the Kerguelen Islands. Based on a nested design (readings of four scales per fish by two independent readers), we decomposed variance in growth and age according to fish (interindividual level), scales (intraindividual level) and readers by using repeatability analysis. The results highlight that most variation is attributable to fish. Readers and scales contribute little to interindividual variance, suggesting that inference was insensitive to intraorganism biological variation. Using additional scales or readers was an inefficient use of sampling resources. We argue that variance decomposition should be widely used for studies aimed at modelling natural variability in life history traits. This would improve our knowledge of the implications of measurement error, helping rationalise and define appropriate sampling strategies.
Additional keywords: introduced species, measurement errors, sampling strategy, scalimetry.
Introduction
Understanding patterns of natural variability is a major issue in evolutionary ecology, because variability can be described at the taxonomic, community, population, individual and evolutionary levels (Landres et al. 1999). However, populations have long been studied without concern for individual variability or inter-relationships within populations (Łomnicki 1999). With the rise of the holistic approach, most recent studies confound the organisational components of ecosystems from the individual level to the ecosystem organisational level. In particular, individuals in a population obviously differ in terms of behaviour, habitat use, reproduction or migratory strategy to optimise their fitness (Roff 1996; Fromentin et al. 2009).
Interindividual variability has attracted much attention during the past two decades because it could have severe consequences on the estimation of population dynamics. Thus, identifying sources of variability underlying interindividual differences is important for developing relevant sampling designs aimed at answering evolutionary questions with appropriate statistical power (Johnson et al. 2015). In this field, significant developments have been based largely on the use of mixed and individual-based modelling that explicitly considers individuals as variable entities (Baayen et al. 2008; Thorson and Minto 2015). As an example, in fish biology, as with many other taxa, individual growth is modelled using the von Bertalanffy growth function (VBGF). Growth parameters are highly dependent upon an accurate description of the individual age–length relationship (Hatch and Jiao 2016). Moreover, estimates of individual growth in population models can be significantly different while accounting for or failing to account for interindividual variability, leading to evolutionary misinterpretations or to inappropriate conservation decisions (Shelton and Mangel 2012; Vincenzi et al. 2014; Harris et al. 2018).
Teleost scales are an important and widely used tool in ichthyological studies (Goodrich 1907; Panfili et al. 2002). Among other applications, scales provide access to life history traits, such as age (Erickson 1983), growth (Kipling 1962; Ottaway 1978) and migration (Bagenal et al. 1973). Readings of the calcified structure can provide accurate estimates of growth and age at both daily and yearly scales. This offer a basis for recording growth patterns from the individual to the population level (Casselman 1990; Schreck and Moyle 1990). Over time, researchers have come to accept that analysing several scales from the same individual provides more reliable information (Panfili et al. 2002). On a theoretical basis, the number of scales required to determine growth and age depends on the species studied (Chilton and Beamish 1982), but the reason for using a given number of scales is rarely mentioned explicitly in the literature. In addition, inconsistency appears among studies dealing with the same fish species for the same purpose. Even if the accuracy of age data has been demonstrated in the published papers initially (Dahl 1907; Ward Cutler 1918; through mark–recapture datasets), Beamish and McFarlane (1983) pointed out that only a few consecutive studies have re-examined the methodology of those initial studies. Campana (2001) and Spurgeon et al. (2015) concluded that over the past 30 years the number of age validation studies has increased; however, there are still some deficiencies in integrating variability in models or in justifying the selected methods. Given the prominent importance of individual variation, the number of scales used for recording relevant individual life history (age, growth, migration) is a matter of interest. Setting up a sampling design with the minimum number of scales required is, indeed, a reasonable shortcut to avoid redundancy and a waste of resources. Variability in growth and age among individuals can be assessed by means of repeatability (characterised as the degree of agreement among measurements). By delineating annuli (yearly rings deposited during winter) and measuring the associated interannuli spacing, one can estimate an individual’s growth trajectory and migratory status (Elliott and Chambers 1996); however, measurements may vary across readers and scales. Therefore, establishing measurement repeatability is important in order to disentangle methodological from biological variance and to increase reliability in the study of evolutionary patterns.
To investigate to what extent biological variability in scale growth and age arises from either individual variation or methodological variation, the brown trout (Salmo trutta) was used as a case study. Variation in scale growth and age was decomposed in an explicit nested quantitative manner (i.e. extracting the respective contribution of readers, scales and individuals). Decomposition of variance is necessary to assess the sensitivity of growth and ageing measurements to realistic levels of scale or reader variability and to efficiently reallocate laboratory time to ecological issues.
Material and methods
Species and study area
The brown trout is a facultative anadromous salmonid species (Acolas et al. 2012; Dodson et al. 2013), with some individuals spending their entire life cycle in fresh water (resident fish), whereas others migrate to sea (anadromous fish). Among other salmonids, brown trout was successfully introduced into a dozen rivers in the subantarctic Kerguelen Islands between 1955 and 1979. This archipelago, located in the Southern Ocean (49°S, 70°E), was previously a fish-free landscape. The complete history of salmonid introduction to the islands is recounted in Lecomte et al. (2013). Since the introduction of fish to the Kerguelen Islands, long-term monitoring has been implemented for a better understanding of the causes and processes of colonisation (Labonne et al. 2013).
To test for the robustness of observations of the growth and age of captured brown trout, three streams with contrasting environments were selected, namely the Norvégienne, Manchot and Rohan rivers (Fig. 1), hereafter named Norvegienne, Manchot and Rohan respectively. The main characteristics of the streams are described in Table 1. Electro- and net fishing were conducted between 2010 and 2016. Because brown trout is a migratory species, resident and anadromous fish (hereafter referred to as ‘phenotype’) were primarily identified based on morphological criteria: length–weight relationship (Jonsson 1985) and colouration (Quigley et al. 2006). A total of 60 brown trout were analysed, with 20 individuals per site in a calibrated resident : anadromous fish ratio of 75% resident : 25% anadromous for Rohan and 55 : 45% for the two other streams (Table 2). The fork length (FL) of the fish at capture ranged from 88 to 770 mm (mean ± s.d., 333.2 ± 183.2 mm).

|
Data collection
Because the scales collected could be damaged and thus rendered useless by regeneration (Borgenson et al. 2014) and resorption (Kacem et al. 2013), numerous scales from each fish were removed from the optimal zone, specifically the second rank, below the dorsal fin and above the lateral line (Elliott and Chambers 1996). For each fish, four scales that were not regenerated nor resorbed were selected and investigated (Bereiter-Hahn and Zylberberg 1993). Selected scales were mounted and photographed (original scale in micrometres) under transmitted light using a stereomicroscope (Olympus SZX-16) and attached camera (Olympus DP72). Photographs were processed and saved using CellSens Entry microimaging software. Ageing and measurements were done by two readers (F. Guéraud and L. Aulus-Giacosa) with different degrees of expertise (2 v. 10 years’ experience) using ImageJ software (ver. 1.51u, National Institutes of Health, see https://imagej.net/Downloads; Abràmoff et al. 2004) on a total of 240 scales in a double-blind and independent manner.
Anadromous fish were distinguished from resident fish because the growth rate of brown trout in fresh water is generally less than the growth rate recorded at sea (Elliott and Chambers 1996; Jarry et al. 2018). Because scale growth is used as a proxy for somatic growth, an increase in the intercirculi spacing on scales is a good proximate indicator of migration. This criterion was used for anadromous fish to determine the size of scales at migration (measured from the core to the circulus corresponding to migration) and age at migration (counts of annuli until the intercirculi spacing increases).
Age was determined by counting the number of annuli on a scale (Borgenson et al. 2014) and total age (TA) was recorded. Freshwater age (FA) corresponds to the number of years spent in freshwater. For anadromous fish, FA was determined by counting the number of annuli before marine migration using the criterion of intercirculi spacing. For resident fish, FA was equal to TA.
Scale growth (interannuli spacing; µm) was measured along the main longitudinal axis from the core to the total radius (TR). The freshwater radius (FR) corresponds to freshwater growth. For anadromous fish, FR was measured on a scale from the core until the circulus before migration according to the criterion of intercirculi spacing. For resident fish, FR was equal to TR. The mean (±s.d.) position of the annuli for freshwater growth are given in Table 3. Further details on the mean position and mean freshwater growth by phenotype are given in Fig. S1, available as Supplementary material to this paper.

|
Hierarchical decomposition of variance
Variance was decomposed hierarchically in a nested and crossed manner, namely fish–reader–scale (Fig. 2) to determine which levels account for the variance in growth and age. Sixty fish were sampled from three populations (Population) with samples taken from two phenotypes (Phenotype). For each fish (Fish), two readers (F. Guéraud and L. Aulus-Giacosa) (Reader) made independent readings on four selected scales (Scale) in a double-blind manner (i.e. two readers independently read each scale; this could be done on several scales for each fish).
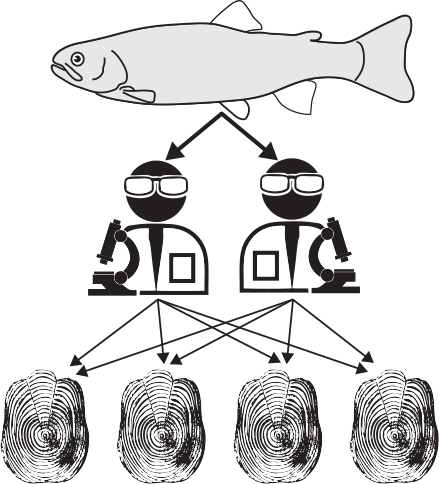
|
To decompose the variance, two response variables were examined through measurements of repeatability (r). The repeatability of scale measurements (an approximation of somatic growth) and age estimates was investigated. Repeatability ranges from 0 to 1 and expresses the proportion of variation explained by the considered level (Bell et al. 2009; Wolak et al. 2012). For each variable, the value taken by r is the proportion of variance explained by the variable and reflects its contribution to overall variance. To estimate repeatability, we used the newly developed method from Stoffel et al. (2017) as implemented in the rptR R package (ver. 0.9.21, see https://cran.r-project.org/web/packages/rptR/index.html; in R, ver. 3.4.4, R Foundation for Statistical Computing, Vienna, Austria). This package fits mixed-effects models by parametric bootstrapping (two Monte Carlo simulation steps) to quantify the uncertainty of repeatability. In our case, we simulated models with 1000 parametric bootstraps and tested the null hypothesis using a likelihood ratio test.
Population and Phenotype were both added as fixed effects in the variance decomposition. Fish, Reader and Scale were considered random variables to explain the variance of scale growth and age. Because growth is sharply contrasted between marine and freshwater habitats, we considered Phenotype as a fixed effect. Similarly, Population was considered a fixed effect because it maximised the log-likelihood.
In addition, we considered Reader as random because we hypothesised that readings subjectively correlated with scales and therefore should more widely reflect the inter-reader effect. Calculations considering Reader as a fixed effect were also performed and did not change the results (Fig. S2). To compare phenotype, we omitted the Phenotype fixed effect and accordingly divided the datasets into two parts, each of them being analysed as stated previously (focusing exclusively on Fish, Reader and Scale effects).
For the present study, variables related to age (FA and TA) were treated as Poisson-distributed data (Chi-Square goodness of fit for Poisson distribution, P = 1.70 × 10–14 for TA and P = 1.00 × 10–8 for FA) and scale growth was approximated and treated as Gaussian (D’Agostino normality test, PSkewness Test = 2.55 × 10–9, PKurtosis Test = 1.30 × 10–1 for TR; PSkewness Test = 1.10 × 10–13, PKurtosis Test = 0.01 for FR). Codes and fully worked examples are available in SCRIPT.R and data.RData of the Supplementary material. The results for r are given with 95% confidence intervals (CI) and the P-value of the likelihood ratio test. For the Poisson-distributed data, the original scale approximations were used because they are the exact solution of the general linear mixed model (GLMM) compared with link scales approximations, which are approximations; however, in this study, the two approximations gave very similar results.
Results
Population accounted for most of the variance (~40% for growth measures (TR, FR) and 15% for annuli counts (TA, FA)), highlighting an important contrast among the three localities in terms of growth and age.
Variance decomposition of scale growth: TR and FR
Variance in growth as interpreted with scale measurements was primarily explained by interindividual differences. Exact values of repeatability are given in Table 4 with 95% CIs and P-values. Fish alone explained more than 96% of the phenotypic variance of TR (Fig. 3a) and 53% of FR (Fig. 4a). By contrast, the proportions of variance explained by Reader and Scale were not consistent in the decomposition of growth (Fig. 3b, c, 4b, c). For both TR and FR, the combined effect of Reader and Scale corresponded to <1% of the total variance and Reader for FR. In addition, growth was harder to decompose for anadromous fish. Although Phenotype was not consistent in accounting for the variance of TR (r = 4.55 × 10–3; 95% CI 6.71 × 10–4–1.36 × 10–2), its effect on FR became greater (r = 0.364; 95% CI 0.202–0.536), reflecting the difficulty of locating the circulus corresponding to migration at sea.
Variance decomposition for TA read on scales and FA
Exact values of repeatability are given in Table 5, with 95% CIs and P-values. Fish explained the main proportion of the variance in ages read on scales: 53% for TA (Fig. 5a) and almost 40% for FA (Fig. 6a). By contrast, Reader and Scale were inconsistent factors for explaining the variance in TA and FA (Fig. 5b, c, 6b, c; Table 5). In addition, Phenotype explained 2% of the variance in TA and 6% in FA. Contrary to measures of growth (TR and FR), Phenotype explained a greater proportion of variance in age models (TA and FA), meaning that environmental conditions (i.e. freshwater v. marine) increase the difficulty of age readings, especially for anadromous fish, where an age at migration had to be determined. The number of annuli counted before migration (FA) was less repeatable than total age (TA) for Fish (r = 0.392 and 0.539 respectively; Fig. 5a, 6a).

|
Comparison of repeatability for resident and anadromous fish
The results obtained by separating Phenotypes are given in Table 6. Because TR was equal to FR and TA was equal to FA for resident fish, the results are the same for both pairs of variables. Variance decomposition was globally similar between resident and anadromous fish, with the notable exception of FA and, to a lesser extent, FR. The variance explained by Fish was reduced for FA and FR compared with TR and TA respectively for anadromous fish, highlighting the difficulty and subjectivity in locating the circulus corresponding to age at migration. The repeatability of interindividual differences in FA was sharply reduced for anadromous fish compared with resident fish (r = 0.167 and 0.584 respectively). In addition to the abovementioned fact that Phenotype has a noteworthy effect on FA decomposition, the proportion of variance in TR explained by Fish remains high for any phenotype, supporting our previous results that total scale growth is primarily explained by interindividual differences, regardless of Reader and Scale.

|
Discussion
The motivating problem for our study was how to most effectively sample, based on biological variance, in order to appropriately model dynamics. Apart from the consensus acceptance that the correct zone for sampling scales in salmonids is the first rows around the lateral line between the pectoral and the anal fins (Ombredane and Richard 1990) and that measures have to be taken along the major scale axis (maximal length from the core of the scale to the border), the number of scales that need to be read to explain relevant individual information is still vague in the literature. Furthermore, a statistical issue in scalimetry is how many scales from fish should be used to improve precision in readings (Haraldstad et al. 2016).
Decomposition of repeatability on growth and age was performed and shows that most of the variability in repeatability is attributable to Fish. More generally, at least 50% of the interindividual variance is related to real interindividual variability, not to methodological or artefactual issues (Scale or Reader related), when investigating growth and TA. TR had the highest Fish repeatability, regardless of the reader and the chosen scale; therefore, increasing the number of scales examined is not necessary for capturing interindividual variability in growth because no significant effect has been recorded for Scale.
This study also suggests further issues associated with identifying migration. Compared with total variables (i.e. TR and TA), both freshwater variables (FR and FA) exhibited lower Fish repeatability, highlighting the difficulty and subjectivity in locating the migration point; however, the results arising from the global dataset encompass two distinct phenotypes. Consequently, when separating the phenotype into two datasets, we observed that the repeatability of Fish increased for FR (by a factor of 2) and decreased for FA (by a factor of 3). Those results globally confirmed that the determination of size through scale size and age at migration is a difficult task. Given the importance of this task to studies aiming to investigate ecological or evolutionary patterns of migration in many anadromous fish species, it is essential to quantify the uncertainty associated with locating the migration point.
In this paper, as in many others (Kimura and Lyons 1991), the percentage of agreement in age estimations between readers was reasonably low: 65 and 60% for TA and FA respectively. The difficulty for readers in ageing fish from multiple structures (scales, otoliths) has long been an issue in many species. To avoid a potential lack of precision, some studies have made the choice to only conserve scales where agreement between scales or readers was established. Nevertheless, by doing so, only a fraction of a fish’s life history may be selected and investigated. Consequently, the variability of life histories present in a population may be biased towards some more understandable pattern that does not necessarily reflect overall natural variability. Alternatively, one can estimate in a quantitative way the respective contributions of readers, scales and individuals to the precision of the information to be analysed. Quantifying the effect of those confounding factors allows extraction of relevant interindividual variability. Only such a decomposition can determine the legitimacy of ignoring scale-related variance. Even if methodological biases in interindividual variability are not significant in this study, they could be substantially reduced by appropriately quantifying reader variance by stream and environment (freshwater v. marine).
The present study provides a case study that quantifies the sources of variance in age and size. Because errors frequently arise either from disagreements between scales or between readers, associated variances should be explicitly integrated into admitting-errors models, such as growth models (Cope and Punt 2007; Shelton and Mangel 2012; Hatch and Jiao 2016). This is particularly true in an evolutionary context when the proper determination of fish length and age at migration, used as threshold traits in the decision to migrate, is necessary to produce reaction norms for migration (Dieckmann and Heino 2007; Hutchings 2011; Jonsson et al. 2016). Indeed, preliminary analysis to quantify errors should be a prerequisite to any study because it could provide valuable insights for accurate modelling of individual variability. Such understanding of interindividual variability should serve to better estimate population dynamics and could have several applications in stock assessment and conservation (Harris et al. 2018).
Inferring growth for fish or other taxa intrinsically depends on an accurate description of the age–length relationship, which may be undermined by measurement errors and ageing errors. Growth is an important life history trait potentially associated with fitness through sexual maturity and the mortality rate (Pettersson et al. 1996; Wysujack et al. 2009). In many taxa, such as mammals (English et al. 2012), birds (Tjørve and Tjørve 2010) or reptiles (Lehman and Woodward 2008), growth is widely modelled using the VBGF (Von Bertalanffy 1938). Not considering individual variability may lead to over- or underestimation of the VBGF parameters such as theoretical maximum length L∞ and the growth coefficient k (Vincenzi et al. 2014, 2016; Harris et al. 2018; see Fig. S3; Table S1). Such errors affect our ability to understand the evolution of life history traits by comparing populations whose locations differ at different times.
A surprisingly high number of studies ignore the decomposition of variance and the implications of their methodologies on the estimation of parameters. Every researcher aims to answer a scientific issue while designing effective studies in terms of both time and funding. Not extending enough effort in data acquisition leads to underpowered analysis, whereas the reverse leads to overpowered analysis. The waste of resources can be considerable in both cases (Wolak et al. 2012; Johnson et al. 2015). Repeatability is an important feature in research, both to be able to reproduce our own studies and to compare with others (Cassey and Blackburn 2006). Unfortunately, the rationale for using a given scalimetric method in fish biology is rarely discussed, and even neglected; therefore, it is sometimes nearly impossible to access the precise methodology (numbers of scales or readers), precluding exact reproduction of experiments. In the present study, the data highlight the importance of individual variability within populations of brown trout in the Kerguelen Islands and enable us to avoid the unnecessary and time-consuming use of multiple scale readings (see Fig. S3; Table S1). In other contexts, the methodological approach (numbers of readers and scales by fish) should be similarly justified and discussed on a case-by-case basis.
In conclusion, decomposition of variance should be a prerequisite to any study aiming to quantify population dynamics through the growth of individuals. If neglecting methodological variance has an effect on the variables studied, the time spent in the laboratory cannot be adequately allocated to focus on biological variability. In addition, failing to disentangle the effects of biological and methodological variance could prevent the relevant investigation of ecological and evolutionary patterns.
Conflicts of interest
The authors declare that they have no conflicts of interest.
Declaration of funding
This research did not receive any specific funding.
Acknowledgements
The authors thank all the ecological and logistic staff from IPEV (Institut polaire français Paul-Emile-Victor, the French Polar Institute) who were involved in the field sampling of scales. The authors thank the experimental facility Ecologie Comportementale des Poissons (ECP) of the UMR INRA/UPPA 1224 ECOBIOP. Moreover, the authors especially thank F. Gueraud for technical help with scalimetry and data acquisition, and J. Labonne and M. Buoro for statistical advice. The authors are also grateful to two anonymous reviewers who helped improve the first version of this manuscript.
References
Abràmoff, M. D., Magalhães, P. J., and Ram, S. J. (2004). Image processing with ImageJ. Biophotonics International 11, 36–42.Acolas, M. L., Labonne, J., Baglinière, J. L., and Roussel, J. M. (2012). The role of body size versus growth on the decision to migrate: a case study with Salmo trutta L. Naturwissenschaften 99, 11–21.
| The role of body size versus growth on the decision to migrate: a case study with Salmo trutta L.Crossref | GoogleScholarGoogle Scholar | 22101839PubMed |
Baayen, R. H., Davidson, D. J., and Bates, D. M. (2008). Mixed-effects modeling with crossed random effects for subjects and items. Journal of Memory and Language 59, 390–412.
| Mixed-effects modeling with crossed random effects for subjects and items.Crossref | GoogleScholarGoogle Scholar |
Bagenal, T. B., Mackereth, F. J., and Heron, J. (1973). The distinction between brown trout and sea trout by the strontium content of their scales. Journal of Fish Biology 5, 555–557.
| The distinction between brown trout and sea trout by the strontium content of their scales.Crossref | GoogleScholarGoogle Scholar |
Beamish, R. J., and McFarlane, G. A. (1983). The forgotten requirement for age validation in fisheries biology. Transactions of the American Fisheries Society 112, 735–743.
| The forgotten requirement for age validation in fisheries biology.Crossref | GoogleScholarGoogle Scholar |
Bell, A. M., Hankison, S. J., and Laskowski, K. L. (2009). The repeatability of behaviour: a meta-analysis. Animal Behaviour 77, 771–783.
| The repeatability of behaviour: a meta-analysis.Crossref | GoogleScholarGoogle Scholar | 24707058PubMed |
Bereiter-Hahn, J., and Zylberberg, L. (1993). Regeneration of teleost fish scale. Comparative Biochemistry and Physiology – A. Physiology 105, 625–641.
| Regeneration of teleost fish scale.Crossref | GoogleScholarGoogle Scholar |
Borgenson, L., Clemens, B., Bowden, K., and Gunckel, S. (2014). Fish life history analysis project: methods for scale analysis. Information Report 2014-10, Oregon Department of Fish and Wildlife, Corvallis, OR, USA.
Campana, S. E. (2001). Accuracy, precision and quality control in age determination, including a review of the use and abuse of age validation methods. Journal of Fish Biology 59, 197–242.
| Accuracy, precision and quality control in age determination, including a review of the use and abuse of age validation methods.Crossref | GoogleScholarGoogle Scholar |
Casselman, J. M. (1990). Growth and relative size of calcified structures of fish. Transactions of the American Fisheries Society 119, 673–688.
| Growth and relative size of calcified structures of fish.Crossref | GoogleScholarGoogle Scholar |
Cassey, P., and Blackburn, T. M. (2006). Reproducibility and repeatability in ecology. Bioscience 56, 958–959.
| Reproducibility and repeatability in ecology.Crossref | GoogleScholarGoogle Scholar |
Chilton, D. E., and Beamish, R. J. (1982). Age determination methods for fishes studied by the Groundfish Program at the Pacific Biological Station. Canadian Special Publication of Fisheries and Aquatic Sciences 60. (Department of Fisheries and Oceans: Ottawa, ON, Canada.) Available at http://publications.gc.ca/collections/collection_2016/mpo-dfo/Fs41-31-60-eng.pdf [Verified 26 August 2019].
Cope, J. M., and Punt, A. E. (2007). Admitting ageing error when fitting growth curves: an example using the von Bertalanffy growth function with random effects. Canadian Journal of Fisheries and Aquatic Sciences 64, 205–218.
| Admitting ageing error when fitting growth curves: an example using the von Bertalanffy growth function with random effects.Crossref | GoogleScholarGoogle Scholar |
Dahl, K. (1907). ‘The Scales of the Herring as a Mean of Determining Age, Growth and Migration. Report on Norwegian Fishery and Marine Investigations, Vol. 2, number 6.’ (Fiskeridirektoratets Havforskningsinstitutt: Bergen, Norway.)
Dieckmann, U., and Heino, M. (2007). Probabilistic maturation reaction norms: their history, strengths and limitations. Marine Ecology Progress Series 335, 253–269.
| Probabilistic maturation reaction norms: their history, strengths and limitations.Crossref | GoogleScholarGoogle Scholar |
Dodson, J. J., Aubin-Horth, N., Thériault, V., and Páez, D. J. (2013). The evolutionary ecology of alternative migratory tactics in salmonid fishes: alternative migratory tactics as threshold traits. Biological Reviews of the Cambridge Philosophical Society 88, 602–625.
| The evolutionary ecology of alternative migratory tactics in salmonid fishes: alternative migratory tactics as threshold traits.Crossref | GoogleScholarGoogle Scholar | 23347290PubMed |
Elliott, J., and Chambers, S. (1996). ‘A Guide to the Interpretation of Sea Trout Scales.’ (National Rivers Authority: Bristol, UK.)
English, S., Bateman, A. W., and Clutton-Brock, T. H. (2012). Lifetime growth in wild meerkats: incorporating life history and environmental factors into a standard growth model. Oecologia 169, 143–153.
| Lifetime growth in wild meerkats: incorporating life history and environmental factors into a standard growth model.Crossref | GoogleScholarGoogle Scholar | 22108854PubMed |
Erickson, C. M. (1983). Age determination of manitoban walleyes using otoliths, dorsal spines, and scales. North American Journal of Fisheries Management 3, 176–181.
| Age determination of manitoban walleyes using otoliths, dorsal spines, and scales.Crossref | GoogleScholarGoogle Scholar |
Fromentin, J.-M., Ernande, B., Fablet, R., and de Pontual, H. (2009). Importance and future of individual markers for the ecosystem approach to fisheries. Aquatic Living Resources 22, 395–408.
| Importance and future of individual markers for the ecosystem approach to fisheries.Crossref | GoogleScholarGoogle Scholar |
Goodrich, E. S. (1907). On the scales of fish, living and extinct, and their importance in classification. Proceedings of the Zoological Society of London 77, 751–773.
| On the scales of fish, living and extinct, and their importance in classification.Crossref | GoogleScholarGoogle Scholar |
Haraldstad, T., Haugen, T. O., Borgstrøm, R., and Jonsson, B. (2016). Increased precision of growth data gained by reading multiple scales from each individual of Atlantic salmon (Salmo salar L.). Fauna Norvegica 36, 1–7.
| Increased precision of growth data gained by reading multiple scales from each individual of Atlantic salmon (Salmo salar L.).Crossref | GoogleScholarGoogle Scholar |
Harris, J. E., Newlon, C., Howell, P. J., Koch, R. C., and Haeseker, S. L. (2018). Modelling individual variability in growth of bull trout in the Walla Walla River Basin using a hierarchical von Bertalanffy growth model. Ecology Freshwater Fish 27, 103–115.
| Modelling individual variability in growth of bull trout in the Walla Walla River Basin using a hierarchical von Bertalanffy growth model.Crossref | GoogleScholarGoogle Scholar |
Hatch, J., and Jiao, Y. (2016). A comparison between traditional and measurement-error growth models for weakfish Cynoscion regalis. PeerJ 4, e2431.
| A comparison between traditional and measurement-error growth models for weakfish Cynoscion regalis.Crossref | GoogleScholarGoogle Scholar | 27688963PubMed |
Hutchings, J. A. (2011). Old wine in new bottles: reaction norms in salmonid fishes. Heredity 106, 421–437.
| Old wine in new bottles: reaction norms in salmonid fishes.Crossref | GoogleScholarGoogle Scholar | 21224878PubMed |
Jarry, M., Beall, E., Davaine, P., Guéraud, F., Gaudin, P., Aymes, J.-C., Labonne, J., and Vignon, M. (2018). Sea trout (Salmo trutta L.) growth patterns during early steps of invasion in the Kerguelen Islands. Polar Biology 41, 925–934.
| Sea trout (Salmo trutta L.) growth patterns during early steps of invasion in the Kerguelen Islands.Crossref | GoogleScholarGoogle Scholar |
Johnson, P. C. D., Barry, S. J. E., Ferguson, H. M., and Müller, P. (2015). Power analysis for generalized linear mixed models in ecology and evolution. Methods in Ecology and Evolution 6, 133–142.
| Power analysis for generalized linear mixed models in ecology and evolution.Crossref | GoogleScholarGoogle Scholar |
Jonsson, B. (1985). Life history patterns of freshwater resident and sea-run migrant brown trout in Norway. Transactions of the American Fisheries Society 114, 182–194.
| Life history patterns of freshwater resident and sea-run migrant brown trout in Norway.Crossref | GoogleScholarGoogle Scholar |
Jonsson, B., Jonsson, M., and Jonsson, N. (2016). Optimal size at seaward migration in an anadromous salmonid. Marine Ecology Progress Series 559, 193–200.
| Optimal size at seaward migration in an anadromous salmonid.Crossref | GoogleScholarGoogle Scholar |
Kacem, A., Baglinière, J. L., and Meunier, F. J. (2013). Resorption of scales in Atlantic salmon (Salmo salar L.) during its anadromous migration: a quantitative study. Cybium 37, 199–206.
Kimura, D. K., and Lyons, J. J. (1991). Between-reader bias and variability in the age-determination process. Fishery Bulletin 89, 53–60.
Kipling, C. (1962). The use of the scales of the brown trout (Salmo trutta L.) for the back-calculation of growth. ICES Journal of Marine Science 27, 304–315.
| The use of the scales of the brown trout (Salmo trutta L.) for the back-calculation of growth.Crossref | GoogleScholarGoogle Scholar |
Labonne, J., Vignon, M., Prévost, E., Lecomte, F., Dodson, J. J., Kaeuffer, R., Aymes, J.-C., Jarry, M., Gaudin, P., Davaine, P., and Beall, E. (2013). Invasion dynamics of a fish-free landscape by brown trout (Salmo trutta L.). PLoS One 8, e71052.
| Invasion dynamics of a fish-free landscape by brown trout (Salmo trutta L.).Crossref | GoogleScholarGoogle Scholar | 23990925PubMed |
Landres, P. B., Morgan, P., and Swanson, F. J. (1999). Overview of the use of natural variability concepts in managing ecological systems. Ecological Applications 9, 1179–1188.
Lecomte, F., Beall, E., Chat, J., Davaine, P., and Gaudin, P. (2013). The complete history of salmonid introductions in the Kerguelen Islands, Southern Ocean. Polar Biology 36, 457–475.
| The complete history of salmonid introductions in the Kerguelen Islands, Southern Ocean.Crossref | GoogleScholarGoogle Scholar |
Lehman, T. M., and Woodward, H. N. (2008). Modeling growth rates for sauropod dinosaurs. Paleobiology 34, 264–281.
| Modeling growth rates for sauropod dinosaurs.Crossref | GoogleScholarGoogle Scholar |
Łomnicki, A. (1999). Individual-based models and the individual-based approach to population ecology. Ecological Modelling 115, 191–198.
| Individual-based models and the individual-based approach to population ecology.Crossref | GoogleScholarGoogle Scholar |
Ombredane, D., and Richard, A. (1990). Détermination de la zone optimale de prélèvement d’écailles chez les smolts de truites de mer (Salmo trutta L.). Bulletin Francais de la Peche et de la Pisciculture 319, 224–238.
| Détermination de la zone optimale de prélèvement d’écailles chez les smolts de truites de mer (Salmo trutta L.).Crossref | GoogleScholarGoogle Scholar |
Ottaway, E. M. (1978). Rhythmic growth activity in fish scales. Journal of Fish Biology 12, 615–623.
| Rhythmic growth activity in fish scales.Crossref | GoogleScholarGoogle Scholar |
Panfili, J., De Pontual, H., Troadec, H., and Wright, P.-J. (2002). ‘Manuel de sclérochronologie des poisons.’ Editions Quae. (IRD: Paris, France.)
Pettersson, J., Johnsson, J. I., and Bohlin, T. (1996). The competitive advantage of large body size declines with increasing group size in rainbow trout. Journal of Fish Biology 49, 370–372.
| The competitive advantage of large body size declines with increasing group size in rainbow trout.Crossref | GoogleScholarGoogle Scholar |
Quigley, D. T. G., Harvey, M. J., Hayden, T. J., Dowling, C., and O’Keane, M. P. (2006). A comparative study of smoltification in sea trout (Salmo trutta L.) and Atlantic salmon (Salmo salar L.): seawater tolerance and thyroid hormone titres. Biology and Environment 106, 35–47.
| A comparative study of smoltification in sea trout (Salmo trutta L.) and Atlantic salmon (Salmo salar L.): seawater tolerance and thyroid hormone titres.Crossref | GoogleScholarGoogle Scholar |
Roff, D. A. (1996). The evolution of threshold traits in animals. The Quarterly Review of Biology 71, 3–35.
| The evolution of threshold traits in animals.Crossref | GoogleScholarGoogle Scholar |
Schreck, C. B., and Moyle, P. B. (Eds) (1990). ‘Methods for Fish Biology.’ (American Fisheries Society: Bethesda, MD, USA.)
Shelton, A. O., and Mangel, M. (2012). Estimating von Bertalanffy parameters with individual and environmental variations in growth. Journal of Biological Dynamics 6, 3–30.
| Estimating von Bertalanffy parameters with individual and environmental variations in growth.Crossref | GoogleScholarGoogle Scholar | 22882022PubMed |
Spurgeon, J. J., Hamel, M. J., Pope, K. L., and Pegg, M. A. (2015). The global status of freshwater fish age validation studies and a prioritization framework for further research. Reviews in Fisheries Science & Aquaculture 23, 329–345.
| The global status of freshwater fish age validation studies and a prioritization framework for further research.Crossref | GoogleScholarGoogle Scholar |
Stoffel, M. A., Nakagawa, S., and Schielzeth, H. (2017). rptR: repeatability estimation and variance decomposition by generalized linear mixed-effects models. Methods in Ecology and Evolution 8, 1639–1644.
| rptR: repeatability estimation and variance decomposition by generalized linear mixed-effects models.Crossref | GoogleScholarGoogle Scholar |
Thorson, J. T., and Minto, C. (2015). Mixed effects: a unifying framework for statistical modelling in fisheries biology. ICES Journal of Marine Science 72, 1245–1256.
| Mixed effects: a unifying framework for statistical modelling in fisheries biology.Crossref | GoogleScholarGoogle Scholar |
Tjørve, K. M. C., and Tjørve, E. (2010). Shapes and functions of bird-growth models: how to characterise chick postnatal growth. Zoology 113, 326–333.
| Shapes and functions of bird-growth models: how to characterise chick postnatal growth.Crossref | GoogleScholarGoogle Scholar |
Vincenzi, S., Mangel, M., Crivelli, A. J., Munch, S., and Skaug, H. J. (2014). Determining individual variation in growth and its implication for life-history and population processes using the empirical Bayes method. PLoS Computational Biology 10, e1003828.
| Determining individual variation in growth and its implication for life-history and population processes using the empirical Bayes method.Crossref | GoogleScholarGoogle Scholar | 25211603PubMed |
Vincenzi, S., Crivelli, A. J., Munch, S., Skaug, H. J., and Mangel, M. (2016). Trade-offs between accuracy and interpretability in von Bertalanffy random-effects models of growth. Ecological Applications 26, 1535–1552.
| Trade-offs between accuracy and interpretability in von Bertalanffy random-effects models of growth.Crossref | GoogleScholarGoogle Scholar | 27755751PubMed |
Von Bertalanffy, L. (1938). A quantitative theory of organic growth (inquiries on growth laws. II). Human Biology 10, 181–213.
Ward Cutler, D. (1918). A preliminary account of the production of annual rings in the scales of plaice and flounders. Journal of the Marine Biological Association of the United Kingdom 11, 470–496.
| A preliminary account of the production of annual rings in the scales of plaice and flounders.Crossref | GoogleScholarGoogle Scholar |
Wolak, M. E., Fairbairn, D. J., and Paulsen, Y. R. (2012). Guidelines for estimating repeatability. Methods in Ecology and Evolution 3, 129–137.
| Guidelines for estimating repeatability.Crossref | GoogleScholarGoogle Scholar |
Wysujack, K., Greenberg, L. A., Bergman, E., and Olsson, I. C. (2009). The role of the environment in partial migration: food availability affects the adoption of a migratory tactic in brown trout Salmo trutta. Ecology Freshwater Fish 18, 52–59.
| The role of the environment in partial migration: food availability affects the adoption of a migratory tactic in brown trout Salmo trutta.Crossref | GoogleScholarGoogle Scholar |









