Free Standard AU & NZ Shipping For All Book Orders Over $80!
Register      Login
Marine and Freshwater Research Marine and Freshwater Research Society
Advances in the aquatic sciences
Shopping Cart: ( empty )
You are here: Home > Journals > MF > MF04187
RESEARCH ARTICLE
Contents Vol 56(2)

Quantifying ecosystem metabolism in the middle reaches of Murrumbidgee River during irrigation flow releases

S. Vink A B , M. Bormans A , P. W. Ford A and N. J. Grigg A
+ Author Affiliations
- Author Affiliations

A CSIRO Land and Water, GPO Box 1666, Canberra, ACT 2601, Australia.

B Corresponding author. Email: sue.vink@csiro.au

Marine and Freshwater Research 56(2) 227-241 https://doi.org/10.1071/MF04187
Submitted: 14 July 2004  Accepted: 31 January 2005   Published: 12 April 2005

Abstract

The relative importance of floodplain carbon inputs and in-stream metabolic processes have not been well quantified in major Australian rivers. We quantified seasonal phytoplankton primary production and net ecosystem production during irrigation flow regimes at four sites each located ~100 km apart in the middle Murrumbidgee River. During flow periods dominated by storage release, ecosystem gross primary productivity, system respiration and phytoplankton chlorophyll concentrations all increased downstream so that overall net ecosystem metabolism was strongly net heterotrophic upstream and closer to balanced downstream. Phytoplankton production dominated ecosystem production throughout the entire reach and was likely to have been phosphorus limited throughout the study. Additionally, phytoplankton biomass was limited by short residence times at the upstream sites and nitrogen limited downstream in summer, despite an increase in turbidity. Both production and respiration rates were generally lower in winter, as expected, owing to lower temperatures.

Extra keywords: carbon cycling, heterotrophic, phytoplankton production, respiration, river metabolism.


Acknowledgments

We thank the following individuals and organisations for help with routine sampling: Peter Pollock and Terry Dowel from Gundagai Shire; Nicole Vonax, Gemma Urquart and the plant operators at Riverina County Water; Richard and Nicholas Hart from Kooba Station; Stephen Thurstan and Matt McLellan from Narrandera Inland Fisheries Research Centre; Roy Zandona, Stuart Paterson and Wendy Minato from CLW Griffith; and Brendan Ebner from Environment-ACT. Thanks also to Rob Cawley (DIPNR) for rating curves, river cross-sections and other data as well as many fruitful discussions. The manuscript was greatly improved by comments from Barbara Robson, Richard Davis and two anonymous reviewers.


References

Alpkem (1992). ‘Flow Solution Methodology #142,156,621,293.’ (Alpkem Pty Ltd: College Station, TX.)

APHA (1992). ‘Standard Methods or the Examination of Water and Wastewater.’ (Eds A. D. Eaton, L. S. Clesceri and A. E. Greenberg.) (APHA: Washington, DC.)

Baldwin, D. S. , Whittington, J. , and Oliver, R. (2003). Temporal variability of dissolved P speciation in a eutrophic reservoir-implications for predicting algal growth. Water Research 37, 4595–4598.
| Crossref | GoogleScholarGoogle Scholar | PubMed | Belanger C., and Brookes S. T. (1999). ‘Rapid 13C Determination from Dissolved Inorganic Carbon (DIC) in Sea and Fresh Water by Continuous Flow IRMS. Presentation to the Stable Isotope Mass Spectrometry Users Group Meeting, Exeter, UK.’

Butler J. N. (1991). ‘Carbon Dioxide Equilibria and their Applications.’ (Lewis: Chelsea, MI.)

Caraco, N. F. , Cole, J. J. , Raymond, P. A. , Strayer, D. L. , Pace, M. L. , Findlay, S. E. , and Fischer, D. T. (1997). Zebra Mussel invasion in a large, turbid river: phytoplankton response to increased grazing. Ecology 78, 588–602.
Chapra S. C. (1997). ‘Surface Water-Quality Modeling.’ (McGraw-Hill: Singapore.)

Chapra, S. C. , and Di Toro, D. M. (1991). The delta method for estimating community production, respiration and reaeration in streams. Journal of Environonmental Engineering 117, 640–655.
Fisher T. R., Melack J. M., Grobbelaar J. U., and Howarth R. W. (1995). Nutrient limitation of phytoplankton and eutrophication of inland, estuarine and marine waters. In ‘Phosphorus in the Global Environment: Transfers, Cycles and Management. Scope 54’. (Ed. H. Tiessen.) (Wiley and Sons: New York.)

Froelich, P. N. (1988). Kinetic control of dissolved phosphate in natural rivers: a primer on the phosphate buffer mechanism. Limnology and Oceanography 33, 649–668.
Hilborn R., and Mangel M. (1997). ‘The Ecological Detective: Confronting Models with Data.’ Monographs in Population Biology 28. (Princeton University Press: Princeton, NJ.)

Holm-Hansen, O. , and Reimann, B. (1978). Chlorophyll a determination: improvements in methodology. Oikos 30, 438–457.
Junk W. J., Bayley P. B., and Sparks R. E. (1989). The flood pulse concept in river-floodplain systems. In ‘Proceedings of the International Large River Symposium. Canadian Special Publications in Fisheries and Aquatic Sciences’. (Ed. D. P. Dodge.) pp. 110–127.

Kelly, M. G. , Hornberger, G. H. , and Cosby, B. J. (1974). Continuous automated measurement of rates of photosynthesis and respiration in an undisturbed river community. Limnology and Oceanography 19, 305–312.
Lachat (1994). ‘QuikChem Method 31-107-04-1-C.’

Leuning, R. , Cleugh, H. A. , Zegelin, S. J. , and Hughes, D. (2005). Carbon and water fluxes over a temperate Eucalyptus forest and a tropical wet/dry Savanna in Australia: Measurements and comparison with MODros. Inf. Serv. remote sensing estimates. Agricultural and Forest Meteorology ,in press.
Likens G. E., and Wetzel R. G. (1990). Diurnal changes in a stream ecosystem: an energy and nutrient budget approach. In ‘Limnological Analyses’. 2nd edn. pp. 325–330. (Springer: New York.)

Lorenzen, C. (1967). Determination of chlorophyll and phaeopigments: Spectrophotometric equations. Limnology and Oceanography 12, 343–346.
Oliver R. L., Hart B. J., Olley J., Grace M., Rees G., and Caitcheon G. (1998). The Darling River: algal growth and the cycling and sources of nutrients. CRC freshwater ecology/CSIRO technical report.

Pace, M. L. , Findlay, S. E. G. , and Lints, D. (1992). Zooplankton in advective environments: the Hudson River community and a comparative analysis. Canadian Journal of Fisheries and Aquatic Sciences 49, 1060–1069.
Read A. (2001). Floodplain inundation frequency response to river regulation: Murrumbidgee, Australia. Honours Thesis, Charles Sturt University, Wagga Wagga, Australia.

Redfield A. C., Ketchum P. H., and Richards F. A. (1963). The influence of organisms on the composition of seawater. In ‘The Sea, Vol. II’. (Ed. M. N. Hill.) pp. 26–77. (Interscience: New York.)

Reynolds C. S. (1984). ‘The Ecology of Freshwater Phytoplankton.’ (Cambridge University Press: Cambridge, UK.)

Richey, J. E. , Hedges, J. I. , Devol, A. H. , Quay, P. D. , Victoria, R. , Martinelli, L. , and Forsberg, B. R. (1990). Biogeochemistry of carbon in the Amazon River. Limnology and Oceanography 35, 352–371.
Watts R. J., Robertson A. I., and Ryder D. S. (2003). The response of biofilm fauna and foodwebs to controlled inundation and desiccation regimes in a lowland river. Ninth International conference on river research and applications. Albury (Australia).

Webster, I. T. , Ford, P. W. , and Hancock, G. (2001). Phosphorus dynamics in Australian lowland rivers. Marine and Freshwater Research 52, 127–137.
| Crossref | GoogleScholarGoogle Scholar | Westhorpe D., Hardwick L., and Chessman B. (2003). Trophic differences between unregulated and regulated rivers, evidence from stable carbon isotopes and C:N ratios. Ninth International conference on river research and applications. Albury (Australia).

Wilcock, R. J. , McBride, G. B. , Nagels, J. W. , and Northcott, G. L. (1995). Water quality in a polluted lowland sream with chronically depressed dissolved oxygen: causes and effects. New Zealand Journal of Marine and Freshwater Research 29, 277–288.
with those computed simultaneously with k20 by curve fitting showed generally good agreement. However for a few (~7% in total) 24 h periods, curve fitting yielded kex values that were close to zero. These kex values were also extremely low relative to values calculated for the previous and following days. Since flow and other general conditions had not changed appreciably between the days in question we concluded that the kex estimated by curve fitting was in error on these days. The exact reason for this discrepancy is not readily apparent at this time and is being investigated further. Consequently, in order to attain the most reliable estimates of GPP and R24, we computed an average daily value for kex using hourly flow and water depth records at each site in Eqn (A1) above. Thus in our analysis, Eqn (1) was solved for only 2 parameters k20 and Pmax.

Optimisation procedure and computation of confidence limits on GPP and R24

Typically, a least-squares method is used to evaluate the optimum parameter values of k20 and Pmax in Eqn (1) (e.g. Kelly et al. 1974); however, we used a maximum-likelihood analysis (Hilborn and Mangel 1997). This method is equivalent to performing a least-squares fit but provides an error estimate to be calculated for each parameter that encompasses the uncertainty associated with the estimated values of the other parameters in addition to measurement/sampling errors.

Initial values for k20 and Pmax were chosen from the literature (Wilcock et al. 1998), we then used Matlab’s ‘ode45’ function to numerically integrate Eqn (1) over each 24 h period to produce a modelled dissolved O2 time series. The goodness of fit between the modelled dissolved O2 time series and the in-situ measured times series was determined by calculating the negative log-likelihood (L):

EA2

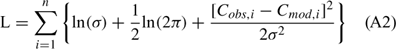
where Cobs,i and Cmod,i are the measured and modelled CO2 values for the ith data point. This method assumes that the CO2 measurement errors are normally distributed with zero mean and known standard deviation, σ. The standard deviation of the dissolved O2 data was determined by placing the multiprobe instruments into water equilibrated with the air for ~1 h. The standard deviation of these measurements for each instrument was averaged and used in the log-likelihood analysis. Note that in this particular case the measurement error is assumed to be normally distributed, and so minimising Eqn (A2) is equivalent to minimising the sum of the squared deviation between measured and modelled values.

Matlab’s ‘fminsearch’ function was used to repeat the integration iteratively and find parameter values that minimise Eqn (5) for each 24 h period. Once optimum values of Pmax and k20 had been estimated for each 24 h period, we quantified the uncertainty in each parameter value using a likelihood ratio test. One parameter was fixed at a given value and the remaining parameter was estimated using the optimisation routine. The fixed parameter was then changed to another value and the process repeated. The negative log-likelihood (L) values calculated from this procedure were used to calculate confidence bounds on GPP, R24 using a likelihood ratio test (Hilborn and Mangel 1997).