Effect of climate variability on water quality trends in New Zealand rivers
T. H. Snelder A D , S. T. Larned
A D , S. T. Larned  B , C. Fraser
B , C. Fraser  A and S. De Malmanche C
A and S. De Malmanche C
A LWP Ltd, Christchurch, New Zealand.
B National Institute of Water and Atmospheric Research, Christchurch, New Zealand.
C Ministry for the Environment, Wellington, New Zealand.
D Corresponding author. Email: ton@lwp.nz
Marine and Freshwater Research 73(1) 20-34 https://doi.org/10.1071/MF21087
Submitted: 21 March 2021 Accepted: 7 September 2021 Published: 30 September 2021
Journal Compilation © CSIRO 2022 Open Access CC BY-NC-ND
Abstract
Associations between temporal variability in 10 water quality variables and the El Niño–Southern Oscillation (ENSO) climate pattern, quantified by the Southern Oscillation Index (SOI), were assessed at 56 river sites in New Zealand over a 31-year period (1989–2019). Fluctuations in monthly observations of water quality at each site were correlated to varying degrees with the corresponding SOI value (ro). Trends for rolling windows of 5-, 10- and 15-year duration were evaluated for each site and variable using Kendall’s tau (τw) and for the SOI using linear regression (δSOIw). Aggregate trends for each variable, duration and time window were quantified as proportions of site trends that were increasing (Pw). Fluctuations in τw and Pw between time windows for all durations were explained by the corresponding SOI trend (δSOIw). Between-site and between-variable differences in the trend responses to the SOI trends were explained by the corresponding ro values and the median of the ro values ( ) respectively. These results indicate that climate variability makes a significant contribution to water quality trends, even at timescales longer than ENSO cycles. Our models can be used to quantify this contribution for individual sites (i.e. τw) and for aggregate trends (i.e. Pw).
) respectively. These results indicate that climate variability makes a significant contribution to water quality trends, even at timescales longer than ENSO cycles. Our models can be used to quantify this contribution for individual sites (i.e. τw) and for aggregate trends (i.e. Pw).
Keywords: climate, El Niño–Southern Oscillation, New Zealand, rivers, trends, water quality.
Introduction
Detection and characterisation of temporal trends are basic objectives of the water quality monitoring programs in operation around the world (Dawe 2006; Rosen and Lapham 2008; Kauffman et al. 2011; Ryberg et al. 2018). The analytical methods used to assess trends are well established, and quality-assured water quality datasets are widely available (e.g. Larned et al. 2016; Civan et al. 2018; Shoda et al. 2019; Helsel et al. 2020). Trend analysis serves multiple purposes, including evaluating changes in environmental state, assessing the effectiveness of management actions and policies, evaluating relationships between environmental conditions and the factors that influence them (i.e. driver or explanatory variables) and providing early warning of environmental problems (McMellor and Underwood 2014; Tomperi et al. 2016; Ministry for the Environment and Statistics New Zealand 2020; Murphy 2020).
In contrast to the widespread assessment of water quality trends, robust attribution of those trends to environmental drivers is less common. Attributing changes in water quality to environmental drivers is challenging due to uncertainty about causation and the interactive effects of multiple drivers, both anthropogenic and natural (Morse and Wollheim 2014; Dupas et al. 2016; Erb et al. 2016; Jackson et al. 2016; Ryberg et al. 2018). In the absence of empirical evidence about drivers, degrading trends in water quality are often casually attributed to anthropogenic drivers, such as agricultural intensification and urban development, based on anecdotal information (e.g. Johnson et al. 2009; Luo et al. 2011). Despite the challenges, arresting and reversing water quality degradation is predicated on the identification of contributing drivers, and predictive relationships between those drivers and water quality conditions.
It is reasonable to expect that water quality trends in most catchments are influenced by both natural and anthropogenic drivers, because both are ubiquitous at regional scales (e.g. natural climate variability, anthropogenic atmospheric nutrient deposition) and at catchment scales (e.g. natural plant succession, anthropogenic land use change). In several recent studies, temporal changes in coastal and fresh water quality were attributed to natural climate variability generated by climatic processes such as the El Niño–Southern Oscillation (ENSO) and the North Atlantic Oscillation (NAO; Mellander et al. 2018; Harding et al. 2019; Murphy and Sprague 2019). These processes produce regional-scale temporal variation in temperature and rainfall that influence catchment processes (e.g. contaminant mobilisation, transport, storage, transformation and dilution), which, in turn, affect water quality conditions (e.g. Gascuel-Odoux et al. 2010; Mellander et al. 2018).
There is continuing concern in New Zealand about water quality in freshwater and coastal environments (Suthanthangjai et al. 2013; Ministry for the Environment and Statistics New Zealand 2019). Water quality trend assessments of regional and national extent are conducted and reported as required by the New Zealand Resource Management Act and the Environmental Reporting Act (Ministry for the Environment and Statistics New Zealand 2017). Assessments of trends in water quality at 600–800 long-term river water quality sites across New Zealand have been conducted at 2- to 5-year intervals since the late 1990s (Larned et al. 2004, 2016; Ministry for the Environment and Statistics New Zealand 2015, 2017, 2019). The analysed trends covered a wide range of time windows and durations, and the reported patterns between successive analyses have been inconsistent. For example, two recent national State of Environment reports reported that 37 and 15% of monitored river sites in New Zealand had increasing nitrate trends for the 10-year windows ending in 2013 and 2017, and that 55 and 46% of the sites had increasing nitrate trends for the 20-year windows with the same end dates (Ministry for the Environment and Statistics New Zealand 2017, 2019). These inconsistencies have not been explained, but the results of an earlier study of water quality trends in New Zealand rivers suggests that climate variability is involved (Scarsbrook et al. 2003). Scarsbrook et al. (2003) found that trends in water quality variables for time windows of 5 and 10 years were reasonably consistent with trends in SOI over the same time windows. That study concluded that attributing changes in water quality to human management is difficult because of the confounding effect of climate variability. However, there has been no investigation of the degree to which climate variability can explain variation in water quality trends pertaining to different time windows and durations.
ENSO is a major source of interannual climatic variation in New Zealand. ENSO reflects a continuum of variation in sea level atmospheric pressure in the tropical Pacific Ocean, the extremes of which are designated El Niño and La Niña (Allan et al. 1996). Variation in ENSO strength is quasi-cyclic, with El Niño and La Niña events occurring on average every 2–7 years. ENSO strength is associated with regionally variable effects on climate conditions in New Zealand (Mullan 1996; Salinger and Mullan 1999). During El Niño events, New Zealand experiences stronger and more frequent westerly winds in summer, leading to dry conditions in eastern regions and increased rainfall in western regions. In winter, El Niño events are associated with more frequent southerly winds and colder than average temperatures. In spring and autumn, south-westerlies tend to be stronger and more frequent during El Niño events, producing higher than average rainfall in the south of the country and decreased rainfall in the east. La Niña events have weaker effects on New Zealand’s climate and are associated with more frequent north-easterly winds, higher than average rainfall in the north-east and decreased rainfall in the south and south-west. Variation in ENSO strength has been linked with regionally variable effects on hydrology in New Zealand (McKerchar et al. 1998; Mosley 2000; Chiew and McMahon 2002). Scarsbrook et al. (2003) showed that ENSO strength was associated with variation in river water quality observations at individual sites. Scarsbrook et al. (2003) also observed that the directions of national-scale trends (based on aggregating individual site trends) for some water quality variables corresponded to trends in ENSO strength.
In this study, we investigated relationships between trends in 10 river water quality variables at 56 New Zealand river monitoring sites and variation in ENSO strength over a 31-year period. The monitoring sites represented large main-stem rivers draining catchments with a wide range of environmental conditions, including near natural and highly modified land cover (Julian et al. 2017). We predicted that the strength and direction of water quality trends measured for specific time windows at both individual river monitoring sites and in aggregate would be associated with ENSO. We used statistical analyses to test these predictions and evaluate the proportions of variation in site and aggregated trends that could be explained by variation in ENSO. Our aim was to produce models that quantified the component of water quality trend strength and direction that can be attributed to ENSO variation for both site and aggregate trends.
Materials and methods
The methods involved multiple steps aimed at providing four primary results, namely to quantify the proportion of variation in site and aggregate water quality trends explained by SOI trends, to explain variation in water quality trend responses to SOI between sites and to explain variation in aggregate water quality trend responses to SOI between variables, as shown schematically in Fig. 1.
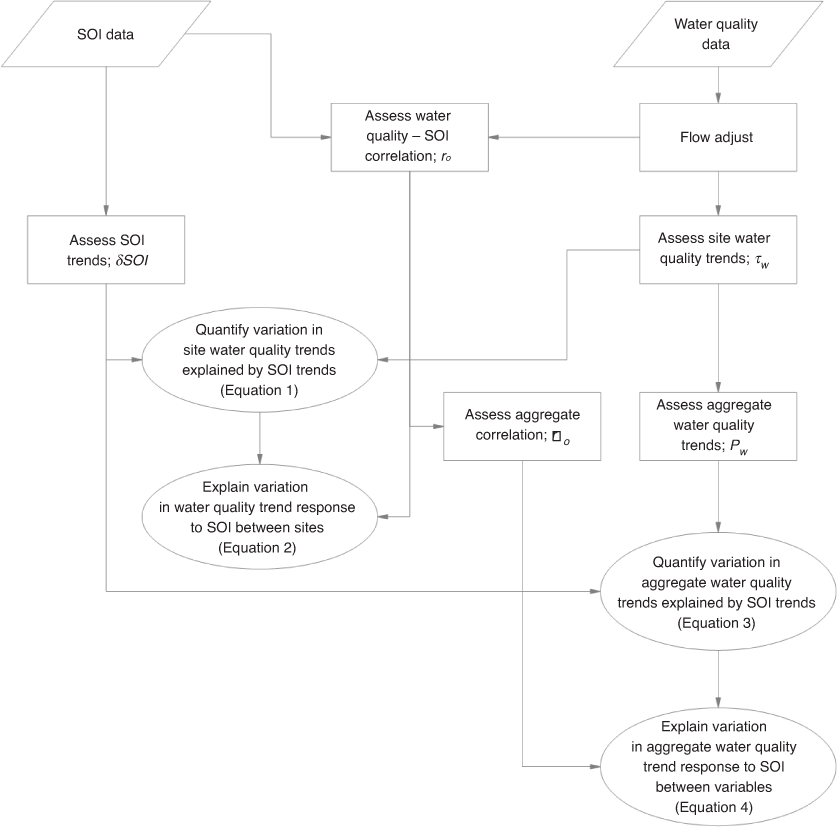
|
Water quality data
This study was based on data from the New Zealand National River Water Quality Network (NRWQN; Smith and Maasdam 1994; Davies-Colley et al. 2011). For the period from 1989 to 2019 (31 years), there was continuous monitoring of 56 sites located on 31 mostly large rivers (mean daily flow ranging from 0.8 to 511 m3 s–1; median flow 96 m3 s–1; Fig. 2). Monitoring records for the NRWQN sites comprise consistent monthly observations of 10 physicochemical variables (including discharge), which are referred to hereafter as ‘water quality variables’ (Table 1), with few censored or missing values. The exceptions were total nitrogen (TN) and ammoniacal nitrogen (NH4-N), for which there are no observations during 1994 (Davies-Colley et al. 2011).

|

|
Flow adjustment
The values of water quality observations in rivers often vary in response to flow fluctuations due to two main mechanisms (Helsel et al. 2020). First, observations may decrease with flow due to dilution if the contaminant is delivered to the river at a constant rate. Second, observations may increase with flow if the contaminant is mobilised in the catchment in association with rainfall or in-stream in association with increasing turbulence. The responses of water quality observations to flow may be a combination of the two mechanisms. When trend analyses are conducted on river water quality data, the observations are often adjusted to account for the effect of flow (flow adjustment) for two reasons. First, flow adjustment can decrease extraneous variation (noise) in the variable of interest, so that trends (i.e. signals) are more confidently detected. Second, flow adjustment can remove the component of a water quality trend that can be attributed to a trend in flow (Helsel et al. 2020).
Flow adjustment is based on regressing the observations against their corresponding flows and then using the residuals of the regression model in the subsequent trend analysis. A variety of regression models may be used for flow adjustment (Helsel et al. 2020). We chose to use ordinary least-squares regression with log (base 10)-transformed values for both the water quality variable observations and flow observations. This form of regression is constrained to be monotonic (increasing or decreasing), which, in our experience, is generally a parsimonious and physically realistic model of the observation–flow relationship. In our experience, more flexible regression methods, such as locally weighted regression scatterplot smoothing, can produce unrealistic models.
Flow adjustment of the observations of each variable at each site, apart from instantaneous discharge at the time of sampling (FLOW), was performed by fitting a regression model to the entire time series. If this model was statistically significant (α = 0.05), the flow-adjusted observations were derived as the residuals of this model. Because the subsequent trend analysis was non-parametric, it was not necessary to back-transform the residuals. If the model was not significant, the variable was not flow adjusted (for further details, see Table S1 of the Supplementary material). At the end of this process, the observations, whether flow adjusted or not, were used in all subsequent analyses and are referred to as the water quality variables. To ensure consistency with studies in which flow adjustments are not used, we repeated all analyses using non-flow adjusted (‘raw’) data, and these results are provided in the Supplementary material.
Analysis of site water quality trends
We evaluated trends in each of the water quality variables at each monitoring site for rolling windows of 5-, 10- and 15-year duration starting in 1989 and incrementing by 1 year to a final window ending in 2019. These durations were chosen because they are typical of the timescales that are widely used in water quality trend assessments in New Zealand and elsewhere (Larned et al. 2016; Oelsner et al. 2017). This resulted in 27, 22 and 17 time windows of 5-, 10- and 15-year duration respectively. Trends were assessed for all site, variable and time window combinations for which data were available for 90% of months and 90% of years.
Trend strength and direction were evaluated using the Mann–Kendall trend test or, in the case that there was a statistically significant difference in the observations grouped by their sampling month (Kruskal–Wallis test, α ≤ 0.05), the seasonal Kendall test (Hirsch et al. 1982). The two procedures are robust to non-normal data distributions, outliers and non-linear trends and are widely used to evaluate the magnitude and significance of environmental trends. Both tests are based on the Mann–Kendall S statistic, which is the difference between the number of positive and negative changes in the water quality variable between all pairs of observations. We converted S to Kendall’s tau (τ) by dividing it by the total number of pairs of observations to provide a standardised measure of trend strength and direction. Kendall’s τ takes values between –1 and +1; a positive value indicates that the observations increased through time, whereas a negative value indicates that the observations decreased through time. Kendall’s τ for each site, water quality variable, duration and time window is denoted τw.
We quantified the aggregate trend for each water quality variable, duration and time window as the proportion of individual site trends with positive τw values; we refer to this statistic as Pw.
Explanatory variables based on the SOI
We used two independent variables based on the SOI to assess the degree to which fluctuations in trend strength and direction between time windows could be explained by variation in ENSO. The SOI is calculated as the normalised anomalies of the monthly mean sea level pressure difference between Tahiti and Darwin, Australia (Salinger and Mullan 1999). Monthly values of the SOI for the period 1989–2017 were obtained from the Australian Bureau of Meteorology (http://www.bom.gov.au/climate/current/soi2.shtml) and we used the Troup convention, whereby index values are multiplied by 10. The SOI typically ranges from –30 to 30 and is quasi-periodic with a typical period of 3–7 years. El Niño conditions are defined as an SOI less than –8 over ≥3 months and La Niña conditions are defined as an SOI >8.
The first independent variable described the trend in the SOI for a given time window. Although the SOI is quasi-cyclic, SOI values exhibit either an increasing or decreasing trend when a time window is defined by arbitrary starting and ending dates. We refer to the trend in the SOI for a specific time window (w) as the SOI trend, denoted by δSOIw. We evaluated δSOIw by linear regression of monthly SOI values against their respective dates for the same rolling windows of 5-, 10- and 15-year duration as the water quality trends.
The second independent variable described the extent to which there was an association between the cyclic fluctuations in the SOI and the corresponding monthly water quality observations at each site. This variable was the Pearson correlation between the monthly water quality observations and corresponding SOI values, which we calculated in four steps (Fig. 3). First, we selected all the observations of the water quality variable in the entire 31-year period of record at each site. Second, because regular seasonal variation in both the water quality measurements and the SOI values obscured their longer-term interannual variation, we deseasonalised both sets of values using classical seasonal decomposition (Hyndman and Athanasopoulos 2021). This analysis used centred annual moving averages to remove the variability associated with regular monthly changes for both the SOI and all water quality variables at each site. Third, because we wanted to assess only the extent to which cyclical fluctuations in the water quality observations and SOI were associated, we removed any secular temporal trend (i.e. any monotonic trend that was exhibited through the entire time series) for both the SOI and the water quality variables. Detrending was performed by regressing the deseasonalised values of the water quality variable and SOI against time using linear models and using the residuals of each model to represent the deseasonalised and detrended time series. Fourth, we calculated the Pearson correlation coefficient between the deseasonalised and detrended time series of the water quality variable and SOI. The correlation coefficients are referred to hereafter as ro.
Relationships between site water quality trends and SOI trends
We quantified the extent to which fluctuations in water quality trend strength and direction could be explained by the SOI for each site, water quality variable and duration in two steps (Fig. 1). First, because we wanted to assess only the extent to which cyclic fluctuations in water quality trends at each site were associated with corresponding fluctuations in the SOI trends, we removed any secular temporal trend that was exhibited in both sets of trends. For each water quality variable and duration, we used linear regression to remove the secular trend that was exhibited through the entire time series of τw values. We also used linear regression to remove any secular trend that was exhibited through the entire time series of the δSOIw values. We regressed the τw and δSOIw values against their corresponding end years and retained both sets of regression residuals (denoted τw′ and δSOIw′ respectively). Second, we fitted the resulting data to models of the form:

where β1 is a fitted coefficient that represents the response of the site water quality trend to the SOI trend. The intercept of Eqn 1 is 0, which represents our expectation that there will be no water quality trend response when the SOI trend for a time window is 0. The individual data points in the above model were not independent because they pertained to a rolling window through time. The models were therefore fitted using generalised least-squares regression, which provides robust estimates of the regression coefficients when there is temporal autocorrelation of the model residuals (Venables and Ripley 2013). In each model, we accounted for temporal autocorrelation by including a first-order autocorrelation structure. We used a pseudo-R2 value (hereafter R2) to quantify the variation in τw′ explained by the model.
For each water quality variable and duration, we inspected the association between the variation in τw′ explained by the models (i.e. R2 values) and the corresponding absolute values of ro. We compared R2 values for sites belonging to four categories defined by the absolute value of ro, namely ≥0 (i.e. all sites), ≥0.1, ≥0.2 and ≥0.3. We expected that sites with larger absolute ro values would have higher R2 values because water quality observations at these sites have higher fidelity to fluctuations in the SOI.
We expected that the between-site variation in the response of water quality trends to the SOI trend for each variable, indicated by the fitted coefficients β1, would be explained by the site ro values. We modelled the between-site variation in responses of the water quality trends to the SOI trend by fitting 30 models (one for each water quality variable and duration) of the form:

where β1 represents the site regression coefficients from Eqn 1 and β2 is a fitted coefficient. The intercept of Eqn 2 is 0, which represents our expectation that there will be no water quality trend response to SOI trends for site and variable combinations with ro of 0. We examined the R2 values and overall significance (F-test P-values) of these models. Because we were examining multiple models (i.e. 10 variables × 3 time window durations), we controlled for false discovery by adjusting the P-values (Benjamini and Hochberg 1995).
Relationships between aggregate water quality trends and SOI trends
We quantified the extent to which fluctuations in the aggregate water quality trends could be explained by the corresponding SOI trends (δSOIw) in two steps. These steps are analogous to the steps described above to quantify the variation in the water quality trends at individual monitoring sites explained by SOI trends (Fig. 1). First, for each water quality variable and duration, we used linear regression to remove any secular temporal trend that was exhibited through the entire time series of both the aggregate water quality trends (i.e. the Pw values) and the corresponding SOI trends (i.e. the δSOIw values). We regressed the Pw and δSOIw values against their corresponding end years and retained both sets of regression residuals (denoted Pw′ and δSOIw′ respectively). Second, for each water quality variable and duration, we fitted a linear regression model of the form:

where β3 is a fitted coefficient that represents the response of the aggregate water quality trend to the SOI trend. The intercept of Eqn 3 is 0, which represents our expectation that there will be no Pw response when the SOI trend for a time window is 0. Because the individual data points in the above model were not independent, the models were fitted using generalised least-squares regression. Temporal autocorrelation was accounted for by including a first-order autocorrelation structure. We used a pseudo-R2 value (hereafter R2) to quantify the variation in Pw′ explained by the models.
We expected that the between-variable variation in the responses of the aggregate trends to the SOI trend, indicated by the fitted coefficients β3, would be explained by the median of the corresponding ro values (denoted  ). This is because, when
). This is because, when 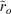 is positive, the majority of sites’ responses to the SOI trend in each time window (δSOIw) will be consistent with the sign of δSOIw. Therefore, the aggregate trend (i.e. Pw) will increase and decrease when δSOIw is positive and negative respectively. Conversely, when
is positive, the majority of sites’ responses to the SOI trend in each time window (δSOIw) will be consistent with the sign of δSOIw. Therefore, the aggregate trend (i.e. Pw) will increase and decrease when δSOIw is positive and negative respectively. Conversely, when  is 0, approximately equal numbers of sites will respond positively and negatively to the SOI trend in every time window. Therefore, the opposing influences of the SOI trend on variables with positive and negative
is 0, approximately equal numbers of sites will respond positively and negatively to the SOI trend in every time window. Therefore, the opposing influences of the SOI trend on variables with positive and negative  values will tend to cancel out and will have little relationship with δSOIw. We modelled the between-variable variation in responses of the aggregate quality trends to the SOI trend by fitting three models (one for each duration) of the form:
values will tend to cancel out and will have little relationship with δSOIw. We modelled the between-variable variation in responses of the aggregate quality trends to the SOI trend by fitting three models (one for each duration) of the form:

where β3 represents the regression coefficients for each water quality variable from Eqn 3, and β4 is a fitted coefficient. The intercept of Eqn 4 is 0, which represents our expectation that there will be no aggregate trend response to SOI trends for variables with  of 0. We examined the R2 values and overall significance (F-test P-values, controlled for false discovery) of these models.
of 0. We examined the R2 values and overall significance (F-test P-values, controlled for false discovery) of these models.
Results
Water quality trends
Trend strength and direction at individual sites (i.e. τw) varied across all water quality variables and time windows (Fig. 4). The aggregate trend (i.e. Pw) oscillated with advancing time window for all variables and durations. For example, for the 5-year duration and turbidity (TURB), the median of values of τw were negative and, consequently, Pw values were <0.5 for four sets of time windows (windows ending 1993 and 1994, 1999–2002, 2005–07 and after 2016). The frequency of the oscillations in the aggregate trend directions decreased with increasing duration. For example, TURB had negative median values of τw and Pw values <0.5, for only two sets of time windows for the 10-year duration and one set for the 15-year duration (Fig. 4).
The amplitude of the oscillation of the Pw values differed between variables. For example, Pw for dissolved reactive phosphorus (DRP) and temperature (TEMP) for the 10-year time window varied from ~0.2 to 0.9, but electrical conductivity (COND) and nitrate and nitrite nitrogen (NNN) varied from ~0.5 to 0.8 (Fig. 4). For some variables, there were obvious secular trends in the Pw values through the time series (i.e. a monotonic trend in the trends) that were a more dominant temporal pattern than the oscillations. This was particularly evident for the 15-year duration for NH4-N (increasing Pw values with advancing time window) and total phosphorus (TP; decreasing Pw values with advancing time window).
SOI trends
The SOI trend (i.e. linear trend in the SOI; δSOIw) differed between time windows, and alternated between increasing and decreasing, for all three durations (Fig. 5). The amplitude of the variation in the linear trend in the SOI decreased with increasing time window duration (Fig. 5).

|
Association between water quality variable observations and the SOI
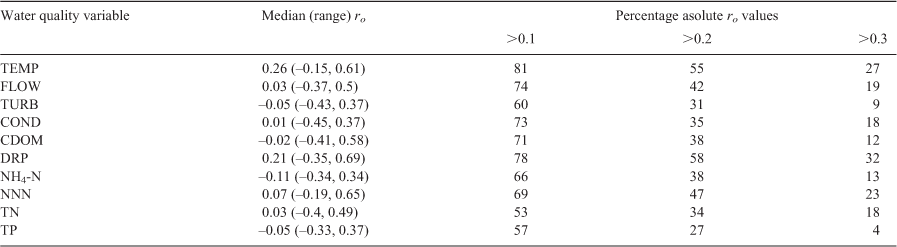
Correlations between the monthly deseasonalised and detrended water quality variable observations and monthly deseasonalised and detrended SOI values (ro) varied in direction across sites and variables, ranging from –0.45 to 0.69 (Table 2). The median values of ro were close to 0 for all variables, except TEMP and DRP, for which median values of ro were >0.2. This indicates that TEMP and DRP were dominated by positive site ro values, whereas there was a relatively even split between sites with positive and negative ro values for the other variables. The proportion of sites with absolute values of ro > 0.1 were lowest for TN and TP and were highest for TEMP, DRP and COND (Table 2).
|
Explanation of site water quality trends by SOI
Examples of the relationship between τw′ and δSOIw′ for TN are shown in Fig. 6 for two sites for time windows of 10-year duration. The ro values were negative for the Waipa River site (Fig. 6a) and positive for the Hurunui River site (Fig. 6b). The relationships in Fig. 6 were consistent with our expectation that fluctuations in water quality trends at individual sites are explained by the SOI trend (i.e. Eqn 1) and that variation in the water quality trend response between sites is explained by the respective ro values (i.e. Eqn 2).

|
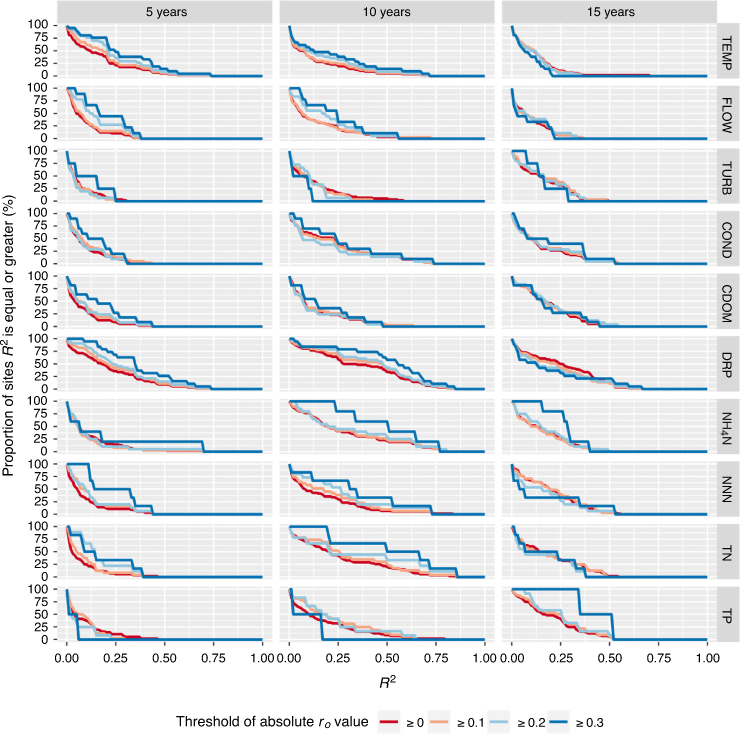
The amount of variation in τw′ that was explained by δSOIw′ (i.e. model represented by Eqn 1) varied for each combination of site, water quality variable and duration (Fig. 7). R2 values tended to be greatest for the 10-year duration and least for the 15-year duration. When averaged across all variables, 13, 32 and 30% of sites had R2 values >0.25 for the 5-, 10- and 15-year time window durations respectively. R2 values tended to increase with increasing absolute values of ro (Fig. 7). When averaged across all variables, 14, 36 and 30% of sites with absolute ro values ≥ 0.1 had R2 values that exceeded 0.25 for the 5-, 10- and 15-year time window durations respectively; this increased to 19, 38 and 30% respectively for absolute ro values ≥0.2 and to 31, 44 and 37 respectively for absolute ro values ≥0.3 (Fig. 7). These results are consistent with our expectation that the explanation of between-time window variation in trends (i.e. R2 values) would be higher for sites with higher ro values.
|
After detrending (i.e. removal of secular trends), the ro values explained between 1 and 79% of the variation in the between-site response of water quality trends to the SOI trends (i.e. β1 coefficients fitted to Eqn 1; Fig. 8). This result was consistent with our expectation that the β1 coefficients, indicating the direction of the response of the water quality trends to the SOI trend at each site, would be consistent with the site’s ro values. The variation in the β1 coefficients explained by ro (R2) was consistently lower for the 15-year duration than for the 5- and 10-year durations (Fig. 8). The TURB, NH4-N and TP models for all durations were not statistically significant (adjusted P > 0.05).

|
Explanation of aggregate water quality trends by SOI
The magnitude of the variation in the aggregate water quality trends (Pw′) associated with δSOIw′ (i.e. β3 in Eqn 3) varied for each combination of water quality variable and duration (Fig. 9). The explained variation in Pw′ was greatest for DRP for the 5- and 10-year durations (R2 values of 0.63 and 0.60 respectively) and TEMP and NNN for the 5-year duration (R2 = 0.41 and 0.40 respectively).

|
The 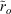 values explained between 52 and 80% of the variation in the between-variable response of the detrended aggregate water quality trends to SOI trends (Eqn 4; Fig. 9). This result was consistent with our expectation that the response of Pw′ to the SOI trend would be consistent with the
values explained between 52 and 80% of the variation in the between-variable response of the detrended aggregate water quality trends to SOI trends (Eqn 4; Fig. 9). This result was consistent with our expectation that the response of Pw′ to the SOI trend would be consistent with the  values. The variation in the β3 coefficients explained by
values. The variation in the β3 coefficients explained by  (R2) was lower for the 15-year duration than for the 5- and 10-year durations, but all models were statistically significant (adjusted P < 0.05; Fig. 9).
(R2) was lower for the 15-year duration than for the 5- and 10-year durations, but all models were statistically significant (adjusted P < 0.05; Fig. 9).
Discussion
Five results of the analyses support our prediction that the strength and direction of water quality trends in New Zealand are associated with ENSO variation. First, for each water quality variable, fluctuations in individual observations of the variables were associated with fluctuations in ENSO indicated by the SOI (ro; Table 2). Second, fluctuations in water quality trends between time windows (i.e. τw′) at individual sites were partly explained by the corresponding SOI trends (Fig. 6, 7). Third, between-site variation in the response of water quality trends to SOI trends was partly explained by ro values (Fig. 8). Fourth, fluctuations in aggregate trends between time windows (i.e. Pw′) were partly explained by the corresponding SOI trends (Fig. 9). Fifth, variation in the response of aggregate trends for individual water quality variables was partly explained by the median of the site ro values ( ; Fig. 9). These results were very similar when the analyses were performed using flow-adjusted and non-flow-adjusted water quality observations (see Fig. S1–S3).
; Fig. 9). These results were very similar when the analyses were performed using flow-adjusted and non-flow-adjusted water quality observations (see Fig. S1–S3).
Because the ENSO process is quasi-cyclic with irregular phases occurring on average every 2–7 years, there tend to be monotonic trends in the SOI at interannual time scales that we refer to here as ‘SOI trends’ (δSOIw; Fig. 5). Partial explanation of the fluctuations in water quality trends between time windows at individual sites (i.e. τw) by the associated SOI trends (δSOIw) indicates that, during periods when the SOI trend is positive, water quality trends tend to increase at sites with positive ro values. The opposite applies to sites with negative ro values. This pattern is reversed during periods when the SOI trend is negative.
Oscillations in aggregate water quality trends (Pw; Fig. 4) are likely to be caused by interannual fluctuations in rainfall and temperature over large spatial scales, which are driven by climatic processes such as ENSO and NAO over large spatial scales (Mullan 1996; Salinger and Mullan 1999; Mellander et al. 2018). In turn, the fluctuations in rainfall and temperature drive synchronous water quality responses (i.e. changes at the same time across sites). However, the strength and direction of those water quality responses depend on the specific response to the SOI at each site (i.e. ro values). Our results also show that the strength of oscillations in aggregate trends, represented by the magnitude of the β3 coefficient in Eqn 3, is influenced by the distribution of ro values across the individual sites. Oscillations of greater magnitude tend to be associated with water quality variables with larger absolute values of 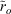 (Fig. 9). These results indicate that some of the inconsistencies in the results of successive water quality trend analyses noted above (Ministry for the Environment and Statistics New Zealand 2017, 2019) are due to the effects of ENSO variation.
(Fig. 9). These results indicate that some of the inconsistencies in the results of successive water quality trend analyses noted above (Ministry for the Environment and Statistics New Zealand 2017, 2019) are due to the effects of ENSO variation.
The methods set out in this study can be used to account for the effects of climate variability on individual and aggregate water quality trends. For an individual water quality variable and site, the combination of the ro value and the SOI trend over a given time window provides an indication of whether climate variability has compensated for or amplified the effects of anthropogenic drivers. For example, for a 10-year duration time window and an SOI trend (δSOIw) of 2.3 year–1, the contribution of the SOI trend to a DRP trend at a site with an ro value of 0.25 can be calculated in two steps. In Step 1, the coefficient β1 for the site can be calculated from Eqn 2, and the β2 coefficient shown in Fig. 8 is 0.045 (i.e. 0.18 × 0.25). In Step 2, the contribution of the SOI trend to the τw value for the site can be calculated from Eqn 1 as 0.1 (i.e. 0.045 × 2.3). This indicates that ENSO variation made a positive contribution to the assessed DRP trend that increased τw by 0.1 compared with a time window with a δSOIw of 0 or compared with a site with an ro value of 0. Similarly, the contribution of the same SOI trend to aggregate trends can be estimated using Eqn 4 and 3. For example, DRP in this study had an 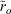 of 0.21 (Table 2) and the β4 coefficient for a time window of 10-year duration was 0.41 (Fig. 9). Therefore, the coefficient β3 is 0.086 (0.41 × 0.21) and the contribution of the SOI trend to the Pw is 0.2 (0.086 × 2.3). That is, for this 10-year window, the influence of ENSO increases the proportion of sites with positive trends in DRP by 20%.
of 0.21 (Table 2) and the β4 coefficient for a time window of 10-year duration was 0.41 (Fig. 9). Therefore, the coefficient β3 is 0.086 (0.41 × 0.21) and the contribution of the SOI trend to the Pw is 0.2 (0.086 × 2.3). That is, for this 10-year window, the influence of ENSO increases the proportion of sites with positive trends in DRP by 20%.
Another way our results can be used to account for climate variability on water quality trends is to use ro values to represent the response of trends for individual sites and variables to the SOI trend for a given time window. If measures of anthropogenic change in the catchments of sites are also available, statistical models can be used to elucidate the influence of those changes on τw by partialling out the variation attributable to the SOI trend (Snelder et al. 2021).
Attribution statements made based on our models could be made more robust by including uncertainty estimates based on the uncertainties of the underlying models. However, attribution of water quality trends to SOI trends should not be construed as comprehensively accounting for the effect of climate variability on water quality trends. Although ENSO strength has an important effect on New Zealand’s climate, it generally accounts for less than 25% of the year-to-year variation in seasonal rainfall and temperature (Salinger and Mullan 1999). Therefore, the SOI is an imprecise representation of the proximate climatic drivers of trends (i.e. rainfall and temperature) at any site. More research is needed to identify rainfall and temperature metrics that best explain variation in water quality trend strength and direction between time windows.
The variable ro is a measure of the specific responses of a water quality variable at a site to fluctuations in ENSO. Understanding the mechanisms that produce the observed correlations may lead to methods that can more comprehensively account for the effect of climate variability on water quality trends. Previous studies have shown that the responses of hydrological metrics (e.g. mean, high and low flows) at river monitoring sites to fluctuations in the SOI are broadly consistent with the known regional effects of ENSO on rainfall (e.g. McKerchar et al. 1998; Mosley 2000). However, although the hydrological responses to variation in ENSO exhibit a degree of regional coherence, these can differ strongly between rivers that are geographically close (Mosley 2000). Similarly, Scarsbrook et al. (2003) showed there were regional patterns in water quality responses to the SOI, but that responses can differ strongly between sites that are geographically close. These findings indicate that flow responses to climate variability are mediated by hydrological processes such as water storage by catchments, which are also likely to mediate water quality responses. Scarsbrook et al. (2003) reported that the responses of some water quality variables to SOI variation were significantly correlated with the flow response to the SOI, but that this was not true for NNN, DRP, NH4-N and coloured dissolved organic matter. This suggests that water quality responses to climate variability, for at least some variables, are mediated by catchment processes such as storage, mobilisation and biogeochemical transformation (Gascuel-Odoux et al. 2010; Green et al. 2014; Mellander et al. 2018). More research is needed to determine the causal links between climate variability and water quality responses. The benefits of this research would be more robust attribution of those trends to environmental drivers and an increased ability to assess the effectiveness of management actions and policies.
Conclusions
Our study shows that the effects of climate variability may amplify or counteract the effects of other drivers of water quality trends, even when those trends are assessed over time windows that are longer than ENSO cycles. Assessing and reporting water quality trends without robust attempts to identify the causes can lead to attribution of the trends to anthropogenic drivers alone, without supporting evidence (Ryberg et al. 2018). Speculative attribution could lead to the application of ineffective management actions to mitigate anthropogenic drivers and, equally, a failure to apply actions because a degrading trend is masked by the effects of climate variability.
In the present study, we used water quality trend directions and magnitudes assessed using Kendall’s τ, which is based on an underlying model of a monotonic trend (Helsel et al. 2020). This approach is a practical way to assess short-term changes in water quality or for analyses associated with hypothesised water quality changes. However, the underlying model of a monotonic trend obscures cyclic temporal patterns, and trend assessments of short duration may be dominated by the effects of climate. As time series of water quality data lengthen, studies that aim to describe patterns in water quality changes should incorporate the entire times series and use more flexible statistical models that detect and fit cyclic components, such as weighted regressions on time, discharge, and season (WRTDS; Hirsch et al. 2010, 2015). This type of more flexible modelling approach to trend analysis will provide a more complete picture of water quality changes as cyclic variation superimposed on longer-term secular trends.
Conflicts of interest
The authors declare that they have no conflicts of interest.
Declaration of funding
This work was funded by the Ministry for the Environment and the Suitability program of the Our Land and Water National Science Challenge (Ministry of Business, Innovation and Employment contract C10X1507).
Acknowledgements
The authors thank the National Institute of Water and Atmospheric Research field and laboratory teams who helped collect and collate the data related to the NRWQN. The authors thank Cathy Kilroy, Anne-Gaelle Ausseil, Lauren Long and Wes Patrick for reviews of earlier manuscripts. The authors also thank two anonymous reviewers whose comments improved the original manuscript.
References
Allan, R., Lindesay, J., and Parker, D. (1996). ‘El Niño Southern Oscillation & Climatic Variability.’ (CSIRO Publishing.)Benjamini, Y., and Hochberg, Y. (1995). Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society. Series B. Methodological 57, 289–300.
| Controlling the false discovery rate: a practical and powerful approach to multiple testing.Crossref | GoogleScholarGoogle Scholar |
Chiew, F. H. S., and McMahon, T. A. (2002). Global ENSO-streamflow teleconnection, streamflow forecasting and interannual variability. Hydrological Sciences Journal 47, 505–522.
| Global ENSO-streamflow teleconnection, streamflow forecasting and interannual variability.Crossref | GoogleScholarGoogle Scholar |
Civan, A., Worrall, F., Jarvie, H. P., Howden, N. J., and Burt, T. P. (2018). Forty-year trends in the flux and concentration of phosphorus in British rivers. Journal of Hydrology 558, 314–327.
| Forty-year trends in the flux and concentration of phosphorus in British rivers.Crossref | GoogleScholarGoogle Scholar |
Davies-Colley, R. J., Smith, D. G., Ward, R. C., Bryers, G. G., McBride, G. B., Quinn, J. M., and Scarsbrook, M. R. (2011). Twenty years of New Zealand’s national rivers water quality network: benefits of careful design and consistent operation 1. Journal of the American Water Resources Association 47, 750–771.
| Twenty years of New Zealand’s national rivers water quality network: benefits of careful design and consistent operation 1.Crossref | GoogleScholarGoogle Scholar |
Dawe, P. (2006). A statistical evaluation of water quality trends in selected water bodies of Newfoundland and Labrador. Journal of Environmental Engineering and Science 5, 59–73.
| A statistical evaluation of water quality trends in selected water bodies of Newfoundland and Labrador.Crossref | GoogleScholarGoogle Scholar |
Dupas, R., Jomaa, S., Musolff, A., Borchardt, D., and Rode, M. (2016). Disentangling the influence of hydroclimatic patterns and agricultural management on river nitrate dynamics from sub-hourly to decadal time scales. The Science of the Total Environment 571, 791–800.
| Disentangling the influence of hydroclimatic patterns and agricultural management on river nitrate dynamics from sub-hourly to decadal time scales.Crossref | GoogleScholarGoogle Scholar | 27422723PubMed |
Erb, K.-H., Fetzel, T., Haberl, H., Kastner, T., Kroisleitner, C., Lauk, C., Niedertscheider, M., and Plutzar, C. (2016) Beyond inputs and outputs: opening the black-box of land-use intensity. In ‘Social Ecology’. pp. 93–124. (Springer.)
Gascuel-Odoux, C., Aurousseau, P., Durand, P., Ruiz, L., and Molenat, J. (2010). The role of climate on inter-annual variation in stream nitrate fluxes and concentrations. The Science of the Total Environment 408, 5657–5666.
| The role of climate on inter-annual variation in stream nitrate fluxes and concentrations.Crossref | GoogleScholarGoogle Scholar | 19497610PubMed |
Green, C. T., Bekins, B. A., Kalkhoff, S. J., Hirsch, R. M., Liao, L., and Barnes, K. K. (2014). Decadal surface water quality trends under variable climate, land use, and hydrogeochemical setting in Iowa, USA. Water Resources Research 50, 2425–2443.
| Decadal surface water quality trends under variable climate, land use, and hydrogeochemical setting in Iowa, USA.Crossref | GoogleScholarGoogle Scholar |
Harding, L. W., Mallonee, M. E., Perry, E. S., Miller, W. D., Adolf, J. E., Gallegos, C. L., and Paerl, H. W. (2019). Long-term trends, current status, and transitions of water quality in Chesapeake Bay. Scientific Reports 9, 6709.
| Long-term trends, current status, and transitions of water quality in Chesapeake Bay.Crossref | GoogleScholarGoogle Scholar | 31040300PubMed |
Helsel, D. R., Hirsch, R. M., Ryberg, K. R., Archfield, S. A., and Gilroy, E. J. (2020). Statistical methods in water resources. Report 4–A3. Reston, VA, USA
| Crossref |
Hirsch, R. M., Slack, J. R., and Smith, R. A. (1982). Techniques of trend analysis for monthly water quality data. Water Resources Research 18, 107–121.
| Techniques of trend analysis for monthly water quality data.Crossref | GoogleScholarGoogle Scholar |
Hirsch, R. M., Moyer, D. L., and Archfield, S. A. (2010). Weighted regressions on time, discharge, and season (WRTDS), with an application to Chesapeake Bay river inputs 1. Journal of the American Water Resources Association 46, 857–880.
| Weighted regressions on time, discharge, and season (WRTDS), with an application to Chesapeake Bay river inputs 1.Crossref | GoogleScholarGoogle Scholar | 22457569PubMed |
Hirsch, R. M., Archfield, S. A., and De Cicco, L. A. (2015). A bootstrap method for estimating uncertainty of water quality trends. Environmental Modelling & Software 73, 148–166.
| A bootstrap method for estimating uncertainty of water quality trends.Crossref | GoogleScholarGoogle Scholar |
Hyndman, R. J., and Athanasopoulos, G. (2021). ‘Forecasting: Principles and Practice.’ (OTexts: Melbourne, Vic., Australia.)
Jackson, M. C., Loewen, C. J., Vinebrooke, R. D., and Chimimba, C. T. (2016). Net effects of multiple stressors in freshwater ecosystems: a meta-analysis. Global Change Biology 22, 180–189.
| Net effects of multiple stressors in freshwater ecosystems: a meta-analysis.Crossref | GoogleScholarGoogle Scholar | 26149723PubMed |
Johnson, H. O., Gupta, S. C., Vecchia, A. V., and Zvomuya, F. (2009). Assessment of water quality trends in the Minnesota River using non-parametric and parametric methods. Journal of Environmental Quality 38, 1018–1030.
| Assessment of water quality trends in the Minnesota River using non-parametric and parametric methods.Crossref | GoogleScholarGoogle Scholar | 19329690PubMed |
Julian, J. P., de Beurs, K. M., Owsley, B., Davies-Colley, R. J., and Ausseil, A.-G. E. (2017). River water quality changes in New Zealand over 26 years: response to land use intensity. Hydrology and Earth System Sciences 21, 1149–1171.
| River water quality changes in New Zealand over 26 years: response to land use intensity.Crossref | GoogleScholarGoogle Scholar |
Kauffman, G. J., Homsey, A. R., Belden, A. C., and Sanchez, J. R. (2011). Water quality trends in the Delaware River Basin (USA) from 1980 to 2005. Environmental Monitoring and Assessment 177, 193–225.
| Water quality trends in the Delaware River Basin (USA) from 1980 to 2005.Crossref | GoogleScholarGoogle Scholar | 20665109PubMed |
Larned, S. T., Scarsbrook, M. R., Snelder, T., Norton, N. J., and Biggs, B. J. F. (2004). Water quality in low-elevation streams and rives of New Zealand. New Zealand Journal of Marine and Freshwater Research 38, 347–366.
| Water quality in low-elevation streams and rives of New Zealand.Crossref | GoogleScholarGoogle Scholar |
Larned, S., Snelder, T., Unwin, M., and McBride, G. (2016). Water quality in New Zealand rivers: current state and trends. New Zealand Journal of Marine and Freshwater Research 50, 389–417.
| Water quality in New Zealand rivers: current state and trends.Crossref | GoogleScholarGoogle Scholar |
Luo, P., He, B., Takara, K., Razafindrabe, B. H., Nover, D., and Yamashiki, Y. (2011). Spatiotemporal trend analysis of recent river water quality conditions in Japan. Journal of Environmental Monitoring 13, 2819–2829.
| Spatiotemporal trend analysis of recent river water quality conditions in Japan.Crossref | GoogleScholarGoogle Scholar | 21842064PubMed |
McKerchar, A. I., Pearson, C. P., and Fitzharris, B. B. (1998). Dependency of summer lake inflows and precipitation on spring SOI. Journal of Hydrology 205, 66–80.
| Dependency of summer lake inflows and precipitation on spring SOI.Crossref | GoogleScholarGoogle Scholar |
McMellor, S., and Underwood, G. J. C. (2014). Water policy effectiveness: 30 years of change in the hypernutrified Colne Estuary, England. Marine Pollution Bulletin 81, 200–209.
| Water policy effectiveness: 30 years of change in the hypernutrified Colne Estuary, England.Crossref | GoogleScholarGoogle Scholar | 24556358PubMed |
Mellander, P.-E., Jordan, P., Bechmann, M., Fovet, O., Shore, M. M., McDonald, N. T., and Gascuel-Odoux, C. (2018). Integrated climate-chemical indicators of diffuse pollution from land to water. Scientific Reports 8, 944.
| Integrated climate-chemical indicators of diffuse pollution from land to water.Crossref | GoogleScholarGoogle Scholar | 29343796PubMed |
Ministry for the Environment & Statistics New Zealand (2015). Environment Aotearoa 2015. Environmental Reporting Series Ministry for Environment and Statistics New Zealand, Wellington, New Zealand. Available at http://www.mfe.govt.nz/publications/environmental-reporting/environment-aotearoa-2015 [Verified 28 February 2018]
Ministry for the Environment & Statistics New Zealand (2017). Our fresh water 2017. Ministry for the Environment & Statistics NZ, Wellington, New Zealand. Available at https://www.mfe.govt.nz/sites/default/files/media/Environmental%20reporting/our-fresh-water-2017_1.pdf
Ministry for the Environment & Statistics New Zealand (2019). Environment Aotearoa 2019. Environmental Reporting Series Ministry for Environment and Statistics New Zealand, Wellington, New Zealand. Available at https://www.mfe.govt.nz/sites/default/files/media/Environmental%20reporting/environment-aotearoa-2019.pdf
Ministry for the Environment & Statistics New Zealand (2020). Our Freshwater 2020. New Zealands Environmental Reporting Series Ministry for the Environment & Statistics NZ, Wellington, New Zealand.
Morse, N. B., and Wollheim, W. M. (2014). Climate variability masks the impacts of land use change on nutrient export in a suburbanizing watershed. Biogeochemistry 121, 45–59.
| Climate variability masks the impacts of land use change on nutrient export in a suburbanizing watershed.Crossref | GoogleScholarGoogle Scholar |
Mosley, M. P. (2000). Regional differences in the effects of El Niño and La Niña on low flows and floods. Hydrological Sciences Journal 45, 249–267.
| Regional differences in the effects of El Niño and La Niña on low flows and floods.Crossref | GoogleScholarGoogle Scholar |
Mullan, B. (1996). Effects of ENSO on New Zealand and the South pacific. Miscellaneous Series 34. The Royal Society of New Zealand, Wellington, New Zealand.
Murphy, J. C. (2020). Changing suspended sediment in United States rivers and streams: linking sediment trends to changes in land use/cover, hydrology and climate. Hydrology and Earth System Sciences 24, 991–1010.
| Changing suspended sediment in United States rivers and streams: linking sediment trends to changes in land use/cover, hydrology and climate.Crossref | GoogleScholarGoogle Scholar |
Murphy, J., and Sprague, L. (2019). Water-quality trends in US rivers: exploring effects from streamflow trends and changes in watershed management. The Science of the Total Environment 656, 645–658.
| Water-quality trends in US rivers: exploring effects from streamflow trends and changes in watershed management.Crossref | GoogleScholarGoogle Scholar | 30529968PubMed |
Oelsner, G. P., Sprague, L. A., Murphy, J. C., Zuellig, R. E., Johnson, H. M., Ryberg, K. R., Falcone, J. A., Stets, E. G., Vecchia, A. V., and Riskin, M. L. (2017). Water-quality trends in the nation’s rivers and streams, 1972–2012—data preparation, statistical methods, and trend results. United States Geological Survey Scientific Investigations Report 2017–5006 Reston, VA, USA.
Rosen, M. R., and Lapham, W. W. (2008). Introduction to the US Geological Survey National Water-Quality Assessment (NAWQA) of ground-water quality trends and comparison to other national programs. Journal of Environmental Quality 37, S-190–S-198.
Ryberg, K. R., Blomquist, J. D., Sprague, L. A., Sekellick, A. J., and Keisman, J. (2018). Modeling drivers of phosphorus loads in Chesapeake Bay tributaries and inferences about long-term change. The Science of the Total Environment 616–617, 1423–1430.
| Modeling drivers of phosphorus loads in Chesapeake Bay tributaries and inferences about long-term change.Crossref | GoogleScholarGoogle Scholar | 29102189PubMed |
Salinger, M. J., and Mullan, A. B. (1999). New Zealand climate: temperature and precipitation variations and their links with atmospheric circulation. International Journal of Climatology 19, 1049–1071.
| New Zealand climate: temperature and precipitation variations and their links with atmospheric circulation.Crossref | GoogleScholarGoogle Scholar |
Scarsbrook, M. R., McBride, C. G., McBride, G. B., and Bryers, G. G. (2003). Effects of climate variability on rivers: consequences for long term water quality analysis. Journal of the American Water Resources Association 39, 1435–1447.
| Effects of climate variability on rivers: consequences for long term water quality analysis.Crossref | GoogleScholarGoogle Scholar |
Shoda, M. E., Sprague, L. A., Murphy, J. C., and Riskin, M. L. (2019). Water-quality trends in US rivers, 2002 to 2012: relations to levels of concern. The Science of the Total Environment 650, 2314–2324.
| Water-quality trends in US rivers, 2002 to 2012: relations to levels of concern.Crossref | GoogleScholarGoogle Scholar | 30292123PubMed |
Smith, D. G., and Maasdam, R. (1994). New Zealand’s national water quality network. 1. Design and physio-chemical characterisation. New Zealand Journal of Marine and Freshwater Research 28, 19–35.
| New Zealand’s national water quality network. 1. Design and physio-chemical characterisation.Crossref | GoogleScholarGoogle Scholar |
Snelder, T. H., Fraser, C., Larned, S. T., Monaghan, R., De Malmanche, S., and Whitehead, A. L. (2021). Attribution of river water-quality trends to agricultural land use and climate variability in New Zealand. Marine and Freshwater Research. [Published online 30 September 2021].
| Crossref |
Suthanthangjai, M., Moore, K., Steel, G., and Hughey, K. F. (2013). Tracking New Zealanders environmental perceptions: a comparison of responses from two survey approaches. The International Journal of Science in Society 4, 25–40.
| Tracking New Zealanders environmental perceptions: a comparison of responses from two survey approaches.Crossref | GoogleScholarGoogle Scholar |
Tomperi, J., Juuso, E., and Leiviskä, K. (2016). Early warning of changing drinking water quality by trend analysis. Journal of Water and Health 14, 433–442.
| Early warning of changing drinking water quality by trend analysis.Crossref | GoogleScholarGoogle Scholar | 27280609PubMed |
Venables, W. N., and Ripley, B. D. (2013). ‘Modern Applied Statistics with S-PLUS.’ (Springer Science & Business Media.)




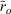 values (
values (