A simple dynamic model of photosynthesis in oak leaves: coupling leaf conductance and photosynthetic carbon fixation by a variable intracellular CO2 pool
Steffen M. Noe A B and Christoph Giersch AA Institut für Botanik, Technische Universität Darmstadt, Schnittspahnstr. 3-5, D-64287 Darmstadt, Germany.
B Present address: Department of Plant Physiology, Institute of Molecular and Cell Biology, Riio 23, EE 51010 Tartu, Estonia.
C Corresponding author. Email: snoe@ut.ee
Functional Plant Biology 31(12) 1195-1204 https://doi.org/10.1071/FP03251
Submitted: 19 December 2003 Accepted: 27 October 2004 Published: 8 December 2004
Abstract
Modelling the diurnal course of photosynthesis in oak leaves (Quercus robur L.) requires appropriate description of the dynamics of leaf photosynthesis of which diurnal variations in leaf conductance and in CO2 assimilation are essential components. We propose and analyse a simple photosynthesis model with three variables: leaf conductance (gs), the CO2 partial pressure inside the leaf (pi), and a pool of Calvin cycle intermediates (aps). The environmental factors light (I) and vapour pressure deficit (VPD) are used to formulate a target function G(I, VPD) from which the actual leaf conductance is calculated. Using this gs value and a CO2 consumption term representing CO2 fixation, a differential equation for pi is derived. Carboxylation corresponds to the sink term of the pi pool and is assumed to be feedback-inhibited by aps. This simple model is shown to produce reasonable to excellent fits to data on the diurnal time courses of photosythesis, pi and gs sampled for oak leaves.
Keywords: leaf conductance, numerical model, oak, photosynthesis, Quercus robur.
Acknowledgments
We thank an anonymous referee for suggesting eqn 2 for the dependence of stomatal response on VPD. The photosynthesis model presented here was developed as part of a process-based model of isoprene emission by trees, which was initiated by Wolfgang Zimmer some time ago. He passed away in August 2002. Stimulating discussions with Wolfgang Zimmer during the earlier stages of this project are gratefully acknowledged.
This work was supported by the German Federal Ministry of Education and Research (BMBF) in context of BEWA2000 (Biogenic emissions of volatile organic compounds from forest ecosystems) which is a subproject of the national joint research project AFO2000 (Atmosphären-Forschungsprogramm 2000).
Assmann SM
(1999) The cellular basis of guard cell sensing of rising CO2. Plant, Cell and Environment 22, 629–637.
| Crossref | GoogleScholarGoogle Scholar |

Ball, JT (1987). Calculations related to gas exchange. In ‘Stomatal function’. pp. 445–476. (Stanford University Press: Stanford)
Cai T, Dang Q-L
(2002) Effects of soil temperature on parameters of a coupled photosynthesis-stomatal conductance model. Tree Physiology 22, 819–827.
| PubMed |

Cohen, SD ,
and
Hindmarsh, AC (1994).
Dewar RC
(1995) Interpretation of an empirical model for the stomatal conductance in terms of guard cell function. Plant, Cell and Environment 18, 365–372.

Farquhar GD, Sharkey TD
(1982) Stomatal conductance and photosynthesis. Annual Review of Plant Physiology 33, 317–345.
| Crossref | GoogleScholarGoogle Scholar |

Farquhar GD,
von Caemmerer S, Berry JA
(1980) A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 149, 78–90.
| Crossref | GoogleScholarGoogle Scholar |

Farquhar GD, Wong SC
(1984) An empirical model of stomatal conductance. Australian Journal of Plant Physiology 11, 191–210.

Gross LJ,
Kirschbaum MUF, Pearcy RW
(1991) A dynamic model of photosynthesis in varying light taking account of stomatal conductance, C3-cycle intermediates, photorespiration and Rubisco activation. Plant, Cell and Environment 14, 881–893.

Heizmann U,
Kreuzwieser J,
Schnitzler J-P,
Brüggemann N, Rennenberg H
(2001) Assimilate transport in the xylem sap of pedunculate oak (Quercus robur) seedlings. Plant Biology 3, 132–138.
| Crossref | GoogleScholarGoogle Scholar |

Jarvis PG
(1976) The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences 237, 593–610.

Katul GG,
Ellsworth DS, Lai CT
(2000) Modelling assimilation and intercellular CO2 from measured conductance: a synthesis of approaches. Plant, Cell and Environment 23, 1313–1328.
| Crossref | GoogleScholarGoogle Scholar |

Kirschbaum MUF,
Gross LJ, Pearcy RW
(1988) Observed and modelled stomatal responses to dynamic light environments in the shade plant Alocasia macrorrhiza.
Plant, Cell and Environment 11, 111–121.

Kirschbaum MUF,
Küppers M,
Schneider H,
Giersch C, Noe S
(1998) Modelling photosynthesis in fluctuating light with inclusion of stomatal conductance, biochemical activation and pools of key photosynthetic intermediates. Planta 204, 16–26.
| Crossref | GoogleScholarGoogle Scholar |

Kreuzwieser J,
Graus M,
Wisthaler A,
Hansel A,
Rennenberg H, Schnitzler J-P
(2002) Xylem-transported glucose as an additional carbon source for leaf isoprene formation in Quercus robur. New Phytologist 156, 171–178.
| Crossref | GoogleScholarGoogle Scholar |

Lambers, H ,
Chapin, FS ,
and
Pons, TL (1998).
Lawlor, DW (1990).
Leuning R
(1995) A critical appraisal of a combined stomatal-photosynthesis model for C3 plants. Plant, Cell and Environment 18, 339–355.

Lösch, R (2001).
Marquardt D
(1963) An algorithm for least-squares estimation of non-linear parameters. Journal of the Society for Industrial and Applied Mathematics 12, 591–612.

Niinemets Ü,
Seufert G,
Steinbrecher R, Tenhunen JD
(2002) A model coupling foliar monoterpene emissions to leaf photosynthetic characteristics in Mediterranean evergreen Quercus species. New Phytologist 153, 257–275.
| Crossref | GoogleScholarGoogle Scholar |

Schultz HR, Matthews MA
(1997) High vapour pressure deficit excerbates xylem cavitation and photoinhibition in shade-grown Piper auritum H.B. & K. during prolonged sunflecks: I relations of plant water relations. Oecologia 110, 312–319.
| Crossref | GoogleScholarGoogle Scholar |

Snaith PJ, Mansfield TA
(1985) Responses of stomata to IAA and Fusicoccin at the opposite phases of an entrained rhythm. Journal of Experimental Botany 36, 937–944.

Snaith PJ, Mansfield TA
(1986) The circadian rhythm of stomatal opening: evidence for the involvement of potassium and chloride fluxes. Journal of Experimental Botany 37, 188–199.

Streubing, L ,
and
Fangmeier, A (1992).
Tenhunen, JD ,
Pearcy, RW ,
and
Lange, OL (1987). Diurnal variations in leaf conductance and gas exchange in natural environments. In ‘Stomatal function’. pp. 323–351. (Stanford University Press: Stanford)
Thornley, JHM ,
and
Johnson, IR (Eds) (1990).
Wong SC,
Cowan IR, Farquhar GD
(1979) Stomatal conductance correlates with photosynthetic capacity. Nature 282, 424–426.

Yong JWH,
Wong SC, Farquhar GD
(1997) Stomatal responses to changes in vapour pressure difference between leaf and air. Plant, Cell and Environment 20, 1213–1216.
| Crossref | GoogleScholarGoogle Scholar |

Zimmer W,
Brüggemann N,
Emeis S,
Giersch C,
Lehning A,
Steinbrecher R, Schnitzler J-P
(2000) Process-based modelling of isoprene emission by oak leaves. Plant, Cell and Environment 23, 585–595.
| Crossref | GoogleScholarGoogle Scholar |

Appendix
Consider a rectangular box with area F and thickness d. We assume that there is a flux Vin [mol m–2 s–1] into the box and a flux Vout leaving the box. The change in concentration n within the box, dn / dt, is then given by:
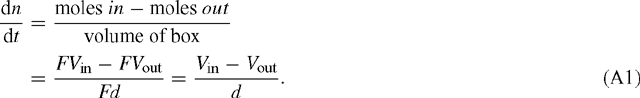
The change in pressure corresponding to that in n is from p = n RT:
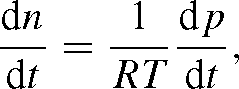
so that (A1) may be written as:
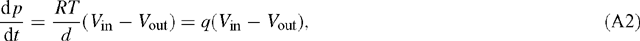
with q = RT / d. Identifying the box with a leaf, F takes the role of the leaf surface and d that of leaf thickness (more exactly, that of a fictitious depth available to diffusion of CO2). Multiplying the flux term gs (pa – pi)/ Patm [μmol m–2 s–1] by RT / d [Pa m² μmol–1] gives the unit of Pa s–1. At T = 300 K and d = 0.1 mm, we have:
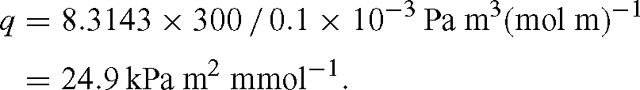
Alternatively, and more convenient when photosynthesis or respiration rates (mm s–1) are of interest, expressing the ps as concentrations (mol m–3), we have:

where q′ = RT / (d Patm). For standard pressure, T = 300 K and d = 0.1 mm, we have:
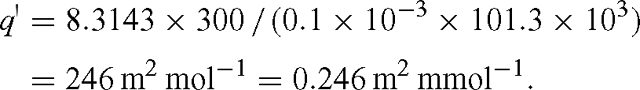
Using q or q′, a differential equation for pi may be formulated using the flux terms that are common in gas-exchange studies (e.g. eqn 11).


