Using Chaos theory fundamentals for analysing temperature, precipitation variability and trends in Northern Patagonia, Argentina
Grethel García Bu Bucogen A * , María Cintia Piccolo
A * , María Cintia Piccolo  B , Vanesa Yael Bohn
B , Vanesa Yael Bohn  C and Gabriel Eduardo Huck
C and Gabriel Eduardo Huck  A
A
A Instituto Argentino de Oceanografía (CONICET-UNS), Bahía Blanca, Buenos Aires, Argentina.
B Instituto Argentino de Oceanografía (CONICET-UNS)–Departamento de Geografía y Turismo, Universidad Nacional del Sur (UNS), Bahía Blanca, Buenos Aires, Argentina.
C Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET)–Departamento de Geografía y Turismo, UNS, Bahía Blanca, Buenos Aires, Argentina.
Journal of Southern Hemisphere Earth Systems Science 72(3) 179-190 https://doi.org/10.1071/ES22009
Submitted: 23 March 2022 Accepted: 26 September 2022 Published: 18 October 2022
© 2022 The Author(s) (or their employer(s)). Published by CSIRO Publishing on behalf of BoM. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)
Abstract
The fundamentals of Chaos theory allow the study of climatic conditions and long-term modifications produced by changes in their spatial and temporal scales. The aim of this work is to analyse the variability and changes produced in the annual cycles of temperature and precipitation in Northern Patagonia, Argentina, applying multifractal analysis as a practical mathematical tool of Chaos theory. Data from the NASA POWER Project (2021) was implemented as an alternative dataset for carrying out climatological studies in the area. Annual mean temperature and precipitation time-series data (1981–2019) were analysed at 72 grid points with 1° of spatial resolution. The Mann–Kendall test was used to calculate the trends through the annual cycles of the meteorological variables. Fractal dimension values were calculated using Multifractal Detrended Fluctuation Analysis. The Hurst exponent, complexity and asymmetry were the multifractal dimensions describing the persistence of time-series trends and climatic variability. The results showed changes in the annual cycles of both variables during the study period. The most significant finding was a large area in the centre and north of the study area, where the decrease in the rainfall regime was persistent. The Hurst exponent detected a sector in the Patagonian Andes mountain range where the temperature increase was constant. This work demonstrates that fractal geometry is useful to describe meteorological variability and obtain better short-, medium- and long-term forecasts.
Keywords: annual cycles, climatic variability, heating, hydric stress, melting, multifractal dimensions, Northern Patagonia, precipitation, temperature, trends.
1. Introduction
Many natural and anthropogenic processes, previously considered deterministic and predictable, currently have severe limitations in terms of predictability (Haro et al. 2012; Santos Burguete 2018). In this context, Chaos theory is fundamental for explaining the inaccuracy and difficulty in obtaining predictable results from a complex and nonlinear system (Selvam 1993). This approach supports the existence of an underlying order in the apparently unpredictable behaviours of nature. The theory establishes that modifications of the initial conditions during the analysis imply significant calculation differences in future trends (Lorenz 1963, 1990, 1991; Selvam 2013, 2017; Martínez Moncaleano 2018). Chaos theory applications have been used in mathematics, meteorology, economy and sociological studies (Hena Rani et al. 2018).
Fractals are the graphical representation of Chaos theory (Mandelbrot 1977; Camacho Velázquez and Vásquez Cruz 2015). Fractal geometry describes structures whose curves, spirals and filaments repeat at different scales (principle of self-similarity) (Mandelbrot and Wheeler 1983) contrasting with traditional Euclidean geometry, which describes artificially created objects. Fractal analysis studies the structure of complex and nonlinear systems using fractal dimensions (Plazas Nossa et al. 2014). The Hurst exponent is the fractal dimension most used for determining how persistent time-series trends are through different scales (Quintero Delgado and Ruiz Delgado 2011).
In meteorology, temperature and precipitation studies are restricted to a specific scale using stochastic methods (Huang et al. 2013; López-Lambraño et al. 2017). This represents a great limitation for performing meteorological forecasts (Lorenz 1963, 1990, 1991). While the spatial and temporal evolution of precipitation is complex (Rangarajan and Sant 2004; Bartos and Jánosi 2006), temperature is a meteorological variable with nonlinear behaviour in its temporal series (Mandelbrot and Wheeler 1983; Bartos and Jánosi 2006; Maofei et al. 2009), therefore, fractal geometry has been used to study the structure of these variables on many occasions (Selvam et al. 1992; Maofei et al. 2009; Selvam 2011; Lovejoy et al. 2012).
Previous research used multifractal methods for characterising temperature and precipitation time-series variability (Svensson et al. 1996; Ghanmi et al. 2013; Domino et al. 2014; Santos da Silva et al. 2020; Morales Martínez et al. 2021). Baranowski et al. (2015) showed that precipitation was the meteorological variable most vulnerable to climate change effects in Europe and these authors, in 2019, also demonstrated how topography and atmosphere patterns influenced the variability of multifractal spectra in Poland (Baranowski et al. 2019). Recently, Santos da Silva et al. (2020) found significant differences between the north and south of Brazil, in terms of stochastic processes that generate fluctuations in air temperature. The Hurst exponent values can be used for describing trends and their persistence in meteorological data (Lovejoy et al. 2012). Pérez et al. (2009) calculated this fractal dimension for precipitation time-series in 10 localities in the west of La Pampa, Argentina, and found an increase in the rainfall regime from 1911 to 2001. There are no examples of multifractal analysis use for temperature record studies in Argentina (López-Lambraño et al. 2017).
According to Paruelo et al. (1998), Garreaud et al. (2009) and Bianchi (2016), research papers about the climatic variability and trends of temperature and precipitation are limited for Northern Patagonia. Temperature analysis detected a clear increasing tendency in annual values in Northern Patagonia, while debate continues about the temporal and spatial evolution of precipitation time series (Romero et al. 2014; Camilloni 2018; Brendel et al. 2020; IPCC 2021; Pessacg et al. 2022). Garreaud et al. (2013) observed absolute changes standardised by the long-term annual precipitation in Patagonia, and revealed a decrease during 1948–2010 in precipitation in a substantial portion of the study area, except in the eastern part where no substantial changes have been registered. Romero et al. (2014) discovered two precipitation trends: an increase in the west and a decrease in the east of Patagonia. The future climatic scenarios described by Camilloni (2018) established the continuity of the trends of Romero et al. (2014) up to 2100. Later, Pessacg et al. (2020) described a decrease in rainfall regime between 2071 and 2100. Pessacg et al. (2022) indicated a slight decrease and a future increase of annual precipitation values for coastal areas to the north of 44°S. IPCC (2021) summarised that annual precipitation values show an increase in the western and a decrease in the eastern part of the Patagonian region. The spatial distribution of precipitation trends differed among these works because of the scarcity of meteorological stations in Patagonia (IPCC 2021).
Most human activities depend on climatic conditions. Changes in the annual values of temperature and precipitation affect ecosystem services, with the provision of water the most affected. Traditionally, a relevant part of Northern Patagonia suffers from water scarcity (Morello et al. 2012). The water reservoirs of this region depend on the rainfall regime and the spring melting of glaciers (Mazzoni and Vázquez 2010). Modifications in the annual precipitation and the water supply towards hydrographic basins can affect the ecosystems in semi-arid and arid areas (Gil Guirado and Bermúdez 2011) and, in addition, temperature rise in the Patagonian Andes mountain range may produce a retreat in ice cover (Johansen et al. 2018; Ferri et al. 2020). For these reasons, this paper analyses climatic variability and determines the changes in the annual cycles of temperature and precipitation in Northern Patagonia from 1981 to 2019.
2. Data and methods
2.1. Study area
The study region extends from the south-east of Mendoza, San Luis, La Pampa and Buenos Aires provinces up to the 44°S parallel (~784 412 km2), being the western limit of the border with Chile and the Espinal ecoregion to the east (Mazzoni and Vázquez 2010; Morello et al. 2012). The Patagonian Andes mountain range, part of the Cordillera de Los Andes, is located on the western boundary. Patagonia presents two different types of relief, with an extensive plateau and riverine valleys that extend to the east and the Patagonian Andes mountains to the west (Mazzoni and Vázquez 2010) (Fig. 1). In the Andean mountains (~42°S) there is a significant concentration of uncovered ice that forms glaciers (García Silva et al. 2019) at 1800 m above sea level (ASL) (Zalazar et al. 2017) (Fig. 1).

|
The study area is under the influence of the semi-permanent anticyclones from both the South Atlantic and Pacific Oceans and the subpolar lows at 60°S (Prohaska 1976; Paruelo et al. 1998; Bianchi 2016). The variation of the circulation patterns, topography and oceanic influence determine the Patagonian climate (Bianchi 2016). Northern Patagonia has four different climates according to the Koppen-Geiger classification (Bianchi and Cravero 2010; Chen and Chen 2013). The climate is Mediterranean (Csb) north of 42°S and west of 65°W, and temperate oceanic (Cfb) south of 42°S in the coastal zone. There is a climatic transition from the east to west, where the Mediterranean climate becomes Arid Cold (BWk) in the centre of Northern Patagonia and finally Cold Semiarid (BSk) near to the coastal sector. According to Morello et al. (2012), 81.6% of the study area has arid and semi-arid characteristics. The Patagonian Andes mountain range influences the zonal distribution of precipitation (Endlichter and Santana 1988; Warren and Sugden 1993; Coronato et al. 2017), with a sharp decrease of annual precipitation from the Andes Mountains to the east (Paruelo et al. 1998). Humid air masses from the Pacific Ocean discharge moisture on the Chilean side of the Andes and on the higher mountain ranges near the Argentine border (Zalazar et al. 2017). Rainfall decreases from west to east, with values between 1500 and 150 mm year–1 (Mazzoni and Vázquez 2010), and mean air temperature varies between 5 and 13°C according to Bianchi and Cravero (2010).
2.2. Dataset
The density of meteorological stations is low in Northern Patagonia (Paruelo et al. 1998; Palese et al. 2001; Garreaud 2009; Garreaud et al. 2013; Bianchi 2016). The NASA MERRA-2 assimilation model system provides the NASA POWER Project with high spatial (0.5°) and temporal (daily) resolution (NASA POWER Project 2021, see https://power.larc.nasa.gov), this meteorological repository was validated as an alternative database for the study region by García Bu Bucogen et al. (2022) and was used to determine temperature and precipitation trends. Annual data from temperature (at 2 m) and precipitation were used for calculating trends, multifractal spectra and their dimensions in 72 grid points (1° spatial resolution) from 1981 to 2019 (Fig. 2).

|
2.3. Methods
The temperature and precipitation trends during 1981–2019 were calculated using the Mann–Kendall test (Mann 1945; Kendall 1975; Goossens and Berger 1986; Yu and Kao 2007; Alencar da Silva Alves and Silva Nóbrega 2017). The results were classified with a confidence level of 90% (significance level of 10%) using the classification criteria of Alves et al. (2015) and Alencar da Silva Alves and Silva Nóbrega (2017).
Multifractal Detrended Fluctuation Analysis (MFDFA) is a method proposed by Kantelhardt et al. (2002), with its main contribution being characterising time series using their multifractal dimensions to detect long-term correlation (Kantelhardt et al. 2002; López-Lambraño et al. 2017; Baranowski et al. 2019). Furthermore, this methodology allows the analysis of signals, even if the time series are affected by non-stationary processes (Gómez and Poveda 2008; Zhou and Leung 2010; Morales Martínez et al. 2021). Another advantage of this technique is that it is less sensitive to the length of the studied time series (Baranowski et al. 2015, 2019) in contrast to traditional methods such as wavelets and the fast Fourier transform. For these reasons, MFDFA is useful for the fractal characterisation of daily, monthly and annual precipitation and temperature time-series (Ghanmi et al. 2013; Domino et al. 2014; Yu et al. 2014; Baranowski et al. 2015; Santos da Silva et al. 2020; Morales Martínez et al. 2021).
MFDFA was implemented for the calculation of the multifractal spectrum and its dimensions from the temperature and precipitation records of Northern Patagonia. The Hurst exponent (α0), complexity (w) and asymmetry (r) were analysed as multifractal dimensions, in particular α0 exposes how persistent or significant the tendency of a meteorological time series is (Rodríguez Aguilar 2012; Nieto et al. 2016). According to Baranowski et al. (2015, 2019) and Santos da Silva et al. (2020) if:
α0 > 0.5, the variable trends are linear and persistent. The series has a long-term memory and the observed changes in the annual cycles will continue to be produced in the near future. For example, if the measurements of a study period were above the historical mean, the time series values will continue to increase in the next period.
α0 < 0.5, the variable has anti-persistent conditions and the tendency is nonlinear. In this case, the series has a short-term memory and the trends will change in the future. For example, if the measurements during the study period were above the historical mean, in the near future they would be under the historical values.
α0 = 0.5, the variable is independent and the future trend forecast has great uncertainty values.
The αmax and αmin values show the extreme measurements of the time series. The width of the multifractal spectrum (w) is the difference between αmax and αmin. This parameter describes how different extreme data are (e.g. drought and extremely humid periods in precipitation time-series), which in the multifractal analysis is known as the complexity of the signal. A larger width of the multifractal spectrum denotes a more complex time-series.
The asymmetry of the multifractal spectrum expresses the dominance of small and large fluctuations around the historical mean. If the multifractal spectrum is skewed to the left, the large fluctuations result in a large variability that describes the time series; however, if it is skewed to the right, small fluctuations are produced by the natural variability of the signal.
The last case is a symmetric spectrum, so both large and small variations are present in the variability of the time series. This multifractal dimension was calculated according to the formula (Santos da Silva et al. 2020) in Eqn 1:
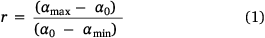
If r > 1, the spectrum is skewed to the right; the fluctuations are slight and respond directly to natural variations in the signal. If r < 1, the spectrum is skewed to the left; the fluctuations are high and the series shows great variability. If r = 1, the spectrum is symmetric; the variability of the time series responds to natural fluctuations and processes that promote high variation in the variable cycles.
The mapping of the spatial distribution of the fractal dimensions was performed in QGIS software (ver. 3.10, see https://github.com/qgis/QGIS). The results were obtained from 72 grid points with the nearest neighbour interpolation method. Four study cases were selected to analyse the climatic variability and locations with persistent and anti-persistent conditions. Study cases were located in the Patagonian Andes mountain range, Península de Valdés and the centre and south-west of Northern Patagonia.
3. Results
3.1. Trends and multifractal dimensions of annual temperature time-series
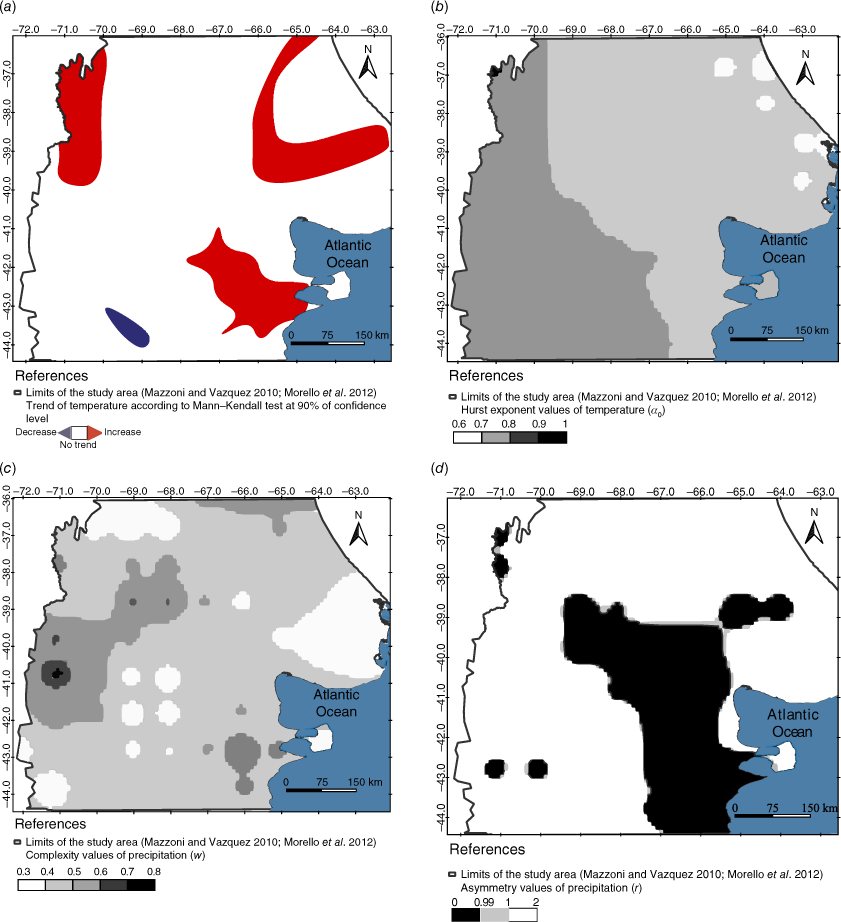
Three sectors of the study area showed a significant increase in temperature (Fig. 3a). The Hurst exponent (α0 > 0.5) showed that the calculated trends were persistent in their annual cycles (Fig. 3b). The time series had long-term memory and what was observed is likely to persist into the near future. The position of the historical records above the historical average determines an upward trend in the future.
|
One sector of the Patagonian Andes mountain range registered a severe temperature rise. The Mann–Kendall tests and the Hurst exponent results were consistent with a persistent temperature increase. Only in the south-west of the study area, the Mann–Kendall tests showed a significant decrease (Fig. 3a) although the Hurst exponent values were persistent for these tendencies. The complexity of the series was low in Northern Patagonia (w < 0.5) (Fig. 3c). The low complexity values were consistent with the high persistence of the variable illustrated in Fig. 3b.
The multifractal spectrum presented skewness to the right on the east side of the study area (r > 1) (Fig. 3d). In this case, variations in annual temperature cycles were associated with natural fluctuations. The asymmetry values showed skewness to the left in the west of the study area (r < 1). This condition described a great variability between annual temperature cycles. The sector where the Mann–Kendall test was significant and persistent towards a temperature increase according to the Hurst exponent coincided with records of low asymmetry (r < 1). The high variability reported (Fig. 3d) could result from gradual increases in the annual temperature.
3.2. Trends and multifractal dimensions of precipitation time-series
The annual precipitation trend was negative in a great part of the northern sector of the study area (Fig. 4a). Only in one sector was the trend of the meteorological variable positive. The Mann–Kendall test detected a significative rise in the rainfall regimen in the south-western sector.

|
The values of the Hurst exponent presented a gradient from the coast to the continental sector (Fig. 4b). Persistent trends (α0 > 0.5) were found in an important part of Northern Patagonia. The decreasing trends in the north and the increasing rainfall pattern reported persisted, meaning this behaviour is likely to persist in the future.
The precipitation was independent (α0 = 0.5) and anti-persistent (α0 < 0.5) for Peninsula de Valdes and surrounding areas. The Hurst exponent values lower than 0.5, indicating a nonlinear trend. For areas with anti-persistent conditions, if the historical mean was lower than the observed values, annual precipitation values would probably increase in the future. In sectors where the variable had independent conditions, the trend forecast has a high level of uncertainty. The complexity was low in Northern Patagonia, except in the north, near Peninsula de Valdez, and a sector in the west (Fig. 4c). High complexity values denoted a major difference between extreme data in the time series, which were located in zones with anti-persistent and independent conditions.
The asymmetry was left-skewed in the south-west, north-west, centre and north-east of Patagonia (r < 1) (Fig. 4d). The multifractal spectrum showed high variability in these areas. Notably, in the northern area with left asymmetry presence, the Mann–Kendall test and the Hurst exponent showed a persistent trend for a precipitation decrease. The skewness to the left was present in the north-west and centre of Northern Patagonia (r < 1) (Fig. 4d). The multifractal spectrum showed a high variability in these areas where the Mann–Kendall test and the Hurst exponent detected a persistent decrease.
3.3. Study cases
Four study cases were selected based on the observed trends illustrated by the Mann–Kendall test and multifractal dimensions values (Fig. 2). The first corresponds to grid point 8, located in the Patagonian Andes mountain range, which showed an area where the temperature trends significantly rose. Grid point 59 (near Peninsula de Valdés) was used to determine how anti-persistent conditions affected the precipitation trends. Finally, grid points 29 and 54, representing the centre and south-west of Northern Patagonia, were studied to describe substantial increase and decrease trends, respectively.
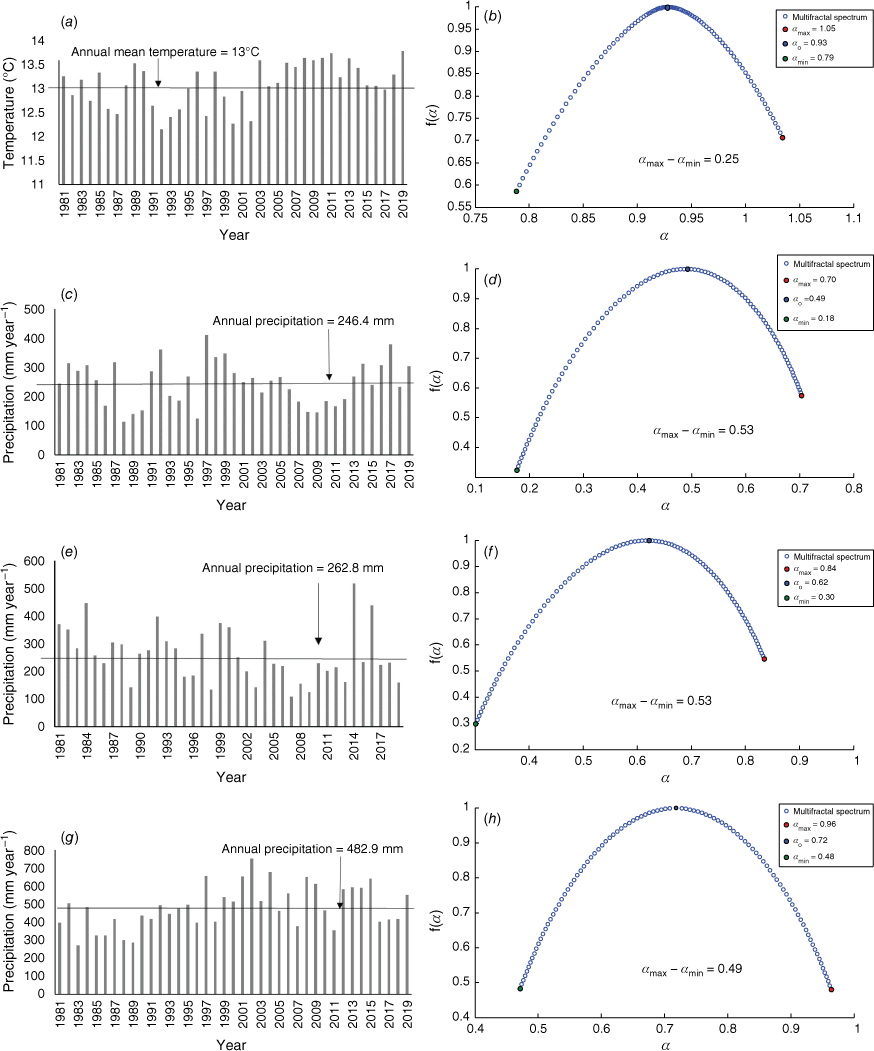
A sector of the Patagonian Andes mountain range presented a significant increase in temperature. Descriptions of climate variability and trends were made using the temperature time-series of grid point 8 (located at 38°S and 71°W) (Fig. 2). The historical record showed that the mean temperature was 13°C and, with the exception of 2017 (12.9°C), from 2003 to 2019, its annual records were higher than the historical value (Fig. 5a). The Mann–Kendall (Z) test value was 2 and the trend was towards an increase in temperature. The Hurst exponent was 0.93 (Fig. 5b), confirming the high persistence of the temperature increase trend. Low complexity was found, so the increase in temperature values was gradual (w = 0.25). The spectrum showed asymmetry to the left, indicating high variability between annual variable cycles.
No clear trends were registered close to Peninsula de Valdés (on the south-east coast). The historical annual precipitation value in grid point 59 (located at 43°S and 65°W) (Fig. 2) was 246.4 mm (Fig. 5c). The Mann–Kendall test value did not detect a clear trend (Z = −0.17) and the Hurst exponent value was 0.49 (anti-persistent) (Fig. 5d). The series was not very complex (w = 0.53) and the multifractal spectrum had a pronounced asymmetry to the left. The results of Hurst exponent, complexity and asymmetry explained the important annual variability registered in the precipitation records (Fig. 5c).
A clear decrease in the precipitation trend was apparent in the centre of the study area. The historical mean annual rainfall was 262.8 mm in grid point 29 (located at 40°S and 67°W) (Fig. 2). The precipitation records were lower than the historical value from 2001 to 2019, except in 2004, 2014 and 2016 (Fig. 5e). This behaviour was consistent with the significant decreasing trend shown by the Mann–Kendall test (Z = −2.03). The Hurst exponent had a value of 0.62 (persistent) (Fig. 5f) with little complexity (w = 0.53). The spectrum had a pronounced asymmetry to the left, which denoted considerable variability.
Meanwhile, in the south-west of Northern Patagonia there was an increasing trend in precipitation. The historical mean annual rainfall was 482.8 mm in grid point 54 (located at 43°S and 70°W) (Fig. 2) and the time series showed that the records tended to be greater than the historical value from 1997 to 2019 (Fig. 5g). The Mann–Kendall test value was 3.43, demonstrating an increase in precipitation at this point. The Hurst exponent value was 0.72 (persistent) (Fig. 5h) and the complexity was low (w = 0.49). The spectrum showed asymmetry to the left, which denoted great variability.
4. Discussion
In the last decade, many studies examined, described and quantified complex and unpredictable dynamics of nonlinear systems that follow mathematical laws, even though their outward appearance appears random (Kantelhardt et al. 2002; Gómez and Poveda 2008; Zhou and Leung 2010; Ghanmi et al. 2013; Domino et al. 2014; Yu et al. 2014; Baranowski et al. 2015; López-Lambraño et al. 2017; Baranowski et al. 2019; Santos da Silva et al. 2020; Morales Martínez et al. 2021) by the evaluation of the physical properties of the time series and their trends (Redondo et al. 2008). In this case, the application of multifractal analysis, based on Chaos theory fundamentals, demonstrated the complexity of conducting climate studies in the study area. The spatial distribution of the meteorological trends was heterogeneous and climatic variability was high in some areas. Additionally, the length of the time series (39 years) limited the results of this paper. The temperature and precipitation time-series analysis showed that these meteorological variables changed from 1981 to 2019 in their spatial and temporal scales for Northern Patagonia.
Lack of positive or negative trends for temperature and precipitation time-series was found in a large portion of Northern Patagonia from 1981 to 2019. The quasi-periodic fluctuations (Bianchi and Cravero 2010) of the rainfall regime and the influence of seasonality on temperature (Das 2009) contribute to the non-linearity of the time series, which translates into an irregular space–time evolution (alternation of increases and decreases in the meteorological variables regimen) that does not necessarily present a significant tendency. Only in a few sectors were persistent trends detected.
Different authors have investigated the temperature trends in Northern Patagonia (Garreaud et al. 2013; Romero et al. 2014; Camilloni 2018; Brendel et al. 2020; IPCC 2021). All studies reported that temperature time-series trends show a clear rise. Our results showed a persistent temperature increase in three areas of Northern Patagonia. However, in the south-west sector of the study area, the annual cycles of the variable presented a persistent decrease.
One finding was detection of a significant temperature rise in a sector of the Patagonian Andes mountain range. The climate in this area is cold and perpetual snow forms glaciers at 1800 m ASL (Bianchi and Cravero 2010; Morello et al. 2012; Coronato et al. 2017); however, the progressive increase in temperature could expose the ice cover to a gradual retreat (Ferri et al. 2020). Andean glaciers are one of the most important freshwater reserves in Argentina because, during spring, melted snow feeds the hydrographic basins of Northern Patagonia with water suitable for human consumption (Masiokas 2008). If the volume of water coming from rain, snow and glacial melting decreases, it could affect the flow of Patagonian rivers (Zalazar et al. 2017) which would be critical during drought periods.
Concerning rainfall, debates continue about how variable trends are in Northern Patagonia. Garreaud et al. (2013) showed a significant decrease in the rainfall regime in the study area from 1948 to 2010 with the exception of the east side, where no substantial changes were found. Romero et al. (2014) described an increase in precipitation in the west and a decrease in the east. The future climate projections of Camilloni (2018) exposed the continuity of the conditions described by Romero et al. (2014). According to Pessacg et al. (2020), the probability is high that the rainfall regime will decrease by 10–30% during the period 2071–2100. Pessacg et al. (2022) found a slight decrease in the rainfall regime in the coastal areas north of 44°S; however, they reported a future increase in annual precipitation values.
This paper detected a significant difference in the spatial distribution of precipitation trends. Precipitation decreased in the north and centre of the study area from 1981 to 2019, while the trend of meteorological variables was positive in a small area to the south-west. The Hurst exponent validated the persistence of these trends in a prominent part of the territory. In Peninsula de Valdés and its surroundings, only anti-persistent and independent conditions were found, meaning that dry periods followed by wet conditions are expected in these areas, coinciding with the observations of Pessacg et al. (2022). However, the variability in annual cycles was high in the areas where there was a decreasing and persistent rainfall regime.
A substantial portion of Northern Patagonia has arid and semi-arid characteristics (Morello et al. 2012). The management of these types of territories is a challenge. A scarcity of water resources aggravated by the effects of climate change, population growth, overexploitation of natural resources and inadequate development policies may cause land degradation with the consequential loss of the biological, productive and economic potential of soils (Collado 2012). If the rainfall regime decreases in the Patagonian region, the desertification process may speed up (González et al. 2017). In addition, high climatic variability in zones with erosion problems may increase the risk associated with meteorological extreme events (floods and drought). The adaptive capacity of ecosystems and human settlements can be severely affected by the negative impact of these events (Meza et al. 2010).
5. Conclusion
Multifractal analysis, based on Chaos theory fundamentals, is a useful tool for studying climatic variability and detecting changes in the annual cycles of meteorological variables. This type of research validates the results obtained with more traditional methods such as the Mann–Kendall test. The present work identified the complexity of the spatial distribution of temperature and precipitation trends in Northern Patagonia. The description of the fractal dimensions showed changes in the annual cycles of the variables from 1981 to 2019.
The spatial distribution of precipitation trends was complex. The decreasing trend of the annual precipitation cycles was persistent in the north and centre of the study area and a rise in rainfall regime trends was reported in the south-west. The Mann–Kendall test and the Hurst exponent values demonstrated that these trends will continue in the near future. The Hurst exponent was anti-persistent and independent in the Peninsula de Valdes and its surroundings, meaning that no clear trend may produce an alternation of wet and dry periods with high climate variability. The temperature trend was positive in three sectors of the study area; only in one area in the south-west was a negative tendency detected. The multifractal dimensions showed high variability and a relevant persistence for temperature rise in one sector of the Patagonian Andes mountain range from 1981 to 2019. Given the persistence of trends, the previously described behaviour of this variable is expected to continue in the near future.
Temperature rise in the Patagonian Andes affects the mountain ice cover and the amplification of zones where the glaciers are retreating will result in eco-systemic imbalances and loss of water resources. This phenomenon is worrisome for territories where the rainfall is decreasing. For Northern Patagonia, precipitation and spring ice melting feed the hydrographic basins of the territory, especially in drought periods. The expansion of hydrological stress periods in a zone affected by aridity could intensify the desertification process.
Predictions about how these variables will behave in the future are possible because fractals replicate their dimensions in an identical way, an infinite number of times at different scales. These analyses will provide complementary information for understanding the actual and future climatic variability in Northern Patagonia; however, scale analyses such as seasonal or synoptic are needed.
Data availability
The authors declare that the entire dataset used in the present study is available (https://power.larc.nasa.gov/data-access-viewer/).
Conflicts of interest
The authors declare that they have no conflicts of interest.
Declaration of funding
The authors thank the National Agency for Scientific and Technological Promotion (ANPCyT), Universidad Nacional del Sur (UNS) and the National Council for Scientific and Technical Research of Argentina (CONICET) for funding this work. Thanks to the Instituto Geográfico Nacional (IGN) Instituto Nacional de Tecnología Agropecuaria (INTA) and POWER NASA Project re-analysis meteorological database (NASA POWER Project 2021) for allowing free access to the data.
Author contributions
Grethel García Bu Bucogen contributed to the investigation, formal analysis, writing, review and editing of the original draft, software and visualisation. María Cintia Piccolo contributed to the investigation, formal analysis, conceptualisation, methodology, review and editing of the original draft, supervision, validation, software and visualisation. Vanesa Yael Bohn contributed to the investigation, conceptualisation, methodology, review and editing of the original draft, supervision and visualisation. Gabriel Eduardo Huck contributed to the review and editing of the original draft, supervision and visualisation.
References
Alencar da Silva Alves KM, Silva Nóbrega R (2017) Tendencia pluviométrica y concentración estacional de precipitación en la cuenca hidrográfica del río Moxotó – Pernambuco – Brasil. Revista Geográfica de América Central 1, 295–313.| Tendencia pluviométrica y concentración estacional de precipitación en la cuenca hidrográfica del río Moxotó – Pernambuco – Brasil.Crossref | GoogleScholarGoogle Scholar | [In Spanish]
Alves TLB, de Azevedo PV, de Farias AA (2015) Comportamento da precipitação pluvial e sua relação com o relevo nas microrregiões do Cariri Oriental e Ocidental do estado da Paraíba. Revista Brasileira de Geografia Física 8, 1601–1614.
| Comportamento da precipitação pluvial e sua relação com o relevo nas microrregiões do Cariri Oriental e Ocidental do estado da Paraíba.Crossref | GoogleScholarGoogle Scholar | [In Spanish]
Baranowski P, Krzyszczak J, Slawinski C, Hoffmann H, Kozyra J, Nieróbca A, Siwek K, Gluza A (2015) Multifractal analysis of meteorological time series to assess climate impacts. Climate Research 65, 39–52.
| Multifractal analysis of meteorological time series to assess climate impacts.Crossref | GoogleScholarGoogle Scholar |
Baranowski P, Gos M, Krzyszczak J, Siwek K, Kieliszek A, Tkaczyk P (2019) Multifractality of meteorological time series for Poland on the base of MERRA-2 data. Chaos, Solitons & Fractals 127, 318–333.
| Multifractality of meteorological time series for Poland on the base of MERRA-2 data.Crossref | GoogleScholarGoogle Scholar |
Bartos I, Jánosi IM (2006) Nonlinear correlations of daily temperature records over land. Nonlinear Processes in Geophysics 13, 571–576.
| Nonlinear correlations of daily temperature records over land.Crossref | GoogleScholarGoogle Scholar |
Bianchi E (2016) Dinámica espacio temporal de la relación entre el clima y el funcionamiento de los ecosistemas en Patagonia Norte. PhD thesis, Universidad Nacional de COMAHUE, San Carlos de Bariloche, Argentina. Available at https://ri.conicet.gov.ar/handle/11336/79967 [In Spanish]
Bianchi A, Cravero S (2010) Atlas climático digital de la República Argentina. (Instituto Nacional de Tecnología Agropecuaria: Salta, Argentina) Available at https://inta.gob.ar/sites/default/files/clima_de_arg._cravero_bianchi_elena_bianchi_100517.pdf [In Spanish]
Brendel AS, del Barrio RA, Mora F, León EAO, Flores JR, Campoy JA (2020) Potencial agroclimático actual de la Patagonia moldeado por patrones térmicos e hídricos. Theoretical and Applied Climatology 142, 855–868.
| Potencial agroclimático actual de la Patagonia moldeado por patrones térmicos e hídricos.Crossref | GoogleScholarGoogle Scholar | [In Spanish]
Camacho Velázquez R, Vásquez Cruz M (2015) Geometría fractal, Teoría del caos, y sus aplicaciones en la Industria Petrolera. Ingeniería Petrolera 55, 718–729. [In Spanish]
Camilloni I (2018) Argentina y el cambio climático. Ciencia e investigación 68, 5–10. [In Spanish]
Chen D, Chen HW (2013) Using the Köppen classification to quantify climate variation and change: an example for 1901–2010. Environmental Development 6, 69–79.
| Using the Köppen classification to quantify climate variation and change: an example for 1901–2010.Crossref | GoogleScholarGoogle Scholar |
Collado A (2012) Desertificación en Argentina: el problema de las 60 millones de hectáreas. [Desertification in Argentina: the problem of 60 million hectares.] (National Institute of Agricultural Technology) Available at https://inta.gob.ar/noticias/desertificacion-en-argentina-el-problema-de-las-60-millones-de-hectareas [In Spanish]
Coronato A, Mazzoni E, Vázquez M, Coronato F (2017) Chapter 3. Clima. In ‘Patagonia: una síntesis de su geografía física’. pp. 101–126. (Universidad Nacional de la Patagonia Austral: Río Gallegos, Argentina) Avaliable at https://www.unpa.edu.ar/publicacion/version-digital-patagonia [In Spanish]
Das P (2009) Nonlinear Analysis of Daily Temperature Data. In ‘2009 ETP International Conference on Future Computer and Communication’, 6–7 June 2009, Wuhan, PR China. INSPEC Accession number 10869078, pp. 273–277. (IEEE)
| Crossref |
Domino K, Błachowicz T, Ciupak M (2014) The use of copula functions for predictive analysis of correlations between extreme storm tides. Physica – A. Statistical Mechanics and its Applications 413, 489–497.
| The use of copula functions for predictive analysis of correlations between extreme storm tides.Crossref | GoogleScholarGoogle Scholar |
Endlichter W, Santana A (1988) El clima del sur de la Patagonia y sus aspectos ecológicos. Anales del Instituto de la Patagonia 484, 57–86. Avaliable at http://www.bibliotecadigital.umag.cl/bitstream/handle/20.500.11893/924/Endlicher_Anales_1988_vol18_pp57‐86.pdf?sequence=1&isAllowed=y [In Spanish]
Farr TG, Rosen PA, Caro E, Crippen R, Duren R, Hensley S, Kobrick M, Paller M, Rodriguez E, Roth L, Seal D, Shaffer S, Shimada J, Umland J, Werner M, Oskin M, Burbank D, Alsdorf D (2007) The Shuttle Radar Topography Mission. Reviews of Geophysics 45, RG2004
| The Shuttle Radar Topography Mission.Crossref | GoogleScholarGoogle Scholar |
Ferri L, Dussaillant I, Zalazar L, Masiokas MH, Ruiz L, Pitte P, Gargantini H, Castro M, Berthier E, Villalba R (2020) Ice mass loss in the Central Andes of Argentina between 2000 and 2018 derived from a new glacier inventory and satellite stereo-imagery. Frontiers in Earth Science 8, 530997
| Ice mass loss in the Central Andes of Argentina between 2000 and 2018 derived from a new glacier inventory and satellite stereo-imagery.Crossref | GoogleScholarGoogle Scholar |
García Bu Bucogen G, Piccolo MC, Bohn VY (2022) Implementación de datos meteorológicos modelados en el norte patagónico argentino. Investigaciones Geográficas 78, 67–87.
| Implementación de datos meteorológicos modelados en el norte patagónico argentino.Crossref | GoogleScholarGoogle Scholar | [In Spanish]
García Silva L, Jover ML, Nahas A, Ferri Hidalgo L, Villalba R, Zalazar L, Sánchez R, Marinsek S (2019) ‘Atlas de Glaciares de la Argentina.’ (Ediciones de la Secretaría de Ambiente y Desarrollo Sustentable de la Nación: Mendoza, Argentina) [In Spanish]
Garreaud RD, Vuille M, Compagnucci R, Marengo J (2009) Present-day South American climate. Palaeogeography, Palaeoclimatology, Palaeoecology 281, 180–195.
| Present-day South American climate.Crossref | GoogleScholarGoogle Scholar |
Garreaud R, Lopez P, Minvielle M, Rojas M (2013) Large-scale control on the Patagonian climate. American Meteorological Society 26, 215–230.
| Large-scale control on the Patagonian climate.Crossref | GoogleScholarGoogle Scholar |
Ghanmi H, Bargaoui Z, Mallet C (2013) Investigation of the fractal dimension of rainfall occurrence in a semi-arid Mediterranean climate. Hydrological Sciences Journal 58, 483–497.
| Investigation of the fractal dimension of rainfall occurrence in a semi-arid Mediterranean climate.Crossref | GoogleScholarGoogle Scholar |
Gil Guirado S, Bermúdez F (2011) Tendencia de las precipitaciones y temperaturas en una pequeña cuenca fluvial del sureste peninsular semiárido. Boletín de la Asociación de Geógrafos Españoles 56, 349–371. [In Spanish]
Gómez J, Poveda G (2008) Estimación del espectro multifractal para series de precipitación horaria en los Andes tropicales de Colombia. Revista de la Academia Colombiana de Ciencias Exactas Físico Naturales 32, 483–502. [In Spanish]
González MH, Romero PE, Garbarini EM (2017) Droughts and floods in northern Argentinean Patagonia. The Andes: geography, diversity, and sociocultural impacts. (NOVA Science Publisher Inc.: New York, NY, USA) Available at https://bibliotecadigital.exactas.uba.ar/collection/paper/document/paper_97815361_v_n_p5_Gonzalez
Goossens C, Berger A (1986) Annual and seasonal climatic variations over the northern hemisphere and Europe during the last century. Annales Geophysicae 4, 385–400.
Haro AX, Limaico CT, Llosas YE (2012) Predicción de datos meteorológicos en cortos intervalos de tiempo en la ciudad de Riobamba usando la teoría del caos. Sistemas, Cibernética e Informática 13, 35–41. [In Spanish]
Hena Rani B, Hasan M, Bala SK (2018) Chaos theory and its applications in our real life. Barishal University Journal 1, 123–140.
Huang H-H, Puente CE, Cortis A, Fernández Martínez JL (2013) An effective inversion strategy for fractal–multifractal encoding of a storm in Boston. Journal of Hydrology 496, 205–216.
| An effective inversion strategy for fractal–multifractal encoding of a storm in Boston.Crossref | GoogleScholarGoogle Scholar |
IPCC (2021) ‘Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change.’ (Eds V Masson-Delmotte, P Zhai, A Pirani, SL Connors, C Péan, S Berger, N Caud, Y Chen, L Goldfarb, MI Gomis, M Huang, K Leitzell, E Lonnoy, JBR Matthews, TK Maycock, T Waterfield, O Yelekçi, R Yu, B Zhou) (Cambridge University Press)
Johansen KS, Alfthan B, Baker E, Hesping M, Schoolmeester T, Verbist K (2018) The Andean glacier and water atlas: the impact of glacier retreat on water resources. UNESCO: Dataset about Global Resources. (UNESCO: Arendal, Norway) Available at https://unesdoc.unesco.org/ark:/48223/pf0000265810
Kantelhardt JW, Zschiegner SA, Koscielny-Bunde E, Havlin S, Bunde A, Stanley H (2002) Multifractal detrended fluctuation analysis of nonstationary time series. Physica – A. Statistical Mechanics and its Applications 316, 87–114.
| Multifractal detrended fluctuation analysis of nonstationary time series.Crossref | GoogleScholarGoogle Scholar |
Kendall M (1975) ‘Rank correlation measures’. p. 120. (Charles Griffin: London, UK)
López-Lambraño A, Carrillo-Yee E, Fuente C, López-Ramos A, López-Lambraño M (2017) Una revisión de los métodos para estimar el exponente de Hurst y la dimensión fractal en series de precipitación y temperatura. Revista Mexicana de Física 63, 244–267. [In Spanish]
Lorenz EN (1963) Deterministic nonperiodic flow. Journal of the Atmospheric Sciences 20, 130–141.
| Deterministic nonperiodic flow.Crossref | GoogleScholarGoogle Scholar |
Lorenz EN (1990) Can chaos and intransitivity lead to interannual variability? Tellus – A. Dynamic Meteorology and Oceanography 42, 378–389.
| Can chaos and intransitivity lead to interannual variability?Crossref | GoogleScholarGoogle Scholar |
Lorenz EN (1991) Dimension of weather and climate attractors. Nature 353, 241–244.
| Dimension of weather and climate attractors.Crossref | GoogleScholarGoogle Scholar |
Lovejoy S, Pinel J, Schertzer D (2012) The global space–time cascade structure of precipitation: satellites, gridded gauges and reanalyses. Advances in Water Resources 45, 37–50.
| The global space–time cascade structure of precipitation: satellites, gridded gauges and reanalyses.Crossref | GoogleScholarGoogle Scholar |
Mandelbrot BB (1977) ‘Fractals: form, chance and dimension.’ (Freeman: San Francisco, CA, USA)
Mandelbrot BB, Wheeler JA (1983) The fractal geometry of nature. American Journal of Physics 51, 286–287.
| The fractal geometry of nature.Crossref | GoogleScholarGoogle Scholar |
Mann HB (1945) Nonparametric tests against trend. Econometrica: Journal of the Econometric Society 13, 245–259.
| Nonparametric tests against trend.Crossref | GoogleScholarGoogle Scholar |
Maofei M, Boming Y, Jianchao C, Liang L (2009) A fractal analysis of dropwise condensation heat transfer. International Journal of Heat and Mass Transfer 52, 4823–4828.
| A fractal analysis of dropwise condensation heat transfer.Crossref | GoogleScholarGoogle Scholar |
Martínez Moncaleano CJ (2018) Teoría del Caos y estrategia empresarial. Tendencias 19, 204–214.
| Teoría del Caos y estrategia empresarial.Crossref | GoogleScholarGoogle Scholar | [In Spanish]
Masiokas M (2008) Climate and glacier variability during past centuries in the North and South Patagonian Andes of Argentina. PhD thesis, The University of Western Ontario, London, ON, Canada. Available at https://www.collectionscanada.gc.ca/obj/thesescanada/vol2/002/NR39303.PDF?is_thesis=1andoclc_number=665191429
Mazzoni E, Vázquez M (2010) Desertificación en la Patagonia. Developments in Earth Surface Processes 13, 351–377.
| Desertificación en la Patagonia.Crossref | GoogleScholarGoogle Scholar | [In Spanish]
Meza L, Corso S, Soza S (2010) ‘Gestión del riesgo de sequía y otros eventos climáticos extremos en Chile.’ (Food and Agriculture Organization of the United Nations: Santiago de Chile, Chile) [In Spanish]
Morales Martínez JL, Segovia-Domínguez I, Rodríguez IQ, Horta-Rangel FA, Sosa-Gómez G (2021) A modified multifractal detrended fluctuation analysis (MFDFA) approach for multifractal analysis of precipitation. Physica – A. Statistical Mechanics and its Applications 565, 125611
| A modified multifractal detrended fluctuation analysis (MFDFA) approach for multifractal analysis of precipitation.Crossref | GoogleScholarGoogle Scholar |
Morello J, Matteucci SD, Rodríguez, AF, Mariana S (2012) ‘Ecorregiones y complejos ecosistemicos argentinos.’ (Orientación Gráfica Editorial: Buenos Aires, Argentina) Available at https://www.researchgate.net/profile/Silvia-Matteucci-2/publication/268447092_Ecorregiones_y_complejos_ecosistemicos_Argentinos/links/598333be0f7e9b2ac353f62e/Ecorregiones-y-complejos-ecosistemicos-Argentinos.pdf [In Spanish]
NASA POWER Project (2021) The Prediction of Worldwide Energy Resource (POWER). (NASA Applied Sciences Program within the Earth Science Division of the Science Mission Directorate) Available at https://power.larc.nasa.gov
Nieto HD, Álvarez JE, Rodríguez EL (2016) Análisis de persistencia en acciones financieras en el mercado colombiano a través de la metodología de Rango Reescalado (R/S). Cuadernos Latinoamericanos de Administración, XII 22, 23–32.
| Análisis de persistencia en acciones financieras en el mercado colombiano a través de la metodología de Rango Reescalado (R/S).Crossref | GoogleScholarGoogle Scholar | [In Spanish]
Palese C, Lassig J, Cogliati M, Bastanski M (2001) Régimen de Viento y potencia eólica en la región Norpatagónica. In ‘IX Encuentro Latinoamericano y del Caribe sobre pequeños aprovechamientos hidroenergeticos’, 5–9 November 2001, Ciudad de Neuquén, Argentina. Available at https://www.researchgate.net/publication/278403844_Regimen_de_Viento_y_potencia_eolica_en_la_region_Norpatagonica [In Spanish]
Paruelo JM, Beltran A, Jobbagy E, Sala OE, Golluscio RA (1998) The climate of Patagonia: general patterns and controls on biotic processes. Ecologia Austral 8, 85–101.
Pérez SP, Sierra EM, Massobrio MJ, Momo FR (2009) Análisis fractal de la precipitación anual en el este de la provincia de La Pampa, Argentina. Revista de Climatología 9, 25–35. [In Spanish]
Pessacg NL, Flaherty S, Solman S, Pascual M (2020) Climate change in northern Patagonia: critical decrease in water resources. Theoretical and Applied Climatology 140, 807–822.
| Climate change in northern Patagonia: critical decrease in water resources.Crossref | GoogleScholarGoogle Scholar |
Pessacg N, Blázquez J, Lancelotti J, Solman S (2022) Climate changes in coastal areas of patagonia: observed trends and future projections. In ‘Global Change in Atlantic Coastal Patagonian Ecosystems’. (Eds EW Helbling, MA Narvarte, RA González, VE Villafañe) pp. 13–42. (Springer: New York, NY, USA)
Plazas Nossa L, Ávila Angulo MA, Moncada Méndez G (2014) Estimación del exponente de Hurst y dimensión fractal para el análisis de series de tiempo de absorbancia UV-VIS. Ciencia e Ingeniería Neogranadina 24, 133–143.
| Estimación del exponente de Hurst y dimensión fractal para el análisis de series de tiempo de absorbancia UV-VIS.Crossref | GoogleScholarGoogle Scholar | [In Spanish]
Prohaska F (1976) El clima de Argentina, Paraguay y Uruguay. Climas de América Central y del Sur. In ‘World Survey of Climatology. Vol. 12’. pp. 57–69. (Elsevier Scientific Publishing Company: Amsterdam, Netherlands) [In Spanish]
Quintero Delgado OY, Ruiz Delgado J (2011) Estimación del exponente de Hurst y la dimensión fractal de una superficie topográfica a través de la extracción de perfiles. UD y la geomática 5, 84–91.
| Estimación del exponente de Hurst y la dimensión fractal de una superficie topográfica a través de la extracción de perfiles.Crossref | GoogleScholarGoogle Scholar | [In Spanish]
Rangarajan G, Sant DA (2004) Fractal dimensional analysis of Indian climatic dynamics. Chaos, Solitons & Fractals 19, 285–291.
| Fractal dimensional analysis of Indian climatic dynamics.Crossref | GoogleScholarGoogle Scholar |
Redondo JM, Grau J, Platonov A, Garzón G (2008) Análisis multifractal de procesos auto similares: imágenes de satélite e inestabilidades baroclinas. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería 24, 25–48. [In Spanish]
Rodríguez Aguilar R (2012) El coeficiente de Hurst y el parámetro α-estable para el análisis de series financieras Aplicación al mercado cambiario mexicano. Contaduría y Administración 59, 149–173.
| El coeficiente de Hurst y el parámetro α-estable para el análisis de series financieras Aplicación al mercado cambiario mexicano.Crossref | GoogleScholarGoogle Scholar | [In Spanish]
Romero PE, Garbarini EM, González MH (2014) Características hídricas y climáticas del norte Patagónico. In ‘II Encuentro de investigadores en formación en Recursos Hídricos’, 9–10 October 2014, Ezeiza, Buenos Aires, Argentina. (INA: Ezeiza, Buenos Aires, Argentina) Available at https://www.ina.gob.ar/ifrh-2014/Eje3/3.33.pdf [In Spanish]
Santos Burguete C (2018) Física del caos en la predicción meteorológica. In ‘AEMET, 2018. Física del caos en la predicción meteorológica - Agencia Estatal de Meteorología - AEMET’. pp. 13–19. (Editorial del Ministerio de Agricultura y Pesca, Alimentación y Medio Ambiente y editada por el Ministerio para la Transición Ecológica) Available at http://www.aemet.es/es/conocermas/recursos_en_linea/publicaciones_y_estudios/publicaciones/detalles/Fisica_del_caos_en_la_predicc_meteo [In Spanish]
Santos da Silva H, Santos Silva JR, Stosic T (2020) Multifractal analysis of air temperature in Brazil. Physica – A. Statistical Mechanics and its Applications 549, 124333
| Multifractal analysis of air temperature in Brazil.Crossref | GoogleScholarGoogle Scholar |
Selvam AM (1993) Universal quantification for deterministic chaos in dynamical systems. Applied Mathematical Modelling 17, 642–649.
| Universal quantification for deterministic chaos in dynamical systems.Crossref | GoogleScholarGoogle Scholar |
Selvam AM (2011) Signatures of universal characteristics of fractal fluctuations in global mean monthly temperature anomalies. Journal of Systems Science and Complexity 24, 14–38.
| Signatures of universal characteristics of fractal fluctuations in global mean monthly temperature anomalies.Crossref | GoogleScholarGoogle Scholar |
Selvam AM (2013) Nonlinear dynamics and chaos: applications in atmospheric sciences. Journal of Advanced Mathematics and Applications 1, 1–24.
| Nonlinear dynamics and chaos: applications in atmospheric sciences.Crossref | GoogleScholarGoogle Scholar |
Selvam AM (2017) Nonlinear dynamics and chaos: applications in meteorology and atmospheric physics. In ‘Self-organized Criticality and Predictability in Atmospheric Flows: The Quantum World of Clouds and Rain’. pp. 1–40. (Springer Atmospheric Sciences: New York, NY, USA)
| Crossref |
Selvam AM, Pethkar JS, Kulkarni MK (1992) Signatures of a universal spectrum for atmospheric interannual variability in rainfall time series over the Indian region. International Journal of Climatology 12, 137–152.
| Signatures of a universal spectrum for atmospheric interannual variability in rainfall time series over the Indian region.Crossref | GoogleScholarGoogle Scholar |
Svensson C, Olsson J, Berndtsson R (1996) Multifractal properties of daily rainfall in two different climates. Water Resources Research 32, 2463–2472.
| Multifractal properties of daily rainfall in two different climates.Crossref | GoogleScholarGoogle Scholar |
Warren CR, Sugden DE (1993) The Patagonian icefields: a glaciological review. Arctic and Alpine Research 25, 316–331.
| The Patagonian icefields: a glaciological review.Crossref | GoogleScholarGoogle Scholar |
Yu J-Y, Kao H-Y (2007) Decadal changes of ENSO persistence barrier in SST and ocean heat content indices: 1958–2001. Journal of Geophysical Research: Atmospheres 112, D13106
| Decadal changes of ENSO persistence barrier in SST and ocean heat content indices: 1958–2001.Crossref | GoogleScholarGoogle Scholar |
Yu Z-G, Leung Y, Chen YD, Zhang Q, Anh V, Zhou Y (2014) Multifractal analyses of daily rainfall time series in Pearl River basin of China. Physica – A. Statistical Mechanics and its Applications 405, 193–202.
| Multifractal analyses of daily rainfall time series in Pearl River basin of China.Crossref | GoogleScholarGoogle Scholar |
Zalazar L, Ferri L, Castro M, Gargantini H, Giménez M, Pitte P, Ruiz L, Masiokas M, Villalba R (2017) Glaciares de Argentina: Resultados Preliminares del Inventario Nacional de Glaciares. Revista de Glaciares y Ecosistemas de Montaña 2, 13–22. Available at https://notablesdelaciencia.conicet.gov.ar/bitstream/handle/11336/60533/CONICET_Digital_Nro.34d18b29-1b97-4bde-8461-3dd79f4ac4fd_B.pdf?sequence=5andisAllowed=y [In Spanish]
Zhou Y, Leung Y (2010) Multifractal temporally weighted detrended fluctuation analysis and its application in the analysis of scaling behaviour in temperature series. Journal of Statistical Mechanics: Theory and Experiment 6, P06021
| Multifractal temporally weighted detrended fluctuation analysis and its application in the analysis of scaling behaviour in temperature series.Crossref | GoogleScholarGoogle Scholar |