Evaluation of climate variability and change in ACCESS historical simulations for CMIP6
Harun A. Rashid A * , Arnold Sullivan A , Martin Dix
A * , Arnold Sullivan A , Martin Dix  A , Daohua Bi A , Chloe Mackallah
A , Daohua Bi A , Chloe Mackallah  A , Tilo Ziehn A , Peter Dobrohotoff
A , Tilo Ziehn A , Peter Dobrohotoff  A , Siobhan O’Farrell A , Ian N. Harman B , Roger Bodman A and Simon Marsland A
A , Siobhan O’Farrell A , Ian N. Harman B , Roger Bodman A and Simon Marsland A
A CSIRO Oceans and Atmosphere, 107–121 Station Street, Aspendale, Vic. 3195, Australia.
B CSIRO Oceans and Atmosphere, Canberra, Australia.
Journal of Southern Hemisphere Earth Systems Science 72(2) 73-92 https://doi.org/10.1071/ES21028
Submitted: 17 November 2021 Accepted: 31 March 2022 Published: 14 July 2022
© 2022 The Author(s) (or their employer(s)). Published by CSIRO Publishing on behalf of BoM. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)
Abstract
We analyse and document the historical simulations performed by two versions of the Australian Community Climate and Earth System Simulator (ACCESS-CM2 and ACCESS-ESM1.5) for the Coupled Model Intercomparison Project Phase 6 (CMIP6). Three ensemble members from each model are used to compare the simulated seasonal-mean climate, climate variability and climate change with observations over the historical period. Where appropriate, we also compare the ACCESS model results with the results from 36 other CMIP6 models. We find that the simulations of the winter and summer mean climates (over the global domain) by the two ACCESS models are similar to or better than most of the other CMIP6 models for surface temperature, precipitation and surface specific humidity. For sea-level pressure, both ACCESS models perform worse than most other models. The spatial structures of the prominent climate variability modes (ENSO, IOD, IPO and AMO) also compare favourably with the corresponding observed structures. However, the results for the simulation of the models’ temporal variability are mixed. In particular, whereas ACCESS-ESM1.5 simulates ENSO events with ~3-year periods (that are closer to the observed periods of 3–7 years), the ACCESS-CM2 simulates ENSO events having quasi-biennial periods. However, ACCESS-CM2 has a much smaller bias (−0.1 W m−2) in present-day top-of-the-atmosphere energy balance than ACCESS-ESM1.5 (−0.6 W m−2). The ACCESS models simulate the anthropogenic climate change signal in historical global-mean surface temperature reasonably well, although the simulated signal variances are ~10% weaker than the observed signal variance (a common bias in most CMIP6 models). Both models also well simulate the major features of observed surface temperature changes, as isolated using a multiple regression model. Despite some identified biases, the two ACCESS models provide high-quality climate simulations that may be used in further analyses of climate variability and change.
Keywords: ACCESS-CM2, ACCESS-ESM1.5, aerosols, climate change, climate variability modes, CMIP6, coupled climate model, earth system model, evaluation, greenhouse gases, historical simulation.
1. Introduction
Understanding historical climate variability and change is important. Among other things, this provides insights into the nature of extreme events, such as droughts, floods and heat waves. Additionally, this gives us confidence in our ability to predict or project climate variations at multiple timescales, ranging from interannual through to century timescales. This understanding is facilitated by the availability of comprehensive observational and reanalysis datasets covering multiple decades, with some datasets going back more than a century. Climate models of varying complexities have also played an important role in uncovering the mechanisms of weather and climatic events. Global climate models (hereafter, GCMs) have been used for providing dynamical predictions for weather and seasonal–interannual climate variability. These models, combined with appropriate forcing datasets, are also predominantly used for providing climate projections. Thanks to continued development over several decades, modern climate models now perform these tasks reasonably well and efforts are continuing to further develop and evaluate these models.
Over the last few decades, the Coupled Model Intercomparison Projects (CMIPs) have been a cornerstone for model development and evaluation. Every few years, modelling centres around the world prepare their climate models and run specified sets of experiments using a standardised forcing dataset. The Australian Community Climate and Earth System Simulator (ACCESS) is one of the models that has contributed to CMIP phases 5 and 6 (Taylor et al. 2012; Eyring et al. 2016). Two versions of ACCESS, ACCESS Coupled Model (ver. 2, ACCESS-CM2) and ACCESS Earth System Model (ver. 1.5, ACCESS-ESM1.5), have been prepared and run for contributing simulations to CMIP6 (Bi et al. 2020; Ziehn et al. 2020). So far, ~500 model runs comprising thousands of years of climate simulations have been performed with ACCESS and have been submitted to the CMIP6 archive (Mackallah et al. 2022). These simulations have been used by many researchers in single-model or multimodel studies to address various scientific questions. It is important that a comprehensive evaluation of the ACCESS model performance is done to help interpret the ACCESS results presented in other studies.
In this work, we analyse the ACCESS historical simulations performed following the CMIP6 protocol (Eyring et al. 2016). The pre-industrial control spin-up simulations for ACCESS-CM2 and ACCESS-ESM1.5 have been documented in Bi et al. (2020) and Ziehn et al. (2020) respectively. These studies described in detail the sea-surface temperature (SST) biases, oceanic mixed layer depth, the Atlantic Meridional Overturning Circulation, and sea-ice in the ACCESS-CM2 simulation and the earth-system aspect of the ACCESS-ESM1.5 simulation, among other things. Here, we examine the simulated mean climate associated with some important variables, climate variability associated with the prominent climate variability modes and climate change associated with important global climate change indices. After describing the CMIP6 historical experiment set-up (Section 2), we document the simulated seasonal-mean climate of surface-air temperature (SAT), precipitation (PR) and sea-level pressure (SLP) and compare the mean climate with the mean climate simulated by other CMIP6 models (Section 3). We then analyse the spatial patterns and power spectral features of the El Niño–Southern Oscillation (ENSO), the Indian Ocean Dipole (IOD), the Interdecadal Pacific Oscillation (IPO) and the North Atlantic SST (NASST) modes (Section 4). This is followed by an investigation of climate change over the CMIP6 historical period (1850–2014) in top-of-the-atmosphere radiation budget, sea-ice extent (SIE) and SATs (Section 5). Finally, some conclusions and discussion are provided (Section 6).
2. Model experiments and evaluation data
2.1. Model configurations and experiment design
The ACCESS-CM2 and ACCESS-ESM1.5 models used for conducting CMIP6 experiments have been described in detail elsewhere (Bi et al. 2020; Ziehn et al. 2020), so only a brief description of the model configurations will be given here. ACCESS-CM2 comprises the UK Met Office Unified Model (UM) Global Atmosphere configuration (ver. 7.1, GA7.1), the Community Atmosphere Biosphere Land Exchange (CABLE) model (ver. 2.5), the Geophysical Fluid Dynamics Laboratory Modular Ocean Model (ver. 5, MOM5) and the Los Alamos sea ice model (ver. 5.1.2, CICE5). These component models are coupled with the CERFACS OASIS3-MCT coupler, with a 3-h coupling time interval. ACCESS-ESM1.5 shares the same ocean model component but slightly different versions of CICE (CICE4.1) and CABLE (CABLE2.4). Also, this model implements the land and ocean carbon cycle components to form the Earth System Model (ESM) version of ACCESS.
The atmospheric models differ significantly in their dynamics, physical parameterisations and vertical resolution between the two ACCESS versions. In addition to a new dynamical core, ACCESS-CM2 incorporates numerous updates for atmospheric physical parameterisations, including radiation, convection, boundary layer and cloud. A detailed description of these updates is found in Walters et al. (2019) and Bi et al. (2020). The atmospheric component of ACCESS-ESM1.5 is based on an earlier version of the UM, with a climate configuration close to GA1 (Hewitt et al. 2011; Bi et al. 2013). Both ACCESS atmospheric models have an N96 horizontal resolution (equivalent to 135-km grid-spacing in mid-latitudes). However, the ACCESS-CM2 atmosphere has a higher vertical resolution with 85 levels reaching a model height of up to 85 km v. 38 levels reaching a height of 40 km in the atmosphere of ACCESS-ESM1.5. The land-surface model CABLE is configured to have 13 surface tile types and six soil layers. The distribution of surface tile types is fixed in time for ACCESS-CM2 but varies in time in ACCESS-ESM1.5 to account for land use change. The ocean component of both ACCESS models, MOM5, has a nominal 1° latitude–longitude resolution with some refinements in the latitudinal spacing (see Bi et al. 2020 for details). There are 50 vertical levels covering depths of 0–6000 m; the upper ocean layers (0–200 m) have a higher resolution, with a 10-m spacing between them, than the deeper ocean layers (the spacing increasing to ~333 m in the abyssal ocean). The sea ice schemes of the two ACCESS models also differ: CICE4.1 has zero-layer thermodynamics, whereas CICE5 has multiple layers and prognostic melt ponds, among other improvements.
ACCESS-CM2 and ACCESS-ESM1.5 were used to perform ensemble simulations using the CMIP6 historical experiment setup (Eyring et al. 2016), which we analyse here. A host of other CMIP6 simulations were also performed, which are listed in Mackallah et al. (2022). In this work, we analyse three ensemble-member historical simulations from each of the ACCESS models (that were available at the start of this analysis). Each ensemble member is run with identical historical forcings for 1850–2014 but starts from different initial conditions taken from the respective pre-industrial control simulations at 50-year intervals (20 years for ACCESS-ESM1.5). The atmosphere-only simulations of ACCESS-CM2 using the same historical experiment setup (but for a shorter period) are documented in Bodman et al. (2020).
2.2. Historical forcings
A summary of the historical forcings is found in Bodman et al. (2020) and a comprehensive description of the preparation of forcing datasets used for ACCESS CMIP6 experiments is given by Mackallah et al. (2022). Briefly, the historical simulations use time-dependent forcings of anthropogenic and natural origins. The prominent anthropogenic forcing agents include the well-mixed greenhouse gases (GHGs), tropospheric aerosols, ozone and land-use changes, and the natural forcings include volcanic aerosols, aerosols from volcanic degassing and the total solar irradiance (TSI) variability. The GHGs (CO2, CH4, N2O, CFCs and HFCs) are prescribed as global and annual mean values, the tropospheric aerosols as monthly varying latitude-longitude fields, the stratospheric aerosols from volcanic eruptions as monthly zonal mean optical parameters in the solar (shortwave) and terrestrial (longwave) spectrum on each model level, and the TSI variability as spectrally resolved monthly mean values. Annual land-use changes are mapped onto the CABLE functional types for ACCESS-ESM1.5. There are differences in the ways these forcings are applied to ACCESS-CM2 and ACCESS-ESM1.5 model simulations; the latter simulation also diagnoses land and ocean carbon fluxes (see Mackallah et al. 2022 for details).
2.3. Evaluation data
We use reanalysis and observational datasets for the evaluation of ACCESS-CM2 and ACCESS-ESM1.5 historical simulations. ERA5 reanalysis (Hersbach et al. 2020) is used for evaluating time-mean SAT and specific humidity (HUSS), the Global Precipitation Climatology Project (GPCP) dataset (ver. 2.3; Adler et al. 2018) for PR, the HadSLP2 dataset (Allan and Ansell 2006) for SLP and CERES-EBAF data for top-of-the-atmosphere (TOA) radiative fluxes (Loeb et al. 2018). The time series of simulated Arctic and Antarctic SIEs are compared against satellite observations made available by the University of Bremen (Spreen et al. 2008). The observed SATs are from the HadCRUT4 dataset, which combines land SATs with SSTs and is expressed as anomalies with respect to the 1961–1990 climatology (Morice et al. 2012). We use the globally filled version of the dataset (Cowtan and Way 2014). The HadISST dataset (ver. 1.1; Rayner et al. 2003) is used for computing the indices of four prominent modes of SST variability: ENSO, IOD, IPO and NASST variability. The indices are then used to obtain the spatial patterns of these modes by regression with SAT anomalies (SATAs). The SATAs are obtained by removing the time-mean and the quadratic trend from annual-mean SATs at each grid point for both observations and simulations.
3. Mean climate
The time-mean surface climate is described separately for the December–January–February (DJF) and June–July–August (JJA) seasons using a few key variables: SAT, PR and SLP. Long-term seasonal means are not very sensitive to small changes in the definition of seasons, so here we use DJF and JJA, which are frequently used in the literature. We highlight the ACCESS model performance by presenting the differences (or biases) between the simulations and observations or reanalyses.
3.1. Seasonal means
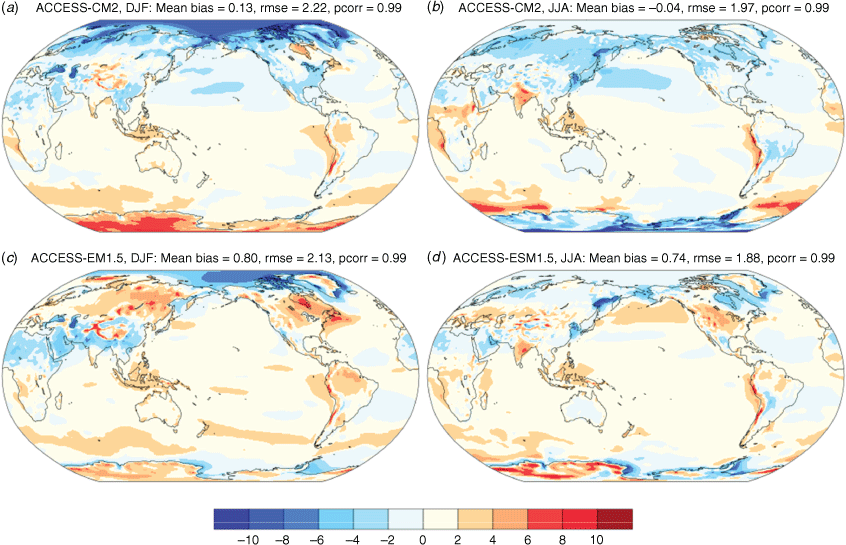
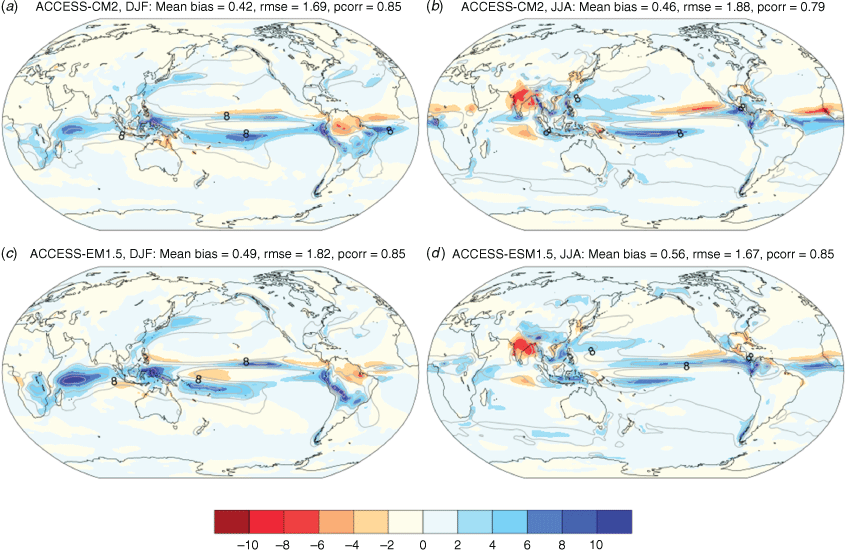
Fig. 1 shows the bias patterns of seasonal mean SATs with respect to the ERA5 reanalysis. In both models, the biases are smallest over the tropical oceans and largest over higher latitudes. For DJF (Fig. 1a, c), the two polar regions exhibit the largest (but oppositely signed) biases and these biases are larger in ACCESS-CM2 (Fig. 1a, b) than in ACCESS-ESM1.5 (Fig. 1c, d). The pronounced cold temperature bias over the Arctic indicates that the ACCESS models do not adequately capture the surface warming observed there over the last few decades. Indeed, the simulated time- and area-averaged (north of 70°N) Arctic SATs are up to 6.6°C colder than in ERA5 (during DJF), with ACCESS-CM2 being the colder of the two models (Supplementary Fig. S1). Large biases are also seen over the continents with warm biases over elevated surfaces (e.g. Antarctica and the Himalayan mountains) and cold biases over the northern hemisphere (NH) sub-tropics. The two models, however, show contrasting temperature biases over the NH extra-tropics. In general, there is a prevalence of cold temperature biases over the NH in ACCESS-CM2, although both models show similar warm biases over the southern hemisphere (SH) oceans. For JJA (Fig. 1b, d), the bias patterns from both models are comparable over the SH, except for the East Antarctic where the ACCESS-CM2 and ACCESS-ESM1.5 models show cold and warm biases respectively. For the NH, many of the two models’ contrasting biases observed in DJF are also seen in JJA (e.g. over the northern extra-tropics), although similar biases are seen over the subtropics (e.g. the South Asian monsoon region). The major SAT biases, especially the widespread NH continental cold bias and the Southern Ocean warm bias, are commonly seen in various configurations of the HadGEM3 model (which shares the same atmospheric model with ACCESS-CM2) and other CMIP-class models (Yamazaki et al. 2021).
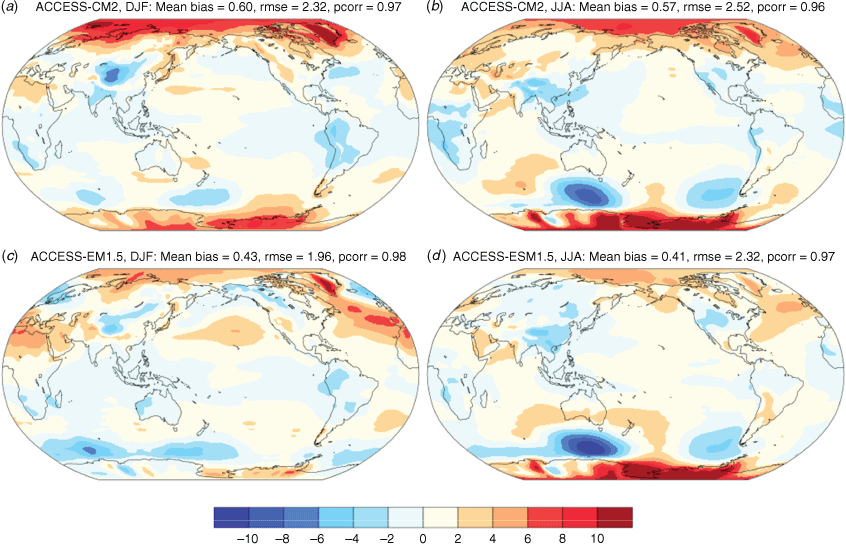
The biases in simulated PR with respect to GPCP observations are shown in Fig. 2; the respective mean PRs are also plotted for comparison. Overall, the models overestimate PR. The largest wet and dry biases are found in the tropics, mainly because the maximum PR occurs there. The bias patterns over the Pacific and Atlantic Oceans take the form of north–south dipoles, with the wet and dry bias regions located respectively to the south and north of the equator during DJF; the dipole moves to the north of the equator during JJA. (This is clearly seen in latitude profiles of zonal-mean PR; Supplementary Fig. S2). This is a long-standing coupled model bias, arising from the simulation of double intertropical convergence zones (ITCZs) and associated cold-tongue biases, in generations of models (Tian and Dong 2020). In observations, a single ITCZ occurs to the north of the equator. There is a large wet bias in the western Indian Ocean during DJF, which is commonly found in many other coupled GCMs (e.g. see fig. 2 of Tian and Dong 2020). Although wet biases over the Pacific and Indian Oceans are larger in DJF than in JJA, the opposite tends to be true over the tropical Atlantic. Notable dry biases occur over the continent during monsoon seasons, especially over the Indian subcontinent and the tropical South America during JJA and DJF respectively.
|
The ITCZ plays an important role in the global energy budget and its north–south location is affected by hemispheric differential heating (e.g. Schneider et al. 2014). ITCZ biases in models, such as that discussed above, have been linked to the biases in simulated extratropical cloud and shortwave radiation. However, other studies disagree with this view, suggesting that reducing the hemispheric energy budget bias alone may not be enough; instead improving the physical parameterisations of rainfall or convection and clouds is important to reduce these ITCZ biases (Hwang and Frierson 2013; Hawcroft et al. 2017).
The model biases in SLP with respect to the HadSLP2 dataset are shown in Fig. 3. Regions with large pressure biases are located mostly in the extra-tropics and over the elevated continental surfaces, e.g. the Tibetan Plateau, the Andes and Antarctica. The biases over these elevated surfaces may partly arise from observational errors and from extrapolation of the data to sea level (Allan and Ansell 2006). The polar regions show high-pressure biases, whereas the southern mid-latitudes and the subtropical mountainous regions have low-pressure biases. The Arctic high-pressure bias is likely linked to the cold biases found there (Fig. 1). There is also a high-pressure bias over much of the North Atlantic Ocean, except in ACCESS-CM2 simulation during DJF. In the SH extra-tropics, the pressure biases form a distinctive wavenumber-3 pattern (van Loon and Jenne 1972; Goyal et al. 2021), which is more pronounced during JJA. This stationary wave pattern can be seen in pressure biases of many CMIP6 models (e.g. Swart et al. 2019), including the UK Met Office models, which share the same atmospheric model code with the ACCESS models. The low-pressure centre south of Australia also features prominently in other CMIP6 models, including in the multimodel mean (not shown). It is not clear what the origin of this distinctive pressure-bias pattern is. However, one can speculate that this may result from a dislocation of the Pacific–South American pattern or shift in tropical convection centres that give rise to the wavenumber-3 pattern through teleconnections (Mo and Higgins 1998; Cai et al. 2011; McIntosh and Hendon 2018; Goyal et al. 2021).
|
Overall, the two ACCESS models perform well in simulating the time-mean SATs, PR and SLP. The biases seen in these models are also commonly found in other state-of-the-science coupled GCMs (Swart et al. 2019; Voldoire et al. 2019; Yamazaki et al. 2021). Below we compare more closely the ACCESS model performance with the performance of other CMIP6 models using the Taylor diagram.
3.2. ACCESS model performances compared to other CMIP6 models
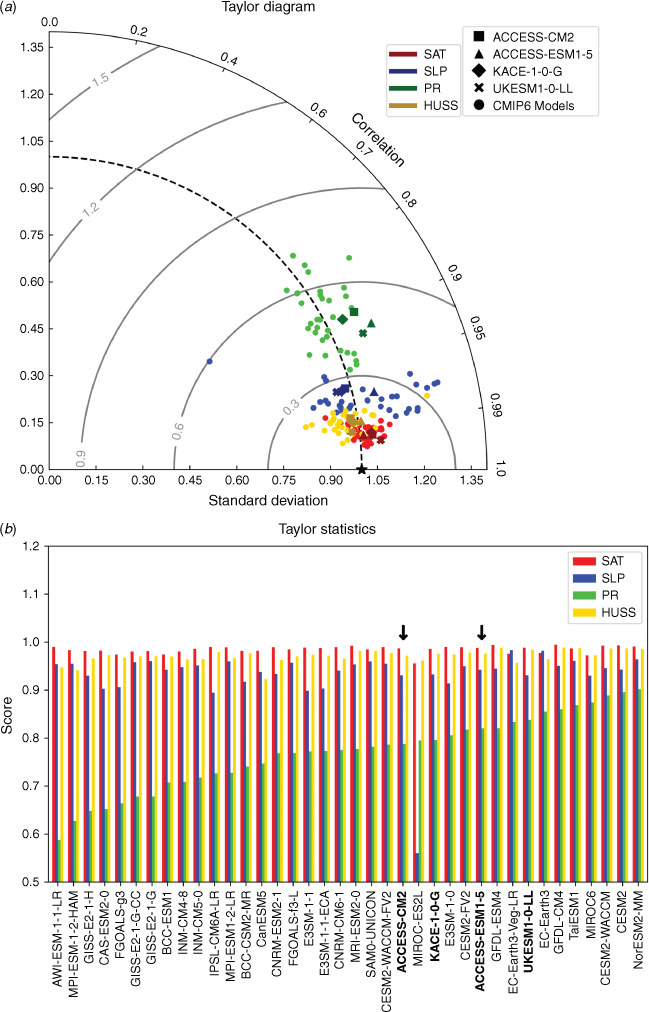
Model performances in simulating the time-mean patterns, relative to a reference dataset, may be efficiently summarised using the Taylor diagram (Taylor 2001). In this diagram, the pattern variances of many time-mean fields and their pattern correlations with the reference dataset are compared. The closer the data points to the reference point, the better the performance. In Fig. 4, we compare the performances of two ACCESS models in simulating the time-mean SAT, PR, SLP and near-surface HUSS with ERA5 reanalysis (Hersbach et al. 2020) and 36 other CMIP6 models (Eyring et al. 2016). Two of these latter models (UKESM1-0-LL and KACE-1-0-G) are specially marked, as they share the same atmospheric model with ACCESS-CM2.
The simulated SAT has the overall best performance, closely followed by HUSS, and PR has the worst performance among the four variables (Fig. 4a). The realistic simulation of PR in GCMs has remained a big challenge for a long time, mainly because this simulation depends on accurate representations of atmospheric convection, cloud microphysics, boundary-layer convergence and atmospheric circulation in the models. Although there has been progress in all these areas, much more is needed for satisfactory PR simulations. The ACCESS models perform similar to or better than most of the other 36 CMIP6 models for SAT, HUSS and PR, but worse for SLP (as quantified by the S statistics discussed below). Similar performances are shown by UKESM1-0-LL and KACE-1-0-G, suggesting that the atmospheric model mainly controls the simulations of these variables.
As a quantitative measure of the model performance, we computed the S statistics proposed by Taylor (2001):
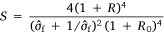
where  is the ratio of pattern standard deviations of a model variable and the reference variable, R is the corresponding pattern correlation between the model and reference variables and R0 is the maximum attainable correlation (taken as 1 in our calculation). The computed S statistics for the ACCESS and other CMIP6 models for four variables are presented in Fig. 4b, arranged in increasing magnitude of the PR score. According to the latter score, the two ACCESS models perform better than most CMIP6 models (as indicated above). The variation of the PR score across the CMIP6 models is large, ranging from a minimum of 0.59 for AWI-ESM-1-1-LR to a maximum of 0.90 for NorESM2-MM. However, the ranges of variation for the other three variables are not as large, with values ~0.9 or higher for most models. Between the two ACCESS models, ACCESS-ESM1.5 outperforms ACCESS-CM2 for all four (annual-mean) variables; for the DJF means, ACCESS-CM2 performs better than ACCESS-ESM1.5 for PR and HUSS. Also, ACCESS-CM2 has smaller mean biases (not included in the Taylor diagram or the statistics) than ACCESS-ESM1.5 for all variables except for SLP (Fig. 1–3).
is the ratio of pattern standard deviations of a model variable and the reference variable, R is the corresponding pattern correlation between the model and reference variables and R0 is the maximum attainable correlation (taken as 1 in our calculation). The computed S statistics for the ACCESS and other CMIP6 models for four variables are presented in Fig. 4b, arranged in increasing magnitude of the PR score. According to the latter score, the two ACCESS models perform better than most CMIP6 models (as indicated above). The variation of the PR score across the CMIP6 models is large, ranging from a minimum of 0.59 for AWI-ESM-1-1-LR to a maximum of 0.90 for NorESM2-MM. However, the ranges of variation for the other three variables are not as large, with values ~0.9 or higher for most models. Between the two ACCESS models, ACCESS-ESM1.5 outperforms ACCESS-CM2 for all four (annual-mean) variables; for the DJF means, ACCESS-CM2 performs better than ACCESS-ESM1.5 for PR and HUSS. Also, ACCESS-CM2 has smaller mean biases (not included in the Taylor diagram or the statistics) than ACCESS-ESM1.5 for all variables except for SLP (Fig. 1–3).
4. Modes of climate variability
Climate variability is also an important indicator of climate models’ performance. Here, we are mainly concerned with the historical variability at interannual to interdecadal timescales. A successful simulation of this variability is central to skilful seasonal and decadal predictions (Meehl et al. 2009; Santoso et al. 2019; Rashid 2020). This may also be important for reliable climate projections by GCMs. The most important modes of interannual to interdecadal variability are ENSO, IOD, IPO and NASST variability (which is closely related to the Atlantic Multi-decadal Oscillation). Below we provide a brief description of the ACCESS models’ performance in simulating these modes. Other important variability modes, such as the Madden–Julian Oscillation and the Southern Annular Mode, occur mostly at the sub-annual timescales and are not described here.
4.1. Spatial patterns
4.1.1. ENSO
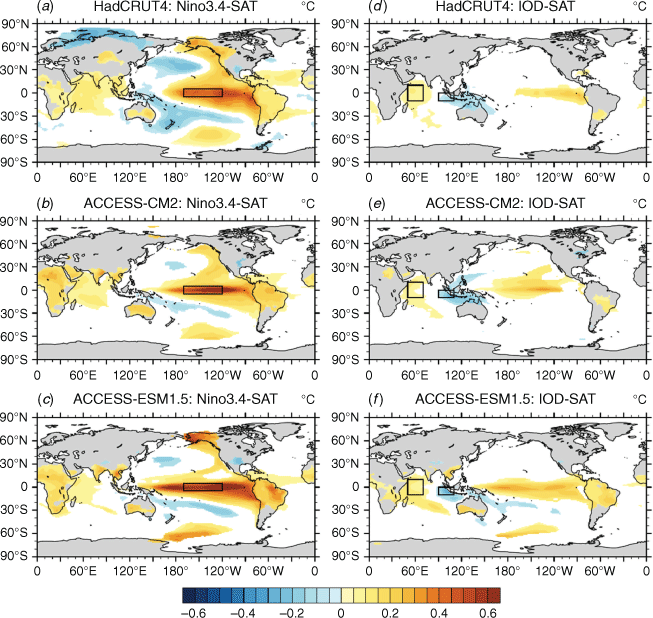
We show the spatial patterns of observed and simulated ENSO events in the left column of Fig. 5 using SAT; the ensemble-mean patterns are shown for ACCESS-CM2 and ACCESS-ESM1.5, obtained by averaging the individual patterns from their three-member ensembles. The SST is also frequently used to depict ENSO structure, but SATs are highly correlated with SSTs over the (ice-free) oceans and also allow us to show ENSO’s teleconnection pattern over the oceans and continents. The ENSO-associated SAT patterns, obtained by regressing the SAT anomalies on the standardised Niño-3.4 index (SST anomalies averaged over 5°S–5°N and 170–120°W), show the maximum warming over the central-to-eastern tropical Pacific (the genesis region of ENSO). Warm anomalies are also observed in the Pacific sector of the Southern Ocean, the western coast of North and South America, and the tropical Indian and Atlantic Oceans (Fig. 5a). The cold anomalies are observed in the south-west and north-west Pacific and to the north of the Eurasian continents. The main features of this observed warm and cold anomaly pattern are seen in the patterns simulated by the two ACCESS models (Fig. 5b, c). However, there are also some differences between the observed and simulated patterns. For example, the warm anomalies in the tropical Pacific are too narrow and the cold anomalies are weak in the model simulations compared to observations. Also, the observed teleconnection between the tropical Pacific and Atlantic Oceans is largely missing in ACCESS-CM2 (Fig. 5b). Improving this teleconnection by imposing observed SSTs over the tropical Atlantic has been found to make the ENSO periodicity more realistic in this model (Bi et al. 2022). Despite these biases, both ACCESS models perform reasonably well for a range of ENSO matrices when compared to other CMIP6 models (Planton et al. 2021).
4.1.2. IOD
The spatial patterns of IOD, computed by regressing SAT anomalies on the standardised IOD index (the difference of SST anomalies averaged over two tropical Indian Ocean boxes: 10°S–10°N, 50–70°E and 10°S–0°, 90–110°E), are shown in Fig. 5d–f. In observations (Fig. 5d), the associated SAT anomalies are confined near the two boxes and in the tropical eastern Pacific. The latter is due to the well-known IOD–ENSO teleconnection (e.g. Hendon 2003; Cai et al. 2011). Additionally, far north Australia experiences cooler temperatures during the positive phase of IOD. The two ACCESS models simulate the IOD-associated SAT patterns well (especially in the ACCESS-CM2 simulation), except that the tropical Pacific teleconnection in ACCESS-ESM1.5 is too strong compared to observations.
4.1.3. NASST variability
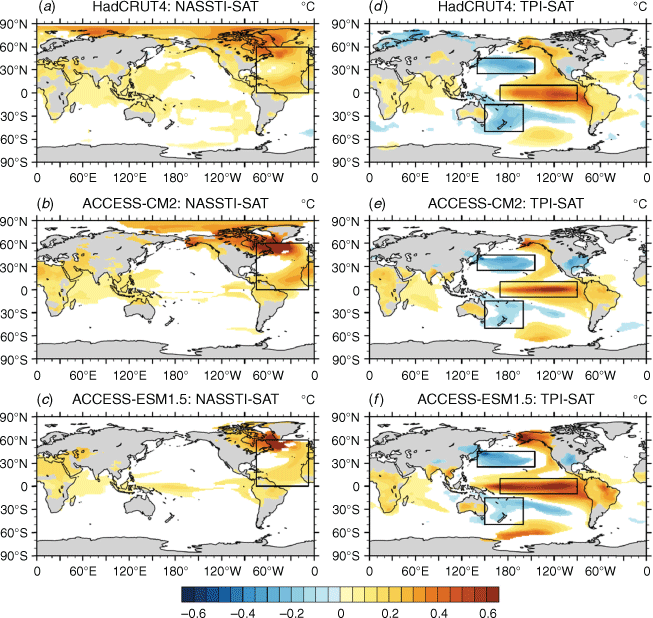
The NASST variability mode, as presented here, includes SST variability both at the interannual and interdecadal timescales (i.e. no low-pass filtering is applied). An index for this mode is calculated by averaging the area-weighted annual-mean SST anomalies over the North Atlantic: 0–60°N, 5–75°W (e.g. Frankcombe et al. 2015). This index is then used to obtain the spatial pattern of SAT anomalies, shown in the left column of Fig. 6, using regression as above. The observed SAT pattern has large magnitudes over the North Atlantic region, as expected, but also over the adjacent polar region (Fig. 6a). There are moderate SAT anomalies over the tropical Indian and western Pacific Oceans, as well as over parts of the South Pacific. The models again simulate the main features of the NASST variability pattern well (Fig. 6b, c), although ACCESS-ESM1.5 simulates a weaker than observed SAT response to the NASST variability index. Some of the differences between the observed and simulated patterns, especially where the anomalies are small, may arise from the fact that the simulated patterns are ensemble means while the observed pattern is not.
|
4.1.4. IPO
In addition to the interannual variability associated with ENSO, the Pacific also exhibits coherent variability at longer timescales characterised by a basin-wide spatial pattern. This variability may be represented by the IPO Tripole Index (TPI), which is computed as the difference between the area-weighted SST anomalies averaged over the central tropical Pacific and those over two boxes in the Northwest and Southwest Pacific (Henley et al. 2015). As expected, the observed SAT regression pattern of the TPI has positive anomalies in the equatorial central and eastern Pacific and negative anomalies in the central and western regions of the extratropical Pacific (Fig. 6d). This is broadly similar to the traditional IPO pattern (e.g. Power et al. 1999) despite no low-pass filtering being applied when computing the TPI. There are also some positive SAT anomalies in remote regions, such as the western parts of the tropical Indian and Atlantic Oceans, parts of Africa and Australia, and South America. The IPO pattern resembles the ENSO pattern in Fig. 5a, which is not surprising given the tropical box of TPI includes most of the Niño-3 and Niño-4 regions. The simulated IPO patterns are similar to the observed pattern, albeit with some differences. For example, the tropical part of the simulated IPO pattern is narrower, and the extratropical anomalies are weaker, in both models than in observations.
4.2. Spectral characteristics
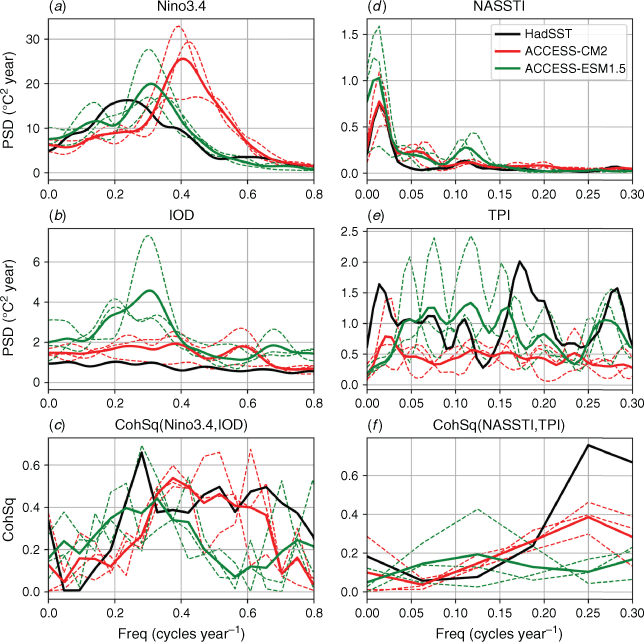
The temporal behaviour of the above climate variability modes is also of interest. Many of these modes exhibit characteristic spectral signatures that are important for diagnosing climate model performance. In Fig. 7, we show the power spectra of the four indices and the coherence spectra between two pairs of those indices. The observed ENSO spectrum has a well-known broad peak at 3–7-year periods (Fig. 7a; black curve). The ensemble-mean spectra of the simulated Niño-3.4 indices (thick red and green curves) also show spectral peaks, but at different periods than in observations. In particular, the ACCESS-CM2 ENSO spectrum peaks at ~2.5-year period and the ACCESS-ESM1.5 spectrum peaks at 3-year period, which is closer to the observed spectral peak. The spectral peaks for ensemble members (thin curves) are located around the peaks of the corresponding ensemble-mean indices. In general, the simulated spectral variances are larger than the observed values. However, there are significant spreads in the simulated spectra, and these are comparable to those found in the corresponding piControl runs. By contrast, the observed IOD spectrum is nearly flat without a discernible spectral peak (Fig. 7b), although there is a hint of a peak near the 5-year period (which may not be statistically significant). The ACCESS-CM2 simulated spectra also do not show any well-defined peaks and are reasonably close to the observed spectrum in magnitude. However, the ACCESS-ESM1.5 simulated IOD spectra show peaks at 3–5-year periods. The IOD variations in this period band are correlated with ENSO-related variations in this model, as shown by the coherence spectra (Fig. 7c).
|
The TPI and NASSTI mainly represent the decadal and longer timescale variability in the Pacific and North Atlantic Oceans respectively. The NASSTI shows a prominent spectral peak at 72.5 years in observations and both ACCESS model simulations, including their individual ensemble members (Fig. 7d). Note, however, that this spectral peak appears to arise from the limited data length (145 years) used for this calculation; any period longer than half the data length would alias into a shorter period, especially because the time means and quadratic trends were removed from the indices. For reference, there is no distinct spectral peak around the 72-year period in the corresponding pre-industrial control simulations (500 years long) of both ACCESS models, although there is a broad peak between 16 and 25 years and a general increase of spectral power towards the lowest frequencies (not shown). There is a secondary peak at a subdecadal period (9 years), which is more pronounced in ACCESS-ESM1.5. The TPI spectra are somewhat noisy (Fig. 7e). The observed TPI spectrum shows both multidecadal and subdecadal peaks at ~72.5 and 6 years; the former peak again appears to be an artifact of the limited sample length. The simulated spectra behave somewhat differently: whereas the ACCESS-ESM1.5 spectrum has magnitudes similar to the observed (in the 6–20-year periods), the ACCESS-CM2 spectrum has markedly smaller magnitudes and has its primary peak at 48 years for the ensemble mean. The coherence spectra between the NASSTI and TPI show no peak at the decadal–multidecadal periods (Fig. 7f).
5. Historical climate change
5.1. Temporal evolution of TOA radiative fluxes and precipitation
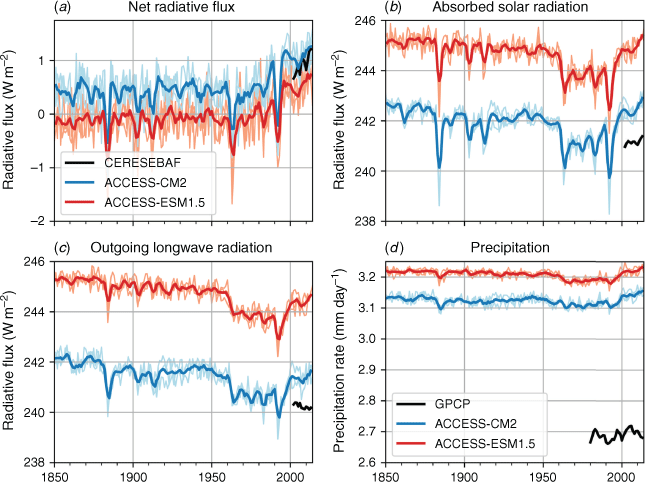
The temporal variations of selected global- and annual-mean climate variables are shown in Fig. 8 for observations and ACCESS simulations. The simulated and observed time-mean values compare well, although there are small differences. In general, the time-mean values from ACCESS-CM2 are closer to the corresponding observed values than those from ACCESS-ESM1.5 (see also Supplementary Fig. S3). The ensemble-mean net TOA radiative fluxes (Qnet) from the two ACCESS simulations evolve slightly differently: ACCESS-CM2 shows variations around a positive balance of 0.4 W m−2 until the middle of the 20th century, whereas ACCESS-ESM1.5 shows variations around a slightly negative balance (−0.1 W m−2) during this period (Fig. 8a). The simulation period is punctuated with large volcanic eruptions; their effects on Qnet are expressed as negative excursions in the time series. Following the eruption of Mount Agung in 1963, the balance for both models shows a strong positive trend, resulting in overall time means of ~0.8 and ~0.3 W m−2 for ACCESS-CM2 and ACCESS-ESM1.5 respectively (Supplementary Fig. S2a). The observed Qnet matches well with that from ACCESS-CM2 simulation over the common period (2001–2014), with a time mean of ~0.9 W m−2. The net positive flux implies a net heat input into the earth–atmosphere system, which is indicative of ensuing global warming.
The ensemble-mean net shortwave fluxes (or absorbed solar radiation; ASR) mostly show a small negative trend until 1960 (Fig. 8b). After this time there is a big drop in ASR, triggered by the Mount Agung eruption in 1963, that persists until the 1990s likely due to the increased anthropogenic aerosols or clouds (Trenberth and Fasullo 2009). The signatures of other large volcanic eruptions are evident in ASR throughout the period. The ASR values start increasing from 1993, in the immediate aftermath of the Mount Pinatubo eruption in 1991, as the tropospheric aerosol concentrations and clouds gradually decline. Both models overestimate the observed time-mean ASR (241 W m−2) over the common period, with the ACCESS-ESM1.5 bias being larger. The outgoing longwave radiation (OLR) shows a similar time evolution to that of ASR, but with slightly smaller time-mean values (Fig. 8c). The similar time evolution is expected as these two radiation components balance each other under equilibrium conditions and their difference yields the net radiative flux (Fig. 8a). As for ASR, both models overestimate the observed time-mean OLR value (~240 W m−2), with ACCESS-ESM1.5’s overestimation being larger. The global- and annual-mean PR rates also show a temporal evolution similar to those of the radiative fluxes (Fig. 8d). This is not surprising, as the global-mean PR change is constrained by changes in the global energy balance (Allen and Ingram 2002; Pendergrass and Hartmann 2014). The simulated PR changes compare favourably with the observed PR change, but the simulated time-mean PRs are again larger than the observed time-mean value (2.7 mm day–1). Note, however, that the GPCP dataset has been shown to underestimate rainfalls, especially over the oceans (Adler et al. 2017; Behrangi and Song 2020).
5.2. Temporal evolutions of polar sea ice
It is well-known that Arctic sea ice cover is sensitive to global-scale climate change and Antarctic sea ice cover shows large variability (Vinnikov et al. 1999; Pezza et al. 2012; Turner et al. 2015). A realistic simulation of the observed sea ice change and variability by climate models is important but has proven challenging. Fig. 9 shows the time series of observed and simulated area-averaged SIEs (total area of ocean grid points with sea ice concentration equal to 15% or more) for the Arctic and Antarctic regions. The observed Arctic SIE for September, i.e. the summer minimum ice coverage, shows a strong negative trend over 1979–2014 (the satellite era), which both ACCESS models simulate well (Fig. 9a). Prior to this period, the modelled SIEs show considerable interannual variability, but no significant trends. The model-simulated mean SIEs compare well with the observed mean (~6.3 × 106 km2) over the common period (1979–2014), although there is an overestimation (of ~10%) by ACCESS-CM2. For March, the winter maximum ice coverage simulated by ACCESS-ESM1.5 matches well with the observations for both time mean and trend (Fig. 9b). ACCESS-CM2, while simulating a negative SIE trend similar to the observed, overestimates the mean value by more than 2 × 106 km2. As discussed in Bi et al. (2020), the cause of the winter maximum SIE in the ACCESS-CM2 model being considerably larger than observed and in ACCESS-ESM1.5 (Fig. 9b), is related to ACCESS-CM2’s winter air temperature over the Arctic Ocean being several degrees colder than observed (Supplementary Fig. S1), consistent with the existence of a stronger than observed high-pressure system over the Beaufort Sea (Fig. 3a). Note, however, that ACCESS-CM2 fares better than ACCESS-ESM1.5, and compares favourably with the multi-model means, in a more detailed study of Arctic sea-ice simulations in 40 CMIP6 models (Notz and SIMIP Community 2020). This study analyses the key metrics of sea-ice process simulation, including the sensitivities of simulated Arctic sea-ice area to anthropogenic CO2 concentration changes and global warming. The apparently better simulation of sea ice by ACCESS-ESM1.5 may be a result of process error cancellations in this model.
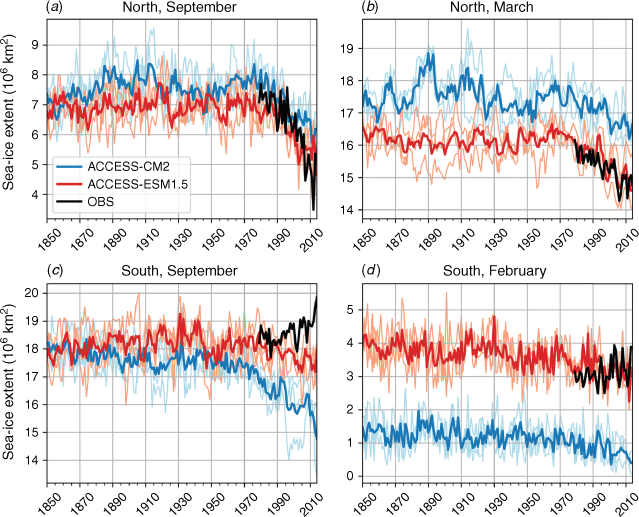
|
The observed Antarctic SIE for September, the winter maximum of sea ice coverage, has a time-mean of 18.6 × 106 km2 over the 1979–2014 period and shows a positive trend during this period (Fig. 9c). The models underestimate the time-mean SIE by up to 2 × 106 km2 mainly because of a simulated negative trend over this period. The simulated negative trend starts from the middle of the 20th century for ACCESS-CM2 and from the mid-1970s for ACCESS-ESM1.5. The Antarctic SIE shows a similar behaviour in February (Fig. 9d, the summer minimum of sea ice coverage), although the observed positive trend and simulated negative trend are both smaller than those in September. The time-mean SIE for ACCESS-ESM1.5 is very close to the observed value; however, the time-mean SIE for ACCESS-CM2 is very small, ~25% of the observed value. The poor simulation of summer sea ice around Antarctica in ACCESS-CM2 is associated with the strong warm biases around the Antarctic continent (see Fig. 1), which leads to SSTs exceeding levels required for the realistic retention of sea ice in summer. Most CMIP5 and CMIP6 models simulate smaller than observed SIE means and negative SIE trends, in contrast to a positive trend in observations (Purich et al. 2016; Roach et al. 2020). The climate models’ inability to simulate the observed positive trend of Antarctic SIE has been a longstanding problem; various causes of this problem have been suggested in the literature, including biases in the simulated Southern Ocean westerly winds and sea ice drift velocity (Sun and Eisenman 2021).
5.3. Analysis of global-mean surface air temperature change
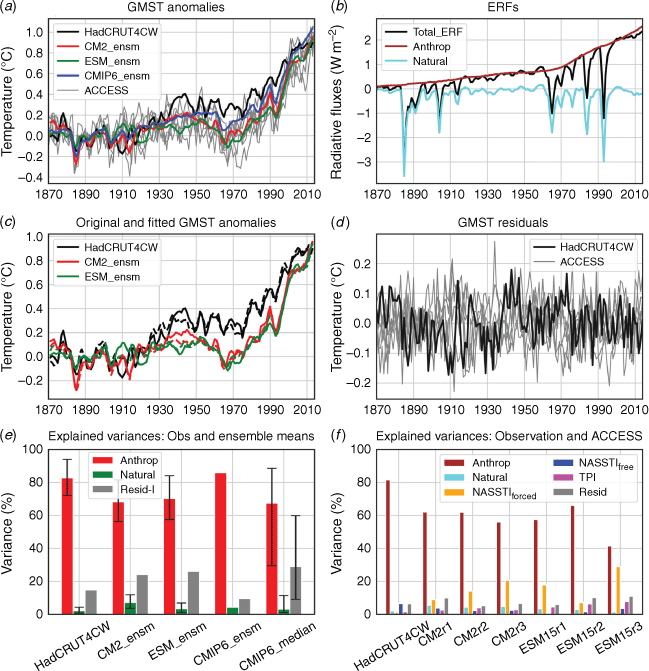
The global mean surface air temperature (GMST) anomalies from ACCESS-CM2, ACCESS-ESM1.5 and 42 CMIP6 model simulations are compared with those from the HadCRUT4 dataset (Fig. 10a). The anomalies are computed with respect to the 1850–1900 time means (hence, the closer match between observations and simulations during that period). There is a common warming trend in the observed and simulated GMST time-series until the 1970s, which is modulated by decadal–multidecadal warming and cooling periods. The evolution of ensemble mean GMSTs (coloured curves) compares well with the observed GMST evolution, except during the middle and second half of the 20th century when the models on average simulate cooler GMSTs (this, however, depends on the chosen reference climatology; see Hawkins and Sutton 2016). Some of the observed mid-20th century warming may be spurious, arising from the uncorrected instrumental biases in the SST record (Thompson et al. 2008). There are sharp drops in GMST associated with large volcanic eruptions. The models tend to show a more pronounced cooling response to volcanic eruptions than observed; this is particularly evident for the large eruptions of 1883, 1963 and 1991. Although the GMST normally recovers within a few years, it took longer after the 1963 event, due to the added influence of anthropogenic aerosols (Wilcox et al. 2013). The observed GMST rises rapidly between 1976 and 1998, followed by a slower rise during 1999–2014 (Fig. 10a). The modelled GMSTs also rise during these periods, but with a larger trend in the latter than the former. This mismatch between the observed and simulated GMST trends after 1998 has been the subject of many studies and is thought to be a result of internal climate variability (e.g. Kosaka and Xie 2016).
It is well-known that the temporal variation of GMST, such as that discussed above, results from a combined influence of various external climate drivers and internal variability modes (e.g. Hegerl et al. 2019). There is, however, a wide variation across climate models in how different forcing agents influence the simulated GMST variations (e.g. Rashid 2021). Here, we use a multiple linear regression (hereafter, MLR) model to estimate the contributions from anthropogenic effective radiative forcing (ERF) due to greenhouse gases and aerosols, natural ERF (due to volcanic eruptions and total solar irradiance variation) (Fig. 10b) and two prominent climate variability modes: the NASST mode (e.g. Frankcombe et al. 2015) and the IPO as represented by the TPI (Henley et al. 2015). The NASST variability has a significant forced signal (Booth et al. 2012), so this mode is separated into forced (NASSTIforced) and free (NASSTIfree) components. The MLR model and its predictor variables are described in detail in Rashid (2021), in an analysis of single-member historical simulations of GMST by 42 CMIP6 models (including ACCESS-CM2 and ACCESS-ESM1.5). Here, we study three-member ensemble simulations from each ACCESS model and compare them with the CMIP6 multimodel mean and observational results.
The MLR model is applied to observed and simulated GMST time-series to obtain variance contributions from the predictors and the residuals. The analysis is done separately for the observed and each of the simulated GMST time-series. The fitted GMSTs, the sum of all the predictor contributions (and ensemble-averaged for the two models), are shown in Fig. 10c. The fitted time-series (dashed curves) match their original counterparts (solid curves) very well, explaining ~89–95% of the respective original time-series (93% for the observation). The residual time-series do not show any discernible trends (Fig. 10d), but have small to moderate autocorrelations that are significant (at the 95% level) for lags up to 4 years (not shown). This indicates that there is still some predictive information left in the residuals, which we do not explore here further. Only small proportions (5–11%) of the observed and simulated GMST variances are left in the respective residual time-series; these originate mainly from GMST variations in the Arctic region (Supplementary Fig. S4).
The anthropogenic ERF explains by far the largest percentage variances of the observed and ensemble mean GMST time-series for the two ACCESS and 42 CMIP6 models, which are compared with the CMIP6 median value (Fig. 10e). The percentage variance for observation (~83%) is comparable to that of the CMIP6 ensemble mean (86%), but is larger than those for ACCESS-CM2 and ACCESS-ESM1.5 ensemble means (68 and 70% respectively). The latter compare well with the CMIP6 median value (67%) of the 42 single-member CMIP6 models. Note that the two ACCESS models have only three ensemble members each, so their explained variances being smaller than that of the CMIP6 ensemble is not unexpected. The percentage variances presented in Fig. 10e are obtained using only the anthropogenic and natural ERFs as predictors in the MLR model to enable the analysis of ensemble mean GMSTs. The results for the observation and individual ACCESS simulations obtained using all five predictors are shown in Fig. 10f. Compared with Fig. 10e, the anthropogenic contributions in individual ACCESS simulations are comparable to the CMIP6 median value, although this contribution is very low in one of the ACCESS-ESM1.5 simulations (~42%, which nevertheless is in the 5th–95th percentile range of the CMIP6 models). This low anthropogenic variance, which is roughly two-thirds of the corresponding variances from the other two ACCESS-ESM1.5 simulations, is compensated by a relatively large NASSTIforced contribution in that simulation. Such a sizable difference in externally forced variance between ensemble simulations is interesting; a full understanding of this will need further investigation. The second largest contribution to the observed GMST variation comes from the North Atlantic internal SST variability, as represented by NASSTIfree; in contrast, the second largest contributor to the simulated GMST variations is NASSTIforced, the North Atlantic forced SST variability. This contrasting relationship with observation is however not unique to the ACCESS models: more than half of the 42 CMIP6 models, analysed in a separate study, have NASSTIforced as the second largest contributor to their simulated GMST variations (Rashid 2021). Also, the NASSTIforced contributions are highly negatively correlated (r = −0.95) with the anthropogenic contributions across different ensemble members, and this is also true for a larger ensemble size of 42 CMIP6 models (not shown but see Rashid 2021). The Pacific SST variability, as represented by the TPI, and the natural ERF both play a minor role in the observed and simulated GMST variability.
5.4. Historical climate change signal in SAT
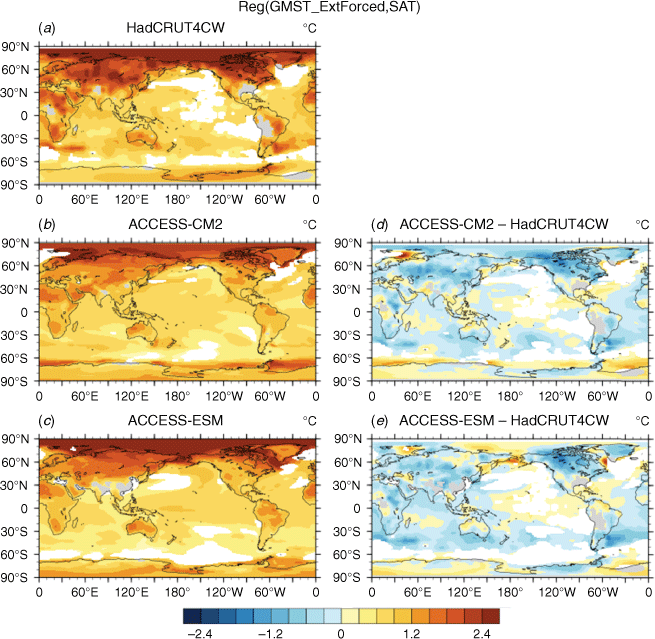
Next, we examine the spatial pattern of anthropogenic climate change in observations and ACCESS models. Although the existence of anthropogenic influence on GMST change has been convincingly shown, the details of the spatial patterns of SAT change and their mechanisms are still being debated. We use the anthropogenic component of GMST, estimated above from the MLR model, to calculate the spatial patterns of anthropogenic SAT changes over 1870–2014 for observations and the two ACCESS models (Fig. 11). The separate GMST components due to the anthropogenic ERF and NASSTIforced are first added together to obtain the total anthropogenic GMST time-series. The global SAT anomalies are then regressed onto this anthropogenic GMST time-series to obtain the spatial patterns of anthropogenic SAT changes. For the two ACCESS models, both the GMST time-series and the SAT anomalies are ensemble-averaged (to reduce the unforced variability) before calculating the regression coefficients. The coefficients are then multiplied by the total GMST change over 1870–2014 (i.e. the GMST range) to give the total SAT changes over the same period.
The pattern of observed SAT changes shows the well-known maximum warming region over the North Pole and the adjacent continents (Fig. 11a), with the maximum SAT anomaly of 3.6°C. Considerable warmings are also observed over the southern half of Australia, northern and southern Africa, central Asia and the eastern part of South America. In general, the oceanic regions show moderate warming compared to the land warming, due mainly to horizontal energy transports (Joshi et al. 2013). The large-scale features of the observed SAT change are captured by the ACCESS models (Fig. 11b, c), although they generally tend to underestimate warming (Fig. 11d, e). There are some regional differences: absence of substantial warming over Southeast Australia and over the isolated oceanic areas near the southern tips of South Africa and South America. Moreover, ACCESS-CM2 shows substantial warming along the edge of Antarctica, which is not seen in observations with the same magnitude. This warming bias may be related to the significant underestimation of summer sea ice by this model in this region (Fig. 9d).
5.5. Comparison with ACCESS DAMIP results
The application of the simple MLR model to the observed and simulated data enables us to separate the externally forced GMST and SAT signals from the climate system’s internal variability, as presented in Fig. 10 and 11 respectively. Similar analyses are also done using comprehensive climate model experiments, e.g. those contributed to the detection and attribution model intercomparison project (DAMIP) under CMIP6 (Gillett et al. 2016). The DAMIP experiments are like the historical experiment, but are driven by separate external forcings, e.g. GHGs-only, aerosols-only and natural forcing-only experiments. It is of interest to compare the above statistical model analysis of ACCESS data with the corresponding result from ACCESS DAMIP experiments. A favourable comparison between these independent analyses will strengthen confidence in the results obtained from either.
Fig. 12 shows the GMST changes obtained from ACCESS historical and DAMIP ensemble mean simulations and from MLR fits to the historical simulations, as well as the observed GMST change for comparison. The DAMIP GMST time-series is the sum of the individual GMSTs from GHGs, aerosols and natural forcing-only simulations. The MLR fits are done to the individual historical simulations and then ensemble averaged. The GMST evolutions from the ACCESS historical and DAMIP simulations compare well (r = 0.94 and 0.81 for ACCESS-CM2 and ACCESS-ESM1.5 respectively), except for some differences after year 2000 (Fig. 12a, b). The differences are likely due to residual internal variability, which does not completely cancel each out on ensemble averaging because of small ensemble size. The ensemble-mean GMSTs from historical simulations and the MLR model match even better, with the MLR model explaining ~90% of the GMST variances (Fig. 10). The anthropogenic (GHGs plus aerosols) and natural forcing contributions to the ACCESS DAMIP simulated and MLR fitted GMSTs also compare well (Fig. 12c, d), to the extent that ACCESS DAMIP and historical simulations compare. The post-2000 mismatches between the latter simulations are associated with the anthropogenic component, although the natural component contributes somewhat for ACCESS-ESM1.5 after 2010. Overall, the simple MLR model isolates the GMST signals due to the anthropogenic and natural radiative forcing as well as in the ACCESS DAMIP simulations. However, the latter are still a very useful set of experiments, as they enable the detection and attribution studies for other climate variables and over global as well as regional domains. Also, the DAMIP experiment can separate the anthropogenic contributions due to GHGs and aerosols; the MLR model cannot do this as the corresponding ERFs are highly (negatively) correlated with each other.
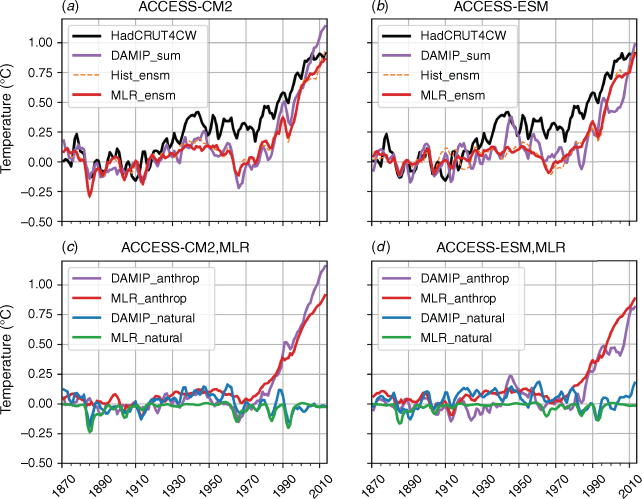
|
Because the MLR model efficiently separates the climate signals of different origins, it is a useful tool for analysing observational as well as model-simulated climate time-series (despite some limitations). Its application to observations and ACCESS model simulations has been demonstrated in this work; elsewhere, we analysed an ensemble of historical simulations from 42 CMIP6 climate models and found a diversity of GMST responses in these models to the anthropogenic and natural forcings (Rashid 2021). The diagnostic results provided by the MLR model may be used to further understand the causes of the differing responses between observations and model simulations and between the model simulations.
6. Conclusions
We analyse and document the historical simulations performed by ACCESS-CM2 and ACCESS-ESM1.5 for CMIP6. Three ensemble members from each model are used to compare the simulated seasonal-mean climate, climate variability and climate change with observations over the historical period. Where appropriate, we also compare the ACCESS model results with results from other CMIP6 models and a MLR model. The main results of this investigation are summarised below.
The seasonal-mean spatial patterns of simulated surface temperature, PR and SLP compare well with the corresponding patterns obtained from reanalysis and observations. The major model biases occur over the polar regions for surface temperature and SLP and the tropical region for PR (Fig. 1–3). The magnitude of these biases is comparable to or less than those found in most other CMIP6 models, except for SLP (Fig. 4). In all models, PR is the most challenging variable to simulate, and the ACCESS models perform better than most CMIP6 models for this variable (Fig. 4b).
The spatial patterns of the dominant climate variability modes in observations and ACCESS historical simulations have reasonably good agreements (Fig. 5, 6). The meridional extent is narrower than observed for the Pacific variability modes (ENSO and IPO), and the simulated IOD mode is stronger than observed. These are long-standing biases commonly found in many climate models (e.g. McKenna et al. 2020). The main features of the observed North Atlantic variability mode are also well captured by the simulated mode. There is, however, only moderate agreement between the power spectra of the observed and simulated modes (Fig. 7). For ENSO, ACCESS-ESM1.5 simulated spectra are in reasonable agreement with the observed spectrum. However, the ACCESS-CM2 simulated spectra are dominated by a quasi-biennial peak, in contrast to the observed spectral peak in the 3–7-year range. For the other modes, the resemblance between the observed and simulated spectra is even weaker. These disagreements may be due to possible model biases, but may also arise from the limited coverage and poor quality of earlier observational data.
It is even harder to assess the realism of model-simulated historical climate changes of radiative fluxes, PR and the polar SIE. This is because the relevant observational data are available for only short periods, which are not adequate for climate change assessment. However, over the common periods, ACCESS-CM2 simulated global-mean TOA radiative fluxes compare favourably with observations, although the biases in ACCESS-ESM1-5 simulated fluxes are relatively larger (Fig. 8a–c). Both models overestimate the global-mean PR relative to GPCP observations (Fig. 8d). For SIE (Fig. 9), ACCESS-CM2 overestimates (underestimates) the sea-ice extent in the NH (SH), most notably during the NH winter season. Both models, however, capture the recent sea ice loss over the Arctic to a varying degree. The situation is different for the SH: although the winter sea ice increases in observations, both ACCESS models show a decreasing trend (Fig. 9c), as for most other CMIP6 models (Roach et al. 2020).
The climate change signal in GMST is analysed in some detail (Fig. 10). The anthropogenic forcing (due to GHGs and aerosols) is by far the largest contributor to the observed and model-simulated GMST changes over the historical period. The free (forced) NASST variability is the second largest contributor to the observed (model simulated) GMST changes. There are differences between the observed and simulated contributions and among the simulated contributions. In particular, the simulated anthropogenic signals are ~10% weaker than the observed signal, a bias also identified in other CMIP6 models (Rashid 2021). The intermodel difference is mainly due to the presence of different levels of internal variability across model realisations. The observed and model-simulated climate change signals in surface temperature show a high degree of spatial agreement, with the largest warming occurring in the Northern polar region (Fig. 11). There are some regional differences between the observed and simulated spatial patterns. The anthropogenic and natural climate change signals detected in GMST using a MLR model compare well with the corresponding signals estimated from the detection and attribution experiments of the much more complex ACCESS models (Fig. 12). This provides confidence in the estimated climate change signals over the historical period; this estimation is challenging because of the presence of significant internal climate variability.
Overall, the two ACCESS models provide high-quality climate simulations that may be used with confidence in further analyses of climate variability and change. Like other complex climate models, the ACCESS models also have biases in their simulated climate. We document some of these biases in this paper, which is expected to help interpret other analyses of ACCESS simulations. It is expected that climate models that simulate historical climate well will also provide reliable climate projections for a particular future climate forcing scenario. It is, however, not clear if (or to what extent) the biases of a particular climate model will remain proportionately the same under different climate forcing regimes, e.g. the historical and future forcing scenarios. Further research is needed to clearly understand this issue.
Data availability
The CMIP6 model outputs used in this study may be downloaded freely from https://esgf-node.llnl.gov/projects/cmip6/ upon registration. The ERF data were downloaded from the KNMI climate explorer website: https://climexp.knmi.nl/selectindex.cgi?id=someone@somewhere. The Cowtan and Way surface temperature dataset is available at https://www-users.york.ac.uk/~kdc3/papers/coverage2013/series.html and the HadISST data were obtained from https://www.metoffice.gov.uk/hadobs/hadisst/data/download.html. Observed sea-ice extent data were downloaded from https://seaice.uni-bremen.de/sea-ice-concentration/amsre-amsr2/time-series/ and the ERA5 reanalysis products from https://cds.climate.copernicus.eu/#!/search?text=ERA5&type=dataset. The HadSLP2 dataset is available at https://www.metoffice.gov.uk/hadobs/hadslp2/data/download.html and the CERES-EBAF data at https://ceres.larc.nasa.gov/order_data.php.
Conflicts of interest
The authors declare that they have no conflicts of interest.
Declaration of funding
This work was partially funded by the National Environmental Science Programme’s Climate Systems Hub. The ACCESS model simulations for CMIP6 were performed using the resources and services from the National Computational Infrastructure (NCI), which is supported by the Australian Government. The other CMIP6 model outputs used in this study were downloaded from the Earth System Grid Federation (ESGF). We acknowledge the World Climate Research Programme’s Working Group on Coupled Modelling, which is responsible for CMIP, and we thank the climate modelling groups for producing and making available their model outputs. For CMIP, the US Department of Energy’s Program for Climate Model Diagnosis and Intercomparison provides coordinating support and led development of software infrastructure in partnership with the Global Organization for Earth System Science Portals.
Supplementary material
Supplementary material is available online.
Acknowledgements
We thank the two anonymous reviewers for their insightful comments, which helped us make the presentation of the results clearer. We also thank Dr Rachel Law for her valuable comments on an earlier version of this manuscript.
References
Adler RF, Gu G, Sapiano M, Wang JJ, Huffman GJ (2017) Global precipitation: means, variations and trends during the satellite era (1979–2014). Surveys in Geophysics 38, 679–699.| Global precipitation: means, variations and trends during the satellite era (1979–2014).Crossref | GoogleScholarGoogle Scholar |
Adler RF, Sapiano MRP, Huffman GJ, Wang J-J, Gu G, Bolvin D, et al. (2018) The Global Precipitation Climatology Project (GPCP) monthly analysis (new version 2.3) and a review of 2017 global precipitation. Atmosphere 9, 138
| The Global Precipitation Climatology Project (GPCP) monthly analysis (new version 2.3) and a review of 2017 global precipitation.Crossref | GoogleScholarGoogle Scholar | 30013797PubMed |
Allan R, Ansell T (2006) A new globally complete monthly historical gridded mean sea level pressure dataset (HadSLP2): 1850–2004. Journal of Climate 19, 5816–5842.
| A new globally complete monthly historical gridded mean sea level pressure dataset (HadSLP2): 1850–2004.Crossref | GoogleScholarGoogle Scholar |
Allen MR, Ingram WJ (2002) Constraints on future changes in climate and the hydrologic cycle. Nature 419, 228–232.
| Constraints on future changes in climate and the hydrologic cycle.Crossref | GoogleScholarGoogle Scholar | 12226678PubMed |
Behrangi A, Song Y (2020) A new estimate for oceanic precipitation amount and distribution using complementary precipitation observations from space and comparison with GPCP. Environmental Research Letters 15, 124042
| A new estimate for oceanic precipitation amount and distribution using complementary precipitation observations from space and comparison with GPCP.Crossref | GoogleScholarGoogle Scholar |
Bi D, Dix M, Marsland SJ, O’Farrell S, Rashid HA, Uotila P, et al. (2013) The ACCESS coupled model: description, control climate and evaluation. Australian Meteorological and Oceanographic Journal 63, 41–64.
| The ACCESS coupled model: description, control climate and evaluation.Crossref | GoogleScholarGoogle Scholar |
Bi D, Dix M, Marsland S, O’Farrell S, Sullivan A, Bodman R, et al. (2020) Configuration and spin-up of ACCESS-CM2, the new generation Australian Community Climate and Earth System Simulator Coupled Model. Journal of Southern Hemisphere Earth Systems Science 70, 225–251.
| Configuration and spin-up of ACCESS-CM2, the new generation Australian Community Climate and Earth System Simulator Coupled Model.Crossref | GoogleScholarGoogle Scholar |
Bi D, Wang G, Cai W (2022) Improved simulation of ENSO variability through feedback from the equatorial Atlantic in a Pacemaker Experiment. Geophysical Research Letters 49, e2021GL096887
| Improved simulation of ENSO variability through feedback from the equatorial Atlantic in a Pacemaker Experiment.Crossref | GoogleScholarGoogle Scholar |
Bodman RW, Karoly DJ, Dix MR, Harman IN, Srbinovsky J, Dobrohotoff PB, Mackallah C (2020) Evaluation of CMIP6 AMIP climate simulations with the ACCESS-AM2 model. Journal of Southern Hemisphere Earth Systems Science 70, 166–179.
| Evaluation of CMIP6 AMIP climate simulations with the ACCESS-AM2 model.Crossref | GoogleScholarGoogle Scholar |
Booth BBB, Dunstone NJ, Halloran PR, Andrews T, Bellouin N (2012) Aerosols implicated as a prime driver of twentieth-century North Atlantic climate variability. Nature 484, 228–232.
| Aerosols implicated as a prime driver of twentieth-century North Atlantic climate variability.Crossref | GoogleScholarGoogle Scholar |
Cai W, van Rensch P, Cowan T, Hendon HH (2011) Teleconnection pathways of ENSO and the IOD and the mechanisms for impacts on Australian rainfall. Journal of Climate 24, 3910–3923.
| Teleconnection pathways of ENSO and the IOD and the mechanisms for impacts on Australian rainfall.Crossref | GoogleScholarGoogle Scholar |
Cowtan K, Way RG (2014) Coverage bias in the HadCRUT4 temperature series and its impact on recent temperature trends. Quarterly Journal of the Royal Meteorological Society 140, 1935–1944.
| Coverage bias in the HadCRUT4 temperature series and its impact on recent temperature trends.Crossref | GoogleScholarGoogle Scholar |
Eyring V, Bony S, Meehl GA, Senior CA, Stevens B, Stouffer RJ, Taylor KE (2016) Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geoscientific Model Development 9, 1937–1958.
| Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization.Crossref | GoogleScholarGoogle Scholar |
Frankcombe LM, England MH, Mann ME, Steinman BA (2015) Separating internal variability from the externally forced climate response. Journal of Climate 28, 8184–8202.
| Separating internal variability from the externally forced climate response.Crossref | GoogleScholarGoogle Scholar |
Gillett NP, Shiogama H, Funke B, Hegerl G, Knutti R, Matthes K, et al. (2016) The Detection and Attribution Model Intercomparison Project (DAMIP v1.0) contribution to CMIP6. Geoscientific Model Development 9, 3685–3697.
| The Detection and Attribution Model Intercomparison Project (DAMIP v1.0) contribution to CMIP6.Crossref | GoogleScholarGoogle Scholar |
Goyal R, Jucker M, Sen Gupta A, Hendon HH, England MH (2021) Zonal wave 3 pattern in the Southern Hemisphere generated by tropical convection. Nature Geoscience 14, 732–738.
| Zonal wave 3 pattern in the Southern Hemisphere generated by tropical convection.Crossref | GoogleScholarGoogle Scholar |
Hawcroft M, Haywood JM, Collins M, Jones A, Jones AC, Stephens G (2017) Southern Ocean albedo, inter-hemispheric energy transports and the double ITCZ: global impacts of biases in a coupled model. Climate Dynamics 48, 2279–2295.
| Southern Ocean albedo, inter-hemispheric energy transports and the double ITCZ: global impacts of biases in a coupled model.Crossref | GoogleScholarGoogle Scholar |
Hawkins E, Sutton R (2016) Connecting climate model projections of global temperature change with the real world. Bulletin of the American Meteorological Society 97, 963–980.
| Connecting climate model projections of global temperature change with the real world.Crossref | GoogleScholarGoogle Scholar |
Hegerl GC, Brönnimann S, Cowan T, Friedman AR, Hawkins E, Iles C, et al. (2019) Causes of climate change over the historical record. Environmental Research Letters 14, 123006
| Causes of climate change over the historical record.Crossref | GoogleScholarGoogle Scholar |
Hendon HH (2003) Indonesian rainfall variability: impacts of ENSO and local air-sea interaction. Journal of Climate 16, 1775–1790.
| Indonesian rainfall variability: impacts of ENSO and local air-sea interaction.Crossref | GoogleScholarGoogle Scholar |
Henley BJ, Gergis J, Karoly DJ, Power S, Kennedy J, Folland CK (2015) A Tripole Index for the Interdecadal Pacific Oscillation. Climate Dynamics 45, 3077–3090.
| A Tripole Index for the Interdecadal Pacific Oscillation.Crossref | GoogleScholarGoogle Scholar |
Hersbach H, Bell B, Berrisford P, Hirahara S, Horányi A, Muñoz-Sabater J, et al. (2020) The ERA5 global reanalysis. Quarterly Journal of the Royal Meteorological Society 146, 1999–2049.
| The ERA5 global reanalysis.Crossref | GoogleScholarGoogle Scholar |
Hewitt HT, Copsey D, Culverwell ID, Harris CM, Hill RSR, Keen AB, et al. (2011) Design and implementation of the infrastructure of HadGEM3: the next-generation Met Office climate modelling system. Geoscientific Model Development 4, 223–253.
| Design and implementation of the infrastructure of HadGEM3: the next-generation Met Office climate modelling system.Crossref | GoogleScholarGoogle Scholar |
Hwang Y-T, Frierson DMW (2013) Link between the double-Intertropical Convergence Zone problem and cloud biases over the Southern Ocean. Proceedings of the National Academy of Sciences of the United States of America 110, 4935–40.
| Link between the double-Intertropical Convergence Zone problem and cloud biases over the Southern Ocean.Crossref | GoogleScholarGoogle Scholar | 23493552PubMed |
Joshi MM, Lambert FH, Webb MJ (2013) An explanation for the difference between twentieth and twenty-first century land–sea warming ratio in climate models. Climate Dynamics 41, 1853–1869.
| An explanation for the difference between twentieth and twenty-first century land–sea warming ratio in climate models.Crossref | GoogleScholarGoogle Scholar |
Kosaka Y, Xie SP (2016) The tropical Pacific as a key pacemaker of the variable rates of global warming. Nature Geoscience 9, 669–673.
| The tropical Pacific as a key pacemaker of the variable rates of global warming.Crossref | GoogleScholarGoogle Scholar |
Loeb NG, Doelling DR, Wang H, Su W, Nguyen C, Corbett JG, et al. (2018) Clouds and the Earth’s Radiant Energy System (CERES) Energy Balanced and Filled (EBAF) top-of-atmosphere (TOA) edition-4.0 data product. Journal of Climate 31, 895–918.
| Clouds and the Earth’s Radiant Energy System (CERES) Energy Balanced and Filled (EBAF) top-of-atmosphere (TOA) edition-4.0 data product.Crossref | GoogleScholarGoogle Scholar |
Mackallah C, Chamberlain MA, Law R, Dix M, Ziehn T, Bi D, Bodman R, Brown J, Dobrohotoff P, Druken K, Evans B, Harman IN, Hayashida H, Holmes R, Kiss A, Lenton A, Liu Y, Marsland S, Meissner K, Menviel L, O Farrell S, Rashid HA, Ridzwan S, Savita A, Srbinovsky J, Sullivan A, Trenham C, Vohralik P, Wang Y, Williams G, Woodhouse M, Yeung N (2022) ACCESS datasets for CMIP6: methodology and idealised experiments. Journal of Southern Hemisphere Earth Systems Science. [Published online XX July 2022].
| Crossref |
McIntosh PC, Hendon HH (2018) Understanding Rossby wave trains forced by the Indian Ocean Dipole. Climate Dynamics 50, 2783–2798.
| Understanding Rossby wave trains forced by the Indian Ocean Dipole.Crossref | GoogleScholarGoogle Scholar |
McKenna S, Santoso A, Gupta A, Sen , Taschetto AS, Cai W (2020) Indian Ocean Dipole in CMIP5 and CMIP6: characteristics, biases, and links to ENSO. Scientific Reports 10, 11500
| Indian Ocean Dipole in CMIP5 and CMIP6: characteristics, biases, and links to ENSO.Crossref | GoogleScholarGoogle Scholar | 32661240PubMed |
Meehl GA, Goddard L, Murphy J, Stouffer RJ, Boer G, Danabasoglu G, et al. (2009) Decadal prediction. Bulletin of the American Meteorological Society 90, 1467–1485.
| Decadal prediction.Crossref | GoogleScholarGoogle Scholar |
Mo KC, Higgins RW (1998) The Pacific–South American modes and tropical convection during the Southern Hemisphere winter. Monthly Weather Review 126, 1581–1596.
| The Pacific–South American modes and tropical convection during the Southern Hemisphere winter.Crossref | GoogleScholarGoogle Scholar |
Morice CP, Kennedy JJ, Rayner NA, Jones PD (2012) Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: the HadCRUT4 data set. Journal of Geophysical Research – D. Atmospheres 117, D08101
| Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: the HadCRUT4 data set.Crossref | GoogleScholarGoogle Scholar |
Notz D (2020) Arctic Sea Ice in CMIP6. Geophysical Research Letters 47, e2019GL086749
| Arctic Sea Ice in CMIP6.Crossref | GoogleScholarGoogle Scholar |
Pendergrass AG, Hartmann DL (2014) The atmospheric energy constraint on global-mean precipitation change. Journal of Climate 27, 757–768.
| The atmospheric energy constraint on global-mean precipitation change.Crossref | GoogleScholarGoogle Scholar |
Pezza AB, Rashid HA, Simmonds I (2012) Climate links and recent extremes in antarctic sea ice, high-latitude cyclones, Southern Annular Mode and ENSO. Climate Dynamics 38, 57–73.
| Climate links and recent extremes in antarctic sea ice, high-latitude cyclones, Southern Annular Mode and ENSO.Crossref | GoogleScholarGoogle Scholar |
Planton YY, Guilyardi E, Wittenberg AT, Lee J, Gleckler PJ, Bayr T, McGregor S, McPhaden MJ, Power S, Roehrig R, Vialard J, Voldoire A (2021) Evaluating climate models with the CLIVAR 2020 ENSO metrics package. Bulletin of the American Meteorological Society 102, E193–E217.
| Evaluating climate models with the CLIVAR 2020 ENSO metrics package.Crossref | GoogleScholarGoogle Scholar |
Power S, Casey T, Folland C, Colman A, Mehta V (1999) Inter-decadal modulation of the impact of ENSO on Australia. Climate Dynamics 15, 319–324.
| Inter-decadal modulation of the impact of ENSO on Australia.Crossref | GoogleScholarGoogle Scholar |
Purich A, Cai W, England MH, Cowan T (2016) Evidence for link between modelled trends in Antarctic sea ice and underestimated westerly wind changes. Nature Communications 7, 10409
| Evidence for link between modelled trends in Antarctic sea ice and underestimated westerly wind changes.Crossref | GoogleScholarGoogle Scholar | 26842498PubMed |
Rashid HA (2020) Factors affecting ENSO predictability in a linear empirical model of tropical air-sea interactions. Scientific Reports 10, 3931
| Factors affecting ENSO predictability in a linear empirical model of tropical air-sea interactions.Crossref | GoogleScholarGoogle Scholar | 32127554PubMed |
Rashid HA (2021) Diverse responses of global‐mean surface temperature to external forcings and internal climate variability in observations and CMIP6 models. Geophysical Research Letters 48, e2021GL093194
| Diverse responses of global‐mean surface temperature to external forcings and internal climate variability in observations and CMIP6 models.Crossref | GoogleScholarGoogle Scholar |
Rayner NA, Parker DE, Horton EB, Folland CK, Alexander LV, Rowell DP, et al. (2003) Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. Journal of Geophysical Research – D. Atmospheres 108, 4407
| Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century.Crossref | GoogleScholarGoogle Scholar |
Roach LA, Dörr J, Holmes CR, Massonnet F, Blockley EW, Notz D, et al. (2020) Antarctic sea ice area in CMIP6. Geophysical Research Letters 47, e2019GL086729
| Antarctic sea ice area in CMIP6.Crossref | GoogleScholarGoogle Scholar |
Santoso A, Hendon H, Watkins A, Power S, Dommenget D, England MH, et al. (2019) Dynamics and predictability of El Niño–Southern Oscillation: an Australian perspective on progress and challenges. Bulletin of the American Meteorological Society 100, 403–420.
| Dynamics and predictability of El Niño–Southern Oscillation: an Australian perspective on progress and challenges.Crossref | GoogleScholarGoogle Scholar |
Schneider T, Bischoff T, Haug GH (2014) Migrations and dynamics of the intertropical convergence zone. Nature 513, 45–53.
| Migrations and dynamics of the intertropical convergence zone.Crossref | GoogleScholarGoogle Scholar | 25186899PubMed |
Spreen G, Kaleschke L, Heygster G (2008) Sea ice remote sensing using AMSR-E 89-GHz channels. Journal of Geophysical Research – C. Oceans 113, C02S03
| Sea ice remote sensing using AMSR-E 89-GHz channels.Crossref | GoogleScholarGoogle Scholar |
Sun S, Eisenman I (2021) Observed Antarctic sea ice expansion reproduced in a climate model after correcting biases in sea ice drift velocity. Nature Communications 12, 1060
| Observed Antarctic sea ice expansion reproduced in a climate model after correcting biases in sea ice drift velocity.Crossref | GoogleScholarGoogle Scholar | 33594079PubMed |
Swart NC, Cole JNS, Kharin VV, Lazare M, Scinocca JF, Gillett NP, et al. (2019) The Canadian Earth System Model version 5 (CanESM5.0.3). Geoscientific Model. Development 12, 4823–4873.
| The Canadian Earth System Model version 5 (CanESM5.0.3). Geoscientific Model.Crossref | GoogleScholarGoogle Scholar |
Taylor KE (2001) Summarizing multiple aspects of model performance in a single diagram. Journal of Geophysical Research – D. Atmospheres 106, 7183–7192.
| Summarizing multiple aspects of model performance in a single diagram.Crossref | GoogleScholarGoogle Scholar |
Taylor KE, Stouffer RJ, Meehl GA (2012) An overview of CMIP5 and the experiment design. Bulletin of the American Meteorological Society 93, 485–498.
| An overview of CMIP5 and the experiment design.Crossref | GoogleScholarGoogle Scholar |
Thompson DWJ, Kennedy JJ, Wallace JM, Jones PD (2008) A large discontinuity in the mid-twentieth century in observed global-mean surface temperature. Nature 453, 646–649.
| A large discontinuity in the mid-twentieth century in observed global-mean surface temperature.Crossref | GoogleScholarGoogle Scholar |
Tian B, Dong X (2020) The Double-ITCZ Bias in CMIP3, CMIP5, and CMIP6 models based on annual mean precipitation. Geophysical Research Letters 47, e2020GL087232
| The Double-ITCZ Bias in CMIP3, CMIP5, and CMIP6 models based on annual mean precipitation.Crossref | GoogleScholarGoogle Scholar |
Trenberth KE, Fasullo JT (2009) Global warming due to increasing absorbed solar radiation. Geophysical Research Letters 36, L07706
| Global warming due to increasing absorbed solar radiation.Crossref | GoogleScholarGoogle Scholar |
Turner J, Hosking JS, Bracegirdle TJ, Marshall GJ, Phillips T (2015) Recent changes in Antarctic sea ice. Philosophical Transactions of the Royal Society – A. Mathematical, Physical and Engineering Sciences 373, 20140163
| Recent changes in Antarctic sea ice.Crossref | GoogleScholarGoogle Scholar |
van Loon H, Jenne RL (1972) The zonal harmonic standing waves in the southern hemisphere. Journal of Geophysical Research 77, 992–1003.
| The zonal harmonic standing waves in the southern hemisphere.Crossref | GoogleScholarGoogle Scholar |
Vinnikov KY, Robock A, Stouffer RJ, Walsh JE, Parkinson CL, Cavalieri DJ, et al. (1999) Global warming and Northern Hemisphere sea ice extent. Science 286, 1934–1937.
| Global warming and Northern Hemisphere sea ice extent.Crossref | GoogleScholarGoogle Scholar | 10583952PubMed |
Voldoire A, Saint-Martin D, Sénési S, Decharme B, Alias A, Chevallier M, et al. (2019) Evaluation of CMIP6 DECK experiments with CNRM-CM6-1. Journal of Advances in Modeling Earth Systems 11, 2177–2213.
| Evaluation of CMIP6 DECK experiments with CNRM-CM6-1.Crossref | GoogleScholarGoogle Scholar |
Walters D, Baran AJ, Boutle I, Brooks M, Earnshaw P, Edwards J, et al. (2019) The Met Office Unified Model Global Atmosphere 7.0/7.1 and JULES Global Land 7.0 configurations. Geoscientific Model Development 12, 1909–1963.
| The Met Office Unified Model Global Atmosphere 7.0/7.1 and JULES Global Land 7.0 configurations.Crossref | GoogleScholarGoogle Scholar |
Wilcox LJ, Highwood EJ, Dunstone NJ (2013) The influence of anthropogenic aerosol on multi-decadal variations of historical global climate. Environmental Research Letters 8, 024033
| The influence of anthropogenic aerosol on multi-decadal variations of historical global climate.Crossref | GoogleScholarGoogle Scholar |
Yamazaki K, Sexton DMH, Rostron JW, McSweeney CF, Murphy JM, Harris GR (2021) A perturbed parameter ensemble of HadGEM3-GC3.05 coupled model projections: part 2: global performance and future changes. Climate Dynamics 56, 3437–3471.
| A perturbed parameter ensemble of HadGEM3-GC3.05 coupled model projections: part 2: global performance and future changes.Crossref | GoogleScholarGoogle Scholar |
Ziehn T, Chamberlain MA, Law RM, Lenton A, Bodman RW, Dix M, et al. (2020) The Australian Earth System Model: ACCESS-ESM1.5. Journal of Southern Hemisphere Earth Systems Science 70, 193–214.
| The Australian Earth System Model: ACCESS-ESM1.5.Crossref | GoogleScholarGoogle Scholar |