Circular Flip-Flop Index: quantifying revision stability of forecasts of direction
Deryn Griffiths A * , Nicholas Loveday A , Benjamin Price A , Michael Foley A and Alistair McKelvie A
A * , Nicholas Loveday A , Benjamin Price A , Michael Foley A and Alistair McKelvie A
A Bureau of Meteorology, GPO Box 1289, Melbourne, Vic. 3001, Australia.
Journal of Southern Hemisphere Earth Systems Science 71(3) 266-271 https://doi.org/10.1071/ES21010
Submitted: 13 May 2021 Accepted: 22 September 2021 Published: 9 December 2021
© 2021 The Author(s) (or their employer(s)). Published by CSIRO Publishing on behalf of BoM. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)
Abstract
The Flip-Flop Index, designed to quantify the extent to which a forecast changes from one issue time to the next, is extended to a Circular Flip-Flop Index for use with forecasts of wind direction, swell direction or similar. The index was devised so we could understand the degree of stability in wind direction forecasts. The Circular Flip Flop Index is independent of observations, has a relatively simple definition and does not penalise a sequence of forecasts that show a trend as long as the forecasts stay within a 180° sector. The Circular Flip-Flop Index is interpreted in terms of the impact of changing forecasts on decisions made by users of the forecast. The Circular Flip-Flop Index has been used to compare the stability of sequences of automated forecast guidance to the official Australian Bureau of Meteorology forecasts, which are prepared manually. It is the first objective assessment of the stability of forecasts of direction. The results show that the forecasts of wind direction from the automated forecast guidance, itself a consensus of many numerical weather models, are more stable than the official, manual forecasts. The Circular Flip-Flop Index does not measure skill but can play a complementary role in characterising and evaluating a forecasting system.
Keywords: flip-flop, forecast assessment, forecast convergence, forecast oscillations, forecast stability, forecast volatility, wind verification.
1 Introduction
The extent and frequency of changes as a forecast is revised, from one issue time to the next, is an aspect of a forecast system that interests forecasters and users. Too much stability may signify issues with the forecast process as may too little stability. This is discussed in Griffiths et al. (2019).
There have been several indices developed to measure forecast stability, each tailored to a specific use and almost all relating to a scalar quantity. For example, see Ruth et al. (2009), Zsoter et al. (2009), Ehret (2010), Griffiths et al. (2019). No-one has tackled a vector quantity, such as wind, or a circular quantity, such as wind direction, although Fowler et al. (2015) tackled the complex question of forecast revisions of tropical cyclone tracks.
We provide an analogous index to the Flip-Flop Index of Griffiths et al. (2019) to extend it to be suitable for a circular quantity, such as wind direction. We provide examples to illustrate the Circular Flip-Flop Index and interpret the index in terms of threshold-based decisions of users of the forecast.
The convention used is that wind direction is the direction from which the wind blows, and is measured clockwise from true north. A forecast wind direction of 360° refers to a wind blowing from north to south, referred to as a northerly wind. Similarly, a wind direction of 180° refers to a southerly wind, blowing from south to north.
2 The Circular Flip-Flop Index
Consider sequences of successive forecasts, or forecast revisions, labelled as f1, f2,…, fn. Each forecast fi is for the same quantity or event, including the same validity time, but is issued at a different time. The forecasts would usually be issued at regular intervals with each subscript representing a different lead time, the time between the forecast being issued and the validity time.
For example, the forecast f7 may be an initial forecast for the chance of rain, or maximum wind speed, on a particular day of interest, issued a week beforehand. A new forecast may be issued each day with f1 the forecast issued the day before the day of interest. In this case the subscripts represent the lead time in days.
For a scalar forecast, the Flip-Flop Index, as per Griffiths et al. (2019), is defined as

For forecasts of wind direction between 0° and 180°, for example, the Flip-Flop Index formula can be used. However, as the directions become more widely varying, possibly rotating around the whole dial, we cannot ignore the circular nature of the forecast parameter and we need to modify the definition.
Let f1, f2,…, fn be a revision sequence of forecasts in degrees. Define
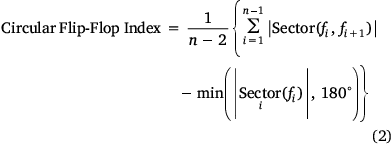
where  is the size of the smallest sector in degrees containing all directions fi, and |Sector (fi, fj)| is the size of the smallest sector in degrees containing the two directions fi and fj.
is the size of the smallest sector in degrees containing all directions fi, and |Sector (fi, fj)| is the size of the smallest sector in degrees containing the two directions fi and fj.
Table 1 shows some forecast sequences and their calculated Circular Flip-Flop Index. Synthetic Examples 1 and 2 are simple rotations of each other. That they have the same Circular Flip-Flop Index is an essential property of any index used to measure stability. As desired, the Circular Flip-Flop Index of Synthetic Example 1 equals the Flip-Flop Index of the same example when interpreted as a scalar forecast.

|
3 Practical interpretation with examples
The Flip-Flop Index can be interpreted in terms of a simple user decision model with a user making one decision when the forecast exceeds a user-defined threshold and changing that decision if a revised forecast is at or below the same threshold. For example, you may plan a picnic if the chance of rain is less than 40% but change your plan to a trip to the museum if the chance of rain is at least 40%. In this case, your user-defined threshold is 40%. When analysing forecast sequences of length 3, the Flip-Flop Index measures the range of thresholds for which users with those decision thresholds will change their mind twice based on the forecast. More generally, the Flip-Flop Index is a measure of the number of times a forecast threshold is crossed (beyond the first time), integrated over all forecast thresholds and normalised according to the length of the forecast revision sequence. For further details, see Griffiths et al. (2019).
We give a similar interpretation of the Circular Flip-Flop Index, interpreting the decision threshold in a way appropriate to directions.
A pilot, Barb, wants to take-off into the wind along a north–south runway. Her decision regarding which end of the runway to start at is informed by whether the wind has a southerly component or a northerly component. That is, her decision is based on directions being within the 180° arc from 90° through southerly to 270° or in the complementary 180° arc from 270° through northerly to 90°. We can think of her decision threshold being 90° and 270°, which are congruent mod 180°. If a forecast revision crosses either 90° or 270°, changing from having a northerly to a southerly component (or vice versa) she will revise her decision. This is illustrated in Fig. 1.

|
Consider the Synthetic Example 1 in Table 1 of forecasts of wind direction (f7, f6, f5, f4, f3, f2, f1 = 50°, 80°, 70°, 120°, 110°, 100°, 60°) all lying within a 70° sector. Applying this sequence of generally easterly wind forecasts to Barb’s decision, her decision threshold is 90°. For the forecasts of wind from 50°, 80° and 70°, Barb plans to take-off from the south. For the forecasts of 120°, 110° and 100°, she plans to take-off from the north. However, with a final forecast revision from 100° to 60°, she reverts to her initial plan. She has changed her plans twice, and experienced a single Flip-Flop.
Consider a nearby runway that is only approximately aligned north–south and has a decision threshold of 75° (or equivalently, 255°). For the same forecast sequence Synthetic Example 1 in Table 1, a pilot would have changed their plans four times.
A similar example might be someone wanting to picnic on the sheltered side of an east–west aligned (north–south facing) wall. Again, their decision will be based on whether the wind has a northerly component or a southerly component, and the decision threshold will be 90° (or equivalently, 270°).
The Synthetic Example 2 in Table 1 is a simple rotation of Synthetic Example 1. In this case it is people with a decision threshold between north and north-east that will change their plans at least once. For both Synthetic Examples 1 and 2, the thresholds that will experience at least one change in plans are those within a 70° sector, being from 50° to 120° (or equivalently, 230° to 300°) for Example 1, and being from 340° to 50° (or equivalently, 160° to 230°) for Example 2.
Note that the most extreme change for a directional forecast is 180°. Forecasts that change by 180° will cause all pilots or picnickers to change their plans regardless of the alignment of their runway or sheltering wall (ignoring the edge case of a runway or wall aligned due east–west).
As with the Flip-Flop Index, when used with a forecast sequence of length 3, the Circular Flip-Flop Index measures the range of thresholds for which users with those decision thresholds will change their mind twice based on the forecast.
In looking at the terms of the Flip-Flop Index (Eqn 1) and Circular Flip-Flop Index (Eqn 2), in Eqn 1 we have |fi − fi+1|, the difference between successive forecasts, which is replaced in Eqn 2 by |Sector(fi, fj)|, which is also the difference between successive forecasts. In both indices, summing the difference between successive forecasts gives a measure of the number of times a forecast threshold is crossed, integrated over all forecast thresholds. In Eqn 1 we subtract 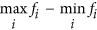 , the magnitude of the smallest interval containing all forecasts, which is replaced in Eqn 2 by the magnitude of the smallest sector containing all forecasts limited by 180°. In both cases, this second term is the range of thresholds crossed at least once by forecast revisions. So, as for the Flip-Flop Index, the Circular Flip-Flop Index can be described as a measure of the number of times a forecast threshold is crossed (beyond the first time), integrated over all forecast thresholds and normalised according to the length of the forecast revision sequence.
, the magnitude of the smallest interval containing all forecasts, which is replaced in Eqn 2 by the magnitude of the smallest sector containing all forecasts limited by 180°. In both cases, this second term is the range of thresholds crossed at least once by forecast revisions. So, as for the Flip-Flop Index, the Circular Flip-Flop Index can be described as a measure of the number of times a forecast threshold is crossed (beyond the first time), integrated over all forecast thresholds and normalised according to the length of the forecast revision sequence.
The maximum value of the Circular Flip-Flop Index is 180°. The maximum value of the Flip-Flop Index is the range of possible forecast values, which will be 100% for probability forecasts and will typically be less than 100°C for forecasts of temperature.
We now consider Synthetic Example 3 from Table 1 (f7, f6, f5, f4, f3, f2, f1 = 360°, 40°, 80°, 120°, 160°, 200°, 240°). The forecast revisions are all gradual and uniform, with each forecast 40° more clockwise than the previous. We note that a user with a decision threshold of 10° (equivalently 190°) changes their decision between f7 and f6 and again between f3 and f2. Indeed, all users with decision thresholds between 360° and 60° experience two changes of decision (a flip-flop). Users with decision thresholds between 60° and 180° change their decision once, but do not experience a flip-flop.
Checking the formula of the Circular Flip-Flop Index, we find the smallest sector containing all forecasts is 240°, so 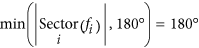 . That is, all users will change their decision at least once. The Circular Flip-Flop Index equals
. That is, all users will change their decision at least once. The Circular Flip-Flop Index equals

This contrasts to the Circular Flip-Flop Index calculated for any three consecutive forecasts in Example 3, which is

Finally, consider Synthetic Example 4 from Table 1 (f7, f6, f5, f4, f3, f2, f1 = 360°, 80°, 360°, 240°, 320°, 80°, 360°). Inspection shows that the forecast is much less stable than Example 3 and this is confirmed by the Circular Flip-Flop Index. The smallest sector containing all directions fi is 200°, so 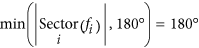 . The Circular Flip-Flop Index equals
. The Circular Flip-Flop Index equals

In Synthetic Example 4, users with decision thresholds between 0° and 60° (equivalently, between 180° and 240°) change their decision four times, experiencing three flip-flops. Users with the decision thresholds of 60° to 80° (equivalently, 240° to 260°) change their decision six times, experiencing five flip-flops. Users with the decision thresholds of 80° to 180° (equivalently, 260° to 360°) change their decision twice, experiencing a single flip-flop. Integrating the number of flip-flops experienced across the different thresholds we get 3 × 60° + 5 × 20° + 1 × 100° = 380° which is divided by n − 2 = 5 to get the Circular Flip-Flop Index.
The example of actual forecasts in Table 1 for Melbourne Airport on 27 December 2020 is typical of most wind forecasts, which display little flip-flopping, especially as the lead days get shorter. In this example, using real forecasts, the Circular Flip-Flop Index for lead days 7–5 is 13°, but for lead days 3–1 it is 0°. For the revision sequence of length seven, the Circular Flip-Flop Index is only 6.4°.
4 Application to forecasts of wind direction
In this section we give examples of using the Circular Flip-Flop Index to analyse and compare properties of some real forecasts of wind direction. We present data from forecasts of wind at forecast sites coinciding with automatic weather stations in Australia valid for each of the 24 hours of each day for 3 months. These were updated daily, giving for each forecast site and validity time a revision sequence (f7, f6, f5, f4, f3, f2, f1) where the subscripts represent the lead time in days, i.e. the number of days before the validity time of the forecast. We had Operational Consensus Forecasts (OCF) and Official forecasts. OCF are a bias corrected blend of Numerical Weather Prediction (NWP) outputs (Bureau of Meteorology 2014). The Official forecasts are as issued by the Bureau of Meteorology. They are often based on a blend of NWP, but the on-duty meteorologists make a judgement call as to which NWP to use and may manually enhance sea breezes, sharpen fronts or otherwise modify the NWP guidance.
When dealing with wind, the direction has no meaning if the forecast wind is calm. In our assessment of forecast stability, we excluded wind direction forecasts when the forecast wind speed was less than 0.05 m/s. If, for example, f4 was excluded due to a forecast wind speed of less than 0.05 m/s, or was missing for some other reason such as a technical fault, then we did not calculate the Circular Flip-Flop Index for any forecast revision sequences that included f4.
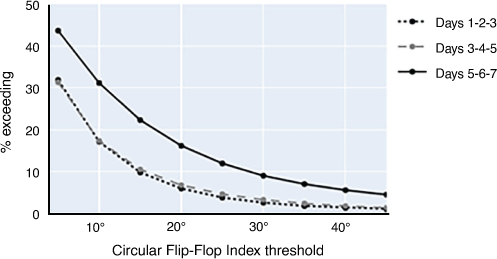
To present our results, we calculated the Circular Flip-Flop Index for all available forecast revision sequences (f7, f6, f5, f4, f3, f2, f1,), (f7, f6, f5), (f5, f4, f3) and (f3, f2, f1). For each of these we, summarised the results over 450 forecast locations and 2200 validity times. We plotted the frequency with which the Circular Flip-Flop Index exceeded values of 5, 10, 15, 20, etc. as shown in Figs 2, 3.
|

|
By plotting the Circular Flip-Flop Index of forecasts of wind direction and the Flip-Flop Index of forecasts of wind speed, we have been able to track changes in forecast stability from year to year and compare forecast stability of different forecast systems. We have been able to compare forecast stability in winter compared to summer and in the mid-latitudes compared to the tropics. We have been able to quantify the stability at shorter lead times compared to longer lead times. Some of these results are shown here.
Reading one value from the graph in Fig. 2 we see that for winter 2020 in southern Australia, the Circular Flip-Flop Index was at least 30° just 9% of the time when considering forecast revisions from lead days 7–5. Interestingly, the forecasts from lead days 5–3 were almost as stable as those for lead days 3–1, with the Circular Flip-Index being at least 30° only 3% of the time for each. Fig. 4 shows the forecast sites included in these results.
|
Fig. 3 shows that in northern Australia the short-term forecasts of wind direction are very stable, but flip-flop more in the summer (December–January–February) than in the winter (June–July–August). Fig. 4 shows the forecast sites included in these results. The difference does not represent varying skill. It is related to the relative stability of the climate in the two seasons.
In Fig. 5, the reference forecast for the Skill Score is sample climatology, calculated for each station and each hour of the day. The error function used to calculate the Skill Score is the Huber Loss function with a transition point from squared to linear penalties at 90° (Huber 1964). The choice of Huber loss, rather than squared error, was made due to not using quality controlled observations and wanting to limit the extent of the impact of large errors. A Skill Score of 1 represents a perfect forecast. The Circular Flip-Flop Index has been calculated for revision sequences of length 3, with the lead days indicated by the lower values labelling the horizontal axis.

|
Fig. 5 shows that the skill and stability of OCF and the Official forecasts in winter 2020 for southern Australia were very similar for lead days 3–7. However, at the shorter lead days, OCF had a slightly higher skill than the Official forecast and greater stability. The Circular Flip-Flop Index for the forecast revisions for lead days 3–1 only exceeded 30° 2.5% of the time for the Official forecasts but even less frequently (0.5% of the time) for the OCF.
5 Discussion and conclusion
The Circular Flip-Flop Index extends the Flip-Flop Index, providing a way to characterise the revision stability of forecasts of direction. This allowed us to make quantitative comparisons between different forecast systems, and for one system, to quantify differences between regions and seasons. It shares the desirable characteristic of the Flip-Flop Index of distinguishing between large and small flip-flops and being insensitive to small perturbations within the revision sequence. The Flip-Flop Index has not been extended to vector forecasts. That is, we have a way to examine the stability of forecasts of magnitude and direction separately, but not together.
Quantifying stability using the Circular Flip-Flop Index, combined with measures of forecast skill, has supported the Bureau of Meteorology in its choice to increasingly rely on consensus forecast guidance.
We recognise that both the Flip-Flop Index and the Circular Flip-Flop Index provide a very generic assessment of forecasts with very simplistic assumptions about users’ decision models. In practice many users will make a decision based on a combination of magnitude and direction, or may be interested in a specific directional sector less than 180°, and may want to create a Flip-Flop Index tailored to their specific decision structure.
Data availability
The data that support this study will be shared upon reasonable request to the corresponding author.
Conflicts of interest
The authors declare no conflicts of interest.
Declaration of funding
This research did not receive any specific funding.
Acknowledgements
Thanks to Robert Taggart, Tim Hume, Beth Ebert and Jenny Farlow for helpful feedback on an early draft of this paper.
References
Bureau of Meteorology (2014) Operations bulletin number 103: upgrades to the operational gridded OCF system. Available at http://www.bom.gov.au/australia/charts/bulletins/apob103.pdf [Accessed 4 February 2021]Ehret U (2010) Convergence index: a new performance measure for the temporal stability of operational rainfall forecasts. Meteorologische Zeitschrif 19, 441–451.
| Convergence index: a new performance measure for the temporal stability of operational rainfall forecasts.Crossref | GoogleScholarGoogle Scholar |
Fowler TL, Brown BG, Halley Gotway J, Kucera P (2015) Spare change: evaluating revised forecasts. Mausam 66, 635–644.
Griffiths D, Foley M, Ioannou I, Leeuwenburg T (2019) Flip-Flop index: quantifying revision stability for fixed-event forecasts. Meteorological Applications 26, 30–35.
| Flip-Flop index: quantifying revision stability for fixed-event forecasts.Crossref | GoogleScholarGoogle Scholar |
Huber PJ (1964) Robust estimation of a location parameter. The Annals of Mathematical Statistics 35, 73–101.
Ruth DP, Glahn B, Dagostaro V, Gilbert K (2009) The performance of MOS in the digital age. Weather and Forecasting 24, 504–519.
| The performance of MOS in the digital age.Crossref | GoogleScholarGoogle Scholar |
Zsoter E, Buizza R, Richardson D (2009) “Jumpiness” of the ECMWF and met office EPS control and Ensemble-Mean forecasts. Monthly Weather Review 137, 3823–3836.
| “Jumpiness” of the ECMWF and met office EPS control and Ensemble-Mean forecasts.Crossref | GoogleScholarGoogle Scholar |

