Influence of the Madden-Julian Oscillation on multiweek prediction of Australian rainfall extremes using the ACCESS-S1 prediction system
Andrew G. Marshall A C , Harry H. Hendon B and Debra Hudson B
A C , Harry H. Hendon B and Debra Hudson B
A Bureau of Meteorology, Hobart, Tas. 7000, Australia.
B Bureau of Meteorology, Docklands, Vic., Australia.
C Corresponding author. Email: andrew.marshall@bom.gov.au
Journal of Southern Hemisphere Earth Systems Science 71(2) 159-180 https://doi.org/10.1071/ES21001
Submitted: 15 January 2021 Accepted: 10 June 2021 Published: 16 July 2021
Journal compilation © BoM 2021 Open Access CC BY-NC-ND
Abstract
We assessed the ability of the Bureau of Meteorology’s ACCESS-S1 dynamical forecast system to simulate and predict high rainfall extremes for each season over Australia, especially focusing on the role of the Madden-Julian Oscillation (MJO). Using retrospective forecasts for the period 1990–2012, we show that ACCESS-S1 simulated the observed modulation of extreme weekly mean rainfall by each phase of the MJO reasonably well; however the simulated changes in probabilities tended to be weaker than those observed, especially across the far north during the austral summer season. The ability of the model to (i) simulate the observed modulation of extreme rainfall and (ii) predict the MJO to a lead time of four weeks, translated to enhanced forecast skill for predicting the occurrence of extreme weekly mean rainfall across much of Australia at times when the MJO was strong, compared to when the MJO was weak, during the austral spring and summer seasons in weeks 2 and 3. However, skill reduced across the central far north during the summer when the MJO was strong, suggesting the model is not good at depicting the MJO’s convective phases as it protrudes southward over northern Australia. During autumn and winter, there was little indication of changes in forecast skill, depending on the strength of the MJO. The results of this study will be useful for regional applications when the MJO is forecast to be strong during spring and summer, particularly where the swing in probability of extreme rainfall is large for specific phases of the MJO.
Keywords: Australia, Bureau of Meteorology, extreme rainfall, Madden-Julian Oscillation, modelling, forecasting, subseasonal prediction, ACCESS-S.
1 Introduction
The Madden-Julian Oscillation (MJO) has been observed to affect subseasonal variation of Australian rainfall both in the tropics and extratropics (e.g. Donald et al. 2006; Wheeler et al. 2009). The MJO affects Australian rainfall via two distinct mechanisms. In the tropical north during the extended summer wet season (roughly extending from October–April), rainfall varies in direct response to the MJO’s convective component, which is shifted into the Southern Hemisphere during these months (e.g. Wheeler et al. 2009; Marshall and Hendon 2019). Subseasonal rainfall (e.g. as embodied by weekly mean anomalies) increases during MJO phases 4–7 (phases defined by Wheeler and Hendon 2004), which corresponds to when the MJO’s convective centre traverses from west to east across the far north of Australia. Similarly, tropical rainfall is suppressed during MJO phases 8 and 1–3, when the suppressed convective phase of the MJO traverses from west to east across northern Australia.
The MJO also affects Australian extratropical rainfall as a result of teleconnections that act to remotely perturb the extratropical circulation (e.g. Matthews et al. 2004), thus affecting the occurrence and locations of rain-bearing weather systems (e.g. Wheeler et al. 2009). Importantly, these remotely driven rainfall variations are not confined to the austral summer season, so the MJO can influence Australian extratropical rainfall even when there is no direct influence of the MJO in tropical portions of Australia. This feature of the MJO means that it can be an important driver and source of predictability of tropical and extratropical Australian subseasonal weather and climate variability year-round.
Another important feature of the MJO’s impact on Australian rainfall is that it not only acts to shift the mean rainfall, it also acts to shift the likelihood of occurrence of extreme rainfall (e.g. Wheeler et al. 2009). Improved understanding of the causes and predictability of extreme rainfall, which we define in this study to be weekly mean accumulations above the 90th percentile (which we refer to as the upper decile), is important because of the potentially large impacts of extreme rainfall on, for instance, human health, agricultural production and infrastructure (e.g. roads and bridges). The focus of this study is thus on the MJO’s influence on Australian subseasonal rainfall extremes and their predictability.
We assessed the predictability of MJO-influenced rainfall extremes using the ACCESS-S1 coupled model seasonal forecast system, which is the Bureau of Meteorology’s operational system (Hudson et al. 2017). In this study, we will provide an assessment of the capability of ACCESS-S1 to predict weekly mean rainfall extremes, highlighting the role of the MJO. This assessment can help build confidence in the uptake of forecasts of extreme rainfall if the role of the MJO, which has been demonstrated to be well predicted to lead times of 3–4 weeks (e.g. Rashid et al. 2011; Marshall and Hendon 2019), can be identified. This assessment will also highlight areas where further model development and improvement may be required, for instance, to improve the depiction of the MJO’s teleconnections to extratropical Australia.
Descriptions of the ACCESS-S1 forecast system, analysis data and MJO index are provided in Section 2. In Section 3, we expand upon the assessment by Marshall and Hendon (2019) of the capability of ACCESS-S1 to predict the MJO using the now-complete set of ACCESS-S1 hindcasts for the period 1990–2012. The model’s depiction of the influence of the MJO on Australian rainfall extremes and the contribution of the MJO to the predictive skill of the extremes are presented in Sections 4 and 5 respectively, and we conclude with a summary of key results in Section 6.
2 Data sets and model description
We explored rainfall variations across Australia using the daily analyses from the Australian Water Availability Project (AWAP; Jones et al. 2009). The AWAP analyses are an optimum interpolation of available station observations on a 5-km horizontal grid. In this study, which focuses on subseasonal rainfall extremes, we defined an extreme occurrence when weekly mean rainfall anomalies exceed the 90th percentile, using 7-day running means calculated from the daily data at each grid point. We calculated the rainfall anomalies relative to climatology and defined the 90th percentile during each standard 3-month season using the 1990–2012 record, so to be compatible with the hindcast record available from the forecast model.
We monitored the MJO using the real-time multivariate MJO (RMM) indices from Wheeler and Hendon (2004). The two RMM indices, RMM1 and RMM2, provide a measure of the strength and phase of the MJO. The RMM indices are the principal components of the leading pair of eigenvectors derived from a combined empirical orthogonal function (EOF) analysis of equatorially averaged outgoing longwave radiation (OLR) and zonal wind at 200 and 850 hPa. Interannual variability was removed by subtracting the previous 120-day mean prior to computing the daily RMM indices. This leading pair of EOFs described the eastward propagation of the combined convection/zonal wind disturbance that characterises the MJO. They were derived from data that are not subject to any band pass filtering and so could be used to assess both real-time evolution of the MJO and its prediction with forecast data. A positive RMM1 corresponds to enhanced convection centred around the maritime continent, whereas a positive RMM2 represents a convection dipole with an enhanced centre over the west Pacific and suppressed centre over the central Indian Ocean. RMM1 and RMM2 may equivalently be expressed as a daily amplitude 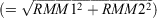 and phase (=tan−1(RMM2/RMM1)), which is useful for the construction of MJO composites. We used the same eight phases as defined by Wheeler and Hendon (2004), with the MJO deemed to be strong/active when the RMM index amplitude was greater than one and weak/inactive when the RMM index amplitude was less than one.
and phase (=tan−1(RMM2/RMM1)), which is useful for the construction of MJO composites. We used the same eight phases as defined by Wheeler and Hendon (2004), with the MJO deemed to be strong/active when the RMM index amplitude was greater than one and weak/inactive when the RMM index amplitude was less than one.
We assessed predictability of rainfall extremes and the role of the MJO using the Australian Community Climate and Earth System Simulator-Seasonal forecast system version 1 (ACCESS-S1), which is the Bureau of Meteorology’s current operational coupled model subseasonal to seasonal prediction system (Hudson et al. 2017). The ACCESS-S1 prediction system is based on the UK Met Office Global Coupled 2.0 model Global Seasonal Forecast System version 5 (MacLachlan et al. 2015). ACCESS-S1 became the operational subseasonal to seasonal prediction system at the Bureau of Meteorology in August 2018, replacing the low resolution-low top model Predictive Ocean Atmosphere Model for Australia (Alves et al. 2003; Marshall et al. 2011; Hudson et al. 2011, 2013). The ACCESS-S1 system has high horizontal resolution (25 km in the ocean and ~60 km in the atmosphere), and its 85 vertical levels in the atmosphere mean that the stratosphere is well resolved to above 1 hPa. Hindcast and real-time initial conditions for sea-ice and the ocean were provided from the assimilation produced at the UK Met Office (e.g. Mogensen et al. 2009, 2012; Maclachlan et al. 2015). The atmospheric initial conditions for the hindcasts were provided by interpolating the European Centre for Medium-Range Weather Forecasts-Interim reanalysis (ERA-I; Dee et al. 2011) of zonal wind (u), meridional wind (v), temperature, humidity and surface pressure onto the ACCESS-S1 atmospheric model grid. In real-time, the atmospheric initial conditions were provided by the Bureau of Meteorology Numerical Weather Prediction system. Soil moisture was initialised with climatology (MacLachlan et al. 2015) and soil temperatures were interpolated from ERA-I data.
The ACCESS-S1 subseasonal hindcasts consist of an 11-member ensemble that extends to 60-day lead time. Ensemble initial conditions were produced by perturbing the atmospheric initial condition (Hudson et al. 2017). In this study, we analysed 11-member ensemble hindcasts initialised on 1st, 9th, 17th and 25th of each month during 1990–2012. For assessing prediction of the MJO, we created predicted RMM indices following the procedure of Rashid et al. (2011). That is, we projected the model’s predicted anomalies, formed by removing the lead time and start time dependent seasonal cycle, of equatorially averaged OLR and zonal winds at 200 and 850 hPa onto the observed pair of eigenvectors derived by Wheeler and Hendon (2004) in order to obtain the predicted RMM1 and RMM2 indices. Prior to projecting the predicted anomalies onto the observed EOF pair, we removed interannual variability by subtracting a 120-day mean that is created for a lead time of τ days as the mean of the previous 120-τ days of observations up to the start of the forecast plus the τ days of the forecast.
We assessed forecast skill for predicting extreme rainfall using the Symmetric Extremal Dependence Index (SEDI), a skill score gaining popularity in its use for verifying extreme events, for which the number of occurrences is small by definition (e.g. North et al. 2013; Marshall et al. 2014; White et al. 2014; Haiden and Duffy 2016; Singh et al. 2017). The SEDI is recognised for its ability to provide meaningful results where many other standard verification scores become degenerate when dealing with rare events and small sample sizes (Ferro and Stephenson 2011; Hogan and Mason 2012). Proposed by Ferro and Stephenson (2011), the SEDI score is based on a 2×2 contingency table and is computed from the hit rate (H) and the false alarm rate (F) at each grid location, using the equation:
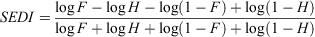
A forecast is deemed to be a ‘hit’ if it and the corresponding observation both exceed a particular threshold (the 90th percentile in our study); and a ‘false alarm’ if the forecast exceeds the threshold but the observed does not. SEDI scores greater (less) than zero indicate skill better (worse) than for random forecasts.
To calculate SEDI scores, we assumed that the forecasts starting 8 days apart in each month (1st, 9th, 17th and 25th) were independent events. This is reasonable given that we verified subseasonal forecasts using weekly averaged periods, and we included data from both weeks 2 and 3 of the forecast (when the MJO was well predicted) in constructing the contingency table. We constructed the 2×2 contingency table based on each individual ensemble member’s forecast exceeding the threshold, whereby the ensemble members were pooled and each added to the counts in the contingency table before the SEDI score was calculated (Marshall et al. 2014). The confidence interval of the SEDI as estimated using the formula for the standard error (SSEDI; Ferro and Stephenson 2011), which was computed at each grid location from the hit rate, false alarm rate, sample size n and base rate p (the relative frequency with which an extreme heat event is observed to occur):
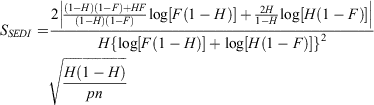
We computed the 95% confidence intervals at each grid point as SEDI ± 2 × SSEDI (where SSEDI estimates the standard deviation) and we considered SEDI scores to represent useful forecast skill (i.e. better than a random forecast) when confidence intervals comprised positive values only.
3 MJO prediction skill
We began by assessing the capability of the ACCESS-S1 system to predict the MJO by verifying the prediction of the RMM indices. A preliminary assessment of MJO forecast skill with ACCESS-S1 was provided in Marshall and Hendon (2019), who used a small subset of the hindcasts that were available at that time. We expanded upon their analysis here using the complete hindcast set (4 start times per month with 11 members for 1990–2012). We group start times together for the standard 3-month seasons and also show some results using all start months.
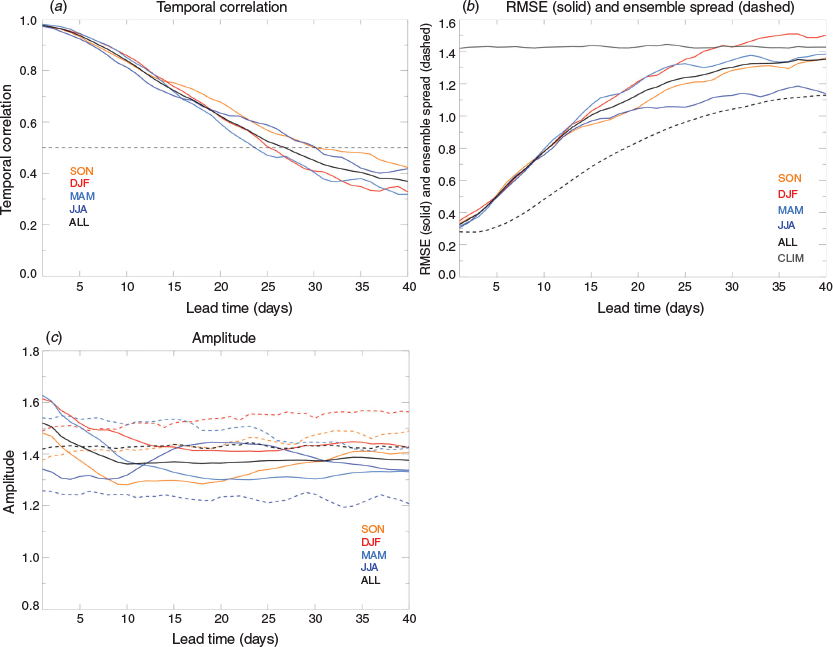
Fig. 1 shows the skill in predicting the daily ensemble mean RMM indices using bivariate correlation (COR) and bivariate root mean square error (RMSE) as defined in Lin et al. (2008):
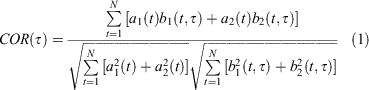
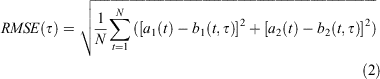
Here, a1(t) and a2(t) are the verification RMM1 and RMM2 indices at time t as provided by Wheeler and Hendon (2004), and b1(t, τ) and b2(t, τ) are the respective ensemble mean forecasts at time t for a lead time of τ days. N is the number of forecasts during each season, or for all times. We calculated COR and RMSE using all hindcasts over the period 1990–2012 for lead times out to 40 days. We also compared to the skill of a climatological forecast, which was obtained by setting to zero the forecast anomalies (b1 = 0 and b2 = 0) in the bivariate RMSE (Eqn. 2). The RMSE for the climatological forecast approximately asymptotes to √2 because the standard deviation of each of the observed RMM indices over all days is one (we denote this as ‘CLIM’ with a grey solid curve in Fig. 1). Forecasts are more skilful than a climatological forecast when the bivariate RMSE <RMSEclim ~√2, which roughly equates to when the bivariate COR> 0.5 (e.g. Murphy and Epstein 1989). Note the RMSE for the climatological forecast is equivalent to the observed bivariate amplitude. We diagnosed the model’s bivariate amplitude by setting to zero the observed anomalies (a1 = 0 and a2 = 0) in (Eqn. 2). We diagnose the bivariate spread of the forecast by substituting the ensemble mean RMM indices for the verification (the ‘a’s) in (Eqn. 2).
The COR shown in Fig. 1a drops below 0.5 at about 25–30 days (longest in spring and shortest in autumn), which agrees well with the earlier assessment of MJO prediction with ACCES-S1 by Marshall and Hendon (2019). The lead time to cross 0.5 correlation (25–30 days) places ACCESS-S1 in the upper tier of models for predicting the MJO (e.g. compare to Lim et al. 2018). A further pleasing result for ACCESS-S1 is that skill for predicting the MJO during boreal summer is now much higher than in its predecessor, POAMA (e.g. compare to results in Rashid et al. 2011 and see Hudson et al. 2017).
Examination of the ensemble spread (black dashed curve in Fig. 1b) indicates that although the ensemble is initially well dispersed (i.e. the spread matches the RMSE at day 1), the spread grows more slowly than the error, especially in the first 5 days of the forecast. This implies that although the initial perturbations are of appropriate size relative to the forecast error, they are not optimally growing. Presumably this stems from ‘spin-up’ of the perturbations in ACCESS-S1, whereby we only added perturbations to dynamical fields (as described in Hudson et al. 2017), with the initial diabatic tendencies (in particular latent heat releases due to deep convection) being zero.
Examination of the bivariate amplitude of the model’s RMM indices (Fig. 1c), here based on individual members and not the ensemble mean, shows that although the model has realistic MJO amplitude at the start of the forecast, for most seasons the MJO then weakens with lead time, resulting in an equilibrated MJO amplitude after about 10-day lead time that is ~10–20% weaker-than-observed. The only exception to this is for forecast start times during boreal summer (June, July, August; JJA), when the equilibrated model amplitude is stronger than observed. We have no further insight as to why this is the case, but the weaker amplitude for the other seasons reflects systematic bias in the eastward extent of the MJO into the western Pacific (Marshall and Hendon 2019).
In summary, the ACCESS-S1 prediction system made skilful forecasts of the MJO well into the week 4 of the forecast. In the following sections, we assess the impact of the MJO on forecasts of extreme rainfall in Australia during weeks 2 and 3 of the forecast when the skill for the MJO is high.
4 Impact of the MJO on extreme rainfall
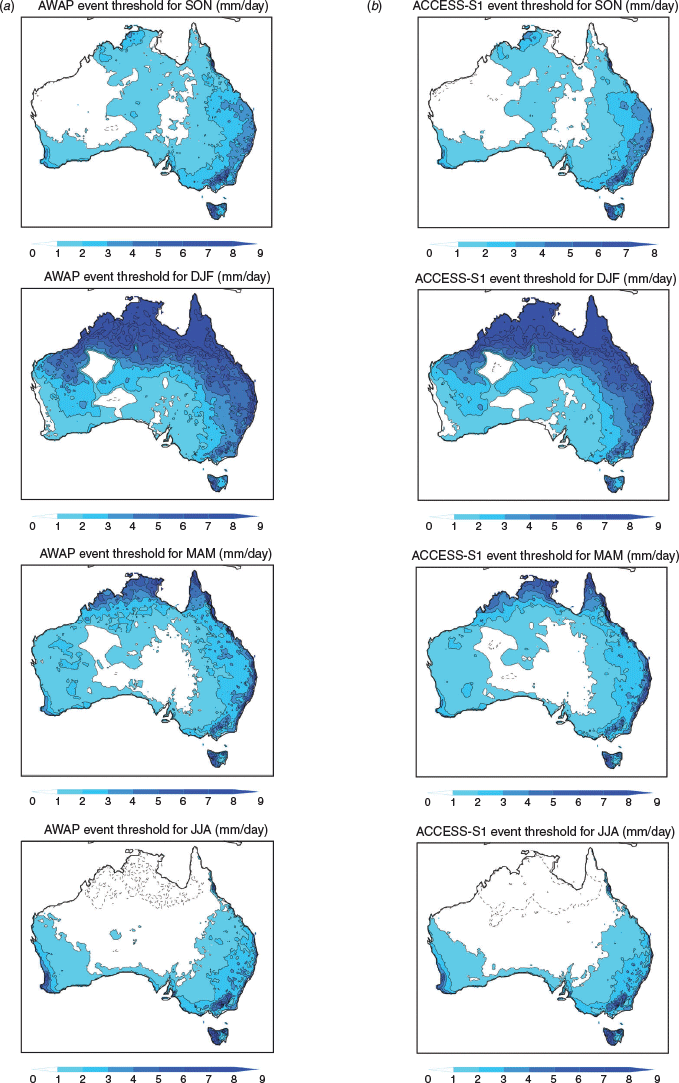
Prior to assessing forecast skill for predicting extreme rainfall and the possible contribution of the MJO, we first diagnosed how the MJO modulates weekly mean extreme rainfall from observations, as simulated in weeks 2 and 3 from the ACCESS-S1 predictions. We began by forming the 90th percentile thresholds for weekly mean rainfall anomalies for the 4 standard seasons (Fig. 2). We did this from the observed AWAP analyses (Fig. 2a) and using data from weeks 2 and 3 from the hindcasts (Fig. 2b). Note that we used predicted rainfall that was calibrated to the daily AWAP analyses using a quantile-quantile matching method applied to daily data and downscaled from 60 to 5 km horizontal resolution (Bureau of Meteorology, 2019; de Burgh-Day et al. 2020). The calibration was done using leave-one-out cross validation (leaving out the year to be calibrated) to increase the robustness of the calibration (so the same data was never used simultaneously for training and calibrating the predictions). All members at each lead time and start time were used to define the quantiles of the predicted data and the calibration was performed in an 11-day window to increase the observed sample size for consistency with the model’s climatology. That is, for a given start date in the hindcast, the climatological mean value for each grid box and each lead day was computed from 11×23 values (11 ensemble members and 23 years). This small sample size resulted in a climatological mean for daily values that was often too noisy. The daily mean climatologies were therefore smoothed with an 11-day window to mitigate this effect, and the calibration was applied to the daily data in an 11-day window for consistency. Further details are provided in Bureau of Meteorology (2019) and de Burgh-Day et al. (2020). The calibration method improved the prediction of the rainfall distribution over large parts of the country at lead times of 2–3 weeks for most start months (not shown).
Fig. 2 shows that the threshold for the 90th percentile of weekly mean rainfall is highest during summer months in the northern portions of the country, reflecting the high rainfall there during the summer monsoon. During winter (JJA), high values lie across the southwest and southeast of the continent, with orographic enhancement apparent along the Great Dividing Range in eastern Victoria and southern New South Wales, and for western Tasmania. Enhanced thresholds are also apparent along the eastern coastal strip, especially during autumn. Comparing the threshold from the model output with the observed indicated remarkably good agreement both in spatial distribution and magnitude. This agreement is not surprising because we used calibrated data. The spatial detail may also partly reflect the high model resolution (e.g. capturing the Great Diving Range, the escarpment to the east of Perth, the coastal enhancement on the central east coast and the west–east contrast across Tasmania) and a good depiction of the relevant dynamics and circulation.
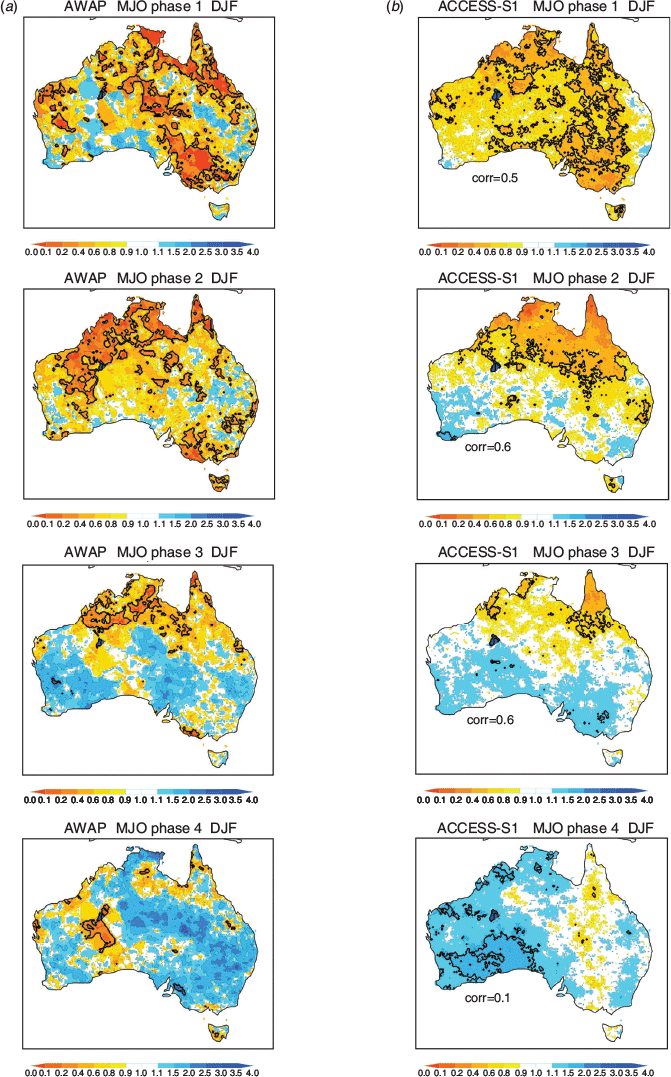
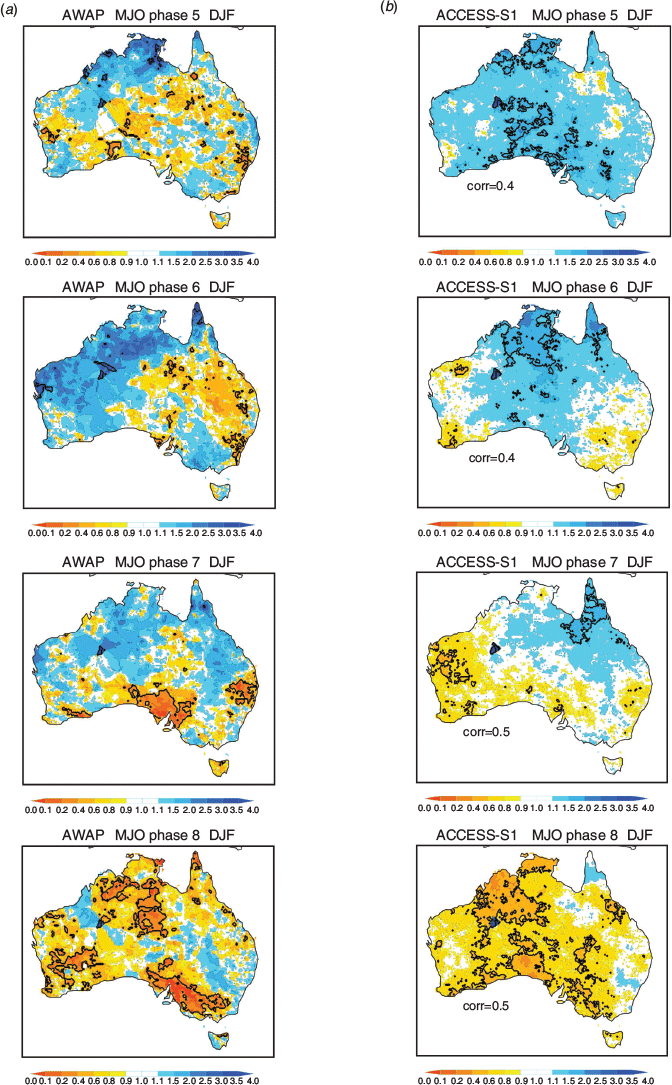
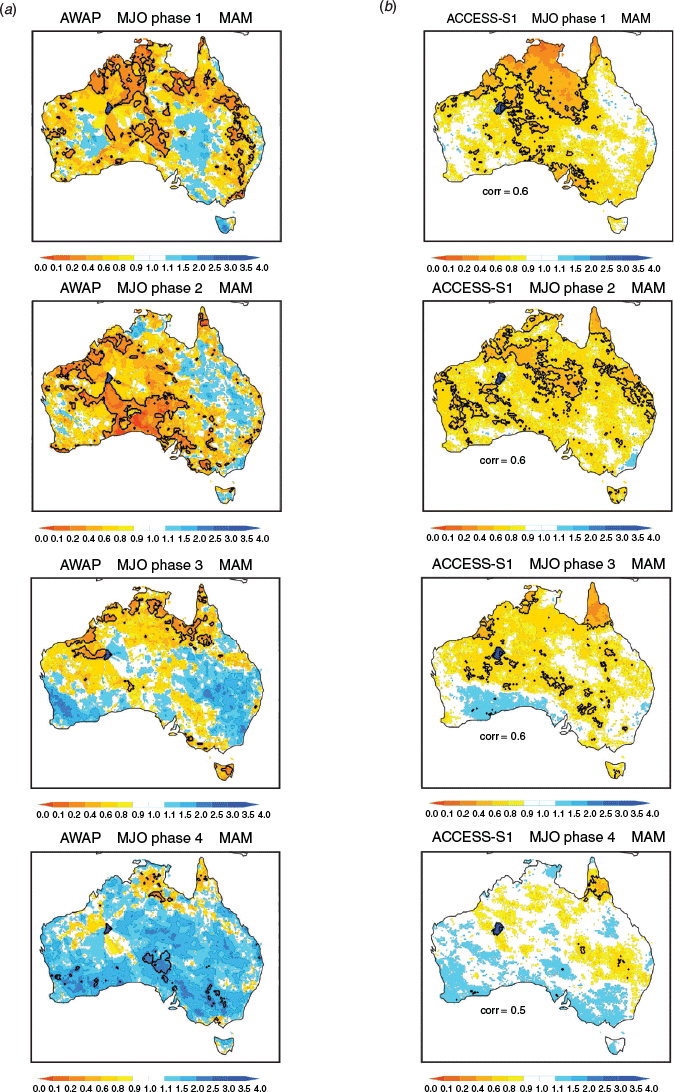
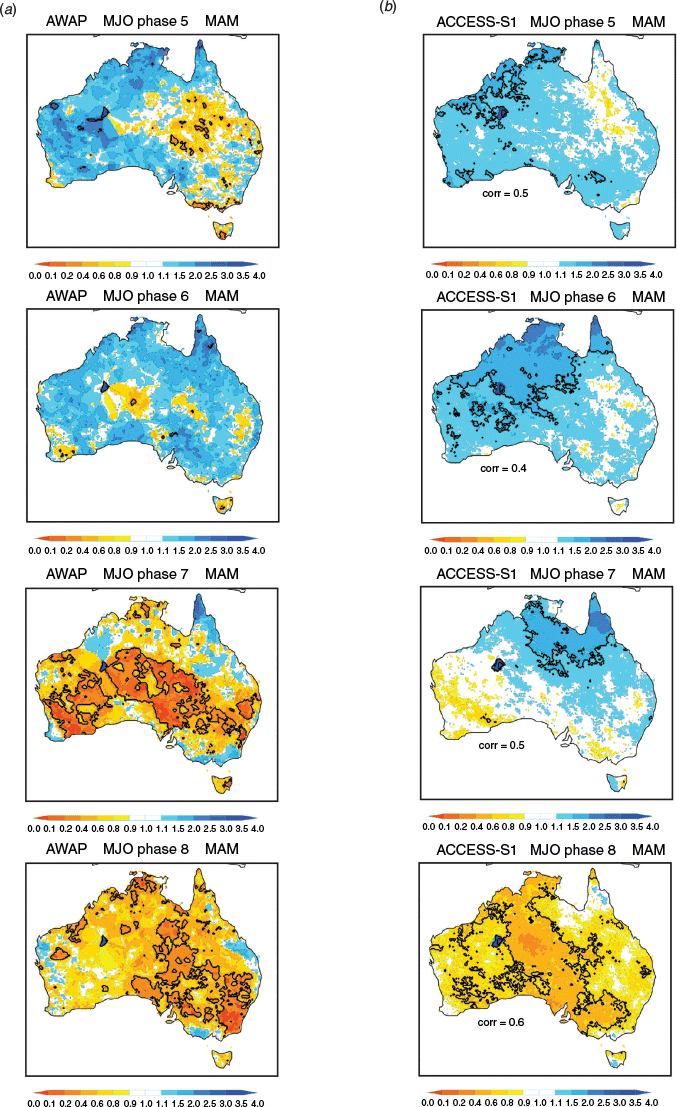
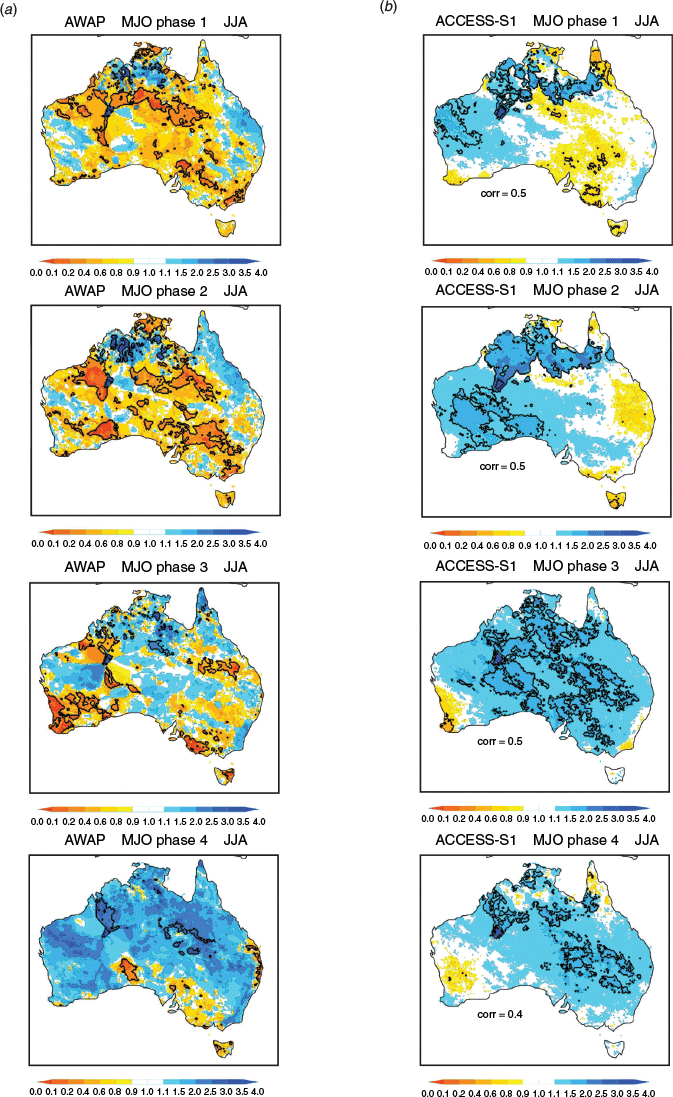
We now turn to assessing the impact of the MJO on the occurrence of extreme rainfall and how well depicted this is in the forecast model (Figs 3–10). Based on exceedance of the 90th percentile thresholds displayed in Fig. 2, we created the composite probability of occurrence of extreme rainfall for each of the eight phases of the MJO when the MJO amplitude is greater than one. Probability composites were computed by counting the number of instances at each grid location for which the weekly mean rainfall value was greater than the event threshold value as displayed in Fig. 2, and then divided by the total number of samples in the composite. We displayed probability composites as ratios relative to the mean decile probability of occurrence (nominally 0.1), so that probabilities greater than one indicate an increased likelihood of an upper decile event, and probabilities less than one indicate a decreased likelihood. Significance was assessed using a z-score test for event probabilities (Spiegel 1961).
For the z-score test, we assumed that the weekly mean data in our composites were comprised of independent samples, of size N, for each MJO phase (e.g. following Marshall et al. 2014, based on an average 6-day progression through each MJO phase). We accounted approximately for the non-independence of ACCESS-S1 ensemble forecast members at lead times of 2–3 weeks by computing the effective sample size, 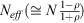 , using the autocorrelation ρ of rainfall at each grid box. The autocorrelation coefficient was calculated by correlating (as a function of hindcast start) each ensemble member with the ensemble mean of the remaining 10 ensemble members at each grid box. The correlation coefficients were then averaged over the 11 realisations, from which we calculated Neff.
, using the autocorrelation ρ of rainfall at each grid box. The autocorrelation coefficient was calculated by correlating (as a function of hindcast start) each ensemble member with the ensemble mean of the remaining 10 ensemble members at each grid box. The correlation coefficients were then averaged over the 11 realisations, from which we calculated Neff.
The probability of occurrence of the weekly mean rainfall exceeding the 90th percentile for each MJO phase was assumed to be significanctly different than the climatological rate when the absolute value of z was greater than 1.96 (two tailed distribution). Note that blue in the maps indicates an increase in the frequency of upper decile weekly rainfall events and red indicates a decrease.
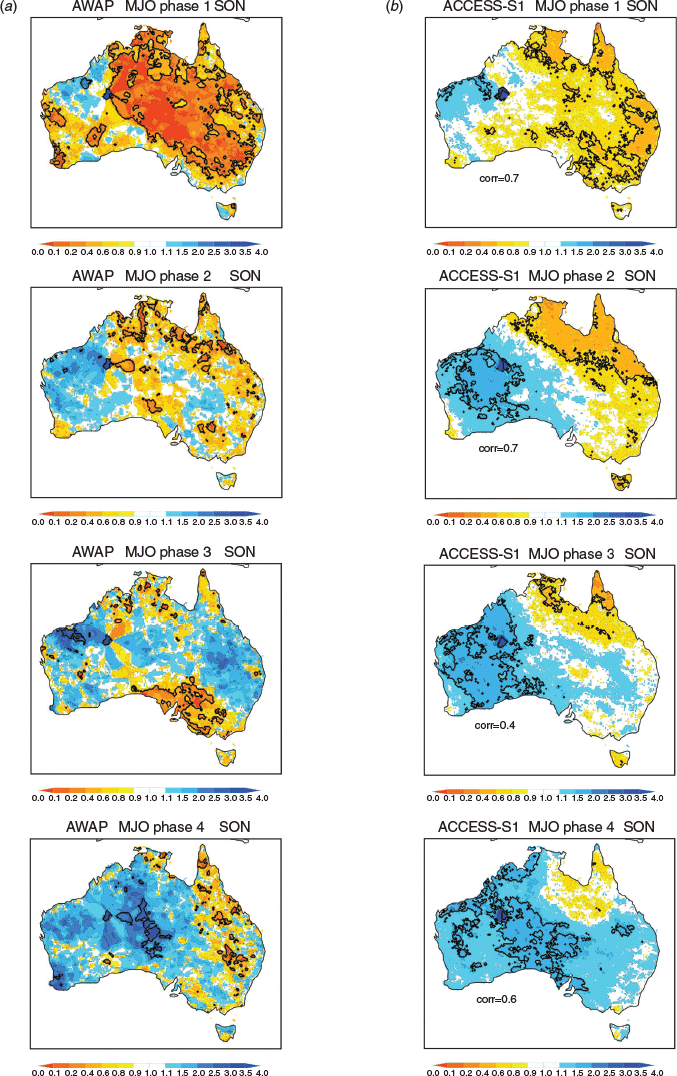
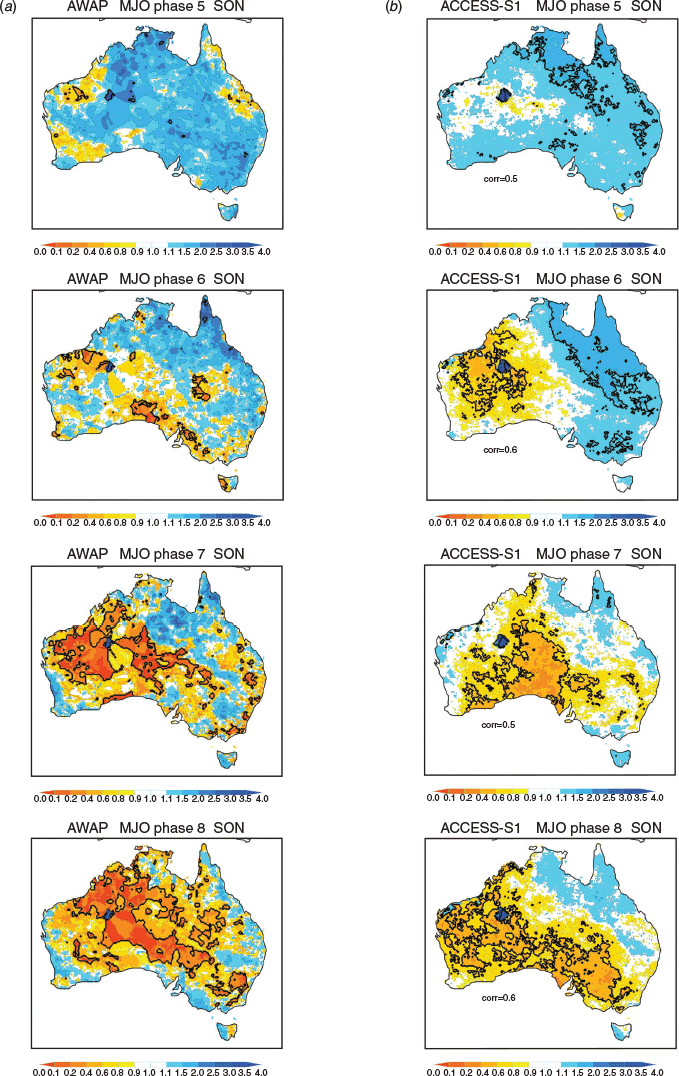
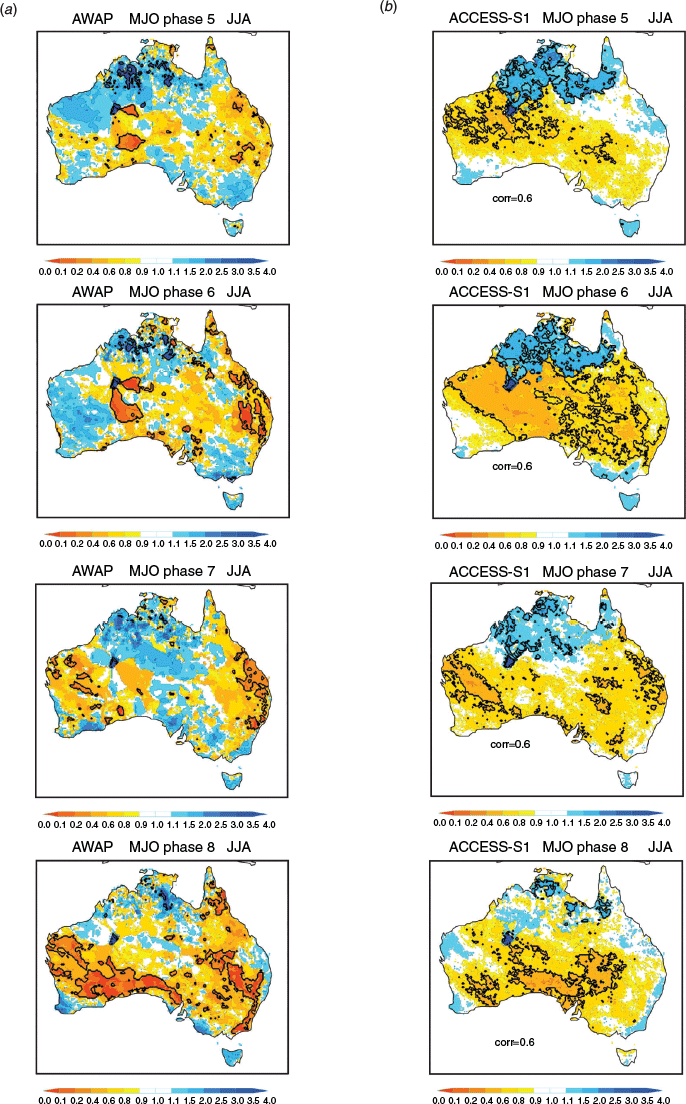
The observed increase in frequency of upper decile weekly rainfall maximises across the north during summer in phases 4–5–6 and is most substantially reduced during phases 8–1–2, corresponding to the occurrence of the active and suppressed convective phases of the MJO over northern Australia. This result is consistent with the observed patterns shown in figure 16 of Wheeler and Hendon (2004) using upper quintile weekly rainfall for the period 1974–1999. However, in all seasons the frequency of upper decile weekly rainfall was also observed to change in various MJO phases throughout Australia, reflecting the importance of the remote impacts of the MJO (e.g. Wheeler et al. 2009). Comparing to the model behaviour, ACCESS-S1 depicts the MJO relationship in all phases and seasons reasonably well, with pattern correlation coefficients ranging 0.4–0.7, except for MJO phase 4 in December, January, February (DJF) when the correlation drops to 0.1 (we discuss some of the possible reasons for this below).
The model’s extreme rainfall event probabilities tend to be slightly weaker than those in AWAP, consistent with the model’s weaker-than-observed representation of MJO rainfall anomalies in ACCESS-S1 (see also Marshall and Hendon 2019). For certain MJO phases, the model also failed to adequately capture the observed strong connections to extreme rainfall, particularly when observed probabilities of wet conditions were low. These include (i) over southeastern Australia in MJO phase 3 during September, October, November (SON, Fig. 3), when anomalous high pressure over southeastern Australia drove a dry signal due to large-scale subsidence (Wheeler et al. 2009), (ii) over eastern Australia in phase 6 during DJF) Fig. 6), (iii) over much of Australia in phase 7 during March, April, May (MAM, Fig. 8), and (iv) over most of the mainland in phase 2 during JJA (Fig. 9), again in association with anomalous high pressure over southern Australia (Wheeler et al. 2009). These examples highlight where the MJO rainfall in ACCESS-S1 was overdone, presumably due to an underrepresentation of the Australian mean sea level pressure/circulation response to the MJO at those times (e.g. Wang and Hendon 2019).
5 Impact of the MJO on prediction of extreme rainfall
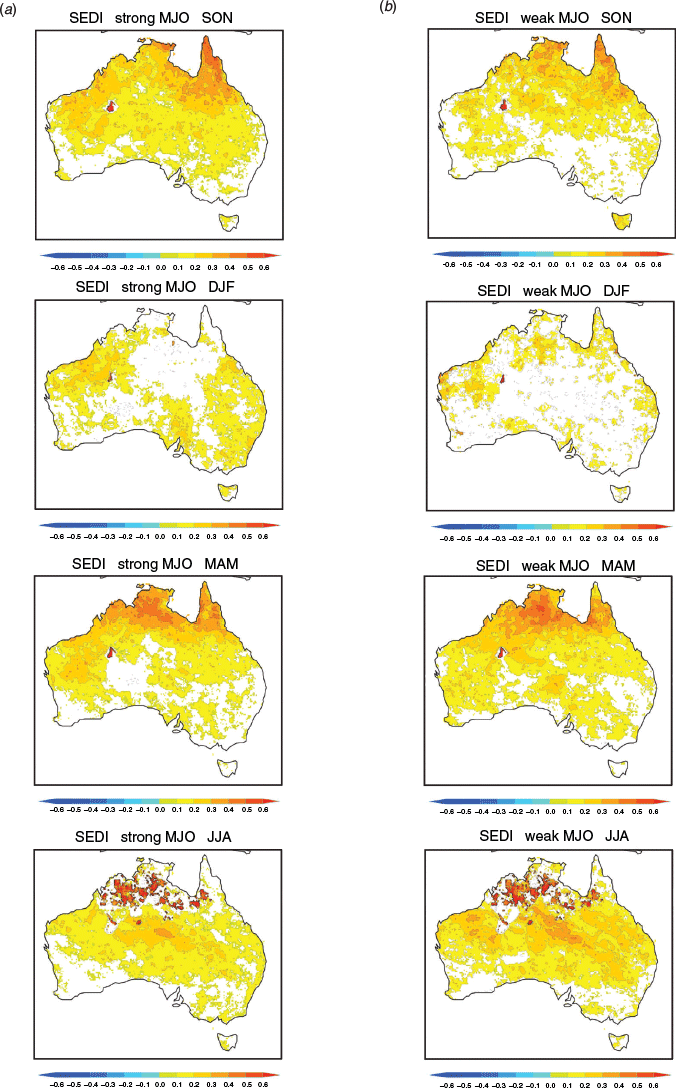
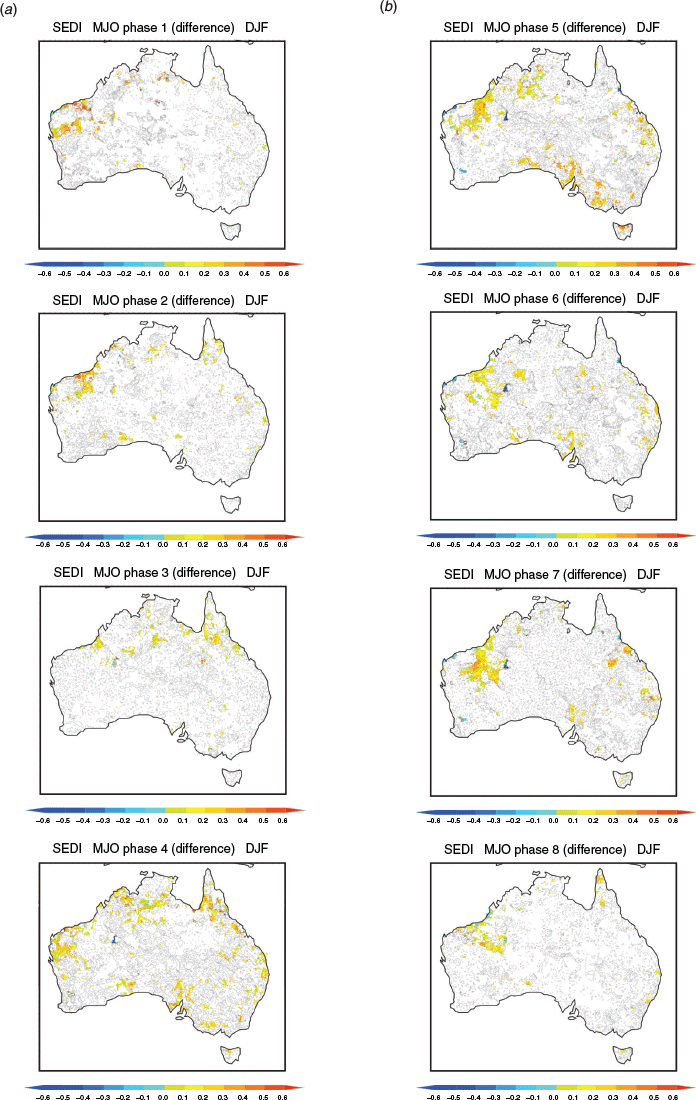
We assessed the overall impact of the MJO on prediction of extreme rainfall by computing the SEDI for all cases when the MJO was predicted to be strong in weeks 2 and 3, and compared this to the SEDI for all cases when the MJO was predicted to be weak. We did this for start times during the four standard seasons (Fig. 11). During SON, the SEDI is positive when the MJO is both strong and weak (i.e. most of the country is covered in orange-yellow positive shades), with highest skill occurring in the far north east. Pleasingly, higher SEDI values extend to the southwest and southeast when the MJO is strong. Similarly, a more positive SEDI occurs in the northwest and central and southeast during DJF when the MJO is strong. Unfortunately, across the far central north, where the MJO’s impact is the strongest during DJF, the SEDI is lower and does not indicate useful skill when the MJO is strong. Presumably, this reflects the inability of the model to properly capture the local convective phase of the MJO over tropical areas, possibly due to misrepresentation of the diurnal cycle of land-based rainfall (e.g. Walters et al. 2017).
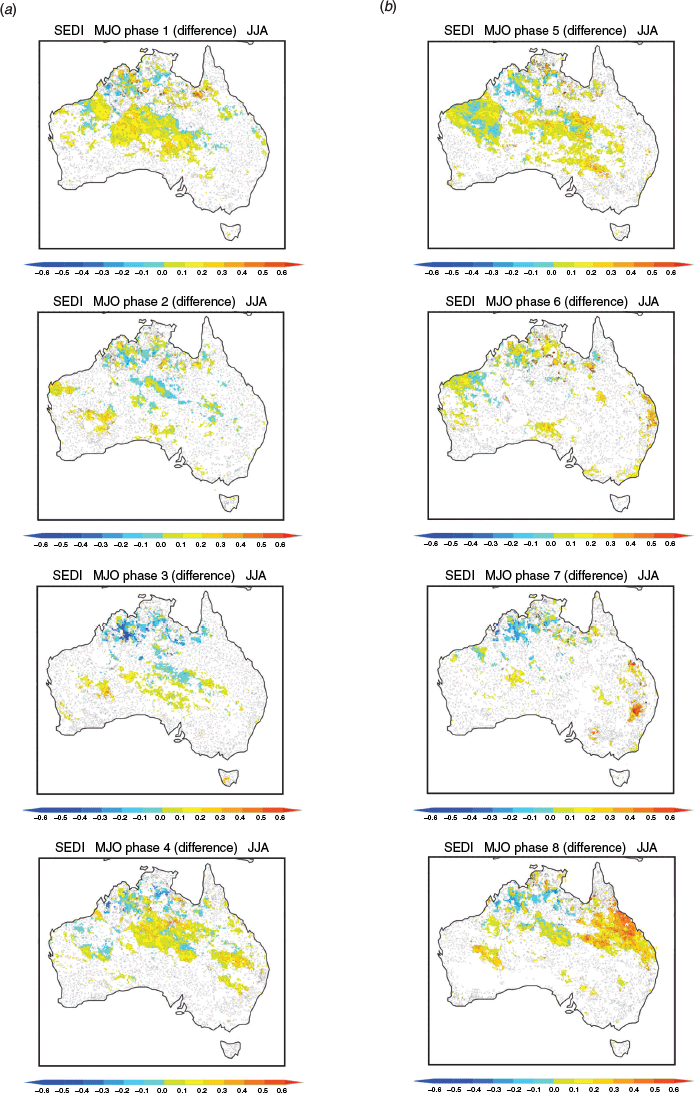
During MAM and JJA, there is little difference in SEDI when the MJO is strong versus weak, with the highest skill in the far north during autumn and across the central portion of the continent in winter occurring for both strong and weak MJO activity. Although the MJO is observed to cause extreme rainfall variability in these regions, the model is apparently unable to convert this into improved predictive skill when the MJO is prominent.
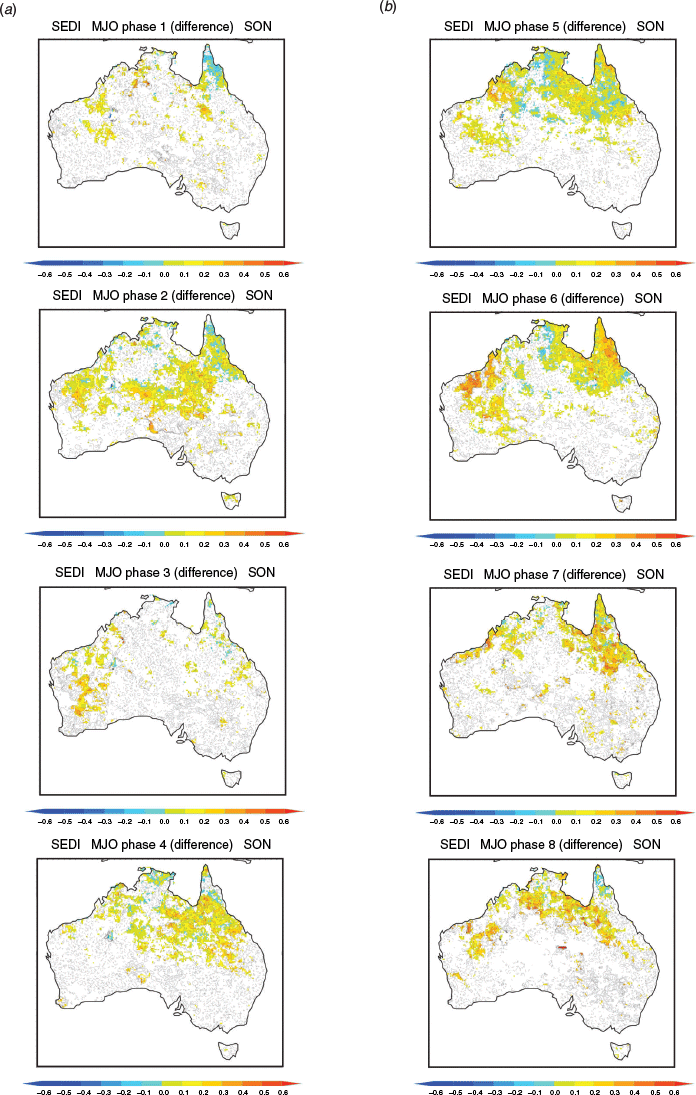
For more insight into how and when the MJO modulates predictive skill, we computed the difference in SEDI for each phase of the MJO when it is strong and weak (Figs 12–15). In SON, the improvements in skill when the MJO is strong occur in most MJO phases (Fig. 12), most notably during phases 5–7 over northern parts of the Northern Territory and Queensland where the odds of extreme rain are elevated when the MJO is strong in these phases (Fig. 4). During DJF (Fig. 13), some improvement in skill for predicting upper decile rain due to the MJO is seen in the northwest Australian Kimberley region, especially during MJO phases 5–6–7 when the MJO acts to increases the chances and during phases 8–1–2 when the MJO acts to decreases the chances (Fig. 5). Otherwise, no clear role for the MJO in improving the prediction of high rainfall extremes is observed during DJF.
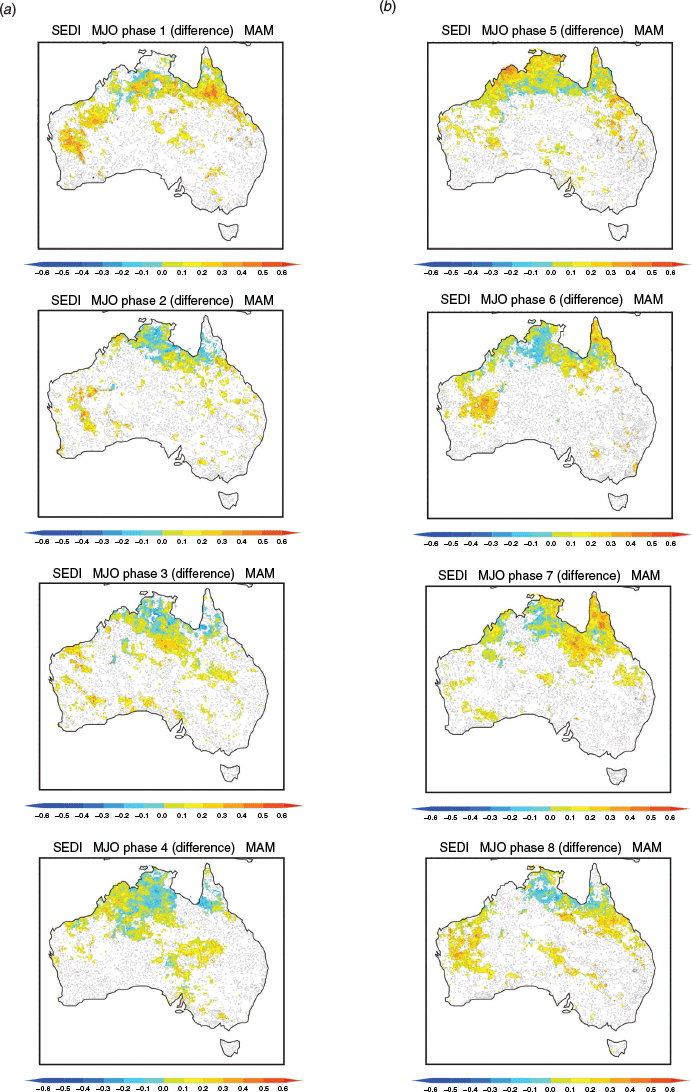
In MAM and JJA, when there is little impact of the MJO on predictive skill (Fig. 11), the variation of skill difference with MJO phase is patchy (Figs 14 and 15). During MAM, improvements in skill are apparent in MJO phase 5 for the Kimberley and Top End, phase 6 for Western Australia’s mid-west, and phase 7 for northern Queensland (Fig. 14), where the chances of high rainfall extremes are elevated (Fig. 8). MJO phase 1 also shows large improvements in skill over parts of western and northern Australia (Fig. 14) where the chances of high rainfall extremes are mostly low (Fig. 7). But, in all phases of the MJO, except phases 1 and 5, skill for predicting upper decile autumn rain over the Top End is lower than when the MJO is weak. This highlights a window of forecast opportunity in phase 5 for the Top End when enhanced tropical rainfall is likely in conjunction with anomalous westerly winds at 850 hPa (Wheeler et al. 2009). The largest improvements in skill for JJA occur over the Australian subtropics between 20°S and 30°S during MJO phases 1, 4, 5 and 8 (Fig. 15) when the convective phases (4 and 5) and suppressed phases (8 and 1) of the MJO occur directly to the north of Australia. These regions coincide with where the observed chances of high rainfall anomalies and extremes are largely enhanced (phases 4 and 5) and reduced (phases 1 and 8) (see also Wheeler et al. 2009).
6 Conclusions
The MJO acts to modulate the occurrence of extreme weekly mean rainfall (i.e. in the upper decile) throughout Australia. During summer, the modulation was prominently in the tropical northern portions of the continent, where the chances of extreme rainfall increase when the convectively active phases of the MJO traverse northern Australia (MJO phases 4–5–6) and decrease during the suppressed phases (MJO phases 8–1–2). However, away from the tropics and in other seasons the MJO also modulated subtropical and mid-latitude extreme rainfall as a result of its teleconnections, which act to alter the extratropical circulation (e.g. Risbey et al. 2009; Wheeler et al. 2009; Marshall et al. 2014). As such, the MJO is a potential source of multiweek predictability of extreme rainfall. In this study, we assessed the contribution of the MJO to predictability of multiweek extreme rainfall using the Bureau of Meteorology’s operational subseasonal–seasonal prediction system ACCESS-S1. The key findings of this study are:
The ACCESS-S1 prediction system is able to predict the MJO, as measured by the RMM indices, to a lead time of ~28 days, which places this system in the upper tier of current S2S models (e.g. compare to Lim et al. 2018).
The ACCESS-S1 model simulates the observed modulation of extreme weekly mean rainfall by each phase of the MJO and in each season reasonably well. However, the variation of the model’s extreme rainfall event probabilities associated with the MJO are generally weaker than those observed, especially across the far north during the summer season.
The MJO is a source of multiweek predictability (forecasts for weeks 2 and 3) during spring and summer seasons, when the forecast skill to predict the occurrence of extreme weekly mean rainfall is enhanced across much of the country at times when the MJO is strong compared to times when the MJO is weak. However, skill is reduced across the central far north during summer when the MJO is strong, suggesting the model is not good at depicting the MJO’s convective phases as it protrudes southward over the northern Australia land mass. During autumn and winter, there is little indication of changes in forecast skill depending on the strength of the MJO.
The overall conclusion is that although the MJO is a driver of extreme rainfall variations across Australia, the MJO is not a strong driver of extreme rainfall predictability with the current forecasting capability provided by the ACCESS-S1 prediction system. However, for certain seasons and for certain MJO phases, forecast skill does increase appreciably. For instance, skill increases markedly across the south and east of the country during summer when the MJO is strong in phases 4 and 5 (Fig. 13), but these are not times when the MJO is causing a large swing either toward increased or decreased chances of extreme rainfall in these regions (Figs 5 and 6). So, although the skill analyses presented in Figs 12–15 could be useful for regional users to refer to when the MJO is forecast to be in certain phases, they need to be used with caution because areas of high skill might not correspond to areas where the swing in probability of extreme rainfall is large for specific phases of the MJO.
Clearly there are systematic errors in the depiction of the MJO and its teleconnection over Australia that are acting to reduce the predictive skill for forecasts of extreme rainfall. The weaker-than-observed MJO amplitude in the model at lead times beyond 1 week contributes to reducing the signal to noise of the MJO’s local impacts and so reduces predictive skill. There is an ongoing concerted effort to improve the depiction of the MJO in the ACCESS-S model in conjunction with the Bureau of Meteorology partner the UK Met Office (e.g. Walters et al. 2017), so we should look forward to improved predictive skill of multiweek extreme rainfall with subsequent upgrades to the model. However, the present results also emphasise the challenge of predicting rainfall extremes and that the MJO is but one of many contributors that must be well predicted in order to produce skilful forecasts.
Conflicts of interest
The authors declare no conflicts of interest.
Declaration of funding
This work is part of the Forewarned is Forearmed project, which is supported by funding from the Australian Government Department of Agriculture and Water Resources as part of its Rural Research and Development for Profit programme.
Acknowledgements
We extend our thanks to Matthew Wheeler and Guomin Wang for generously giving their time to help improve the overall quality of this paper.
References
Alves, O., Wang, G., Zhong, A., Smith, N., Tzeitkin, F., Warren, G., Schiller, A., Godfrey, S., and Meyers, G. (2003). POAMA: Bureau of Meteorology Operational Coupled Model Forecast System. In ‘Proceedings of national drought forum’, Brisbane, April 2003. (Eds R. Stone and I. Partridge.) pp. 49–56. (DPI Publications: Department of Primary Industries, Brisbane, Qld)Bureau of Meteorology (2019). Operational Implementation of ACCESS-S1 Forecast Post-Processing. Melbourne. Available at http://www.bom.gov.au/australia/charts/bulletins/opsull-124-ext.pdf.
de Burgh-Day, C., Griffiths, M., Yan, H., Young, G., Hudson, D., and Alves, O. (2020). An adaptable framework for development and real time production of experimental sub-seasonal to seasonal forecast products. Bureau Research Report 042. (Bureau of Meteorology: Melbourne, Vic.).
Dee, D. P., Uppala, S. M., Simmons, A. J., et al. (2011). The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Quart. J. R. Meteorol. Soc. 137, 553–597.
| The ERA-Interim reanalysis: Configuration and performance of the data assimilation system.Crossref | GoogleScholarGoogle Scholar |
Donald, A., Meinke, H., Power, B., Maia, A. D. H., Wheeler, M. C., White, N., Stone, R. C., and Ribbe, J. (2006). Near‐global impact of the Madden‐Julian Oscillation on rainfall. Geo. Res. Lett. 33, L09704.
| Near‐global impact of the Madden‐Julian Oscillation on rainfall.Crossref | GoogleScholarGoogle Scholar |
Ferro, C. A. T., and Stephenson, D. B. (2011). Extremal Dependence indices: Improved Verification Measures for Deterministic Forecasts of Rare Binary Events. Wea. Forecast 26, 699–713.
| Extremal Dependence indices: Improved Verification Measures for Deterministic Forecasts of Rare Binary Events.Crossref | GoogleScholarGoogle Scholar |
Haiden, T., and Duffy, S. (2016). Use of high-density observations in precipitation verification. ECMWF Newsletter 147, 20–25.
Hogan, R. J., and Mason, I. B. (2012). Deterministic forecasts of binary events. In ‘Forecast verification: a practitioner’s guide in atmospheric science’. (Eds I. T. Jolliffe and D. B. Stephenson.) 2nd Edn (Wiley)
Hudson, D., Alves, O., Hendon, H. H., and Wang, G. (2011). The impact of atmospheric initialisation on seasonal prediction of tropical Pacific SST. Clim. Dyn. 36, 1155–1171.
| The impact of atmospheric initialisation on seasonal prediction of tropical Pacific SST.Crossref | GoogleScholarGoogle Scholar |
Hudson, D., Marshall, A., Yin, Y., Alves, O., and Hendon, H. (2013). Improving intraseasonal prediction with a new ensemble generation strategy. Mon. Wea. Rev. 141, 4429–4449.
| Improving intraseasonal prediction with a new ensemble generation strategy.Crossref | GoogleScholarGoogle Scholar |
Hudson, D., Alves, O., Hendon, H., Lim, E.-P., Liu, G., Luo, J.-J., MacLaughlan, C., Marshall, A. G., Shi, L., Wang, G., Wedd, R., Young, G., Zhao, M., and Zhou, X. (2017). ACCESS-S1: The new Bureau of Meteorology multi-week to seasonal prediction system. J. South. Hemisph. Earth. Sys. Sci. 67, 132–159.
| ACCESS-S1: The new Bureau of Meteorology multi-week to seasonal prediction system.Crossref | GoogleScholarGoogle Scholar |
Jones, D. A., Wang, W., and Fawcett, R. (2009). High-quality spatial climate data-sets for Australia. Aust. Meteorol. Oceanogr. J. 58, 233–248.
| High-quality spatial climate data-sets for Australia.Crossref | GoogleScholarGoogle Scholar |
Lim, Y., Son, S., and Kim, D. (2018). MJO Prediction Skill of the Subseasonal-to-Seasonal Prediction Models. J. Clim. 31, 4075–4094.
| MJO Prediction Skill of the Subseasonal-to-Seasonal Prediction Models.Crossref | GoogleScholarGoogle Scholar |
Lin, H., Brunet, G., and Derome, J. (2008). Forecast skill of the Madden-Julian Oscillation in two Canadian atmospheric models. Mon. Wea. Rev. 136, 4130–4149.
| Forecast skill of the Madden-Julian Oscillation in two Canadian atmospheric models.Crossref | GoogleScholarGoogle Scholar |
MacLachlan, C., Arribas, A., Peterson, K. A., Maidens, A., Fereday, D., Scaife, A. A., Gordon, M., Vellinga, M., Williams, A., Comer, R. E., Camp, J., Xavier, P., and Madec, G. (2015). Global seasonal forecast system version 5 (GloSea5): a high-resolution seasonal forecast system. Quart. J. Roy. Meteorol. Soc. 141, 1072–1084.
| Global seasonal forecast system version 5 (GloSea5): a high-resolution seasonal forecast system.Crossref | GoogleScholarGoogle Scholar |
Marshall, A. G., and Hendon, H. H. (2019). Multi-week prediction of the Madden–Julian oscillation with ACCESS-S1. Clim. Dyn. 52, 2513–2528.
| Multi-week prediction of the Madden–Julian oscillation with ACCESS-S1.Crossref | GoogleScholarGoogle Scholar |
Marshall, A. G., Hudson, D., Wheeler, M. C., Hendon, H. H., and Alves, O. (2011). Assessing the simulation and prediction of rainfall associated with the MJO in the POAMA seasonal forecast system. Clim. Dyn. 37, 2129–2141.
| Assessing the simulation and prediction of rainfall associated with the MJO in the POAMA seasonal forecast system.Crossref | GoogleScholarGoogle Scholar |
Marshall, A. G., Hudson, D., Wheeler, M. C., Alves, O., Hendon, H. H., Pook, M. J., and Risbey, J. S. (2014). Intra-seasonal drivers of extreme heat over Australia in observations and POAMA-2. Clim. Dyn. 43, 1915–1937.
| Intra-seasonal drivers of extreme heat over Australia in observations and POAMA-2.Crossref | GoogleScholarGoogle Scholar |
Matthews, A. J., Hoskins, B. J., and Masutani, M. (2004). The global response to tropical heating in the Madden–Julian oscillation during the northern winter. Quart. J. Roy. Meteorol. Soc. 130, 1991–2011.
| The global response to tropical heating in the Madden–Julian oscillation during the northern winter.Crossref | GoogleScholarGoogle Scholar |
Mogensen, K., Balmaseda, M., Weaver, A. T., Martin, M., and Vidard, A. (2009). NEMOVAR: A variational data assimilation system for the NEMO ocean model. ECMWF Newsletter. 120, 17–21.
Mogensen, K., Balmaseda, M. A., and Weaver, A. T. (2012). The NEMOVAR ocean data assimilation system as implemented in the ECMWF ocean analysis for System 4. Tech Rep TR-CMGC-12-30. CERFACS Toulouse France.
Murphy, A. H., and Epstein, E. S. (1989). Skill scores and correlations in model verification. Mon. Wea. Rev. 117, 572–582.
| Skill scores and correlations in model verification.Crossref | GoogleScholarGoogle Scholar |
North, R., Truman, M., Mittermaier, M., and Rodwell, M. J. (2013). An assessment of the SEEPS and SEDI metrics for the verification of 6 h forecast precipitation accumulations. Meteor. Applic. 20, 164–175.
| An assessment of the SEEPS and SEDI metrics for the verification of 6 h forecast precipitation accumulations.Crossref | GoogleScholarGoogle Scholar |
Rashid, H., Hendon, H. H., Wheeler, M., and Alves, O. (2011). Prediction of the Madden-Julian Oscillation with the POAMA dynamical seasonal prediction system. Clim. Dyn. 36, 649–661.
| Prediction of the Madden-Julian Oscillation with the POAMA dynamical seasonal prediction system.Crossref | GoogleScholarGoogle Scholar |
Risbey, J. S., Pook, M. J., McIntosh, P. C., Wheeler, M. C., and Hendon, H. H. (2009). On the Remote Drivers of Rainfall Variability in Australia. Mon Weather Rev. 137, 3233–3253.
| On the Remote Drivers of Rainfall Variability in Australia.Crossref | GoogleScholarGoogle Scholar |
Singh, H., Arora, K., Ashrit, R., and Rajagopal, E. N. (2017). Verification of pre-monsoon temperature forecasts over India during 2016 with a focus on heatwave prediction. Nat. Hazards Earth. Syst. Sci. 17, 1469–1485.
| Verification of pre-monsoon temperature forecasts over India during 2016 with a focus on heatwave prediction.Crossref | GoogleScholarGoogle Scholar |
Spiegel, M. R. (1961). Schaum’s outline of theory and problems of Statistics. (Schaum Publishing Company: New York.)
Walters, D., Brooks, M., Boutle, I., Melvin, T., Stratton, R., Vosper, S., Wells, H., Williams, K., Wood, N., Allen, T., Bushell, A., Copsey, D., Earnshaw, P., Edwards, J., Gross, M., Hardiman, S., Harris, C., Heming, J., Klingaman, N., Levine, R., Manners, J., Martin, G., Milton, S., Mittermaier, M., Morcrette, C., Riddick, T., Roberts, M., Sanchez, C., Selwood, P., Stirling, A., Smith, C., Suri, D., Tennant, W., Vidale, P. L., Wilkinson, J., Willett, M., Woolnough, S., and Xavier, P. (2017). The Met Office Unified Model Global Atmosphere 6.0/6.1 and JULES Global Land 6.0/6.1 configurations. Geosci. Mod. Dev. 10, 1487–1520.
| The Met Office Unified Model Global Atmosphere 6.0/6.1 and JULES Global Land 6.0/6.1 configurations.Crossref | GoogleScholarGoogle Scholar |
Wang, G., and Hendon, H. H. (2019). Impacts of the Madden-Julian Oscillation on wintertime Australian minimum temperatures and Southern Hemisphere circulation. Clim. Dyn. 55, 3087–3099.
| Impacts of the Madden-Julian Oscillation on wintertime Australian minimum temperatures and Southern Hemisphere circulation.Crossref | GoogleScholarGoogle Scholar |
Wheeler, M. C., and Hendon, H. H. (2004). An all-season real-time multivariate MJO index: Development of an index for monitoring and prediction. Mon. Wea. Rev. 132, 1917–1932.
| An all-season real-time multivariate MJO index: Development of an index for monitoring and prediction.Crossref | GoogleScholarGoogle Scholar |
Wheeler, M. C., Hendon, H. H., Cleland, S., Meinke, H., and Donald, A. (2009). Impacts of the Madden–Julian Oscillation on Australian Rainfall and Circulation. J. Clim. 22, 1482–1498.
| Impacts of the Madden–Julian Oscillation on Australian Rainfall and Circulation.Crossref | GoogleScholarGoogle Scholar |
White, C. J., Hudson, D., and Alves, O. (2014). ENSO, the IOD and the intraseasonal prediction of heat extremes across Australia using POAMA-2. Clim. Dyn. 43, 1791–1810.
| ENSO, the IOD and the intraseasonal prediction of heat extremes across Australia using POAMA-2.Crossref | GoogleScholarGoogle Scholar |