Australian climate warming: observed change from 1850 and global temperature targets
Michael R. Grose A * , Ghyslaine Boschat B C , Blair Trewin
A * , Ghyslaine Boschat B C , Blair Trewin  B , Vanessa Round A , Linden Ashcroft C D , Andrew D. King C D , Sugata Narsey B and Edward Hawkins E
B , Vanessa Round A , Linden Ashcroft C D , Andrew D. King C D , Sugata Narsey B and Edward Hawkins E
A CSIRO Climate Science Centre, Hobart, Tas., Australia.
B Bureau of Meteorology, Docklands, Vic., Australia.
C ARC Centre of Excellence for Climate Extremes, Melbourne, Vic., Australia.
D School of Geography, Earth and Atmospheric Sciences, University of Melbourne, Melbourne, Vic., Australia.
E Department of Meteorology, National Centre for Atmospheric Science, University of Reading, Reading, UK.
Journal of Southern Hemisphere Earth Systems Science 73(1) 30-43 https://doi.org/10.1071/ES22018
Submitted: 15 May 2022 Accepted: 31 January 2023 Published: 20 February 2023
© 2023 The Author(s) (or their employer(s)). Published by CSIRO Publishing on behalf of the Bureau of Meteorology. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)
Abstract
Mean annual temperature is often used as a benchmark for monitoring climate change and as an indicator of its potential impacts. The Paris Agreement of 2015 aims to keep the global average temperature well below 2°C above pre-industrial levels, with a preferred limit of 1.5°C. Therefore, there is interest in understanding and examining regional temperature change using this framework of ‘global warming levels’, as well as through emissions pathways and time horizons. To apply the global warming level framework regionally, we need to quantify regional warming from the late 19th century to today, and to future periods where the warming levels are reached. Here we supplement reliable observations from 1910 with early historical datasets currently available back to 1860 and the latest set of global climate model simulations from CMIP5/CMIP6 to examine the past and future warming of Australia from the 1850–1900 baseline commonly used as a proxy for pre-industrial conditions. We find that Australia warmed by ~1.6°C between 1850–1900 and 2011–2020 (with uncertainty unlikely to substantially exceed ±0.3°C). This warming is a ratio of ~1.4 times the ~1.1°C global warming over that time, and in line with observed global land average warming. Projections for global warming levels are also quantified and suggest future warming of slightly less than the observed ratio to date, at ~1.0–1.3 for all future global warming levels. We also find that to reliably examine regional warming under the emissions pathway framework using the latest climate models from CMIP6, appropriate weights to the ensemble members are required. Once these weights are applied, results are similar to CMIP5.
Keywords: Australian mean annual temperature, climate projections, climate warming, future mean annual temperature, global surface air temperature, global temperature targets, global warming levels, historical change, observed change.
1. Introduction
Global surface air temperature (GSAT) is used as a guide to the magnitude of climate change we experience, and as an indicator of the level of potential impacts. Since the Paris Agreement in 2015, there has been strong interest in assessing regional climate change at defined global warming levels of 1.5 and 2°C since the pre-industrial era, and then comparing these to higher levels of global warming such as 3 and 4°C, whenever they might be reached during transient climate change this century. This framework has been titled ‘global warming levels’ (James et al. 2017). There is now interest in what these levels mean regionally. Quantifying the regional warming and climate impacts associated with future global warming targets is a topic of great interest as countries seek to mitigate the impacts of climate change (e.g. Harrington et al. 2018). However, there is also interest in examining climate change according to diverging future emission or concentration pathways, commonly using the Representative Concentration Pathways (RCPs) of van Vuuren et al. (2011) or the Shared Socio-economic Pathways (SSPs) of Meinshausen et al. (2019). Under the pathway framework, change can be reported from a historical baseline to useful future time horizons, commonly 20-year periods such as 2040–2059 or 2080–2099. Both the global warming level framework and the pathway framework are presented in products such as the Intergovernmental Panel on Climate Change Sixth Assessment Report (IPCC AR6, Masson-Delmotte et al. 2021), featuring prominently in the Atlas chapter and Interactive Atlas (Gutiérrez et al. 2021). However, there are some remaining knowledge gaps when applying either framework in Australia.
To use the global warming levels framework, an estimate of regional warming since pre-industrial times is needed, or at least since 1850–1900 as an ‘early industrial’ baseline (Hawkins et al. 2017; Schurer et al. 2017). Estimating climate warming is also useful for simply understanding the climate change already experienced in Australia. However, both the global and especially the regional change since 1850–1900 are uncertain since data are sparse prior to the 20th century in many places (e.g. Morice et al. 2012). Limited standardisation of instruments and observational procedures in the 19th century adds additional uncertainty to global and regional averages. There are few regions of the world where high-quality long-term observational temperature series are available for the full post-1850 period. Australia has a quality-controlled temperature series only back to 1910 in the Australian Climate Observations Reference Network – Surface Air Temperature (ACORN-SAT) dataset (Trewin et al. 2020), and a more limited range of observations available from 1860 (e.g. Ashcroft et al. 2012). The linear trend during 1910–2019 from the ACORN-SAT dataset is 1.44 ± 0.24°C (Trewin et al. 2020), but there are likely to be changes between 1850 and 1910 that remain unaccounted for. Climate models can also be used to examine past changes in conjunction with observations to fill gaps in space and time, either through the use of reanalysis of the actual climate or examining the forced response through free-running climate models.
The global warming levels framework also needs model estimates of change to a future period when the global warming levels are reached. Here we rely heavily on climate models, since they provide a physically based simulation of future conditions. To examine future conditions at global warming levels, model outputs from the Coupled Model Inter-comparison Project phase 5 (CMIP5; Taylor et al. 2012) and phase 6 (CMIP6; Eyring et al. 2016) can be examined using the ‘time sampling’ method (James et al. 2017). This method accounts for the different rates of warming between models by sampling in windows around the time that each model reaches a global warming level rather than a consistent timeframe. By sampling in time when each model reaches the global warming levels, the results are standardised for the circumstances where climate sensitivity is higher (reaching warming levels sooner) or lower (reaching warming levels later).
To apply the emissions pathway and time horizon framework, ideally a balanced sampling of various uncertainties should be made, including climate sensitivity, which is not standardised under this framework. The CMIP simulations are ‘ensembles of opportunity’, so do not represent a balanced sample of model uncertainty, and modelled climate sensitivity presents a challenge in the latest round of CMIP models. Compared to the range estimated by an independent assessment (e.g. Sherwood et al. 2020), the CMIP5 spread is a reasonable approximation of this assessed range, but the CMIP6 spread is not, with sensitivity above the likely range over-represented and two models below the very likely range (Zelinka et al. 2020; Hausfather et al. 2022). It has been noted that the ‘hot models’ cannot be entirely discounted (Bloch-Johnson et al. 2022), but just should not be over-represented in an ensemble. For the assessment of global temperature change in IPCC AR6, it was acknowledged that the uneven spread of climate sensitivity in CMIP6 means that the ‘one model one vote’ approach does not produce balanced ensemble statistics for global mean temperature change (Arias et al. 2021). Instead, an assessment of warming to date and climate sensitivity was combined with the outputs from CMIP models using weighting schemes, as well as Earth System Model emulators, to generate warming estimates in Arias et al. (2021). Weighting schemes for CMIP6 that attempt to address the climate sensitivity issue include those by Brunner et al. (2020) and Tokarska et al. (2020). Emulators have been used regionally (e.g. Beusch et al. 2022), and could be used as a part of comprehensive and balanced warming projections for Australia. However, weighting scheme methods have not been applied regionally before, including in Australia.
Here we address these knowledge gaps by examining temperature change in Australia from the early industrial baseline of 1850–1900 using various methods, and then projected change to various global warming levels and for the SSPs using an example weighting scheme. We examine the national average as well as sub-regions including states and territories, as a picture of past, present and future warming in our region.
2. Data and methods
2.1. Datasets and models
The Australian mean annual temperature anomaly (using a 1961–1990 baseline) for the 1910–2021 period is derived from the homogenised, Australia-wide temperature records in the ACORN-SAT version 2.1 (ACORN-SATv2.1; Trewin et al. 2020). The ACORN-SATv2.1 comprises daily temperature observations from 112 locations across Australia that have been thoroughly examined for non-climatic influences and inhomogeneities.
There are challenges in assessing Australian temperature change prior to 1910, as there are very limited data available outside mainland south-east Australia before the mid-1870s, apart from some for Western Australia (Gergis et al. 2021) and limited records from the Northern Territory. There are also substantial inhomogeneities in the dataset as a result of the wide range of instrument exposures prior to the introduction of the Stevenson thermometer screen as a standard. The change to Stevenson screens was largely complete by the mid-1890s in Queensland, South Australia and the Northern Territory, but did not occur in New South Wales and Victoria until 1906–1908 (Nicholls et al. 1996). The observed dataset for south-east Australia in Ashcroft et al. (2012) is used, as this addresses these homogeneity issues (e.g. adjusting for the introduction of the Stevenson screen), and uses monthly observations from 38 long-term stations to calculate a regional average over 138–154°E, 24–40°S (land-masked) and from 1860 onwards. The inter-annual temperature variability in this region is higher than for Australia as a whole, but the longer-term trends for this region may still be a proxy for trends in the nation. Supporting this, the correlations between the ACORN-SAT and Ashcroft datasets from 1910 to 2010 are R = 0.90 for annual data, R = 0.97 for 11-year running averages and the differences in the 30-year changes calculated as rolling linear trends over 1910–2016 are all less than 0.1°C.
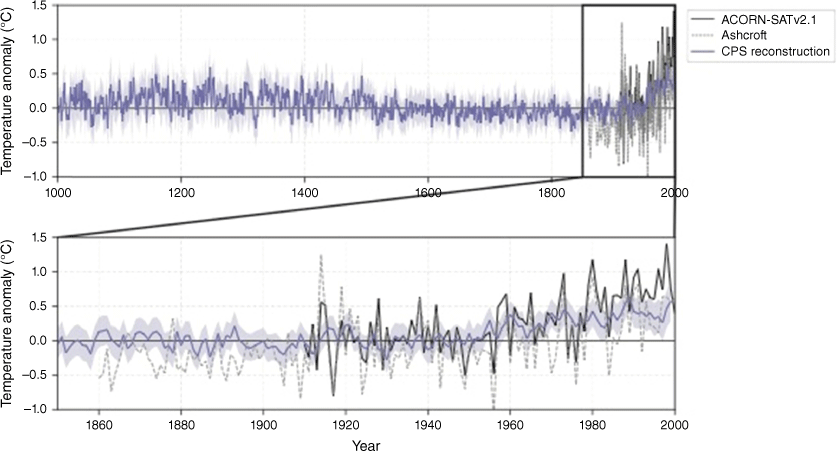
We also examine the paleo-climate reconstruction of the years 1000–2000 from Gergis et al. (2016) for broader context. This 1000-member reconstruction of regional temperature is based on the composite plus scale technique, where data from temperature-sensitive proxies are standardised and combined, then scaled using an instrumental target record. The reconstruction covers the entire region of Australasia (0–50°S, 110–180°E) and is relevant to land and ocean, so likely underestimates trends over Australian land only. Also, the reconstruction is for the September–February season rather than the entire year.
For comparison to the regional high-quality dataset from ACORN-SATv2.1, mean annual temperature values (median estimate) for the land area of Australia are derived from the following global gridded datasets: HadCRUT5 (Morice et al. 2021), Berkeley Earth (Rohde and Hausfather 2020), NOAA GlobalTemp (Huang et al. 2020; Zhang et al. 2019), Cowtan and Way (2014) and GISTEMP (Lenssen et al. 2019). Note that NOAA GlobalTemp and GISTEMP are available from 1880, the others from 1850.
Mean annual temperature was examined in CMIP5 models for the historical and RCP simulations, and from CMIP6 models for the historical and SSP simulations (Table 1). At the global scale, two aspects to be considered are (a) that model fields are globally complete whereas observed datasets have gaps in spatial coverage, which are treated differently, and (b) observed global mean annual temperature anomalies are surface air temperature over land and sea surface temperature over ocean, whereas models use surface air temperature for the whole globe. Globally complete observed datasets (which, in this context, include reanalyses) show stronger recent warming than datasets that have spatial gaps, largely because the latter underrepresent areas in high northern latitudes that are warming faster than the global mean (Simmons et al. 2017). The IPCC AR6 finds that estimates of change in GSAT and global mean surface temperature are likely to be slightly different, but that there is no clear evidence of the sign of this difference (Gulev et al. 2021). Neither issue would be expected to have an impact on model–observation comparisons over the Australian continent, since there is complete coverage in all datasets here and we only examine temperature over land.

|
2.2. Estimating warming from 1850 to 1900
Temperature change from the early industrial baseline to the recent past is estimated by the difference in mean temperature between the 1850–1900 and 2011–2020 periods, consistent with the IPCC’s Sixth Assessment Report (Masson-Delmotte et al. 2021). This method is used rather than a linear trend, as used in Trewin et al. (2020), since a linear fit is an inaccurate description of the data for this longer period (see Fig. 1, see Section 3.2). The ACORN-SATv2.1 dataset is used from 1910, and we focus here on an estimate of the difference between 1850 and 1900 and the early part of this observed series (1910–1930 is used), to use as an addition to the series to account for change prior to 1910.
Six different methods were used to estimate this offset using different datasets and models: (1) the paleo-climate reconstruction, (2) the early historical observational dataset, (3) global gridded observation datasets, (4) CMIP5 and CMIP6 global climate model outputs, (5) global climate model outputs with bias corrections applied and (6) a statistical model based on global mean temperature.
The bias correction (method 5) is applied to climate model outputs to adjust the simulated output from each model for 1850–1909 based on differences between the observations (ACORN-SATv2.1) and the model output over a training period (here 1910–1960). The method we use is the Empirical Quantile Mapping method which calibrates the simulated cumulative distribution function (CDF) based on a nonparametric function that amends mean, variability and shape errors in the CDF (for more detail, see Amengual et al. 2012).
A regression model (method 6) is generated between global mean temperature, which is likely to be more reliably estimated in 1850–1910 than regional temperature, and local temperature. The linear regression model is calculated from 1910 to 2019, then used to generate a predicted regional time series with confidence bounds for the entire 1850–2019 period.
2.3. Projections
Projected change for global warming levels was calculated using time sampling (James et al. 2017) of CMIP5 models. Results from CMIP5 are the main focus of this study, as they are the most developed, but we briefly compare these findings to those from CMIP6 to assess any difference. Choices on the method are similar to that of the IPCC Atlas (Gutiérrez et al. 2021), using Run 1 from up to 40 CMIP5 models. Only RCP8.5 simulations are used, to ensure a consistent and sufficiently large ensemble size for each warming level, as higher warming levels (e.g. 4°C) are not met under the lower pathways. This is consistent with other studies including Schleussner et al. (2016). For example, fewer than one-third of models reach a global warming level of 3°C or above under RCP4.5, whereas almost all models could provide data on global warming levels up to 4°C under RCP8.5. It is worth noting that a high-end emissions scenario is used for a consistent sample size in each warming level, but results are similar between RCP8.5 and other RCPs for all lower warming levels (not shown). Changes for the 1.5, 2, 3 and 4°C warming levels are presented but we make no comment on the likelihood of reaching any one of these levels. Also, our results should be interpreted as representing Australian temperature changes for a transient climate rather than a stabilised climate where net-zero emissions is achieved in line with policy goals (Rogelj et al. 2017). Regional temperature changes under transient and stabilised global warming levels differ (e.g. King et al. 2020).
To identify the global warming level epoch in each model, a 10-year running mean is first applied to the globally averaged temperature anomaly from 1850 to 1900. Years where the running mean global temperature falls within ±0.2°C tolerance of the warming level are selected (e.g. 1.8–2.2°C for a 2°C global warming level), along with the ±5 years on either side, as used in King et al. (2017). These years are then used to time sample for regional temperatures under each global warming level. The 10–90th percentile and model mean are then given.
For the emissions pathway and time horizon framework, first the ensemble spread of equal weighting is calculated, then the 10–90th percentile range and mean of Run 1 from CMIP5 and CMIP6 models (Table 1). Following this, weighting based on global warming and model independence by Brunner et al. (2020) is applied to the same models, ensemble members and SSP (SSP5–8.5) specific to that study, and again the 10–90% range and model mean are shown. Weights vary between 0.0013 for models with poor evaluation and match to historical trends, through to 0.13 for models with higher evaluation and match to historical trends. This weighting is not applied to other SSPs, as the same ensemble members are not all available for all SSPs. This result is not presented as a comprehensive assessment of future warming in CMIP6, but rather as an illustration of the relevant issues using an example approach for a very high concentration pathway.
3. Results
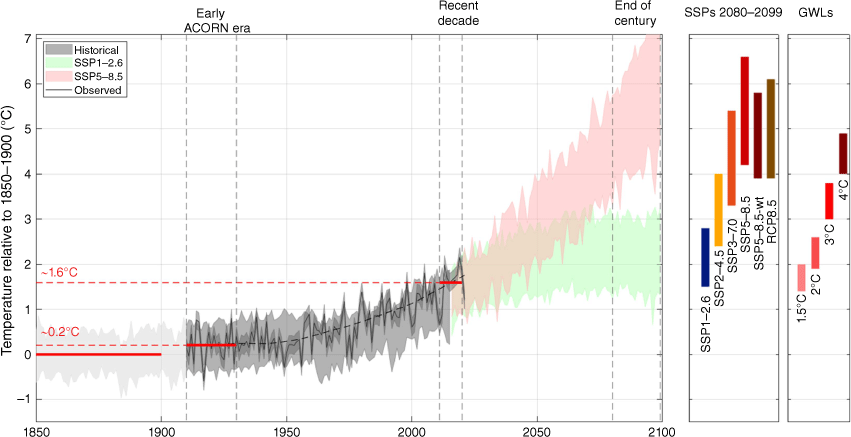
The summary graphic (Fig. 1) and table (Table 2) of mean annual temperature shows a central estimate of warming of 0.2°C between the late 19th century (1850–1900) and the first 20 years of the official observed record (1910–1930), and of 1.6°C between the late 19th century (1850–1900) and the recent decade (2011–2020) for Australia, as well as projected regional warming under all global warming levels and selected concentration pathways. These components are examined in the following sections.

|
3.1. Temperature difference 1850–1900 to 1910–1930
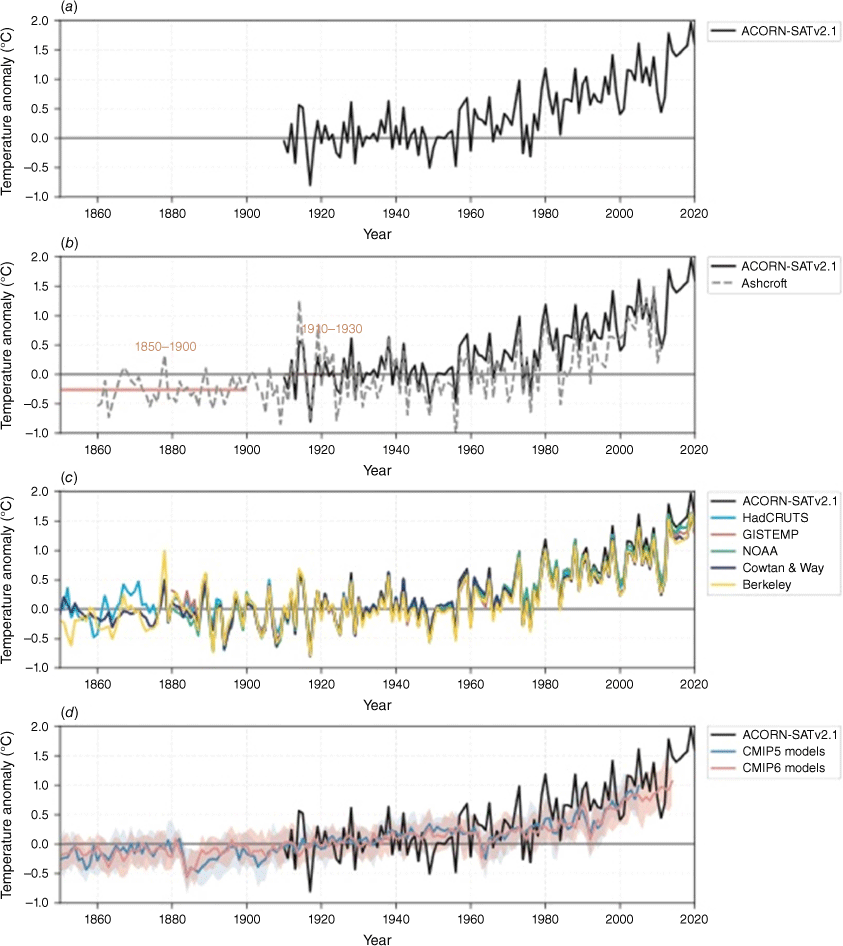
The paleo-climate reconstruction indicates a warming of 0.04°C between 1850–1900 and 1910–1930 for land and ocean regions of Australasia (Fig. 2). This is likely an underestimate of land-only change for Australia specifically, as trends over ocean and New Zealand are lower than for the Australian landmass (e.g. Gulev et al. 2021). However, the whole series provides useful context for further investigations, as it shows that temperature likely varied by less than ±0.3°C for the period 1000–1850, and trends were all much less than in the recent period. Note that the early historical record and observed ACORN-SATv2.1 record overlaid on this proxy record are for Australian land specifically, so have higher interannual variability.
|
The early historical record shows a difference of 0.26°C between 1860–1900 and 1910–1930 (Fig. 2, 3). The higher interannual variability in south-east Australia compared to the national average is seen in the overlapping series (Fig. 3b). But as mentioned above, this does not necessarily mean it is not a useful proxy for trends at the national scale over multiple decades.
Global gridded datasets align closely with each other and with ACORN-SATv2.1 since 1910 but show some different variability and trends in the earlier part of the record (Fig. 3c). The difference between 1850–1900 (or 1880–1900 for GISTEMP and NOAA) and 1910–1930 varies between 0.0 and 0.1°C, with a median of 0.07°C.
In CMIP5 and CMIP6 models there is a spread of temperature changes between 1850–1900 and 1910–1930. The CMIP5 results are shown in Fig. 3, with a model median at 0.21°C. Apart from some outliers, most models are grouped around this value, with the 25–75% range of 0.08–0.26°C. There is a range of cooling responses to the Krakatoa volcanic eruption in 1883 in the models, explaining some differences. Natural variability, possibly related to trends in land surface variables and rainfall, may also explain some differences in the model results, from strong warming in GFDL-ESM2G (0.6°C) that may be related to the strong drying over the inland region in this model over the period, to slight cooling in MRI-ESM1 (−0.1°C) that may be related to the simulated rainfall increase over the period (rainfall analysis not shown). Applying the bias adjustment to CMIP5 gives a median difference of 0.17°C and slightly reduces the spread between all models but retains a similar 25–75% range (0.08–0.25°C). Results are similar for uncorrected CMIP6 data (median 0.17°C, 25–75% range 0.04–0.26°C).
The regression model based on observed global warming to local warming gives a difference of 0.0–0.2°C between 1850–1900 and 1910–1930. However, the model shows considerable noise, with a confidence interval of ~0.2°C through the series, and this relationship is commonly used to estimate ‘noise’ when estimating climate emergence (Hawkins et al. 2020). Therefore, the result is not useful to quantify the difference between the two periods but is helpful as an independent check that the broad magnitude of change aligns with other results.
The paleo-climate record and observed datasets all have limitations, but nevertheless all indicate a difference in the range of 0.0–0.26°C between the two periods. This range is supported by the regression model for global temperature. The dataset with the most in situ measurements, the early historical record, gives the higher value of change. However, the presence of various uncertainties suggests that the change value cannot be estimated with statistical reliability using these observations alone.
The various uncertainties in the different data sources (observed datasets, paleo records and models) differ in nature, and cannot be easily combined to produce a single estimate of this change value, so here we choose a single source to use. We take the median of CMIP5/CMIP6 models as a useful estimate (0.2°C), since it has complete spatial and temporal coverage and has a coherent representation of the effect of early climate forcings. We note that this is more conservative than the historical dataset with the most in situ data from Ashcroft et al. (2012) at 0.27°C but is broadly consistent with the order of magnitude of change from other sources. The value is slightly higher than that obtained from the global gridded datasets, but we note that some of these datasets do not include the station records used in Ashcroft et al. (2012) and interpolate data over long distances in some cases. Also, historical trends in the 1910–2021 period are typically lower in the global datasets than in ACORN-SAT, suggesting that they generally have suppressed trends compared to high-quality regional observation datasets. The ACORN-SATv.2 showed stronger recent warming than ACORN-SATv.1 for Australia, partly because of improved treatment of the large number of site moves from in-town to out-of-town locations in the 1990s and 2000s (Trewin et al. 2020), and it is likely that global datasets have to date not fully captured the changes corrected for in ACORN-SATv.2. Note we report a precision of only one decimal place here, at 0.2°C. No formal confidence bounds are given due to the different forms of uncertainties involved. However, the maximum and minimum value found from any method or model (using the 10–90% model range, which excludes outliers such as those mentioned above) are used as an approximate guide to uncertainty. For Australia this is 0.0°C (HadCRUT5) to 0.4°C (highest model change), resulting in a 0.2 ± 0.2°C range. This convention is adopted henceforth, with the minimum and maximum values shown in parentheses.
For states and territories within Australia (Table 2), the median modelled warming between these periods is 0.1°C (−0.1°C to 0.4°C) for Tasmania and 0.2°C for all others. The maximum and minimum values from any method are all in the range −0.2°C to 0.5°C for all, with the lowest coming from global gridded datasets and the highest coming from models.
3.2. Historical temperature change
Adding the 0.2°C estimate of early warming to the ACORN-SATv2.1 time series after it is already calculated as an anomaly from 1910 to 1930 gives us an estimated change relative to 1850–1900 (Fig. 1). This shows a difference between 1850–1900 and 2011–2020 of 1.6°C (Fig. 1). Internal variability is larger at the national scale compared to the global scale, so its effect on the 10-year mean will be larger for Australia compared to the globe. An increased frequency of warmer or cooler years by chance during this recent decade may bias the estimated warming. However, with a 41-year Lowess filter through the data to remove variability at this scale (Fig. 1), the mean in the decade is also 1.6°C above 1850–1900, suggesting variability does not unduly affect the estimate. Applying this filter also allows the calculation of warming to the most recent year of 2021 in a long-term trend perspective, and this value is 1.76°C. A warming of 1.6°C between these periods is directly in line with the global land average of 1.6°C, and ~1.4 times the global average including land and ocean of 1.1°C reported in the IPCC’s Sixth Assessment Report (Masson-Delmotte et al. 2021). Accounting for the indicative uncertainty range, the ratio is 1.3–1.6 to the global average. The equivalent warming between 1850–1900 and 2011–2020 for states and territories is 1.1°C in Tasmania, 1.4°C in Victoria, 1.5°C in Western Australia and the Northern Territory, 1.6°C in New South Wales and the Australian Capital Territory, and 1.7°C in Queensland and South Australia (Table 2).
The difference between this central estimate of 1.6°C change and that of 1.44°C value from Trewin et al. (2020) is the net result of three factors. The first is the addition of 0.2°C rise between 1850–1900 and 1910–1930. The second is the effect of using a difference rather than linear trend. Owing to the accelerating warming trend, a linear trend over this longer 1850–2021 period is lower than the smoothed data at the start and end of the record and higher in the middle, illustrated using a typical model simulation blended with ACORN-SATv2.1 (Fig. 4). For comparison, the linear trend for this example blended series and the mean of all models is 1.8°C (and ranges within 1.4–2.1°C using different models), and the difference using this example model is 1.6°C, chosen to be similar to the model average. For reference, the linear trend of 1.44°C from 1910 to 2019 compares with a difference of 1.31°C between the 1910–1930 and 2010–2019 means. The third factor is the addition of one more year of data; Trewin et al. (2020) used 1910–2019, and here we report for the decade 2011–2020, which is 0.07°C warmer than 2010–2019, with the relatively cool year of 2010 replaced in the decadal average by the warm year of 2020.

|
The warming in Australia is higher than the global average and similar to the global land average since c. 1960, with some differences in the decadal trends before this (Fig. 4b). The ratio of Australian warming to global and global land average warming is noisy due to low values until c. 2000 but has been more stable at ~1.4 (global) and 1 (land) since then (Fig. 4c).
The confidence bound from the core ACORN-SATv2.1 record is reported as 1.44 ± 0.24 for 1910–2019 in Trewin et al. (2020), calculated as the random error on the linear trend. Such a confidence bound cannot be reproduced for the analysis presented here, as it does not use a linear trend. A more formal uncertainty estimate of the ACORN-SATv2.1 record is produced by Grainger et al. (2022), incorporating observation error, grid point uncertainty and area-average uncertainty. This analysis found a change of 1.42 ± 0.28°C over the slightly shorter record of 1910–2018, again using a regression model. This estimate is consistent with Trewin et al. (2020), but the analysis cannot be reproduced for this estimate either, as the forms of uncertainty are not commensurate. The estimate of warming between 1850–1900 and 1910–1930 does not use the same ACORN set of station observations only, change is measured as difference rather than a linear trend, and some errors are correlated between the two estimates. Therefore, no formal confidence bounds are given to this estimate; however, we note that the range from the early historical warming alone may be ~±0.2°C. Uncertainties (2-sigma) in annual mean values of Australian temperature in ACORN-SAT range from ±0.176°C in 1910 to ±0.084°C in 2018 (Grainger et al. 2022). Using this as a basis for assessing uncertainties in decadal means and combining with the ±0.2°C uncertainty estimate for the 1850–1900 to 1910–1930 change, it is considered unlikely that the uncertainty in the total 1850–1900 to 2011–2020 change substantially exceeds 0.3°C, making a range of 1.3–1.9°C (Table 2). An equivalent is calculated for each state and territory (Table 2). The uncertainty estimate in the 20-year running mean value for Australia in Berkeley for the 1850–1900 period is 0.2°C relative to 1951–1980 (Rohde and Hausfather 2020), supporting an uncertainty of this magnitude. For reference, the CMIP6 warming of Australian land between 1850–1900 and 2011–2020 is generally lower than observed, with a mean of 1.3°C (model range 0.9–2.3°C), and only three of 44 models have warming of 1.6°C or above.
3.3. Projected change for global warming levels
Results here are for transient climate change this century, noting that stabilised climates at these global warming levels will differ. Projected change in Australian mean annual temperature (land only) from 1850 to 1900 to all four global warming levels (1.5, 2, 3 and 4°C) are all ~0.9–1.3 times the global average including oceans (Fig. 1, Table 2). For example, 2°C global warming is projected to be 1.7–2.4°C in Australia (10–90% range of models). These results match those in the IPCC Atlas and Interactive Atlas (Gutiérrez et al. 2021) within 0.2°C tolerance. For example, the Atlas reports 2°C global warming as 1.9–2.6°C for Australia. Results are very similar when using CMIP6 (e.g. 2°C gives 1.8–2.4°C), reflecting that this framework standardises for different spreads of climate sensitivity and other model differences in the two model ensembles.
These projected changes differ from the observed changes to date in terms of the ratio to global average including oceans, and global land average. First, the simulated Australian warming is at a lower ratio compared to global warming (including oceans) than the ratio found in observations: 0.9–1.3 compared to 1.4 times (and at the low end of the range accounting for the indicative uncertainty estimate). Also, the observed warming in Australia is similar to the global land average, but the projected warming of Australia is in fact lower than the global land average. For example, in CMIP6 at 2°C global warming, the global land average is projected to be 2.6–2.8°C warmer (Gutiérrez et al. 2021), which is higher than the 1.7–2.4°C for Australia.
The simulated ratios between Australian and global warming are generally highly persistent through time and for each warming level, hence the consistent ratio to global warming through each level. The precise ratio in the observed world is likely influenced by natural variability, and noisy at lower levels of global warming, including the current level (Fig. 4c). However, the results presented here suggest that all models may underestimate the current ratio of Australian to global warming, and further research is required into the cause of this difference if the difference persists and is not a function of natural variability in observations. Interestingly, the ratio of global land to global ocean warming (~1.8×, Masson-Delmotte et al. 2021) is higher in observations than in models as well.
3.4. Projected change for RCPs and SSPs
The 10–90% range of projected changes of Australian land average temperature between 1850–1900 and 2080–2099 for the SSPs using CMIP6 with equal model weighting reported in Gutiérrez et al. (2021), are 1.5–2.8°C under SSP1–2.6, 2.4–4.0°C under SSP2–4.5, 3.3–5.4°C under SSP3–7.0 and 4.2–6.6°C under SSP5–8.5 (Fig. 1). Ranges are very similar when using the slightly expanded model list (Table 1), for example SSP5–8.5 is 4.2–6.8°C. However, these ranges are not a balanced sampling of an independent assessment of the underlying uncertainty, as they are affected by the uneven spread in climate sensitivity in CMIP6. The issue is reflected in the notable difference between the CMIP5 and CMIP6 projections for this period under a very high pathway of RCP8.5/SSP5–8.5 (Fig. 1). Part of this difference is explained by the concentration pathways not being identical, i.e. they both result in ~8.5 W m−2 radiation imbalance by 2100, but the mix of different forcings including greenhouse gas concentrations differ in how this is reached. However, the more notable reason for the difference is the different spread in climate sensitivity in CMIP6 compared to CMIP5, where CMIP6 has more models in the high range and by chance CMIP5 more closely matches the likely range (Zelinka et al. 2020). As a demonstration of one potential solution to this issue, the Brunner et al. (2020) weighting system was applied, and the resulting range is narrower at both the upper and lower bound, at 3.9–5.8°C, and is closer to the CMIP5 RCP8.5 result (3.9–6.1°C).
4. Discussion
The increase in GSAT since the pre-industrial era is frequently used as a measure of the magnitude of climate change and an indication of its impacts. Therefore, the mean annual temperature of Australia is also a useful quantity to consider when examining our changing climate in the past and future and provides relevant context in discussions around climate change impacts and adaptation. A calculation of mean annual temperature based around a network of reliable station observations is the most credible and accepted approach to estimate mean annual Australian temperature but this record for Australia is only available for 1910 to the present. Various other datasets and models can be used to go further back in time and forward into the future under various scenarios of human development.
The analysis provided here suggests that the Australian mean temperature rose slightly between 1850–1900 and 1910–1930, based on different observed datasets and models. This finding is consistent with a small external forcing from an enhanced greenhouse effect present at the time. A central estimate of 0.2°C and an uncertainty range of ±0.2°C between 1850–1900 and 1910–1930 was taken from models but is consistent with an uncertainty range of ±0.2°C from the available observational data. Climate models are expected to give an estimated response to external forcings, including the increasing concentrations of greenhouse gases in 1850–1930, along with natural forcings such as volcanic eruptions like Krakatoa. Models simulate their own internal variability adding ‘noise’ to this simulated climate response. The median of CMIP5 climate models gives a change of 0.21°C, and 0.17°C for both corrected CMIP5 and uncorrected CMIP6. These changes (all can be rounded to 0.2°C), represent the central estimate of different model responses, averaging out each model’s independent internal variability. A further analysis of a 40-member large ensemble of the CMIP6 model ACCESS-ESM1.5 gives a median estimate of 0.14°C, but with a range of −0.2 to 0.4°C, indicating that internal variability may be larger than the signal, but that the externally forced response is likely to be a small increase. Trends from observed datasets suggest natural variability did not produce a difference between these two periods that is dramatically different from the average response to forcings of a small increase; all datasets show a difference of 0.0–0.3°C.
The change in Australian temperature cannot be estimated precisely before 1910, and various factors may have affected it that are difficult to fully account for, including the transient cooling due to the Krakatoa eruption, rainfall trends or changes to aerosols. However, we present an estimate of 0.2°C (with this limited precision) as a best estimate based on the range from different datasets of early temperature change. Adding this value to the more established dataset that is available from 1910 and calculating change as a difference between periods rather than as a linear trend, the warming of Australia between 1850–1900 and 2011–2020 can be estimated at ~1.6°C with an uncertainty unlikely to exceed ±0.3°C. The ±0.3°C range is included throughout the entire series in Fig. 1 as a guide of uncertainty around this value. This change of 1.6°C is slightly greater than that from the linear trend in 1910–2021 of 1.44°C, mainly due to the warming in the early period and the effect of using a difference rather than a trend. This estimate of Australian historical climate warming is in line with the global land average, faster than the ocean average and the global average including oceans, but less than regions such as the Arctic or the large northern hemisphere continents. The CMIP models generally simulate a ratio of Australian to global warming that is lower than this new estimate of observed change (Section 3.3). This may be due to noise and uncertainty in this ratio from observations (Fig. 4), but if the ratio is persistently higher in observations than models with further warming, it may suggest a bias in models. A recent estimate of warming in the Arctic since 1979 is higher than previously suggested, and the amplification ratio is higher than in many models (Rantanen et al. 2022), and perhaps there are similar but less pronounced issues in Australia.
Into the future, the CMIP models also suggest that Australia warms at a ratio to global warming that is slightly lower than that in observations (1.0–1.3 times, compared to 1.4), but similar to the ratio in the historical period in models. If this is not explained by uncertainty in the observed ratio or model bias, as discussed above, and is in fact a reliable finding, then it may be due to an increasingly enhanced warming in the northern hemisphere compared to the southern hemisphere, especially over the large northern hemisphere continents and Arctic region (Friedman et al. 2013), but the precise details and causes of this need further investigation.
Projections for global warming levels are relevant to policy, as they are the framework used in the Paris Agreement and are a convenient way of overcoming issues around CMIP6 as an ‘ensemble of opportunity’ with an uneven spread of climate sensitivity. Projections for global warming level can be contextualised by providing the timing of reaching different global warming levels under different future emissions pathways.
Projected warming for Australia from CMIP6 under the very high SSP5–8.5 pathway with equal model weighting differed from those with an example model weighting scheme applied in this study and those from CMIP5 by up to ~0.8°C at the high end. This supports the view that that ‘one model one vote’ projections using CMIP6 give unbalanced estimates of warming (Hausfather et al. 2022), and a misleading view of the plausible range of temperature change. The effect is greater at the high end of the temperature range and under higher SSPs and near the end of the century, but will affect the projection under all SSPs. This analysis supports not using a ‘one model one vote’ approach when producing climate projections for SSPs and time horizons using CMIP6 for temperature projections and projections of variables that correlate with warming.
Various other solutions were used to produce balanced estimates of global warming for the SSPs by the IPCC’s Sixth Assessment Report (Masson-Delmotte et al. 2021), including the use of other weighting schemes, emulators and an explicit accounting for climate sensitivity. Alternatively, only the global warming level results can be produced, and these can be contextualised in terms of SSP and timeframe using the thorough assessment of the timing of reaching those warming levels produced using an assessment of more than just CMIP models given in IPCC’s Sixth Assessment Report (Masson-Delmotte et al. 2021). To apply a similarly thorough exercise to regional warming in Australia is beyond the scope of this study; however, we present this analysis as an illustration of the problem and to flag the need for further work.
The 10–90% range with weighting presented here shows a relatively balanced presentation of the bulk of the range but not the tails. Warming above the 90% percentile of the model range after weighting, including the models with very high climate sensitivity, also cannot be ruled out, but can be considered as a ‘low likelihood high warming outcome’, as in IPCC’s Sixth Assessment Report (Masson-Delmotte et al. 2021).
A more detailed analysis is required to give reliable estimates of Australian warming under the SSPs, involving CMIP5/CMIP6 models, the various weighting schemes, as well as an assessment of climate sensitivity and the use of emulators. The unequal sampling of climate sensitivity and warming in CMIP6 has flow-on effects to projected changes in temperature extremes, where changes to some extremes broadly follow the change in the mean, as illustrated by the initial assessment in Grose et al. (2020). However, it is also likely to affect the projected change in some other climate variables or features, and this needs careful assessment. Alternatively, users of climate projections can give a greater focus to global warming levels rather than time horizons, and the conditions and timing of reaching those global warming levels can be drawn from the independent assessment. This standardises for climate sensitivity and warming rates, then reintroduces the time and emissions pathway dimensions using a balanced assessment, as suggested in Hausfather et al. (2022).
5. Conclusions
Mean warming is often used for gauging and benchmarking climate changes, so quantifying past and likely future warming is useful. The estimate of ~1.1°C global warming between 1850–1900 and 2011–2020 is a highly cited statistic, and to estimate the equivalent Australian land area we must use various lines of imperfect evidence. Here we find that Australia likely warmed slightly between 1850 and 1910, and likely warmed by ~1.6°C between 1850–1920 and 2011–2020. This amount is similar to the global land average and ~1.4 times the global average including oceans. Uncertainty around this 1.6°C estimate is unlikely to substantially exceed ±0.3°C.
The future Australian mean annual temperature to 2100 depends very strongly on the emissions pathway the world follows. Future Australian warming is projected to likely remain higher than the global average but perhaps lower than the global land average, with variations across the region (lowest in Tasmania, highest inland). Owing to an uneven spread of climate sensitivity, the CMIP6 global climate models can be used for the ‘global warming levels’ framework with equal weighting, but not for time horizons and emissions pathways, where weighting or other modelling must be used.
Australia has experienced statistically significant and substantial warming to date, and further warming is projected proportional to the global emissions pathway. This mean warming is associated with substantial changes to climate extremes and impacts.
Data availability
Data are all publicly available at the various observed data sources (e.g. ACORN-SAT: http://www.bom.gov.au/climate/data/acorn-sat/) and model data are available through the World Climate Research Programme (WCRP) at the Program for Climate Model Diagnosis & Intercomparison (PCMDI; https://pcmdi.llnl.gov/CMIP6/).
Conflicts of interest
Blair Trewin is an Associate Editor for the Journal of Southern Hemisphere Earth Systems Science but did not at any stage have editor-level access to this manuscript while in peer review, as is the standard practice when handling manuscripts submitted by an editor to this journal. The Journal of Southern Hemisphere Earth Systems Science encourages its editors to publish in the journal and they are kept totally separate from the decision-making processes for their manuscripts. The authors have no further conflicts of interest to declare.
Declaration of funding
This work was funded and supported by the Australian Government’s National Environmental Science Program Climate Systems hub (NESP-CS). E. Hawkins was funded by the UK National Centre for Atmospheric Science and the NERC GloSAT project.
Acknowledgements
The authors acknowledge the various providers of model, observed and paleo-reconstruction datasets. We also thank the internal and external reviewers.
References
Amengual A, Homar V, Romero R, Alonso S, Ramis C (2012) A statistical adjustment of regional climate model outputs to local scales: application to Platja de Palma, Spain. Journal of Climate 25, 939–957.| A statistical adjustment of regional climate model outputs to local scales: application to Platja de Palma, Spain.Crossref | GoogleScholarGoogle Scholar |
Arias P, Bellouin N, Coppola E, Jones R, Krinner G, Marotzke J, Naik V, Palmer M, Plattner G-K, Rogelj J, Rojas M, Sillmann J, Storelvmo T, Thorne P, Trewin B, Achutarao K, Adhikary B, Allan R, Armour K, Bala G, Barimalala R, Berger S, Canadell JG, Cassou C, Cherchi A, Collins WD, Collins WJ, Connors S, Corti S, Cruz F, Dentener FJ, Dereczynski C, Di Luca A, Diongue Niang A, Doblas-Reyes P, Dosio A, Douville H, Engelbrecht F, Eyring V, Fischer EM, Forster P, Fox-Kemper B, Fuglestvedt J, Fyfe J, Gillett N, Goldfarb L, Gorodetskaya I, Gutierrez JM, Hamdi R, Hawkins E, Hewitt H, Hope P, Islam AS, Jones C, Kaufmann D, Kopp R, Kosaka Y, Kossin J, Krakovska S, Li J, Lee J-Y, Masson-Delmotte V, Mauritsen T, Maycock T, Meinshausen M, Min S, Ngo Duc T, Otto F, Pinto I, Pirani A, Raghavan K, Ranasighe R, Ruane A, Ruiz L, Sallée J-B, Samset BH, Sathyendranath S, Monteiro PS, Seneviratne SI, Sörensson AA, Szopa S, Takayabu I, Treguier A-M, van den Hurk B, Vautard R, Von Schuckmann K, Zaehle S, Zhang X, Zickfeld K (2021) Technical summary. In ‘Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change’. (Eds V Masson-Delmotte, P Zhai, A Pirani, SL Connors, C Péan, S Berger, N Caud, Y Chen, L Goldfarb, MI Gomis, M Huang, K Leitzell, E Lonnoy, JBR Matthews, TK Maycock, T Waterfield, O Yelekçi, R Yu, B Zhou) pp. 33−144. (Cambridge University Press)
| Crossref |
Ashcroft L, Karoly D, Gergis J (2012) Temperature variations of southeastern Australia, 1860–2011. Australian Meteorological and Oceanographic Journal 62, 227–245.
Beusch L, Nicholls Z, Gudmundsson L, Hauser M, Meinshausen M, Seneviratne SI (2022) From emission scenarios to spatially resolved projections with a chain of computationally efficient emulators: coupling of MAGICC (v7.5.1) and MESMER (v0.8.3). Geoscientific Model Development 15, 2085–2103.
| From emission scenarios to spatially resolved projections with a chain of computationally efficient emulators: coupling of MAGICC (v7.5.1) and MESMER (v0.8.3).Crossref | GoogleScholarGoogle Scholar |
Bloch-Johnson J, Rugenstein M, Gregory J, Cael BB, Andrews T (2022) Climate impact assessments should not discount ‘hot’ models. Nature 608, 667
| Climate impact assessments should not discount ‘hot’ models.Crossref | GoogleScholarGoogle Scholar |
Brunner L, Pendergrass AG, Lehner F, Merrifield AL, Lorenz R, Knutti R (2020) Reduced global warming from CMIP6 projections when weighting models by performance and independence. Earth System Dynamics 11, 995–1012.
| Reduced global warming from CMIP6 projections when weighting models by performance and independence.Crossref | GoogleScholarGoogle Scholar |
Cowtan K, Way RG (2014) Coverage bias in the HadCRUT4 temperature series and its impact on recent temperature trends. Quarterly Journal of the Royal Meteorological Society 140, 1935–1944.
| Coverage bias in the HadCRUT4 temperature series and its impact on recent temperature trends.Crossref | GoogleScholarGoogle Scholar |
Eyring V, Bony S, Meehl GA, Senior CA, Stevens B, Stouffer RJ, Taylor KE (2016) Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geoscientific Model Development 9, 1937–1958.
| Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization.Crossref | GoogleScholarGoogle Scholar |
Friedman AR, Hwang Y-T, Chiang JCH, Frierson DMW (2013) Interhemispheric temperature asymmetry over the twentieth century and in future projections. Journal of Climate 26, 5419–5433.
| Interhemispheric temperature asymmetry over the twentieth century and in future projections.Crossref | GoogleScholarGoogle Scholar |
Gergis J, Neukom R, Gallant AJE, Karoly DJ (2016) Australasian temperature reconstructions spanning the last millennium. Journal of Climate 29, 5365–5392.
| Australasian temperature reconstructions spanning the last millennium.Crossref | GoogleScholarGoogle Scholar |
Gergis J, Baillie Z, Ingallina S, Ashcroft L, Ellwood T (2021) A historical climate dataset for southwestern Australia, 1830–1875. International Journal of Climatology 41, 4898–4919.
| A historical climate dataset for southwestern Australia, 1830–1875.Crossref | GoogleScholarGoogle Scholar |
Grainger S, Fawcett R, Trewin B, Jones D, Braganza K, Jovanovic B, Martin D, Smalley R, Webb V (2022) Estimating the uncertainty of Australian area-average temperature anomalies. International Journal of Climatology 42, 2815–2834.
| Estimating the uncertainty of Australian area-average temperature anomalies.Crossref | GoogleScholarGoogle Scholar |
Grose MR, Narsey S, Delage FP, Dowdy AJ, Bador M, Boschat G, Chung C, Kajtar JB, Rauniyar S, Freund MB, Lyu K, Rashid H, Zhang X, Wales S, Trenham C, Holbrook NJ, Cowan T, Alexander L, Arblaster JM, Power S (2020) Insights from CMIP6 for Australia’s future climate. Earth’s Future 8, e2019EF001469
| Insights from CMIP6 for Australia’s future climate.Crossref | GoogleScholarGoogle Scholar |
Gulev SK, Thorne PW, Ahn J, Dentener FJ, Domingues CM, Gerland S, Gong D, Kaufman DS, Nnamchi HC, Quaas J, Rivera JA, Sathyendranath S, Smith SL, Trewin B, von Schuckmann K, Vose RS (2021) Changing state of the climate system. In ‘Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change’. (Eds V Masson-Delmotte, P Zhai, A Pirani, SL Connors, C Péan, S Berger, N Caud, Y Chen, L Goldfarb, MI Gomis, M Huang, K Leitzell, E Lonnoy, JBR Matthews, TK Maycock, T Waterfield, O Yelekçi, R Yu, B Zhou) pp. 287–422. (Cambridge University Press)
| Crossref |
Gutiérrez JM, Jones RG, Narisma GT, Alves LM, Amjad M, Gorodetskaya IV, Grose M, Klutse NAB, Krakovska S, Li J, Martínez-Castro D, Mearns LO, Mernild SH, Ngo-Duc T, van den Hurk B, Yoon J-H (2021) Atlas. In ‘Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change’. (Eds V Masson-Delmotte, P Zhai, A Pirani, SL Connors, C Péan, S Berger, N Caud, Y Chen, L Goldfarb, MI Gomis, M Huang, K Leitzell, E Lonnoy, JBR Matthews, TK Maycock, T Waterfield, O Yelekçi, R Yu, B Zhou) pp. 1927–2058. (Cambridge University Press)
| Crossref |
Harrington LJ, Frame D, King AD, Otto FEL (2018) How uneven are changes to impact-relevant climate hazards in a 1.5 °C world and beyond? Geophysical Research Letters 45, 6672–6680.
| How uneven are changes to impact-relevant climate hazards in a 1.5 °C world and beyond?Crossref | GoogleScholarGoogle Scholar |
Hausfather Z, Marvel K, Schmidt GA, Nielsen-Gammon JW, Zelinka M (2022) Climate simulations: recognize the ‘hot model’ problem. Nature 605, 26–29.
| Climate simulations: recognize the ‘hot model’ problem.Crossref | GoogleScholarGoogle Scholar |
Hawkins E, Ortega P, Suckling E, Schurer A, Hegerl G, Jones P, et al. (2017) Estimating changes in global temperature since the preindustrial period. Bulletin of the American Meteorological Society 98, 1841–1856.
| Estimating changes in global temperature since the preindustrial period.Crossref | GoogleScholarGoogle Scholar |
Hawkins E, Frame D, Harrington L, Joshi M, King A, Rojas M, Sutton R (2020) Observed emergence of the climate change signal: from the familiar to the unknown. Geophysical Research Letters 47, e2019GL086259
| Observed emergence of the climate change signal: from the familiar to the unknown.Crossref | GoogleScholarGoogle Scholar |
Huang B, Menne MJ, Boyer T, Freeman E, Gleason BE, Lawrimore JH, et al. (2020) Uncertainty estimates for sea surface temperature and land surface air temperature in NOAAGlobalTemp version 5. Journal of Climate 33, 1351–1379.
| Uncertainty estimates for sea surface temperature and land surface air temperature in NOAAGlobalTemp version 5.Crossref | GoogleScholarGoogle Scholar |
James R, Washington R, Schleussner C-F, Rogelj J, Conway D (2017) Characterizing half-a-degree difference: a review of methods for identifying regional climate responses to global warming targets. WIREs Climate Change 8, e457
| Characterizing half-a-degree difference: a review of methods for identifying regional climate responses to global warming targets.Crossref | GoogleScholarGoogle Scholar |
King AD, Karoly DJ, Henley BJ (2017) Australian climate extremes at 1.5 °C and 2 °C of global warming. Nature Climate Change 7, 412–416.
| Australian climate extremes at 1.5 °C and 2 °C of global warming.Crossref | GoogleScholarGoogle Scholar |
King AD, Lane TP, Henley BJ, Brown JR (2020) Global and regional impacts differ between transient and equilibrium warmer worlds. Nature Climate Change 10, 42–47.
| Global and regional impacts differ between transient and equilibrium warmer worlds.Crossref | GoogleScholarGoogle Scholar |
Lenssen NJL, Schmidt GA, Hansen JE, Menne MJ, Persin A, Ruedy R, Zyss D (2019) Improvements in the GISTEMP Uncertainty Model. Journal of Geophysical Research: Atmospheres 124, 6307–6326.
| Improvements in the GISTEMP Uncertainty Model.Crossref | GoogleScholarGoogle Scholar |
Masson-Delmotte V, Zhai P, Pirani A, Connors SL, Péan C, Berger S, Caud N, Chen Y, Goldfarb L, Gomis MI, Huang M, Leitzell K, Lonnoy E, Matthews JBR, Maycock TK, Waterfield T, Yelekçi O, Yu R, Zhou B (Eds) (2021) ‘Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change.’ (Cambridge University Press, Cambridge, UK, and New York, NY, USA)
| Crossref |
Meinshausen M, Nicholls Z, Lewis J, Gidden MJ, Vogel E, Freund M, et al. (2019) The SSP greenhouse gas concentrations and their extensions to 2500. Geoscientific Model Development Discussions 2019, 1–77.
| The SSP greenhouse gas concentrations and their extensions to 2500.Crossref | GoogleScholarGoogle Scholar |
Morice CP, Kennedy JJ, Rayner NA, Jones PD (2012) Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: The HadCRUT4 data set. Journal of Geophysical Research: Atmospheres 117, D08101
| Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: The HadCRUT4 data set.Crossref | GoogleScholarGoogle Scholar |
Morice CP, Kennedy JJ, Rayner NA, Winn JP, Hogan E, Killick RE, Dunn RJH, Osborn TJ, Jones PD, Simpson IR (2021) An updated assessment of near-surface temperature change from 1850: the HadCRUT5 Data Set. Journal of Geophysical Research: Atmospheres 126, e2019JD032361
| An updated assessment of near-surface temperature change from 1850: the HadCRUT5 Data Set.Crossref | GoogleScholarGoogle Scholar |
Nicholls N, Tapp R, Burrows K, Richards D (1996) Historical thermometer exposures in Australia. International Journal of Climatology 16, 705–710.
| Historical thermometer exposures in Australia.Crossref | GoogleScholarGoogle Scholar |
Rantanen M, Karpechko AY, Lipponen A, Nordling K, Hyvärinen O, Ruosteenoja K, Vihma T, Laaksonen A (2022) The Arctic has warmed nearly four times faster than the globe since 1979. Communications Earth & Environment 3, 168
| The Arctic has warmed nearly four times faster than the globe since 1979.Crossref | GoogleScholarGoogle Scholar |
Rogelj J, Schleussner C-F, Hare W (2017) Getting it right matters: temperature goal interpretations in geoscience research. Geophysical Research Letters 44, 10,662–10,665.
| Getting it right matters: temperature goal interpretations in geoscience research.Crossref | GoogleScholarGoogle Scholar |
Rohde RA, Hausfather Z (2020) The Berkeley Earth Land/Ocean Temperature Record. Earth System Science Data 12, 3469–3479.
| The Berkeley Earth Land/Ocean Temperature Record.Crossref | GoogleScholarGoogle Scholar |
Schleussner CF, Lissner TK, Fischer EM, Wohland J, Perrette M, Golly A, Rogelj J, Childers K, Schewe J, Frieler K, Mengel M, Hare W, Schaeffer M (2016) Differential climate impacts for policy-relevant limits to global warming: the case of 1.5 °C and 2 °C. Earth System Dynamics 7, 327–351.
| Differential climate impacts for policy-relevant limits to global warming: the case of 1.5 °C and 2 °C.Crossref | GoogleScholarGoogle Scholar |
Schurer AP, Mann ME, Hawkins E, Tett SFB, Hegerl GC (2017) Importance of the pre-industrial baseline for likelihood of exceeding Paris goals. Nature Climate Change 7, 563–567.
| Importance of the pre-industrial baseline for likelihood of exceeding Paris goals.Crossref | GoogleScholarGoogle Scholar |
Sherwood SC, Webb MJ, Annan JD, Armour KC, Forster PM, Hargreaves JC, Hegerl G, Klein SA, Marvel KD, Rohling EJ, Watanabe M, Andrews T, Braconnot P, Bretherton CS, Foster GL, Hausfather Z, von der Heydt AS, Knutti R, Mauritsen T, Norris JR, Proistosescu C, Rugenstein M, Schmidt GA, Tokarska KB, Zelinka MD (2020) An assessment of earth’s climate sensitivity using multiple lines of evidence. Reviews of Geophysics 58, e2019RG000678
| An assessment of earth’s climate sensitivity using multiple lines of evidence.Crossref | GoogleScholarGoogle Scholar |
Simmons AJ, Berrisford P, Dee DP, Hersbach H, Hirahara S, Thépaut J-N (2017) A reassessment of temperature variations and trends from global reanalyses and monthly surface climatological datasets. Quarterly Journal of the Royal Meteorological Society 143, 101–119.
| A reassessment of temperature variations and trends from global reanalyses and monthly surface climatological datasets.Crossref | GoogleScholarGoogle Scholar |
Taylor KE, Stouffer RJ, Meehl GA (2012) An overview of CMIP5 and the experiment design. Bulletin of the American Meteorological Society 93, 485–498.
| An overview of CMIP5 and the experiment design.Crossref | GoogleScholarGoogle Scholar |
Tokarska KB, Stolpe MB, Sippel S, Fischer EM, Smith CJ, Lehner F, Knutti R (2020) Past warming trend constrains future warming in CMIP6 models. Science Advances 6, eaaz9549
| Past warming trend constrains future warming in CMIP6 models.Crossref | GoogleScholarGoogle Scholar |
Trewin B, Braganza K, Fawcett R, Grainger S, Jovanovic B, Jones D, Martin D, Smalley R, Webb V (2020) An updated long-term homogenized daily temperature data set for Australia. Geoscience Data Journal 7, 149–169.
| An updated long-term homogenized daily temperature data set for Australia.Crossref | GoogleScholarGoogle Scholar |
van Vuuren DP, Edmonds J, Kainuma M, Riahi K, Thomson A, Hibbard K, et al. (2011) The representative concentration pathways: an overview. Climatic Change 109, 5–31.
| The representative concentration pathways: an overview.Crossref | GoogleScholarGoogle Scholar |
Zelinka MD, Myers TA, McCoy DT, Po-Chedley S, Caldwell PM, Ceppi P, Klein SA, Taylor KE (2020) Causes of higher climate sensitivity in CMIP6 models. Geophysical Research Letters 47, e2019GL085782
| Causes of higher climate sensitivity in CMIP6 models.Crossref | GoogleScholarGoogle Scholar |
Zhang H-M, Huang B, Lawrimore J, Menne M, Smith TM (2019) NOAA Global Surface Temperature Dataset (NOAAGlobalTemp), Version 5 [Dataset]. NOAA National Centers for Environmental Information.
| Crossref |