Redefining southern Australia’s climatic regions and seasons
Sonya Fiddes A B D , Acacia Pepler
A B D , Acacia Pepler  A , Kate Saunders
A , Kate Saunders  C and Pandora Hope
C and Pandora Hope  A
A
A Bureau of Meteorology, Melbourne, Australia.
B Present Address. Australian Antarctic Program Partnership, Institute of Marine and Antarctic Studies, University of Tasmania, Hobart, Australia.
C Delft Institute of Applied Mathematics, Delft University of Technology, Delft, Netherlands.
D Corresponding author. Email: sonya.fiddes@utas.edu.au
Journal of Southern Hemisphere Earth Systems Science 71(1) 92-109 https://doi.org/10.1071/ES20003
Submitted: 5 August 2020 Accepted: 16 February 2021 Published: 16 March 2021
Journal Compilation © BoM 2021 Open Access CC BY-NC-ND
Abstract
Climate scientists routinely rely on averaging over time or space to simplify complex information and to concisely communicate findings. Currently, no consistent definitions of ‘warm’ or ‘cool’ seasons for southern Australia exist, making comparisons across studies difficult. Similarly, numerous climate studies in Australia use either arbitrarily defined areas or the Natural Resource Management (NRM) clusters to perform spatial averaging. While the NRM regions were informed by temperature and rainfall information, they remain somewhat arbitrary. Here we use weather type influence on rainfall and clustering methods to quantitatively define climatic regions and seasons over southern Australia. Three methods are explored: k-means clustering and two agglomerative clustering methods, Ward linkage and average linkage. K-means was found to be preferred in temporal clustering, while the average linkage method was preferred for spatial clustering. For southern Australia as a whole, we define the cool season as April–September and warm season as October–March, though we note that a three-season split may provide more nuanced climate analysis. We also show that different regions across southern Australia experience different seasons and demonstrate the changing spatial influence of weather types with the seasons, which may aid regionally or seasonally specific climate analysis. Division of southern Australia into 15 climatic regions shows localised agreement with the NRM clusters where distinct differences in rainfall amounts exist. However, the climate regions defined here better represent the importance of topographical aspect on weather type influence and the inland extent of particular weather types. We suggest that the use of these regions would provide consistent climate analysis across studies if widely adopted. A key requirement for climate scientists is the simplification of data sets into both seasonally or regionally averaged subsets. This simplification, by grouping like regions or seasons, is done for a number of reasons both scientific and practical, including to help understand patterns of variability, underlying drivers and trends in climate and weather, to communicate large amounts of data concisely, to reduce the amount of data required for processing (which becomes increasingly important with higher resolution climate model output), or to more simply draw a physical boundary between regions for other purposes, such as flora and fauna habitat analysis, appropriate agricultural practices or water management.
Keywords: climate regions, Natural Resource Management (NRM), rainfall, topography, weather type, Southern Australia, k-means clustering, seasons, regions.
1 Introduction
The grouping of climate regions has been a problem long considered by climate and weather scientists, with the physicality of such groupings often limited by the type of data used to develop the regionalisation (for example by relying on just rainfall or temperature data at coarse resolutions or as station data in earlier attempts). As a result, these subsets of regions or seasons often included a level of subjectively defined groupings of data or methods of grouping that cannot take into account certain physical characteristics of the climate. We suggest that if scientists are tying to understand the physical reason for trends or variability in the weather or climate system (or systems dependant on weather and climate), inappropriate or arbitrary subsetting may dampen true signals or enhance false ones.
With increasing high-quality observational records and modelling capacity, climate data are becoming ever more comprehensive in time, space and information. Although the statistical methods employed in this study are well established within climate science, the application of such methods to these new and comprehensive data sets is providing important knowledge and new perspectives. For example, Drosdowsky (1993) used clustering to define rainfall regions over Australia, but was significantly limited by the quality and spatial extent of the data available at the time. Recent examples where clustering has been used with high-quality data include for the development of appropriate statistical modelling of rainfall extremes for different regions across Australia (Saunders et al. 2020) or to understand the synoptic effects of the El Niño Southern Oscillation (ENSO) over southeastern Australia (Hauser et al. 2020). In this work, we evaluate three different clustering methods and apply them in time and space using a new data set of daily weather types across southern Australia (Pepler et al. 2020). While we note that a subjective decision is still required for cluster analysis (as discussed in the methods section), the actual allocation of data points to a cluster is entirely quantitative. This quantitative allocation is where cluster analysis provides more meaningful results than the more subjectively chosen clusters, such as those discussed below.
In past analysis, ‘warm’ and ‘cool’ or ‘wet’ and ‘dry’ seasons (or clusters of time) have been used to provide information on the characteristics and trends of two distinct times of year. These half-year seasons are typically referred to as the ‘warm’ and ‘cool’ seasons in Australian climate studies, rather than ‘wet’ or ‘dry’, as the latter labels can mean quite different periods depending on the location (e.g. the wet period in northern Australia coincides with the warm season, while in southern Australia, it coincides with the cool season). The ‘warm’ and ‘cool’ season terminology is used in this study, and while describing different seasons on a temperature basis, is also applied to rainfall indices.
The South East Australia Climate Initiative (CSIRO 2012), the Climate Change in Australia (CCIA) project (CSIRO and Bureau of Meteorology 2015) and the Victorian Climate Initiative (Hope et al. 2017) have used the months November–March as the ‘warm’ season and April–October as the ‘cool’ season. However, other researchers have used a varying array of seasonal breakdowns including (but not limited to) considering the cool season as: May–October (Grose et al. 2015; Pepler et al. 2019b, 2020), May–September (Larsen and Nicholls 2009), April–October (Pook et al. 2006; Risbey et al. 2009b; Rauniyar and Power 2020), April–September (Freund et al. 2017), June–October (Pepler et al. 2014), May–November (Fiddes and Timbal 2017) or a more traditional autumn plus winter approach: March–August (Nicholls 2009). In most of these studies, the warm season was defined as the opposite months. The warm season has also been defined as the traditional spring plus summer approach to best represent the period influenced by the ENSO (for example in Lim et al. 2019).
We note that the definition of a season can depend on the topic of interest and extends beyond the climate into areas such as hydrology and water resource management. For example, many water resource managers define a ‘water year’ instead of a normal calendar year, where the ‘wet’ or ‘filling’ season encompasses the months that climatologically have the greatest streamflow. Similarly, seasonal definitions can also extend to the biosphere (e.g. breading or flowering seasons), including agricultural growth seasons and how people interact with their environment – for example: Indigenous seasonal calendars. While we note that such definitions may help simplify the process of evaluating resources and aid decision making, we suggest that such seasonal definitions may not be appropriate for understanding the physical weather and climate trends and variability behind the changes in the field of interest, if that field is intrinsically dependant on weather and climate. A clear and physically-based definition of seasons for southern Australia as a whole and for the regions within will enable more meaningful analysis of such physical mechanisms and easier comparison across studies leading to greater transferability of knowledge.
In a similar vein, analysis or averaging of climate data over broad regions is an important aspect of providing useable information to stakeholders or the scientific community. Australia experiences a variety of climatic zones which are heavily influenced by regional topography and nearby oceans. For example, we can see that the topography shown in Fig. 1a is clearly influencing total annual rainfall along the east coast shown in Fig. 1b, with large differences depending on the aspect relative to the mountains. However, analysis of rainfall and temperature alone cannot distinguish between regions that experience or are influenced by fundamentally different weather. Several current methods that are used to divide Australia based on climate information are discussed below. We also note that a number of studies in the literature use arbitrarily defined regions of southern Australia for their climate analysis, for example Dey et al. (2019).
For biodiversity, land and water management, Australia is divided into Natural Resource Management (NRM) regions, shown by white contours in Fig. 1c. The boundaries of these regions are somewhat arbitrary, being defined according to land management authorities on a state by state basis, rather than by climate information.
In the CCIA project undertaken by CSIRO and BoM, Australia was divided into eight clusters, in part based on these NRM regions, known as the ‘NRM clusters’ and shown in colours in Fig. 1c. The method used to identify these eight regions considered climatic and biophysical information from Stern et al. (2000), who provided a modified version of the Koeppen climate regions for Australia. Where possible the clusters were aligned with the NRM regions (of 2013) (CSIRO and Bureau of Meteorology 2019). These NRM clusters are now regularly used in climate science to provide regional information to stakeholders and authorities (Freund et al. 2017; Di Virgilio et al. 2019; Grose et al. 2020).
Koeppen climate classifications are determined based on seasonal rainfall and temperatures, but do not take into account broader scale climatic or weather type influences. An updated Koeppen climate classification scheme is shown in Fig. 1d (Peel et al. 2007). By comparing Fig. 1b with Fig. 1d, we can see that the influence of rainfall is clearly evident. One significant limitation of Koeppen climate regions is its inability to differentiate between topographical aspects. It is well understood that the east/west or north/south aspects of the Great Dividing Range (GDR) experience significantly different rainfall regimes (e.g. Timbal 2010; Fiddes et al. 2015). Systems such as cold fronts and cyclones embedded in the westerly storm track or cut-off lows, also propagating from the west, play an important role to the west of the GDR (Risbey et al. 2009a, 2013). On the other hand, cyclones that propagate towards Australia from the east, such as East Coast Lows or moist onshore flow, have a much greater influence on the east coast (Pepler et al. 2014).
In this work, a new weather types dataset (Pepler et al. 2020) allows us to quantitatively determine for the first time the seasonal periods and spatial regions of southern Australia in which rainfall is brought by similar weather types. Using this information we can evaluate commonly used regionalisation methods and assess whether they are appropriate for continued use in climate science.
2 Data and methods
2.1 Weather type and rainfall data
A new dataset of weather types that influence rainfall in southern Australia (south of 25°S), presented in Pepler et al. (2020), is used for this study. The Pepler et al. (2020) dataset uses multiple automated methods of front and low pressure (cyclonic) system detection, combined with environmental conditions relevant to thunderstorms (Dowdy 2020) as well as detection of warm fronts and a dataset of anticyclones (Pepler et al. 2019a, 2019b) to provide a comprehensive summary of the daily weather types important for rainfall for southern Australia. While each of these weather types are represented, fronts, cyclones and thunderstorms are also considered when they occur concurrently, resulting in compounding events with large impacts on rainfall (e.g. front-thunderstorm events). Pepler et al. (2020) use the ERA-Interim (Dee et al. 2011) product at a resolution of 0.75° to produce a gridded, daily dataset of weather types for the period of 1979–2015. Rainfall has been associated with these weather types using the Australian Water Availability Project (AWAP) gridded (0.05°), daily rainfall data set (Jones et al. 2009), shown in Fig. 1b. Maximum temperatures have also been taken from the AWAP dataset.
By using a comprehensive dataset of weather types for every day over 1979–2015 for southern Australia, we have been able to identify unique regions of Australia in the most robust way currently available. However, it is important to note that there are a large number of ways to potentially classify rain-bearing systems in Australia, including the role of upper-level systems such as cut-off lows (Risbey et al. 2013), distinguishing between lows with a tropical or extratropical nature (Cavicchia et al. 2019), or other rain-bearing systems such as atmospheric rivers and northwest cloudbands (Reid et al. 2019), so the choices used for defining weather systems will likely influence the results of the clustering.
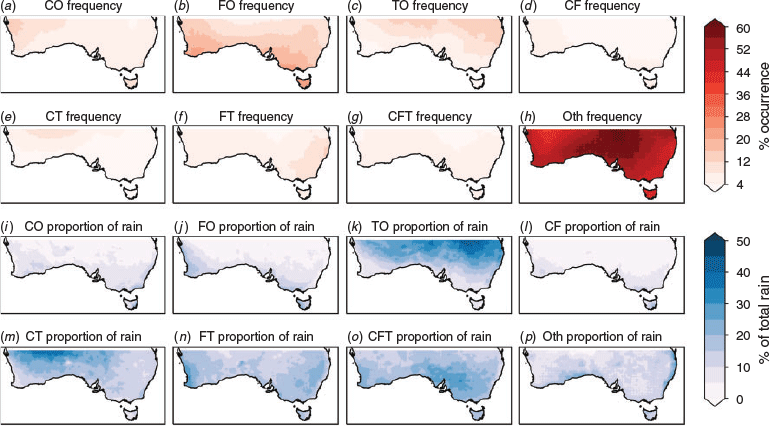
The weather types data in this study have been organised into the proportion of rain each weather type delivered to each grid point per month (Fig. 2). The major rain-bearing weather types (fronts, cyclones and thunderstorms), and the combinations thereof (e.g. cyclone-fronts or cyclone-fronts-thunderstorms), each provide a point to cluster on. Little change in results are found when non-major rain-bearing weather types (highs and warm fronts) are considered their own data point compared to if they are included into the ‘other’ category. Hence, non-major rain-bearing weather types, undefined types and unconfirmed cyclones or fronts are grouped into an ‘other’ category. Subsequently, at each grid cell we have eight fractions of the total rainfall.
The Euclidean distance between the fractions of rainfall at different cells is used for clustering. Using the proportion of rain associated with each weather type enables us to understand southern Australia’s seasons and climate zones with respect to rainfall and to easily perform averaging statistics over regions. The choice of distance is vitally important to the final assignment of grid cells to clusters, and here we make a conscious decision to use proportions of rainfall instead of totals to calculate the distance. This ensures the final clustering is related to all weather types, and avoids the situation where the rainfall delivered by one weather type dominates all others, dwarfing the contribution of the other weather types in the Euclidean distance calculation, and biasing the resulting regions. The trade off is that in using proportions we do lose some sensitivity. For example, if one point has a 10% contribution, we cannot distinguish whether this is 1 mm in 10 mm, or 100 mm in 1000 mm. While normalisation or other statistical processing, such as principal component analysis (PCA), can be used to ‘flatten’ the data, for rainfall at a daily scale this is non-trivial. Hence proportionality was used.
Other distances were also considered, including using the the frequency of weather types (without the relationship to rainfall). However, a frequency based distance was unable to capture important physical influences, such as from topography. Also given neither totals or proportions reflect the dry climate, we explored adding a ninth component to the vector of 8 weather types. The ninth point represented the normalised total rainfall of the period (annual or seasonal) in an attempt to reduce sensitivity in low rainfall regions. The results were very similar using this ninth component and hence are not shown.
For the seasonal analysis, we have calculated the monthly spatial average rainfall proportion associated with each weather pattern (resulting in a sample size of 12), upon which the clustering was performed. For the spatial analysis, the average annual or seasonal proportion of rainfall associated with each weather type was calculated for each grid box over the specified region.
2.2 Clustering methods
There are a number of different methods that can be used to identify spatially coherent regions with similar climate characteristics. One common approach is to identify areas that have similar temporal variability, such that the rainfall within the region is strongly correlated. This is frequently achieved through PCA or empirical orthogonal functions (EOFs), and is often applied to spatial data such as sea surface temperatures (Saji et al. 1999; Yuan Zhang et al. 1997). This approach has been also applied to identifying regions of Australia with coherent rainfall patterns (e.g. Drosdowsky 1993). PCA can also be used to ‘flatten’ a large array of data (especially when considering multiple fields) into a subset that can be more easily treated using Euclidean clustering analysis (Wilks 2011; Jiang et al. 2012). Studies interested in individual extreme events also frequently apply self-organising mapping (SOM) to large gridded datasets such as mean sea level pressure in order to divide the data into a small number of coherent spatial patterns (e.g. Alexander et al. 2010; Gibson et al. 2017).
In this paper, rather than identifying regions with similar temporal variability, we instead want to identify regions with similar rainfall characteristics. This means that rather than areas such as south west Western Australia and south east Australia being separated due to their different relationships with drivers such as ENSO (as in Drosdowsky 1993), we can identify areas which are affected by fundamentally the same types of weather, regardless of their spatial location. To achieve this we use two distinct clustering methodologies: k-means clustering and hierarchical clustering. These methods of clustering are a form of unsupervised learning that is highly flexible and can be used with minimal assumptions. This makes it well suited to simplifying large datasets and uncovering hidden structure (Hastie et al. 2001). We further note that k-means clustering can be considered a special subset of SOM (Gibson et al. 2017).
2.3 K-means clustering
K-means clustering is one of the most popular and commonly used methods for finding structure within a dataset (Hastie et al. 2001; Wilks 2011). The k-means method separates a set of N points into k clusters by minimising the sum of squared distances within each cluster. For Euclidean distances, this is the same as minimising the within cluster variances or the inertia (sum of squares).
2.4 Hierarchical clustering
Agglomerative-hierarchical clustering in contrast, takes a bottom-up approach (Hastie et al. 2001). Each point initially forms its own cluster, two clusters are merged together according to a linkage criterion and this merging of cluster pairs is repeated until all points are in the same cluster. This sequential merging of clusters creates a hierarchical tree-like structure, also known as a dendrogram (see Fig. 3). The final assignment of points to clusters is determined by cutting across the dendrogram and grouping points in the same branch of the tree. At low cut heights, the strength of association between points in a cluster is strongest and lots of small clusters are produced. At higher cut heights, the strength of association is weaker, and fewer, larger clusters are created.

|
The linkage criterion determines which two branches (clusters) are merged in the tree, with different linkage criterion producing different dendrograms and different clusters. Two common linkage criteria for merging branches are Ward linkage and average linkage. The Ward linkage is similar to k-means. The two clusters with the smallest sum of squared distances between points will be merged. For the average linkage, the two clusters with the smallest average distance between the clusters are merged.
2.5 Selecting the number of clusters
Deciding upon the number of clusters can be a somewhat subjective process, and, strictly speaking, there is no ‘true’ structure to recover. Therefore, there may not be a definitive answer to how many clusters to select. Different statistical methods can be used to aid in making a decision about the number of clusters. These methods are subject to interpretation and different methods may infer different numbers of clusters. It is therefore equally important to take into consideration the physical meaning of the resultant clusters (e.g. do they make sense with what we know about the region’s topography, dominant flow?) as well as the practicality of the clusters (e.g. are the clusters defined useful for end users, are they too large or too small?).
Several methods have been used to help identify an appropriate number of clusters for this work in an effort to make a less subjective decision. The elbow method plots the inertia over a range of cluster numbers. The optimal number of clusters can be found where an ‘elbow’ can be identified in a plot of the inertia, i.e. the point after which the inertia start decreasing linearly. This method is particularly useful for k-means clustering. Three other metrics for cluster number evaluation were employed in this work, including the Calinski–Harabasz score, the Silhouette score and the Davies–Bouldin index (Calinski and Harabasz 1974; Rousseeuw 1987; Davies and Bouldin 1979). However, these metrics provided little additional or useful guidance in the applications of this work and subsequently are not shown or discussed. For hierarchical clustering, multiple cut heights were considered and user knowledge based on known topographic and climate features was used to make a final decision of the number of clusters. The Pedregosa et al. (2011) python package was again used to perform each of these analysis.
2.6 Method considerations
There are some implicit assumptions and statistical considerations to be aware of when choosing between the different cluster methods. For example, k-means is susceptible to outliers and has underlying Gaussian assumptions that influence the resulting clusters. This can create problems for irregularly shaped or high-dimension data. In contrast, for flatter point geometries (lower dimensional data), k-means often creates clusters of similar size. This characteristic is undesirable for the application of spatial clustering in this study, as coastal clusters are expected to be smaller compared with large inland desert clusters.
The Ward linkage is similar to k-means, in that it also minimises the variance when using an Euclidean distance. Again, as data underpinning this work do not necessarily have a Gaussian distribution, the clustering may not reflect the application well. This is why the average linkage is also considered. The average linkage is well suited for both Euclidean and non-Euclidean distances. It is also flexible in the sense that the clusters can occur of uneven sizes.
In contrast to k-means, in hierarchical clustering once points are assigned to a branch and grouped, the points cannot be separated again later. In some instances this may be considered a drawback. For this application, nearby points in space are expected to experience similar weather. The imposed hierarchy should therefore help ensure the spatial coherence of clusters. Also the bottom-up approach should provide useful information about how regions evolve and how different weather type impacts occur on different spatial scales.
3 Annual average clusters for southern Australia
To identify the regional clusters for southern Australia, we have calculated the annual mean proportion of rainfall brought by each weather type for each grid box. Clustering was performed for the three methods discussed in Section 2. The k-means and Ward methods produced a remarkably similar regional breakdown of southern Australia (not shown), irrespective of the number of clusters. However, as suggested in Section 2, both these methods are biased toward clusters of a similar size and susceptible to spurious allocation of samples to clusters. In particular, north–south banding of clusters in the dry regions of southern Australia was found, in part demonstrating the increasing dominance of thunderstorms heading northwards and their localised nature. While the increasing northwards dominance of thunderstorms is a physically robust result, we do not believe that the regions produced by k-means and Ward clustering over the desert regions (where less than 250 mm year−1 of rain falls) are as climatically different as these methods suggest. By comparison, the average linkage method showed a reduced tendency towards north–south banding in the dry regions of Australia, while similarly capturing many of the clusters found in wetter parts of Australia. For this reason, the average linkage method will be used for spatial clustering going forwards.
To investigate an appropriate number of clusters to choose from, the dendrogram using the average linkage method is shown in Fig. 3. Each vertical line, or branch, represents a cluster at a certain step in the algorithm, where the bottom represents individual grid points at the beginning through to the point where just one cluster exists at the top. The horizontal lines show where in this processes two branches have been merged to form a larger cluster. We can use dendrograms to inform us of what the best ‘cut height’ or number of clusters is, by looking at how much distance (on the y-axis) exists between merges (horizontal lines). A larger distance indicates a greater difference between the two clusters being merged. The dendrogram is also able to provide information about when the clusters have been merged, their size and their structure.
Seven branches have been identified in Fig. 3 (shown by the colours) in which the distance from the most recent merge of clusters is relatively large. From the structure of the dendrogram we should expect three large clusters (dark blue, red and light brown), two small clusters (light blue and dark brown) and two very small clusters (note that the purple branch is actually two – see the two grey lines above), highlighting the average linkage method’s ability to form clusters of uneven size.
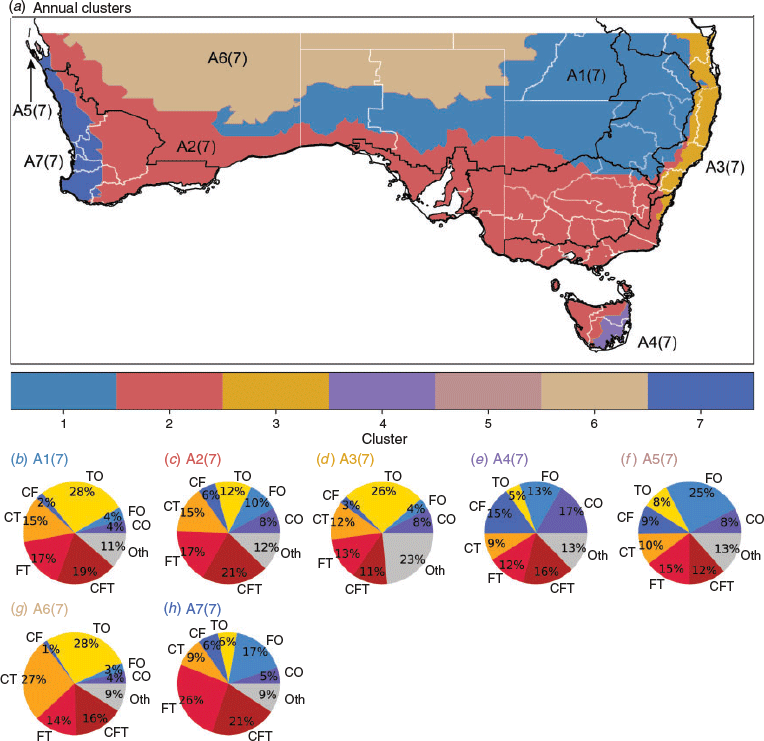
When the seven clusters are plotted spatially (Fig. 4 – note the naming convention A–annual, cluster number and total number of clusters), we can see the three large clusters make up the interior of southern Australia, while the remaining four smaller clusters are restricted to coastal regions. We note that the smallest cluster (A5(7)) is located in the north-west corner of the plot, over the peninsulas surrounding Shark Bay in Western Australia. The Shark Bay cluster sees a large proportion of rainfall from fronts (26%) with little thunderstorm activity. For large-scale climate analysis, merging this region into the west coast cluster (A7(7)), which also receives a large amount of rainfall from frontal activity, is deemed practically appropriate if using coarse resolution gridded products. However for regional-scale analysis, we recommend that this region remains as an individual cluster as it has been found by the clustering to have an independent influence from rain-bearing weather systems. This recommendation is also applied to the remaining small clusters identified in this study unless otherwise stated.
Similar to the Shark Bay cluster, the west coast cluster is dominated by frontal activity and appears to show the extent of frontal dominance into Western Australia’s interior. This cluster also aligns well with the region that experiences the most rainfall, however, the boundaries of A7(7) and A2(7) do not align well with NRM regions in south-western Australia.
On the east coast, cluster A3(7) is clearly constrained by the GDR, aligning it well with the east coast NRM cluster. Interestingly, however, the east coast cluster does not extend into Victoria, likely highlighting the dominant nature of moist onshore flow generating rainfall along the mid-east coast, and less so along the south-east coast. Similarly, for the A4(7) cluster on the Tasmanian east coast, the weather types of influence are also clearly influenced by the topography, resulting in a clear lack of rain on the leeward side of the mountains (see Fig. 1c,d).
The three interior clusters, A1(7) (north-east interior), A2(7) (southern coast) and A6(7) (north-west interior) show a degree of north–south banding, however in the two northern clusters an east–west divide is also apparent. Comparing the north-west and north-east interior clusters, we can see that they are both dominated by thunderstorm only activity, bringing 28% of rain to each region. However, the north-west interior cluster is also heavily influenced by cyclone-thunderstorm events making up another 27% of rain, compared to 15% for the north-east interior cluster, which appears to have more front-thunderstorm and cyclone-front-thunderstorm events. While some arguments could be made for the merging of these two regions given their dependence on thunderstorms, similar to that of the NRM clusters, we suggest that the differences between cyclone and frontal activity warrants separate clusters.
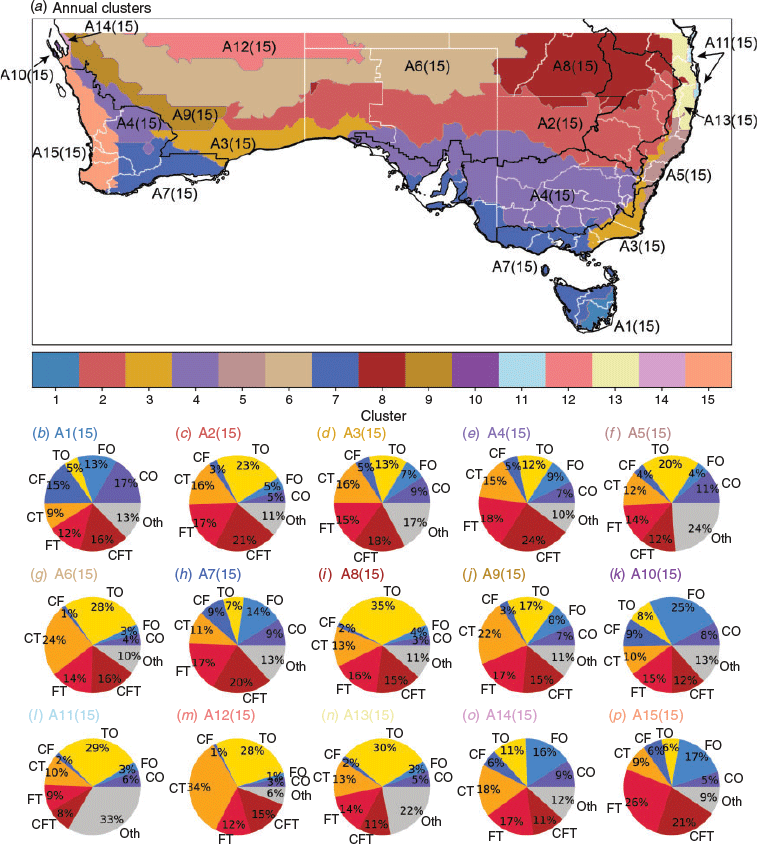
The clusters presented in Fig. 4 represent the structure shown in the dendrogram in Fig. 3 when a high cut height is taken. However, our knowledge of these areas suggests that different climate regions exist within some of the larger clusters, in particular the southern coast cluster, which may be of use for regional climate studies. To overcome this issue, we take a lower cut height in the dendrogram presented in Fig. 3. Figure 5 presents clustering using the average linkage method over 15 clusters. The number 15 was selected after careful consideration as it provided the best representation of physical climate regions to our knowledge while also ensuring meaningful differences between the clusters.
At first glance, the clusters presented in Fig. 5 agree relatively well with the NRM clusters shown in black (and in Fig. 1c). The NRM clusters were informed by a previous version of the Koeppen climate regions and so by nature, the clusters presented here also agree well with the broader Koeppen climates. This result is encouraging, given that the dataset used to perform clustering in this study, unlike the Koeppen climate zones, has no knowledge of either temperature or total rainfall. With this in mind, we can be satisfied that the regions developed in this study are a good reflection of different climate regions with the additional benefit of weather type information.
More specifically, we can see that the southernmost cluster found in Fig. 4 has now been separated into six separate clusters. The two northern interior clusters presented in Fig. 4 have been further split into two main clusters each. Examination of clusters A2(15) and A8(15) in Fig. 5 indicate that these two regions do represent different climatic regimes, with increasing thunderstorm activity northwards and increasing cyclone and front activity southwards. Clusters A6(15) and A12(15) show an equal proportion of rainfall from thunderstorms, while further north a greater dependence on cyclone-thunderstorm activity is the dominant source of rainfall. However, A12(15) is in a region of Australia with very low observation density (and low rainfall), impacting the reliability of the gridded rainfall products over the area (Jones et al. 2009; King et al. 2013). Hence lower confidence is given to the results of cluster A12(15).
Over south-western Australia and south-eastern Australia, clusters A3(15), A4(15) and A7(15) together align relatively well with the NRM clusters over the respective regions. While these three clusters discontinuously span the extent of southern Australia, the individual regions shown are sensible given current climate knowledge. Furthermore, the spanning of these clusters over both south-western and south-eastern Australia supports the zones identified in the Koeppen climate regions (Fig. 1d) as well as current thought that the two regions have many climatic similarities in terms of both trends and variability. However, although from this analysis we have found that these split regions are impacted by similar types of weather, we know that the origins of these weather types are different and that some climatic or physical characteristics are also fundamentally different (for example, the role of topography in the two regions of cluster A3(15)). For this reason, we suggest that the physically separated region of clusters A3(15), A4(15) and A7(15) may, when appropriate, be considered as separate climate regions.
More specifically, over Victoria, clusters A3(15), A4(15) and A7(15) reflect remarkably well the division of the state presented in Hope et al. (2017) and Timbal et al. (2017), primarily forced by the GDR. In addition, Cluster 4, over eastern Australia, reflects well some of the most productive agriculture regions, including much of the southern Murray–Darling Basin. Over south-western Australia, cluster A15(15) is heavily influenced by frontal activity where the majority of rainfall for the region is received (Hope et al. 2015), while clusters A4(15) and A7(15) show a more mixed contribution of rainfall from weather types, with thunderstorms more important in A4(15) and cyclones and fronts in A7(15).
Two very small clusters are found over north-west Western Australia, including the Shark Bay region (A10(15) in Fig. 5) previously discussed as well as a region along the north-western coastline, A14(15). Cluster A14(15) is somewhat comparable to A15(15) and A10(15) with respect to front only activity, though some differences remain when considering the combined weather events. Again, given their very small areal representation, merging clusters A10(15) and A14(15) into A15(15) and A9(15) respectively is deemed appropriate for instances where coarse resolution gridded products are being used.
Along the mid-east coast, two main clusters have been found, clusters A5(15) and A13(15). Both clusters receive a large proportion of rain from the ‘other’ category. Easterly onshore winds in this region produce a proportion of this ‘other’ rainfall (Pepler et al. 2014), which, if they do not generate thunderstorm activity, are unable to be classified with this data set. If we analyse the breakdown of the ‘other’ rainfall in cluster A5(15), we find that 11% of rainfall is associated with a nearby anticyclone, 6% from a warm front, and 4% each for unconfirmed cyclones/fronts or undefined weather types. Cluster A5(15) also sees a relatively large proportion of rainfall from cyclone only and cyclone-thunderstorm events, likely to represent the influence of East Coast Lows, which produce a large proportion of rainfall in the southern half of the eastern seaboard (Pepler et al. 2014). In contrast, thunderstorm-related types contribute a larger proportion of rainfall in cluster A13(15) which is more subtropical in nature (Fig. 1). The ‘other’ weather type category is approximately equally split between the four subcategories, indicating that anticyclones are playing a less important role in cluster A13(15).
Figure 5 shows that cluster A11(15) has been separated from A13(15). Both clusters have an important source of rainfall from thunderstorms, however A11(15) has more rainfall from the ‘other’ category, which also breaks down approximately equally into the four subcategories. In additional, A11(15) receives significantly more rainfall than A13(15) (median of 1460 mm year−1 compared to 1015 mm year−1), and hence it is interesting that this has been picked up by the clustering method. However, given the limited areal coverage of A11(15), we consider merging this cluster with A13(15) appropriate for large-scale climate analysis, although we note that for other purposes this may not be desirable.
These results have found 15 distinct climatic regions of varying sizes annually. However, we note that these regions may not be stationary as different weather types affect different regions throughout the year. For example as the westerly stormtrack moves equatorwards during winter, cyclones and fronts are more likely to effect southern parts of Australia, while warmer temperatures over the summer months provide better conditions for thunderstorm development. Subsequently, in the next section, we evaluate the southern Australian seasons, again using clustering, but in time instead of space. With quantitatively defined seasons, we repeat the spatial clustering for each season in order to detect how these climate regions may change throughout the year.
4 Defining southern Australia’s seasons by weather type
In order to identify the best definition of a season, we are using the monthly mean proportion of rainfall attributed to each weather type, resulting in a sample size of 12. The three methods of clustering described in Section 2 were evaluated. Little practical guidance was provided by the cluster number evaluation metrics (the Calinski–Harabasz score, the Silhouette score and the Davies–Bouldin index), each of which suggested that 12 clusters (of 12 samples) was the most suitable. For this reason, we have focused on the elbow plot for the k-means method and dendrograms for the Ward and average linkage methods, shown in Fig. 6.

|
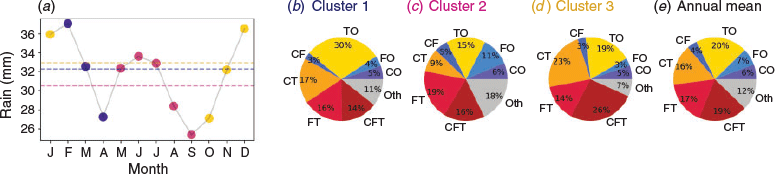
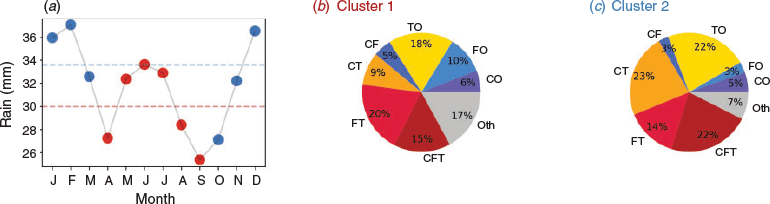
Figure 6a shows a weak elbow at around four clusters, after which the distances more linearly decrease. The structure of the Ward linkage dendrogram (Fig. 6b) suggests that there are two seasonal clusters for southern Australia. The average and Ward method dendrograms are similar in structure, however, the timing of amalgamation varies. The average dendrogram shows a cluster with just a single month, which also occurs for k-means when four clusters are selected. For this work, we do not consider a single month to be representative of a season. Hence, we show below the seasonal clustering for three seasons (Fig. 7), where the Ward and average linkage hierarchical methods and the k-means non-hierarchical method provide the same results.
Figure 7a divides the year into an ‘early summer’ from October–January (Cluster 3), a ‘late summer’ from February–April (Cluster 1) and a ‘winter’ season from May–September (Cluster 2). The early summer season receives the most rainfall of the three seasons (32.9 mm month−1), which is largely a result of the combination of cyclones, fronts and thunderstorms (bringing 26% of rain, see Fig. 7d). Other weather types that include thunderstorms (thunderstorm only, cyclone-thunderstorm or front-thunderstorm combinations) make up the majority of the remaining rainfall. The early summer season is also the warmest compared to the late summer and winter, with average maximum temperatures of 31°C, 30°C and 20°C respectively. Late summer rainfall is, on average, slightly lower than the early summer rainfall (32.3 mm month−1) and is dominated by thunderstorm only events, making up 30% of rainfall. The late summer season receives less rainfall from combined events (cyclone-thunderstorm and cyclone-front-thunderstorm) than the early summer, and a higher proportion of rainfall on ‘other’ days. The winter season is the coolest and driest (30.5 mm month−1) cluster and receives less rainfall from thunderstorms than the warm seasons. Instead, this season receives an increased proportion of rainfall from front-only (11%) and cyclone only (6%) events, as well as an increase in unclassified (17%) rainfall, which is predominantly associated with high pressure systems and warm fronts.
The division of the annual cycle into three seasons provides some practical purpose for climate science. For example, in southeastern Australia, autumn (March–May) rainfall has been found to have the largest declines in rainfall in the region (Nicholls 2009; Timbal 2009; Dey et al. 2019), a considerable concern for the agricultural growing season (Pook et al. 2009). Having more appropriately defined seasons may help understand these trends in greater detail and without confounding influences. The breakdown into three seasons here may also reflect the diverse nature of climates found across southern Australia.
While a three season breakdown can be useful, a two season breakdown is commonly used in recent climate science (as discussed in the introduction) and hence is also provided here. The definition of the two seasons varies depending on clustering technique. The k-means method suggests two evenly distributed seasons: a ‘warm’ season of October–March and a ‘cool’ season of April–September. Alternatively, both the hierarchical methods suggests a warm season of October–April, and a cool season of May–September. One important difference between these methods is in the ability for k-means to move samples into different clusters throughout the iterative process in order to minimise the inertia. For hierarchical methods, once a sample is grouped it cannot change, even if it may fit better elsewhere, as seen from the dendrograms. This strictness in the hierarchical clustering is beneficial for spatial clusters, as discussed in Section 2, though less so for temporal clusters. We suggest in this instance that the k-means method may better reflect the true seasonal distribution and these results are presented in Fig. 8.
Figure 8c shows that the warm season (October–March), is dominated by thunderstorm activity both in isolation (22%) and in combinations with cyclones and fronts (22%). The cool season (April–September) shows reduced thunderstorm activity and a higher proportion of front only activity, cyclone only events and ‘other’ weather events.
5 Seasonal non-stationarity of climate regions
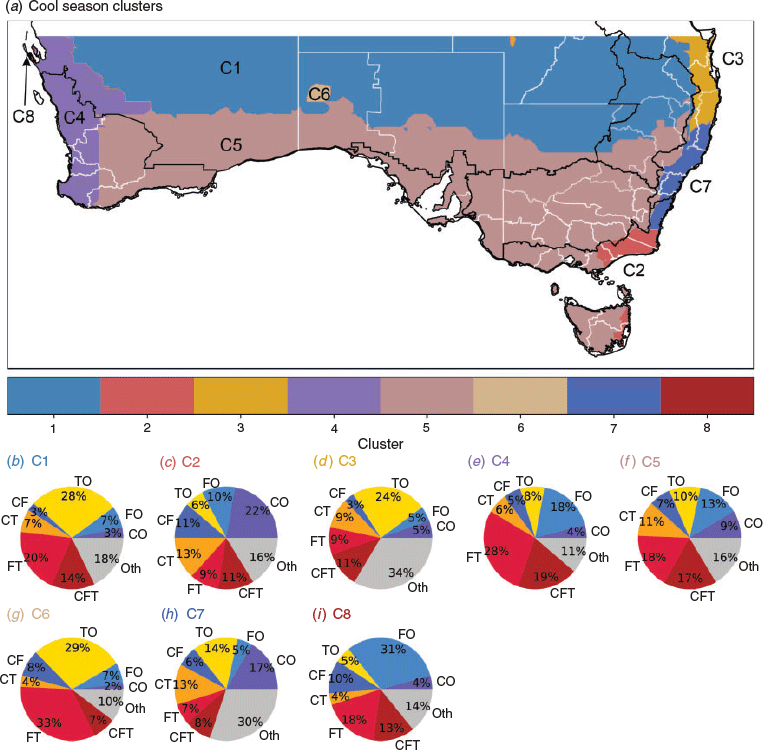
The quantitative breakdown of seasons performed above now allows us to examine the non-stationarity of the climate regions for the first time. For this section, we employ the average linkage method, as for the annual climate regions clustering in Section 3, and we use the two season breakdown found in Section 4: October–March (warm) and April–September (cool). Dendrograms of both seasons (not shown) indicate structures with six separate groups. However, as for the annual region, we understand that greater climate regionality exists than what the six groups provide (not shown). For this reason, eight clusters have been selected and are believed to appropriately represent the climate regions of southern Australia, while reducing unphysical behaviour over desert regions.
For the warm season, Fig. 9 shows eight clusters of varying size with some interesting differentiations. The two large northern clusters, W1 and W2, are dominated by thunderstorms, with the north-eastern clusters receiving 35% of rain from thunderstorm only events. The north-western cluster, similar to that of the annual period, is dominated by combined cyclone-thunderstorm events, bringing 36% of rain. Cluster W3, on the north-west coast, while similar to W2 further inland with respect to cyclone-thunderstorm events, also sees 14% of rain from cyclone only weather types. Cluster W8 has been split between the east coast and parts of the south coast of Western Australia, with the majority of rain arising from thunderstorm-related weather types as well as other days. Cluster W4 has also been dispersed across the southern coastline and Tasmania, with a fairly high proportion of rainfall from fronts and cyclones. Finally, cluster W5, in southeast Australia has the largest proportion of rainfall from cyclone-front-thunderstorm activity, with less cyclone and/or front activity than the coastal clusters over southeast Australia.
Compared to the warm season and the annual clustering, the cool season sees a more consistent north–south spread of clusters, with two major regions in the north and south making up the majority of southern Australia (Fig. 10). We note that even with up to 15 clusters, these two large areas remain consistent, indicating a strong association within each cluster. The low east–west separation (bar the east and west coast) reflects the dominance of westerly flow over southern parts of Australia during the cool season.
Cluster C1, in the north, is dominated by thunderstorm only events, making up 28% of rainfall, while cyclone and front only or combined events contribute little rainfall. Cluster C5 on the other hand has a larger proportion of cyclone and frontal activity that when all combined (cyclone only, front only plus cyclone-front) make up 29% of rainfall. Along the the east coast, clusters C3 and C7 show clear influences of easterly propagating weather systems, with 34% and 30% of rain from ‘other’ weather types, likely to be from moist onshore flow. The influence of cyclone only and cyclone-thunderstorm systems are clearly evident in clusters C2 and C7, likely to be associated with East Coast Low type events, making up 35% and 30% of rain.
On the west coast, cluster C4 is shown to have an important source of rainfall from frontal and front-thunderstorm activity, making up 46% of rainfall in the cool season. Similar to that found for the annual clusters, a small region over Shark Bay, Western Australia has been isolated (C8), where the influence of frontal activity stands out (31%) and thunderstorm activity is at a minimum. Finally, a very small region in central Australia (C6) is found, where front-thunderstorm rainfall is very important (33%). This region is an area of very low cool season rainfall and low station density (King et al. 2013). The authors have less confidence in the AWAP data over this region and believe that this cluster may be identified due to artefacts in the data rather than being a separate climate regime. For this reason we recommend that this cluster should be merged with the larger C1 region in all circumstances.
We note that the clusters shown in this section are for the average linkage clustering method, which retains inherent structural information, such as spatial awareness, and does not require clusters to be of a similar size. The k-means and Ward linkage methods show some similar features over regions such as south-western Australia and the east coast, but have many more inland clusters of similar sizes (as apposed to some very small clusters found in the average method) that were not thought to be appropriate climate regions.
The cool and warm seasonal clusters have shown how the changing seasonality of weather types influences the distribution of rainfall over southern Australia. For studies examining seasonally isolated trends historically or into the future these climate regions may provide more nuanced results. At the same time however, we note that the regions identified in Section 3 may experience a different seasonal cycle to that of the broad southern Australian average, depending on their major influences. We address this in the next section.
6 Climate region seasonality
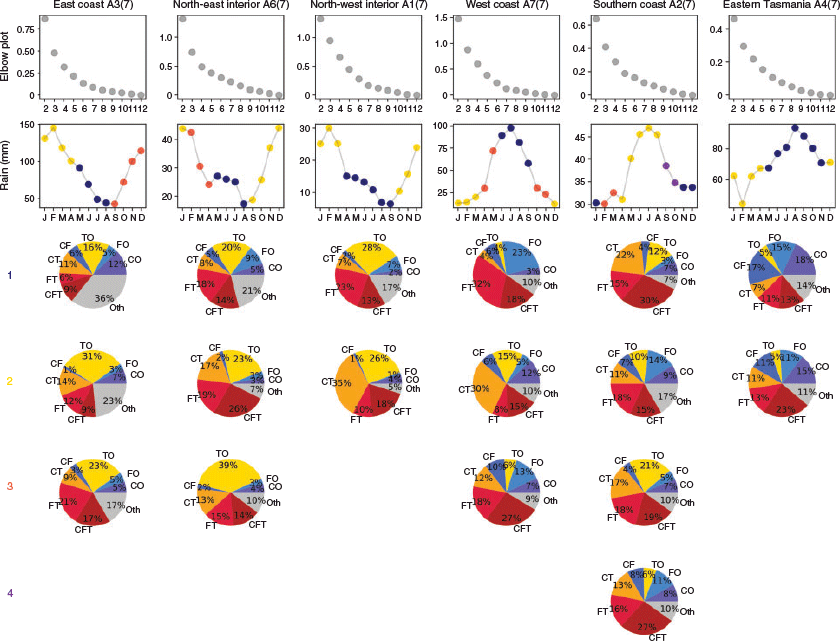
While a broad-scale, geographically averaged seasonal cycle provides a useful point upon which to compare climate analysis over different regions, localised studies may be better suited to using a more targeted seasonal breakdown. In this section, we use the k-means clustering method, as in Section 4 and the six main annual average regional clusters found in Section 3 to evaluate the different seasonal cycles across southern Australia. For simplicity, we use the six seasonal clusters identified in Fig. 4, where the Shark Bay cluster has been merged with the West Coast cluster.
The elbow plots shown in Fig. 11 suggest between three and eight clusters for the six regions shown, although many with low confidence. The dendrograms for each region (not shown) for both the Ward and average methods predominately recommend two clusters. In addition, we require ‘seasons’ to be of at least two months duration. The numbers of clusters presented here offer the best balance between physically different seasons, according to the breakdown of weather types, and the recommended number of clusters according to the metrics.
Figure 11 shows a varying definition of seasons depending on the region. All regions display a relatively consistent ‘winter’ season, starting in April or May (June for the west coast) and ending in August or September (November for eastern Tasmania). However, the warmer month seasons tend to be much more varied with respect to timing and number of seasons.
On the east coast, the winter season (Cluster 1) is defined as May–August, with most rainfall generated from ‘other’ weather types (36%). Examining this more closely, we find that 13% of rain is associated with a nearby high pressure system causing moist onshore winds, 8% from warm fronts, 6% from unconfirmed cyclones or fronts and the remainder is undefined. In addition, cyclone-related weather types are collectively responsible for 38% of rainfall respectively and are most likely associated with East Coast Lows. Thunderstorm-only days generate 23% of rainfall in the early summer season (September–December, Cluster 3), with a further 47% of early summer rainfall generated by the combination of a thunderstorm and a cyclone or front, and a smaller proportion of rainfall on other days. In the late summer (January–April, Cluster 2), thunderstorm-only days are responsible for 31% of rain, and ‘other’ weather types 23% (highs 5%, warm fronts 7%, unconfirmed cyclones or fronts 7% and undefined 5%), with smaller contributions from combined thunderstorms than in early summer.
Moving inland, three seasonal clusters have been selected for the north-east interior region. The winter season (Cluster 1), May–August, similar to the east coast, receives most rainfall from thunderstorms (20%) and ‘other’ weather types (highs 7%, warm fronts 6%, unconfirmed cyclones or fronts 4% and undefined 4%). Front-only days also generate 9% of rainfall during the winter season, but little rain at other times of the year. An early summer season, September–January (Cluster 2), receives most of its rainfall during cyclone-front-thunderstorm events, with the combination of a thunderstorm with a cyclone or front events collectively generating 64% of early summer rainfall. Combined thunderstorms are less important during the late summer season (Cluster 3), February–April, when 39% of rain is from thunderstorm only events.
Comparatively, in the north-west interior only two seasons have been defined. When three seasons were defined, April was singled out as a season, in which 45% of rainfall was generated from thunderstorm activity. However, as mentioned previously, we do not consider single months to be representative of a ‘season’ and hence two seasons are shown. The winter season, Cluster 1, is defined as April–September and is dominated by thunderstorm only rainfall (28%) as well as a large proportion of rainfall from front-thunderstorm days (23%) and other days (17%). The summer season, Cluster 2, October–March, receives most of its rainfall from cyclone-thunderstorm events (35%) as well as thunderstorm only events (26%), with reduced frontal activity.
On the west coast, rainfall in the winter season (Cluster 1, June–September) is clearly dominated by frontal activity. The four front-related types collectively explain 79% of winter rainfall, including 23% on front-only days and 32% when combined with thunderstorms. Unlike the other regions, instead of having an early and late summer season, the west coast has a summer season (December–March, Cluster 2) and a ‘transition’ season that is split over April–May and October–November (Cluster 3). The summer season is heavily influenced by cyclone activity combined with thunderstorms (30%), while the majority of rainfall generated in Cluster 3 is from cyclone-front-thunderstorm activity (27%) reflecting the transitional nature of this season.
The southern coast region is the only region to have four separate seasons defined. The winter season, Cluster 2, is defined as April–August and displays a relatively even spread of rainfall attribution by weather type, with front-thunderstorm activity or other weather types (7% highs, 3% warm fronts and 3% unconfirmed cyclones) the predominant source of rain. The early summer season rainfall (Cluster 1, November–January) is predominately brought by the combination of a thunderstorm with a cyclone and/or front (67%). These combined events continue to produce 54% of rainfall during the late summer (February–March, Cluster 3) but there is an increase in rainfall from thunderstorm-only days (21%). Lastly, Cluster 4 is considered a spring season, from September–October. This season still receives 56% of rainfall from combined thunderstorms, particularly cyclone-front-thunderstorm activity (27%), but has less thunderstorm-only rainfall than any of the other seasons (6%). Instead, 27% of rainfall is generated by a cyclone and/or front without thunderstorms, only slightly below the contribution during the winter season (30%).
Finally, two seasons have been found for eastern Tasmania: a winter season (May–November) and summer season (December–April). Three seasons were originally identified (May–August, September–November, December–April) however the ‘winter’ and ‘spring’ seasons were found to have very similar synoptic makeup. In total, 50% of rain during the winter season (Cluster 1) is from a cyclone and/or front, including 18% of rainfall from cyclones alone and 17% from cyclone-fronts. The summer season (Cluster 2), sees the proportion of rainfall from these systems decrease to 37%, with an increase in rainfall from the combination of cyclones and/or fronts with thunderstorms (47%). In contrast to elsewhere in Australia, thunderstorm-only events generate little rainfall in either season for this region.
The results presented here highlight that while it is easy to simply apply one seasonal definition to the whole country, the seasonal breakdown of rainfall and weather patterns can vary significantly across the country. While using a consistent definition of cool and warm seasons for southern Australia is useful in aiding comparisons between studies, for regional analyses it is useful to consider local factors in determining the seasons that best reflect the local climate.
7 Discussion and conclusions
A range of climate regions have been used in the past to perform averaging. This work presents the first definitions of climate regions based on clustering methods with high-quality weather type and rainfall information. We have found that the NRM clusters that follow topography or significant rainfall and temperature boundaries (as suggested by the Koeppen climate zones) satisfactorily capture climate regions in ‘coastal’ regions of south-west Western Australia and along the southern eastern seaboard. However, we note that inland, the NRM and Koeppen climate zones tend to consider all desert regions as one. This study has found some important differences between the eastern and western desert areas related to the influence of cyclone activity. In addition, we note that the Koeppen climate zones are unable to take into account the effect of topographical aspects on how different weather types influence rainfall, which is overcome in this analysis. We suggest that the climate regions produced in this study are more appropriate for climate analysis than the NRM regions or Koeppen climate zones.
This study has provided the first quantitatively defined definition of seasons for southern Australia as a whole and for six significant climate regions (and a seventh smaller region). On average, we find that the cool season should be defined as April–September and the warm season from October–March. A three season breakdown was also provided, where a winter season from May–September was defined in addition to an early and late summer season from October–January and February–April respectively. For the regional definitions of seasons the number of seasons found varies with the region. In general, the cool season was found to begin in April or May and end in August–September, with some outliers. However, much greater variation exists over the warmer months, with between one and three distinct seasons in different parts of Australia over a range of timings.
This work has not only been able to identify distinct climatic regions and season, but to also characterise them with respect to the most important weather types for bringing rainfall. Using the average two season split as defined above, we have also been able to show that the regional breakdown of rainfall bearing weather types over Australia varies in different seasons. We find a strong north–south divide in the cool season over the entire study area, with the exception of the east and west coasts. This divide reflects the dominance of the westerly storm track, with the largest impact on the west coast and the blocking nature of the GDR along the east coast. In the warm season, the influence of fronts and cyclones in the westerly flow is reduced in the southern-most regions, while thunderstorms and their interaction with fronts and cyclones cause a greater east–west divide over the study area. Knowledge such as this is useful in understanding not only the variability of a region, but can also help give context to trends in weather patterns and how these may disproportionately affect regions or times of year.
Although these climate regions were defined based on the proportion of rainfall brought by selected weather types, their alignment in some areas with the Koeppen or NRM regions or alternately, with our knowledge of the regional climate, gives us some expectation that the regions defined here will be useful outside of rainfall or weather type studies. This will be the focus of future work. A further useful application may be to advance the connection between Indigenous understanding of weather and climate and data driven understanding. An attempt was made to compare our comparatively broad regional analysis of seasons to local Indigenous seasonal calendars available via the BoM Indigenous knowledge website without success. We suspect that this misalignment of seasons is due to the length of seasons identified in this work (although shorter seasons were also compared) and the broad areas over which our seasonal analysis was performed. However, using a similar method to that presented here, with localised weather information in combination with Indigenous climate knowledge, may improve our understanding of how seasons and their respective weather types influence the biosphere.
While the clustering methods used in this work are able to quantitatively assign grid points or seasons to the respective clusters, some subjectivity remains surrounding the choice of the number of clusters. While this was thoroughly tested, ranging up to 30 for the regional clustering and up to six for the seasonal clustering, and statistical guidance was considered, the number of clusters remains a choice with no ‘wrong’ or ‘right’ answer. We have provided the number of clusters that we deemed the most appropriate give what we know about the physical region and how such clusters are used.
We further acknowledge that different results can be gained by using a different weather typing data set, although no other dataset as comprehensive as the one presented in Pepler et al. (2020) currently exists for Australia. Clustering upon absolute rainfall or weather type frequency were also tested in this study. While these tests provided different results, they were not considered to be as meaningful for the regional analysis, behaving more similarly to the Koeppen Climate Zones and unable to capture important influence from topography. Furthermore, with respect to the regional clustering, early merging of clusters that corresponded to geographically separated regions was found in the hierarchical clustering. This merging was counter to our expectations of how rainfall behaves but in keeping with expectations of the weather type behaviour.
The combination of the weather types data sets and clustering methods demonstrates how, with improved observations, modelling and computational methods, such techniques can be applied to new, complex data sets, offering new insights into our climate system. The regions and seasons defined here can provide researchers with more tailored information about where or when averaging should be performed in order to achieve results that are the most meaningful. With consistent definitions, greater reproducability and transferability of knowledge can be achieved. It is our hope that the regions and seasons defined in the work can be broadly applied across climate science in southern Australia.
Code and data availability
The Scikit learn clustering package was used to perform this analysis and is available online (Pedregosa et al. 2011). The weather type data is available by contacting Acacia Pepler and will be shared for research purposes as an output of the Victorian Water and Climate Initiative. The AWAP rainfall data is available from the Bureau of Meteorology website. Mask files (as netCDF) of the regional clusters presented in this work are available online DOI:10.5281/zenodo.4265471 (Fiddes et al. 2020).
Conflicts of interest
The authors have no conflicts of interest to declare.
Acknowledgements
The authors would like to acknowledge Jennifer Catto, Andrew Dowdy and Irina Rudeva for their contributions to the weather types dataset. Sonya Fiddes, Acacia Pepler and Pandora Hope were supported by the Victorian Department of Environment, Land, Water and Planning as part of the Victorian Water and Climate Initiative. This research was undertaken with the assistance of resources and services from the National Computational Infrastructure (project eg3), which is supported by the Australian Government. The authors would like to acknowledge the traditional owners of the lands upon which this research was performed and pay our respect to elders past, present and emerging.
References
Alexander, L. V., Uotila, P., Nicholls, N., and Lynch, A. (2010). A new daily pressure dataset for Australia and its application to the assessment of changes in synoptic patterns during the last century. J. Climate 23, 1111–1126.| A new daily pressure dataset for Australia and its application to the assessment of changes in synoptic patterns during the last century.Crossref | GoogleScholarGoogle Scholar |
Calinski, T., and Harabasz, J. (1974). A dendrite method for cluster analysis. Commun. Stat. Theory Methods 3, 1–27.
| A dendrite method for cluster analysis.Crossref | GoogleScholarGoogle Scholar |
Cavicchia, L., Pepler, A., Dowdy, A., and Walsh, K. (2019). A physically based climatology of the occurrence and intensification of Australian east coast lows. J. Climate 32, 2823–2841.
| A physically based climatology of the occurrence and intensification of Australian east coast lows.Crossref | GoogleScholarGoogle Scholar |
CSIRO (2012). Climate and water availability in south-eastern Australia: A synthesis of findings from Phase 2 of the South Eastern Australian Climate Initiative (SEACI). Technical report, CSIRO, Melbourne, Australia.
CSIRO and Bureau of Meteorology (2015). Technical Report. In ‘Climate Change in Australia Projections for Australia’s Natural Resource Management Regions: Cluster Reports’, page 218. CSIRO and Bureau of Meteorology, Australia.
CSIRO and Bureau of Meteorology (2019). Regionalisation Schemes. Available at https://www.climatechangeinaustralia.gov.au/en/climate-projections/about/modelling-choices-and-methodology/regionalisation-schemes/
Davies, D. L., and Bouldin, D. W. (1979). A Cluster Separation Measure. IEEE Transactions on Pattern Analysis and Machine Intelligence PAMI-1, 224–227.
| A Cluster Separation Measure.Crossref | GoogleScholarGoogle Scholar |
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., Mcnally, A. P., Monge-Sanz, B. M., Morcrette, J. J., Park, B. K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J. N., and Vitart, F. (2011). The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Quart. J. Roy. Meteor. Soc. 137, 553–597.
| The ERA-Interim reanalysis: Configuration and performance of the data assimilation system.Crossref | GoogleScholarGoogle Scholar |
Dey, R., Lewis, S. C., Arblaster, J. M., and Abram, N. J. (2019). A review of past and projected changes in Australia’s rainfall. WIRES: Clim. Change 10, 1–23.
| A review of past and projected changes in Australia’s rainfall.Crossref | GoogleScholarGoogle Scholar |
Di Virgilio, G., Evans, J. P., Di Luca, A., Olson, R., Argüeso, D., Kala, J., Andrys, J., Hoffmann, P., Katzfey, J. J., and Rockel, B. (2019). Evaluating reanalysis-driven CORDEX regional climate models over Australia: model performance and errors. Clim. Dyn. 53, 2985–3005.
| Evaluating reanalysis-driven CORDEX regional climate models over Australia: model performance and errors.Crossref | GoogleScholarGoogle Scholar |
Dowdy, A. J. (2020). Climatology of thunderstorms, convective rainfall and dry lightning environments in Australia. Clim. Dyn. 54, 3041–3052.
| Climatology of thunderstorms, convective rainfall and dry lightning environments in Australia.Crossref | GoogleScholarGoogle Scholar |
Drosdowsky, W. (1993). An analysis of Australian seasonal rainfall anomalies: 1950–1987. Int. J. Climatol. 13, 1–30.
| An analysis of Australian seasonal rainfall anomalies: 1950–1987.Crossref | GoogleScholarGoogle Scholar |
Fiddes, S. L., and Timbal, B. (2017). Future impacts of climate change on streamflows across Victoria, Australia: making use of statistical downscaling. Clim. Res. 71, 219–236.
| Future impacts of climate change on streamflows across Victoria, Australia: making use of statistical downscaling.Crossref | GoogleScholarGoogle Scholar |
Fiddes, S. L., Pezza, A. B., and Barras, V. (2015). Synoptic climatology of extreme precipitation in alpine Australia. Int. J. Climatol. 35, 172–188.
| Synoptic climatology of extreme precipitation in alpine Australia.Crossref | GoogleScholarGoogle Scholar |
Fiddes, S., Pepler, A., Saunders, K., and Hope, P. (2020). Southern Australia's climate regions (Version 1.0.0) [Data set]. Zenodo. Available at http://doi.org/10.5281/zenodo.4265471
Freund, M., Henley, B. J., Karoly, D. J., Allen, K. J., and Baker, P. J. (2017). Multi-century cool- and warm-season rainfall reconstructions for Australia’s major climatic regions. Clim. Past 13, 1751–1770.
| Multi-century cool- and warm-season rainfall reconstructions for Australia’s major climatic regions.Crossref | GoogleScholarGoogle Scholar |
Gibson, P. B., Perkins-Kirkpatrick, S. E., Uotila, P., Pepler, A. S., and Alexander, L. V. (2017). On the use of self-organizing maps for studying climate extremes. J. Geophys. Res. 122, 3891–3903.
| On the use of self-organizing maps for studying climate extremes.Crossref | GoogleScholarGoogle Scholar |
Grose, M., Abbs, D., Bhend, J., Chiew, F. H. S., Church, J., Ekstrom, M., Lucas, C., McInnes, K., Moise, A. F., Monselesan, D., Mpelasoka, F., Webb, L., and Whetton, P. H. (2015). Southern Slopes Cluster Report. In ‘Climate Change in Australia Projections for Australia’s Natural Resource Management Regions: Cluster Reports’ (Eds M. Ekstrom, P. H. Whetton, C. Gerbring, M. Grose, L. Webb, and J. S. Risbey) page 65. (CSIRO and Bureau of Meteorology, Australia.)
Grose, M. R., Narsey, S., Delage, F. P., Dowdy, A. J., Bador, M., Boschat, G., Chung, C., Kajtar, J. B., Rauniyar, S., Freund, M. B., Lyu, K., Rashid, H., Zhang, X., Wales, S., Trenham, C., Holbrook, N. J., Cowan, T., Alexander, L., Arblaster, J. M., and Power, S. (2020). Insights From CMIP6 for Australia’s Future Climate. Earth’s Future 8, .
| Insights From CMIP6 for Australia’s Future Climate.Crossref | GoogleScholarGoogle Scholar |
Hastie, T., Friedman, J., and Tibshirani, R. (2001). The Elements of Statistical Learning. Springer Series in Statistics. (Springer: New York, NY.)
Hauser, S., Grams, C. M., Reeder, M. J., McGregor, S., Fink, A. H., and Quinting, J. F. (2020). A weather system perspective on winter-spring rainfall variability in southeastern Australia during El Niño. Quart. J. Roy. Meteor. Soc. 146, 2614–2633.
| A weather system perspective on winter-spring rainfall variability in southeastern Australia during El Niño.Crossref | GoogleScholarGoogle Scholar |
Hope, P., Abbs, D., Bhend, J., Chiew, F., Church, J., Ekström, M., Kirono, D., Lenton, A., Lucas, C., McInnes, K., Moise, A., Monselesan, D., Mpelasoka, F., Timbal, B., Webb, L., and Whetton, P. (2015). Southern and South-Western Flatlands Cluster Report. In ‘Climate Change in Australia Projections for Australia’s Natural Resource Management Regions: Cluster Reports’ (Eds M. Ekstrom, P. H. Whetton, C. Gerbring, M. Grose, L. Webb, and J. S. Risbey) page 64. (CSIRO and Bureau of Meteorology, Australia.)
Hope, P., Timbal, B., Hendon, H., Ekström, M., and Potter, N. (2017). A synthesis of findings Victorian Climate Initiative. Technical report, Bureau of Meteorology, Melbourne, Australia.
Jiang, N., Cheung, K., Luo, K., Beggs, P. J., and Zhou, W. (2012). On two different objective procedures for classifying synoptic weather types over east Australia. Int. J. Climatol. 32, 1475–1494.
| On two different objective procedures for classifying synoptic weather types over east Australia.Crossref | GoogleScholarGoogle Scholar |
Jones, D. A., Wang, W., and Fawcett, R. (2009). High-quality spatial climate data-sets for Australia. Aust. Meteor. Ocean. J. 58, 233–248.
| High-quality spatial climate data-sets for Australia.Crossref | GoogleScholarGoogle Scholar |
King, A. D., Alexander, L. V., and Donat, M. G. (2013). The efficacy of using gridded data to examine extreme rainfall characteristics: A case study for Australia. Int. J. Climatol. 33, 2376–2387.
| The efficacy of using gridded data to examine extreme rainfall characteristics: A case study for Australia.Crossref | GoogleScholarGoogle Scholar |
Larsen, S. H., and Nicholls, N. (2009). Southern Australian rainfall and the subtropical ridge: Variations interrelationships, and trends. Geophys. Res. Lett. 36, 1–5.
| Southern Australian rainfall and the subtropical ridge: Variations interrelationships, and trends.Crossref | GoogleScholarGoogle Scholar |
Lim, E. P., Hendon, H. H., Hope, P., Chung, C., Delage, F., and McPhaden, M. J. (2019). Continuation of tropical Pacific Ocean temperature trend may weaken extreme El Niño and its linkage to the Southern Annular Mode. Sci. Rep. 9, 1–15.
| Continuation of tropical Pacific Ocean temperature trend may weaken extreme El Niño and its linkage to the Southern Annular Mode.Crossref | GoogleScholarGoogle Scholar |
Nicholls, N. (2009). Local and remote causes of the southern Australian autumn-winter rainfall decline, 1958–2007. Clim. Dyn. 34, 835–845.
| Local and remote causes of the southern Australian autumn-winter rainfall decline, 1958–2007.Crossref | GoogleScholarGoogle Scholar |
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P., Weiss, R., Dubourg, V., Vanderplas, J., Passos, A., Cournapeau, D., Brucher, M., Perrot, M., and Duchesnay, E. (2011). Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 12, 2825–2830.
Peel, M. C., Finlayson, B. L., and McMahon, T. A. (2007). Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Sys. Sci. 11, 1633–1644.
| Updated world map of the Köppen-Geiger climate classification.Crossref | GoogleScholarGoogle Scholar |
Pepler, A. S., Timbal, B., Rakich, C., and Coutts-Smith, A. (2014). Indian Ocean Dipole Overrides ENSO’s Influence on Cool Season Rainfall across the Eastern Seaboard of Australia. J. Climate 27, 3816–3826.
| Indian Ocean Dipole Overrides ENSO’s Influence on Cool Season Rainfall across the Eastern Seaboard of Australia.Crossref | GoogleScholarGoogle Scholar |
Pepler, A., Dowdy, A., and Hope, P. (2019a). A global climatology of surface anticyclones, their variability, associated drivers and long-term trends. Clim. Dyn. 52, 5397–5412.
| A global climatology of surface anticyclones, their variability, associated drivers and long-term trends.Crossref | GoogleScholarGoogle Scholar |
Pepler, A., Hope, P., and Dowdy, A. (2019b). Long-term changes in southern Australian anticyclones and their impacts. Clim. Dyn. 53, 4701–4714.
| Long-term changes in southern Australian anticyclones and their impacts.Crossref | GoogleScholarGoogle Scholar |
Pepler, A. S., Dowdy, A. J., van Rensch, P., Rudeva, I., Catto, J. L., and Hope, P. (2020). The contributions of fronts, lows and thunderstorms to southern Australian rainfall. Clim. Dyn. 55, 1481–1505.
| The contributions of fronts, lows and thunderstorms to southern Australian rainfall.Crossref | GoogleScholarGoogle Scholar |
Pook, M. J., McIntosh, P. C., and Meyers, G. A. (2006). The synoptic decomposition of cool-season rainfall in the southeastern Australian cropping region. J. Appl. Meteor. Climatol. 45, 1156–1170.
| The synoptic decomposition of cool-season rainfall in the southeastern Australian cropping region.Crossref | GoogleScholarGoogle Scholar |
Pook, M., Lisson, S., Risbey, J., Ummenhofer, C. C., McIntosh, P., and Rebbeck, M. (2009). The autumn break for cropping in southeast Australia: trends, synoptic influences and impacts on wheat yield. Int. J. Climatol. 29, 2012–2026.
| The autumn break for cropping in southeast Australia: trends, synoptic influences and impacts on wheat yield.Crossref | GoogleScholarGoogle Scholar |
Rauniyar, S. P., and Power, S. B. (2020). The impact of anthropogenic forcing and natural processes on past, present and future rainfall over Victoria, Australia. J. Climate , 1–58.
Reid, K. J., Simmonds, I., Vincent, C. L., and King, A. D. (2019). The Australian Northwest Cloudband: Climatology, mechanisms, and association with precipitation. J. Climate 32, 6665–6684.
| The Australian Northwest Cloudband: Climatology, mechanisms, and association with precipitation.Crossref | GoogleScholarGoogle Scholar |
Risbey, J. S., Pook, M. J., McIntosh, P. C., Ummenhofer, C. C., and Meyers, G. A. (2009a). Characteristics and variability of synoptic features associated with cool season rainfall in southeastern Australia. Int. J. Climatol. 29, 1595–1613.
| Characteristics and variability of synoptic features associated with cool season rainfall in southeastern Australia.Crossref | GoogleScholarGoogle Scholar |
Risbey, J. S., Pook, M. J., McIntosh, P. C., Wheeler, M. C., and Hendon, H. H. (2009b). On the Remote Drivers of Rainfall Variability in Australia. Mon. Wea. Rev. 137, 3233–3253.
| On the Remote Drivers of Rainfall Variability in Australia.Crossref | GoogleScholarGoogle Scholar |
Risbey, J. S., Mcintosh, P. C., and Pook, M. J. (2013). Synoptic components of rainfall variability and trends in southeast Australia. Int. J. Climatol. 33, 2459–2472.
| Synoptic components of rainfall variability and trends in southeast Australia.Crossref | GoogleScholarGoogle Scholar |
Rousseeuw, P. J. (1987). Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 20, 53–65.
| Silhouettes: A graphical aid to the interpretation and validation of cluster analysis.Crossref | GoogleScholarGoogle Scholar |
Saji, N. H., Goswamim, B. N., Vinayachandran, P. N., and Yamagata, T. (1999). A dipole mode in the tropical indian ocean. Nature 401, 360–363.
| A dipole mode in the tropical indian ocean.Crossref | GoogleScholarGoogle Scholar | 16862108PubMed |
Saunders, K. R., Stephenson, A. G., and Karoly, D. J. (2020). A regionalisation approach for rainfall based on extremal dependence. Extremes , .
| A regionalisation approach for rainfall based on extremal dependence.Crossref | GoogleScholarGoogle Scholar |
Stern, H., De Hoedt, G., and Ernst, J. (2000). Objective classification of Australian climates. Aust. Meteor. Mag. 49, 87–96.
Timbal, B. (2009). The continuing decline in South-East Australian rainfall - Update to May 2009. CAWCR Res. Lett. , 4–12.
Timbal, B. (2010). The climate of the Eastern Seaboard of Australia: A challenging entity now and for future projections. IOP Conf. Ser.: Earth Environ. Sci. 11, 012013.
| The climate of the Eastern Seaboard of Australia: A challenging entity now and for future projections.Crossref | GoogleScholarGoogle Scholar |
Timbal, B., Fiddes, S., and Brown, J. R. (2017). Understanding south-east Australian rainfall projection uncertainties: the influence of patterns of projected tropical warming. Int. J. Climatol. 37, 921–939.
| Understanding south-east Australian rainfall projection uncertainties: the influence of patterns of projected tropical warming.Crossref | GoogleScholarGoogle Scholar |
Wilks, D. S. (2011). Statistical Methods in the Atmospheric Sciences. Elsevier, 3rd edition.
Zhang, Y., Wallace, J. M., and Battisti, D. S. (1997). ENSO-like interdecadal variability: 1900–93. J. Climate 10, 1004–1020.
| ENSO-like interdecadal variability: 1900–93.Crossref | GoogleScholarGoogle Scholar |