Response time of temperature measurements at automatic weather stations in Australia

Keywords: automatic weather station, AWS, field air temperature, resistance thermometer, response time, temperature measurement, WMO, World Meteorological Organization.

Recently, temperature measurements at the Bureau of Meteorology’s automatic weather stations (AWS) have been criticised publicly as not following World Meteorological Organization (WMO) guidelines that recommend 1-min data as the basic measurement, because it is 1-s data that are logged. The Bureau records the measurement in the last second of each minute as its 1-min value. It considers this appropriate, arguing that AWS temperature systems have a response time such that each measurement is not a spot measurement, but an average smoothed over the previous 40–80 s, consistent with the WMO guidelines (BoM 2017).

To test whether the 1-s air temperature data (air T) are averaged over a longer period by slow measurement system response time Ayers (2019) compared the Bureau’s 1-min data (recorded as the value in the last second of each minute) with a value averaged from five 1-s measurements in the minute, centred on that second. This was possible since the Bureau records not only the 1-s value for the last second in each minute, but also the highest and lowest 1-s values in each minute, T_max and T_min. For any minute, i, and adopting the Bureau’s labelling of the seconds in each minute from 0 to 59, the comparison made by Ayers (2019) was between T₅₉ and the 5-value average incorporating that value and the four T_max and T_min values recorded in the minute either side of that value. That methodology is depicted schematically in Fig. 1, reproduced from Ayers (2019).

Fig. 1.  Schematic depicting the five 1-s air temperature measurements averaged for comparison with the value from the last second of each minute, the central T_59i value (Ayers 2019).

Ayers (2019) concluded that the frequency distribution of the difference between the 1-s value at the end of each minute and the 5-point average centred on that second was consistent with the Bureau’s stated position that the 1-s data were already smoothed appropriately over the prior 40–80 s. Ayers (2019) further suggested that any additional averaging would likely be inappropriate as it might lead to over-damped 1-min values. However, in the absence of measured 1 Hz temperature data, explicit confirmation of these conclusions based on just the 5-point average rather than a full 60-point (60 s) 1-min average was not possible.

This work describes an experiment carried out at two AWS sites, Darwin (NT) and Noarlunga (SA), to provide 1 Hz air temperature data. The purpose was to determine the effects of measurement system response time on smoothing of 1-s data under field conditions, based on measurements every second (60 1-s data points each minute). Properties of the measured 1 Hz datasets were analysed by comparison with the properties of a synthetic dataset of 1-s values smoothed with e-folding times varied from 1 to 180 s.

The specific objective was to estimate measurement system response time, expressed as e-folding time, with this response time being the overall response time for the AWS measurement system (Stevenson Screen plus resistance thermometer).

The Darwin site is located at latitude –12.4239, longitude 130.8925 at a Station Height of 30.4 m. A standard Bureau AWS at the site has air temperature measured by a Rosemount Model ST2041 resistance thermometer mounted in a 60 L Stevenson screen. The AWS is located within the boundary of the observations enclosure, an open grassed area.

The Noarlunga site is located at latitude –35.1586, longitude 138.5057 at a Station Height of 55 m. As at Darwin the air temperature measurement is made with a standard Bureau AWS using a Rosemount Model ST2401 resistance thermometer mounted in a 60 L Stevenson screen. The AWS is located within the boundary of the observations enclosure, an open area of natural grass with some small shrubs 20 m to the west and east.

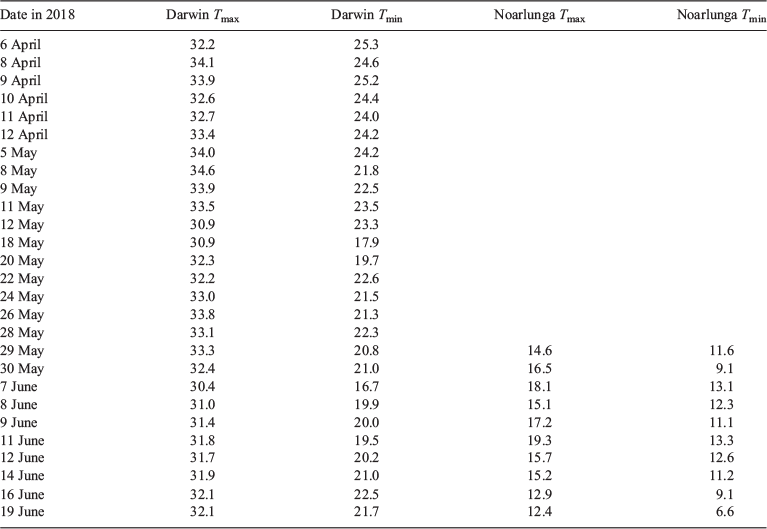
Table 1 lists the 27 days at Darwin and 10 days at Noarlunga in 2018 for which 1 Hz data were recorded, along with the highest daily T_min and T_max values recorded in the 1-minuted data.

Table 1.  Days on which 1 Hz data were recorded at Darwin and Noarlunga AWS

The 1 Hz data collected from Darwin and Noarlunga were analysed by comparison with a synthetic dataset of 1 Hz values produced by Ayers (2019). That dataset mimicked the statistical properties of instantaneous air temperature data measured using fast response sensors by Costa Frola et al. (2014), scaled to approximate the standard deviation of the measured daytime temperature fluctuations in the Australian data analysed (for further details see Ayers 2019).

A randomly selected 1-h period of 3600 s drawn from the synthetic instantaneous data was subjected to two different averaging methods. The first employed smoothing by applying a given e-folding time to the data, varying the time constant used across the range 1–180 s, the second was to take the running mean of 60 data points centred on a point 30 s earlier to provide a 1-min average that would approximate in time the Bureau’s assertion that the measurement system time constants at any point in time smooth the data over the previous 40–80 s.

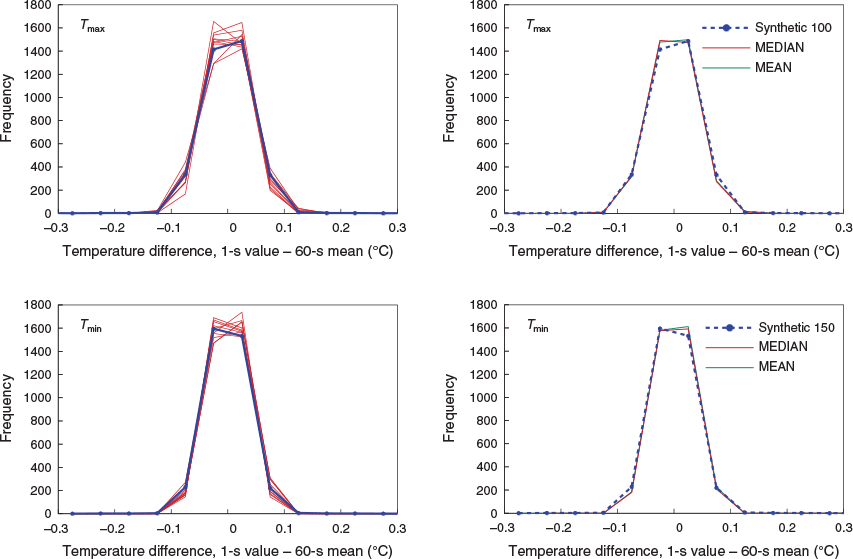
The frequency distributions of the difference between synthetic data subjected to different e-folding times and the 60-s arithmetic mean values for each of the 3600 s in the synthetic hour of data are plotted in Fig. 2 on the same scale as used by Ayers (2019). The most important feature of Fig. 2 is that the difference between the data smoothed by the various e-folding times and the 60-s mean reduces significantly as the e-folding time increases, the distribution narrows. This provides an opportunity to evaluate the smoothing of the 1 Hz data measured under field conditions by comparing the shape of the frequency distribution for the difference between measured 1 Hz data and the 60-s mean of those data with the varying shapes of the synthetic difference frequency curves in Fig. 2.

Fig. 2.  Synthetic 1 Hz air temperature data showing the difference between the data set smoothed with the indicated e-folding times (20 s to 180 s) and smoothed with a 60-s running mean, based on 3600 data points (1 h of 1-s data).

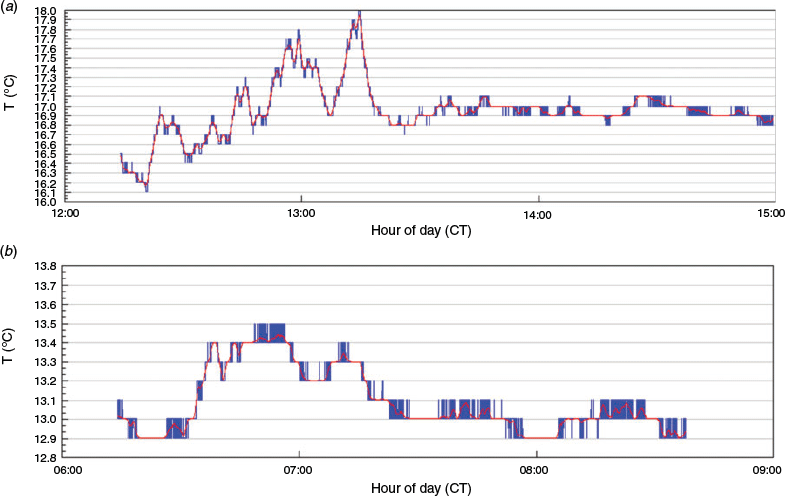
To span the measured daily range of air T, comparisons were made using 1 h of 1-s measured data taken at the times of the daily maximum in T_max in early afternoon and daily minimum in T_min early morning the following day. Fig. 3 provides an example of the measured 1-s data from Darwin, Fig. 4 provides an example from Noarlunga.

Fig. 3.  Blue lines: example of 1 Hz air temperature from Darwin, (a) afternoon 12 May 2018, (b) morning 13 May 2018. Red line: 60-s running mean.

Fig 4.  Blue lines: example of 1 Hz air temperature from Noarlunga, (a) afternoon 7 June 2018, (b) morning 8 June 2018. Red line: 60-s running mean.

Fig. 5 shows the frequency distributions of the difference between the 1 Hz data and the 60-s running mean from each day at Darwin overlaid by the best-fit theoretical distribution (see Fig. 1) (blue line). The estimated system e-folding time in seconds is shown in the right hand panel. Fig. 6 presents the comparable data from Noarlunga.

Fig 5.  Frequency distributions of the difference between measured 1-s air temperature data and the 60-s running mean for the minute represented by that second. Data from 27 days of 1 Hz measurements at Darwin. Individual datasets used were for the hour (3600 s) in which T_max occurred each day and T_min occurred on the following day. Blue lines represent best fit synthetic distributions calculated as for Figure 1.

Fig 6.  Frequency distributions of the difference between measured 1-s air temperature data and the 60-s running mean for the minute represented by that second, from 10 days of 1 Hz measurements at Noarlunga. Individual datasets used were for the hour (3600 s) in which T_max occurred each day and T_min occurred on the following day. Blue lines represent best fit synthetic distributions calculated as for Figure 1.

There are two notable features of Figs 3 and 4. The first is that, consistent with the observations of Ayers (2019), there is very little difference evident between the measured 1 Hz data and the 60-s running means of those data. This lack of major additional smoothing despite the 60-point average provides a strong indication that the 1 Hz data are already well smoothed in terms of variability at the minute level. The second point is that the small scale variability is larger at the time of T_max than at the time of T_min, again consistent with the observation by Ayers (2019) that standard deviation of air T fluctuations was highly correlated with solar irradiance throughout the day, as expected if turbulence in the planetary boundary layer is driven by solar heating that causes small scale convective overturning.

Three initial observations may also be made concerning Figs 5 and 6. The first is that a consistently good fit can be found between the measured differences between the 1 Hz data and 60-s means and best-fit theoretical equivalents. The second is that, as noted regarding Figs 4 and 5, there is a systematic difference between the results for T_max and T_min with the estimated measurement system e-folding time doubling at both sites in going from the hour around T_max to the hour around T_min. The third point is that there is also a systematic difference apparent between the results from Darwin and those from Noarlunga, with the estimated measurement system e-folding times for both the T_max and T_min data being significantly larger for Noarlunga than for the Darwin data.

The objective of this work was to explore the proposition that 1-s air temperature data measured at Bureau of Meteorology AWSs represent good measurement practice as required by WMO, via measurement system time constants that average the data over the previous 40–80 s, to meet the WMO recommendations for recording 1-min data. Based on statistical analysis of Bureau AWS data recorded for the last second in each minute combined with T_max and T_min from the two adjacent minutes Ayers (2019) concluded that this proposition was sound. However an additional test using field data based on explicit measurement of 1 Hz data was recommended to put any conclusion beyond doubt. This work describes the results of that additional test.

Because Ayers (2019) found a strong relationship between the standard deviation of air T fluctuations and solar exposure two sites were chosen for recording of 1 Hz AWS data. The tropical site of Darwin at 12°S has high solar exposure all year in comparison with mid-latitude sites so should well reflect solar-driven variability in air T at short time scales during the day at all times of year. In contrast, the mid-latitude site of Noarlunga at 35°S in winter has significantly less solar exposure and considerably lower air T, so these two sites span a range of environmental and measurement conditions.

Both the Darwin and Noarlunga 1 Hz data sets reproduce the conclusion of Ayers (2019) based on far more limited data (5-point average each minute rather than 60-point average): averaging the 1-s AWS data produces only very minor additional smoothing. The most plausible explanation for this is that the 1-s data are already smoothed at ~1-min timescale so additional smoothing has only minimal effect (see also relevant commentary in WMO 2014, and Bendat and Piersol, 1986). This is consistent with the Bureau’s statement that AWS 1-s data are effectively an average over ~40–80 s.

The overlay of probability distribution functions (pdf) for 1-s data minus 60-s mean data from Darwin (Fig. 5) and Noarlunga (Fig. 6) with the best-fit theoretical pdf provides a more explicit demonstration that the 1-s data reflect smoothing of instantaneous air T data as the Bureau has asserted. The 1-s data in the four of the panels in Figs 5 and 6 closely reproduce the behaviour of the synthetic data smoothed with e-folding times ranging from 50–150 s.

The lower estimated e-folding times for T_max compared with T_min at both sites, and the lower estimated e-folding times for both T_min and T_max at Darwin compared with T_min and T_max at Noarlunga are consistent with the conclusion reached by Ayers (2019) that fluctuations in air temperature scale with solar-driven turbulence in the planetary boundary layer, which is higher in daytime than night-time and higher at Darwin than at Noarlunga. Clearly all air temperature measurement systems will experience the same significant day-night, winter-summer differences in solar-driven turbulent mixing. So no matter how 1-min averages are produced, irrespective of the different approaches that vary by country while still meeting WMO requirements (as noted by Ayers 2019), the data themselves will always reflect these systematic effects of turbulence on the 1-min values that are recorded.

The study reported here independently confirms the conclusion reached by Ayers (2019) that the measurement of air temperature by the Bureau’s AWS stations is robust and consistent with WMO requirements. The Bureau’s position that ‘each one second temperature value is not an instantaneous measurement of the air temperature but an average of the previous 40 to 80 seconds’ (BoM 2017) is supported here based on 1 Hz air temperature data measured at Darwin and Noarlunga. Hence, it is appropriate for the Bureau to record the value at the last second of each minute as satisfying WMO sampling requirements for 1-min data.

The author is Editor in Chief of this journal. He was blinded from the review process and had no editorial involvement with this paper, which was handled independently by other members of the Editorial Board. There are no other conflicts.