Progress in understanding the use of diffusive gradients in thin films (DGT) – back to basics
William Davison A B and Hao Zhang AA Lancaster Environment Centre, Lancaster University, Lancaster, LA1 4YQ, UK.
B Corresponding author. Email: w.davison@lancaster.ac.uk
Environmental Chemistry 9(1) 1-13 https://doi.org/10.1071/EN11084
Submitted: 22 June 2011 Accepted: 13 September 2011 Published: 31 January 2012
Journal Compilation © CSIRO Publishing JYEAR Open Access CC BY-NC-ND
Environmental context. It is now nearly 20 years since the introduction of the technique of diffusive gradients in thin films, which can provide information on solute concentrations and dynamics in sediments, soils and water. The interpretation of these measurements in terms of concentrations relies on simple equations and associated assumptions. This review examines how well they have stood the test of time.
Abstract. Diffusive gradients in thin films (DGT) is now widely used to measure a range of determinands in waters, soils and sediments. In most cases the mass accumulated is interpreted in terms of a labile form of the component being measured using a simple equation that applies to steady-state conditions. During the past decade several publications have revealed phenomena that question some of the assumptions necessary for use of the simple equation. This review systematically examines the available evidence relating to appropriate geometry, possible charge effects, binding of solutes and ligands to the diffusive gel and filter, the rate of reaction with the binding layer, the effects of solution complexation and kinetic limitation, necessary time for deployment and the measurement of nanoparticles. DGT emerges as a robust monitoring tool for labile components in solution. Although there is evidence, for some conditions, of binding of metals and, more moderately, humic substances to the diffusive gel and filter membrane, this is unlikely to affect DGT measurement in natural waters for deployment times exceeding a few days. Detailed speciation and kinetic studies require a more thorough interpretation of the mass accumulated by DGT. A coherent theory has emerged for relatively simple solutions, but systems with complex heterogeneous ligands, as is the case for natural waters, are challenging. The size discrimination of DGT is still poorly known. Systematic measurements with well characterised nanoparticles are required to define the distribution of pore sizes in the gels and to establish the contribution of natural colloids to the DGT measurement.
Introduction
Diffusive gradients in thin films (DGT) is now an established technique that is used in different fields of research, including water quality monitoring,[1,2] chemical speciation in solution,[3,4] sediment geochemistry,[5,6] dynamic processes in waters[7–9] and soils[10,11] and bioavailability in waters[12,13] and soils.[14,15] By using different binding agents the range of determinands has been extended from trace metals[16] to include other cations,[17,18] oxyanions[19,20] and targeted species, for example sulfide,[21] uranium,[22] radium[23] and technetium.[24] This burgeoning use of the technique in different areas of research has been facilitated by its simplicity, ease of use and the straightforward interpretation of measured mass (MDGT) in terms of the DGT-labile concentration (CDGT) which in sediments and soils is an interfacial concentration.[16,25]
From the outset it was recognised that use of Eqn 1 to obtain CDGT from the well defined quantities (see Fig. 1) of physical (geometric) area of the exposure window (Ap), diffusion layer thickness (Δg) and deployment time (t) requires several assumptions.[26]


|
Put simply these are: (i) geometric values of exposure area and Δg apply with a negligible diffusion boundary layer; (ii) interactions of solution species with the gel and membrane filter comprising Δg are negligible; (iii) measured species interact at the binding layer surface without penetration; and (iv) the time taken by the initial transient before steady-state is negligible compared with the deployment time. Further interpretation of in-situ measurements in natural waters also assumed that there would be negligible contribution from colloidal species, other than very small nanoparticles such as complexes with fulvic and humic acid, which are usually regarded as solution species.[16,27] Initially these assumptions were largely untested, but over time they have been investigated by several research groups. By examining the available evidence this review considers the likely validity of Eqn 1 for a range of determinands and conditions, presents alternative approaches where necessary and highlights remaining uncertainties. The focus is on deployments in solutions, which provide controlled conditions for performance testing, but the findings relate directly to in-situ deployments in natural waters and are very relevant to deployments in soils and sediments.
Appropriate area and thickness
A thin layer of solution adjacent to an immersed surface is quiescent and transport of solutes in this layer, known as the diffusive boundary layer (DBL), is exclusively by diffusion. Therefore the complete diffusion gradient for a deployed DGT device extends through the DBL. In this paper we use the term material diffusion layer (MDL) when referring to the gradients through the diffusion layer and filter, of total thickness (Δg) (Fig. 1).
Although early work appreciated that the diffusion gradient would extend into the adjacent solution where there is a DBL, the thickness of the DBL was initially assumed to be negligible in well mixed solutions and natural waters.[16] The DBL was soon shown to be significant in stirred solutions at low stirring speeds[26] and in 1998 Zhang et al.[28] took it into account in their in-situ measurements of phosphate by deploying DGT devices with different thicknesses (g) of diffusive gel. They stated that the DBL thickness (δ) can be derived from the intercept divided by the slope of a plot of 1/MDGT v. Δg according to Eqn 2 (Ae, the effective surface area, is explained below).[29,30]
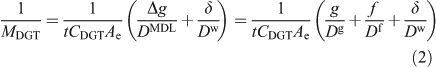
The gel originally used in DGT and most commonly used since is APA, which is polyacrylamide crosslinked with an agarose derivative.[31] Measurements using a diffusion cell have shown that the diffusion coefficient of simple metal cations in the filter membrane (Df) of thickness f, is indistinguishable from that in the APA gel (Dg).[32] Consequently, a single value can be used for the MDL (DMDL = Dg = Df), but a separate value for water (Dw) should be used for the DBL.[32]
When Warnken et al.[33] measured Cd in well stirred solutions using MDL thicknesses of 0.14 to 1.34 mm, they were able to obtain estimates of δ, which decreased with increasing stirring speed. The consistency of the data when only the filter membrane was used (for the 0.14 mm thickness) also confirmed that Dg = Df. As Webb and Keough[34] have demonstrated, it is difficult to estimate δ precisely using just two MDL thicknesses, but by using four MDL thicknesses and replicate measurements Warnken et al.[33] obtained very reproducible values, as have other workers.[35] It was shown later that when metals are present as organic complexes the DBL obtained using this method can be higher than the physical value, as it incorporates a kinetic term if slowly dissociating complexes contribute to the accumulated metal.[8,36] As complexes of Cd and Zn in natural waters are generally weak, with no measurable kinetic limitation, the value of δ obtained from measurements of these metals is the true physical DBL.
The precise values of CDGT obtained for each metal in simple, non-complexing, inorganic solutions, taking into account the DBL, were systematically higher than the concentrations measured directly in solution, Csoln.[33] This was attributed to the effective surface area (Ae) of the standard DGT holders being 3.80 cm2 whereas the geometric area was 3.14 cm2. Similar experiments also showed that for standard soil devices: Ap = 2.54 cm2 and Ae = 3.08 cm2. Measurements using laser ablation inductively coupled plasma–mass spectrometry (ICP-MS) showed that the metal accumulates in an area of resin gel greater than Ap.[33] However the major reason for Ae > Ap is that the diffusion pathway into the front membrane is not just perpendicular to the membrane, as implicitly assumed using the simple one-dimensional representation of diffusion of Eqns 1 and 2 (Fig. 2). Extra material is supplied at the edges in curved diffusion paths as shown using numerical modelling (O. A. Garmo, pers. comm.). Similarly, there are likely to be edge effects for the DBL. Therefore, derived values of δ are also really effective values, as δ is unlikely to be constant over the whole area of the filter.

|
According to the above evidence, Eqn 3 is generally most appropriate for calculating CDGT.
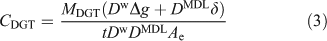
However, it can be simplified when a 0.8 mm-thick gel layer is used with a typically 0.14 mm-thick membrane filter in a standard DGT solution device. There are then two valid ways of calculating CDGT for a given value of MDGT. Eqn 1 can be used with the geometric area (Ap) making no account for the DBL. Alternatively the same value of CDGT will be obtained by using Eqn 3 with Ae = 3.8 cm2 when the actual DBL is 0.23 mm. This is why in practise Eqn 1 has been found to work quite well. The DBL is typically ~0.2 mm in well stirred solutions, as created by immersing a DGT device in a solution stirred by a magnetic follower to create a well defined vortex. In-situ measurements of the DBL using DGT vary from 0.26 mm (fast flowing waters), 0.31 mm (Lake Epilimnion) to 0.39 mm (stagnant pond). Therefore, for all but the last case, the error in using Eqn 1 with the geometric area and neglecting the DBL would be much less than 10 %. This greatly simplifies measurements, as there is no need to measure the DBL thickness, but clearly this only applies to DGT devices with this standard geometry and size. Note that errors will be larger when other thicknesses of gel are used. Eqn 3 should then be the preferred calculation route, in which case δ should be measured using a suite of DGT devices having the same geometry, but equipped with a range of gel layer thicknesses.
Inert diffusive gel?
Effect of gel charge
The APA diffusive gel commonly used in DGT devices was previously used in experiments employing the technique of diffusive equilibration in thin films (DET).[37–39] As part of the DET studies, the gel was equilibrated with known solutions and the total solute concentrations in the gel compared with their known concentrations in solution. The generally good agreement established that there was no significant attachment to the gel of the solutes studied, including major cations and anions, FeII, MnII and ammonia.
Early measurements of trace metals using DGT assumed that any interactions with the diffusive gel were minimal, as indicated by the good agreement between CDGT and Csoln in non-complexing solutions.[26] However, measurements undertaken at very low ionic strengths (I) (I ≤ 1 mM) began to reveal inconsistencies. Using an APA diffusive gel, Alfaro-De la Torre et al.[29] observed values of CDGT/Csoln systematically greater than 1, which they attributed to diffusion of metal ions being enhanced to preserve electroneutrality under dynamic conditions. Peters et al.[40] speculated that their observed values of CDGT/Csoln, ranging from 0.5 to 3, were attributable to an apparently variable charge on the gel. An earlier study had shown that diffusion coefficients of metal ions in the APA gel, measured using a diffusion cell, were also erratic at very low ionic strengths.[31] An explanation for the apparent inconsistencies was provided by Warnken et al.[41] Their systematic experiments showed that the extent of washing determines the value of CDGT/Csoln. If polyacrylamide gels are not very well washed they have a negative charge because of the presence of excess reagent products. A simple test involves measuring the pH of the rinse solution: values greater than 7 indicate incomplete removal of reagent products. With copious washing the pH can become less than 7 and a value of CDGT/Csoln < 1 may be observed if the ionic strength is very low (~0.1 mM), indicating a small positive charge stemming from hydrogen ions in the wash water (CO2 at atmospheric partial pressure dissolving as carbonic acid). At ionic strengths of 1 mM or higher, CDGT/Csoln = 1 using well washed gels, due to electrolytic screening of the charge.
Fatin-Rouge et al.[42] considered quantitatively several solute–gel interactions, including steric hindrance and specific binding of metals to the gel. They provided a mechanistic basis for observed values of CDGT/Csoln greater than 1 in pure agarose gel, based on the effect of gel charge, which creates a Donnan potential. Their explanation for DGT applications was elaborated in detail by Yesek and van Leeuwen,[43] who supported their theory by deriving the Donnan potential from measurements of the conductivity of polyacrylamide gels copolymerised with sodium acrylate to ensure a high charge. They were crosslinked with N,N′-methylene-bis-acrylamide, commonly known as bis-acrylamide or simply bis, with 0.3 g of bis and 15.3 g of acrylamide in 100 mL of the initial gel solution. When gels are negatively charged, cations become electrostatically associated with the gel. Their concentrations on either side of the gel–solution interface are then unequal, with an enhanced concentration inside the gel (Fig. 3). In practise the gel contacts a membrane filter rather than solution, but if the filter has zero charge (which may not be the case) the gel–solution interface is effectively the interface between the gel and the porewater of the membrane filter. The consequence of the charged-induced cation enhancement is that the diffusion gradient of metal ions through the gel is elevated compared with a comparable situation where the gel is uncharged, and CDGT is higher than expected if calculated using Eqn 1. The Donnan potential (ψ) established between gel and solution, because of the charge density of the gel (ρ), can be used to calculate the elevation of the concentration in the gel (Cgel) over the adjoining solution (Eqns 4, 5).
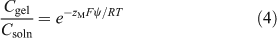
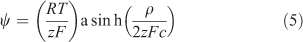

|
The valence of the metal ion is zM, and that of the supporting electrolyte, of concentration c, is z. The Faraday constant is F, R is the gas constant and T is the absolute temperature. If gels are positively charged, cations are repelled and the concentration at the gel side of the interface is lowered. The concentration gradient in the gel is then lowered so that CDGT/Csoln becomes less than 1 in very low ionic strength solutions, as observed by Warnken et al.[41] and supported by comparable lower fluxes observed in diffusion cell experiments, that were interpreted as lower apparent diffusion coefficients.[32] Eqn 5 shows that the effect of gel charge is reduced as ionic strength (related to zc) is increased.
Yesek and van Leeuwen[43] found that for the bis crosslinked gel without any sodium acrylate the Donnan potential was too small to measure (<10 mV) in solutions where I ≥ 1 mM, indicating negligible effects due to charge. As ionic strength was lowered further, there was an increasingly negative Donnan potential. DGT measurements with this gel gave values for CDGT/Csoln = ~1.7 at I = 0.1 mM and slightly higher than 1 at I = 1 and 10 mM. From consideration of Eqns 4 and 5 it appears that at these low ionic strengths the Donnan potential resulting from the gel charge is not negligible.[44] Sangi et al.[45] had earlier used bis gels (0.8 g of bis and 30 g of acrylamide in 100 mL of gel solution) in DGT to measure metals in situ in a stream with a very low ionic strength. Their calibrations produced values of CDGT/Csoln = ~1 for Cd at I ≥ 1 mM, but systematically increasing values as the ionic strength was lowered. They showed, using simple DET experiments, that the ratio of Cd concentrations in the gel (Cgel) to Csoln increased with decreasing ionic strength below I = 1 mM, consistent with the gels having a negative charge whose effects were apparent at these low ionic strength solutions. When all the above measurements with bis gels were made the critical importance of gel washing was not appreciated, so the results should be regarded cautiously.
Use of the above theory (Eqns 4, 5) implies a high density of charged sites, which may not be the case for the APA gel, which has minimal charge effects. However, it is also presumed that charges are distributed uniformly so that the potential is constant within the gel. If this does not hold there may be a negligible net charge, even though locally within the gel there may be charged groups.[42]
So how do the charges on the gel discussed above affect DGT measurements? Where DGT incorporates the most commonly used APA gel and measurements are made at ionic strengths of 1 mM or above there is no effect. This is consistent with the very small positive charge on the gel, provided it has been well washed during preparation.[41] Several papers authored by van de Veeken and van Leeuwen[46–48] state that there is a negative charge on the APA gel, but they refer to their measurements made using bis gels.[43,44] Even for their bis gels they found it difficult to measure a Donnan potential at I = 1 mM. The restricted gel that has been used in DGT is a bis crosslinked gel of a different composition (0.8 g of crosslinker and 15 g of monomer).[9,31,32] It is referred to as a ‘restricted’ gel because diffusion coefficients of metal complexes with large ligands in this gel have been shown to be lower than in the APA gel, which may be attributed to a more restricted diffusion path. Verification that CDGT/Csoln = 1 forms part of the quality control for each batch of gels produced by DGT Research Limited, but this is only performed at I = 10 mM. Ideally more detailed measurements at low ionic strength should be performed with well washed examples of the restricted gel to emulate the detailed study of the APA gel.[41]
Effects of binding of measured species
The above discussion of the effects of gel charge have focussed on their direct effects on DGT measurements and therefore on CDGT/Csoln. However, as Sangi et al.[45] showed experimentally, a negative charge within the gel will promote accumulation of cations and therefore when the diffusive gel is simply equilibrated in solution, as in a DET experiment, the ratio of metal concentrations measured in the gel to that in solution (Cgel/Csoln) will be greater than 1. When the enrichment of metal cations within the gel is because of the gel charge, the value of Cgel/Csoln should depend markedly on ionic strength (Eqns 4, 5). Fatin-Rouge et al.[42] recognised that their observed ratios of Cgel/Csoln for Cu, Cd, Hg and Pb in an agarose gel were partly attributable to charge effects, which develop a Donnan potential, and were partly attributable to specific binding between the metal ions and the gel. The values of Cgel/Csoln >1 observed earlier for solutions of 0.83 mg L–1 of Cd, using a bis gel, increased markedly as ionic strength decreased below 1 mM, but for I = 1 to 100 mM they were fairly constant between 1.5 and 1.7.[45] The virtual invariance to ionic strength is consistent with weak specific binding that is observable above 1 mM when associations because of charge are negligible. Cd was also observed to bind specifically to the APA gel.[41] The Cgel/Csoln ratio was ~9 and independent of I (0.01 to 10 mM) when Cd was 1 µg L–1. At 10 µg L–1 of Cd, the much reduced ratio of ~2 declined a little with decreasing ionic strength and at 60 µg L–1 of Cd, the ratio was close to 1. The specific binding of low concentrations of Cd obscures any Donnan effects for the 1 µg L–1 Cd solution. The marked dependence on the concentration of Cd indicates a low capacity of binding sites. At 10 µg L–1 of Cd some of the binding may be related to the slight positive charge observed on these gels for I < 1 mM.[41]
DET experiments have shown some slight binding (Cgel/Csoln = 1.1) of U (400 nM), Mo (1 µM) and Re (5 nM) to a bis crosslinked gel.[49] Similarly, there was at most very slight binding of AsV and SeVI to an APA gel (Cgel/Csoln = 1.1–1.2) when Csoln = 25 µg L–1 (see supporting information in Williams et al.[50]). For phosphate at 1 mg L–1 and at much lower concentrations in rivers there was no evidence of binding to APA gels.[51] No enrichment in an agarose gel was observed for Cd, Cu, Mn, chloride, bromide, sulfate and nitrate, but concentrations in solution were high at 10 mg L–1.[52]
In a comprehensive study of cationic trace metal binding to APA, restricted and agarose gels and to the polyethersulfone membrane filter (Supor-450, Pall) commonly used within DGT,[53] the concentration of metals, the ionic strength and the solution composition were systematically varied. Enrichment of trace metals in the APA and restricted gels was observed under some conditions. It decreased with increasing trace metal concentration, so low concentrations of 10 and 100 nM were used to maximise the effect. Enrichment was almost insensitive to ionic strength and concentrations of Ca and Mg, consistent with high affinity, but low capacity, specific binding to the polyacrylamide gel structure. Cu, Pb and Ni were the most strongly bound, with Cgel/Csoln = 14, 2 and 1.4 at 10 nM metal concentrations. Cd and Co binding was so slight that it was difficult to measure. Complexes of metal with fulvic acid also appeared to bind to the polyacrylamide gels, but there was less evidence for fulvic acid complexes binding to the filter and agarose gels. Binding of metals to the filter and agarose gel was also generally less than observed for the APA gel, but binding of Cu and Pb was again most pronounced. Although these metals clearly bind specifically, the enrichment of, for example Cd, decreased with increasing ionic strength, suggesting that it is attributable, at least in part, to electrostatic interactions.
The most pronounced binding of a cation to a diffusive gel was reported for Hg where a value of Cgel/Csoln = 700 was found for an APA gel and 4.5 for an agarose gel.[54] It is well known that Hg binds with high affinity to amide groups, which are a prime constituent of polyacrylamide gels. However, Hg has been measured successfully with DGT using both these gel types.[6,54]
Collectively the measurements on specific binding show that in many cases when DGT is used it would be incorrect to assume there is no interaction between solutes and the materials of the diffusion layer. The influence of such binding on measurements of metals by DGT has been investigated both experimentally and using a numerical model, which includes binding to the diffusive layer as well as binding to the resin layer.[55] As metal enters the diffusive layer it binds, with metal accumulating until the capacity (usually low) of the gel binding sites is reached. Consequently the time it takes to reach the steady-state concentration gradient of unbound metal through the gel is lengthened. At this steady-state, when all binding sites on the gel are equilibrated with the local metal concentration in solution, the concentration gradient and hence the flux will be no different to the normal situation for DGT, when there is no binding to the gel. Therefore, if the deployment time is sufficiently long, use of the simple Eqn 1 will provide the correct answer. A more detailed discussion of the transient state and necessary deployment times is provided in a subsequent section. However, it should be appreciated here that when metals are present at high concentrations, as in contaminated systems, affects associated with specific binding will be negligible. Even at low concentrations, noticeable effects in terms of a significantly delayed approach to a steady-state concentration gradient are only likely to occur for Cu and Pb.
It is relevant to mention here a further effect related to binding of solute to the gel. DGT devices are often left for hours or days before they are dismantled. During this resting time the metal bound to the diffusive layer will be stripped out by the stronger Chelex sink. For very short deployment times, typically less than 2 h, this could produce an erroneously high DGT measurement, especially if there is appreciable binding that elevates the total concentration of metal in the MDL.[55] For the more usual longer deployment times, however, this release from the diffusive gel effectively shortens the deployment time necessary before the effect of the initial transient conditions on the DGT measurement are negligible.
Possible ligand binding
Simple inorganic ligands, such as sulfate, chloride and phosphate are not enriched or depleted in gels according to the available evidence of DET-type experiments.[39,51,52] To our knowledge the binding of simple organic ligands has not been directly tested, although measurements of metals by DGT in solutions where they are present have been sensibly interpreted without invoking such effects.[56–58] An experimental study has considered directly the enrichment in an APA gel of Suwannee River fulvic acid (SRFA) and humic acid extracted from forest soil (FSHA). Deployment solutions were buffered with the sodium salt of 2-(N-morpholino)ethanesulfonic acid (MES) to pH 6.1 and contained NaNO3 (0.001–0.1 M).[47,48] The humic material associated with the gel was measured spectroscopically at 280 nm by simply inserting a part of the gel into a cuvette. There was little systematic evidence for any enrichment of SRFA from the measured ratio of Cgel/Csoln, which was 1.0 at Csoln =50 mg L–1.[47] At concentrations of SRFA of 5 mg L–1, Cgel/Csoln was 1.9 at I = 11 mM, but 0.6 at I = 2 mM. The observed concentration dependence of Cgel/Csoln does not suggest a charge related phenomenon, but a negative Donnan potential was assumed in rationalising the results, even though experiments at very low ionic strength with well washed gels indicate a small positive charge.[41] A separate experiment, which measured Cgel/Csoln for SRFA when Cd was present in solution, found the ratio did not differ from 1 for concentrations of SRFA in the range 2.6 to 50 mg L–1.[48] Consistently high values of Cgel/Csoln were observed for FSHA of 50–56 at I = 2 mM and 12–17 at I = 11 mM, independent of the concentration of FSHA (0.3–10 mg L–1).[47] In the presence of Cd the ratio for FSHA declined to ~30 (I = 2 mM) and ~5 (I = 11 mM).[48] Cadmium was enriched in the gel, most markedly at I = 2 mM, with the enrichment increasing with the concentration of FSHA. In interpreting their data the authors assumed, without supporting measurements, that the gel was negatively charged and, with this premise, pointed out that the higher accumulation factor they observed for negatively charged humic acid (pH 6.1) at lower ionic strength is counterintuitive. To account for their observations, they invoked micelle formation at the higher ionic strength, with the micelles having less hydrophobic affinity. This may be true, but equally a slight positive charge on the gel, as has been observed from measurements at very low ionic strength,[41] would explain the data without invoking micelle formation.
Clearly, if humic acid does substantially bind to the APA gel it is likely to affect the performance of DGT for measuring trace metals. So far the main evidence comes from a single study and is confined to humic acid derived from a forest soil. Attempts to replicate this work found measurements of the absorbance loss from solution were much more sensitive than measuring absorbance on the gel (Y. Gao and C. Lin, pers. comm.). Ratios of Cgel/Csoln of 2 for SRFA and Suwannee River humic acid (SRHA) and 11 for a soil derived humic acid were obtained at pH 6.1 and I = 2 mM. Molecular weight and hydrophobicity, which is likely to promote binding to gels, is known to decrease in the order: soil derived humic acid > aquatic humic acid > fulvic acid. Most laboratory work with DGT or DET and humic substances has used fulvic acid. Garmo et al.[53] found that fulvic acid slightly increased the enrichment of some metals on polyacrylamide gels, presumably by either fulvic acid or its complexes binding to the gel. DGT experiments in solutions of Cu and SRFA were able to measure Cu accurately, provided deployments were sufficiently long to accommodate the longer time required to reach steady-state conditions because of binding of the complexes in the diffusive layer.[55] No exceptional behaviour associated with adsorption was reported when diffusion coefficients of fulvic and humic acids from an aquatic source and humic acid extracted from peat were measured using a diaphragm cell in a medium of 0.1-M NaNO3 at pH 7.8.[31]
DGT measurements of metals do not appear to have been affected by binding of humic substances to the MDL. In solutions of 1-µM Pb and either 5 mg L–1 SRHA or 25 mg L–1 SRFA over the pH range 5 to 6.9, DGT measurements could be interpreted by simply considering complexation in solution, without invoking possible effects associated with binding of either metal or humic substances to the gel.[59] In natural waters both fulvic acid and humic acid are present, with the former usually dominant. Good agreement has normally been observed between DGT and filterable metal where complexation in solution was predicted to be unimportant.[60–62] Where complexation is dominant, as is often the case for Cu, the measured signal could be explained by accounting for the lower diffusion coefficient of the complex and, if necessary, the dissociation kinetics of species in solution.[61,63,64] These studies embraced a wide range of dissolved organic carbon, for example from 0.6 to 13.2 mg L–1 in 34 streams.[64]
The weight of evidence suggests that effects associated with possible enrichment in the gel of humic substances do not affect significantly the interpretation of in-situ measurements in freshwater of metals by DGT. It is even more unlikely that there will be any effects for measurements made in marine systems. However, as the indications are that for some conditions humic acid can bind to gels, further direct investigations of the binding and its effects on DGT measurements are required. This particularly applies to DGT measurements made in soils where the humic substances may be more hydrophobic and have a greater affinity for the gels. It should be recognised that humic acid in soil solution may not bind to gels as well as humic acid extracted from soil using a strong base, as this latter procedure will extract more hydrophobic fractions attached to solid phases. Given the sensible interpretation of DGT data for deployments in soils without invoking binding of humic acid to the gel,[10,11,15,50] the present position is that a problem associated with ligand binding has yet to be demonstrated in practice.
Concentration of analyte in the binding layer
Application of Eqn 1 requires that the concentration of the measured species at the interface between the binding and diffusion layers is negligibly small. This condition implies that binding is very fast. The usual good agreement between CDGT and the directly measured concentration in solution indirectly confirms that the condition holds. Measurement of the time dependence of the binding of solutes to binding gels, simply immersed without DGT holders in well stirred solutions, provides direct information on the rate of binding, as shown for binding of phosphate, molybdate, and cationic metals to a mixed binding layer.[65] The amount bound usually increases progressively over a timescale of minutes, as it is controlled by mass transport. However, to have an effectively zero interfacial concentration in DGT, binding needs to be efficient within a minute. As Luo et al.[66] have pointed out, the measured mass accumulated in this time by the immersed binding gel equates to a flux that is usually orders of magnitude higher than the maximum flux required by DGT, confirming that the rate of binding is not limiting for DGT.
Levy et al.[35] investigated penetration of metal into the binding gel by using DGT devices equipped with multiple resin binding layers. In simple solutions at pH 7 they found no evidence of penetration beyond the first binding layer, but at lower pH there was measurable penetration of Mn (pH 4 and 5) and Cd and Co (pH 4). The results were consistent with rapid binding of metals in circum-neutral waters and slower binding of Mn, Cd and Co at lower pH. A penetration parameter expressing the mean distance that metals penetrate into the resin (λM) was derived. Other than for very low pH, it was no greater than the diameter of the Chelex 100 resin.
When the accumulated analyte is near to the maximum capacity of the binding layer, the case of a near infinite sink no longer applies. The concentration in the pores of the gel at the interface of the diffusion and binding layers becomes significant and the increase in DGT measured mass with increasing concentration or deployment time declines as the capacity is approached. However, when the accumulated mass is less than approximately one-tenth of the capacity, the sensitivity of the DGT response is unaffected. Competition for the binding sites with other components in solution effectively lowers the capacity and induces a progressive decline in sensitivity as the capacity is approached. Using a simple ion exchange equation incorporated into a model of DGT accumulated mass, Degryse et al.[67] showed how measurement of Zn was affected by competitive binding of Ca. Similar competition by protons for sites on Chelex most probably accounts for the declining performance of DGT for measuring cationic metals as pH is lowered.[68,69] Problems with measuring MnII, which binds weakly to Chelex, in the presence of very high concentrations of FeII have been reported[70] and phosphate measurements were affected by very high concentrations of bicarbonate.[71] Where analytes have high concentrations, as for Ca, measurements must be restricted to fairly short deployment times, typically <1 day, to ensure capacity is not approached.[17] Use of thicker diffusion gels is also then a sensible strategy.
Different slopes of mass v. time have been observed when using DGT devices with different binding agents, as for measurements of Hg in simple solutions using Chelex and Spheron-thiol[54] and, for times exceeding 24 h, when measuring phosphate in seawater using ferrihydrite and titanium oxide.[72] If capacity was approached in the latter case, competitive binding by the anions in seawater may be responsible, as suggested. However, the former case of different slopes throughout the time regime is more puzzling. For simple solutions, relatively weak binding is sufficient to lower analytes to negligible concentrations and so the measurement is expected to be independent of the binding agent.[73] Possible explanations include the binding of Hg to Chelex being kinetically limited and the binding agent affecting Hg hydrolysis.
Accounting for complexation
If complexes of a metal measured by DGT are present, and they dissociate rapidly (fully labile) and have the same diffusion coefficient as the free metal, Eqns 1, 2 and 3 can be used, with CDGT being the total concentration of metal. Simple inorganic complexes including carbonates, hydroxides, sulfates and chlorides are within this category. Dealing fully with the effects of complexation for situations other than this simple case is, as for any technique, quite complicated and would require a review in its own right. This section therefore only provides a brief outline of progress.
Natural organic ligands, including humic substances, may be sufficiently large that their complexes have a smaller diffusion coefficient. For simplicity and brevity the subsequent discussion will consider only the simple case where the labile inorganic metal (M) reacts with an organic ligand (L) to form a complex (ML) but some of the cited literature includes fuller treatments. When the complex is fully labile (dissociates rapidly), the accumulated mass is simply derived from the sum of the fluxes attributable to each species present, resulting in Eqn 6 where the diffusion coefficient in the DBL is taken to be the same as that in the gel layer.[74]
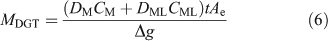
This treatment, allied to in-situ deployments of DGT with different gels, each with different diffusion coefficients for fulvic acid, was used to derive the concentration of metals bound to fulvic acid in freshwater.[74,75] The DBL thickness was derived in the same water by deploying DGT devices with different thickness and δ was incorporated within Δg, with the assumption that diffusion coefficients in water, DMw and DMLw, were the same as those in the MDL and diffusive gel, DMg and DMLg. If this assumption does not hold, Eqn 7 applies (remember DMDL = Dg = Df).[8]
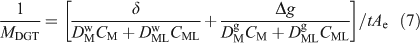
When a single measurement of MDGT is made in an unknown solution containing a fully labile complex, CM and CML cannot be derived even if DM and DML are known. However, if the concentrations of CM and CML are estimated independently by modelling, it is possible to calculate the expected value of CDGT, which has been termed Cmaxdyn (Eqn 8).[61,63] This maximum dynamic concentration is the maximum concentration, corresponding to the situation where all complexes are labile, that can be measured in a solution using a dynamic technique (where metal species must be transported by diffusion before measurement). Eqn 8 again disregards different values for diffusion coefficients in the DBL.
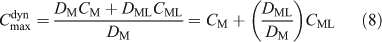
Where ML is a metal complex with fulvic acid, to a good approximation DML/DM = 0.2 in an APA gel.[31,32] Eqn 8 has been used with this ratio to calculate Cmaxdyn for several freshwaters using a speciation code such as WHAM[76] and total filterable concentrations.[3,61–64] Where expected, for example for weakly complexing metals such as Cd and Mn in slightly acidic waters, Cmaxdyn has agreed quite well with CDGT. Values of CDGT appreciably less than Cmaxdyn have been taken to indicate either slow complex dissociation rates or the presence of colloidal species that are sufficiently immobile or inert not to be measured by DGT. These observations are consistent with predictions of complex lability, which indicate that for DGT with an ~1 mm thick MDL, most metal complexes can be expected to be labile, with Cu and Pb at very low ratios of metals to humic substances being the only exceptions.[77,78]
An appreciation of how kinetic factors influence the DGT measurement has been approached in two ways: by developing analytical equations and using dynamic numerical models. A simplified equation requiring many assumptions was first used to obtain information on the rate of dissociation of NiNTA complexes (NTA, nitrilotriacetic acid) from DGT measurements using several diffusion layer thicknesses.[79] Similar measurements performed in situ in a natural water were interpreted using the more complete Eqn 9 derived from an approach used to interpret voltammetric data.[8,80]
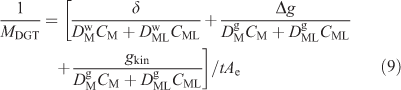
The kinetic term (gkin) was obtained from plots of 1/MDGT v. Δg. A fuller interpretation of data obtained when Δg is varied, which accommodates penetration according to the theory of Mongin et al.[58] and Uribe et al.,[81] will soon be available (J. Galceran, J. L. Levy and J. Puy, pers. comm.). It confirms that it is appropriate to use Eqn 9 to obtain gkin. However, the earlier quantitative interpretation of gkin, which failed to consider penetration into the resin gel of the relatively slowly dissociating complexes, did not generally represent the DGT case.[8] Town et al.[7] have pointed out that only a narrow kinetic window is accessed by this approach. They have suggested that this can be extended by varying the metal-to-ligand ratio.
Tusseau-Vuillemin et al.[82] used the first dynamic numerical model of DGT immersed in a solution of metal ion and ligand to demonstrate that, depending on its dissociation rate, the complex could diffuse into the resin layer before dissociating (Fig. 4). They demonstrated quantitatively that the contribution of DGT accumulated metal from the complex is governed by DML/DM and the proportion of the complex that can dissociate. Cu-citrate and Cu-EDTA (EDTA, ethylenediaminetetraacetate) were used as examples of labile and inert systems. Penetration into the resin layer was experimentally demonstrated using lanthanide complexes of a multidentate ligand.[83] It was successfully modelled using a similar approach to Tusseau-Vuillemin et al.[82] but assuming that binding of metal to the resin was controlled by stability and rate constants rather than being instantaneous.[73] The DGT measurement was shown to be independent of the stability constant for metal binding to the resin, provided it was greater than a threshold value. A similar model was used to calculate the lability degree defined as the ratio of the actual contribution of the complex to the metal flux to the maximum contribution reached if the complex was labile (Eqn 10).[58]

Metal fluxes, J, are subscripted according to the actual measured value, the value when all complexes are inert (supply only from free metal) and for the case when all complexes are labile. Model simulations showed that a complex system is likely to appear more labile when measured by DGT, where complexes can penetrate into the binding layer, than when measured by other techniques where complexes are restricted to the diffusion layer. This work was extended to provide approximate analytical expressions for calculating the metal flux, lability degree and concentration profiles in a DGT experiment.[81] The diffusion layer for DGT is typically 100 times greater than for voltammetry, which means that even without considering resin layer penetration, complexes are ~10 000 times more labile when measured using DGT. Penetration of partially labile complexes into the resin layer enhances this effect.
Collectively these developments provide increased understanding of how the DGT measurement is affected by the complexities of solution speciation. One of the great advantages of the modelling approach is as an aid to conceptual appreciation, especially by the images it provides of temporal changes in the distribution of each species through the DGT device (Fig. 4). The accumulated mass can be successfully predicted for well defined metal-ligand systems. However, interpreting measurements in truly unknown and very complicated systems, such as natural waters, is far more challenging. Comparison with Cmaxdyn and use of multiple devices with a range of diffusion layer thickness are useful approaches. If the only data available are from a single type of DGT device, the measurement must simply be interpreted as labile and mobile metal, as there are too many unknown solution parameters (e.g. speciation, dissociation rates, colloidal composition) that can affect measurements made with DGT or any other dynamic technique. An additional complication is that the heterogeneous ligands of natural waters have a distribution of stability and dissociation rate constants. Plots of CDGT v. the ratio of moles of bound metal to weight of DOC have provided information on the variation in the affinities of binding sites that can be available to a metal (heterogeneity).[7] However, this procedure did not provide conclusive information when applied to data for 34 streams, which may be a general outcome when applied to natural waters, where other variables, such as pH and the nature of the DOC, will be important.[64]
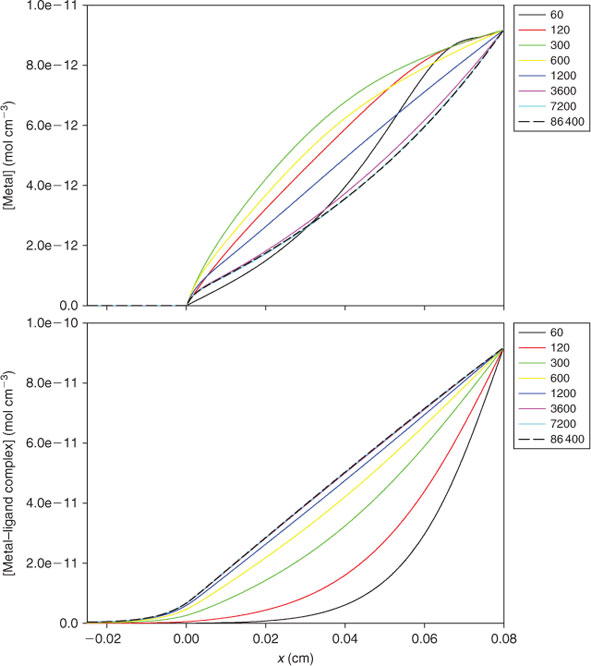
|
Necessary time for DGT deployment
If the metal accumulated by DGT is modelled dynamically the initial transient before steady-state will automatically be accommodated and interpretation of the measured accumulated mass will be valid irrespective of deployment time. However, Eqns 1–3 and 6–9 apply to the steady-state case. A necessary condition for their valid application is that the actual mass accumulated is not significantly different from the mass that would have accumulated if there was no initial transient.
The time required to reach steady-state has been reported to be approximated by Δg2/yD, with the coefficient y having values from 1[84] to π.[16,26] To be meaningful these values of y and associated times need to be accompanied by some measure of the degree to which steady-state is approached. Dynamic modelling of the DGT system has shown that the instantaneous flux will be ~99 % of the steady-state value at time Δg2/D.[55] A more realistic approach, when considering typical DGT measurement errors, might be to consider 95 % of the steady-state value, which is approximated by Δg2/2D.[55,81]
The potential error incurred when interpreting the measured mass solely in terms of steady-state is not simply obtained by expressing the time to steady-state as a percentage of the deployment time. The mass that accumulates before steady-state being reached should be considered. Lehto et al.[73] used a dynamic numerical model that accommodates the time to steady-state to calculate mass accumulated for various values of t, Δg and D, and compared the mass to that obtained assuming steady-state throughout (i.e. using Eqn 1). The difference between the two, which provides the error associated with neglecting the steady-state, can, to a good approximation, be calculated using Δg2/yD, but this time y = 6 (Eqn 11).
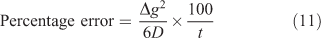
Strictly the whole of the regime where diffusion applies, including the DBL, should be considered and so it is more appropriate to use Δg + δ rather than Δg, with the implicit assumption that Dw = Dg. For typical trace metals in simple solutions, with a diffusion coefficient of 5 × 10–6 cm2 s–1, the error when using a 0.8 mm-thick diffusive gel (filter = 0.13 mm; δ = 0.27 mm, (Δg + δ) = 1.2 mm) is 3.3 % (t = 4 h), 1.3 % (t = 10 h) and 0.56 % (t = 24 h). Increasing the gel layer thickness will increase these errors, but even with an exceptionally large value of Δg + δ of 2.4 mm the error after 24 h is only 2.2 %.
Two factors can increase substantially the time necessary to reach steady-state and therefore the associated errors. They are the slower diffusion of complexes and the binding of metals, complexes or ligands to the materials of the diffusion layer. If there is no binding in the MDL, the greatest effect that labile complexes can have on the time required to reach steady-state is when the metal is fully complexed. In the APA gel, D for complexes of fulvic acid is ~2 × 10–6 cm2 s–1, and for humic acid ~1 × 10–6 cm2 s–1, whereas in the restricted gel it is ~1 ×10–6 cm2 s–1 for fulvic acid.[32] Using Eqn 11 with D = 1 ×10–6 cm2 s–1, the error when using a 0.8 mm-thick diffusive gel is 17 % (t = 4 h), 6.7 % (t = 10 h) and 2.8 % (t = 24 h), indicating that deployment times of at least 24 h should be used when humic substances are present. Tusseau-Vuillemin et al.[82] and Lehto et al.[73] (within the supporting information) have shown that the evolution of the concentration of each species with time can be quite complex and highly variable, depending on diffusion coefficients of metals and complexes, the initial ligand-to-metal ratio, extent of complexation and the rate of dissociation (Fig. 4). When appreciable labile or partially labile complexes are present, during the initial approach to steady-state the concentration of free metal within the diffusive layer may be greater than the steady-state values represented by a linear concentration gradient, due to resupply from the complex (Fig. 4).
Recent simulations of DGT fluxes in complexing media have shown how the lability of complexes rather than their diffusion characteristics affect the time required to reach steady-state (J. Galceran and J. Puy, pers. comm.). Inert or very labile complexes do not affect appreciably the time required to reach steady-state, but for partially labile complexes it may be increased by as much as a factor of 5.
Binding of components in solution to the diffusive gel or filter membrane can increase the time required to establish steady-state. To achieve steady-state, equilibrium must be established between the metal on the MDL binding sites and the metal in solution at each location. As these sites must be effectively ‘filled’ by the metal diffusing into the layer, more metal is required than for the case where there is no binding within the MDL, lengthening the necessary time before the linear concentration gradient of free metal is established. The maximum rate at which metal can diffuse into the diffusive layer is proportional to the concentration in solution. As there appears to be a fixed capacity of sites for binding metals, the time required to achieve steady-state increases as the concentration in solution declines and the thickness of the diffusive layer increases.[55] Of the metals tested, Cu binds most markedly.[53] Garmo et al.[55] used a numerical model, which they validated experimentally, to calculate the error on the DGT measurement associated with this effect. For a 1 mm-thick diffusion layer and the very low concentration of 0.1 nM, the error would be negligible (<3 %) for deployments >5 days, acceptable at <5 % after 3 days, but for 1 day it is ~15 % and still ~7 % for 2 days. Copper (then Pb) is the worst case; the effect for other metals will generally be considerably less. At more realistic environmental concentrations for Cu of 10 and 100 nM, the error for a 24-h deployment would be ~7 and ~3 %.
Binding of a metal complex to the diffusive gel will also increase the time required to reach steady-state. This case has been modelled, but there is no experimental evidence to support the findings. Van Leeuwen’s[85] graphically presented modelled outputs did not have good temporal resolution, but they indicated that the time to reach steady-state increased from 700 s to 5 × 103 s to 5 × 105 s for the respective cases of free metal ion, metal plus slowly diffusing complex and metal plus slowly diffusing complex that also binds to the gel (at a very high ratio of 25 bound to 1 in solution). In these calculations DM =7 × 10–6 cm2 s–1 and DML = 1 × 10–6 cm2 s–1, but no information on the concentrations of species were provided and it is not known whether binding of humic substances is concentration dependent. However, the simulations usefully point to two interesting effects. First, short deployments of DGT, under conditions where the time to steady-state is long, are likely to provide a measure of the total labile inorganic species. Second, if there is pronounced binding of the complex to the materials of the diffusive layer, very long deployment times of several weeks may be necessary to ensure that the DGT measurement accurately reflects the total labile species in solution.
Collectively the information available on the time required to reach steady-state suggests that short deployment times of 1 day or less should be avoided in uncontaminated natural waters. In principle, binding of Cu and probably Pb to the diffusive gel may considerably increase the time required to reach steady-state, but only when the metals are present at very low concentrations (very low nanomolar range or less). Under these conditions it was suggested that measurements of accumulated mass with respect to time may have two slopes, initially proportional to the uncomplexed metal concentration and then to the total metal concentration.[85] However, because of the low metal concentrations, deployment times in excess of 3 days will most likely be required to ensure adequate pre-concentration by DGT for reliable analytical measurement. Consequently the time taken to reach steady-state will not be a problem and an initially lower slope will not be observed. Binding of metal complexes to the diffusive gel will further increase the time taken to steady-state. Although moderate promotion of metal binding by fulvic acid has been observed, there was no significant effect on the time taken to reach steady-state.[55] The similar weak binding of aquatic humic acid suggests that the time to steady-state will not be increased appreciably by its presence. For measurements of aquatic systems contaminated with metals, times at least as short as 1 day can be used because effects due to adsorption of metals will be minimised and their complexes will be less dominant in solution. As there appears to be more binding to the gel of humic acid extracted from soils, assessment of possible binding of the presumed more hydrophobic humic acid in soil (and peat) solution is urgently needed. It is worth noting, however, that time-dependent DGT measurements on soils have been explained without invoking a very slow approach to pseudo steady-state associated with binding to the gel of metal complexes or ligands.[11,86]
Measurement of nanoparticulate species
Possible measurement by DGT of solute that forms a component of colloids or nanoparticulate species will depend on whether the particle can diffuse through the gel and filter, and sufficiently rapidly release solute when it encounters the binding layer. In solution without the hindrance of a gel the diffusion coefficient (m2 s–1) decreases as the radius of a spherical particle (r, m) increases according to the Stokes–Einstein equation, which at 25 °C for neutral buoyancy particles in water reduces to Eqn 12,[87,88] provided the molecular weight (Mwt) ≤ 50 000 Da.[89]
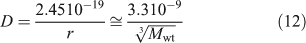
Therefore, particles with a Mwt of ~50 000 Da and a diameter of 5–6 nm can expect to have a diffusion coefficient in water of ~9 × 10–11 m2 s–1 (= 9 × 10–7 cm2 s–1). This is approximately a factor of 8 less than that of free metal ions, and consequently measurement of metal attached to such particles by a technique relying on diffusional transport will inherently have poor sensitivity. In DGT, particles within the filter and gel will diffuse more slowly than in water. Lead et al.[90] used ultracentrifugation to estimate molecular weights (in parentheses) of fulvic acid isolated from water (AFA) (2400 Da), humic acid isolated from water (AHA) (6300 Da) and humic acid from a peat soil (PHA) (16 500 Da). Their diffusion coefficients (×10–6 cm2 s–1) in an APA gel (italicised) and a restricted gel (underlined) were substantially less than in water (normal text): AFA (2.46, 1.15, 0.37); AHA (1.79, 0.60, 0.18); PHA (1.30, 0.35), and in agreement with values for SRFA and SRHA.[31,32] The decrease compared with water was proportionally greatest for the larger molecules and the restricted gel, suggesting that size affects diffusion in these gels, even for these relatively modest sizes (r = ~1 nm (AFA), 1.4 nm (AHA) and 1.9 nm (PHA)). Given that D in the APA gel for the 3.8 nm-diameter nanoparticle is 27 % of the value in water, a much greater attenuation might be expected for a 10-nm nanoparticle, further reducing its sensitivity to measurement by DGT. The restricted gel impedes even AHA quite markedly (only 10 % of the D value in water), which has prompted the suggestion that when used in DGT it provides an approximate measure of inorganic species, especially when complexation is not dominated by humic substances.[75]
Diffusion coefficients (×10–6 cm2 s–1) in agarose gel of AFA (1.92), AHA (1.19) and PHA (0.74) are higher than in polyacrylamide gels, indicating a larger pore size.[31] Fluorescence correlation spectroscopy of defined particles or molecules with a range of sizes showed that agarose gel had a mean pore diameter of 74 nm.[87] However, because of the distribution of pore sizes, particles with a diameter >60 nm were considered to be trapped. That is they may be able to diffuse locally, within a set of large pores, but could not diffuse through an entire gel. Particles with diameters up to 140 nm could participate in the locally trapped diffusion.
Similar detailed information on pore size characteristics is unfortunately not yet available for the gels commonly used in DGT. DGT measurements, using both APA and restricted gels, were made of Pb in solutions containing free Pb and Pb bound to monodisperse carboxylated latex nanospheres with diameters of 81 and 259 nm.[88] There was no evidence of Pb from the larger particles contributing to the measurement, but some indication that, in solutions containing the smaller particles, there was more Pb accumulated than expected from the free ion alone. In DET experiments performed with the same solutions the measured concentration of Pb in the gels was greater than the free ion concentration in solution and the time to equilibration was longer than for the free ion. The authors considered this as evidence that both sizes of particles could diffuse through both types of gel. However, the results would be equally consistent with Pb2+ binding to the gel. According to the paper there was no evidence of such binding, but this is contrary to the data of Garmo et al.[53] Given that only particles <60 nm in diameter can diffuse through an agarose gel, which is more permeable to humic substances than APA, it is surprising that particles as large as 259 nm equilibrate to a high concentration within both APA and restricted gels. Van der Veeken et al.[88] postulated that the restricted gel in particular, which attenuates markedly the diffusion of humic substances, has a very wide pore size distribution. Although the structures of APA and restricted gels are probably different from that of agaraose, it is worth noting that according to the measured characteristics of agarose, large particles (e.g. 259 nm) would be expected to display trapped diffusion and so would not penetrate to populate the entire gel.
Comparisons of metal speciation using in-situ DGT (APA gel) and ultrafiltration showed very good agreement between the <1-kDa fraction and DGT measurements for Mn, Cd and Zn in the Baltic Sea and for Mg in a river.[17,91] DGT measurements of Cu and Ni in the Baltic Sea were lower than the <1-kDa fraction, consistent with the presence of inert colloids, which may be strong organic complexes.[91] These measurements suggest that in practise DGT may only be measuring particles smaller than 2 nm.
More data are required on diffusion of well defined nanoparticles in the APA and restricted gels. Recent evidence indicates that the pore sizes are greater than an earlier assessment of the literature indicated,[31] which opens up the exciting possibility of using DGT to determine nanoparticles. However, the slow diffusion of nanoparticles will confer poor sensitivity. Labille et al.[92] have demonstrated that the gel structure at the surface of an agarose gel differs from that of the bulk gel, with the diffusion coefficients of solutes in this ~100 µm-thick region being appreciably less than their values in the bulk gel. Such a phenomenon may not occur in acrylamide gels, whose structures and casting procedures differs from that of agarose, but, if it did, there would effectively be a ‘surface filter’ for larger nanoparticles. Although lability, as expressed by Eqn 10, increases with nanoparticle size this is simply because of the lower diffusive flux as a result of slower diffusion.[78] These diffusional constraints may explain why field data indicate that only very small nanoparticles (colloids) are measured by DGT. More general modelling of fluxes of metal ions at consuming interfaces, which include organisms, has shown that natural colloids are expected to make a negligible contribution to the total flux.[77,78]
Conclusions
It is wholly appropriate that the assumptions accompanying use of the simple steady-state DGT equation have been the focus of a considerable body of research. The accumulated evidence suggests that these assumptions hold for most conditions, but not surprisingly there are exceptions. There remains robust support for use of DGT as a monitoring tool of labile solute species in natural waters. The simple Eqn 1 still holds within typical experimental errors when a 0.8 mm-thick diffusion layer is used. Although trace metals and, to a lesser extent, humic substances have been shown to accumulate within the diffusive gel, they are unlikely to affect the DGT measurement provided deployment times of a few days are used. Early work suggested that effects related to gel charge affected measurements made at low ionic strength, but for the most commonly used APA gel this is now known to be an artefact associated with inadequate washing of the gel. More definitive data on possible charge effects is required for the restricted gel. Use of DGT for speciation and kinetic studies is more demanding and requires use of equations with fewer assumptions, which adequately accommodate effects associated with an effective rather than geometric area, a DBL, appropriate diffusion coefficients for each species and dissociation kinetics. Interpretation in these circumstances is greatly improved by having a suite of DGT measurements, which may include ranges of gel layer thicknesses, gel composition and deployment times, as well as other data, such as filterable metal. Good progress has been made on measurements in well defined systems, but in-depth interpretation of measurements in natural waters is complicated by the distribution of binding and rate constants associated with metal complexed with humic substances. Apart from humic substances, we know little about the contribution of nanoparticles to the DGT measurement. Definitive data obtained with well-characterised particles are urgently required and further data are needed on the interactions of humic substances in soil solution with the diffusive gel and filter.
The above account has focussed largely on trace metals, for which the DGT measurement has been most systematically investigated. Increasingly, however, DGT is being used to measure other components. As the use of DGT is extended to new determinands and new media, it is essential that performance characteristics of DGT, including possible interactions with the gel, continue to be thoroughly evaluated.
Acknowledgements
The authors thank J. Buffle, J. Galceran. O. A. Garmo, J. Puy and two anonymous reviewers for their constructive comments on the manuscript, and N. J. Lehto for providing Fig. 4.
References
[1] M. Schintu, B. Marras, L. Durante, P. Meloni, A. Contu, Macroalgae and DGT as indicators of available trace metals in marine coastal waters near a lead–zinc smelter. Environ. Monit. Assess. 2010, 167, 653.| Macroalgae and DGT as indicators of available trace metals in marine coastal waters near a lead–zinc smelter.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXos1Wqsbw%3D&md5=dfb0f8772f1e1aa40612f0c879ff24feCAS |
[2] J. E. Sherwood, D. Barnett, N. W. Barnett, K. Dover, J. Howitt, H. Li, P. Kew, J. Mondon, Deployment of DGT units in marine waters to assess the environmental risk from a deep sea tailings outfall. Anal. Chim. Acta 2009, 652, 215.
| Deployment of DGT units in marine waters to assess the environmental risk from a deep sea tailings outfall.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXhtF2htbvM&md5=8ac8a3fe5233b2677b3e474847ebb357CAS |
[3] L. S. Balistrieri, R. G. Blank, Dissolved and labile concentrations of Cd, Cu, Pb, and Zn in the South Fork Coeur d’Alene River, Idaho: comparisons among chemical equilibrium models and implications for biotic ligand models. Appl. Geochem. 2008, 23, 3355.
| Dissolved and labile concentrations of Cd, Cu, Pb, and Zn in the South Fork Coeur d’Alene River, Idaho: comparisons among chemical equilibrium models and implications for biotic ligand models.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXhsVWms73K&md5=0499bdee3c4b364183dd0a80f0436dddCAS |
[4] M. Pesavento, G. Alberti, R. Biesuz, Analytical methods for determination of free metal ion concentration, labile species fraction and metal complexation capacity of environmental waters: a review. Anal. Chim. Acta 2009, 631, 129.
| Analytical methods for determination of free metal ion concentration, labile species fraction and metal complexation capacity of environmental waters: a review.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXhsFWis73L&md5=df0202ebdfdb5983255588567842c580CAS |
[5] M. V. Ardelan, E. Steinnes, Changes in mobility and solubility of the redox sensitive metals Fe, Mn and Co at the seawater-sediment interface following CO2 seepage. Biogeosciences 2010, 7, 569.
| Changes in mobility and solubility of the redox sensitive metals Fe, Mn and Co at the seawater-sediment interface following CO2 seepage.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXltlCju7s%3D&md5=0b042049c5eee0efde06c7edc3725d59CAS |
[6] O. Clarisse, B. Dimock, H. Hintelmann, E. P. H. Best, Predicting net mercury methylation in sediments using diffusive gradient in thin films measurements. Environ. Sci. Technol. 2011, 45, 1506.
| Predicting net mercury methylation in sediments using diffusive gradient in thin films measurements.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXjvFCntg%3D%3D&md5=ba56d6f4c7adb347b062854864d995f9CAS |
[7] R. M. Town, P. Chakraborty, H. P. van Leeuwen, Dynamic DGT speciation analysis and applicability to natural heterogeneous complexes. Environ. Chem. 2009, 6, 170.
| Dynamic DGT speciation analysis and applicability to natural heterogeneous complexes.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXotVyqtrY%3D&md5=6fa1fd7e25cb6bcc1b0df5e917bf659eCAS |
[8] K. W. Warnken, W. Davison, H. Zhang, J. Galceran, J. Puy, In situ measurements of metal complex exchange kinetics in freshwater. Environ. Sci. Technol. 2007, 41, 3179.
| In situ measurements of metal complex exchange kinetics in freshwater.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXjsV2mur0%3D&md5=e131291b45e2e877a09c01c25768aa8dCAS |
[9] R. Dahlqvist, K. Andersson, J. Ingri, T. Larsson, B. Stolpe, D. Turner, Temporal variations of colloidal carrier phases and associated trace elements in a boreal river. Geochim. Cosmochim. Acta 2007, 71, 5339.
| Temporal variations of colloidal carrier phases and associated trace elements in a boreal river.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXht1GhurbF&md5=a24f2c73ddf7eaa21c737d282c7ab283CAS |
[10] C. Oporto, E. Smolders, F. Degryse, L. Verheyen, C. Vandecasteele, DGT-measured fluxes explain the chloride-enhanced cadmium uptake by plants at low but not at high Cd supply. Plant Soil 2009, 318, 127.
| DGT-measured fluxes explain the chloride-enhanced cadmium uptake by plants at low but not at high Cd supply.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXltVWrs7k%3D&md5=9cf90f149a342381ad1b8ec3d99d460cCAS |
[11] H. Ernstberger, H. Zhang, A. Tye, S. Young, W. Davison, Desorption kinetics of Cd, Zn and Ni measured in intact soils by DGT. Environ. Sci. Technol. 2005, 39, 1591.
| Desorption kinetics of Cd, Zn and Ni measured in intact soils by DGT.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2MXht1yhu7Y%3D&md5=d3024588c2935cb88695e4e59c36cea6CAS |
[12] D. Ferreira, N. Tousset, C. Ridame, M. H. Tusseau-Vuillemin, More than inorganic copper is bioavailable to aquatic mosses at environmentally relevant concentrations. Environ. Toxicol. Chem. 2008, 27, 2108.
| More than inorganic copper is bioavailable to aquatic mosses at environmentally relevant concentrations.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXht1SgurzM&md5=8e365e0c6591ca6b294c64f0a595456aCAS |
[13] P. Bradac, R. Behra, L. Sigg, Accumulation of cadmium in periphyton under various freshwater speciation conditions. Environ. Sci. Technol. 2009, 43, 7291.
| Accumulation of cadmium in periphyton under various freshwater speciation conditions.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXpslClt74%3D&md5=ae1b15e03c357b5a0844a9afc8f5c0f3CAS |
[14] A. L. Pérez, K. A. Anderson, DGT estimates cadmium accumulation in wheat and potato from phosphate fertilizer applications. Sci. Total Environ. 2009, 407, 5096.
| DGT estimates cadmium accumulation in wheat and potato from phosphate fertilizer applications.Crossref | GoogleScholarGoogle Scholar |
[15] I. Cattani, E. Capri, R. Boccelli, A. A. M. Del Re, Assessment of arsenic availability to roots in contaminated Tuscany soils by a diffusion gradient in thin films (DGT) method and uptake by Pteris vittata and Agrostis capillaris. Eur. J. Soil Sci. 2009, 60, 539.
| Assessment of arsenic availability to roots in contaminated Tuscany soils by a diffusion gradient in thin films (DGT) method and uptake by Pteris vittata and Agrostis capillaris.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXhtVGis7zO&md5=80a6e9a0c29058a3f3734796f28cea0cCAS |
[16] W. Davison, H. Zhang, In situ speciation measurements of trace components in natural waters using thin-film gels. Nature 1994, 367, 546.
| In situ speciation measurements of trace components in natural waters using thin-film gels.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2cXhsVemtrc%3D&md5=a46668663a8de3d4c887158bbe7ebbcfCAS |
[17] R. Dahlqvist, H. Zhang, W. Davison, J. Ingri, Performance of DGT (diffusive gradients in thin films) for measuring Ca and Mg in freshwater. Anal. Chim. Acta 2002, 460, 247.
| Performance of DGT (diffusive gradients in thin films) for measuring Ca and Mg in freshwater.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD38XjvF2ktrY%3D&md5=a16efe62bd59080e6f7ce35b421ff606CAS |
[18] L. Chang, W. Davison, H. Zhang, M. Kelly, Performance characteristics for the measurement of Cs and Sr by diffusive gradients in thin films (DGT). Anal. Chim. Acta 1998, 368, 243.
| Performance characteristics for the measurement of Cs and Sr by diffusive gradients in thin films (DGT).Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1cXjtlOnsLY%3D&md5=2ad7730f7a06eea2fe23befc5b876997CAS |
[19] H. Österlund, S. Chlot, M. Faarinen, A. Widerlund, I. Rodushkin, J. Ingri, D. C. Baxter, Simultaneous measurements of As, Mo, Sb, V and W using a ferrihydrite diffusive gradients in thin films (DGT) device. Anal. Chim. Acta 2010, 682, 59.
| Simultaneous measurements of As, Mo, Sb, V and W using a ferrihydrite diffusive gradients in thin films (DGT) device.Crossref | GoogleScholarGoogle Scholar |
[20] S. M. Ding, D. Xu, Q. Sun, H. B. Yin, C. S. Zhang, Measurement of dissolved reactive phosphorus using the diffusive gradients in thin films technique with a high-capacity binding phase. Environ. Sci. Technol. 2010, 44, 8169.
| Measurement of dissolved reactive phosphorus using the diffusive gradients in thin films technique with a high-capacity binding phase.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXht1eisrrI&md5=bcbd89763817c880dbc6dee2568505e2CAS |
[21] C. R. DeVries, F. Wang, In situ two-dimensional high-resolution profiling of sulfide in sediment interstitial waters. Environ. Sci. Technol. 2003, 37, 792.
| In situ two-dimensional high-resolution profiling of sulfide in sediment interstitial waters.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3sXksFChsA%3D%3D&md5=3e2b18ace8db43660c595b3e8b687a92CAS |
[22] M. Gregusova, B. Docekal, New resin gel for uranium determination by diffusive gradient in thin films technique. Anal. Chim. Acta 2011, 684, 142.
| New resin gel for uranium determination by diffusive gradient in thin films technique.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXhsF2msbnJ&md5=977c3619306e35db476b2837a400f315CAS |
[23] M. Leermakers, Y. Gao, J. Navez, A. Poffijn, K. Croes, W. Baeyens, Radium analysis by sector field ICP-MS in combination with the Diffusive Gradients in Thin Films (DGT) technique. J. Anal. At. Spectrom. 2009, 24, 1115.
| Radium analysis by sector field ICP-MS in combination with the Diffusive Gradients in Thin Films (DGT) technique.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXovVShtrc%3D&md5=7c9c1109d0fd4b1417272722fcebaeafCAS |
[24] M. A. French, H. Zhang, J. M. Pates, S. E. Bryan, R. C. Wilson, Development and performance of the diffusive gradients in thin films technique for the measurement of technetium-99 in seawater. Anal. Chem. 2005, 77, 135.
| Development and performance of the diffusive gradients in thin films technique for the measurement of technetium-99 in seawater.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2cXhtValsLfI&md5=5ad100e8eae4a751fbbf4f32f9948718CAS |
[25] M. Harper, W. Davison, H. Zhang, W. Tych, Solid phase to solution kinetics in sediments and soils interpreted from DGT measured fluxes. Geochim. Cosmochim. Acta 1998, 62, 2757.
| Solid phase to solution kinetics in sediments and soils interpreted from DGT measured fluxes.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1cXnslOjs7k%3D&md5=0ef15f4fdb491273c2335530aa317bc1CAS |
[26] H. Zhang, W. Davison, Performance characteristics of the technique of diffusion gradients in thin-films (DGT) for the measurement of trace metals in aqueous solution. Anal. Chem. 1995, 67, 3391.
| Performance characteristics of the technique of diffusion gradients in thin-films (DGT) for the measurement of trace metals in aqueous solution.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2MXnslKgtrc%3D&md5=bb9658e99f6d0c6ad7950f14c6e2b63dCAS |
[27] M. R. Twiss, J. W. Moffett, Comparison of copper speciation in coastal marine waters measured using analytical voltammetry and diffusion gradient in thin-film techniques. Environ. Sci. Technol. 2002, 36, 1061.
| Comparison of copper speciation in coastal marine waters measured using analytical voltammetry and diffusion gradient in thin-film techniques.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD38XosV2ntA%3D%3D&md5=7321e3a505357603c8ab12955fa1fc52CAS |
[28] H. Zhang, W. Davison, R. Gade, T. Kobayashi, In situ measurement of phosphate in natural waters using DGT. Anal. Chim. Acta 1998, 370, 29.
| In situ measurement of phosphate in natural waters using DGT.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1cXjvFeqs78%3D&md5=0c26e2c1924ad9f97e675df442fd6b65CAS |
[29] M. C. Alfaro-De la Torre, P. Y. Beaulieu, A. Tessier, In situ measurement of trace metals in lakewater using the dialysis and DGT techniques. Anal. Chim. Acta 2000, 418, 53.
| In situ measurement of trace metals in lakewater using the dialysis and DGT techniques.Crossref | GoogleScholarGoogle Scholar |
[30] W. Davison, G. Fones, M. Harper, P. Teasdale, H. Zhang, Dialysis, DET and DGT: in situ diffusional techniques for studying water, sediments and soils, in In Situ Monitoring of Aquatic Systems: Chemical Analysis and Speciation (Eds J. Buffle, G. Horvai) 2000, pp. 495–570 (Wiley: New York).
[31] H. Zhang, W. Davison, Diffusional characteristics of hydrogels used in DGT and DET techniques. Anal. Chim. Acta 1999, 398, 329.
| Diffusional characteristics of hydrogels used in DGT and DET techniques.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1MXmvFeqtLk%3D&md5=4b258c91e60376e3c73b902e9e6083edCAS |
[32] S. Scally, W. Davison, H. Zhang, Diffusion coefficients of metals and metal complexes in hydrogels used in diffusive gradients in thin films. Anal. Chim. Acta 2006, 558, 222.
| Diffusion coefficients of metals and metal complexes in hydrogels used in diffusive gradients in thin films.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28XotFygtw%3D%3D&md5=0fb760c892c4443b28eebf4d1c1dea84CAS |
[33] K. W. Warnken, H. Zhang, W. Davison, Accuracy of the diffusive gradients in thin-films technique: diffusive boundary layer and effective sampling area considerations. Anal. Chem. 2006, 78, 3780.
| Accuracy of the diffusive gradients in thin-films technique: diffusive boundary layer and effective sampling area considerations.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28XktVSktrg%3D&md5=53fe9af778efe5a42da4d35f8f606ad9CAS |
[34] A. W. Webb, M. J. Keough, Quantification of copper doses to settlement plates in the field using diffusive gradients in thin films. Sci. Total Environ. 2002, 298, 207.
| Quantification of copper doses to settlement plates in the field using diffusive gradients in thin films.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD38XnvVOhtrc%3D&md5=5bf1f7f96340362b5a18cd7c943ffc8eCAS |
[35] J. L. Levy, H. Zhang, W. Davison, J. Puy, J. Galceran, Assessment of trace metal binding kinetics in dynamic techniques. Anal. Chim. Acta in press.
[36] K. W. Warnken, W. Davison, H. Zhang, Interpretation of in situ speciation measurements of inorganic and organically complexed trace metals in freshwater by DGT. Environ. Sci. Technol. 2008, 42, 6903.
| Interpretation of in situ speciation measurements of inorganic and organically complexed trace metals in freshwater by DGT.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXpvFSmurk%3D&md5=17f2f452321aa807afb8c92d86c87b8eCAS |
[37] W. Davison, G. W. Grime, J. A. W. Morgan, K. Clarke, Distribution of dissolved iron in sediment pore waters at submillimetre resolution. Nature 1991, 352, 323.
| Distribution of dissolved iron in sediment pore waters at submillimetre resolution.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK3MXkvFyrtL4%3D&md5=9971de58e2fd78d7cadb51ad7ffa5b35CAS |
[38] W. Davison, H. Zhang, G. W. Grime, Performance characteristics of gel probes used for measuring the chemistry of pore waters. Environ. Sci. Technol. 1994, 28, 1623.
| Performance characteristics of gel probes used for measuring the chemistry of pore waters.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2cXltFOju7c%3D&md5=9d9f4d34dc5a0b93439a95a03166c0b1CAS |
[39] M. D. Krom, P. Davison, H. Zhang, W. Davison, High resolution pore water sampling using a gel sampler: an innovative technique. Limnol. Oceanogr. 1994, 39, 1967.
| High resolution pore water sampling using a gel sampler: an innovative technique.Crossref | GoogleScholarGoogle Scholar |
[40] A. Peters, H. Zhang, W. Davison, Investigation of the application of DGT devices for measurement of trace metals in low ionic strength freshwaters. Anal. Chim. Acta 2003, 478, 237.
| Investigation of the application of DGT devices for measurement of trace metals in low ionic strength freshwaters.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3sXkvV2iug%3D%3D&md5=f2c7f73cbb1ad74c191ba7d0010907aeCAS |
[41] K. Warnken, H. Zhang, W. Davison, Trace metal measurements in low ionic strength solutions by diffusive gradients in thin-films (DGT). Anal. Chem. 2005, 77, 5440.
| Trace metal measurements in low ionic strength solutions by diffusive gradients in thin-films (DGT).Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2MXms1Kntb4%3D&md5=5af5e2e974108f0e79d46fd6ecff929aCAS |
[42] N. Fatin-Rouge, A. Milon, J. Buffle, R. R. Goulet, A. Tessier, Diffusion and partitioning of solutes in agarose hydrogels: the relative influence of electrostatic and specific interactions. J. Phys. Chem. B 2003, 107, 12 126.
| Diffusion and partitioning of solutes in agarose hydrogels: the relative influence of electrostatic and specific interactions.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3sXnvFWkt74%3D&md5=2340102e504aa955b17afcdeb94b3757CAS |
[43] L. P. Yezek, H. P. van Leeuwen, An electrokinetic characterization of low charge density cross-linked polyacrylamide gels. J. Colloid Intface Sci 2004, 278, 243.
| An electrokinetic characterization of low charge density cross-linked polyacrylamide gels.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2cXms1Cmsbc%3D&md5=062c208c0bd2b962b859c10f7cb4b362CAS |
[44] L. P. Yezek, H. P. van Leeuwen, Donnan effects in the steady-state diffusion of metal ions through charged thin films. Langmuir 2005, 21, 10 342.
| Donnan effects in the steady-state diffusion of metal ions through charged thin films.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2MXhtVGqsrjJ&md5=67e4bf9f193db8a34eafc99a2909dc46CAS |
[45] M. R. Sangi, M. J. Halstead, K. A. Hunter, Use of the diffusion gradient thin film method to measure trace metals in fresh waters at low ionic strength. Anal. Chim. Acta 2002, 456, 241.
| Use of the diffusion gradient thin film method to measure trace metals in fresh waters at low ionic strength.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD38XitFWgt70%3D&md5=3a32fa8018dd9a3c0cb58796a8750776CAS |
[46] L. P. Yezek, L. R. van der Veeken, H. P. van Leeuwen, Donnan effects in metal speciation analysis by DET/DGT. Environ. Sci. Technol. 2008, 42, 9250.
| Donnan effects in metal speciation analysis by DET/DGT.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXhtlKlsrjN&md5=7b7decf27e3b2b01be07180e19b166b4CAS |
[47] L. R. van der Veeken, P. Chakraborti, H. P. van Leeuwen, Accumulation of humic acid in DET/DGT gels. Environ. Sci. Technol. 2010, 44, 4253.
| Accumulation of humic acid in DET/DGT gels.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXlslWgsL8%3D&md5=c20cc011e02d1021351a648b754dce47CAS |
[48] L. R. van der Veeken, H. P. van Leeuwen, DGT/DET gel partition features of humic acid/metal species. Environ. Sci. Technol. 2010, 44, 5523.
| DGT/DET gel partition features of humic acid/metal species.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXnsFGitbw%3D&md5=f6e35ebe8aa4792c4ba69159520c8c82CAS |
[49] J. Morford, L. Kalnejais, W. Martin, R. Francois, I.-M. Karle, Sampling marine porewaters for Mn, Fe, U, Re, and Mo: modifications on diffusional gradients in thin film gel probes. J. Exp. Mar. Biol. Ecol. 2003, 285–286, 85.
| Sampling marine porewaters for Mn, Fe, U, Re, and Mo: modifications on diffusional gradients in thin film gel probes.Crossref | GoogleScholarGoogle Scholar |
[50] P. N. Williams, H. Zhang, W. Davison, A. A. Meharg, M. H. Sumon, G. J. Norton, H. Brammer, R. Islam, Organic matter–solid phase interactions are critical for predicting arsenic release and plant uptake in Bangladesh paddy soils. Environ. Sci. Technol. 2011, 45, 6080.
| Organic matter–solid phase interactions are critical for predicting arsenic release and plant uptake in Bangladesh paddy soils.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXnvVKitLY%3D&md5=a00573b5d51ee3e399a0769d1210c6e9CAS |
[51] H. P. Jarvie, R. J. G. Mortimer, E. J. Palmer-Felgate, K. St. Quinton, S. A. Harman, P. Carbo, Measurement of soluble reactive phosphorus concentration profiles and fluxes in river-bed sediments using DET gel probes. J. Hydrol. (Amst.) 2008, 350, 261.
| Measurement of soluble reactive phosphorus concentration profiles and fluxes in river-bed sediments using DET gel probes.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXisFSru7g%3D&md5=6698d272f517c5c494db2c1b2eedf949CAS |
[52] H. Docekalová, O. Clarisse, S. Salomon, M. Wartel, Use of constrained DET probe for a high resolution determination of metals and anions distribution in the sediment pore water. Talanta 2002, 57, 145.
| Use of constrained DET probe for a high resolution determination of metals and anions distribution in the sediment pore water.Crossref | GoogleScholarGoogle Scholar |
[53] O. A. Garmo, W. Davison, H. Zhang, Interactions of trace metals with hydrogels and filter membranes used in DET and DGT techniques. Environ. Sci. Technol. 2008, 42, 5682.
| Interactions of trace metals with hydrogels and filter membranes used in DET and DGT techniques.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXns1Wjsrg%3D&md5=3ca4684e1ceaa31de19b47cbd6cfac98CAS |
[54] H. Docekalova, P. Divis, Application of diffusive gradient in thin films technique (DGT) to measurement of mercury in aquatic systems. Talanta 2005, 65, 1174.
| Application of diffusive gradient in thin films technique (DGT) to measurement of mercury in aquatic systems.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2MXit1Cks7Y%3D&md5=26dc5dc546ac3ab5c50d0f2c7346f242CAS |
[55] O. A. Garmo, W. Davison, H. Zhang, Effects of binding of metals to the hydrogel and filter membrane on the accuracy of the diffusive gradients in thin films technique. Anal. Chem. 2008, 80, 9220.
| Effects of binding of metals to the hydrogel and filter membrane on the accuracy of the diffusive gradients in thin films technique.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXhtlWqu73E&md5=1c546ca69c3315c7f19c5c0ee2def7a0CAS |
[56] M. H. Tusseau-Vuillemin, R. Gilbin, E. Bakkaus, J. Garrie, Performance of diffusion gradient in thin films to evaluate the toxic fraction of copper to Daphnia magna. Environ. Toxicol. Chem. 2004, 23, 2154.
| Performance of diffusion gradient in thin films to evaluate the toxic fraction of copper to Daphnia magna.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2cXms1GhsLk%3D&md5=0053ef725a4b68843a52aa019959b910CAS |
[57] E. Unsworth, H. Zhang, W. Davison, Use of DGT to measure cadmium speciation in solutions with synthetic and natural ligands: comparison with model predictions. Environ. Sci. Technol. 2005, 39, 624.
| Use of DGT to measure cadmium speciation in solutions with synthetic and natural ligands: comparison with model predictions.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2cXhtVKit7fL&md5=b165eaf86aeac4d40d3cdcc7c2154e79CAS |
[58] S. Mongin, R. Uribe, J. Puy, J. Cecilia, J. Galceran, H. Zhang, W. Davison, Key role of the resin layer thickness in the lability of complexes measured by DGT. Environ. Sci. Technol. 2011, 45, 4869.
| Key role of the resin layer thickness in the lability of complexes measured by DGT.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXmtVCmsL0%3D&md5=d9e3bb0b37ba1e52c70d04b80b7901beCAS |
[59] S. Scally, W. Davison, H. Zhang, Measurements of Pb speciation in synthetic solutions using DGT. Aust. J. Chem. 2004, 57, 925.
| Measurements of Pb speciation in synthetic solutions using DGT.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2cXps1Sjsr0%3D&md5=651abd1874d418d7fa4d5b2f34ed529dCAS |
[60] S. Denney, J. Sherwood, J. Leyden, In situ measurements of labile Cu, Cd and Mn in river waters using DGT. Sci. Total Environ. 1999, 239, 71.
| In situ measurements of labile Cu, Cd and Mn in river waters using DGT.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1MXmtleiu74%3D&md5=1df940f3133c86465b80681813de457eCAS |
[61] J. Gimpel, H. Zhang, W. Davison, In-situ trace metal speciation in lake surface waters using DGT, dialysis and filtration. Environ. Sci. Technol. 2003, 37, 138.
| In-situ trace metal speciation in lake surface waters using DGT, dialysis and filtration.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD38XptFCht7g%3D&md5=cc7585a65f4d9308b9886a20dacf180dCAS |
[62] L. S. Balistrieri, R. R. Sear, N. M. Piatak, B. Paul, Assessing the concentration, speciation, and toxicity of dissolved metals during mixing of acid-mine drainage and ambient river water downstream of the Elizabeth Copper Mine, Vermont, USA. Appl. Geochem. 2007, 22, 930.
| Assessing the concentration, speciation, and toxicity of dissolved metals during mixing of acid-mine drainage and ambient river water downstream of the Elizabeth Copper Mine, Vermont, USA.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXkvFGmtrw%3D&md5=492ec6dfbbac26d543dc775fcd4bd61eCAS |
[63] E. R. Unsworth, K. W. Warnken, H. Zhang, W. Davison, F. Black, J. Buffle, J. Cao, R. Cleven, J. Galceran, P. Gunkel, E. Kalis, D. Kistler, H. P. Van Leeuwen, M. Michel, S. Noel, Y. Nur, N. Odzak, J. Puy, W. Van Riemsdijk, L. Sigg, E. Temminghoff, M.-L. Tercier-Waeber, S. Toepperwien, R. M. Town, L. Weng, H. Xue, Model predictions of metal speciation in freshwaters compared to measurements by in situ techniques. Environ. Sci. Technol. 2006, 40, 1942.
| Model predictions of metal speciation in freshwaters compared to measurements by in situ techniques.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28XhtlSku7o%3D&md5=f1372c913c38a7567823d9613a4bb5f1CAS |
[64] K. W. Warnken, A. J. Lawlor, S. Lofts, E. Tipping, W. Davison, H. Zhang, In situ speciation measurements of trace metals in headwater streams. Environ. Sci. Technol. 2009, 43, 7230.
| In situ speciation measurements of trace metals in headwater streams.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXmsFGlsbw%3D&md5=3185a3f804945b6bbb28e10120bda836CAS |
[65] S. Mason, R. Hamon, A. Nolan, H. Zhang, W. Davison, Performance of a mixed binding layer for measuring anions and cations in a single assay using the diffusive gradients in thin films technique. Anal. Chem. 2005, 77, 6339.
| Performance of a mixed binding layer for measuring anions and cations in a single assay using the diffusive gradients in thin films technique.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2MXosVGhu78%3D&md5=deb1b9eca708204f3089ddb8c6728208CAS |
[66] J. Luo, H. Zhang, J. Santner, W. Davison, Performance characteristics of diffusive gradients in thin films equipped with a binding gel layer containing precipitated ferrihydrite for measuring arsenic(V), selenium(VI), vanadium(V), and antimony(V). Anal. Chem. 2010, 82, 8903.
| Performance characteristics of diffusive gradients in thin films equipped with a binding gel layer containing precipitated ferrihydrite for measuring arsenic(V), selenium(VI), vanadium(V), and antimony(V).Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXht1OgsrvF&md5=12133eb1f69635f329296cdaaaa85d82CAS |
[67] F. Degryse, E. Smolders, I. Oliver, H. Zhang, Relating soil solution Zn concentrations to diffusive gradients in thin films measurements in contaminated soils. Environ. Sci. Technol. 2003, 37, 3958.
| Relating soil solution Zn concentrations to diffusive gradients in thin films measurements in contaminated soils.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3sXlvVyqtLc%3D&md5=9cc9185148b73faf0f63a5ad7ca57fa0CAS |
[68] J. Søndergaard, In situ measurements of labile Al and Mn in acid mine drainage using diffusive gradients in thin films. Anal. Chem. 2007, 79, 6419.
| In situ measurements of labile Al and Mn in acid mine drainage using diffusive gradients in thin films.Crossref | GoogleScholarGoogle Scholar |
[69] H. M. Conesa, R. Schulin, B. Nowack, Suitability of using diffusive gradients in thin films (DGT) to study metal bioavailability in mine tailings: possibilities and constraints. Environ. Sci. Technol. 2010, 17, 657.
| 1:CAS:528:DC%2BC3cXitVSisrc%3D&md5=d17caa716d62e7b12a6545a14de272cfCAS |
[70] S. Tankere-Muller, H. Zhang, W. Davison, N. Finke, O. Larsen, H. Stahl, R. N. Glud, Fine scale remobilisation of Fe, Mn, Co, Ni, Cu and Cd in contaminated marine sediment. Mar. Chem. 2007, 106, 192.
| Fine scale remobilisation of Fe, Mn, Co, Ni, Cu and Cd in contaminated marine sediment.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXovFSmur0%3D&md5=48c0a4b1875ed971546566329d4465a7CAS |
[71] S. Mason, R. Hamon, H. Zhang, J. Anderson, Investigating chemical constraints to the measurement of phosphorus in soils using diffusive gradients in thin films (DGT) and resin methods. Talanta 2008, 74, 779.
| Investigating chemical constraints to the measurement of phosphorus in soils using diffusive gradients in thin films (DGT) and resin methods.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXjtV2msA%3D%3D&md5=0a2269acd299eb40d7a44a4193c03f61CAS |
[72] J. D. Panther, P. R. Teasdale, W. M. Bennett, D. T. Welsh, H. J. Zhao, Titanium dioxide-based DGT technique for in situ measurement of dissolved reactive phosphorus in fresh and marine waters. Environ. Sci. Technol. 2010, 44, 9419.
| Titanium dioxide-based DGT technique for in situ measurement of dissolved reactive phosphorus in fresh and marine waters.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXhsVGkt7jP&md5=16a8eca49566fc0b0d55119f89f1cf06CAS |
[73] N. J. Lehto, W. Davison, H. Zhang, W. Tych, An evaluation of DGT performance using a dynamic numerical model. Environ. Sci. Technol. 2006, 40, 6368.
| An evaluation of DGT performance using a dynamic numerical model.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28XptFahurg%3D&md5=ac36a76424fbbfd5f5bf7555cfaddb8dCAS |
[74] H. Zhang, W. Davison, Direct in situ measurements of labile inorganic and organically bound metal species in synthetic solutions and natural waters using diffusive gradients in thin films. Anal. Chem. 2000, 72, 4447.
| Direct in situ measurements of labile inorganic and organically bound metal species in synthetic solutions and natural waters using diffusive gradients in thin films.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3cXls1Oku70%3D&md5=d413eae3075abca5abe0b85b9434b2c0CAS |
[75] H. Zhang, Competition effects on the binding of Ni, Zn and Cu by organic matter. Environ. Sci. Technol. 2004, 38, 1421.
| Competition effects on the binding of Ni, Zn and Cu by organic matter.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2cXmtlWguw%3D%3D&md5=19fedd8f10c863500904247ff6e7b2ccCAS |
[76] E. Tipping, Cation Binding by Humic Substances 2002 (Cambridge University Press: Cambridge, UK).
[77] Z. Zhang, J. Buffle, Metal flux and dynamic speciation at (bio)interfaces. Part V: the role of simple, fulvic and aggregate complexes on Pb flux in freshwater ligand mixtures, computed at planar consuming interfaces. Geochim. Cosmochim. Acta 2009, 73, 1223.
| Metal flux and dynamic speciation at (bio)interfaces. Part V: the role of simple, fulvic and aggregate complexes on Pb flux in freshwater ligand mixtures, computed at planar consuming interfaces.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXhvFajtbg%3D&md5=9a0c456f78ed8cb55f746fc4a736b0c7CAS |
[78] Z. Zhang, J. Buffle, Metal flux and dynamic speciation at (bio)interfaces. Part VI: the roles of simple, fulvic and aggregate complexes on computed metal flux in freshwater ligand mixtures; comparison of Pb, Zn and Ni at planar and microspherical interfaces. Geochim. Cosmochim. Acta 2009, 73, 1236.
| Metal flux and dynamic speciation at (bio)interfaces. Part VI: the roles of simple, fulvic and aggregate complexes on computed metal flux in freshwater ligand mixtures; comparison of Pb, Zn and Ni at planar and microspherical interfaces.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXhvFajtbk%3D&md5=437bf93dad3ebc2c3198587d6860a0f9CAS |
[79] S. Scally, W. Davison, H. Zhang, In situ measurements of dissociation kinetics and labilities of metal complexes in synthetic solutions using DGT. Environ. Sci. Technol. 2003, 37, 1379.
| In situ measurements of dissociation kinetics and labilities of metal complexes in synthetic solutions using DGT.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3sXhsFWjt7s%3D&md5=9f11e49a0e4e65820121c621096d0651CAS |
[80] J. Salvador, J. Puy, J. Cecilia, J. Galceran, Lability of complexes in steady state finite planar diffusion. J. Electroanal. Chem. 2006, 588, 303.
| Lability of complexes in steady state finite planar diffusion.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28XitVSmuro%3D&md5=fbac2acc7dcb35510b7a0d744f9b1776CAS |
[81] R. Uribe, S. Mongin, J. Puy, J. Cecilia, J. Galceran, H. Zhang, W. Davison, Contribution of partially labile complexes to the DGT metal flux. Environ. Sci. Technol. 2011, 45, 5317.
| Contribution of partially labile complexes to the DGT metal flux.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXmsVWlsLs%3D&md5=6cc3cab7c0bd2fd208333710ea6dfa92CAS |
[82] M. H. Tusseau-Vuillemin, R. Gilbin, M. A. Taillefert, A dynamic numerical model to characterise labile metal complexes collected with diffusive gradients in thin-films devices. Environ. Sci. Technol. 2003, 37, 1645.
| A dynamic numerical model to characterise labile metal complexes collected with diffusive gradients in thin-films devices.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3sXitFGnu7o%3D&md5=0a17a4000a44db6a02e17869296668ecCAS |
[83] O. A. Garmo, N. J. Lehto, H. Zhang, W. Davison, O. Røyset, E. Steinnes, Dynamic aspects of DGT as demonstrated by experiments with lanthanide complexes of a multidentate ligand. Environ. Sci. Technol. 2006, 40, 4754.
| Dynamic aspects of DGT as demonstrated by experiments with lanthanide complexes of a multidentate ligand.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28XmsVaisrs%3D&md5=b03212374de59448303dc3ecc8b1efefCAS |
[84] H. P. van Leeuwen, Dynamic aspects of in situ speciation processes and techniques, in In Situ Monitoring of Aquatic Systems: Chemical Analysis and Speciation (Eds J. Buffle, G. Horvai) 2000, pp. 525–528 (Wiley: New York).
[85] H. P. Van Leeuwen, Steady-state DGT fluxes of nanoparticulate metal complexes. Environ. Chem. 2011, 8, 525.
| 1:CAS:528:DC%2BC3MXhtlykt73F&md5=74244b53ebf1888b15500aab2ad17fe1CAS |
[86] B. Nowack, S. Koehler, R. Schulin, Use of diffusive gradients in thin films (DGT) in undisturbed field soils. Environ. Sci. Technol. 2004, 38, 1133.
| Use of diffusive gradients in thin films (DGT) in undisturbed field soils.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2cXksFOisg%3D%3D&md5=53fb00f1961c427bc299b25f1e98bd16CAS |
[87] N. Fatin-Rouge, K. Starchev, J. Buffle, Size effects on diffusion processes within agarose gels. Biophys. J. 2004, 86, 2710.
| Size effects on diffusion processes within agarose gels.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2cXjvVyjtLs%3D&md5=5e7661bbdd71ce0d6adf5c7914a72c14CAS |
[88] P. L. R. van der Veeken, J. P. Pinheiro, H. P. van Leeuwen, Metal speciation by DGT/DET in colloidal complex systems. Environ. Sci. Technol. 2008, 42, 8835.
| Metal speciation by DGT/DET in colloidal complex systems.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXhtlSnu7zE&md5=10bda423c06978d7e223337d72083568CAS |
[89] J. Buffle, Complexation Reactions in Aquatic Systems; an Analytical Approach 1988 (Ellis Horwood: Chichester, UK).
[90] J. R. Lead, J. Hamilton-Taylor, N. Nesketh, M. N. Jones, A. E. Wilkinson, E. Tipping, A comparative study of proton and alkaline–earth metal-binding by humic substances. Anal. Chim. Acta 1994, 294, 319.
| A comparative study of proton and alkaline–earth metal-binding by humic substances.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK2cXlslyksr8%3D&md5=83f6af6a5de8759ce38854a1b482e86aCAS |
[91] J. Forsberg, R. Dahlqvist, J. Gelting-Nystrom, J. Ingri, Trace metal speciation in brackish water using diffusive gradients in thin films and ultrafiltration: comparison of techniques. Environ. Sci. Technol. 2006, 40, 3901.
| Trace metal speciation in brackish water using diffusive gradients in thin films and ultrafiltration: comparison of techniques.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28XksFKku7s%3D&md5=3357ccad93020bcb21718c51b200d0f4CAS |
[92] J. Labille, N. Fatin-Rouge, J. Buffle, Local and average diffusion of nanosolutes in agarose gel: the effect of the gel–solution interface structure. Langmuir 2007, 23, 2083.
| Local and average diffusion of nanosolutes in agarose gel: the effect of the gel–solution interface structure.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28XhtlCqtrrJ&md5=a749eb20d543dbbdd3903e86312b26e2CAS |


