A comparison of characterisation and modelling approaches to predict dissolved metal concentrations in soils
Judith M. Garforth A B D , Andrew M. Tye C , Scott D. Young B , Elizabeth H. Bailey B and Stephen Lofts A *
A *
A
B
C
D Present address:
Abstract
It is useful to know the concentration of ‘labile’, or chemically active, metal in soils because it can be used to predict metal solubility and environmental impact. Several methods for extracting the labile metal from soils have been proposed, and here we have tested two of these to see how well the resulting data can be used to model metal solubility. Such mixed approaches can be applied to different soil types with the potential to model metal solubility over large areas.
Predicting terrestrial metal dynamics requires modelling of metal solubility in soils. Here, we test the ability of two geochemical speciation models that differ in complexity and data requirements (WHAM/Model VII and POSSMs), to predict metal solubility across a broad range of soil properties, using differing estimates of the labile soil metal concentration.
Using a dataset of UK soils, we characterised basic properties including pH and the concentrations of humic substances, mineral oxides and metals. We estimated labile metal by extraction with 0.05 mol L−1 Na2H2EDTA and by multi-element isotopic dilution (E-value). Dissolved concentrations of Ni, Cu, Zn, Cd and Pb were estimated in 0.01 mol L−1 Ca(NO3)2 soil suspensions using the total metal ({M}total), the EDTA-extracted pool ({M}EDTA) and the E-value ({M}E) as alternative estimates of the chemically reactive metal concentration.
Concentrations of {M}EDTA were highly correlated with values of {M}E, although some systematic overestimation was seen. Both WHAM/Model VII and POSSMs provided reasonable predictions when {M}EDTA or {M}E were used as input. WHAM/Model VII predictions were improved by fixing soil humic acid to a constant proportion of the soil organic matter, instead of the measured humic and fulvic acid concentrations.
This work provides further evidence for the usefulness of speciation modelling for predicting soil metal solubility, and for the usefulness of EDTA-extracted metal as a surrogate for the labile metal pool. Predictions may be improved by more robust characterisation of the soil and porewater humic substance content and quality.
Keywords: analytical chemistry, chemical extraction, isotopic dilution, modelling, partitioning, soil chemistry, speciation, trace metals.
Introduction
The dynamics of soil metals are known to be controlled, at least partly, by the solid–solution partitioning of a labile or ‘geochemically active’ pool of soil-associated metal, rather than by the total soil metal concentration (Degryse et al. 2004). Partitioning measurements, along with modelled predictions of metal speciation, form the basis of our understanding of metal transport in soils and aquifers. The solid–solution partitioning of soil metals may be predicted using either empirical or mechanistic ‘assemblage’ models. These predict metal adsorption and solution speciation using the concentrations of soil components having proton and metal binding capabilities, including soil organic matter (SOM), Fe, Mn and Al hydroxides, and clay. Over a number of years, studies have compared predicted and measured results to test this approach (Groenenberg et al. 2012). The majority of these studies have used either WHAM/Model V–VII (Tipping and Hurley 1992; Tipping 1998; Tipping et al. 2011), the NICA-Donnan model (Kinniburgh et al. 1996) or the Stockholm Humic Model (SHM) (Gustafsson 2001) as the sub-model to describe metal binding to organic matter in the assemblage model. Models VI and VII have been incorporated into the assemblage model, WHAM, which also contains models for surface complexation at oxide surfaces and ion exchange on clays (Lofts and Tipping 1998). The NICA-Donnan model has been incorporated into modelling frameworks such as ECOSAT (Keizer and van Riemsdijk 2009) and ORCHESTRA (Meeussen 2003), in order to describe metal binding in whole soils.
Assemblage models require, as an input, a measurement of the concentration of soil metal that is active in adsorption processes. Various measurements have been used to determine estimates of the ‘active pool’. These include metal extracted by 0.05 mol L−1 EDTA (Quevauviller 1998), 2 mol L−1 HNO3 (Weng et al. 2001, 2002a), 0.43 mol L−1 HNO3 (Tipping et al. 2003; Dijkstra et al. 2004), 0.22 mol L−1 HNO3 (Almås et al. 2007) and pseudo-total metal concentration determined by aqua regia digestion (Schröder et al. 2005). It has been noted that discrepancies between predicted and measured results in the aforementioned studies may be partly due to overestimation or underestimation of the ‘active pool’ of metal (Weng et al. 2001, 2002a; Almås et al. 2007) by these extraction measurements. However, over the past two decades, methods using isotopic dilution (ID) with radio-isotopes (e.g. Tye et al. 2003) and stable metal isotopes (Ahnstrom and Parker 2001; Nolan et al. 2004) have been used to estimate the ‘E-value’ or isotopically exchangeable metal concentration. Conceptually, such measurements represent the best description of the pool of soil metal that is active in rapid (de)sorption processes. Results have shown that the E-value of a metal is dependent on: (i) the source of contamination, (ii) soil physiochemical properties such as pH and redox potential and (iii) soil–metal contact time (Ayoub et al. 2003). Consideration of contact time is particularly important in measuring E-values to allow the added isotope to equilibrate with the soil while not undergoing any significant removal from the labile pool due to fixation or precipitation (Mao et al. 2017). A further advantage of the ID approach is that, since it involves suspension of soil in a weak electrolyte solution, it allows for simultaneous determination of metal solubility. For example, Marzouk et al. (2013) measured Zn, Cd and Pb solution concentrations in 246 soil suspensions in 0.01 mol L−1 Ca(NO3)2 when undertaking E-value measurements.
Whilst assemblage modelling is based on sound mechanistic and technical understanding, it requires considerable amounts of input data, and this may be expensive or impractical when analysis of large datasets is required. Simpler, empirical approaches may therefore be useful to obtain the relationships between adsorbed metal and solution variables including the total and free ion concentrations in soil pore waters. The recently published POSSMs model (Lofts 2022) seeks to emulate the outputs of mechanistic models by calculating the free, solution-bound and sorbed soil metal within a single calculation, whilst restricting input parameters to an estimate of the labile (or geochemically active) metal, SOM content, solution phase pH and dissolved organic matter (DOM) concentrations. The POSSMs model has been largely tested on organic rich and lower pH soils. Previous work on multiphase modelling (Mao et al. 2017) has shown that at higher pH and lower organic matter concentrations, other phases such as the mineral oxides are predicted to become increasingly important in metal binding. The aim of this paper is to compare the outputs of (i) the geochemical assemblage model WHAM/Model VII and (ii) POSSMs, to predict soluble Ni, Cu, Zn, Cd and Pb concentrations using a dataset of soils with a range of pH values similar to that of Mao et al. (2017), but with a wider range of organic matter contents. In particular we compare measured dissolved metal concentrations with model predictions computed using three expressions of the ‘geochemically active pool’. These included total soil metal ({M}total), metal extracted using the EU recommended extractant of 0.05 mol L−1 EDTA ({M}EDTA) and the labile pool as measured by multi-element ID ({M}E) with solution concentrations measured in 0.01 mol L−1 Ca(NO3)2 soil suspensions.
Experimental
A glossary of terms is provided in Table 1.
| Term | Meaning | Units | |
|---|---|---|---|
| {M}total | Soil metal concentration obtained by extraction with HNO3 and HClO4 (2 mL:1 mL) followed by digestion with 2.5 mL HF. | mol kg−1 | |
| {M}EDTA | Soil metal concentration obtained by extraction with 0.05 mol L−1 Na2H2EDTA. | mol kg−1 | |
| {M}E | Soil metal concentration obtained by ID (E-value). | mol kg−1 | |
| pHca | pH measured in 0.01 mol L−1 Ca(NO3)2 suspension at a soil/solution ratio of 33 g L−1. | – | |
| AMsoil | Average atomic mass of metal in the un-spiked control soil. | g mol−1 | |
| AMsp | Average atomic mass of metal in the isotope spike. | g mol−1 | |
| Csp | Concentration of metal in the isotope spike. | mol L−1 | |
| Vsp | Volume of the isotope spike in the spiked soil suspension. | L | |
| W | Mass of soil in suspension. | kg | |
| sIAsp | Isotopic abundance of spike isotope in the isotope spike solution. | g g−1 | |
| rIAsp | Isotopic abundance of reference isotope in the isotope spike solution. | g g−1 | |
| sIAsus | Isotopic abundance of spike isotope in the solution phase of an un-spiked control suspension. | g g−1 | |
| rIAsus | Isotopic abundance of reference isotope in the solution phase of an un-spiked control suspension. | g g−1 | |
| sIAsp−sus | Isotopic abundance of spike isotope in the solution phase of the spiked suspension. | g g−1 | |
| rIAsp−sus | Isotopic abundance of reference isotope in the solution phase of the spiked suspension. | g g−1 | |
| 204Pb cps/208Pb cps | Ratio of ICP-MS count rates of the isotopes 204Pb and208Pb. | – | |
| NIST 204Pb IA/208Pb IA | Ratio of isotopic abundances of 204Pb and 208Pb in NIST certified reference standard SRM-981. | – | |
| FeOx | Iron(iii) oxide. | – | |
| MnOx | Manganese oxide. | – | |
| pM | Negative logarithm of solution metal concentration (with units of mol L−1). | – | |
| ΔpM | Measured pM – modelled pM for a single soil. | – | |
| MBE | Mean bias error, mean measured pM – mean modelled pH. | – | |
| RSD | Residual standard deviation. | – |
Soils
The comparison of modelling approaches used a dataset of 109 UK soils, which were selected for their wide range of total soil metal concentrations, metal sources and soil characteristics. A total of 56 soils were collected specifically for this investigation, from field sites chosen because of their metal contamination histories, or underlying geology. The remaining soils were selected from archives held by the British Geological Survey (G-BASE, 44 soils; Rawlins et al. 2012) and the University of Nottingham (nine soils; Thornton et al. 2008; Atkinson 2010).
All soils, whether freshly collected or archived, were air dried and sieved to < 2 mm. Sub samples of both archived and freshly collected soils were agate ball-milled (Fritsch Pulverisette, Germany) for total metal analysis. Loss on ignition (LOI; g (g dry weight soil)−1) was measured after heating soils (~1 g, < 2 mm) to 550°C for 2 h in a muffle furnace, and used as an estimate of SOM content (Karam 1993).
Soil metal binding phases
To predict soil solution metal concentrations using the chemical speciation model WHAM/Model VII the following soil phases were quantified. Metal oxides (MnOx and FeOx) were extracted in a solution containing 0.07 mol L−1 Na2S2O4, 0.3 mol L−1 C6H5Na3O7 and 1 mol L−1 NaHCO3 (‘DCB’ solution), shaken for 24 h at 20°C (Pansu and Gautheyrou 2006). Extraction suspensions were centrifuged at 2200g and 10°C for 15 min, and supernatant solutions filtered to < 0.2 μm (Filtropur S without prefilter). Samples were analysed by inductively coupled plasma–mass spectrometry (ICP-MS). Concentrations of FeOx and MnOx were calculated from the concentrations of Fe and Mn (mol kg−1) in the DCB extractions and converted into relative concentrations of Fe2O3.H2O and MnO2. Humic and fulvic acids (HAs and FAs) were quantified by an extraction procedure adapted from the typical extraction schemes used to remove and fractionate humic substances (HS) from soils (Tipping 2002; Anderson and Schoenau 2007), but simplified by omitting certain steps (e.g. acid pretreatment to remove inorganic C, N, P and S) as the focus was on quantifying HS rather than extracting them for experimental use. Extraction was done by suspending 1–2 g, < 2 mm soil in 20 mL of 0.1 mol L−1 NaOH, and shaking for 24 h at 20°C to solubilise the HA and FA fractions. Extraction suspensions were centrifuged at 2200g and 10°C for 15 min, and a 5 mL aliquot of the supernatant stored for analysis of the HA and FA fractions. A 10 mL aliquot of the supernatant was acidified with 1 mL of 1.5 mol L−1 HNO3 and left overnight, allowing HA to precipitate out of solution. After centrifugation at 2200g and 10°C for 15 min, the supernatant was stored at 4°C for analysis of the FA fraction. All samples were analysed for dissolved organic carbon (DOC) content (Shimadzu TOC-VCPH, Total Organic Carbon Analyser, Model TNM-1). Particulate FA and HA concentrations were calculated assuming that FA and HA comprise 50% carbon (Weng et al. 2002b).
Soil metal concentrations
Soil total metal concentrations, {M}total, were determined following a HF digestion procedure in preference to the aqua regia digestion commonly used, since the latter may not be able to access metal held within silicate matrices. Two replicate ball-milled soil samples (~0.2 g) were extracted with concentrated HNO3 and HClO4 (2 mL:1 mL) at 80°C for 8 h followed by 100°C for 2 h. After addition of concentrated HF (2.5 mL), samples were then digested at 120°C for 1 h, 140°C for 3 h, 160°C for 4 h and 50°C for 1 h. Samples were left overnight, before addition of concentrated HNO3 (2.5 mL) and ultrapure water (2.5 mL). Samples were warmed to 50°C for 1 h, and then cooled and diluted to 50 mL with high purity water, and stored prior to multi-element analysis by ICP-MS (X-Series II; Thermo Fisher Scientific, Bremen, Germany).
Isotopic dilution assays
Enriched stable isotopes, with certified isotopic abundances (IAs) of 97.0% 62Ni, 99.2% 65Cu, 99.9% 70Zn, 70.3% 108Cd and 99.4% 204Pb, were obtained as metal foils from Isoflex, San Francisco, CA, USA. The foils were dissolved in HNO3 to create dilute isotope stock solutions of concentrations 603, 840, 154, 192 and 442 μg mL−1 for 62Ni, 65Cu, 70Zn, 108Cd and 204Pb, respectively. Dilute isotope stock solutions were mixed to create multi-element isotope spike solutions specific to each soil. In general, the multi-element isotope spike solution concentrations were intended to increase the values of the natural abundances of the spike isotopes in the soil by between 10 and 30%, based on a spike volume of 0.4 mL. However, for soils with low total metal concentrations and for practical purposes, it was necessary to sometimes use spike concentrations resulting in values outside this range. In the soils used for modelling in this work, the means (and ranges) of the percentages by which the natural abundance of the spike isotope was raised by spiking were 3.60 (0.235–23.3), 7.35 (1.03–20.5), 0.368 (0.0356–1.72), 10.9 (0.152–42.8) and 1.03 (0.0813–6.16) for Ni, Cu, Zn, Cd and Pb, respectively.
The effect of the isotope on the pH of the soil suspensions may influence the derived E-value. Sterckeman et al. (2009) found that the spiking approach had a significant effect on the soil suspension pH and recommended adjusting the pH of the spike solution to a sufficiently high value to minimise the possibility of acidification effects. In contrast, Marzouk et al. (2013) investigated the effect on the soil suspension pH of adding variable spike volumes, using a broadly similar approach to spike composition and concentration for 70Zn, 111Cd and 204Pb isotopes as was taken here. They found that the pH values of soil suspensions, spiked to give 10 and 100% changes in the natural abundance of the labile pools of 70Zn, 108Cd and 204Pb, were not significantly different (P < 0.05) from suspensions of unspiked soils. Given the similarity of our spiking approach to that of Marzouk et al. (2013), we have assumed that there was no significant effect on suspension pH due to our procedures.
ID assays required six replicate soil samples (~1 g, < 2 mm). Initially, these were each suspended in 30 mL of 0.01 mol L−1 Ca(NO3)2 solution and shaken for 72 h at room temperature. Three of the replicate suspensions were then spiked with 0.4 mL of a multi-element isotope spike solution (62Ni, 65Cu, 70Zn, 108Cd, 204Pb), before all replicates were shaken for a further 72 h. Suspensions were centrifuged at 2200g and 10°C for 15 min and supernatant solutions filtered to < 0.2 µm (Filtropur S without prefilter, Sarstedt) to exclude non-labile metal bound to larger colloids. Samples were acidified to 2% HNO3 prior to isotope ratio analysis by ICP-MS.
For all the metals, it was found that, in some cases, the concentration of metal solubilised by the electrolyte was so low that the measurements of isotopic ratios required to compute E-values could be considered unreliable. The numbers of soils affected were 10, 18, 16, 20 and 27 for Ni, Cu, Zn, Cd and Pb, respectively. Therefore, the assays for these soil/metal combinations were repeated using 10−5 mol L−1 (NH4)2EDTA as the suspending electrolyte. This matrix has previously been shown to increase the concentration of labile metal in solution, due to complexation of metal ions by EDTA, but to mobilise negligible non-labile metal (Degryse et al. 2004; Atkinson et al. 2011; Izquierdo et al. 2013). For comparative purposes, assays using 10−5 mol L−1 (NH4)2EDTA were also done on a number of soils for which satisfactory results were obtained using Ca(NO3)2 as suspending electrolyte: 21, 18, 15, 16 and 7 for Ni, Cu, Zn, Cd and Pb, respectively.
Values of {M}E (mol kg−1) were determined from the IA of the spike isotope (sIA) and a reference isotope (rIA) measured in three solutions: the isotope spike solution (IAsp), the solution phase of the spiked suspension (IAsp−sus) and the solution phase of an un-spiked control suspension (IAsus). Values of {M}E were calculated from Eqn 1 (Heumann 1988; Gäbler et al. 2007):
where AMsoil and AMsp are the average atomic masses of the metal in the un-spiked control soil and the isotope spike respectively (g mol−1), Csp and Vsp are the concentration (g L−1) and volume (L) of the isotope spike respectively, and W is the mass of the soil (kg).
The IAs of the isotopes in the spiked and un-spiked soil solutions were calculated from the measured isotope ratios, and the natural abundance ratios of the unmeasured isotopes for each metal. For Pb, however, natural abundance ratios were not used, because lead isotope abundance varies depending on the source of the lead in the soil. For this reason, the isotope ratios for all Pb isotope combinations were measured. The isotope ratios 62Ni/60Ni, 65Cu/63Cu, 70Zn/66Zn, 108Cd/111Cd, 204Pb/208Pb, 206Pb/208Pb and 207Pb/208Pb, were measured by quadrupole ICP-MS, operating in CCT-KED (collision cell technology with kinetic energy discrimination) mode, particularly to minimise interference from the chlorine dimer (35Cl–35Cl) in some extractions which interferes with measurements of 70Zn. The isobaric interference of 204Hg on 204Pb was corrected by assay of 202Hg, although this was a very small adjustment. Where necessary, samples were diluted to ensure measurement by the electron multiplier detector in pulse-counting mode. The ions of each isotope of a metal are transported with different efficiencies within the ICP-MS due to their different mass to charge ratios, and this effect is referred to as mass discrimination (MD). Corrections for MD were calculated from measured count rate ratios of ICP-MS calibration standards for Ni, Cu, Zn and Cd and the certified reference standard NIST SRM-981 for Pb. An example for Pb is given in Eqn 2 (Marzouk et al. 2013). The standards were run approximately every 20 samples and MD factors implemented as a drift correction.
Additional measurements for modelling
Soil suspension pH (pHCa) was determined in the un-spiked 0.01 mol L−1 Ca(NO3)2 soil suspensions (~1 g, < 2 mm/30 mL) after 144 h shaking, using a pH meter and combined pH electrode (Radiometer Analytical SAS). The pH electrode was calibrated using pH 1, 4 and 7 buffer solutions (Fixanal, Fluka Analytical) at 20°C. Solution concentrations of Ni, Cu, Zn, Cd and Pb were also measured in these solutions, for the purpose of testing the model outputs. DOC concentrations were measured on filtered, unacidified aliquots of the un-spiked 0.01 mol L−1 Ca(NO3)2 soil suspensions, after 144 h shaking, using a total organic carbon analyser (Shimadzu TOC-V CPH, Model TNM-1).
WHAM/Model VII application
Default parameter settings and input files were used for the speciation modelling. The soil concentration was set equal to the soil/solution ratio (33 g L−1), and the pH to the pHCa value. The total Ni, Cu, Zn, Cd and Pb concentrations were set to the measured values of either {M}total, {M}EDTA or {M}E. Soil binding phases used in the computations were particulate HA, FA, MnOx and FeOx. Measured concentrations of particulate HA, FA and DCB-extractable Mn were used to compute the phase concentrations. The concentration of particulate FeOx was computed by inputting the DCB-extractable concentration of iron as the total FeIII and allowing FeOx to precipitate from this iron pool as a particulate solid with a chemically active surface. The solution electrolyte was represented by inputting concentrations of dissolved Ca and NO3 (0.01 and 0.02 mol L−1, respectively). DOM in the suspensions was represented by colloidal FA concentrations, calculated from the DOC concentrations assuming that 65% of the measured DOC was ‘active’ FA in respect to binding, and that FA is 50% C (Weng et al. 2002b). The temperature was set to 293 K (20°C) and for computing carbonate chemistry, the atmospheric partial pressure of CO2 was set to 0.0004. The variables used for model application are summarised in Table 2.
| Input parameter | Phase | Unit | Notes | |
|---|---|---|---|---|
| {M} E for Ni, Cu, Zn, Cd, Pb | Solute. Total concentration. | mol L−1 | ||
| {M}EDTA for Ni, Cu, Zn, Cd and Pb | Solute. Total concentration. | mol L−1 | ||
| Ca, NO3 | Solute. Total concentration. | mol L−1 | From background electrolyte. | |
| Fulvic acid | Colloidal. A | g L−1 | From measured [DOC]. | |
| Soil humic acid concentration | Particulate. B | g L−1 | ||
| Soil fulvic acid concentration | Particulate. B | g L−1 | ||
| DCB-extractable Fe | Solute. Total concentration. | g L−1 | Allowed to precipitate to form particulate iron(iii) oxide B. | |
| Mn oxide concentration | Particulate. B | g L−1 | Computed from the concentration of DCB-extractable Mn. | |
| Suspended particulate matter | – | g L−1 | Calculated from the suspension soil to solution ratio 1 g/30 mL. | |
| Temperature | – | K | 293 K | |
| Atmospheric partial pressure of CO2 | – | – | 0.0004 | |
| Soil suspension pH | – | – |
A check on the possibility of mineral control of metal solubility was undertaken by separate speciation of the soil supernatants, using the measured solution metal concentrations as input, and calculating saturation indices for a range of hydroxide and carbonate-containing minerals.
An alternative parameterisation of the model was also run, using an assumption that the SOM comprised 50% HA. This assumption was previously used by Buekers et al. (2008) and Marzouk et al. (2013).
The WHAM outputs used were (1) the total aqueous concentrations of Ni, Cu, Zn, Cd and Pb (mol L−1), which were compared to the concentrations measured in solution (section Additional measurements for modelling), and (2) the proportion of each metal predicted to be bound to each particulate and colloidal phase.
POSSMs application
POSSMs was developed (Lofts 2022) to provide a model for the equilibrium soil–solution partitioning of Ni, Cu, Zn, Cd and Pb with minimal data requirements and thus suitable for application at large scale, where the relatively detailed data requirements of WHAM or other geochemical speciation models might not be achievable. The model represents the system of chemical equilibria acting on metals in soils via two ‘lumped’ equilibria: those between the free and adsorbed metal, and between the free and metal complexed in the soil solution. These equilibria are expressed as
The terms Kads, Kcomp, A, B, Δ, , β and δ are empirical parameters obtained by directly fitting the model to data of matched soil solution pH, solid phase and DOM, and geochemically active, soil solution and free metal concentrations. Lofts (2022) parameterised the model by fitting it to datasets where porewaters were extracted from intact soils prior to characterisation, in order to provide the best possible analogue to field porewaters. Where free ion in the porewaters was not measured directly, it was obtained by modelling using WHAM/Model VII. Best fit values of the parameters are provided in Table 3.
Results
General soil characteristics
Of the 109 soils studied, 84 were successfully analysed for all the determinants required to perform the desired speciation for all five metals. To allow robust comparison of modelling outcomes across the metals and modelling approaches, only the results for these soils are presented and analysed here.
Graphical summaries of the ranges of pH, soil LOI and [DOC] (in the 0.01 mol L−1 Ca(NO3)2 suspensions) are shown in Supplementary Fig. S1. Table 4 shows summary statistics for the total and EDTA-extractable metal concentrations, and the E-values. Soil metal concentrations span several orders of magnitude, reflecting the wide range of soil characteristics, from uncontaminated rural soils to those impacted by urban, industrial and mining activity. Values of {M}total, {M}EDTA and {M}E for each soil are shown in the Supplementary material (Supplementary Table S1).
| Ni (mol kg−1) | Cu (mol kg−1) | Zn (mol kg−1) | Cd (mol kg−1) | Pb (mol kg−1) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| {M}total | {M}EDTA | {M} E | {M}total | {M}EDTA | {M} E | {M}total | {M}EDTA | {M} E | {M}total | {M}EDTA | {M} E | {M}total | {M}EDTA | {M} E | ||
| Geomean | −3.29 | −4.40 | −4.39 | −3.03 | −3.69 | −2.64 | −2.30 | −3.11 | −3.09 | −4.93 | −5.25 | −5.23 | −2.94 | −3.48 | −3.26 | |
| Median | −3.36 | −4.61 | −4.56 | −3.09 | −3.74 | −3.58 | −2.36 | −3.15 | −3.11 | −5.06 | −5.33 | −5.30 | −2.98 | −3.45 | −3.21 | |
| IQR | −3.26 | −4.41 | −4.55 | −2.72 | −3.28 | −3.17 | −1.96 | −2.68 | −2.62 | −4.75 | −5.06 | −5.03 | −2.64 | −3.19 | −2.92 | |
| Min | −4.25 | −5.77 | −5.76 | −4.11 | −5.15 | −5.28 | −3.43 | −4.81 | −5.02 | −5.97 | −7.20 | −7.29 | −3.98 | −5.05 | −4.74 | |
| Max | −1.17 | −2.03 | −2.02 | −0.81 | −1.65 | −1.69 | −0.74 | −1.11 | −1.04 | −2.96 | −3.11 | −3.12 | −0.86 | −1.61 | −1.40 | |
Humic and fulvic acid contents
Supplementary Fig. S2 shows the proportion of SOM (as LOI) present as HS, and the measured ratio of HA to FA. The proportion of HS ranged widely, from below 0.05 g g−1 to approximately 0.5 g g−1. There was no clear relationship between the humic content of the SOM and the LOI, although when the humic content is plotted against pHCa a trend to lower humic content with higher pHCa can be seen (correlation coefficient 0.55, P < 0.001). The proportion of the base-extractable organic matter (the sum of HA and FA) that is humic in nature increases with increasing SOM, but in a non-linear manner. Correlation between the HA proportion and the logarithm of the LOI has a coefficient of 0.44 (P < 0.001). Conversely, there was no clear relationship between the HA proportion and pHCa, other than a tendency to a higher proportion on average when pHCa < 4.
Comparison of {M}EDTA and {M}E as geochemically reactive metal pools
Figs 1 and 2 show the ratios of metal extracted by EDTA in each soil to the corresponding E-value, as a function of pH in the Ca(NO3)2 suspension. Standard errors in ratios were computed by bootstrapping using the standard deviations of measured {M}E and {M}EDTA concentrations and a sample size of 2000. Median relative standard errors (RSEs) were all 3%, with the exception of Pb for which it was 4%. Maximum RSEs were 54, 25, 15, 21 and 32% for Ni, Cu, Zn, Cd and Pb, respectively.
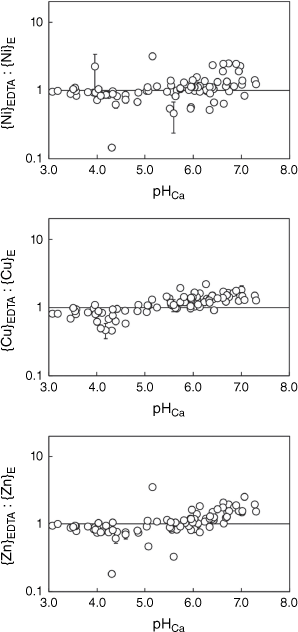
Values of {M}EDTA as a proportion of {M}E as a function of pH in 0.01 mol L−1 Ca(NO3)2, for Ni, Cu and Zn. The horizontal line represents equal values of {M}EDTA and {M}E. Error bars represent ±1 standard error.
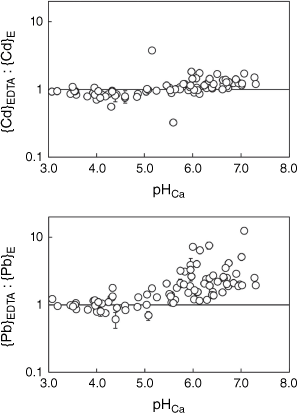
Values of {M}EDTA as a proportion of {M}E as a function of pH in 0.01 mol L−1 Ca(NO3)2, for Cd and Pb. The horizontal line represents equal values of {M}EDTA and {M}E. Error bars represent ±1 standard error.
Values of {M}EDTA and {M}E represent two estimates of the labile or ‘geochemically active’ metal – by wet chemical extraction and by ID analysis. Values of {M}E expressed as a proportion of {M}total ranged from 0.01–0.64 for Ni, 0.02–0.65 for Cu, 0.01–1.08 for Zn, 0.01–1.08 for Cd and 0.03–1.16 for Pb. These ranges exceed the literature values compiled by Izquierdo et al. (2013) in contaminated flood plain soils of 0.10–0.33 for Zn, 0.03–1.00 for Cd and 0.31–0.78 for Pb. They also exceed those reported by Mao et al. (2017) for urban soils in two UK cities.
On average, Cd was most isotopically labile and Ni least; the mean {M}E:{M}total ratios were 0.12, 0.25, 0.22, 0.54 and 0.35 for Ni, Cu, Zn, Cd and Pb, respectively. Pairwise t-testing showed that only the means for Cu and Zn were not significantly different (P < 0.05). Supplementary Fig. S3 shows the distribution of individual ratios for each metal; for Zn, Cd and Pb there is considerable variation in individual ratios, covering almost the entire range of possible values. This is in line with results previously reported by Marzouk et al. (2013) and Izquierdo et al. (2013), who found that {M}E:{M}total ratios decreased in the order Cd > Pb > Zn for sets of 246 minespoil-contaminated soils and 27 alluvial soils respectively. Supplementary Fig. S4 further compares the mean ratios found here with those found from other studies in UK soils. Although the mean values vary among the studies, there is a consistent pattern to the relative ratios: Cd > Pb > Cu ~ Zn > Ni.
The E-values were found to exceed {M}Total concentrations for Pb in soil 65, Zn and Cd in soil 72, and Cd and Pb in soil 86. All these soils were acidic (pHCa < 5) with relatively high organic matter contents (>0.24 g g−1 LOI). Previous research on fixation of labile Zn and Cd in soils has shown that the extent of fixation is relatively low in acidic soils (Degryse et al. 2004; Marzouk et al. 2013). It is likely that such E-values reflect near complete lability of the soil metal coupled with natural heterogeneity of the sampled soil.
Values of {M}EDTA and {M}E were highly correlated (Table 5). On average, the ratio of {M}EDTA to {M}E was 1.03, 1.16, 1.22, 1.17 and 1.48 for Ni, Cu, Zn, Cd and Pb, respectively. Overall, the Na2H2EDTA extraction provided a reasonable match to the more conceptually precise isotopically exchangeable pool. For Ni, Cu, Zn and Cd the match between {M}EDTA and {M}E was reasonable but for Pb the {M}EDTA values were more clearly biased to higher values. Investigation of the relationship between the {M}EDTA:{M}E ratio and pHCa (Figs 1 and 2) showed that, in general, ratios for Ni, Cu, Zn and Cd were below unity when pHCa ≤ 5.0 (0.90, 0.80, 0.82 and 0.86 respectively) and over unity when pHCa > 5.0 (1.23, 1.33, 1.29 and 1.20 respectively). The mean {Pb}EDTA:{Pb}E ratio was 1.02 when pHCa ≤ 5.0 and 2.51 when pHCa > 5.0. A single soil (Port Talbot 1) showed a {Pb}EDTA:{Pb}E ratio of over 10.
| Metal | Pearson correlation coefficient | Regression equation | |
|---|---|---|---|
| Ni | 0.996 | {M}EDTA = 1.04∙{M} E − 5.63 × 10−6 | |
| Cu | 0.976 | {M}EDTA = 0.99∙{M} E + 0.000143 | |
| Zn | 0.994 | {M}EDTA = 1.19∙{M} E + 0.000121 | |
| Cd | 0.978 | {M}EDTA = 1.06∙{M} E + 3.44 × 10−6 | |
| Pb | 0.988 | {M}EDTA = 1.56∙{M} E − 4.87 × 10−5 |
Overall, it was found that if the non-labile metal pool is smaller at low pH, there is less likelihood of a difference between {M}EDTA and {M}E. However, some exceptions were found. For example, Ni, Zn and Cd {M}EDTA and {M}E in the soils Wemyss Mine Horizon 1 and Wemyss Mine Horizon 2, with pHCa 5.6 and 5.1 respectively, showed notable contrasts. The E-values for Ni, Zn and Cd for the Horizon 1 soil (the upper horizon) were underestimated by the Na2H2EDTA extraction ({M}EDTA:{M}E ratios were 0.45, 0.33 and 0.32 of {M}E for Ni, Zn and Cd respectively). In contrast, the E-values for Horizon 2 (the lower horizon) were overestimated by the Na2H2EDTA extraction ({M}EDTA: {M}E ratios were 3.16, 3.53 and 3.76 for Ni, Zn and Cd respectively). Although the underestimation of E-values by the EDTA extraction was unexpected, a similar finding was made for Pb in acidic organic soils by Marzouk et al. (2013). It may also be that the particular history of such a site, being in the vicinity of an abandoned Pb/Zn mine, has resulted in metals occurring in specific forms that produce the unusual result seen.
No significant relationships were found between the {M}EDTA:{M}E ratio and LOI or DCB-extractable Mn or Fe, for any of the metals (data not shown).
WHAM/Model VII modelling
The mineral solubility control check showed that predicted concentrations of metals in the supernatants were all below saturation with respect to any of the mineral phases considered (Supplementary Table S3).
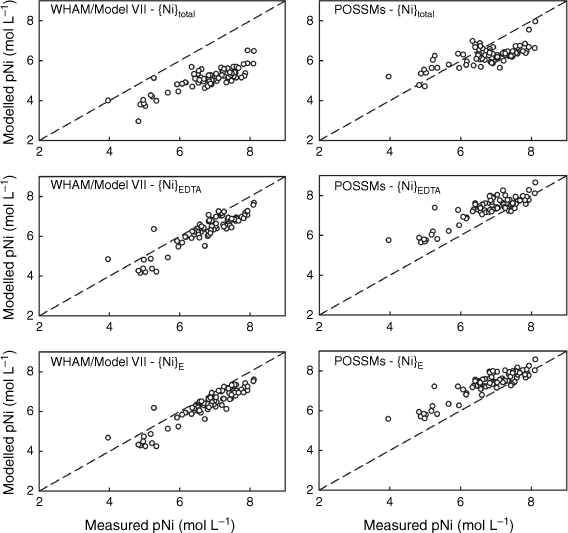
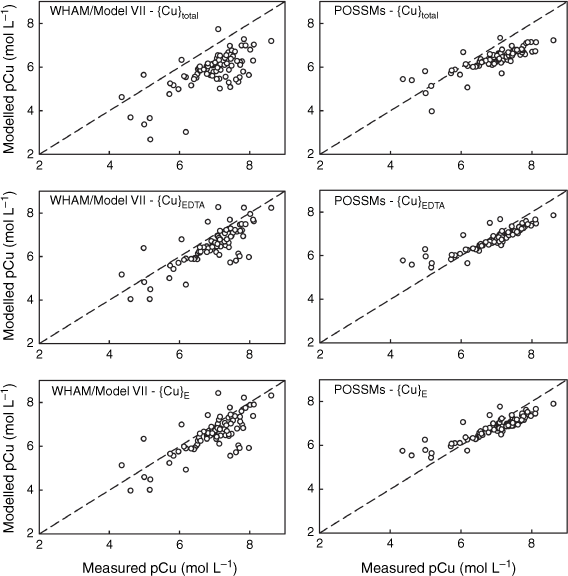
Comparisons were made using WHAM/Model VII, where values of {M}total, {M}EDTA and {M}E were used as the reactive solute concentrations for modelling purposes. Outputs from both models were compared to the measured total soluble Ni, Cu, Zn, Cd and Pb concentrations in the un-spiked 0.01 mol L−1 Ca(NO3)2 soil suspensions. Goodness of fit parameters (r2 values, RMSD and mean bias error (MBE, mean measured pM – mean modelled pM)) are shown in Table 6, and comparisons of observations and predictions are shown in Figs 3–7. When using {M}total as the estimate of geochemically reactive soil metal, both models generally overestimated metal solubility (MBE > 0), with the exception of POSSMs for Cd where a small underestimation was seen on average. By contrast, when using {M}EDTA or {M}E, there was a consistent shift towards smaller values of MBE. This is to be expected given that {M}EDTA and {M}E were, on average, smaller than {M}total for each soil.
| WHAM/Model VII measured HA, FA | WHAM/Model VII HA = 50% SOM | POSSMs | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| r2 | RSD | MBE | r2 | RSD | MBE | r2 | RSD | MBE | ||
| {Ni}total | 0.68 | 1.76 | 1.69 | 0.70 | 1.56 | 1.48 | 0.48 | 0.82 | 0.53 | |
| {Ni}EDTA | 0.81 | 0.59 | 0.46 | 0.86 | 0.39 | 0.23 | 0.75 | 0.72 | −0.57 | |
| {Ni} E | 0.85 | 0.53 | 0.42 | 0.88 | 0.36 | 0.20 | 0.80 | 0.70 | −0.58 | |
| {Cu}total | 0.50 | 1.27 | 1.10 | 0.48 | 1.07 | 0.84 | 0.69 | 0.75 | 0.58 | |
| {Cu}EDTA | 0.61 | 0.70 | 0.44 | 0.58 | 0.60 | 0.16 | 0.80 | 0.45 | 0.16 | |
| {Cu} E | 0.57 | 0.70 | 0.39 | 0.53 | 0.64 | 0.10 | 0.80 | 0.45 | 0.14 | |
| {Zn}total | 0.55 | 1.48 | 1.33 | 0.64 | 1.20 | 1.05 | 0.49 | 0.91 | 0.57 | |
| {Zn}EDTA | 0.71 | 0.66 | 0.40 | 0.80 | 0.46 | 0.14 | 0.61 | 0.63 | −0.17 | |
| {Zn} E | 0.84 | 0.55 | 0.36 | 0.87 | 0.38 | 0.10 | 0.75 | 0.56 | −0.19 | |
| {Cd}total | 0.67 | 1.00 | 0.88 | 0.78 | 0.76 | 0.66 | 0.66 | 0.47 | −0.10 | |
| {Cd}EDTA | 0.74 | 0.61 | 0.45 | 0.84 | 0.39 | 0.23 | 0.72 | 0.58 | −0.40 | |
| {Cd} E | 0.84 | 0.52 | 0.41 | 0.90 | 0.31 | 0.19 | 0.82 | 0.54 | −0.42 | |
| {Pb}total | 0.73 | 1.13 | 0.87 | 0.73 | 1.11 | 0.84 | 0.56 | 1.10 | 0.66 | |
| {Pb}EDTA | 0.72 | 0.85 | 0.40 | 0.72 | 0.84 | 0.39 | 0.60 | 0.94 | 0.37 | |
| {Pb} E | 0.75 | 0.80 | 0.13 | 0.75 | 0.80 | 0.12 | 0.76 | 0.74 | 0.17 | |
Comparison of measured Ni solution concentrations (pNi, −log10 of the total solution Ni in mol L−1) in 0.01 mol L−1 Ca(NO3)2 soil suspensions with model outputs using {Ni}total, {Ni}EDTA and {Ni}E as model inputs. Left: predictions using WHAM/Model VII, right: predictions using POSSMs. The dashed lines indicate the 1:1 line.
Comparison of measured Cu solution concentrations (pCu, −log10 of the total solution Cu in mol L−1) in 0.01 mol L−1 Ca(NO3)2 soil suspensions with model outputs using {Cu}total, {Cu}E and {Cu}EDTA as model inputs. Left: predictions using WHAM/Model VII, right: predictions using POSSMs. The dashed lines indicate the 1:1 line.
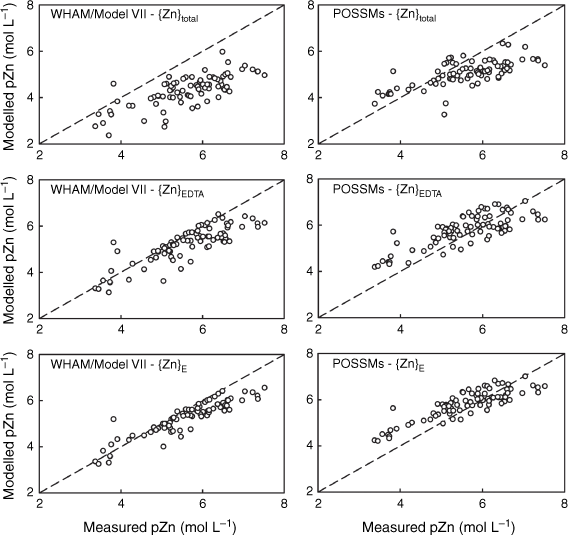
Comparison of measured Zn solution concentrations (pZn, −log10 of the total solution Zn in mol L−1) in 0.01 mol L−1 Ca(NO3)2 soil suspensions with model outputs using {Zn}total, {Zn}E and {Zn}EDTA as model inputs. Left: predictions using WHAM/Model VII, right: predictions using POSSMs. The dashed lines indicate the 1:1 line.
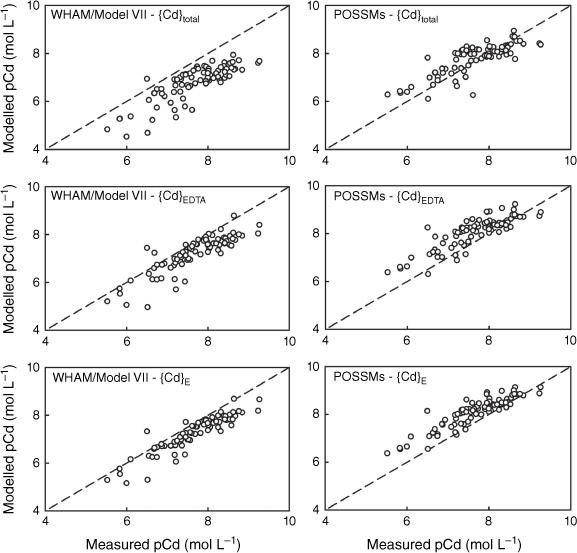
Comparison of measured Cd solution concentrations (pCd, −log10 of the total solution Cd in mol L−1) in 0.01 mol L−1 Ca(NO3)2 soil suspensions with model outputs using {Cd}total, {Cd}E and {Cd}EDTA as model inputs. Left: predictions using WHAM/Model VII, right: predictions using POSSMs. The dashed lines indicate the 1:1 line.
Comparison of measured Pb solution concentrations (pPb, −log10 of the total solution Pb in mol L−1) in 0.01 mol L−1 Ca(NO3)2 soil suspensions with model outputs using {Pb}total, {Pb}E and {Pb}EDTA as model inputs. Left: predictions using WHAM/Model VII, right: predictions using POSSMs. The dashed lines indicate the 1:1 line.
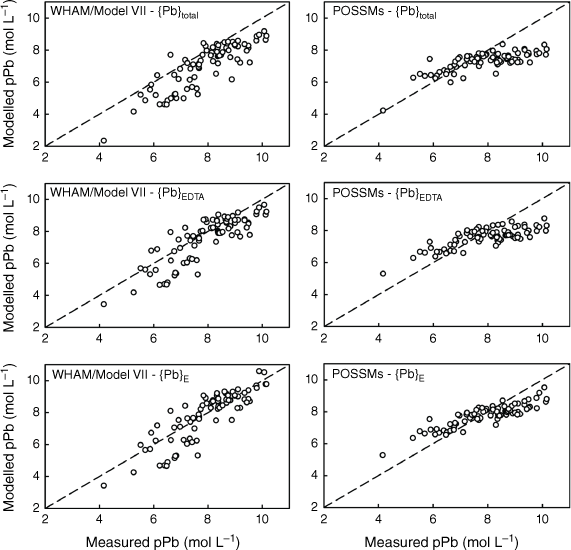
The WHAM/Model VII predictions using {M}EDTA or {M}E all showed positive MBE, i.e. overestimation of metal solubility on average. Generally, the MBE values obtained from WHAM/Model VII were rather similar when using either {M}EDTA or {M}E as input, though there was a consistent tendency to slightly smaller MBE when using {M}E. The largest difference in MBE was seen for Pb, which may be related to the differences seen between {M}EDTA and {M}E for this metal at the higher end of the soil pHCa range. Overall goodness-of-prediction, quantified by the RMSD value, showed similar trends to MBE, with the use of {M}EDTA or {M}E as input generally resulting in lower RMSDs, with the RMSD when using {M}E generally the same or lower than the RMSD when using {M}EDTA. The exception was Pb, where all the RMSD values were similar. Patterns in r2 were similar, with the highest r2 for all the metals except Cu being found when using the {M}E. Supplementary Fig. S5 shows the patterns in observed and modelled metal solubility as a function of pHCa, using the model with {M}E as input. WHAM/Model VII reproduced the general trends in solubility well using the measured soil HA and FA concentrations, albeit with a general tendency to overestimate the solubility of Ni, Zn and Cd across the pHCa range, particularly in the most acidic soils (pHCa < 5.5). Both the relatively weak trend in Cu solubility and the strong trend in Pb solubility were reproduced, however, for both metals the model predicted near complete solubility below pHCa ~3.75, which overestimated observed solubility by over an order of magnitude in most cases.
The alternative parameterisation of the model, where active soil HA was set to 50% of LOI and active FA not used, increased the modelled HA + FA concentration in the soils by a factor of 2.3 on average, with only five soils having lower HA + FA than under the standard parameterisation. The outcome was consistently lower RSD and MBE values than were found when using the measured HA and FA concentrations (Table 6), with the exception of Pb for which the RSD and MBE under both assumptions were essentially identical. Supplementary Fig. S6 shows the predictions made using the alternative parameterisation and values of {M}E as input. Supplementary Fig. S5 shows that the improvements in model prediction when assuming soil HA to be 50% of LOI became larger at higher pHCa values, and that in the most acidic soils (lowest pHCa quintile, 3.08–4.24), the improvement in prediction was small to negligible.
Adjusting the activity of DOM generally had a smaller effect on model goodness-of-prediction. For example, halving active DOM decreases MBE by 0.01 for Ni and had no effect on RSD, while doubling active DOM increased both RSD and MBE by small amounts (RSD from 0.53 to 0.55 and MBE from 0.41 to 0.43). Similar patterns were found for Zn and Cd. A larger response was seen for Cu: halving DOM activity decreased RSD slightly (0.70–0.68) but reduced MBE by about a half (0.39–0.19), while doubling active DOM increased RSD (0.70–0.80) and MBE (0.39 and 0.60). Changing DOM activity had little effect on the RSD for Pb (0.80–0.84 when halving DOM activity and to 0.81 when doubling it). The MBE changed from 0.13 to −0.02 on halving DOM activity.
Supplementary Fig. S7 shows the predicted distribution of each metal among the solution and the individual solid phases (SOM, iron oxide and manganese oxide) when modelling using values of {M}E as input. For Cu, Zn and Cd, there was a general trend of increasing adsorption with increasing pH, with organic matter generally being the dominant adsorption phase. The metal oxides become more significant as adsorption phases as pH increases and, for Zn and Cd, iron oxide is the most important adsorbing phase in soils with pHCa above ~6.6. Manganese oxide is a relatively unimportant contributor to binding, particularly for Cu, and tended to be most important in soils of pHCa ~5.5–6.0, becoming less important at higher pH. Somewhat different trends were seen for Ni and Pb. Soil adsorption of Ni exhibited a maximum in the pHCa range ~5.5–6.0, in contrast to the other metals. Manganese oxide was also predicted to be a relatively important contributor to Ni adsorption, comparable to that of HA and FA, with iron oxide playing a relatively minor role. Lead adsorption was dominated by the metal oxides, and binding to HA and FA played only a minor role. The relative importance of iron and manganese oxides as Pb sorbents is predicted to vary considerably with pH, with manganese oxide being most important up to a pHCa of ~6.0, above which iron oxide is predicted to play an increasingly important role and to dominate adsorption above pHCa ~6.6.
As the soil pH is a key variable influencing most chemical equilibria, the relationship between pHCa and prediction bias (ΔpM, measured pM – modelled pM) was investigated further. When {M}E was used as the input to WHAM/Model VII, ΔpM for Ni, Zn and Cd had significant positive correlations with pHCa, with Pearson correlation coefficients of 0.26 (P = 0.015), 0.47 (P < 0.001) and 0.44 (P < 0.001) respectively. Copper and lead were found to have significant negative correlations (Pearson correlation coefficients −0.51 and −0.52, both P < 0.001). This indicates a systematic tendency for solubility in soils at lower pH to be overestimated to a greater extent than at higher pH. Calculation of Cu and Pb MBE values for the pHCa quintiles shows that there was considerable overestimation of solubility in the lowest quintile (3.08–4.24) (MBE for Cu was 1.08 and for Pb was 1.23). Across the remaining pHCa range, MBE for Cu was 0.24 and for Pb was −0.15. Buekers et al. (2008) noted that overestimation of Ni, Cu, Zn and Cd solubility occurred mainly for soils with pH > 6 and suggested that this may result from an underestimation of sorption on oxyhydroxides, which becomes increasingly important as pH increases (Supplementary Fig. S7). Previously, predictions of Pb solubility have been found to be pH dependent, with over prediction at low pH and under predictions at high pH (Marzouk et al. 2013).
Similar correlation patterns were found between pH and {M}EDTA concentrations when used as inputs to WHAM/Model VII. For Ni, Zn and Cd, significant positive correlations between ΔpM and pHCa were found, with coefficients of 0.45, 0.60 and 0.54 respectively (P < 0.001 for all). Copper and lead ΔpM values again had significant negative correlations with pHCa (correlation coefficients −0.35 and −0.30 respectively, P = 0.001 and 0.006 respectively). The Cu and Pb correlations were again driven by overestimation of metal solubility in the lowest pHCa quintile, with the MBE for Cu being 0.98 and for Pb 1.21, compared with MBEs of 0.30 and 0.20 for the other quintiles.
When the alternative model parameterisation was used, clear changes were seen in the relationship between model bias and pHCa. Pearson correlation coefficients between ΔpM and pHCa for Ni, Zn and Cd changed to −0.19 (P = 0.088), 0.11 (P = 0.332) and 0.00 (P = 0.979); thus, the alternative parameterisation did not result in significant relationships between model bias and pHCa for these metals. Supplementary Fig. S5 shows that the predicted decrease in metal solubility caused by the change in model assumptions did not occur for the soils in the lowest pHCa quintile. The change in assumptions thus not only reduced MBE for the whole dataset, but made the model bias more consistent across the whole pHCa range.
POSSMs modelling
POSSMs gave broadly similar goodness-of-prediction results compared to WHAM/Model VII, yet there were some notable differences. In particular, when using either {M}EDTA or {M}E as input, dissolved Ni and Cd were underestimated on average across the range of pHCa quintiles, while WHAM/Model VII overestimated solubility on average. When using {M}E as input, goodness-of-prediction (RSD, Table 6) for Ni was inferior to that for WHAM/Model VII, while for cadmium it was similar. Goodness-of-prediction and MBE for copper were superior to that of WHAM/Model VII, while for zinc RSD was similar, with a lower MBE for POSSMs. Goodness-of-prediction and MBE for lead were similar, with RSD being marginally lower for POSSMs and MBE being marginally higher.
As with the WHAM/Model VII results, we investigated further the relationship between prediction bias (ΔpM) and pHCa for POSSMs. When {M}E was used as the input, ΔpM for Ni, Zn, Cd and Pb had significant positive correlations (P < 0.001) with pHCa, with Pearson correlation coefficients of 0.56, 0.66, 0.63 and 0.69 respectively. Copper showed a weaker negative correlation coefficient of −0.23 (P = 0.034). These trends can also be seen by inspecting Supplementary Fig. S7. With the exception of Cu, POSSMs underestimated the trend in average solubility across the quintiles of pHCa. This was particularly notable in the case of Pb, where the model underestimated solubility on average in the two lowest pHCa quintiles, but then overestimated it at higher pHCa. This pHCa-dependent bias in predictions can also be seen in the overall solubility prediction (Fig. 7), since there was a strong pH dependence of absolute Pb solubility. So, despite the fact that overall goodness-of-prediction measures for Pb were quite similar for POSSMs and WHAM/Model VII, a more detailed look at how goodness-of-prediction varies showed clear patterns that suggest areas in which the model could be improved; in this case, to better describe the dependence of solubility on pH. Correlation patterns and significance when using {M}EDTA as input were very similar, with the exception that the correlation for Cu was not significant (P = 0.53).
Discussion
The approach to assessing and modelling metal solubility in this study is broadly similar to that taken previously by a number of authors (e.g. Izquierdo et al. 2013; Marzouk et al. 2013; Mao et al. 2017), but we have used a range of soils covering a broader spectrum of land use and potential contamination sources. The range of pHCa values in our study (3.08–7.31) is broader than those of Izquierdo et al. (2013) (5.3–8.0) and Mao et al. (2017) (3.6–8.1), as is the range of SOM contents (this study 0.028–0.939 g g−1; Izquierdo et al. (2013) 0.04–0.18 g g−1, Mao et al. (2017) 0.020–0.502 g g−1). The ranges of pHCa and SOM in this study are similar to those of Marzouk et al. (2013) (2.58–7.58 and 0.034–0.961 g g−1, respectively), however, this study covers a far wider range of locations, land use and metal source types than Marzouk et al. (2013), which focused on a single mining-impacted upland catchment.
The proportion of metal in labile form in a given soil is a complex function of factors including contamination history, soil chemistry and mineralogy and metal properties. Factors suggested to influence rates of fixation of labile metal to non-labile forms include the ionic radius (Degryse et al. 2009), solid-phase diffusion into metal (hydr)oxides (Bruemmer et al. 1988; Trivedi and Axe 2001) or carbonates (Hamon et al. 2002; Buekers et al. 2007), surface precipitation (Ma et al. 2006), substitution into iron (oxy)hydroxides (Manceau et al. 2000) or fixation into natural organic matter (Mao et al. 2015). Processes may be metal-specific, such as the formation of surface precipitates, or they may be favoured by intrinsic metal properties, such as the role of ionic radius in substitution reactions (Xu et al. 2006), which favours metals having smaller ionic radii (Ni, Cu, Zn) over those with larger radii (Cd, Pb). Thus, it is not surprising, and highly consistent with previous research, to see both high variation in the labile proportions of individual metals and patterns in the degree of mean lability.
Our results suggest that in general the 0.05 mol L−1 EDTA extraction is a reasonable analogue for isotopically labile metal, although we can see systematic differences between determinations as a function of pH. These differences may arise due to the ability of EDTA to promote ligand-induced dissolution of soil solid phases such as metal oxides and carbonates (Izquierdo et al. 2013). Other researchers have found somewhat different results. Izquierdo et al. (2013) performed isotopic lability measurements and 0.05 mol L−1 EDTA extractions for Zn, Cd and Pb on floodplain soils of central England, and found a concentration-dependent relationship between {Pb}EDTA and {Pb}E, with the majority of their soils having EDTA-extractable Pb three to four times higher than the isotopically determined labile Pb. We do not see such a relationship in this work. This is likely due to the broader range of soil types used, which causes any concentration relationship to be swamped by the relationship with pH (Fig. 2). Marzouk et al. (2013) compared isotopic lability and chemical extractability of Zn, Cd and Pb for soils of a mining-impacted catchment in Northern England. They found that while there was reasonable correspondence between isotopically labile metal and metal extracted by 0.05 mol L−1 EDTA or 0.43 mol L−1 HNO3 in acidic organic soils, the extractions overestimated the isotopically labile pool in circumneutral and alkaline soils. Similarly, Garforth et al. (2016) found that extraction with 0.05 mol L−1 EDTA provided the best agreement with isotopically labile pools of Ni, Cu, Zn, Cd and Pb in four UK soils, compared with 0.43 mol L−1 HNO3, 0.43 mol L−1 acetic acid and 1 mol L−1 CaCl2.
The prediction of metal solubilities by WHAM/Model VII clearly demonstrates that the use of total metal as a speciation model input for prediction of metal solubility is inferior to the use of a measure of labile or ‘geochemically active’ metal. This provides further confirmation of a result already observed by a number of authors (Izquierdo et al. 2013; Marzouk et al. 2013). It also demonstrates that although good predictions of metal solubility are obtained using 0.05 mol L−1 EDTA-extracted metal as the model input (RSD < 1 for all the metals), the use of isotopically labile metal as input consistently provides predictions that are at least as good, and usually better, than those obtained using EDTA. This is in agreement with the results previously found by Izquierdo et al. (2013) for Zn and Cd in a more restricted set of soils, although these authors did find a lower MBE and similar RSD for Pb when using 0.05 mol L−1 EDTA. In contrast, we obtained a notable improvement in MBE from 0.40 when using EDTA-extracted Pb, to 0.13 when using isotopically labile Pb. This contrast may well be due to the better agreement between {Pb}EDTA and {Pb}E in soils where pHCa < 5.0. In soils in this study with pHCa < 5.0 (n = 26) the mean absolute difference in predicted pPb between the two methods of estimating labile metal was 0.0056, whereas for soils of pHCa > 5.0 it was 0.39.
Comparing the goodness-of-prediction values obtained from the speciation modelling (using {M}E as input) to those obtained in previous similar studies may be useful in providing clues as to the causes of model error. The most similar previous study to this one is that of Mao et al. (2017), conducted on urban soils. The RSD values obtained in this study were similar to those of Mao et al. (2017) for Ni, superior for Zn and Cd but inferior for Cu and Pb. Conversely, in comparison to Marzouk et al. (2013) this study shows a superior prediction for Pb but inferior predictions for Zn and Cd, while for Izquierdo et al. (2013) this study is superior for Zn and Cd but inferior for Pb. So there is little apparent consistency in the RSD values, which possibly indicates that the RSD is dependent on the nature of the soils within each separate dataset.
Patterns in the mean bias error (MBE) across studies may be indicative of inaccurate formulation of model assumptions, or bias in one or more supporting measurements. In this study we observed a consistent positive MBE for all metals, indicating overestimation of metal solubility on average. The same pattern was observed by Mao et al. (2017), with the exception of Pb, and by Izquierdo et al. (2013) for Zn, Cd and Pb. Marzouk et al. (2013) also observed this pattern for Cd and Pb but found a small overestimation of Zn solubility on average. There is thus a reasonably consistent pattern across studies, most notably between this study and that of Mao et al. (2017). We investigated the possibility of systematic model bias by performing additional WHAM/Model VII simulations with the soil HA concentration set to 50% of LOI, after Marzouk et al. (2013). The results show that the model outcomes are somewhat sensitive to the concentration of HA (and FA) representing SOM, and that setting HA and FA to measured concentrations tends to underestimate solid phase binding for Ni, Cu, Zn and Cd. The reasons for this warrant further examination. A possibility is that the base extraction method used for the determination of soil HA and FA might be underestimating the amount of ‘active’ HS, possibly because the extraction is not efficient enough to remove the humics from the soil matrix in a single step. Alternatively, there may be components of the SOM active in metal binding that are not extractable using base. Izquierdo et al. (2013) suggested that overestimation may be due to a proportion of the soil metal being adsorbed to soil carbonates, a process not considered in WHAM/Model VII. This was because the soils they worked with were sourced from a limestone-based catchment. However, metal adsorption to carbonate surfaces is unlikely to be important for many of the soils in the current study given their provenance. Interestingly, the apparent underestimation of the ‘activity’ of particulate organic matter was also seen by Lofts and Tipping (1998), when using base extraction to estimate the HS content of riverine suspended sediment for modelling using WHAM/Model V.
The influence of DOM activity on the predictions was generally more metal-dependent than the influence of SOM activity. The influence was broadly related to the strength of metal–DOM binding, with the relatively weakly DOM-binding metals (Ni, Zn and Cd) being less sensitive to varying the DOM activity than the relatively strongly binding Cu and Pb. The use of a single value of ‘DOM activity’ to estimate concentrations of ‘active’ FA for modelling is a clear simplification. Previous research (Amery et al. 2008; Djae et al. 2017; Ouédraogo et al. 2022) has shown that fitting the DOM activity on an individual soil basis results in a broad range of activities (as low as 10% and as high as 215% in the cited studies, compared to the range of 32.5–130% used for sensitivity testing in this work). Currently, no single approach to estimating DOM activity, based on ancillary quantifications of DOM quality such as fluorescence indices or specific UV absorbance at 254 nm (SUVA254), appears to be appropriate for estimating activity. For example, Amery et al. (2008) found that SUVA254 variations could improve the prediction of DOM-bound Cu in soil solutions, but Ouédraogo et al. (2022) could not improve the prediction of free copper using either SUVA254 or fluorescence indices.
An important element of studies such as ours is the choice of the binding surface assemblage to be used in simulation of the solid phase. Other researchers (Bonten et al. 2008; Dijkstra et al. 2009) have used alternative assemblages including clay and aluminium oxide, which we have not used here. Their use of aluminium oxide was limited by lack of data to the assumption of identical binding parameters as for iron oxide. The results suggested that clay might be important for Zn and Cd binding in soils of particularly high clay content, but it is not possible to tease out the possible importance of aluminium oxide from their results. Nevertheless, the choice of solid phase assemblage components remains key to studies of trace element solubility in soil. A standard approach to soil characterisation for solubility modelling would be a way forward here, allowing a higher degree of data interoperability across studies and thus of model application and comparison. Key here is the fact that other trace elements, particularly those that occur as anions, may have different preferences for binding surfaces to the metals studied here.
Compared to the other metals, predictions of Pb solubility resulted in the highest RSD value (Table 6). These results are in contrast to those of Izquierdo et al. (2013) who reported that accuracy of predictions decreased in the order Pb > Zn > Cd. However, weaker predictions of Pb solubility compared to Zn and Cd have previously been reported by Marzouk et al. (2013). They suggested that this may be due to Pb binding in the solid phase being more distributed between organic matter and Fe and Mn oxides, compared to Zn and Cd which were predominantly adsorbed to organic matter (Supplementary Fig. S7). The predictions of Pb solubility are therefore sensitive to uncertainties in a greater number of measurements than the other metals, which may well explain the greater scatter seen in the WHAM/Model VII predictions.
The POSSMs model is intended to provide a means of computing a simplified soil metal speciation with practical minimum input requirements. Therefore, in contrast to WHAM, there is relatively little scope for the application of different assumptions regarding factors such as SOM and DOM activities. The parameter sets used by the model were derived by Lofts (2022) from datasets of British and Dutch soils. The labile metal in the British soils was estimated by extraction with 0.1 mol L−1 EDTA, and in the Dutch soils by extraction with 2 mol L−1 HNO3. The solution phase was obtained by extraction of porewater following soil incubation; thus the soil/solution ratios were far higher (up to approximately two orders of magnitude) than the ratios employed in this work. The porewater pH range was 3.35–8.28, the SOM range was 0.004–0.98 g g−1 and the DOM range was 0.0106–0.942 g L−1. The pH and DOM ranges of the dataset used in this study extend slightly below those of the training dataset (3.08 and 0.0069 g L−1 respectively) but the SOM range is within that of the training dataset. The range of land use is narrower in the training dataset, comprising semi-natural UK soils and Dutch soils from an agricultural field experiment.
Overall, the results show that POSSMs provides a useful and plausible alternative approach for modelling metal solubility compared to the more complex and data-intensive WHAM/Model VII and similar models. It may provide a useful alternative approach for situations where the data required for more complex models are not available, for example when there is a need to model solubility using large scale soil geochemical datasets. Although the dataset produced in this study covered a similar range of soil conditions to the POSSMs parameterisation dataset, the parameterisation dataset used reactive metal concentrations obtained by extraction, as opposed to E-values. In this context, the quality of the predictions obtained here when using {M}E is encouraging, as are the small differences in predictions obtained when using either {M}EDTA or the E-value as input. The systematic bias in the predictions seen for some metals suggests that broader testing and ultimately reparameterisation of the model to the largest possible dataset is desirable. Parameterisation to data containing metal E-values is desirable, however, the results found here suggest that it may have little influence on predictions with the possible exception of Pb.
Conclusions
We applied two geochemical speciation models, WHAM/Model VII and POSSMs, to model the solubility of Ni, Cu, Zn, Cd and Pb in a broad range of soils from the UK, using {M}total, {M}EDTA and {M}E to represent the labile pool of metal controlling solubility.
In agreement with previous work, representing the labile metal by the total measured pool resulted in overestimation of metal solubility on average.
Estimation of labile soil metal by EDTA extraction provided concentrations largely comparable to the isotopically exchangeable pool, although some systematic deviations were observed, particularly for Pb.
Both EDTA-extracted and isotopically exchangeable metal pools provided reasonable predictions of metal solubility using WHAM/Model VII with measured concentrations of soil humic substances. Predictions were generally improved by applying the assumption that soil organic matter comprised 50% humic acid. This suggests that further testing of the method for estimating soil humic substance concentrations may be warranted.
The relatively simple POSSMs model provided predictions comparable to WHAM/Model VII, further indicating its potential usefulness for large scale application.
Quantification of the variability in the ‘activity’ of the dissolved organic matter in the solution phase may further improve the predictive capabilities of the models.
Supplementary material
Details of the datasets and a range of additional figures are provided in the Supplementary material online.
Data availability
The data used in this study may be obtained by emailing Stephen Lofts (stlo@ceh.ac.uk).
Acknowledgements
The authors dedicate this paper to Professor Edward Tipping with grateful thanks for his major scientific contributions to the field of soil metal chemistry modelling, and for his generous and continuing advice, mentorship, scientific collaboration and friendship over many years. They also thank three anonymous reviewers for their constructive and useful comments on the initial version of the manuscript.
References
Ahnstrom ZAS, Parker DR (2001) Cadmium reactivity in metal-contaminated soils using a coupled stable isotope dilution-sequential extraction procedure. Environmental Science & Technology 35, 121-126.
| Crossref | Google Scholar | PubMed |
Almås ÅR, Lofts S, Mulder J, Tipping E (2007) Solubility of major cations and Cu, Zn and Cd in soil extracts of some contaminated agricultural soils near a zinc smelter in Norway: modelling with a multisurface extension of WHAM. European Journal of Soil Science 58, 1074-1086.
| Crossref | Google Scholar |
Amery F, Degryse F, Cheyns K, De Troyer I, Mertens J, Merckx R, Smolders E (2008) The UV-absorbance of dissolved organic matter predicts the fivefold variation in its affinity for mobilizing Cu in an agricultural soil horizon. European Journal of Soil Science 59, 1087-1095.
| Crossref | Google Scholar |
Atkinson NR (2010) Heavy metal geochemistry of contaminated fenland soils in NW England. PhD Thesis, University of Nottingham, Nottingham, England. Available at https://eprints.nottingham.ac.uk/id/eprint/27795
Atkinson NR, Bailey EH, Tye AM, Breward N, Young SD (2011) Fractionation of lead in soil by isotopic dilution and sequential extraction. Environmental Chemistry 8, 493-500.
| Crossref | Google Scholar |
Ayoub AS, McGaw BA, Shand CA, Midwood AJ (2003) Phytoavailability of Cd and Zn in soil estimated by stable isotope exchange and chemical extraction. Plant and Soil 252, 291-300.
| Crossref | Google Scholar |
Bonten LTC, Groenenberg JE, Weng L, van Riemsdijk WH (2008) Use of speciation and complexation models to estimate heavy metal sorption in soils. Geoderma 146, 303-310.
| Crossref | Google Scholar |
Bruemmer GW, Gerth J, Tiller KG (1988) Reaction kinetics of the adsorption and desorption of nickel, zinc and cadmium by goethite: I. Adsorption and diffusion of metals. Journal of Soil Science 39, 37-52.
| Crossref | Google Scholar |
Buekers J, Van Laer L, Amery F, Van Buggenhout S, Maes A, Smolders E (2007) Role of soil constituents in fixation of soluble Zn, Cu, Ni and Cd added to soils. European Journal of Soil Science 58, 1514-1524.
| Crossref | Google Scholar |
Buekers J, Degryse F, Maes A, Smolders E (2008) Modelling the effects of ageing on Cd, Zn, Ni and Cu solubility in soils using an assemblage model. European Journal of Soil Science 59, 1160-1170.
| Crossref | Google Scholar |
Degryse F, Buekers J, Smolders E (2004) Radio-labile cadmium and zinc in soils as affected by pH and source of contamination. European Journal of Soil Science 55, 113-122.
| Crossref | Google Scholar |
Degryse F, Smolders E, Parker DR (2009) Partitioning of metals (Cd, Co, Cu, Ni, Pb, Zn) in soils: concepts, methodologies, prediction and applications – a review. European Journal of Soil Science 60, 590-612.
| Crossref | Google Scholar |
Dijkstra JJ, Meeussen JCL, Comans RN (2004) Leaching of heavy metals from contaminated soils: an experimental and modeling study. Environmental Science & Technology 38, 4390-4395.
| Crossref | Google Scholar | PubMed |
Dijkstra JJ, Meeussen JCL, Comans RNJ (2009) Evaluation of a Generic Multisurface Sorption Model for Inorganic Soil Contaminants. Environmental Science & Technology 43, 6196-6201.
| Crossref | Google Scholar |
Djae T, Bravin MN, Garnier C, Doelsch E (2017) Parameterizing the binding properties of dissolved organic matter with default values skews the prediction of copper solution speciation and ecotoxicity in soil. Environmental Toxicology and Chemistry 36, 898-905.
| Crossref | Google Scholar | PubMed |
Gäbler HE, Bahr A, Heidkamp A, Utermann J (2007) Enriched stable isotopes for determining the isotopically exchangeable element content in soils. European Journal of Soil Science 58, 746-757.
| Crossref | Google Scholar |
Garforth JM, Bailey EH, Tye AM, Young SD, Lofts S (2016) Using isotopic dilution to assess chemical extraction of labile Ni, Cu, Zn, Cd and Pb in soils. Chemosphere 155, 534-541.
| Crossref | Google Scholar | PubMed |
Groenenberg JE, Dijkstra JJ, Bonten LTC, de Vries W, Comans ENJ (2012) Evaluation of the performance and limitations of empirical partition–relations and process–based multisurface models to predict trace element solubility in soils. Environmental Pollution 166, 98-107.
| Crossref | Google Scholar | PubMed |
Gustafsson JP (2001) Modeling the acid–base properties and metal complexation of humic substances with the Stockholm Humic Model. Journal of Colloid and Interface Science 244, 102112.
| Crossref | Google Scholar |
Hamon RE, McLaughlin MJ, Cozens G (2002) Mechanisms of attenuation of metal availability in in situ remediation treatments. Environmental Science & Technology 36, 3991-3996.
| Crossref | Google Scholar | PubMed |
Izquierdo M, Tye AM, Chenery SR (2013) Lability, solubility and speciation of Cd, Pb and Zn in alluvial soils of the River Trent catchment UK. Environmental Science: Processes & Impacts 15, 1844-1858.
| Crossref | Google Scholar | PubMed |
Kinniburgh DG, Milne CJ, Benedetti MF, Pinheiro JP, Filius J, Koopal LK, Vanriemsdijk WH (1996) Metal ion binding by humic acid: application of the NICA-Donnan model. Environmental Science & Technology 30, 1687-1698.
| Crossref | Google Scholar |
Lofts S (2022) POSSMs: a parsimonious speciation model for metals in soils. Environmental Chemistry 18, 335-351.
| Crossref | Google Scholar |
Lofts S, Tipping E (1998) An assemblage model for cation binding by natural particulate matter. Geochimica et Cosmochimica Acta 62, 2609-2625.
| Crossref | Google Scholar |
Ma Y, Lombi E, Nolan AL, McLaughlin MJ (2006) Short-term natural attenuation of copper in soils: effects of time, temperature, and soil characteristics. Environmental Toxicology and Chemistry 25, 652-658.
| Crossref | Google Scholar | PubMed |
Manceau A, Schlegel ML, Musso M, Sole VA, Gauthier C, Petit PE, Trolard F (2000) Crystal chemistry of trace elements in natural and synthetic goethite. Geochimica et Cosmochimica Acta 64, 3643-3661.
| Crossref | Google Scholar |
Mao LC, Young SD, Bailey EH (2015) Lability of copper bound to humic acid. Chemosphere 131, 201-208.
| Crossref | Google Scholar | PubMed |
Mao LC, Young SD, Tye AM, Bailey EH (2017) Predicting trace metal solubility and fractionation in Urban soils from isotopic exchangeability. Environmental Pollution 231, 1529-1542.
| Crossref | Google Scholar | PubMed |
Marzouk ER, Chenery SR, Young SD (2013) Measuring reactive metal in soil: a comparison of multi-element isotopic dilution and chemical extraction. European Journal of Soil Science 64, 526-536.
| Crossref | Google Scholar |
Meeussen JCL (2003) ORCHESTRA: An object-oriented framework for implementing chemical equilibrium models. Environmental Science & Technology 37, 1175-1182.
| Crossref | Google Scholar | PubMed |
Nolan AL, Ma YB, Lombi E, McLaughlin MJ (2004) Measurement of labile Cu in soil using stable isotope dilution and isotope ratio analysis by ICP-MS. Analytical and Bioanalytical Chemistry 380, 789-797.
| Crossref | Google Scholar | PubMed |
Ouédraogo F, Cornu J-Y, Janot N, Nguyen C, Sourzac M, Parlanti E, Denaix L (2022) Do DOM optical parameters improve the prediction of copper availability in vineyard soils? Environmental Science and Pollution Research 29, 29268-29284.
| Crossref | Google Scholar | PubMed |
Quevauviller P (1998) Operationally defined extraction procedures for soil and sediment analysis I. Standardization. Trends in Analytical Chemistry 17, 289-298.
| Crossref | Google Scholar |
Schröder TJ, Hiemstra T, Vink JPM, van der Zee SEATM (2005) Modeling of the solid-solution partitioning of heavy metals and arsenic in embanked flood plain soils of the rivers Rhine and Meuse. Environmental Science & Technology 39, 7176-7184.
| Crossref | Google Scholar | PubMed |
Sterckeman T, Carignan J, Srayeddin I, Baize D, Cloquet C (2009) Availability of soil cadmium using stable and radioactive isotope dilution. Geoderma 153, 372-378.
| Crossref | Google Scholar |
Thornton I, Farago ME, Thums CR, Parrish RR, McGill RAR, Breward N, Fortey NJ, Simpson P, Young SD, Tye AM, Crout NMJ, Hough RL, Watt J (2008) Urban geochemistry: research strategies to assist risk assessment and remediation of brownfield sites in urban areas. Environmental Geochemistry and Health 30, 565-576.
| Crossref | Google Scholar | PubMed |
Tipping E (1998) Humic Ion-Binding Model VI: an improved description of the interactions of protons and metal ions with humic substances. Aquatic Geochemistry 4, 3-47.
| Crossref | Google Scholar |
Tipping E, Hurley MA (1992) A unifying model of cation binding by humic substances. Geochimica et Cosmochimica Acta 56, 3627-3641.
| Crossref | Google Scholar |
Tipping E, Rieuwerts J, Pan G, Ashmore MR, Lofts S, Hill MTR, Farago ME, Thornton I (2003) The solid-solution partitioning of heavy metals (Cu, Zn, Cd, Pb) in upland soils of England and Wales. Environmental Pollution 125, 213-225.
| Crossref | Google Scholar | PubMed |
Tipping E, Lofts S, Sonke JE (2011) Humic Ion-Binding Model VII: a revised parameterisation of cation binding by humic substances. Environmental Chemistry 8, 225-235.
| Crossref | Google Scholar |
Trivedi P, Axe L (2001) Predicting divalent metal sorption to hydrous Al, Fe, and Mn oxides. Environmental Science & Technology 35, 1779-1784.
| Crossref | Google Scholar | PubMed |
Tye AM, Young SD, Crout NMJ, Zhang H, Preston S, Barbosa–Jefferson VL, Davison W, McGrath SP, Paton GI, Kilham K, Resende L (2003) Predicting the activity of Cd2+ and Zn2+ in soil pore water from the radio-labile metal fraction. Geochimica et Cosmochimica Acta 67, 375-385.
| Crossref | Google Scholar |
Weng LP, Temminghoff EJM, van Riemsdijk WH (2001) Contribution of individual sorbents to the control of heavy metal activity in sandy soil. Environmental Science & Technology 35, 4436-4443.
| Crossref | Google Scholar | PubMed |
Weng LP, Temminghoff EJM, Lofts S, Tipping E, van Riemsdijk WH (2002a) Complexation with dissolved organic matter and solubility control of heavy metals in a sandy soil. Environmental Science & Technology 36, 4804-4810.
| Crossref | Google Scholar |
Weng LP, Fest EPMJ, Filus J, Temminghoff EJM, van Riemsdijk WH (2002b) Transport of humic and fulvic acids in relation to metal mobility in a copper-contaminated acid sandy soil. Environmental Science & Technology 36, 1699-1704.
| Crossref | Google Scholar |
Xu Y, Boonfueng T, Axe L, Maeng S, Tyson T (2006) Surface complexation of Pb(II) on amorphous iron oxide and manganese oxide: spectroscopic and time studies. Journal of Colloid and Interface Science 299, 28-40.
| Crossref | Google Scholar | PubMed |


