POSSMs: a parsimonious speciation model for metals in soils
Stephen Lofts A *
A *
A UK Centre for Ecology and Hydrology, Lancaster Environment Centre, Lancaster, LA1 4AP, UK.
Environmental Chemistry 18(8) 335-351 https://doi.org/10.1071/EN21100
Submitted: 21 July 2021 Accepted: 18 November 2021 Published: 22 February 2022
© 2021 The Author(s) (or their employer(s)). Published by CSIRO Publishing. This is an open access article distributed under the Creative Commons Attribution 4.0 International License (CC BY)
Environmental context. Predicting the chemistry of metals is important for understanding their movement and impacts in the environment. Metal chemistry models are generally complex and difficult to apply, but a simpler model, which does not need large amounts of input data, can also provide good results. A simpler model can be more easily included in large-scale models of metal transport and impacts in the environment.
Abstract. Mechanistic geochemical models are useful for detailed study of the speciation of metals in well-characterised soils, but can be challenging to apply when driving soil compositional data are sparse, for example, at large scales. Empirical models, using minimal driving data, have been developed either for prediction of solid–solution partitioning or for the computation of the free metal ion from the total or geochemically active metal. This work presents an empirical speciation model, POSSMs (ParsimOniouS Speciation of Metals in soils), which predicts the free, solution-bound and sorbed metal in a soil in a single calculation, using a minimal set of soil parameters. The model has been parameterised for Ni, Cu, Zn, Cd and Pb using datasets of geochemically active soil metal and solution phase composition. The parameterised model can also be used to compute the free metal ion from the solution metal. The model was tested by applying it to literature datasets on the speciation of metals in soil solutions and extracts, and on the metal solid–solution partitioning. The performance of the model was comparable to other empirical models of similar complexity. Some test datasets produced biased predictions, particularly in the underestimation of measured free ion at circumneutral and alkaline pH, where the model predicted low free ion concentrations. The model is not a replacement for mechanistic geochemical models, but is a useful tool for soil metal speciation where comprehensive driving data are not available.
Keywords: chemical speciation, dissolve dorganic matter, free metal ion, modelling, partition coefficient, pH, soil organic matter, soils, trace metals.
Introduction
Modelling of the equilibrium speciation of metals is a well-established approach in a range of research areas related to their environmental behaviour, such as their transport in soils and aquifers (Bonten et al. 2011; Bea et al. 2013), and their environmental bioavailability and toxicity (Crawford et al. 2017; Fornaroli et al. 2018). Speciation modelling may be used to predict metal forms in a solution alone or in a system also containing sorbing solid phases. The latter approach is useful to predict metal solubility in soils and so may be linked to modelling of metal transport and losses to deeper soil and/or surface waters.
Mechanistic speciation modelling has the advantage of technical defensibility and, in principle, a broad range of applications, but at the costs of complexity, driving data requirements and model execution time. The issues of driving data and execution time become particularly onerous when an intensive model application is required. This may occur, for example, in large-scale application or where assessment of uncertainty and sensitivity is required using Monte Carlo techniques. There has thus been considerable interest in the development of simpler models that emulate the predictions of mechanistic models. Empirical approaches have been employed, for example, to derive relationships between the sorbed metal and the free ion in soil solution (Tipping et al. 2003; Groenenberg et al. 2010a) or to predict the dissolved metal in the solution phase from the sorbed concentration (Groenenberg et al. 2012). Such approaches have been applied in dynamic modelling of metals in soils (Lofts et al. 2013). The use of the current empirical models does have limitations, most notably that they are limited to predicting the concentration of one species or form of metal (e.g. free ion, solution metal) from another (e.g. sorbed metal). Combined application of separate solubility and free ion models is technically feasible but there is a risk of inconsistency in the outcomes if the parameterisations are independent of each other. Thus, a modelling approach combining minimal data requirements and the prediction of both the free ion and solubility in a single computation would be a useful addition to existing approaches. The simultaneous computation of the free ion and the soluble concentration would make a model potentially suitable for combined assessment of metal solubility and bioavailability.
This study outlines the development of a metal speciation framework for soils (POSSMs – ParsimOniouS Speciation of Metals in soils) that extends the empirical approach of Tipping et al. (2003) and Groenenberg et al. (2010a) for metal binding to solution phase ligands as well as sorption to the soil solid phase. The model can also be used to compute the free ion and bound metal in the solution phase only. The model is calibrated for Ni, Cu, Zn, Cd and Pb using existing datasets of soil and solution phase composition, and its performance is evaluated against literature datasets of soil–solution partitioning and solution phase speciation.
Experimental
Model structure
Table 1 provides a glossary of terms used in equations, including their units, and the reader is referred to this table for an explanation of the terms used within the text.

|
We take the calculation framework of a mechanistic equilibrium model as a starting point and construct expressions for the concentrations of solution-bound and sorbed forms of metal as functions of the free metal ion. The model is applied by supplying a ‘geochemically active’ concentration of metal, which comprises the sum of three forms (groups of metal species):
metal present in its free ionic form, i.e. not bound to any ligand in solution or to the solid phase. This metal is termed ‘free’;
metal bound to ligands in the solution, whether specifically bound (complexed) or electrostatically associated. This metal is termed ‘solution-bound’;
metal bound to solid phase ligands, either specifically or electrostatically. This metal is termed ‘sorbed’.
The concentrations of metal in each form are computed by iterative adjustment of the free ion concentration until the sum of the three computed forms equals the supplied ‘geochemically active’ concentration. The modelling initially took the approach of subdividing the water in the system into the water electrostatically held by the soil solids, the water held electrostatically by organic matter dissolved in the solution phase and the water not electrostatically held (the true solution). This approach mimics that taken by mechanistic models such as WHAM, although unlike such models, the bound metal is not subdivided into that bound by bond formation with organic molecules and that within the electrostatically held water. The concentration of the free ion is defined as the moles of free ion per litre of the true solution, and the concentration of solution-bound metal is defined as the moles of solution-bound metal per litre of the aqueous phase. The mass balance of metal in the system is given by
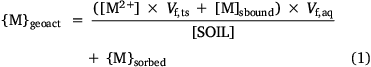
where Vf,ts is the volume of true solution per unit volume of the aqueous phase in the system and Vf,aq is the volume of water in the aqueous phase (not held electrostatically by the solid phase) per unit volume of total water in the system. The electrostatically held water in both the solid and solution phases is assumed to be held by organic matter, and the volumes vD,solution and vD,solid thus have units of L (g OM)−1. Initial model fitting and adjustment of vD,solution and vD,solid showed that their presence and variation exerted negligible influence on the model predictions, and so a simplified mass balance was adopted:
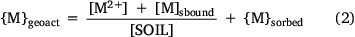
The concentrations of solution-bound and sorbed metal are given by
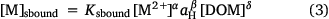
and
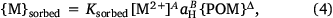
where Ksbound, α, β, δ and Ksorbed, A, B, Δ are fitting parameters. The form of Eqn 4 is similar to the C–Q relationship of Groenenberg et al. (2010a), but here a non-logarithmic form of the expression is used. The pH dependence of binding is computed as a function of proton activity rather than pH, so the sign of the coefficient B is the opposite of that of the pH coefficient in the C–Q relationship. In fitting, the coefficients α and A are constrained to be less than or equal to unity. This provides relationships between the solution-bound or sorbed metal and the free ion that are in accordance with the binding behaviour of metals to heterogeneous complexants, i.e. that the incremental strength of complexation decreases with increasing loading of the complexant.
Preliminary modelling of the solution speciation using WHAM7 (Lofts and Tipping 2011; Tipping et al. 2011) (see Section Calibration dataset and modelling approach for details) suggested that with the exception of Pb, binding to DOM was a dominant mechanism across the full range of pH. In the case of Pb, precipitated iron(III) oxyhydroxide (FeOx) was predicted to largely be the main binding phase above pH 7 (data not shown). Therefore, to investigate the possible importance of FeOx as a variable in the solution speciation of Pb, Eqn 3 was extended to include solution phase Fe as a variable:
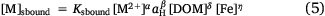
with [Fe] being the Fe concentration in solution (mol (L aqueous phase)−1).
The model was applied by supplying values of {M}geoact, [SOIL], aH, [DOM] and {POM}. Speciation was computed by iterative estimation of [M2+], computation of [M]sbound and {M}sorbed using Eqns 3 and 4, respectively, then computation of {M}geoact according to Eqn 1, until the computed value matched the supplied value within tolerance limits. Iterative improvement of the estimate of [M2+] was done using the one-dimensional Newton–Raphson approach. The dissolved metal concentration in the solution phase (i.e. the porewater or an aqueous extraction of the soil), [M]diss, was the sum [M2+] + [M]sbound.
A truncated version of the model may be used to compute the solution phase free metal ion from the total solution metal. In this case, a modified mass balance is used:
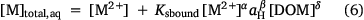
The partition coefficient, Kd (L (kg soil)−1) may also be computed:
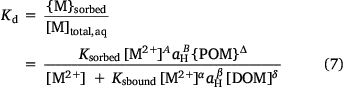
Model parameterisation was done using a bespoke script in R (R Core Team 2019). A version was also implemented as a Microsoft Excel user-defined function. This version, with additional function for data entry, is available from https://www.ceh.ac.uk/services/possms, or by contacting the author.
General dataset considerations
Application of POSSMs, both in calibration and for prediction, requires measurements of the geochemically active soil metal concentration and soil organic matter content, and the solution phase pH and DOM concentration. Geochemically active soil metal may be estimated by a number of methods. The most commonly used methods involve extraction of the soil using either a dilute mineral acid (e.g. 0.43 M nitric acid, Groenenberg et al. 2017) or a dilute solution of a strong metal-binding ligand (e.g. 0.05 M EDTA, Quevauviller 1998) to remove metal reversibly sorbed to the soil surface, either by providing a high concentration of an ion that competes with the metal for surface binding (H+ in the case of mineral acids) or a solution ligand that outcompetes the surface binding sites for metal. In practice, researchers have used a range of acid and/or strong ligand concentrations for estimation of the geochemically active metal. Pragmatically, it is not possible to identify a single ‘best’ extraction because all have potential artefacts that may affect their performance in certain soil types, for example causing dissolution of readily soluble solid phases containing metal. Therefore, in this work, datasets where geochemically active metal has been estimated by room temperature extraction using either dilute mineral acid or EDTA have been accepted for calibration and testing purposes.
The soil organic matter content, {SOM}, is typically measured either by soil loss on ignition or by the difference between total and inorganic C measured using elemental analysis. In the latter case, conversion to organic matter is done by assuming a percentage of carbon content in the organic matter. This work used a carbon content of 50% throughout. Computation of sorbed metal within POSSMs requires the particulate organic matter content of the soil, {POM}. This must be computed from {SOM} by correcting for the organic matter in solution, [DOM]:
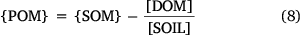
This computation is done automatically in the model.
Calibration dataset and modelling approach
Three calibration datasets from the literature were used: (i) the dataset of Tipping et al. (2003); (ii) the dataset of Shotbolt and Ashmore (2004) and (iii) the datasets of Weng and co-workers (Weng et al. 2001, 2002). These will be referred to as the ‘UK1’, ‘UK2’ and ‘NL’ datasets respectively. Variable ranges within each dataset are shown in Table 2.

|
The UK1 dataset comprises measurements on 98 non-forested upland surface soils (0–5 cm) sampled from five upland areas of England and Wales. The data used comprises: (i) measurements of loss on ignition (LOI) by ashing at 450°C; (ii) estimates of geochemically active Cu, Zn, Cd and Pb by extraction with EDTA (0.1 mol L−1); (iii) measurements of pH, dissolved organic carbon (DOC) and filtered (0.2 µm) metals (Na, Mg, Al, K, Ca, Fe, Cu, Zn, Cd, Pb) in porewaters extracted from soil blocks previously saturated with deionised water to field capacity and incubated for a week prior to porewater extractions using Rhizon™ samplers. Further details of the analysis and sampling are provided by Tipping et al. (2003). The experimental approaches taken provide a dataset that has a reasonable degree of realism and field relevance, with soil:solution ratios that are closer to those expected in the field than those ratios typical of laboratory sorption experiments. The solid : liquid ratios of the saturated soils were calculated by the same method as Tipping et al. (2003).
The UK2 dataset comprises measurements on 56 lowland and forested upland soils, and 23 soils from historic mining sites and nearby uncontaminated locations. Soil solutions were extracted using a method similar to that for the soils of dataset UK1. Solutions were analysed for pH and the concentrations of DOC, Na, Mg, Al, K, Ca, Fe, Cl, NO3 and SO4, and Ni, Cu, Zn, Cd and Pb. Geochemically active Ni, Cu, Zn, Cd and Pb were estimated by soil extraction with 0.1 mol L−1 EDTA. Loss on ignition was measured by the same method as for dataset UK1.
The NL dataset comprises measurements on 32 soil samples taken from a field site near Wageningen, NE Netherlands, comprising plots with pH and Cu input rate adjusted (Weng et al. 2001, 2002). Surface samples (0–20 cm) were taken from eight plots and profiles (eight further samples, down to a depth of 1 m) from three of the plots. Soil organic matter content was estimated by LOI at 550°C and geochemically active metals were estimated using 2 mol L−1 HNO3 extraction. Free metal ion concentrations in the solution phase were measured using the Donnan membrane technique (DMT), using 100 g of air-dried soil and 218 mL of solution (0.002 M Ca(NO3)2), giving a soil concentration of 459 g L−1. The pH and DOC concentrations of the solution phase were measured following equilibration of the solution with the soil. Because of the detection limit of the DMT approach, the free metal ion could not always be quantified. The number of determinations was 24, 20, 32, 21 and 19 for Ni, Cu, Zn, Cd and Pb respectively.
Because free metal ion concentrations were not measured for the UK1 and UK2 datasets, they were estimated by speciation of the porewater using WHAM/Model VII (Tipping et al. 2011). In the UK1 dataset, the concentrations of Cl and SO4 in the porewater were not measured, and so they were estimated by speciation, fixing the charge equivalent ratio of Cl : SO4 to 3 : 1 and adjusting the sum of Cl and SO4 to match the computed and observed pH values. Dissolved organic carbon was assumed to comprise 65% fulvic acid. Porewater Fe was assumed to be FeIII and allowed to form a colloidal oxyhydroxide precipitate (suspended in the porewater) if solubility limits were exceeded, using the parameters given in Lofts and Tipping (2011). The oxyhydroxide was assumed to have a chemically active surface, simulated using the model of Lofts and Tipping (1998). Aluminium was allowed to precipitate as its oxyhydroxide with a standard log solubility product of 8.5 and an enthalpy of −106.9 kJ mol−1.
Sorbed metal concentrations, {M}ads, were computed by correcting {Mgeoact} for the metal in the solution phase:
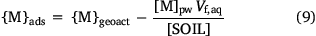
The median percentages of metal in the solution phase were 0.4, 0.3, 0.9, 0.3 and 0.02% for Ni, Cu, Zn, Cd and Pb respectively. The highest percentages of metal in the solution phase were 27, 3.6, 43, 27 and 0.9 respectively, and, with the exception of Pb, were found in acidic (pH < 5), low SOM subsoils of the Netherlands dataset.
Model parameters were optimised by minimising a composite root-mean-squared error term:
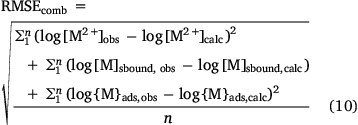
Optimal parameters, including uncertainties, and standard errors of prediction were computed by bootstrapping using bespoke R code. Parameter best estimates were obtained as the medians of estimates derived by model fitting to 2000 sampled datasets. Parameter uncertainties were obtained by taking the 15.9 and 84.1 percentiles of each set of parameter estimates. Standard errors of prediction were obtained using the 0.632 estimator approach (Efron 1983).
Application to literature studies
To test the performance of the model, data on the speciation of Ni, Cu, Zn, Cd and Pb in soils and soil solutions were gathered from the literature. To be included in the testing, a dataset had to provide data allowing testing of (i) soil–solution partitioning and/or the relationship between the sorbed metal and the free ion, or (ii) the relationship between the solution metal concentration and the free ion. For prediction of the full speciation, therefore, measurements of (i) the geochemically active metal, (ii) dissolved and/or free metal activity or concentration in the solution phase, (iii) soil organic matter content and (iv) solution pH and DOC concentration were required. For prediction of the free ion in the solution phase, measurements of (i) solution and free metal activity or concentration and (ii) solution pH and DOC concentration were needed.
The datasets are summarised in Supplementary Table S1. Two datasets (Koopmans et al. 2008; Groenenberg et al. 2010b; DMT3) and Ren et al. (2015a, 2017) (DMT6) allowed full prediction of free, solution and sorbed forms for all the metals. Cancès et al. (2003) (DMT1) allowed full prediction for all metals except Ni, and Pampura et al. (2006) (DMT2, ISE1) allowed full assessment for Cu, using two analytical techniques for the free ion. Duffner et al. (2014) (DMT6) allowed prediction of free Zn2+ and sorbed zinc, but not the solution metal. de Groot et al. (1998) (KD1), Gooddy et al. (1995) (KD2) and Izquierdo et al. (2013) (KD3) allowed assessment of soil–solution partitioning. Twenty five datasets were found allowing prediction of the free metal from the solution phase only, including DMT1, DMT2/ISE1 and DMT3. Of these, five allowed predictions of Ni speciation, all making measurements using DMT. For Cu, 15 datasets allowed predictions, making measurements using DMT. Pampura et al. (2006) additionally measured Cu2+ activity using ISE. Five other datasets included free Cu measurements using ISE. Sixteen datasets had free Zn measurements, nine by DMT, four by cation exchange and one by a combination of anodic stripping voltammetry measurement of voltammetrically labile Zn, coupled with speciation to obtain free Zn (Stephan et al. 2008) (V1). One dataset (Chito et al. 2012) (DMT14, AGNES1) comprised comparative measurements of free Zn by DMT and AGNES. Free Cd was measured in 13 datasets, nine by DMT, three by cation exchange and one by a combination of differential pulse anodic stripping voltammetry and speciation calculations (Sauvé et al. 2000) (V2). Free Pb was measured in ten datasets, nine by DMT and once by anodic stripping voltammetry and speciation calculations (Sauvé et al. 1997) (V3).
The exact form of the quoted free ion measurements (activities or concentrations) in each dataset was obtained from the published experimental description, where explicitly given. The DMT method measures the true solution free ion concentration, and this assumption was made for all DMT datasets unless otherwise stated. Pampura et al. (2006) converted their measured DMT Cu2+ concentrations to activities.
For consistency across the datasets, comparisons of measured and computed free ion were made on the true solution ion concentration. Where free ion activities were quoted in the dataset, they were converted to true solution concentrations by the use of activity coefficient, γM:

This correction was done for ten datasets, each of which required estimation of ionic strength of the solution phase for activity coefficient calculation. For the studies of Sauvé and co-workers on the speciation of Zn, Cd and Pb (Sauvé et al. 1997, 2000; Stephan et al. 2008) and the dataset of Sanders (1982), an ionic strength of 0.01 M was assumed, being the ionic strength of the electrolyte used for soil solution extraction. Nolan et al. (2003) provided solution phase ionic strengths estimated from electrical conductivity. Vulkan et al. (2000) provided electrical conductivity measurements on the solution phase, which were converted to ionic strength using the relationship of Simón and García (1999). In Pampura et al. (2006), ionic strengths were estimated using soil solution compositions. Salam and Helmke (1998) provided solution phase major ion concentrations, which were used to compute ionic strength using WHAM/Model VII (Cl concentrations were not provided and were estimated by forcing a charge balance in WHAM). All activity coefficients were computed using the Davies equation.
Where required, soil concentrations were computed directly from soil masses and solution volumes provided. Where this information was not present, the soil concentration was computed from the soil composition and the % saturation of soil pores (% water holding capacity) (see Supplementary material, default computation of soil concentration).
Results
POSSMs fitting
No significant differences in the model fits for Pb were seen when Eqn 5 was used instead of Eqn 3, i.e. when the solution Fe concentration was included as an additional variable for modelling of solution-bound Pb. Therefore, all modelling of Pb was done using aH and [DOM] only as the variables for solution binding, as for the other metals.
Fig. 1, 2 show the free ion concentrations and partition coefficients resulting from the model parameterisation respectively. Table 3 shows the optimised parameters for each metal, including ranges of uncertainty. Root-mean-squared errors (RMSEs), and the proportions of fitted values within half and one order of magnitude of observations, are shown in Table 4. Generally POSSMs fitted well to the observations, with a majority of fitted values of [M2+]aq, [M]total,aq and Kd consistently predicted to within half an order of magnitude of observation, and almost all fitted values consistently within one order magnitude of observation. Prediction of aqueous phase free ions from the observed solution phase concentrations, in terms of RMSEs, was consistently better than the prediction from the whole soil fitting. The parameters for the relationship between the sorbed metal and the free ion concentration were comparable to those obtained by Groenenberg et al. (2010a) (note that both models include the UK1 data in the training set). Coefficients of pH had absolute values in the range 0.4–0.5 for Ni, Zn and Cd in both models, and for Cu and Pb, the absolute values were approximately unity or greater. For Pb, the coefficient of the Groenenberg model was slightly greater (1.21 versus an absolute value of 1.05 for POSSMs). Coefficients of SOM in POSSMs were higher for all the metals with the exception of Pb, for which the POSSMs coefficient (0.60) was notably lower than the coefficient of Groenenberg et al. (2010a) (1.07). The coefficient of sorbed metal concentration in POSSMs was always predicted to be the maximum allowed value of unity, while Groenenberg et al. (2010a), who allowed the coefficient to take a value above unity, obtained values below unity except for Cd.

|
To evaluate the performance of POSSMs in predicting solution metal and Kd values, the training datasets were fitted to a single equation for metal solubility, where the solution metal was predicted from the sorbed metal and soil properties:
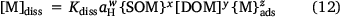
where Kdiss, w, x, y and z are fitting parameters. This expression provides a single, more direct relationship between solution and sorbed metal than POSSMs, and thus provides a benchmark against which to compare POSSMs performance. The differences in the goodness-of-fits for POSSMs and Eqn 12 were marginal (data not shown) with the largest differences in RMSE being 0.02 for solution Ni, and 0.01 for log Kd in Cd.
No comparison with previous modelling was possible for the relationship between predicted free metal ion and solution-bound metal, but an evaluation of the fitted coefficients was possible. The dependence of solution binding on pH (β) increases in the order Cd < Zn < Ni < Cu < Pb, which is a similar order to the pH dependence of sorption (Β). With the exception of Ni, the coefficient for solution binding was smaller than the coefficient for sorption.
Supplementary Fig. S1 compares the free ion concentrations computed by WHAM/Model VII with POSSMs predictions by speciation of the solution only. Standard errors of prediction and numbers of points within half and one order of magnitude are shown in Table 4. Both the standard errors and the number of points within half and one order of magnitude were consistently lower than the corresponding values obtained for prediction of the free ion from the whole soil calibration. This suggested that the calibration approach taken is robust for deriving parameter sets for computation of the free ion from the whole soil or the solution phase.
Application to literature data: (i) whole soil
Fig. 3 compares the observed free ion concentrations with those predicted from whole soil speciation. Generally, the model predicted the majority of observed concentrations to within an order of magnitude. The RMSEs for the individual datasets (Supplementary Table S2) were somewhat variable, particularly for Ni and Pb owing to the presence of a small number of poorly predicted points. The overall RMSEs are shown in Supplementary Table S4. With the exception of Cd, for which values were comparable, these errors were somewhat higher than the standard errors of prediction for the training dataset (Table 4). The overall RMSEs for Ni and Pb were somewhat skewed by outliers (predictions of over two orders of magnitude different to the observation).
Fig. 4 compares observed Kds in whole soil studies with POSSMs predictions. Predictions were generally satisfactory, with over 80% of predictions being within an order of magnitude of observations and over 50% being within half an order of magnitude, for all the metals. No systematic bias between observation and prediction was seen, with the possible exception of copper, for which low Kds (>101 L kg−1) were consistently overestimated by the model, mostly by over an order of magnitude. These points were all derive from dataset KD2 (Gooddy et al. 1995). Supplementary Table S4 provides overall RMSEs. As was the case with the free ion predictions, the RMSEs were rather higher than the standard errors of prediction in the training dataset.
Fig. 5 shows the prediction of average Kds in porewaters sampled from soil of the Elbe floodplain, Germany (Rennert et al. 2017, dataset F1). The model provided a reasonable prediction of the Kds, with the exception of Pb, for which Kds were on average overestimated, with two of the four predictions over an order of magnitude different from observation.

|
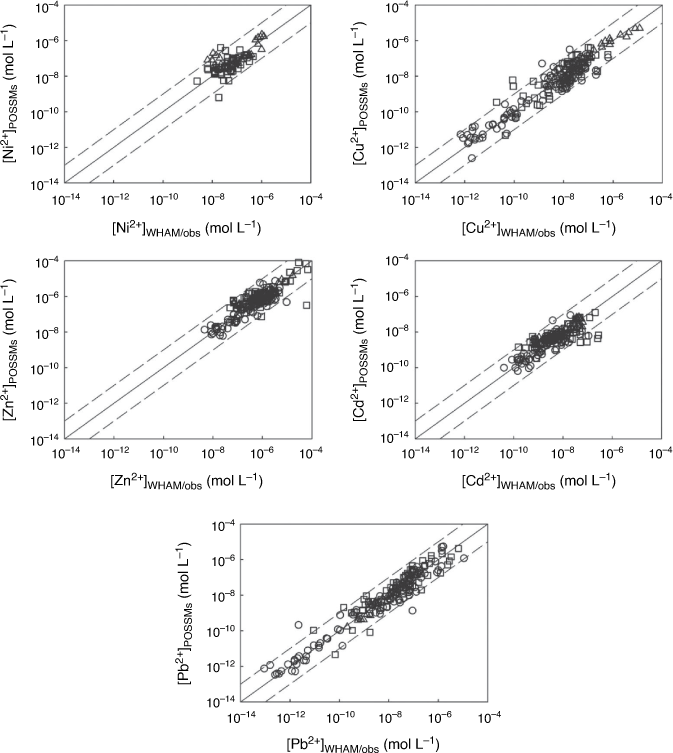
Application to literature data: (ii) dissolved phase
Measured and predicted concentrations of metal free ions, as a proportion of the dissolved metal, are compared in Fig. 6, and RMSEs are shown in Supplementary Table S3. The model largely predicted the observed free ion to within an order of magnitude, although some larger differences were seen, particularly for Cu (66 of 259 observations) and Pb (37 of 147 observations). In the case of Cu, seven predicted values differed by more than three orders of magnitude from observation, while a further nine values differed by over two orders of magnitude. Two predicted Pb2+ concentrations differed from observation by more than three orders of magnitude and ten further predictions differed by more than two orders of magnitude. In all these cases, POSSMs gave a prediction of the free metal ion that was lower than observation. Plotting the ratio of calculated to observed free ion against the pH (Supplementary Fig. S2, S3) showed that underestimation of the free Cu2+ or Pb2+ by two orders of magnitude or more occurred at the upper end of the pH range: pH > 6 for Cu2+ and pH > 7 for Pb2+. Furthermore, the underestimation largely arose from observations in datasets DMT8 (Kim and Owens 2009) and DMT9 (Nolan et al. 2003). These two datasets exerted a strong influence on the prediction RMSEs for Cu and Pb in the DMT studies. Removing the datasets from the computation reduced the overall RMSEs to 0.651 and 0.591 for Cu and Pb respectively. Further inspection of the larger DMT8 dataset showed no strong trend in the measured free Cu and Pb ion as a function of pH, in disagreement with what is known about the competitive effects of pH on metal ion binding to organic matter. Furthermore, Nolan et al. (2003) applied WHAM/Model VI to their data and found similar discrepancies between observations and predictions.
For Ni, Zn and Cd, model predictions were generally close to observations, with some specific exceptions. Free ionic Zn and Cd were underestimated in DMT9, and the voltammetric analyses of Sauvé and co-workers (datasets V1 and V2) were generally overestimated by the model. The reasons why this might be are not clear. The voltammetric approach entails measurement of voltammetrically labile metal and speciation to obtain the free ion on the assumption that the voltammetrically labile metal comprises the free ion and inorganic complexes. Stephan et al. (2008) showed that in fact the voltammetrically labile Zn might comprise relatively weakly organically bound metal also. However, if this were occurring in the soil solutions, it would result in overestimation of the voltammetrically labile metal and free ion, the opposite of what is found. It was also notable that the DOC concentrations in each study differed by approximately an order of magnitude on average, even though the datasets overlapped in terms of site locations and the soil extraction procedure was the same, and that in dataset V1 DOC was directly measured, while in dataset V2 it was estimated using UV absorbance. Differences in soil storage and extent of drying may cause considerable changes in the concentration and metal-binding properties of DOM in soil solutions (Amery et al. 2007). Therefore it is worth considering these results with some caution. It is also notable that the prediction of Pb2+ in dataset V3 was done using DOC taken from dataset V2 and showed scatter but only small bias (RMSE = 0.69, bias in log [M2+] = 0.026).
For all the types of prediction, the influence of extending the model beyond the range of variables in the training dataset was assessed. RMSEs were recomputed after removing predictions for which one or more of the metal concentration, pH, SOM or DOM was outside the ranges in the training datasets (Table 2). The adjusted RMSEs are provided in Supplementary Tables S2–S5. Generally, there was no obvious pattern of increasing or reducing RMSEs once outlying points were discarded. This is likely to result, in part, from the nature of the specific datasets, some of which (e.g. DMT2, ISE1) are of soils known to be contaminated with one or more metals. The clearest difference was seen for Cu Kd prediction, for which the RMSE dropped from 0.83 to 0.46 when outlying data were discarded. This improvement in the fit was largely owing to the removal of most of the KD3 dataset, which largely has very low active soil Cu concentrations (excluding the two highest concentrations, which are from topsoil samples, the mean geochemically active Cu is 2.3 × 10−9 mol g−1, or 0.15 µg g−1). These soils exhibit relatively low Kd values for copper, ranging from 10−1.64 to 101.18, and POSSMs cannot reproduce these values (predicted range 100.86–102.01). Conversely, the RMSEs for Cu free ion and Kd in the DMT2 dataset increased after removal of data lines having geochemically active Cu concentrations above the range in the calibration dataset.
Comparison with other models
Parts of the testing dataset could be speciated using existing models for the prediction of either the free metal ion or solution phase metal concentration. The C–Q model of Groenenberg et al. (2010a) was used to predict free ion concentration from pH, SOM and geochemically active metal concentration, for datasets DMT1–7 and ISE1 (Supplementary Fig. S4). The goodness-of-prediction (RMSE) values were 1.18, 0.96, 0.48, 0.45 and 1.10 for Ni, Cu, Zn, Cd and Pb respectively. For the same datasets, the POSSMs RMSEs were 1.18, 0.64, 0.53, 0.46 and 0.95 respectively. The solubility model of Groenenberg et al. (2012) predicts the solution phase metal concentration from the geochemically active soil metal, pH, solution phase DOC and up to three solid phase parameters (SOM, clay content and the sum of oxalate-extractable soil Al and Fe). It was applied to datasets DMT3, KD1 and KD3, and partly to KD2. For DMT3 and KD1 (Supplementary Fig. S5), the RMSEs in the log of solution metal were 0.53, 0.51, 0.68, 0.73 and 0.54 respectively, while for POSSMs they were 0.59, 0.51, 0.75, 0.78 and 0.56 respectively. For dataset KD2, the solubility model could not be applied for Ni and Zn owing to the requirement for the % clay content of soil, which was not supplied. For Cu, Cd and Pb, predictions were made on the basis of SOM, the sum of oxalate-extractable soil Al and Fe, solution phase pH and DOC (Supplementary Fig. S6). For Cu, the RMSEs were comparable (0.91 for the solubility model and 1.24 for POSSMs), although the performance of both models was relatively poor. For both Cd and Pb, the performance of POSSMs (RMSEs of 0.28 and 0.48 respectively) was superior to that of the solubility model (RMSEs of 0.93 and 1.42) despite the latter using an additional soil property variable compared with POSSMs. For dataset KD3, predictions were possible for Zn, Cd and Pb (Supplementary Fig. S7). The performance of POSSMs was inferior to the solubility model for Zn and Pb (POSSMs RMSEs 0.59 and 0.72, solubility model RMSE 0.36 and 0.59) but was somewhat better for Cd (POSSMs RMSE 0.61, solubility model RMSE 0.79).
Discussion
The POSSMs approach builds closely upon previous empirical models of soil metal chemistry (Tipping et al. 2003; Groenenberg et al. 2010a). The distinctive feature of the model is its ability to predict both the free metal concentration and the solid–solution partitioning of the geochemically active metal, using a minimal data set. Application to literature data suggests that POSSMs is capable of providing estimates of solid–solution partitioning and free ion concentration comparable to those obtained from models that predict these variables singly.
The model provides similar goodness-of-prediction to existing empirical models of metal solubility and speciation, where comparative calculations can be made. The ability to predict the free ion concentrations in the training dataset as a function of the solution metal is a useful test of the robustness and realism of the parameterisation. Because the parameterisation is based largely on predictions of free ion using WHAM/Model VII, this part of the model is largely an emulator of WHAM. Predictions of free ion concentrations in literature datasets were variable across dataset and metal, which likely reflects the technical complexity of the measurement techniques. The large discrepancies observed in some datasets between observed and predicted Cu and Pb, for example, warrant further investigation. More rigorous, systematic investigation of the comparative performance of speciation approaches is needed, particularly under conditions where the free ion is expected to form a small proportion (e.g. <1%) of the solution phase metal. Variability in predictions of Kds may reflect the range of approaches to separating a solution phase from the soil, although, at least in the case of Cu, there are clear issues with extending the model beyond its calibration range. Further, systematic investigation of how Kds may change with separation approach, and of partitioning under extreme conditions of pH, SOM/DOM and geochemically active metal, are needed to better establish a useful working range for POSSMs.
The model requires a concentration of soil solids for computing metal mass balance, a requirement not found in models for predicting the free ion or solubility alone. Within the likely range of soil concentrations relevant for field application, the model predictions are not greatly sensitive to soil concentration (Supplementary Fig. S8). It is notable that although a range of soil concentrations are present in the fitting and testing datasets (Supplementary material, summaries of literature datasets), there is no indication that this influences the model goodness-of-fit nor the predictive capabilities. In the absence of information on the moisture content of a field soil, a reasonable prediction of soil concentration can be made using a plausible moisture content as a percent pore saturation, for example by applying the approach set out in the Supplementary material (computation of soil concentration).
The POSSMs model is not intended to be a replacement for mechanistic geochemical speciation modelling, which can be a powerful tool in aiding understanding of the mechanisms driving speciation, such as the importance of different solid phases in sorption. Because it is designed for application to field situations, it has been parameterised using data from soils not spiked with metal salts. As such spiking induces chemical changes, such as increased ionic strength in the solution phase, applying POSSMs to such soils should be done with caution. Neither does the model allow for the control of metal speciation by solid phase dissolution–precipitation equilibria, so its application to soils where such controls occur is not recommended at present.
POSSMs is intended, as far as possible, to be a general model of soil metal chemistry applicable to a wide range of soils. The calibration datasets used do emphasise acidic and organic matter-rich soils (Supplementary Fig. S9). Acidic low organic matter soils and circumneutral high organic matter soils are also represented, but there are relatively few soils with both pH > 6 and {SOM} > 0.05 g (g soil)−1. It is therefore to be expected that using the parameterisation derived here, the model is most suitable for acidic, organic-rich soils and least suitable for circumneutral, organic-poor soils. It is in this range of soil compositions that other phases such as mineral oxides may become important for binding metals. The potential importance of other phases as model variables is clear from both mechanistic and empirical modelling, particularly at higher pH values. For example, Duffner et al. (2014) modelled Zn soil binding mechanistically and suggested that although organic matter was the main sorbent, iron oxides (goethite and hydrous ferric oxide) and clay were non-negligible contributors. Groenenberg et al. (2012) empirically modelled soil–solution partitioning of metals including clay and the sum of oxalate-extractable Al and Fe as explanatory variables (the latter acting as a surrogate for amorphous Al and FeIII oxides). They found that clay content was a significant variable for Ni and Zn partitioning, and the oxalate-extractable Al and Fe to be significant for Cu, Zn, Cd and Pb.
Application of POSSMs to circumneutral, organic-poor soils with the current parameterisation needs to be done with care and to acknowledge the lack of calibration for the model to such soils. Some soils of this type are present within the datasets to which the model has been applied, namely datasets DMT6, KD1 and KD3 (Supplementary Fig. S9). Comparison of modelled Kds in these soils with the Kds for the remaining soils does not show any systematic deviation in predictions across the metals. A small number of outliers can be seen for Ni, Zn and Pb. For the latter two metals, these outliers include a small number of soils having particularly high observed Kd values. This suggests, albeit weakly, that the model may be underestimating metal sorption in particularly strongly sorbing soils. This is suggestive of a failure to consider additional soil binding phases for a relatively small number of soils. Systematic evaluation of the model parameterisation against greater numbers of soils of this type is needed to justify the reparameterisation of the model, or the inclusion of additional binding phases.
POSSMs could also be adapted readily to account for the effects of variability in SOM and DOM composition on speciation. This is a key area of research (e.g. Ren et al. 2015b). Ideally, a training dataset covering as wide a range of soil types as possible, and including measurement of DOM and SOM composition, would be needed to explore the possibility of improving model prediction by consideration of organic matter composition.
Conclusions
The POSSMs model is an empirical model for soil metal speciation that predicts both the free ion and partitioning in a single calculation using minimal driving data.
Following calibration using literature datasets, the model was applied to a number of datasets of metal speciation in soil–solution and solution phase only systems. The model produced predictions broadly comparable with empirical models designed for prediction of the free ionic or solution metal alone.
Predictions of the free ion in the solution phase alone were reasonable but some datasets produced large differences between observation and prediction, particularly at circumneutral and alkaline pH. More research is needed into the performance of free ion measurement approaches under conditions where extensive metal complexation is expected to occur.
The POSSMs parameterisation is oriented towards acidic and organic-rich soils. Predictions in circumneutral, organic-poor soils do not suggest any systematic bias, but application to such soils should be done with caution.
POSSMs complements mechanistic speciation models by providing a means to predict key metal species in soils using a minimal driving dataset. It is most likely to find use in applications requiring large-scale chemistry datasets, such as large-scale modelling.
Data availability
The data that support this study will be shared upon reasonable request to the corresponding author.
Conflicts of interest
The author declares no conflict of interest.
Declaration of funding
This work was supported by the Natural Environment Research Council award number NE/R016429/1 as part of the UK-SCAPE programme delivering National Capability.
Supplementary material
Details of the datasets used for testing, their parameter ranges and prediction errors, the default approach to computation of the soil concentration and a range of additional figures are available in supplementary material online.
Acknowledgements
Thanks go to Sam Tomlinson and Sam Harrison for comments on a draft of the text. I thank an anonymous reviewer for comments which helped in the improvement of the manuscript.
References
Amery F, Degryse F, Degeling W, Smolders E, Merckx R (2007). The copper-mobilizing-potential of dissolved organic matter in soils varies 10-fold depending on soil incubation and extraction procedures. Environmental Science and Technology 42, 2277–2281.| The copper-mobilizing-potential of dissolved organic matter in soils varies 10-fold depending on soil incubation and extraction procedures.Crossref | GoogleScholarGoogle Scholar |
Bea SA, Wainwright H, Spycher N, Faybishenko B, Hubbard SS, Denham ME (2013). Identifying key controls on the behavior of an acidic-U(VI) plume in the Savannah River Site using reactive transport modeling. Journal of Contaminant Hydrology 151, 34–54.
| Identifying key controls on the behavior of an acidic-U(VI) plume in the Savannah River Site using reactive transport modeling.Crossref | GoogleScholarGoogle Scholar | 23707874PubMed |
Bonten LTC, Groenenberg JE, Meesenburg H, de Vries W (2011). Using advanced surface complexation models for modelling soil chemistry under forests: Solling forest, Germany. Environmental Pollution 159, 2831–2839.
| Using advanced surface complexation models for modelling soil chemistry under forests: Solling forest, Germany.Crossref | GoogleScholarGoogle Scholar |
Cancès B, Ponthieu M, Castrec-Rouelle M, Aubry E, Benedetti MF (2003). Metal ions speciation in a soil and its solution: experimental data and model results. Geoderma 113, 341–355.
| Metal ions speciation in a soil and its solution: experimental data and model results.Crossref | GoogleScholarGoogle Scholar |
Chito D, Weng L, Companys E, Puy J, van Riemsdijk WH, van Leeuwen HP (2012). Determination of free Zn2+ concentration in synthetic and natural samples with AGNES (Absence of Gradients and Nernstian Equilibrium Stripping) and DMT (Donnan Membrane Technique). Science of the Total Environment 421–422, 238–244.
| Determination of free Zn2+ concentration in synthetic and natural samples with AGNES (Absence of Gradients and Nernstian Equilibrium Stripping) and DMT (Donnan Membrane Technique).Crossref | GoogleScholarGoogle Scholar |
Crawford SE, Lofts S, Liber K (2017). Predicting the bioavailability of sediment-bound uranium to the freshwater midge (Chironomus dilutus) using physicochemical properties. Environmental Toxicology and Chemistry 37, 1146–1157.
| Predicting the bioavailability of sediment-bound uranium to the freshwater midge (Chironomus dilutus) using physicochemical properties.Crossref | GoogleScholarGoogle Scholar |
de Groot AC, Peijnenburg WJGM, van den Hoop MAGT, Ritsema R, van Veen RPM (1998) ‘Heavy metals in Dutch field soils: an experimental and theoretical study on equilibrium partitioning. Report no. 607220001’. (RIVM: Bilthoven, The Netherlands)
Duffner A, Weng L, Hoffland E, van der Zee SEATM (2014). Multi-surface modeling to predict free zinc ion concentrations in low-zinc soils. Environmental Science and Technology 48, 5700–5708.
| Multi-surface modeling to predict free zinc ion concentrations in low-zinc soils.Crossref | GoogleScholarGoogle Scholar | 24742258PubMed |
Efron B (1983). Estimating the error rate of a prediction rule: improvement on cross-validation. Journal of the American Statistical Association 78, 316–331.
| Estimating the error rate of a prediction rule: improvement on cross-validation.Crossref | GoogleScholarGoogle Scholar |
Fornaroli R, Ippolito A, Tolkkinen MJ, Mykra H, Muotka T, Balistrieri LS, Schmidt TS (2018). Disentangling the effects of low pH and metal mixture toxicity on macroinvertebrate diversity. Environmental Pollution 235, 889–898.
| Disentangling the effects of low pH and metal mixture toxicity on macroinvertebrate diversity.Crossref | GoogleScholarGoogle Scholar | 29351889PubMed |
Gooddy DC, Shand P, Kinniburgh DG, van Riemsdijk WH (1995). Field–based partition coefficients for trace elements in soil solutions. European Journal of Soil Science 46, 265–285.
| Field–based partition coefficients for trace elements in soil solutions.Crossref | GoogleScholarGoogle Scholar |
Groenenberg JE, Romkens PFAM, Comans RNJ, Luster J, Pampura T, Shotbolt L, Tipping E, de Vries W (2010a). Transfer functions for solid-solution partitioning of cadmium, copper, nickel, lead and zinc in soils: derivation of relationships for free metal ion activities and validation with independent data. European Journal of Soil Science 61, 58–73.
| Transfer functions for solid-solution partitioning of cadmium, copper, nickel, lead and zinc in soils: derivation of relationships for free metal ion activities and validation with independent data.Crossref | GoogleScholarGoogle Scholar |
Groenenberg JE, Koopmans GF, Comans RNJ (2010b). Uncertainty analysis of the nonideal competitive adsorption−Donnan model: effects of dissolved organic matter variability on predicted metal speciation in soil solution. Environmental Science and Technology 44, 1340–1346.
| Uncertainty analysis of the nonideal competitive adsorption−Donnan model: effects of dissolved organic matter variability on predicted metal speciation in soil solution.Crossref | GoogleScholarGoogle Scholar | 20047312PubMed |
Groenenberg JE, Dijkstra JJ, Bonten LTC, de Vries W, Comans RNJ (2012). Evaluation of the performance and limitations of empirical partition–relations and process based multisurface models to predict trace element solubility in soils. Environmental Pollution 166, 98–107.
| Evaluation of the performance and limitations of empirical partition–relations and process based multisurface models to predict trace element solubility in soils.Crossref | GoogleScholarGoogle Scholar | 22484504PubMed |
Groenenberg JE, Romkens PFAM, Van Zomeren A, Rodrigues SM, Comans RNJ (2017). Evaluation of the single dilute (0.43M) nitric acid extraction to determine geochemically reactive elements in soil. Environmental Science and Technology 51, 2246–2253.
| Evaluation of the single dilute (0.43M) nitric acid extraction to determine geochemically reactive elements in soil.Crossref | GoogleScholarGoogle Scholar | 28164700PubMed |
Izquierdo M, Tye AM, Chenery SR (2013). Lability, solubility and speciation of Cd, Pb and Zn in alluvial soils of the River Trent catchment UK. Environmental Science – Processes & Impacts 15, 1844–1858.
| Lability, solubility and speciation of Cd, Pb and Zn in alluvial soils of the River Trent catchment UK.Crossref | GoogleScholarGoogle Scholar |
Kim KR, Owens G (2009). Chemodynamics of heavy metals in long-term contaminated soils: metal speciation in soil solution. Journal of Environmental Science 21, 1532–1540.
| Chemodynamics of heavy metals in long-term contaminated soils: metal speciation in soil solution.Crossref | GoogleScholarGoogle Scholar |
Koopmans GF, Schenkeveld WDC, Song J, Luo Y, Japenga J, Temminghoff EJM (2008). Influence of EDDS on metal speciation in soil extracts: measurement and mechanistic multicomponent modeling. Environmental Science and Technology 42, 1123–1130.
| Influence of EDDS on metal speciation in soil extracts: measurement and mechanistic multicomponent modeling.Crossref | GoogleScholarGoogle Scholar | 18351082PubMed |
Lofts S, Tipping E (1998). An assemblage model for cation binding to particulate matter. Geochimica et Cosmochimica Acta 62, 2609–2625.
| An assemblage model for cation binding to particulate matter.Crossref | GoogleScholarGoogle Scholar |
Lofts S, Tipping E (2011). Assessing WHAM/Model VII against field measurements of free metal ion concentrations: model performance and the role of uncertainty in parameters and inputs. Environmental Chemistry 8, 501–516.
| Assessing WHAM/Model VII against field measurements of free metal ion concentrations: model performance and the role of uncertainty in parameters and inputs.Crossref | GoogleScholarGoogle Scholar |
Lofts S, Tipping E, Lawlor AJ, Shotbolt L (2013). An intermediate complexity dynamic model for predicting accumulation of atmospherically-deposited metals (Ni, Cu, Zn, Cd, Pb) in catchment soils: 1400 to present. Environmental Pollution 180, 236–245.
| An intermediate complexity dynamic model for predicting accumulation of atmospherically-deposited metals (Ni, Cu, Zn, Cd, Pb) in catchment soils: 1400 to present.Crossref | GoogleScholarGoogle Scholar | 23792383PubMed |
Nolan AL, McLaughlin MJ, Mason SD (2003). Chemical speciation of Zn, Cd, Cu, and Pb in pore waters of agricultural and contaminated soils using Donnan dialysis. Environmental Science and Technology 37, 90–98.
| Chemical speciation of Zn, Cd, Cu, and Pb in pore waters of agricultural and contaminated soils using Donnan dialysis.Crossref | GoogleScholarGoogle Scholar | 12542296PubMed |
Pampura T, Groenenberg JE, Rietra RPJJ (2006). Comparison of methods for copper free ion activity determination in soil solutions of contaminated and background soils. Forest Snow and Landscape Research 80, 305–322.
Quevauviller P (1998). Operationally defined extraction procedures for soil and sediment analysis I. Standardization. Trends in Analytical Chemistry 17, 289–298.
| Operationally defined extraction procedures for soil and sediment analysis I. Standardization.Crossref | GoogleScholarGoogle Scholar |
R Core Team (2019) R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. Available at https://www.R-project.org/
Ren Z-L, Sivry Y, Dai J, Tharaud M, Cordier L, Benedetti MF (2015a). Multi-element stable isotopic dilution and multi-surface modelling to assess the speciation and reactivity of cadmium and copper in soil. European Journal of Soil Science 66, 973–982.
| Multi-element stable isotopic dilution and multi-surface modelling to assess the speciation and reactivity of cadmium and copper in soil.Crossref | GoogleScholarGoogle Scholar |
Ren Z-L, Tella M, Bravin MN, Comans RNJ, Dai J, Garnier J-M, Sivry Y, Doelsch E, Straathof A, Benedetti MF (2015b). Effect of dissolved organic matter composition on metal speciation in soil solutions. Chemical Geology 398, 61–69.
| Effect of dissolved organic matter composition on metal speciation in soil solutions.Crossref | GoogleScholarGoogle Scholar |
Ren Z-L, Sivry Y, Tharaud M, Cordier L, Li Y, Dai J, Benedetti MF (2017). Speciation and reactivity of lead and zinc in heavily and poorly contaminated soils: Stable isotope dilution, chemical extraction and model views. Environmental Pollution 225, 654–662.
| Speciation and reactivity of lead and zinc in heavily and poorly contaminated soils: Stable isotope dilution, chemical extraction and model views.Crossref | GoogleScholarGoogle Scholar | 28392241PubMed |
Rennert T, Rabus W, Rinklebe J (2017). Modelling the concentrations of dissolved contaminants (Cd, Cu, Ni, Pb, Zn) in floodplain soils. Environmental Geochemistry and Health 39, 331–344.
| Modelling the concentrations of dissolved contaminants (Cd, Cu, Ni, Pb, Zn) in floodplain soils.Crossref | GoogleScholarGoogle Scholar | 27472945PubMed |
Salam AK, Helmke PA (1998). The pH dependence of free ionic activities and total dissolved concentrations of copper and cadmium in soil solution. Geoderma 83, 281–291.
| The pH dependence of free ionic activities and total dissolved concentrations of copper and cadmium in soil solution.Crossref | GoogleScholarGoogle Scholar |
Sanders JR (1982). The effect of pH upon the copper and cupric ion concentrations in soil solutions. Journal of Soil Science 33, 679–689.
| The effect of pH upon the copper and cupric ion concentrations in soil solutions.Crossref | GoogleScholarGoogle Scholar |
Sauvé S, McBride MB, Hendershot W (1997). Speciation of lead in contaminated soils. Environmental Pollution 98, 149–155.
| Speciation of lead in contaminated soils.Crossref | GoogleScholarGoogle Scholar |
Sauvé S, Norvell WA, McBride M, Hendershot W (2000). Speciation and complexation of cadmium in extracted soil solutions. Environmental Science and Technology 34, 291–296.
| Speciation and complexation of cadmium in extracted soil solutions.Crossref | GoogleScholarGoogle Scholar |
Shotbolt L, Ashmore MR (2004) ‘Extension of critical loads mapping to forests and lowland vegetation: derivation of new transfer functions. annexes to the final report to Defra EPG 1/3/188’. pp. 137–163. (Defra: London)
Simón M, Garcı́a I (1999). Physico-chemical properties of the soil-saturation extracts: estimation from electrical conductivity. Geoderma 90, 99–109.
| Physico-chemical properties of the soil-saturation extracts: estimation from electrical conductivity.Crossref | GoogleScholarGoogle Scholar |
Stephan CH, Courchesne F, Hendershot WH, McGrath SP, Chaudri AM, Sappin-Didier V, Sauvé S (2008). Speciation of zinc in contaminated soils. Environmental Pollution 155, 208–216.
| Speciation of zinc in contaminated soils.Crossref | GoogleScholarGoogle Scholar | 18222022PubMed |
Tipping E (1998). Humic ion-binding model VI: an improved description of the interactions of protons and metal ions with humic substances. Aquatic Geochemistry 4, 3–48.
| Humic ion-binding model VI: an improved description of the interactions of protons and metal ions with humic substances.Crossref | GoogleScholarGoogle Scholar |
Tipping E, Rieuwerts J, Pan G, Ashmore MR, Lofts S, Hill MTR, Farago ME, Thornton I (2003). The solid-solution partitioning of heavy metals (Cu, Zn, Cd, Pb) in upland soils of England and Wales. Environmental Pollution 125, 213–225.
| The solid-solution partitioning of heavy metals (Cu, Zn, Cd, Pb) in upland soils of England and Wales.Crossref | GoogleScholarGoogle Scholar | 12810315PubMed |
Tipping E, Lofts S, Sonke JE (2011). Humic ion-binding model VII: a revised parameterisation of cation-binding by humic substances. Environmental Chemistry 8, 225–235.
| Humic ion-binding model VII: a revised parameterisation of cation-binding by humic substances.Crossref | GoogleScholarGoogle Scholar |
Vulkan R, Zhao F-J, Barbosa-Jefferson V, Preston S, Paton GI, Tipping E, McGrath SP (2000). Copper speciation and impacts on bacterial biosensors in the pore water of copper-contaminated soils. Environmental Science and Technology 34, 5115–5121.
Weng L, Temminghoff EJM, Van Riemsdijk WH (2001). Contribution of individual sorbents to the control of heavy metal activity in sandy soil. Environmental Science and Technology 35, 4436–4443.
| Contribution of individual sorbents to the control of heavy metal activity in sandy soil.Crossref | GoogleScholarGoogle Scholar | 11757598PubMed |
Weng LP, Temminghoff EJM, Lofts S, Tipping E, van Riemsdijk WH (2002). Complexation with dissolved organic matter and solubility control of heavy metals in a sandy soil. Environmental Science and Technology 36, 4804–4810.
| Complexation with dissolved organic matter and solubility control of heavy metals in a sandy soil.Crossref | GoogleScholarGoogle Scholar |