Simple assessment of shallow velocity structures with small-scale microtremor arrays: interval-averaged S-wave velocities
Ikuo Cho 1 3 Atsushi Urabe 2 Tsutomu Nakazawa 1 Yoshiki Sato 1 Kentaro Sakata 11 Geological Survey of Japan, AIST, 1-1-1 Higashi, Tsukuba, Ibaraki 305-8567, Japan.
2 Research Institute for Natural Hazards and Disaster Recovery, Niigata University, 8050 Ikarashi 2-no-cho, Niigata 950-2181, Japan.
3 Corresponding author. Email: ikuo-chou@aist.go.jp
Exploration Geophysics 49(6) 922-927 https://doi.org/10.1071/EG18020
Submitted: 11 February 2018 Accepted: 18 February 2018 Published: 20 April 2018
Journal compilation © ASEG 2018 Open Access CC BY-NC-ND
Abstract
This article describes a method for processing microtremor records from a small-scale seismic array that allows interval-averaged S-wave velocities to be estimated for 10-m depth ranges down to a depth of 30 m. The method was applied to microtremor data obtained in the town of Mashiki, Kumamoto Prefecture, Japan, and the analysis results were evaluated through a comparison with available PS logs and sections obtained by surface-wave methods. It turned out that the interval-averaged S-wave velocity estimates may be subject to errors of up to 20–30% in absolute values, but it was shown that the method can help evaluate relative spatial variations in those S-wave velocities. In view of the simplicity of analysis, the analyser-independent nature of the results and the limitations of analysis accuracy, the interval-averaged S-wave velocity estimation method presented here could be used as an effective tool for the preliminary analysis of microtremor data from small-scale seismic arrays.
Key words: arrays, exploration methodologies, noise, passive, shallow, surface wave, velocity.
Introduction
Microtremor array methods refer to techniques that use seismic-array records of microtremors to estimate S-wave velocity structures beneath the seismic arrays. We have been working to develop simpler and more robust microtremor methods that use small-scale seismic arrays, such as miniature arrays measuring only 1 m or less in radius and compact arrays of three unevenly spaced sensors measuring only several metres in radius (Cho et al., 2004, 2008, 2013). The simpler and more robust microtremor method has enabled large-scale surveys to be conducted in recent years by using large numbers of compact seismic arrays of similar types (Senna et al., 2017).
When it comes to the specific topic of estimating velocity structures by using small-scale seismic arrays, however, we have only published one report on estimating average S-wave velocities for the topmost 10-, 20- and 30-m depth intervals beneath the ground surface (AVS0_10, AVS0_20, AVS0_30) (Cho et al., 2008).
This article describes an extension to that method, in which the depth range being studied is divided into several intervals and average S-wave velocities are estimated for each interval. The estimation method is very simple, but few reports and publications are available that deal with such techniques. Our method is illustrated here through application to data from the town of Mashiki, Kumamoto Prefecture, which sustained serious damage during the M7.3 Kumamoto earthquake of April 16, 2016, and its M6.5 foreshock two days earlier.
Method
The interval-averaged S-wave velocity AVSD1_D2 for a depth range between D1 and D2 is given by

where  and Vs(z) represents the S-wave speed at depth z. It follows from the definition of ΔTD1_D2 that
and Vs(z) represents the S-wave speed at depth z. It follows from the definition of ΔTD1_D2 that

so

Solving the above equation for AVS10_20 gives
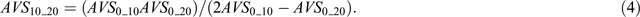
A similar procedure gives
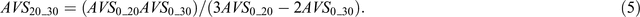
The interval-averaged S-wave velocities for depth ranges of 10–20 m and 20–30 m (AVS10_20, AVS20_30) can be obtained from Equations 4 and 5 if the microtremor array method helps identify Rayleigh-wave phase velocities corresponding to wavelengths of 13, 25 and 40 m (C13, C25, C40) and if they are used as substitutes for the average S-wave velocities for the topmost 10-, 20- and 30-m depth intervals beneath the surface (AVS0_10, AVS0_20, AVS0_30) (e.g. Konno and Kataoka, 2000; Cho et al., 2008).
Application
We conducted array measurements of microtremors at 18 sites along the 1.2-km-long survey line M in Mashiki (Figure 1) during 7–9 June 2016. A regular four-sensor array with a radius of 0.6 m, consisting of three sensors spaced evenly around a circle and another at the centre (Cho et al., 2013), and an irregular array of three unevenly spaced sensors (Cho et al., 2004) with side lengths of 5–7 m, were deployed at each site for 15-min recordings at a sampling frequency of 100 Hz.

|
We also carried out observations along survey line L on 1 February 2017. We took 30-min recordings with a linear array of six seismic sensors spaced at 4-m intervals, and we conducted four sessions of the procedure to cover the total survey line length of 88 m. Further, we also took array recordings of the same type we had conducted along survey line M at three sites along an extension of survey line L. Hakusan Corporation’s JU215/JU410 servo accelerometer, which integrates a sensor with a data logger and is time-calibrated with a Global Positioning System, was used in all measurements.
The centreless circular array method of Cho et al. (2004, 2008, 2013) was applied to records of the regular four-sensor arrays and of the irregular three-sensor arrays, to obtain dispersion curves of Rayleigh-wave phase velocities. We also considered a set of three consecutive sensors in a linear array to be a ‘centred circular’ array of three sensors with a radius of 4 m and applied the spatial autocorrelation method of Aki (1957) to their records. The spectral analysis method, the procedure for estimating Rayleigh-wave phase velocities and the analysis parameters were the same as described in Cho et al. (2004), except that the fast Fourier transform segment length was set at 5.12 s. The method described here was applied to the Rayleigh-wave phase velocities evaluated at the individual sites to obtain estimates for interval-averaged S-wave velocities.
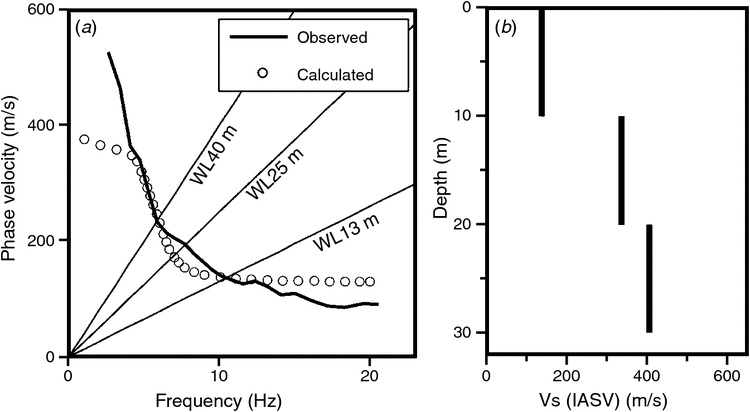
Figure 2 shows the Rayleigh-wave phase velocities estimated with the microtremor array method at the site of an available PS log (Yoshimi et al., 2016) (Figure 1). The figure also shows interval-averaged S-wave velocities calculated from the readings of C13, C25 and C40. The relative residual errors of the interval-averaged S-wave velocities from those obtained directly from the PS log amounted to 2%, –14% and 20% for the AVS0_10, AVS10_20 and AVS20_30, respectively. For the sake of reference, we also conducted microtremor measurements at the site of another available PS log at KiK-net Mashiki seismic station (KMMH16) (Figure 1) and carried out similar comparisons. A circular array with a 26-m radius was also deployed there. The relative residual errors at that site were –30%, 3% and –19% for the AVS0_10, AVS10_20 and AVS20_30, respectively.
Konno and Kataoka (2000) said that the AVS0_30 estimate from C40 only represents a first approximation, partly because the C40–AVS0_30 correlation is based only on numerical simulations and partly because the Rayleigh-wave phase velocity estimates from real microtremor array data contain measurement errors. The same can be said of C13 and C25, so the interval-averaged S-wave speeds that are derived from them should also be understood to be first approximations. In fact, they differed by up to 30% from the values based on PS logs.
The method presented here thus has its own limitations of accuracy, but it is recognisably effective in visualising relative spatial variations in S-wave speeds. For example, Figure 3 compares an S-wave velocity section, drawn by using the interval-averaged S-wave speed estimates from the microtremor data along survey line L, with available output of a surface-wave method at the same location (MLIT, 2017). It should be noted that the microtremor section shown here was drawn by spatial interpolation of the AVS0_10, AVS10_20 and AVS20_30 values, which were taken to be representative S-wave velocities at depths of 5, 15 and 25 m, respectively. In other words, everything except at the X symbols is an interpolated value. It should also be noted that the two section drawings have different velocity scale bars.

|
The surface-wave method indicated low velocities in the neighbourhood of the arrow in the figure. An earthquake fault cropped out on the surface at the location of the arrow during the Kumamoto earthquake (Shirahama et al., 2016), which invites the question whether the low-velocity zone continues to greater depths. Low velocities were also indicated by the microtremor method at the same location. In addition, the microtremor section shows that velocities remain relatively low at least to a depth of 30 m beneath the earthquake fault outcrop, whereas the surface-wave method only visualised structures down to a depth of 15 m.
Figure 4 shows a microtremor section along survey line M. The line passes through an area of serious damage from the Kumamoto earthquake, with building collapse rates of 75% or more (MLIT, 2017), near an along-line distance of 1.0 km. A surface-wave study has also been conducted in the neighbourhood of that area (MLIT, 2017). Comparison found that the microtremor method produced an output pattern that was similar to the results of the surface-wave method in that area as well.

|
Certain differences, indeed, were recognised in the absolute velocity values. That led us to compare interval-averaged S-wave velocity estimates at representative points in the microtremor sections with corresponding S-wave velocity estimates in the surface-wave sections (Figure 5), although the two sets of quantities are primarily unsuited for direct comparison. That produced a correlation coefficient of 0.81, and the ratio between S-wave velocity estimates from the microtremor method and from the surface-wave method was found to be 1.04 ± 0.28 (standard deviation). The results indicated that there is meaningful correlation, despite the large variations.

|
It should of course be noted that, as is evident from the figure, deviations grow with increasing depth. Quantitatively speaking, the estimates from the microtremor method turned out to be ~15% smaller on average than the estimates from the surface-wave method at a depth of 5 m and 23% larger at a depth of 15 m. The data from the deepest parts correspond to the lower boundary of the area covered by the surface-wave method, which is surrounded by a broken line in Figure 4. We believe there is a need to take account of both the question of the reliability of surface-wave methods (reliability of inverse analysis) and the question of the accuracy of the microtremor method presented here.
Discussion
Small-scale seismic arrays excel in the flexibility of measurements. In the case of the present study, the introduction of miniature and irregular seismic arrays allowed efficient measurements, although very little space was available for deploying microtremor arrays because of seismic damage. That said, conducting dense and haphazard measurements would still be inefficient, no matter how efficient the measurement method may be in its own right, unless the method allows the velocity structure to be estimated on-site, so that decisions can be made on the next measurement location on the priority list. This is where our present method comes in handy. Our method allows the velocity structure to be visualised on the spot without putting a load on the computer, requiring only a system for estimating Rayleigh-wave phase velocities to be available at the measurement site. The analysis results do not depend on the analyser, because there is no leeway for the intervention of inversion parameters that might be selected arbitrarily by the analyser. Everybody can replicate the same results, so re-examination is easy even if a problem arises later. Our present method, therefore, has characteristics that make it suitable for use in preliminary on-site analysis.
In fact, we initially conducted measurements at 12 locations in a matter of only 6 h, including transit time, in order to get a rough picture of the pattern shown in Figure 4. We processed the data on the night of Day 1, whereupon we made decisions on the areas where we thought we needed denser records, and we carried out additional measurements at four sites on Day 2 and two sites on Day 3. As a result, Figure 4 captures a relatively good picture of the characteristics of steep changes in the velocity structure near along-line distances of 0.7 and 1.0 km. This illustrates the utility of our present method as a preliminary analysis tool for making the most of the flexibility of microtremor measurements using small-scale seismic arrays.
In the field of surface-wave methods, a simple conversion of the Rayleigh-wave phase velocity dispersion curve, more commonly known as the ‘one-third of the wavelength’ law (Gazetas, 1982; Standardization Committee of the Society of Exploration Geophysicists of Japan (SEGJ), 2008), has often been used as a classical tool for preliminary analysis. This technique consists of multiplying a wavelength value and a phase velocity value by respective scaling factors and assuming that the products represent the depth and the S-wave velocity, respectively. Empirically, that method indeed produces natural results, but its resolution fails significantly at depth. This is an inevitable problem, given that Rayleigh-wave phase velocities in long-wavelength (low-frequency) ranges correspond to subsurface properties integrated all the way from the surface to depth (Aki and Richards, 2002). Our present method has improved the resolution at depth by splitting the information contained in the Rayleigh-wave phase velocities into fragments of information by 10-m depth intervals. In that sense, our method could be recognised as an extension to the above-described simple conversion method.
Our method associates Rayleigh-wave phase velocities with subsurface structure models only through an empirical law. There is, therefore, no guarantee that theoretical Rayleigh-wave phase velocities, calculated from a subsurface structure model obtained with our method, will replicate the observed phase velocities. This represents a fundamental difference from more typical inversion methods, such as genetic algorithms and linearised inversion. But it is not hard to imagine that a theoretical Rayleigh-wave phase velocity dispersion curve based on a subsurface structure model obtained from our present method will explain observations to a certain extent, given that empiricism and theory have been so built to avoid too much deviation.
Figure 6, for example, compares a Rayleigh-wave phase velocity dispersion curve, calculated theoretically (Hisada, 1994, 1995) by using the interval-averaged S-wave velocity estimates, with a corresponding observed dispersion curve (site KMMH16). In the figure, the theoretical values represent fundamental-mode Rayleigh-wave phase velocities calculated by assuming a horizontally layered structure consisting of a semi-infinite medium underlying two 10-m-thick layers. The figure shows that theory agrees relatively well with the observations in a frequency range (5–10 Hz) corresponding to wavelengths from 13 to 40 m.
The above discussions, of course, are only intended to show the soundness of our present method and do not mean to say that more typical inversion methods are unnecessary. In fact, we do need, in various situations, approaches that are based on physical (theoretical) models. For example, our present method cannot even deal with the simple request that layering of the subsurface structure should be modelled after drilling data from the neighbourhood. An empirical law, before everything else, has limitations of accuracy.
At site KMMH16, array measurements of microtremors were taken and Rayleigh-wave phase velocity dispersion curves were shown by Arai and Kashiwa (2017) and Chimoto et al. (2016) as well. We have read their dispersion curves, applied our present method to each of them and compared the results with the interval-averaged S-wave speeds obtained in this study (Figure 6b). The differences in the interval-averaged S-wave speed estimates were found to grow with increasing depth. More specifically, the AVS0_10, AVS10_20 and AVS20_30 were found to have standard deviations of 7%, 17% and 30%, respectively. Those variations are comparable in magnitude to the deviations from available PS logs as shown in the section ‘Application’ and likely indicate the limitations of our present method in terms of accuracy.
However, the so-called inverse analysis methods also require careful work. For example, the distribution of layers of a subsurface structure strongly influences the analysis results, and therefore, requires time for validation; an interested reader can compare between the inversion results in the publications of Arai and Kashiwa (2017) and Chimoto et al. (2016). Our present method has a different application. It is inferior to more typical inversion methods in terms of flexibility and accuracy, but we still believe it can be used effectively as a preliminary analysis tool for obtaining a rough picture of spatial variations in shallow structures by juxtaposing measurement and analysis results from a large number of sites.
Conclusion
We have presented a simple method for estimating interval-averaged S-wave velocities for depth ranges of 0–10, 10–20 and 20–30 m by using a Rayleigh-wave phase velocity dispersion curve obtained from array measurements of vertical-motion microtremors. This method could be understood as an extension, with enhanced resolution, on a conventional technique that consists of a simple conversion of a Rayleigh-wave phase velocity dispersion curve into an S-wave velocity profile. Our method is based on an empirical law that associates average S-wave velocities of subsurface structures with their Rayleigh-wave phase velocities. It uses only part of the information contained in Rayleigh-wave phase velocity dispersion curves and no other information on subsurface structures. It should be remembered, therefore, that the method only has limited precision, or in other words, may be subject to errors of up to a few tens of percent.
It has been shown, however, that our method produces output images that are similar to the results of surface-wave techniques insofar as the objective is to get an approximate picture of spatial variations in shallow structures by juxtaposing measurement and analysis results from a large number of sites. The output does not depend on the analyser, and it takes only simple algebra to obtain results once a Rayleigh-wave phase velocity dispersion curve has been estimated, so our method could be used effectively as a tool of preliminary analysis, particularly from the viewpoint of making the most of the flexibility of small-scale seismic arrays.
Conflicts of interest
The authors declare no conflicts of interest.
Acknowledgements
The authors thank two anonymous reviewers for their useful comments that improved the original manuscript. The microtremor data used in this paper were recorded with seismometers borrowed from the National Research Institute for Earth Science and Disaster Resilience (NIED). A soil profile at KMMH16 was provided by NIED. Masayuki Yoshimi provided us with an S-wave velocity profile obtained at the site of a PS log on survey line M. Hiroshi Arai provided us with high quality image data of a PS log and microtremor analysis results. The Generic Mapping Tools were used to generate the figures. This research was financially supported in part by the Japan Society for the Promotion of Science (JSPS) KAKENHI Grant Numbers JP15H04080 and JP17K18962.
References
Aki, K., 1957, Space and time spectra of stationary stochastic waves, with special reference to microtremors: Bulletin of the Earthquake Research Institute, University of Tokyo, 35, 415–457Aki, K., and Richards, P. D., 2002, Quantitative seismology (2nd edition): University Science Books.
Arai, H., and Kashiwa, H., 2017, Geotechnical boring and microtremor array surveys at KiK-net Mashiki Station: Summaries of technical papers of annual meeting Architectural Institute of Japan (in Japanese).
Chimoto, K., Yamanaka, H., Tsuno, S., Miyake, H., and Yamada, N., 2016, Estimation of shallow S-wave velocity structure using microtremor array exploration at temporary strong motion observation stations for aftershocks of the 2016 Kumamoto earthquake: Earth, Planets, and Space, 68, 206
| Estimation of shallow S-wave velocity structure using microtremor array exploration at temporary strong motion observation stations for aftershocks of the 2016 Kumamoto earthquake:Crossref | GoogleScholarGoogle Scholar |
Cho, I., Tada, T., and Shinozaki, Y., 2004, A new method to determine phase velocities of Rayleigh waves from microseisms: Geophysics, 69, 1535–1551
| A new method to determine phase velocities of Rayleigh waves from microseisms:Crossref | GoogleScholarGoogle Scholar |
Cho, I., Tada, T., and Shinozaki, Y., 2008, A new method of microtremor exploration using miniature seismic arrays: quick estimation of average shear velocities of the shallow soil: Butsuri Tansa, 61, 457–468
| A new method of microtremor exploration using miniature seismic arrays: quick estimation of average shear velocities of the shallow soil:Crossref | GoogleScholarGoogle Scholar |
Cho, I., Senna, S., and Fujiwara, H., 2013, Miniature array analysis of microtremors: Geophysics, 78, KS13–KS23
| Miniature array analysis of microtremors:Crossref | GoogleScholarGoogle Scholar |
Gazetas, G., 1982, Vibrational characteristics of soil deposits with variable wave velocity: International Journal for Numerical and Analytical Methods in Geomechanics, 6, 1–20
| Vibrational characteristics of soil deposits with variable wave velocity:Crossref | GoogleScholarGoogle Scholar |
Hisada, Y., 1994, An efficient method for computing Green’s functions for a layered half-space with sources and receivers at close depths: Bulletin of the Seismological Society of America, 84, 1456–1472
Hisada, Y., 1995, An efficient method for computing Green’s functions for a layered half-space with sources and receivers at close depths (Part 2): Bulletin of the Seismological Society of America, 85, 1080–1093
Konno, K., and Kataoka, S., 2000, An estimating method for the average S-wave velocity of ground from the phase velocity of Rayleigh wave: Proceedings of Japan Society of Civil Engineers, 2000, 415–423
Ministry of Land, Infrastructure, Transport and Tourism (MLIT), 2017, Report on the way of safety measures towards the urban reconstruction of the Mashiki Town suffering from the 2016 Kumamoto Earthquakes: Final report. pp. 126. Available at: http://www.mlit.go.jp/report/press/toshi08_hh_000034.html (in Japanese)
Senna, S., Wakai, A., Jin, K., Matsuyama, H., Maeda, T., and Fujiwara, H., 2017, Modeling of the subsurface from the seismic bedrock to the ground surface for a broadband strong motion evaluation in Kanto Area (Part 2): JpGU-AGU Joint Meeting 2017, S-SS15–19.
Shirahama, H., Yoshimi, M., Awata, Y., Maruyama, T., Azuma, T., Miyashita, Y., Mori, H., Imanishi, K., Takeda, N., Ochi, T., Otsubo, M., Asahina, D., and Miyakawa, A., 2016, Characteristics of the surface ruptures associated with the 2016 Kumamoto earthquake sequence, central Kyushu, Japan: Earth, Planets, and Space, 68, 191
| Characteristics of the surface ruptures associated with the 2016 Kumamoto earthquake sequence, central Kyushu, Japan:Crossref | GoogleScholarGoogle Scholar |
Standardization Committee of the Society of Exploration Geophysicists of Japan (SEGJ), 2008, Applications manual of geophysical methods to engineering and environmental problems: Society of Exploration Geophysicists of Japan, 111–126 (in Japanese).
Yoshimi, M., Hata, Y., Goto, H., Hosoya, T., Morita, S., and Tokumaru, T., 2016, Borehole exploration in heavily damaged area of the 2016 Kumamoto Earthquake, Mashiki Town, Kumamoto: Proceedings of Annual Fall Meeting, 2016, of the Japanese Society for Active Fault Studies, Tokyo, Japan, Paper No. 17. Available at: http://jsaf.info/pdf/meeting/2016/2016fall_S.pdf (in Japanese)