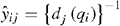From rainfall to farm incomes—transforming advice for Australian drought policy. I. Development and testing of a bioeconomic modelling system
Philip Kokic A , Rohan Nelson B F , Holger Meinke C , Andries Potgieter D and John Carter EA ABARE, GPO Box 1563, Canberra, ACT 2601, Australia, and CSIRO Wealth from Oceans Flagship, GPO Box 284, Canberra, ACT 2601, Australia.
B CSIRO Wealth from Oceans Flagship, GPO Box 284, Canberra, ACT 2601, Australia, and formerly ABARE, GPO Box 1563, Canberra, ACT 2601, Australia.
C Crop and Weed Ecology, Department of Plant Sciences, Wageningen University, PO Box 430, 6700 AK Wageningen, The Netherlands.
D Queensland Department of Primary Industries, PO Box 102, Toowoomba, Qld 4350, Australia.
E Queensland Department of Natural Resources and Water, GPO Box 2454, Brisbane, Qld 4001, Australia.
F Correspondence author. Email: rohan.nelson@csiro.au
Australian Journal of Agricultural Research 58(10) 993-1003 https://doi.org/10.1071/AR06193
Submitted: 14 June 2006 Accepted: 21 June 2007 Published: 30 October 2007
Abstract
In this paper we report the development of a bioeconomic modelling system, AgFIRM, designed to help close a relevance gap between climate science and policy in Australia. We do this by making a simple econometric farm income model responsive to seasonal forecasts of crop and pasture growth for the coming season. The key quantitative innovation was the use of multiple and M-quantile regression to calibrate the farm income model, using simulated crop and pasture growth from 2 agroecological models. The results of model testing demonstrated a capability to reliably forecast the direction of movement in Australian farm incomes in July at the beginning of the financial year (July–June). The structure of the model, and the seasonal climate forecasting system used, meant that its predictive accuracy was greatest across Australia’s cropping regions. In a second paper, Nelson et al. (2007, this issue), we have demonstrated how the bioeconomic modelling system developed here could be used to enhance the value of climate science to Australian drought policy.
Acknowledgments
The research carried out in this project was partially funded by the Managing Climate Variability Research and Development Program, and the Grains Research and Development Corporation. Their support is gratefully acknowledged. The authors acknowledge helpful comments on earlier drafts by Graeme Hammer, Fred Chudleigh, Beverly Henry, Ken Day, Grant Stone, Jozef Syktus, Greg Griffiths, Ahmed Hafi, David Pannell, and an anonymous referee. For their efforts in preparing data, the authors also thank Caroline Levantis and Dorine Bruget.
Anderson JR
(2003) Risk in rural development: challenges for managers and policy makers. Agricultural Systems 75, 161–197.
| Crossref | GoogleScholarGoogle Scholar |
obtained optimum values of Qij, which maximise the profit function (A1) subject to (A2) given a set of expected prices {Pij*; j = 1,…,m} at the forecast time point. At this optimum the cost function reduces to:

where

is the farm’s unit cost of producing commodity, and λi is a Lagrange multiplier from constraint (A2).
Predicting income when commodity prices change
Partial derivatives of the quantity of each commodity produced (Qij) and λi with respect to expected prices (Pij*) are used to simulate the production of each commodity given an expected price change between the base and forecast time points. This means that the resulting change in unit costs can also be predicted (using Eqn A4). Profit is simulated by using Eqns A1 and A3 and the realised price. In other words, provided that a farm is managed so that its outputs are always adjusted to maximise its expected profit subject to Eqn A2, its micro-level supply response (change in its outputs) to price changes can be simulated.
Details of the estimation and application of the model to forecast incomes in response to changes in commodity prices have been presented by Kokic et al. (1993, 2000).
Predicting income when yields change
The CPMs were used to forecast the quantity of each commodity in the FIM (beef, wool, lamb, wheat, winter crops, and summer crops). The quantity of each commodity in the FIM is adjusted in proportion to yields forecast by the CPMs (y*ij) relative to the base year (yij):
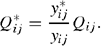
Unit costs are modified using Eqn A3, and profit is simulated by using Eqns A1 and A3.
Appendix 2. M-quantile regression
The role of M-quantile regression in predicting farm incomes has been discussed in detail by Kokic et al. (2000). The productivity of individual farms varies with farm-specific factors such as soil moisture availability, soil fertility, management practices, and on-farm infrastructure. This means that productivity can vary dramatically among farms that share broadly similar characteristics such as location, size, and enterprise mix. The use of standard regression methods implicitly assumes that the parameters relating productivity to farm incomes are the same for all farms, resulting in aggregation or averaging bias. This can be partly overcome using M-quantile regression (Breckling and Chambers 1988) to estimate farm-specific productivity coefficients.
M-quantile regression is a method of modelling that implicitly allows for ‘missing variables’ in a regression specification, effectively replacing the conventional OLS ‘average line plus noise’ model by a family of lines indexed by a coefficient q (Fig. B1). Different values of q then correspond to different levels of the missing variables. The regression surface passing through the ith dependent value corresponds to a particular quantile value qi and a set of regression coefficients di. The advantage of this approach over OLS regression is that the regression coefficients are disaggregated down to each data point. While this disaggregation may not be complete because of the smoothing effect of regression, M-quantile regression has the advantage that it is non-parametric and so the estimates of regression coefficients are dictated solely by the data.

|
In research reported in this paper, M-quantile regression was applied to the livestock components of Eqn A2. Corresponding to each value of q there are regression coefficient estimates dj(q) for j = 1,…, m. These regression coefficients can be interpreted as a set of non-parametric functions dj(q), which map the livestock productivity index q to estimates of the yields of lamb, beef, and wool from the AAGIS survey data. The value qi for any given farm is chosen so as to equate the livestock component of Eqn A2 to the area of the farm used for livestock production. The estimates of yield for that farm i are given by: