An improved method for biometric analysis of soil test – crop response data sets

Maheswaran Rohan; Mark Conyers

doi:10.1071/CP24162

RESEARCH ARTICLE (Open Access)

Previous Next Contents Vol 76(1)

An improved method for biometric analysis of soil test – crop response data sets

Maheswaran Rohan

^A ^* and Mark Conyers

^B

+ Author Affiliations

- Author Affiliations

^A Wagga Wagga Agricultural Institute, Wagga Wagga, NSW 2650, Australia.

^B Retired. Formerly of: Wagga Wagga Agricultural Institute, Wagga Wagga, NSW 2650, Australia.

^* Correspondence to: maheswaran.rohan@dpi.nsw.gov.au

Handling Editor: Davide Cammarano

Crop & Pasture Science 76, CP24162 https://doi.org/10.1071/CP24162

Submitted: 19 May 2024 Accepted: 11 December 2024 Published: 17 January 2025

© 2025 The Author(s) (or their employer(s)). Published by CSIRO Publishing. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)

Abstract

Context

To increase cereal production, primary producers want to know the amount of fertiliser that needs to be applied to achieve high yield. To calculate the critical soil test value (CSTV) especially in Colwell-P, several models were found in the literature. The arcsine-log calibration curve has been commonly used in Australia to estimate the CSTV. However, this method has some mathematical weaknesses, which tend to give underestimated values for CSTV.

Aim

In this paper, we describe the mathematical issues and propose a model to overcome these issues. The simplified model proposed allows us to estimate the CSTV and its standard error.

Method

We have applied the regression and the delta method to the data used in the arcsine-log calibration curve (ALCC) method.

Key results

Based on the given data, a soil test value of 31.5 mg P kg⁻¹ soil is required to achieve 90% relative yield of wheat, which is the middle ground of previously published critical values between the underestimate (21.4 mg kg⁻¹) generated by the ALCC algorithm and the overestimate (40 mg kg⁻¹) generated by the conventional Mitscherlich method.

Conclusions

Advantages of this method are: (1) simple to apply to any data sets; and (2) easy to incorporate other covariates into the models. This method should be applied for computing estimates of CSTV and its standard error because it overcomes the contentious issue of the division of the y-axis by the correlation coefficient.

Implication

The proposed method should replace the ALCC algorithm and the current P values used in farming may need to be updated.

Keywords: delta method, phosphorus, soil test calibration, statistical models, wheat.

Introduction

To manage the increasing population, a significant increase in cereal production is greatly demanded (Alexandratos and Bruinsma 2012). Soil fertility is one of the primary factors required for increasing that cereal production. To minimise the cost, primary producers want to know the amount of fertiliser that is sufficient to achieve high yield. To answer this question, mathematical models need to be developed that make optimal use of the available data. In the literature, the crop yield against soil test value (STV) is algebraically discussed (Colwell 1963; Brennan and Bell 2013; Bell et al. 2013; Dyson and Conyers 2013; Speirs et al. 2013a, 2013b; Correndo et al. 2017). Instead of yield, the relative yield (RY) was also used as a response variable for standardising the data regarding locations, soil quality, seasons, etc. Algebraically, RY = (Y₀/Y_max) × 100, where Y₀ is a yield without fertiliser and Y_max is the maximum yield with fertilser for a given STV. For example, RY = 90% at STV = δ mg kg⁻¹ means that the change between Y_max and Y₀ was only 10% when the soil test value is δ mg kg⁻¹. A detailed discussion on RY was given in Dyson and Conyers (2013).

Mathematical models were often developed to predict the yield for a given STV. In most previous studies, the non-linear relationship between RY and STV was described as linear after transforming the original data. That means it ends up with simple linear regression in the transformed scale. In simple linear regression, the explanatory variable STV is to be fixed, but in practice, it is generally observed as an association with RY. One of the aims of developing these models was to estimate a critical soil test value (CSTV) for a given yield or RY. Due to the complexity of the model, the demonstration of uncertainty of the CSTV was limited in the literature. However, the arcsine-log calibration curve (ALCC) method was introduced by switching the axes to determine the confidence interval (CI) for the CSTV (Dyson and Conyers 2013; Correndo et al. 2017). We believe that switching axes may be mathematically unwarranted and its estimates of CSTV are possibly underestimated or overestimated, depending on the data.

The purpose of this study was to develop an alternative procedure for mathematically describing weakly associated data such as soil test calibrations. We compare the results of the proposed method with previous results on the same data set, involving the response to P fertiliser by wheat.

Materials and methods

Data

Data was collected through the Grains Research and Development Corporation (GRDC) funded project that constructed the national soil test – crop response data base (Speirs et al. 2013a, 2013b). Here, we give a very brief detail of the data because secondary data, discussed in the ALCC algorithm paper (Dyson and Conyers 2013), was used for our investigation. It is helpful to compare the results and insights. There were 105 trial sites, but two of them were excluded from the analysis due to the high leverage that their high STV and 100% RY produced in the transformed domain. Dyson and Conyers (2013) give further details of the data. Specifically, we focused on the relationship between the RY and STV (Colwell-P) using this data set.

Scope of the paper

In this paper, we show that the estimates obtained by regressing y on x and x on y are mathematically equivalent, where y and x are vectors of (n × 1) whose elements are (y₁, y₂, …, y_n) and (x₁, x₂, …, x_n), respectively, with the primary aim to improve and simplify the existing models including ALCC method, and calculate the CSTV using the proposed model and its standard error algebraically, which will allow us to provide improved the CIs.

Mathematical equivalent

The mathematical equivalent may be defined if a set of estimates generated from the standard regression can be mathematically used to predict exactly another set of estimates, obtained by switching the regression axis. It can be simply explained below.

When regressing y on x, the estimates ${\hat{β}}_{0}$ and ${\hat{β}}_{1}$ for parameters intercept and slope are:

(1)

{\hat{β}}_{1} = \frac{s_{x y}}{s_{x x}} and {\hat{β}}_{0} = \bar{y} - {\hat{β}}_{1} \bar{x}

where $\bar{x} = \frac{\sum_{i = 1}^{n} x_{i}}{n}$ ; $\bar{y} = \frac{\sum_{i = 1}^{n} y_{i}}{n}$ ; $s_{x y} = \sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})$ ; $s_{x x} = \sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}$ ; and $s_{y y} = \sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}$ . In addition, the estimated correlation coefficient = $\hat{r} = \frac{s_{x y}}{\sqrt{s_{x x}} \sqrt{s_{y y}}}$ . In contrast, if we regress x on y (rotating the axes; it was done in the ALCC algorithm), the new estimates ${\tilde{β}}_{0}$ and ${\tilde{β}}_{1}$ for parameters intercept and slope are:

{\tilde{β}}_{1} = \frac{s_{x y}}{s_{y y}} = {\hat{β}}_{1} \frac{s_{x x}}{s_{y y}};

{\tilde{β}}_{0} = \bar{x} - {\tilde{β}}_{1} \bar{y} = \bar{x} - {\hat{β}}_{1} (\frac{s_{x x}}{s_{y y}}) \bar{y}

and

(2)

The estimated correlation coefficient = \tilde{r} = \frac{s_{x y}}{\sqrt{s_{x x}} \sqrt{s_{y y}}} = \hat{r}

when switching the axes, the new estimates can be predicted exactly from the standard regression estimates and were influenced by the term $\frac{s_{x x}}{s_{y y}}$ , plus the correlation coefficient did not change. Algebraically, they are related. However, in the ALCC algorithm, ${\tilde{β}}_{0}$ was used to compute the estimate of CSTV, which may lead to a biased estimate.

Calibration RY vs STV

Clearly stated, RY can be predicted by STV, but not the reverse (Dyson and Conyers 2013). We prefer to stay with an original structure for the rest of the analysis, rather than switching the axes. The RY values were bounded at 0 and 100%, the conventional transformation of arcsine with the square root of the proportion of RY was used as a response variable. To address the large STV values, the natural logarithm transformation (ln(STV)) was made. The model may be described in a linear form:

(3)

\arcsin (sqrt (\frac{{RY}_{i}}{100})) = β_{0} + β_{1} \ln ({STV}_{i}), i = 1, \dots, 103;

The estimates ${\hat{β}}_{0}$ and ${\hat{β}}_{1}$ for parameters β₀ and β₁, respectively, can be easily computed using freely or commercially available statistical software.

Computation of CSTV

This section aims to calculate the critical soil test value (CSTV_α) for a given RY of α, which we define C_α. The value α may be defined as 70, 80, 90, and 95%. In the case of α = 90%, the transformed value of C_α is 1.249 $(= \arcsin (sqrt (\frac{90}{100})))$ . To compute the CSTV_α, substitute C_α in the right-hand side of Eqn 3 and replace β₀ and β₁ in Eqn 3 by their estimates ${\hat{β}}_{0}$ and ${\hat{β}}_{1}$ :

C_{α} = {\hat{β}}_{0} + {\hat{β}}_{1} \ln ({CSTV}_{α})

\ln ({CSTV}_{α}) = \frac{C_{α} - {\hat{β}}_{0}}{{\hat{β}}_{1}}

(4)

{CSTV}_{α} = \exp (\frac{C_{α} - {\hat{β}}_{0}}{{\hat{β}}_{1}})

Computation of CSTV_α is simple, but the computation of uncertainty in the CSTV_α is not easy due to the complex form. To avoid this complexity, the axes were switched in the ALCC method (Dyson and Conyers 2013; Correndo et al. 2017). However, we introduce a method to calculate the standard error of the estimate CSTV_α using the delta method.

Delta method

The delta method is often used to compute the variance for a complex form of the estimate (Seber and Wild 1989). In general, the variance of the smooth function f of asymptotically normal random variables with known variance-covariance Σ can be computed using the formulae:

(5)

V (f (x)) = {(\frac{\partial f (x)}{\partial x})}^{t} \sum (\frac{\partial f (x)}{\partial x})

where $\frac{\partial f (x)}{\partial x}$ is the partial derivative of f(x) with respect to x and the t in the superscript of the Eqn 5 indicates transposition of the matrix. Hence, the standard error is $\sqrt{V (f (x))}$ . Rohan and Sarmah (2023) explained how to calculate the standard error for the half-life of kinetic dissipation models. This helps us to describe an algebraic method to drive the standard error of the CSTV_α.

Computation of standard error of CSTV_α

Let us define the function f of the parameters $β_{0}$ and $β_{1}$ :

(6)

{CSTV}_{α} = f (β_{0}, β_{1}) = \exp (\frac{C_{α} - β_{0}}{β_{1}})

(7)

\frac{\partial f (β_{0}, β_{1})}{\partial β_{0}} = \exp (\frac{C_{α} - β_{0}}{β_{1}}) (\frac{- 1}{β_{1}}) = - (\frac{1}{β_{1}}) f (β_{0}, β_{1})

(8)

\frac{\partial f (β_{0}, β_{1})}{\partial β_{1}} = \exp (\frac{C_{α} - β_{0}}{β_{1}}) (\frac{- (C_{α} - β_{0})}{β_{1}^{2}}) = - (\frac{C_{α} - β_{0}}{β_{1}^{2}}) f (β_{0}, β_{1})

V (f (β_{0}, β_{1})) = (\begin{matrix} \frac{\partial f (β_{0}, β_{1})}{\partial β_{0}} & \frac{\partial f (β_{0}, β_{1})}{\partial β_{1}} \end{matrix}) \sum (\begin{matrix} \frac{\partial f (β_{0}, β_{1})}{\partial β_{0}} \\ \frac{\partial f (β_{0}, β_{1})}{\partial β_{1}} \end{matrix})

V (f (β_{0}, β_{1})) = (\begin{matrix} - (\frac{1}{β_{1}}) f (β_{0}, β_{1}) & - (\frac{C_{α} - β_{0}}{β_{1}^{2}}) f (β_{0}, β_{1}) \end{matrix}) (\begin{matrix} σ_{β_{0}}^{2} & σ_{β_{0}, β_{1}} \\ σ_{β_{0}, β_{1}} & σ_{β_{1}}^{2} \end{matrix}) (\begin{matrix} - (\frac{1}{β_{1}}) f (β_{0}, β_{1}) \\ - (\frac{C_{α} - β_{0}}{β_{1}^{2}}) f (β_{0}, β_{1}) \end{matrix})

(9)

V (f (β_{0}, β_{1})) = {(\frac{f (β_{0}, β_{1})}{β_{1}})}^{2} (σ_{β_{0}}^{2} + 2 [\frac{C_{α} - β_{0}}{β_{1}}] σ_{β_{0}, β_{1}} + {[\frac{C_{α} - β_{0}}{β_{1}}]}^{2} σ_{β_{1}}^{2})

where $σ_{β_{0}}^{2}$ and $σ_{β_{1}}^{2}$ are the variance of ${\hat{β}}_{0}$ and ${\hat{β}}_{1}$ respectively, and $σ_{β_{0}, β_{1}}$ is the covariance of ${\hat{β}}_{0}$ and ${\hat{β}}_{1}$ . The above regression analysis in Eqn 3 provided all components of $\sum$ . To evaluate the variance of CSTV_α, $β_{0}$ and $β_{1}$ are replaced by the estimates ${\hat{β}}_{0}$ and ${\hat{β}}_{1}$ , and C_α is the known constant. Hence, the standard error of the estimate CSTV_α is the square root of $V (f (β_{0}, β_{1}))$ .

Results

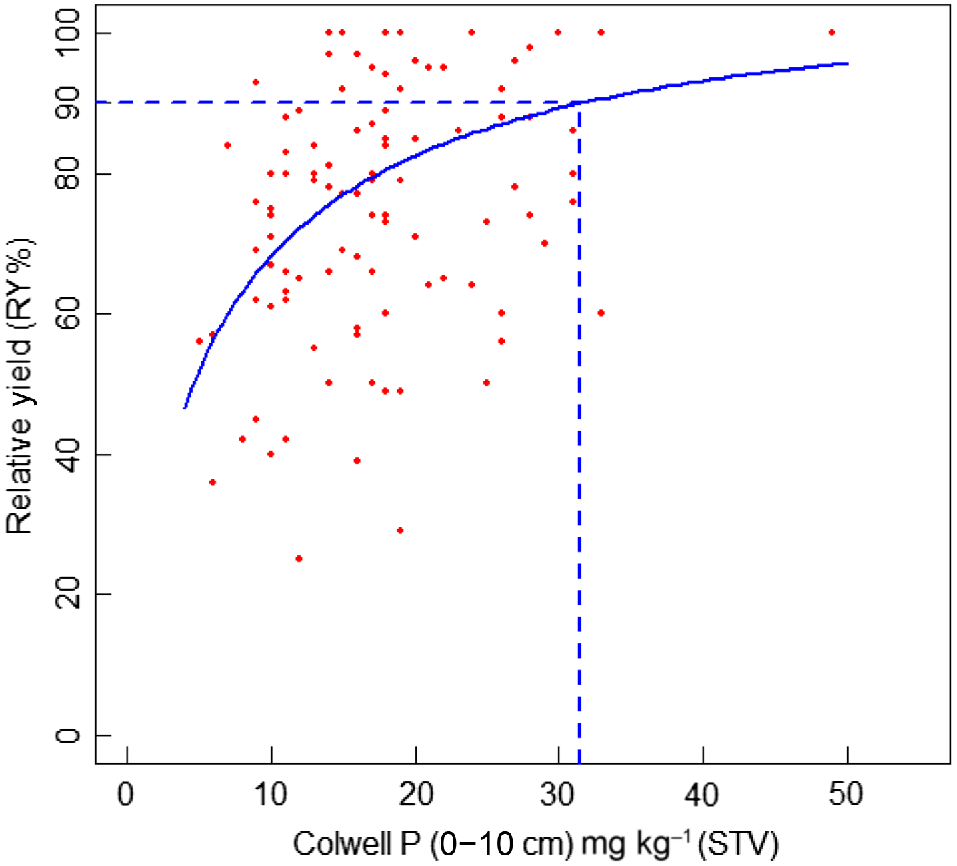
Fig. 1 shows the linear fit for the scatter plot of arcsine with the square root of the proportion of RY against the natural logarithm of Colwell-P. The fitted equation is:

\arcsin (sqrt (\frac{\hat{RY}}{100})) = 0.417 + 0.241 \times \ln (Colwell P),

and the estimated variance-covariance, $\hat{Σ}$ , of the regression estimates $\hat{β} = {({\hat{β}}_{0}, {\hat{β}}_{1})}^{t}$ is:

\hat{Σ} = (\begin{matrix} 0.023 & - 0.008 \\ - 0.008 & 0.003 \end{matrix})

To calculate the CSTV_α for various α = 70, 80, 90, and 95%, the C_α takes the values 0.991, 1.107, 1.249, and 1.345 respectively. Hence, ${CSTV}_{90 %} = \exp (\frac{1.249 - {\hat{β}}_{0}}{{\hat{β}}_{1}}) = 31.498$ and using Eqn 9 to compute its standard error, which is 5.55. It is expected to be reasonably large because the data was highly variable due to variations in locations, soil types, seasons, etc. (Dyson and Conyers 2013). The 95% CI for CSTV_90% is (20.6, 42.4).

Fig. 1.

Fitted calibration curve using Eqn 3 with the raw data (103 points).

Similarly, CSTV_α for various α = 70, 80, and 95% can be computed and results are in Table 1. We found that the standard error increases with (Table 1). This seems to be expected because high yield depends not only on Colwell-P but also on other variables, which interact to produce relatively large variations.

Table 1.CSTV_α for various α with their confidence interval.

α	C_α	CSTV_α	Standard error	95% CI
70%	0.991	10.806	1.41	(8.0, 13.6)
80%	1.107	17.484	1.69	(14.2, 20.8)
90%	1.249	31.498	5.55	(20.6, 42.4)
95%	1.345	46.954	12.00	(23.4, 70.5)

Discussion

Many approaches were developed to calculate the CSTV_α in the literature (Colwell 1963; Dyson and Conyers 2013; Correndo et al. 2017). Switching the axes is required in the ALCC algorithm (Dyson and Conyers 2013). We believe that it is unnecessary and that it can be numerically described using the data employed to obtain Eqn 2 in Dyson and Conyers (2013).

After switching the axes, the equation $lnColwell P = 2.894 + 0.692 \times arcsinRY rel 90 %$ was found by Dyson and Conyers (2013) to estimate CSTV_90%, which is 18.06 (=exp(2.894)). In our notation, they are ${\tilde{β}}_{0} = 2.894$ and ${\tilde{β}}_{1} = 0.692$ . However, we prefer to do regression without changing the concept of the response variable vs the independent variable. We obtained $arcsinRY rel 90 % = - 0.832 + 0.241 \times lnColwell P$ . In the case of direct regression notation, ${\hat{β}}_{0} = - 0.832, {\hat{β}}_{1} = 0.241, \bar{x} = 2.782, \bar{y} = - 0.161,$ s_xx = 18.718, s_yy = 6.547 and s_xy = 4.527. Applying the Eqn 2 in section 2, ${\tilde{β}}_{0}$ and ${\tilde{β}}_{1}$ can be derived using above the quantities, ${\tilde{β}}_{1} = {\hat{β}}_{1} \times (\frac{s_{x x}}{s_{y y}}) = 0.692$ and ${\tilde{β}}_{0} = \bar{x} - {\tilde{β}}_{1} \bar{y} = 2.894$ . They are exactly the same result as that of Dyson and Conyers (2013) without switching the axes. Using this direct regression approach, CSTV_90% is $\exp (\frac{0.83161}{0.24105}) = 31.498$ , which is far away from the previously reported value of 18.06. This difference is caused by the ${\tilde{β}}_{0}$ because it was used to calculate the CSTV_90% in the paper (Dyson and Conyers 2013). We can now see that ${\tilde{β}}_{0}$ is influenced by many factors such as $\bar{x}, \bar{y},$ s_xx, and s_yy and that will give an underestimated value CSTV_90%.

The subsequent r-modified-y on x regression was used to drive the CSTV_90% from Eqn 3 of the Dyson and Conyers (2013) paper, where it was reported as 21.4 (up from 18.06). However, the left-hand side of Eqn 3 in Dyson and Conyers (2013) was an r-adjusted centroid ln (Colwell-P), which is $2.7824 + (\frac{\ln (Colwell P) - 2.7824}{0.408})$ . This adjustment of the left-hand side of the equation was not considered when they computed the CSTV_90%. Based on this model and giving attention to left-hand adjustment, our calculation shows the CSTV_90% remains 18.06, which is the effect of switching axes. We believe the estimate of CSTV_90% should not be modified with algebraic adjustments.

Correndo et al (2017) followed the ALCC algorithm but improved the CI by discarding division by r. However, rotation of the axes was also used in this method. Eqns 2, 3, 4, 5 and 6 in the Correndo et al. (2017) paper were used to compute CSTV_90%. There is a potential issue between the Eqn 2 and its reference of Legendre and Legendre (1998, p. 503), where it is stated that ${\tilde{β}}_{1} = \frac{r^{2}}{{\hat{β}}_{1}}$ . We believe that the stated result by Legendre and Legendre (1998, p. 503) is mathematically correct. Further discussion of this paper was minimised due to the similar rotation issue and use of Eqn 2 (Correndo et al. 2017).

The original calibration for wheat (Triticum aestivum) and Colwell-P (Colwell 1963) produced an estimated critical STV of about 30 mg kg⁻¹ based on a 7.5-cm (3 inches) deep soil sample. This corresponds to a range of 23–30 mg kg⁻¹ with the current 10 cm soil sampling depth, depending on the degree that the concentration of P at 0–7.5 cm depth is either diluted or maintained at 7.5–10 cm. While Colwell (1963) produced a single critical STV, it soon became apparent that the 90% critical STV varied with soil type, ranging from 10 mg kg⁻¹ on a sand in Western Australia to 32 mg kg⁻¹ on cooler Tasmanian soils (Moody and Bolland 1999). The critical STV for wheat and P was then shown to vary from 17 to 40 mg kg⁻¹ (Moody and Bolland 1999) as the P buffering capacity of a soil ranged from 6 to 279 (using the PBC method; Dear et al. 1992). Hence, soil test calibration needs to take account of relevant soil properties as more recently affirmed by Bell et al. (2013) in their calculations of critical STV for wheat and P across Australia. Further, the scatter within soil test calibrations has been shown to be influenced by sowing date and growing season rainfall (Conyers et al. 2020; Mason and McDonald 2021). Therefore, the issue of importance in this discussion is not the absolute critical soil test value and its uncertainty (i.e. the critical range for the soil test (Dyson and Conyers 2013) for this particular data set), but the optimal method of calculation of that critical range for any given data set of soil test – plant response. We now compare different analyses of the data set used here and in two other studies (Table 2).

Table 2.Comparison of curve fit determinations to the data set.

	Mitscherlich method Dyson and Conyers (2013)	ALCC method Dyson and Conyers (2013)	Modified ALCC method Correndo et al. (2017)	Proposed in this study
_90%	40	21.4	21.9	31.5
95% CI for CSTV_90%	Not determined	(17.0–26.6)	(19.4–24.5)	(20.6–42.4)
70% CI for CSTV_90%	Not determined	(18.9–23.9)	Not determined	(26.0–37.0)

It is not surprising that the conventionally used Mitscherlich method, which asymptotes to infinity, drags the CSTV to a higher value than other methods. Confidence intervals for the Mitscherlich method were not determined by Dyson and Conyers (2013). The ALCC method (Dyson and Conyers 2013) produced a CSTV of 18.06 or 21.4 (r modified), approximately half of that of the Mitscherlich method. The authors acknowledged the conservative nature of their method relative to potential P responsiveness (Dyson and Conyers 2013). Correndo et al. (2017) modified the ALCC method, being critical of the division by r of the transformed (and rotated) STVs. Their procedure reduced the 95% CI compared with the original analysis. The proposed method, without axes rotation and using the delta method, produced an intermediate estimate of the CSTV but broader 70% and 95% CI’s. It will be noted from our Table 1 that the size of the CI wider as STV increases, a result of the shape of the data in Fig. 1 and soil test calibration curves in general.

The present situation is that the ALCC method can be regarded as producing low CSTVs and sometimes broader CIs than alternative methods. For example, Correndo et al (2017) modified the ALCC method and tightened the CIs. This study provides a CSTV that is higher than that from the ALCC method but less than that from the conventional method of the Mitscherlich method. In fact, the present method bisects the Mitscherlich method and the ALCC method at 80, 90, and 95% in this data set.

These methods (Mitscherlich, ALCC, modified ALCC, and the present delta method) should be tested and compared over a range of data sets so that the best approach to weak associations, such as soil test calibrations, can be established. The National BFDC Data Base (Watmuff et al. 2013) provides such an opportunity.

Conclusion

We propose that the method described here should be widely applied for computing the estimates CSTV and its standard error. The advantage of this method is that no rotation of the axes is required, and the regression is therefore direct, and it is more flexible for incorporating other covariates into the model. The proposed method also overcomes the contentious issue of the division of the y-axis by the correlation coefficient, identified by Correndo et al. (2017). The proposed method is useful for developing other standardised CSTVs by analysing various data sets featuring weak associations between related variables, as commonly occurs with soil test calibrations. For this specific data set, the proposed method provides a reasonably suitable critical soil test value of P for achieving 90% relative yield of wheat.

Data availability

The data used are available from the corresponding author.

Conflicts of interest

The authors declare that they have no conflicts of interest.

Declaration of funding

This research did not receive any specific funding.

Acknowledgement

We acknowledge the provision of the data from the Better Fertiliser Decisions for Crops database owned and managed by the Grains Research and Development Corporation, Australia.

References

Alexandratos N, Bruinsma J (2012) World agriculture towards 2030/2050: the 2012 revision. In ‘ESA Working Paper No. 12-03.’ FAO, Rome. Available at https://www.fao.org/4/ap106e/ap106e.pdf

Bell R, Reuter D, Scott B, Sparrow L, Strong W, Chen the late W (2013) Soil phosphorus–crop response calibration relationships and criteria for winter cereal crops grown in Australia. Crop & Pasture Science 64(5), 480-498.
| Crossref | Google Scholar |

Brennan RF, Bell MJ (2013) Soil potassium–crop response calibration relationships and criteria for field crops grown in Australia. Crop & Pasture Science 64, 514-522.
| Crossref | Google Scholar |

Colwell JD (1963) The estimation of the phosphorus fertilizer requirements of wheat in southern New South Wales by soil analysis. Australian Journal of Experimental Agriculture and Animal Husbandry 3(10), 190-197.
| Crossref | Google Scholar |

Conyers M, Bell R, Bell M (2020) Factors influencing the soil-test calibration for Colwell P and wheat under winter-dominant rainfall. Crop & Pasture Science 71(2), 113-118.
| Crossref | Google Scholar |

Correndo AA, Salvagiotti F, García FO, Gutiérrez-Boem FH (2017) A modification of the arcsine-log calibration curve for analysing soil test value-relative yield relationships. Crop & Pasture Science 68(3), 297-304.
| Crossref | Google Scholar |

Dear BS, Helyar KR, Muller WJ, Loveland B (1992) The P fertilizer requirements of subterranean clover, and the soil P status, sorption and buffering capacities from two P analyses. Australian Journal of Soil Research 30(1), 27-43.
| Crossref | Google Scholar |

Dyson CB, Conyers MK (2013) Methodology for online biometric analysis of soil test-crop response datasets. Crop & Pasture Science 64(5), 435-441.
| Crossref | Google Scholar |

Legendre P, Legendre L (1998) Interpretation of ecological structures. In ‘Numerical ecology. Vol. 20’. 2nd English edn. (Eds P Legendre, L Legendre) pp. 497–545. (Elsevier: Amsterdam)

Mason S, McDonald G (2021) Time of sowing influences wheat responses to applied phosphorus in alkaline calcareous soils in a temperate climate. Crop & Pasture Science 72(11), 861-873.
| Crossref | Google Scholar |

Moody PW, Bolland MDA (1999) Phosphorus. In ‘Soil analysis: an interpretation manual’. (Eds KI Peverill, LA Sparrow, DJ Reuter) pp. 187–220. (CSIRO Publishing: Melbourne, Australia)

Rohan M, Sarmah AK (2023) Computation of standard error for half-life estimation using various dissipation models for regulatory purposes. Science of The Total Environment 893, 164773.
| Crossref | Google Scholar | PubMed |

Seber G, Wild C (1989) ‘Non-linear regression.’ (John Wiley & Sons: New York, NY, USA)

Speirs SD, Reuter DJ, Peverill KI, Brennan RF (2013a) Making better fertiliser decisions for cropping systems in Australia: an overview. Crop & Pasture Science 64(5), 417-423.
| Crossref | Google Scholar |

Speirs SD, Scott BJ, Moody PW, Mason SD (2013b) Soil phosphorus tests II: a comparison of soil test–crop response relationships for different soil tests and wheat. Crop & Pasture Science 64(5), 469-479.
| Crossref | Google Scholar |

Watmuff G, Reuter DJ, Speirs SD (2013) Methodologies for assembling and interrogating N, P, K, and S soil test calibrations for Australian cereal, oilseed and pulse crops. Crop & Pasture Science 64(5), 424-434.
| Crossref | Google Scholar |

An improved method for biometric analysis of soil test – crop response data sets

Abstract

Introduction

Materials and methods

Data

Scope of the paper

Mathematical equivalent

Calibration RY vs STV

Computation of CSTV

Delta method

Computation of standard error of CSTVα

Results

Discussion

Conclusion

Data availability

Conflicts of interest

Declaration of funding

Acknowledgement

References

Computation of standard error of CSTV_α