Mapping the impact of subsoil constraints on soil available water capacity and potential crop yield
Mikaela J. Tilse A * , Thomas F. A. Bishop A , John Triantafilis B and Patrick Filippi A
A * , Thomas F. A. Bishop A , John Triantafilis B and Patrick Filippi A
A Precision Agriculture Laboratory, Sydney Institute of Agriculture, School of Life and Environmental Sciences, Faculty of Science, The University of Sydney, Sydney, NSW 2006, Australia.
B Manaaki Whenau – Landcare Research, Lincoln, New Zealand.
Crop & Pasture Science 73(6) 636-651 https://doi.org/10.1071/CP21627
Submitted: 9 August 2021 Accepted: 25 January 2022 Published: 25 February 2022
© 2022 The Author(s) (or their employer(s)). Published by CSIRO Publishing. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)
Abstract
Context: The depth-to a constraint determines how much of the soil profile, and the water it contains, can be accessed by plant roots. Information describing the impacts of soil constraints on available water capacity (AWC) and yield is important for farm management, but is rarely considered in a spatial context.
Aims and methods: The depth-to three yield-limiting constraints (sodicity, salinity, and alkalinity) was mapped across ∼80 000 ha in northern New South Wales, Australia using machine learning and digital soil mapping techniques. Soil AWC was calculated using soil data and pedotransfer functions, and water use efficiency equations were used to determine potential yield loss due to the presence of soil constraints. From this, the most-limiting constraint to yield was mapped.
Key results: One or more constraints were found to be present across 54% of the study area in the upper 1.2 m of the soil profile, overall reducing the AWC by ∼50 mm and potential yield by an average of 1.1 t/ha for wheat and 0.8 bales/ha for cotton. Sodicity (Exchangeable Sodium Percentage > 15%) was identified as the most-limiting constraint to yield across the study area.
Implications: The simplification of multiple sources of information into a single decision-making tool could prove valuable to growers and farm managers in managing soil constraints and understanding important interactions with available water and yield.
Keywords: decision trees, digital soil mapping, pedotransfer function, precision agriculture, Random Forest, soil constraints, soil water, yield potential.
Introduction
Crop yields vary spatially, and season to season, in response to the interactions between climate, soil, and management (Filippi et al. 2019b). A large part of this variability is due to the heterogeneity of soil physical and chemical properties (Dang et al. 2010). Capturing and understanding this variability is important for informing management decisions to drive more profitable, and sustainable, cropping systems.
Soil constraints are chemical or physical properties of the soil that may impede root growth and limit crop yields (van Gool et al. 2005). While approximately 10% of Australia’s land mass is considered arable (Looney 1991) and features many desirable physical and chemical soil characteristics, over three-quarters of these soils have one or more constraints in the surface and/or subsoil (Bot et al. 2000). The alluvial cotton and grain growing valleys of eastern Australia have highly productive soils, however agricultural production is still limited by the presence of soil constraints, with the most prevalent being high levels of soil salinity, sodicity, and alkalinity.
Sodic soils can significantly limit plant growth and yields, causing dispersion, soil structural decline, and a reduction in the soils’ plant-available water capacity (AWC) (Hazelton and Murphy 2016; Isbell 2016). Soil salinity, measured by the electrical conductivity (EC) of the soil, imposes water stress via osmotic effects or high salt concentrations, negatively impacting the yields of most crops (Shaw 1997; Dang et al. 2006; Hazelton and Murphy 2016). Extremely alkaline pH values restrict root growth via nutrient deficiencies and toxicities (Hazelton and Murphy 2016). The values at which soil sodicity, salinity, or alkalinity become constraining to crop growth and yield varies due to the interactions between different soils and crop types, and environmental conditions such as rainfall and temperature.
Through chemical or physical impediments, the presence of one or more constraints in the soil profile limits the ability of a crop to utilise stored soil moisture (Dang et al. 2004). The depth-to a particular constraint determines how much of the soil profile, and the water it contains, can be accessed by roots (van Gool et al. 2005). It is possible to ameliorate or manage constraints to optimise crop yields. However, the efficacy and economic viability of such management decisions depends on the nature and impact of the constraint(s) (Bennett et al. 2015). If the depth-to a constraint is not known, resources such as fertiliser and irrigation may be applied unnecessarily, and therefore be wasted (Filippi et al. 2020a). Currently, information describing the distribution of several subsoil constraints, and the depth at which they occur, is not widely available to growers and farm managers.
Many broadacre farmers now have access to vast amounts of publicly accessible and farm-sourced data (Bramley and Ouzman 2019), including proximal and remote sensing information, soil surveys, and yield monitoring data such as Landsat and MODIS imagery, gamma radiometric surveys, rainfall grids, and terrain attribute data. Advancements in digital soil mapping (DSM), computing technologies, and available covariates for mapping, are enabling the integration of information from across a range of spatial and temporal extents to inform management decisions (e.g. Dang et al. 2011). Despite these advancements however, much of this information is underutilised by growers and farm managers, and the translation of this knowledge into useful decision-making tools is limited.
A suite of nation-wide maps for several soil properties is available, collectively known as the Soil and Landscape Grid of Australia (SLGA) (Grundy et al. 2015). Maps for 13 soil properties, including EC for salinity and pH for acidity/alkalinity, are provided at a 90 m spatial resolution. However, some agronomically-important constraints such as soil sodicity [i.e. Exchangeable Sodium Percentage (ESP)] are not included and predictions for some soil properties such as AWC may be imprecise as estimates are based on a small number of in-field measurements (Austin et al. 2019). Also, the six depth intervals, which are provided at the standards of the GlobalSoilMap project (i.e. 0–0.05, 0.05–0.15, 0.15–0.30, 0.30–0.60, 0.60–1.00, 1.00–2.00 m; Arrouays et al. 2014), and coarse vertical resolutions in the subsoil (e.g. 0.60–1.00 m) make it difficult to accurately determine the depth at which a constraint is reached.
Several agronomically-important soil constraints have been mapped at the regional, farm, and field scale. Dang et al. (2010) mapped the spatial distribution of pH, EC, ESP, and chloride constraints across the northern grains region of Queensland, although the depth at which a constraint threshold was reached was not considered. In a study of soil salinity and sodicity constraints in a semi-arid irrigation region of southern Australia, Filippi et al. (2018a) produced individual maps for several depth increments down the soil profile to capture the vertical distribution of soil salinity and sodicity constraints. While informative, these maps are difficult for growers to interpret due to the overwhelming volume of information they provide. Leenaars et al. (2018) estimated and mapped the influence of a range of soil properties on rootzone depth, effectively mapping the depth-to root-constraining factors, across sub-Saharan Africa. In this study, the relatively coarse-resolution GlobalSoilMap standard depths were used and conservative assumptions were made about where constraints were being met, as the authors assumed that the upper depth of the shallowest layer a constraint was reached was the depth that a constraint was first reached.
The depth-to individual soil constraints has successfully been mapped at the field and catchment- scales at a fine vertical resolution. Filippi et al. (2019a) and Filippi et al. (2020a) mapped the depth-to pH and ESP constraints, respectively, on a single map at a 1 cm vertical resolution. Both studies mapped individual soil constraints in 3D to successfully build a single decision-making tool that simplified volumes of data. However, the assessment of multiple constraints in a single analysis and an assessment of their interactions with other soil processes was not considered. While Dang et al. (2010) and Sadras et al. (2003) modelled the relationship between soil constraints, AWC and yield at single points throughout north-eastern and southern Australia, respectively, these interactions were not considered spatially and the impacts of constraints on soil AWC was not quantified or mapped.
This study aims to build upon previous research to map the depth-to multiple subsoil constraints and quantify their impact on AWC and potential cotton and wheat yield across multiple fields and farms. Different subsoil constraints at agronomically-important thresholds, specifically pH 1:5 soil:water ( ) > 9 for alkalinity, EC 1:5 soil:water (EC1:5) > 1 dS/m for salinity, and ESP > 15% for sodicity, were mapped across the Ashley Irrigation Area in the Gwydir Valley of northern NSW, and a fine-scale (30 m) map of the most-limiting constraint to yield was produced. The workflow developed in this study aims to integrate multiple sources of information about the interactions between subsoil constraints, AWC, and yield to provide a single decision-making tool for the on-farm management of subsoil constraints.
) > 9 for alkalinity, EC 1:5 soil:water (EC1:5) > 1 dS/m for salinity, and ESP > 15% for sodicity, were mapped across the Ashley Irrigation Area in the Gwydir Valley of northern NSW, and a fine-scale (30 m) map of the most-limiting constraint to yield was produced. The workflow developed in this study aims to integrate multiple sources of information about the interactions between subsoil constraints, AWC, and yield to provide a single decision-making tool for the on-farm management of subsoil constraints.
Materials and methods
The study area
The study was conducted across a collection of farms to the north–west of the Ashley Irrigation Area (centered approximately on latitude 29°20′45″S, longitude 149°49′7″E), which is located north of Moree in the Gwydir Valley of northern NSW, Australia (Fig. 1). The total study area encompassed ∼81 877 hectares (ha) and included grazing areas, and dryland and irrigated cropping fields. Irrigated cotton (Gossypium hirsutum) and grains including wheat (Triticum aestivum) are the most common crops grown in the study region. The climate of the region is semi-arid with long, hot summers, cool to mild winters and an annual mean temperature range between 26.9 and 12.6°C (Bureau of Meteorology (BOM) 2021). Rainfall is summer dominant, averaging 561.3 mm annually with a mean monthly maximum precipitation of 79.1 mm in January and minimum of 22.7 mm in April (Bureau of Meteorology (BOM) 2021). Grey and Brown Vertosols are the dominant soil types of the region according to the Australian Soil Classification (Isbell 2016).
|
|
Soil datasets
The soil data used in this study were obtained from two surveys conducted across the Ashley Irrigation Area (Fig. 1). Soil samples for Survey 1 were collected from a single field to the north–west of the Ashley Irrigation Area. A detailed description for the soil sampling design for Survey 1 can be found in Triantafilis et al. (2001). Briefly, soil samples were collected at 81 sites and subsampled at depth increments of 0–0.3, 0.3–0.6, 0.6–0.9, 0.9–1.2 m, resulting in a total of 405 individual samples available for Survey 1. Samples for Survey 2 were collected across the Ashley Irrigation Area from a mixture of soil cores subsampled at 30 cm depth increments down to 1.2 m and via an electromagnetic (EM) induction survey. A total of 145 sites and 1156 individual samples were available for Survey 2. A detailed description of data collection, soil sampling and laboratory analysis for Survey 2 can be found in Zhao et al. (2019). In each of the surveys, measurements were taken for  , EC1:5, ESP, and particle size fractions (Triantafilis et al. 2001; Zhao et al. 2019).
, EC1:5, ESP, and particle size fractions (Triantafilis et al. 2001; Zhao et al. 2019).
The number of sampling sites, and the number of and depth of sampling intervals varied between the two legacy soil surveys. Only soil data from the top 120 cm of the soil profile was used in this study. The total soil dataset included 1561 samples from 226 individual sites (Fig. 1).
Spatial covariates for modelling and mapping
The covariates used for modelling and mapping consisted of satellite imagery, gamma radiometrics, a silica index map, elevation, and derived terrain attributes. These covariates were at different spatial and temporal resolutions.
Landsat 7 satellite imagery was accessed through the Google Earth Engine (GEE) (Gorelick et al. 2017). All tier 1 surface reflectance imagery from 1 January 2000 to 31 December 2017 was accessed at a 30 m spatial resolution. Landsat 7 satellite imagery was chosen as it provides data over a longer time period compared to other products (e.g. Sentinel 2), and can be used to represent long-term trends using consistent data with a ∼16-day revisit time. The banding error generated by the failure of the Scale Line Corrector (SLC) in the Landsat 7 imagery was negated as statistics were obtained from many images over the available time period (Filippi et al. 2020b). A cloud-masking filter was applied to all images to remove pixels affected by cloud cover, and the 5th, 50th and 95th percentile statistics were calculated for each pixel for the entire data time-series to reflect the full range of the data. The Landsat 7 imagery was used to derive Red Band and Normalised Difference Vegetation Index (NDVI) imagery. The 5th, 50th and 95th percentiles of the NDVI imagery were selected to reflect crop growth and vigour through time and to indicate patterns of production potential. The Red Band imagery (5th, 50th and 95th percentiles) was used to represent topsoil colour. The timing of the remote sensing imagery and soil samples was not considered to be an issue as soil constraints are expected to remain relatively stable over time (Dang et al. 2011). The imagery was used to represent long-term trends to filter out more temporary, seasonal effects, rather than the surface reflectance at the time of sampling.
A digital elevation model (DEM) was obtained from the ELVIS (ELeVation Information System) platform at a 30 m resolution (Department of Finance, Services and Innovation 2020). Terrain attributes, derived from the Shuttle Radar Topography Mission (SRTM), were obtained from CSIRO’s Data Access Portal at a 30 m spatial resolution, including slope percent, degree, relief, topographic wetness index (TWI), multi-resolution ridge top flatness (MrRTF), multi-resolution valley bottom flatness (MrVBF), aspect, plan and profile curvature, and topographic position index (TPI).
Airborne gamma radiometric dose rate, uranium (Rad U), thorium (Rad Th) and potassium (Rad K) data, and their respective ratios (Rad U:Th, Rad U:K, Rad U2:Th, Rad Th:K), were obtained through the Geophysical Archive Data Delivery System (GADDS), Geoscience Australia, at a ∼100 m spatial resolution. All radiometric products were processed with low-pass filtering (Minty et al. 2009).
A silica index map at a resolution of 1:250 000, as described by Gray et al. (2016), was also used as a covariate for modelling. This index map represents the silica content of a soils’ parent material, relating to soil texture and influencing other important soil properties.
Spatial modelling of soil properties
Across the study area, soil pH, EC, and ESP were modelled. These were considered the most agronomically-important subsoil constraints to irrigated and dryland cropping in the region. Clay, sand, and soil organic carbon (SOC) content was also mapped across the area as inputs for the pedotransfer function (PTF; Padarian Campusano 2014) to estimate AWC. All data analyses were performed in the open-source software R, ver. 4.0.4 (R Core Team 2021).
Vertical resampling of soil data to 120 cm
The number of sampled increments and depth intervals varied between the two legacy soil surveys. To overcome these inconsistencies, equal-area quadratic smoothing splines (Bishop et al. 1999), which apply a set of local quadratic functions to describe a smooth curve through a set of points, were used to standardise depth increments. Data for all soil properties were re-sampled to 1 cm depth increments to 120 cm to give an estimate of the depth-to-constraint at a fine vertical resolution down the profile.
Model validation
The accuracy and quality of each Random Forest model was tested using leave-one-site-out cross validation (LOSOCV). The LOSOCV involved removing all data from one site, using this as the validation data, and leaving the remaining sites as a calibration dataset. This LOSOCV process was repeated for all sites (i.e. a total of 226 times). For each iteration, whole profiles were removed during the LOSOCV to ensure that soil samples from the same site were not used in both the calibration and validation datasets. Model quality was assessed using the Lin’s Concordance Correlation Coefficient (LCCC) (Lin 1989) and Root Mean Square Error (RMSE).
Modelling soil properties
At each of the 226 sites, the associated spatial covariates described above were extracted for the study area. The 1 cm splined soil data for all soil properties were then stacked and combined with these covariates to create a single dataset. The mid-depth between the upper and lower depth of each splined interval (i.e. 0.5 cm for the 0–1 cm depth interval) was also calculated and added as a predictor variable.
Random Forest models (Breiman 2001), which are a suite of decision trees, were used to build a relationship between each soil property and the predictor variables (Table 1). Random Forests were chosen due to their efficiency in terms of identifying relationships between the response and predictor variables that can be non-linear and involve interactions (Breiman 2001). Spatial covariates were selected based on their variable importance measure, discussed below, and the combination of covariates that resulted in the best model quality. All depths were modelled together instead of modelling each depth increment individually.

|
For the Random Forest models, the ‘ranger’ package, ver. 0.12.1 (Wright and Ziegler 2017), in the software R was used, which enables the fast implementation of Random Forest models that is well suited to high-dimensional data (Wright and Ziegler 2017). For each Random Forest model, the number of trees was set to 500 and the number of variables to possibly split at in each node (mtry) was set to the default option, which was the rounded-down square root of the number of variables within each model (Wright and Ziegler 2017).
Variable importance
The ‘permutation’ variable importance measure within the ‘ranger’ package in R (ver. 0.12.1; Wright and Ziegler 2017) was used to assess the importance of predictor variables in each of the Random Forest models. The permutation variable importance approach is a measure of the importance of a variable on the final prediction, measured as the difference in prediction accuracy with and without the help of the predictor variable (Strobl et al. 2008; Wright et al. 2016). Covariates with a poor relationship to the response variable, in this case the relevant soil attributes, will have a variable importance close to zero. For more strongly related covariates, the variable importance score will increase and the prediction performance will be improved following the addition of the covariate to the model (Filippi et al. 2020a).
Mapping the depth-to constraint
To map the depth-to a constraint, a 30 m resolution spatial covariate grid of the Ashley Irrigation Area was created. All spatial covariates were then extracted onto this grid using the nearest neighbour method. The Random Forest models were used to predict the spatial distribution of pH, EC, and ESP constraints onto the spatial covariate grid. Predictions were made at each 1 cm depth increment down to 120 cm, resulting in 120 maps for each soil constraint. All 120 maps were combined and stacked. From this, the depth-to which pH, EC, and ESP constraints were first reached in the soil profile were identified for each grid point by nominating a threshold value. The threshold values of 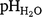 > 9, EC1:5 > dS/m, and ESP > 15% were chosen as they were determined to be the values for each constraint that significantly impeded root growth, resulting in negative impacts on crop growth and yield for wheat and cotton (Hazelton and Murphy 2016; Isbell 2016). This information was then mapped across the study area, showing the depth to each soil constraint threshold.
> 9, EC1:5 > dS/m, and ESP > 15% were chosen as they were determined to be the values for each constraint that significantly impeded root growth, resulting in negative impacts on crop growth and yield for wheat and cotton (Hazelton and Murphy 2016; Isbell 2016). This information was then mapped across the study area, showing the depth to each soil constraint threshold.
Modelling available water capacity
The AWC of the top 120 cm of the soil profile was calculated using PTFs from modelled clay and sand content, and bulk density derived from SOC (Padarian Campusano 2014). The PTFs were applied at each 1 cm depth increment down to 120 cm to calculate field capacity (FC) and permanent wilting point (PWP), and AWC was calculated as the difference between the two for each layer. In the PTF, the FC was defined as the volumetric water content of an initially saturated soil following 2–3 days of drainage, also known as the drained upper limit (DUL; Veihmeyer and Hendrickson 1949). The PWP was defined as the volumetric water content remaining in the soil after a healthy crop has reached maturity in water-limited conditions with uninterrupted root development, also referred to as the crop lower limit (CLL; Hochman et al. 2001).
Interactions between depth-to-constraint and available water capacity
The interactions between the depth-to a constraint (pH, EC, and/or ESP) and AWC was assessed. For constraints reached within the top 30 cm of the soil profile, the depth-to-constraint was fixed at 30 cm as constraints were assumed to be non-limiting to plant access to water above this depth. ‘Unconstrained’ AWC was calculated as the AWC without considering the presence of constraints. The AWC for each 1 cm soil layer was summed down to the depth any constraint was reached so that the ‘constrained’ AWC map excluded soil water beyond the depth-to a constraint. The total unavailable water due to the presence of constraints was calculated as the difference between unconstrained and constrained AWC. The unconstrained and constrained AWC, and unavailable water due to the presence of any constraint, was mapped across the study area. The impact of individual pH, EC, and ESP constraints on AWC was also calculated to estimate potential yield loss (see Results - Potential yield loss due to the presence of constraints) and most-limiting constraint to yield (see Results - Most-limiting constraint to yield) but are not presented.
Potential yield loss due to the presence of constraints
The map of unavailable water due to the presence of all constraints combined, and of each individual constraint (described above), was used to determine the potential lost yield for wheat and cotton crops. Water use efficiency (WUE) equations developed by French and Schultz (1984) and Roth et al. (2013) were used to estimate potential lost yield for wheat and cotton, respectively. The French and Schultz (1984) equation estimated WUE for wheat grain yield to be 20 kg/ha.mm water. The WUE equation developed by Roth et al. (2013) estimated cotton lint yield to be >3 kg/ha.mm water, so in this study 3 kg/ha.mm water was used as a conservative estimate of yield loss. For cotton, potential yield loss was presented in bales/ha as the standard industry measurement of lint yield is 1 bale = 227 kg (Roth et al. 2013). A land-use map of NSW, obtained from the Office of Environment and Heritage (OEH), NSW Government (Office of Environment and Heritage – OEH 2017), was simplified into two categories – cropping (arable) and other. The maps of potential yield loss were masked to only include arable land across the study area.
Most-limiting constraint
The potential yield loss maps for the depth-to pH, EC, and ESP constraints were stacked and the greatest potential yield loss was calculated at each grid point. This value was assigned to the corresponding constraint (pH, EC, or ESP) and was determined to be the most-limiting constraint to yield. This was then mapped across the study area.
Results
Soil analytical results
The range, mean, and median values were calculated for soil pH, EC, ESP, clay, sand, and SOC contents (Table 2). Soil pH was generally constant with depth (Fig. 2) with a range of 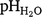 6.60–10.44 and a mean of 8.58 (Table 2). On average, soil EC1:5 was 0.60 dS/m and increased with depth up to a value of 3.30 dS/m (Fig. 2, Table 2). Soil ESP averaged 10.99% across the study area and steadily increased with depth (Fig. 2, Table 2). Most samples were classified as medium-heavy clays, with a mean clay content of 53.97% that remained relatively constant down the profile (Fig. 2, Table 2). Sand content was steady with depth, averaging 19.56% (Fig. 2, Table 2). SOC content ranged between 0.18% and 1.06%, averaging 0.47% overall and decreased down the soil profile (Fig. 2, Table 2).
6.60–10.44 and a mean of 8.58 (Table 2). On average, soil EC1:5 was 0.60 dS/m and increased with depth up to a value of 3.30 dS/m (Fig. 2, Table 2). Soil ESP averaged 10.99% across the study area and steadily increased with depth (Fig. 2, Table 2). Most samples were classified as medium-heavy clays, with a mean clay content of 53.97% that remained relatively constant down the profile (Fig. 2, Table 2). Sand content was steady with depth, averaging 19.56% (Fig. 2, Table 2). SOC content ranged between 0.18% and 1.06%, averaging 0.47% overall and decreased down the soil profile (Fig. 2, Table 2).

|
Model quality
After performing the LOSOCV by whole soil profiles, the LCCC and RMSE were used to assess model predictions. The quality statistics showed that clay content was predicted with greatest accuracy (LCCC = 0.64) (Table 3). Soil EC, sand, and SOC were predicted with comparable accuracy (LCCC = 0.60), followed by ESP (LCCC = 0.50). The model used to predict soil pH performed most poorly (LCCC = 0.38) (Table 3).

|
Variable importance
The top five most important covariates for each soil property and model are presented (Table 4). Generally, a mixture of covariates representing terrain attributes, radiometrics, and satellite imagery were important within each of the six models (Table 4). All available covariates were required to build the clay model (Table 1). Conversely, the pH model was built using the least number of covariates, using predominately satellite imagery and terrain attributes (Tables 1 and 4). Overall, radiometrics and satellite imagery, including both NDVI and Red Band imagery, were the most important groups of covariates used within all models (Table 4). Mid-depth, MrRTF, Rad U:Th, and RED 95 imagery were used consistently across each of the six models (Tables 1 and 4).

|
Depth-to-constraint maps
Overall, there was little similarity in the spatial distribution of the depth-to a constraint when comparing each of the soil constraint thresholds (i.e. pH, EC, and ESP) (Fig. 3). Approximately 54% of the study area was affected by at least one constraint in the top 120 cm of the soil profile. Less than 1% of the total study area was constrained by a 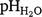 of 9 (Fig. 3, Table 5). Over 25% of soils were found to be constrained by an EC1:5 constraint of 1 dS/m somewhere in the top 120 cm of the soil profile, mostly between 30 and 90 cm (Fig. 3, Table 5). These were found throughout the east of the study area, as well as a smaller central region and areas to the north–west (Fig. 3). The map of the depth-to an ESP constraint of 15% showed a high degree of spatial variability and revealed that over 35% of soils were constrained by sodicity somewhere in the top 120 cm of the soil profile (Fig. 3, Table 5). Most soils constrained by an ESP of 15% were within the top 30 cm of the soil profile and were widely distributed throughout the study area (Fig. 3, Table 5).
of 9 (Fig. 3, Table 5). Over 25% of soils were found to be constrained by an EC1:5 constraint of 1 dS/m somewhere in the top 120 cm of the soil profile, mostly between 30 and 90 cm (Fig. 3, Table 5). These were found throughout the east of the study area, as well as a smaller central region and areas to the north–west (Fig. 3). The map of the depth-to an ESP constraint of 15% showed a high degree of spatial variability and revealed that over 35% of soils were constrained by sodicity somewhere in the top 120 cm of the soil profile (Fig. 3, Table 5). Most soils constrained by an ESP of 15% were within the top 30 cm of the soil profile and were widely distributed throughout the study area (Fig. 3, Table 5).
Interactions between depth-to-constraint and available water capacity
The interactions between the depth-to shallowest constraint (i.e. pH, EC, or ESP) and AWC was mapped across the study area. Without the presence of constraints, there was little spatial variability in AWC and much of the study area was predicted to have a moderate-to-high AWC that averaged 161.89 mm (Fig. 4). As expected from the methodology, total constrained AWC averaged 111.15 mm across the study area and a lower AWC due to the presence of constraints was apparent across the north–east of the study area (Fig. 4). Soils with a higher constrained AWC were located predominately to the south of the study area and within narrow bands running throughout central regions (Fig. 4). Soil AWC with or without constraints ranged between 14.13 and 282.15 mm. The total unavailable water due to the presence of constraints was highly spatially variable and averaged 50.73 mm across the study area, ranging between 0 and 206.44 mm. More water was unavailable due to constraints in clearly defined fields to the far west and north–east of the study area, as well as a small central region (Fig. 4).
|
|
Potential yield loss due to the presence of constraints
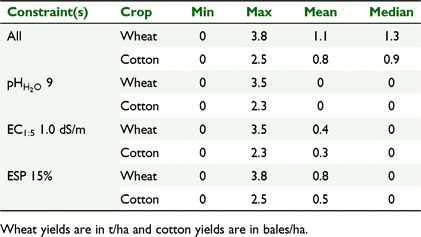
Based on calculations from WUE equations (French and Schultz 1984; Roth et al. 2013) using AWC estimates (Fig. 4), the distribution of potential yield losses for wheat and cotton due to the presence of all constraints (i.e. pH, EC, and ESP) across arable regions of the study area (Fig. 5) were spatially similar to the distribution of unavailable AWC due to the presence of constraints (Fig. 4). On average, potential yield loss due to all constraints for wheat was 1.1 tonnes (t)/ha and ranged from 0 to 3.8 t/ha (Table 6). For cotton, potential losses in lint yield averaged 0.8 bales/ha with a range between 0 and 2.5 bales/ha (Table 6).
|
|
|
As for the depth-to-constraint maps (Fig. 3), there was little similarity in the spatial distribution of yield losses due to the presence of each individual pH, EC, and ESP constraint (Fig. 5). Therefore, the greatest potential yield losses were predicted to be attributed to an ESP constraint of 15%, averaging 0.4 t/ha for wheat (range 0–3.8 t/ha) and 0.8 bales/ha for cotton (range 0–2.5 bales/ha) (Table 5). Maximum potential yield losses due to an EC1:5 constraint of 1 dS/m were 3.5 t/ha for wheat and 2.3 bales/ha for cotton, averaging 0.4 t/ha and 0.3 t/ha, respectively (Table 5). Potential yield losses due to a 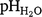 constraint of 9 ranged between 0 and 3.5 t/ha for wheat and 0–2.3 bales/ha for cotton, however these impacts were negligible as <1% of the total study area was constrained (Table 5, Fig. 5).
constraint of 9 ranged between 0 and 3.5 t/ha for wheat and 0–2.3 bales/ha for cotton, however these impacts were negligible as <1% of the total study area was constrained (Table 5, Fig. 5).
Most-limiting constraint to yield
The most-limiting constraints to yield were identified from the potential yield loss maps, and the predictions were mapped across arable regions of the study area (Fig. 6). Over 36% of arable soils were most-limited by a sodicity constraint (ESP > 15%), followed by salinity (EC1:5 1 dS/m) which affected approximately 23% of arable soils (Fig. 6). Less than 1% of arable soils were most-limited by an alkalinity constraint (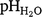 > 9) (Fig. 6). Yields across the remaining 38% of arable land were not limited by any constraint within the top 120 cm of the soil profile (Fig. 6).
> 9) (Fig. 6). Yields across the remaining 38% of arable land were not limited by any constraint within the top 120 cm of the soil profile (Fig. 6).
|
|
Discussion
Model quality and modelling approach
Random Forest models were developed to predict soil properties in 3D. As whole soil profiles were removed from the model during LOSOCV, potential interactions with other samples at different depths from the same site were eliminated. A comparison of LOSOCV techniques performed by Filippi et al. (2020a) found that validating models with splined data, as was applied in this study, is a robust approach that is comparable with using un-splined data, therefore giving us confidence in our predictions and model quality assessment used here.
Various soil properties have been modelled on comparable soils across northern NSW. Soil ESP was predicted with moderate accuracy and model performance in the current study was similar to the Random Forest-based estimates made by Filippi et al. (2020a) at the catchment scale. The quality of predictions for pH in this study were better than those obtained by Ma et al. (2021) across the Edgeroi District but poorer than those from Filippi et al. (2019a). The substantially lower sampling density here and uneven distribution of samples across the study area may explain the poorer model performance, with over 35% of all legacy soil survey samples obtained from a single field in the north–west of the study area (i.e. Survey 1, Fig. 1) potentially contributing to a more accurate prediction of soil properties in this region compared to the south of the study area. This is a common problem when using legacy soil data, as new data are expensive to obtain.
Good predictions were obtained for clay and were comparable to estimates across the Cox’s River catchment made by Bishop et al. (2015) and better than those obtained by Ma et al. (2021) across the Edgeroi District, both located just south of the Ashley Irrigation Area. Similar model quality statistics were obtained by Filippi et al. (2018b) when estimating soil EC across similar cotton-growing soils in southern NSW. Predictions of SOC content made across the Edgeroi District by Malone et al. (2009) and Ma et al. (2021) were both poorer than those obtained in this study, as were predictions obtained for the sand particle size fraction by Buchanan et al. (2012) further west across the Bourke Irrigation District.
The most important covariate for soil pH, EC, ESP, and SOC models was mid-depth, which is unsurprising considering these properties were most variable with depth (Fig. 2). The relatively high importance of radiometric covariates within almost all models makes sense, as these factors provide information about soil parent material and relate to soil forming processes (Bishop et al. 2015).
Depth-to-constraint
While subsoil alkalinity is considered an inherent property of the alluvial cotton-growing valleys of northern NSW, less than 1% of the study area was constrained by alkalinity within the top 120 cm of the soil profile. This is substantially less than predictions across the Namoi Valley, located south of the Gwydir Valley (Filippi et al. 2019a), but is not unexpected as soil pH values for the Namoi Valley area are higher than those for the lower Gwydir Valley (Singh et al. 2003).
Both soil EC and ESP values increased with depth and EC threshold limits were mostly exceeded in the subsoil between 30 and 60 cm (Fig. 3), which is typical of soils across the plains of northern NSW (Dang et al. 2006). The distribution of salinity and sodicity constraints across the study area were largely contrasting, despite soil salinity and sodicity constraints being commonly found together across the shrink-swell clay soils of northern NSW (Dang et al. 2006). The majority of soils across Australia’s cotton growing regions are considered sodic (Northcote and Srene 1972; Naidu et al. 1995), and similar proportions of an ESP constraint of 15% have been found across the Namoi Catchment (Filippi et al. 2020a).
This study mapped the depth-to fixed constraint threshold values for pH, EC, and ESP based on known agronomic impacts to yield potential (Hazelton and Murphy 2016; Isbell 2016). While fixed constraint thresholds are useful in theory, in practice they do not reflect the complex interactions between different soil properties or the different conditions under which potential yield may be constrained. This study assumed that the presence of a constraint at a fixed threshold value was an immediate barrier to root exploration down the profile (van Gool et al. 2005). However, a plants’ physical response to a soil constraint is not defined by a set value, and the magnitude of impact on root growth may vary for a range of constraint values. The use of ‘fuzzy’ boundaries that capture a range of potentially constraining threshold values and have relative impacts on root growth (and therefore yield), as opposed to rigid limits, may be more appropriate in future studies to capture the variation in response by different crops. Likewise, not all crops may incur a growth or yield penalty at the same threshold value, and future work should consider different constraint threshold limits for a range of crop types and growth conditions.
Interactions between depth-to-constraint and AWC
Uncertainty about the availability of water is considered one of the most significant limitations to irrigated and dryland crop production in Australia (Roth et al. 2013). Estimates of AWC made in this study were comparable with others across northern NSW soils (Cull et al. 1981; Malone et al. 2009). However, these estimates were either limited to single points (Cull et al. 1981), or did not explicitly consider the influence of constraints on AWC (Cull et al. 1981; Malone et al. 2009). Sadras et al. (2003) and Dang et al. (2010) developed conceptual models to estimate plant available water and plant available water capacity, respectively, considering the influence of soil constraints. However, these relationships were derived from point-based observations and were not considered spatially.
Soil AWC has been mapped across large spatial extents and at the sub-field scale. Based on in-field observations of DUL and CLL, Padarian et al. (2014) used DSM techniques to map AWC across the Australian wheat belt. However, direct measurements of FC/DUL and PWP/CLL are time-consuming and expensive (Rab et al. 2009). The application of PTFs enables the estimation of soil properties using more readily available or more easily measured soil information that can provide more accurate predictions of AWC compared to DSM techniques (Austin et al. 2019). Both Rab et al. (2009) and Malone et al. (2009) applied PTFs to estimate AWC at the district level, however neither study considered, quantified, or mapped the impact of constraints on AWC.
The PTFs applied in this study to estimate DUL and CLL for AWC were generated and calibrated in an Australian context on similar (predominately Vertosol) soils (Padarian Campusano 2014). Thus, the AWC estimates produced here (Fig. 4) address precautions around model transportability (Padarian Campusano 2014), giving us confidence in our estimations.
Lost yield potential
Many agricultural soils across Australia feature physical or chemical characteristics that constrain crop production (Bot et al. 2000). Although interactions between subsoil constraints impact yields in different ways, as discussed, the deeper a constraint is reached in the soil, the higher crop yields will be (Filippi et al. 2019a, 2020a). Dalal et al. (2002) showed that a decrease in rooting depth from 105 to 45 cm resulted in a yield reduction for wheat from 3.5 to 1.5 t/ha across southern Queensland cropping soils. However, we cannot accurately state the degree to which subsoil constraints reduce AWC across the region without appropriate validation with observed yield data. Future work should validate potential crop yield losses with real yield maps to assess the validity of WUE equation-based estimates of constrained AWC and potentially identify other drivers of yield variability.
The interactions between subsoil constraints and yield have been extensively studied. Filippi et al. (2019a) and Filippi et al. (2020a) mapped the depth-to pH and ESP constraints, respectively, and assessed their impact on crop yields at the sub-field scale. While both studies found clear relationships between the depth-to a constraint and crop yield, the impact of constraints on AWC was not quantified and much of the available literature does not consider these interactions with yield. Although the conceptual model developed by Dang et al. (2010) considered realistic yield potential as a function of the interactions between constraints and AWC, the realistic yield potential was not explicitly calculated, and this relationship was also not considered spatially.
The map of unavailable water due to the presence of constraints produced in this study was integrated with WUE equations developed from French and Schultz (1984) and Roth et al. (2013) to estimate the potential yield loss due to individual and all constraints. Potential yield loss for cotton was lower than for wheat, although this is to be expected as cotton has a lower WUE of the harvestable component compared to wheat. Although similar constraint thresholds were considered for both cotton and wheat in this study, it should be acknowledged that these theoretical threshold values may not capture the full extent to which constraints impact AWC for different crop species.
In their simplest form, the French and Schultz (1984) and Roth et al. (2013) WUE equations do not account for the influence of soil factors on available water, nor do they consider the timing of rainfall, length of growing season, or variation in soil evaporation. This study attempted to account for interactions between soil constraints and AWC, while still maintaining the original simplicity of the WUE frameworks. By calculating potential crop yield with respect to constraint-limited AWC, the impact of subsoil constraints on yield and the soil environment has been accounted for and provides a more simplistic estimation of the extent of these interactions. Future work should use soil water balance models, for example that described by Wimalathunge and Bishop 2019 to assess the true impact of reduced AWC on yield rather than assuming lost AWC equals lost water over the entire season.
Practical applications
The effective amelioration and management of subsoil constraints relies on useful decision-making tools. Mapping the spatial distribution of subsoil constraints in 3D is not a novel approach, however, the integration of this information with PTFs to estimate AWC has not been explored in detail. This study explored a potential new workflow for identifying the most-limiting constraint to yield by considering the interactions between depth-to subsoil constraints, AWC, and potential crop yield. This single map presents these combined interactive effects and simplifies multiple sources of information into a single decision-making tool. This can then be used by growers and farm managers to guide the targeted amelioration or management of soil constraints.
The identification of limiting constraints to yield has long been a goal in research. Shatar and McBratney (2004) applied the boundary-line analysis (BLA) method to compare actual and potential yields and identify the most-limiting constraints to yield at the field scale. While the map produced by Shatar and McBratney (2004) is visually similar to the map identifying the most-limiting constraint produced in this study (Fig. 6), a BLA requires high-quality and accurate yield and soil information that is often not attainable by growers on-farm. Further, many BLA studies fail to consider the depth at which constraints were reached in the soil profile, nor do they consider the impact of constraints on AWC.
From this study, it is evident that ameliorating or managing subsoil sodicity across much of the study area should be a priority, while particular fields to the north should be managed to address salinity constraints (Fig. 6). While chemical and mechanical amelioration strategies, such as the application of gypsum in combination with cultivation, have been shown to be effective in treating soil sodicity (Page et al. 2018), understanding the depth-to and nature of a constraint is important for determining the feasibility of amelioration strategies and minimising unnecessary expenditure on resources.
Conclusions
Over 54% of the study area was constrained by one or more soil constraints (i.e. pH, EC, or ESP) somewhere in the top 120 cm of the soil profile. Soil sodicity (ESP > 15%) was identified as the most-limiting constraint to yield compared to salinity (EC1:5 1 dS/m) and alkalinity (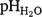 9). Total unconstrained AWC averaged 161.9 mm across the study area and total constrained AWC averaged 111.2 mm, with constraints reducing total AWC and soil water available for plant uptake by an average of 50.7 mm. Through WUE equations, potential yield loss was estimated to average 1.1 t/ha for wheat and 0.8 bales/ha for cotton, due to the presence of all constraints.
9). Total unconstrained AWC averaged 161.9 mm across the study area and total constrained AWC averaged 111.2 mm, with constraints reducing total AWC and soil water available for plant uptake by an average of 50.7 mm. Through WUE equations, potential yield loss was estimated to average 1.1 t/ha for wheat and 0.8 bales/ha for cotton, due to the presence of all constraints.
The workflow developed in this study effectively demonstrates the development of a useful decision-making tool to identify the most-limiting constraint to yield on a single map using readily available soil information, DSM techniques, and PTFs to better understand the impact of subsoil constraints. A map of the most-limiting constraint to yield, and its use in conjunction with additional independent information such as maps of the depth-to a constraint, is potentially useful for guiding decision-making for the amelioration and management of subsoil constraints, and the feasibility of such decisions. This work should be extended by validating potential yield loss estimations with farm-sourced yield data. Future work should consider including a greater range of threshold values for constraints and incorporating a soil water balance model into the framework.
Data availability
The data that support this study cannot be shared publicly due to privacy reasons.
Conflicts of interest
The authors declare no conflicts of interest.
Declaration of funding
This research was funded by the University of Sydney.
References
Arrouays D, Grundy MG, Hartemink AE, Hempel JW, Heuvelink GBM, Hong SY, Lagacherie P, Lelyk G, McBratney AB, McKenzie NJ, Mendonca-Santos MdL, Minasny B, Montanarella L, Odeh IOA, Sanchez PA, Thompson JA, Zhang G (2014) Chapter Three - GlobalSoilMap: toward a fine-resolution global grid of soil properties. In ‘Advances in agronomy’. (Ed. DL Sparks) pp. 94–134. (Elsevier)| Crossref |
Austin JM, Stockmann U, Verburg K (2019) Using pedotransfer functions to improve the precision of spatially predicted available water capacity. In ‘23rd International congress on modelling and simulation’. The National Convention Centre, Canberra, ACT, Australia, 1–6 December 2019. pp. 372–378. (Modelling and Simulation Society of Australia and New Zealand: Canberra)
| Crossref |
Bennett JMcL, Cattle SR, Singh B (2015) The efficacy of lime, gypsum and their combination to ameliorate sodicity in irrigated cropping soils in the Lachlan Valley of New South Wales. Arid Land Research and Management 29, 17–40.
| The efficacy of lime, gypsum and their combination to ameliorate sodicity in irrigated cropping soils in the Lachlan Valley of New South Wales.Crossref | GoogleScholarGoogle Scholar |
Bishop TFA, McBratney AB, Laslett GM (1999) Modelling soil attribute depth functions with equal-area quadratic smoothing splines. Geoderma 91, 27–45.
| Modelling soil attribute depth functions with equal-area quadratic smoothing splines.Crossref | GoogleScholarGoogle Scholar |
Bishop TFA, Horta A, Karunaratne SB (2015) Validation of digital soil maps at different spatial supports. Geoderma 241–, –249.
| Validation of digital soil maps at different spatial supports.Crossref | GoogleScholarGoogle Scholar |
Bot A, Nachtergaele F, Young A (2000) ‘Land resource potential and constraints at regional and country levels’, (Food and Agriculture Organization: Rome)
Bramley RGV, Ouzman J (2019) Farmer attitudes to the use of sensors and automation in fertilizer decision-making: nitrogen fertilization in the Australian grains sector. Precision Agriculture 20, 157–175.
| Farmer attitudes to the use of sensors and automation in fertilizer decision-making: nitrogen fertilization in the Australian grains sector.Crossref | GoogleScholarGoogle Scholar |
Breiman L (2001) Random forests. Machine Learning 45, 5–32.
| Random forests.Crossref | GoogleScholarGoogle Scholar |
Buchanan S, Triantafilis J, Odeh IOA, Subansinghe R (2012) Digital soil mapping of compositional particle-size fractions using proximal and remotely sensed ancillary data. Geophysics 77, WB201
| Digital soil mapping of compositional particle-size fractions using proximal and remotely sensed ancillary data.Crossref | GoogleScholarGoogle Scholar |
Bureau of Meteorology (BOM) (2021) Summary statistics - Moree Aero. Climate statistics for Australian locations. Available at http://www.bom.gov.au/climate/averages/tables/cw_053115.shtml. [Accessed 5 August 2021]
Cull PO, Hearn AB, Smith RCG (1981) Irrigation scheduling of cotton in a climate with uncertain rainfall. Irrigation Science 2, 127–140.
| Irrigation scheduling of cotton in a climate with uncertain rainfall.Crossref | GoogleScholarGoogle Scholar |
Dalal RC, Blasi M, So HB (2002) DNR6 – High sodium levels in subsoil limits yields and water use in marginal cropping areas. Grains Research & Development Corporation Project No. DNR 6.
Dang YP, Routley RD, McDonald M, Dalal R, Alsemgeest V, Orange D (2004) Effects of chemical subsoil constraints on lower limit of plant available water for crops grown in southwest Queensland. In ‘New directions for a diverse planet: Proceedings for the 4th International Crop Science Congress in conjunction with the 12th Australian Agronomy Conference and the 5th Asian Crop Science Conference’. 26 September–1 October 2004, Brisbane, Australia. (Ed. T Fischer) (Australian Society of Agronomy: Brisbane)
Dang YP, Dalal RC, Routley R, Schwenke GD, Daniells I (2006) Subsoil constraints to grain production in the cropping soils of the north-eastern region of Australia: an overview. Australian Journal of Experimental Agriculture 46, 19–35.
| Subsoil constraints to grain production in the cropping soils of the north-eastern region of Australia: an overview.Crossref | GoogleScholarGoogle Scholar |
Dang YP, Dalal RC, Mayer DG, McDonald M, Routley R, Schwenke GD, Buck SR, Daniells IG, Singh DK, Manning W, Ferguson N (2008) High subsoil chloride concentrations reduce soil water extraction and crop yield on Vertosols in north-eastern Australia. Australian Journal of Agricultural Research 59, 321–330.
| High subsoil chloride concentrations reduce soil water extraction and crop yield on Vertosols in north-eastern Australia.Crossref | GoogleScholarGoogle Scholar |
Dang YP, Dalal RC, Buck SR, et al. (2010) Diagnosis, extent, impacts, and management of subsoil constraints in the northern grains cropping region of Australia. Soil Research 48, 105–119.
| Diagnosis, extent, impacts, and management of subsoil constraints in the northern grains cropping region of Australia.Crossref | GoogleScholarGoogle Scholar |
Dang YP, Pringle MJ, Schmidt M, Dalal RC, Apan A (2011) Identifying the spatial variability of soil constraints using multi-year remote sensing. Field Crops Research 123, 248–258.
| Identifying the spatial variability of soil constraints using multi-year remote sensing.Crossref | GoogleScholarGoogle Scholar |
Department of Finance, Services and Innovation (2020) NSW Foundation Spatial Data Framework – elevation and depth – digital elevation model. (Department of Customer Service) Available at https://data.nsw.gov.au/data/dataset/ee5e06a2-255b-48e4-9f55-ec3c0e7bcec8. [Accessed 8 August 2021]
Filippi P, Cattle SR, Bishop TFA, Odeh IOA, Pringle MJ (2018a) Digital soil monitoring of top- and sub-soil pH with bivariate linear mixed models. Geoderma 322, 149–162.
| Digital soil monitoring of top- and sub-soil pH with bivariate linear mixed models.Crossref | GoogleScholarGoogle Scholar |
Filippi P, Cattle SR, Bishop TFA, Pringle MJ, Jones EJ (2018b) Monitoring changes in soil salinity and sodicity to depth, at a decadal scale, in a semiarid irrigated region of Australia. Soil Research 56, 696–711.
| Monitoring changes in soil salinity and sodicity to depth, at a decadal scale, in a semiarid irrigated region of Australia.Crossref | GoogleScholarGoogle Scholar |
Filippi P, Jones EJ, Ginns BJ, Whelan BM, Roth GW, Bishop TFA (2019a) Mapping the depth-to-soil pH constraint, and the relationship with cotton and grain yield at the within-field scale. Agronomy 9, 251
| Mapping the depth-to-soil pH constraint, and the relationship with cotton and grain yield at the within-field scale.Crossref | GoogleScholarGoogle Scholar |
Filippi P, Jones EJ, Wimalathunge NS, Somarathna PDSN, Pozza LE, Ugbaje SU, Jephcott TG, Paterson SE, Whelan BM, Bishop TFA (2019b) An approach to forecast grain crop yield using multi-layered, multi-farm data sets and machine learning. Precision Agriculture 20, 1015–1029.
| An approach to forecast grain crop yield using multi-layered, multi-farm data sets and machine learning.Crossref | GoogleScholarGoogle Scholar |
Filippi P, Jones EJ, Bishop TFA (2020a) Catchment-scale 3D mapping of depth to soil sodicity constraints through combining public and on-farm soil databases – a potential tool for on-farm management. Geoderma 374, 114396
| Catchment-scale 3D mapping of depth to soil sodicity constraints through combining public and on-farm soil databases – a potential tool for on-farm management.Crossref | GoogleScholarGoogle Scholar |
Filippi P, Whelan BM, Vervoort RW, Bishop TFA (2020b) Mid-season empirical cotton yield forecasts at fine resolutions using large yield mapping datasets and diverse spatial covariates. Agricultural Systems 184, 102894
| Mid-season empirical cotton yield forecasts at fine resolutions using large yield mapping datasets and diverse spatial covariates.Crossref | GoogleScholarGoogle Scholar |
French RJ, Schultz JE (1984) Water use efficiency of wheat in a Mediterranean-type environment. I. The relation between yield, water use and climate. Australian Journal of Agricultural Research 35, 743–764.
| Water use efficiency of wheat in a Mediterranean-type environment. I. The relation between yield, water use and climate.Crossref | GoogleScholarGoogle Scholar |
Gorelick N, Hancher M, Dixon M, Ilyushchenko S, Thau D, Moore R (2017) Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sensing of Environment 202, 18–27.
| Google Earth Engine: Planetary-scale geospatial analysis for everyone.Crossref | GoogleScholarGoogle Scholar |
Gray JM, Bishop TFA, Wilford JR (2016) Lithology and soil relationships for soil modelling and mapping. Catena 147, 429–440.
| Lithology and soil relationships for soil modelling and mapping.Crossref | GoogleScholarGoogle Scholar |
Grundy MJ, Viscarra Rossel RA, Searle RD, Wilson PL, Chen C, Gregory LJ (2015) Soil and landscape grid of Australia. Soil Research 53, 835–844.
| Soil and landscape grid of Australia.Crossref | GoogleScholarGoogle Scholar |
Hazelton P, Murphy B (2016) ‘Interpreting soil test results: what do all the numbers mean?.’ (CSIRO Publishing: Melbourne)
| Crossref |
Hochman Z, Dalgliesh NP, Bell K (2001) Contributions of soil and crop factors to plant available soil water capacity of annual crops on Black and Grey Vertosols. Australian Journal of Agricultural Research 52, 955–961.
| Contributions of soil and crop factors to plant available soil water capacity of annual crops on Black and Grey Vertosols.Crossref | GoogleScholarGoogle Scholar |
Isbell R (2016) ‘The Australian soil classification.’ (CSIRO Publishing: Melbourne)
| Crossref |
Leenaars JGB, Claessens L, Heuvelink GBM, Hengl T, Ruiperez González M, van Bussel LGJ, Guilpart N, Yang H, Cassman KG (2018) Mapping rootable depth and root zone plant-available water holding capacity of the soil of sub-Saharan Africa. Geoderma 324, 18–36.
| Mapping rootable depth and root zone plant-available water holding capacity of the soil of sub-Saharan Africa.Crossref | GoogleScholarGoogle Scholar | 30122789PubMed |
Lin LI-K (1989) A concordance correlation coefficient to evaluate reproducibility. Biometrics 45, 255–268.
| A concordance correlation coefficient to evaluate reproducibility.Crossref | GoogleScholarGoogle Scholar |
Looney JW (1991) Land degradation in Australia: the search for a legal remedy. Journal of Soil and Water Conservation 46, 256–259.
Ma Y, Minasny B, McBratney A, Poggio L, Fajardo M (2021) Predicting soil properties in 3D: should depth be a covariate? Geoderma 383, 114794
| Predicting soil properties in 3D: should depth be a covariate?Crossref | GoogleScholarGoogle Scholar |
Malone BP, McBratney AB, Minasny B, Laslett GM (2009) Mapping continuous depth functions of soil carbon storage and available water capacity. Geoderma 154, 138–152.
| Mapping continuous depth functions of soil carbon storage and available water capacity.Crossref | GoogleScholarGoogle Scholar |
Minty B, Franklin R, Milligan P, Richardson M, Wilford J (2009) The radiometric map of Australia. Exploration Geophysics 40, 325–333.
| The radiometric map of Australia.Crossref | GoogleScholarGoogle Scholar |
Naidu R, Rengasamy P, De Lacy NJ, Zarcinas BA (1995) Soil solution composition of some sodic soils. In ‘Australian sodic soils: distribution, properties and management’. (Eds R Naidu, M Sumner, P Rengasamy) pp. 155–161. (CSIRO Publishing: Melbourne)
Northcote KH, Srene JKM (1972) ‘Australian soils with saline and sodic properties.’ (CSIRO Publishing: Melbourne)
Office of Environment and Heritage - OEH (2017) ‘NSW landuse.’ pp. 2007 (NSW Government: Australia)
Padarian J, Minasny B, McBratney AB, Dalgliesh N (2014) Predicting and mapping the soil available water capacity of Australian wheatbelt. Geoderma Regional 2–3, 110–118.
| Predicting and mapping the soil available water capacity of Australian wheatbelt.Crossref | GoogleScholarGoogle Scholar |
Padarian Campusano JS (2014) Provision of soil information for biophysical modelling. Masters Thesis, The University of Sydney, NSW, Australia. Available at http://hdl.handle.net/2123/12278
Page KL, Dalal RC, Wehr JB, Dang YP, Kopittke PM, Kirchhof G, Fujinuma R, Menzies NW (2018) Management of the major chemical soil constraints affecting yields in the grain growing region of Queensland and New South Wales, Australia – a review. Soil Research 56, 765–779.
| Management of the major chemical soil constraints affecting yields in the grain growing region of Queensland and New South Wales, Australia – a review.Crossref | GoogleScholarGoogle Scholar |
Rab MA, Fisher PD, Armstrong RD, Abuzar M, Robinson NJ, Chandra S (2009) Advances in precision agriculture in south-eastern Australia. IV. Spatial variability in plant-available water capacity of soil and its relationship with yield in site-specific management zones. Crop & Pasture Science 60, 885–900.
| Advances in precision agriculture in south-eastern Australia. IV. Spatial variability in plant-available water capacity of soil and its relationship with yield in site-specific management zones.Crossref | GoogleScholarGoogle Scholar |
R Core Team (2021) R: a language and environment for statistical computing. Available at https://www.r-project.
Roth G, Harris G, Gillies M, Montgomery J, Wigginton D (2013) Water-use efficiency and productivity trends in Australian irrigated cotton: a review. Crop & Pasture Science 64, 1033–1048.
| Water-use efficiency and productivity trends in Australian irrigated cotton: a review.Crossref | GoogleScholarGoogle Scholar |
Sadras V, Baldock J, Roget D, Rodriguez D (2003) Measuring and modelling yield and water budget components of wheat crops in coarse-textured soils with chemical constraints. Field Crops Research 84, 241–260.
| Measuring and modelling yield and water budget components of wheat crops in coarse-textured soils with chemical constraints.Crossref | GoogleScholarGoogle Scholar |
Shatar TM, McBratney AB (2004) Boundary-line analysis of field-scale yield response to soil properties. The Journal of Agricultural Science 142, 553–560.
| Boundary-line analysis of field-scale yield response to soil properties.Crossref | GoogleScholarGoogle Scholar |
Shaw RJ (1997) Salinity and sodicity. In ‘Sustainable crop production in the sub-tropics: an Australian perspective’. (Eds AL Clarke, PB Wylie) pp. 79–96. (Queensland Department of Primary Industries: Brisbane)
Singh B, Odeh IOA, McBratney AB (2003) Acid buffering capacity and potential acidification of cotton soils in northern New South Wales. Soil Research 41, 875–888.
| Acid buffering capacity and potential acidification of cotton soils in northern New South Wales.Crossref | GoogleScholarGoogle Scholar |
Strobl C, Boulesteix A-L, Kneib T, Augustin T, Zeileis A (2008) Conditional variable importance for random forests. BMC Bioinformatics 9, 307
| Conditional variable importance for random forests.Crossref | GoogleScholarGoogle Scholar | 18620558PubMed |
Triantafilis J, Huckel AI, Odeh IOA (2001) Comparison of statistical prediction methods for estimating field-scale clay content using different combinations of ancillary variables. Soil Science 166, 415–427.
| Comparison of statistical prediction methods for estimating field-scale clay content using different combinations of ancillary variables.Crossref | GoogleScholarGoogle Scholar |
van Gool D, Tille P, Moore G (2005) Land evaluation standards for land resource mapping: assessing land qualities and determining land capability in south-western Australia. Report 298. Department of Primary Industries and Regional Development, Western Australia, Perth.
Veihmeyer FJ, Hendrickson AH (1949) Methods of measuring field capacity and permanent wilting percentage of soils. Soil Science 68, 75–94.
| Methods of measuring field capacity and permanent wilting percentage of soils.Crossref | GoogleScholarGoogle Scholar |
Wimalathunge NS, Bishop TFA (2019) A space-time observation system for soil moisture in agricultural landscapes. Geoderma 344, 1–13.
| A space-time observation system for soil moisture in agricultural landscapes.Crossref | GoogleScholarGoogle Scholar |
Wright MN, Ziegler A (2017) ranger: a fast implementation of random forests for high dimensional data in C++ and R. Journal of Statistical Software 77, 1–17.
| ranger: a fast implementation of random forests for high dimensional data in C++ and R.Crossref | GoogleScholarGoogle Scholar |
Wright MN, Ziegler A, König IR (2016) Do little interactions get lost in dark random forests? BMC Bioinformatics 17, 145
| Do little interactions get lost in dark random forests?Crossref | GoogleScholarGoogle Scholar | 27029549PubMed |
Zhao X, Wang J, Zhao D, Li N, Zare E, Triantafilis J (2019) Digital regolith mapping of clay across the Ashley irrigation area using electromagnetic induction data and inversion modelling. Geoderma 346, 18–29.
| Digital regolith mapping of clay across the Ashley irrigation area using electromagnetic induction data and inversion modelling.Crossref | GoogleScholarGoogle Scholar |


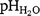 (a), EC1:5 (b), ESP (c), clay (d), sand (e), and SOC (f) attribute values with depth. Median values represented by solid black lines inside boxes, and the dashed vertical red lines indicate the threshold values deemed to be constraining to crop growth for pH, EC, and ESP (
(a), EC1:5 (b), ESP (c), clay (d), sand (e), and SOC (f) attribute values with depth. Median values represented by solid black lines inside boxes, and the dashed vertical red lines indicate the threshold values deemed to be constraining to crop growth for pH, EC, and ESP (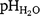 9, EC1:5 1 dS/m, ESP 15%). No data for SOC were available for a depth > 90 cm.
9, EC1:5 1 dS/m, ESP 15%). No data for SOC were available for a depth > 90 cm. > 9, EC1:5 > 1 dS/m, ESP > 15%.
> 9, EC1:5 > 1 dS/m, ESP > 15%.
