Magnetic properties and neutron spectroscopy of lanthanoid-{tetrabromocatecholate/18-crown-6} single-molecule magnets
Maja A. Dunstan A , Marina Cagnes B , Wasinee Phonsri C , Keith S. Murray C , Richard A. Mole B * and Colette Boskovic A *
A *
A School of Chemistry, The University of Melbourne, Parkville, Vic. 3010, Australia.
B Australian Nuclear Science and Technology Organisation, Locked Bag 2001, Kirrawee, NSW 2232, Australia.
C School of Chemistry, Monash University, Clayton, Vic. 3800, Australia.
Australian Journal of Chemistry 75(9) 595-609 https://doi.org/10.1071/CH21306
Submitted: 28 November 2021 Accepted: 12 January 2022 Published: 14 March 2022
© 2022 The Author(s) (or their employer(s)). Published by CSIRO Publishing. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)
Abstract
Lanthanoid single-molecule magnets (Ln-SMMs) exhibit slow magnetic relaxation at low temperatures. This arises from an energy barrier to magnetisation reversal associated with the crystal field (CF) splitting of the Ln(III) ion. The magnetic relaxation is impacted by the interaction of the molecule with the crystal lattice, so factors including particle size and crystal packing can play an important role. In this work, a family of compounds of general formula [Ln(18-c-6)(NO3)(Br4Cat)]·X (Ln = La, Tb, Dy; 18-c-6 = 18-crown-6; Br4Cat2− = tetrabromocatecholate) has been studied by inelastic neutron scattering (INS) and magnetometry to elucidate the effects of crystal packing on the slow magnetic relaxation of the Tb(III) and Dy(III) compounds. The deuterated analogues [Ln(18-c-6-d24)(NO3)(Br4Cat)]·CH3CN-d3 (1-LnD; Ln = La, Tb, Dy) have been synthesised, with 1-TbD and the diamagnetic analogue 1-LaD measured by INS. The dynamic magnetic properties of 1-TbD and 1-DyD have also been measured and compared for two samples with different particle sizes. To probe packing effects on the slow magnetic relaxation, two new solvatomorphs of the hydrogenous compounds [Ln(18-c-6)(NO3)(Br4Cat)]·X (2-Ln: X = CH2Cl2; 3-Ln: X = 0.5 toluene) have been obtained for Ln = Tb and Dy. The CF splitting between the ground and first excited CF pseudo-doublets has been experimentally determined for 1-TbD by INS, and strongly rare earth dependent and anharmonic lattice vibrational modes have also been observed in the INS spectra, with implications for slow magnetic relaxation. Dynamic magnetic measurements reveal significant particle-size dependence for the slow magnetic relaxation for 1-TbD, while a previously reported anomalous phonon bottleneck effect in the 1-DyD analogue does not change with particle size. Further dynamic magnetic measurements of 2-Ln and 3-Ln show that the slow magnetic relaxation in these Ln-SMMs is strongly dependent on lattice effects and crystal packing, which has implications for the future use of Ln-SMMs in devices.
Keywords: deuteration, inelastic neutron scattering, lanthanides, magnetic properties, phonon bottleneck, rare earths, single-molecule magnets, spectroscopy.
Introduction
Single-molecule magnets (SMMs) are discrete metal-based compounds that exhibit slow relaxation of magnetisation and magnetic hysteresis at low temperatures. Their magnetic bistability makes SMMs potential candidates for high density data storage applications, and efforts are underway to immobilise single molecules on surfaces to allow for individual addressing.[1–4] Quantum effects such as quantum tunnelling of magnetisation (QTM), a through barrier relaxation process, have recently afforded applications for the use of SMMs as qubits in quantum computing. There are recent reports of long quantum coherence times in the order of microseconds at low temperatures in SMM materials, showing promise for their use in this application.[5,6] Since the report of slow magnetic relaxation in a terbium bis phthalocyanine complex [TbPc2]− (PcH2 = phthalocyanine) in 2003,[7] SMMs incorporating trivalent lanthanoid ions have dominated the field. Significant advances have been made in the last few years with a recent example of a dysprosium metallocene [(CpiPr5)Dy(Cp*)]+ (CpiPr5 = penta-iso-propylcyclopentadienyl; Cp* = pentamethylcyclopentadienyl) showing magnetic hysteresis loops above liquid nitrogen temperature.[8]
The magnetic properties of the trivalent lanthanoid ions arise mainly from crystal field (CF) splitting of the ground Russell-Saunders J multiplet into mJ microstates. If the Ln(III) ion has a doubly degenerate ground microstate with a large magnetic anisotropy, and a sizeable energy gap between the ground and lowest lying excited microstate, slow magnetic relaxation can occur.[9] To improve SMM behaviour, the CF splitting can be tuned through modification of the coordination geometry and ligands. An electrostatic approach is often used in the design of Ln-SMMs, where the geometry of the ligands around the Ln(III) ion are used to stabilise the highest mJ microstate.[10] This relies on using a coordination environment with the strongest crystal field in the axial positions for Ln(III) where the electron density of the f-orbitals can be described as ‘oblate’ (e.g. Tb(III), Dy(III)), and a coordination environment that has the strongest crystal field in the equatorial plane for ‘prolate’ Ln(III) (e.g. Er(III), Yb(III)). Additionally, magnetic exchange coupling[11,12] and dipolar coupling[13,14] can influence the magnetic properties of Ln(III) systems.
Magnetic relaxation of Ln-SMMs can occur via various mechanisms. Quantum-tunnelling of magnetisation, a through barrier relaxation process, occurs at low temperature, but a judicious choice of symmetry at the Ln(III) centre, or the application of a small magnetic field can reduce the rate of QTM.[15] Thermally activated relaxation processes are important for bistability in applications. Over barrier thermally activated relaxation, known as Orbach relaxation, occurs through an excited CF level within the ground electronic multiplet, and can be tuned by modifying the CF splitting. There are also additional thermally activated relaxation processes with a Tn dependence – Raman relaxation through a virtual excited state, with n > 1, and direct relaxation in applied magnetic fields, where n = 1. Thermally activated processes rely on energy transfer from a ‘bath’ of infinite heat capacity to the sample – meaning that there must be energy that can be transferred to the lattice as lattice vibrations (phonons) and spin-phonon coupling to couple these phonon modes to the spin of the Ln(III). The importance of these non-Orbach thermally activated processes in the slow magnetic relaxation of high performing SMMs has become apparent in the last few years, particularly for Ln-SMMs.[16]
In general, there is sufficient coupling between the thermal bath, the phonon system, and the spin system to allow magnetic relaxation. However, in cases where there is an inefficient exchange between the bath and the spin system, a phonon bottleneck occurs, slowing down relaxation at low temperatures.[17] This effect can depend on several factors – crystallite size, concentration of paramagnetic ions, the phonon spectrum, and spin-phonon coupling. This phenomenon has been recently observed in a family of compounds [Ln(18-c-6)(NO3)(X4Cat)]·CH3CN, (18-c-6 = 18-crown-6; X4Cat2− = tetrahalocatecholate; X = Cl, Br), where a low temperature T6 phonon bottleneck regime was observed for Ln = Ce and Dy.[18]
Inelastic neutron scattering (INS) is a spectroscopic technique that uses neutrons to measure phenomena such as lattice vibrations and magnetic excitations in materials. It has many advantages for the study of magnetic materials, as it can be used to measure transitions such as CF excitations of a sample in zero-field, unlike techniques such as EPR spectroscopy or far-infrared spectroscopy.[19] The use of INS to study CF transitions in Ln(III) molecular compounds is somewhat limited, although it has been used successfully to identify CF splitting in Ln-SMMs such as Na9[Ln(W5O18)2] (Ln = Nd, Ho, Er),[20] (NBu4)[DyPc2]·2DMF,[21] and Er[N(SiMe3)2]3.[22] Additionally, it can be employed to measure the phonon spectra for a variety of compounds,[23] and has recently been used to observe spin-phonon coupling in a SMM.[24]
Our group is interested in the properties of Ln ions with redox-active ligands such as dioxolenes [25] and tetraoxolenes,[26,27] for applications in single-molecule magnetism and other areas.[28] Previously, the magnetic behaviour of the family of compounds [Ln(18-c-6)(NO3)(Br4Cat)]·CH3CN (I-Ln) was reported by some of us, with slow magnetic relaxation observed for Ce, Nd, Tb, and Dy analogues.[18] Herein, we report the INS spectra of deuterated analogues of [Ln(18-c-6-d24)(NO3)(Br4Cat)]·CH3CN-d3, (1-LnD)[18] with the aim of measuring the CF splitting to provide an additional verification of the published calculated CF splitting. The Tb(III) and diamagnetic La(III) analogues were chosen for this study due to their low neutron absorption cross-sections compared to Dy(III). We also present additional magnetic studies on 1-TbD and 1-DyD, where we examine the effects of deuteration and particle size on the slow magnetic relaxation observed for these compounds. Additionally, we report the synthesis and characterisation of two new solvatomorphs, [Ln(18-c-6)(NO3)(Br4Cat)]·X, 2-Ln (X = CH2Cl2) and 3-Ln (X = 0.5 toluene), demonstrating the impact crystal packing can have on the slow magnetic relaxation of Ln-SMMs that relax by Raman and phonon bottleneck relaxation processes.
Results and discussion
Synthesis
Deuterated samples of [Ln(18-c-6-d24)(NO3)(Br4Cat)]·CH3CN-d3 (1-LnD; Ln = La, Tb) for INS and magnetic measurements were obtained using an analogous method to the hydrogenous samples reported in the literature.[18] The ligand 18-crown-6-d24 was obtained from the National Deuteration Facility, ANSTO. The only other source of hydrogen in the compounds is from the co-crystallised acetonitrile, and so acetonitrile-d3 was used as the solvent. The syntheses of large INS samples of 1-TbD and 1-LaD were undertaken at a 100 mg scale and combined, allowing recollection of acetonitrile-d3. The synthesis was adapted slightly from the literature procedure for the hydrogenous analogues to use less deuterated solvent. A hot acetonitrile-d3 solution of lanthanoid nitrate was refluxed with the 18-crown-6-d24 for 15 min (Ln = La), 30 min (Ln = Tb) or 1 h (Ln = Dy). The solution was cooled, and Br4CatH2 deprotonated with two equivalents of triethylamine in acetonitrile-d3 was added dropwise. Within 5 min, yellow needles appeared and were filtered after 30 min and washed with a small volume of chilled acetonitrile-d3. The overall deuteration of the compounds was found to be 67%, from H/D isotope analysis.
Using a similar method, two new solvates of the hydrogenous 1-Ln have been synthesised, one with dichloromethane [Ln(18-c-6)(NO3)(Br4Cat)]·CH2Cl2 (Ln = Tb, Dy; 2-Ln) and the other with toluene [Ln(18-c-6)(NO3)(Br4Cat)]·0.5C7H8 (Ln = Tb, Dy; 3-Ln). A hot solution of the Ln(NO3)3·xH2O and 18-crown-6 in CH2Cl2 (2-Ln) or toluene (3-Ln), with a small amount of methanol to aid the dissolution of the lanthanoid nitrate salt, was refluxed with for 45 min (Ln = Tb) or 1.5 h (Ln = Dy). The solution was cooled, and Br4CatH2 deprotonated with two equivalents of triethylamine in CH2Cl2 (2-Ln), or toluene (3-Ln) was added dropwise. Within 5 min, yellow rod-like crystals appeared for 2-Ln, while plate-like crystals of 3-Ln took a few hours to appear. The solutions were left overnight to fully crystallise, collected by vacuum filtration, washed well, and air-dried. All the samples are insoluble, so were characterised in the solid state.
Structure descriptions
The single crystal X-ray diffraction data for the new solvatomorphs 2-Ln and 3-Ln are presented in Table 1, as well as the previously unpublished crystal structure of 1-Dy. Compound 1-Dy crystallises in the triclinic space group P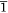 , with one lanthanoid complex and one disordered acetonitrile per unit cell, consistent with the published La and Ce compounds.[18] The crystals of 1-Dy are highly twinned, and as such the data quality is low, however, it is presented here for comparison with 2-Ln and 3-Ln. Compounds 2-Tb and 2-Dy crystallise as bright yellow rods in the monoclinic space group P21/n, with one lanthanoid complex and one dichloromethane solvent molecule per asymmetric unit. Compounds 3-Tb and 3-Dy crystallise as bright yellow plate-like blocks in the monoclinic space group P21/c, with one lanthanoid complex and half a toluene solvent molecule per asymmetric unit.
, with one lanthanoid complex and one disordered acetonitrile per unit cell, consistent with the published La and Ce compounds.[18] The crystals of 1-Dy are highly twinned, and as such the data quality is low, however, it is presented here for comparison with 2-Ln and 3-Ln. Compounds 2-Tb and 2-Dy crystallise as bright yellow rods in the monoclinic space group P21/n, with one lanthanoid complex and one dichloromethane solvent molecule per asymmetric unit. Compounds 3-Tb and 3-Dy crystallise as bright yellow plate-like blocks in the monoclinic space group P21/c, with one lanthanoid complex and half a toluene solvent molecule per asymmetric unit.
|
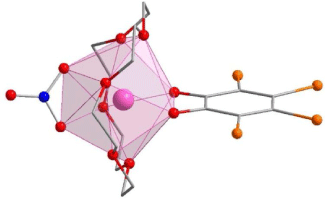
The lanthanoid complexes in 1-Dy, 2-Ln and 3-Ln (Fig. 1, Supplementary Fig. S1) are isostructural with the previously reported complexes 1-Ln,[18] with slight differences in coordination geometry. The lanthanoid(III) centres all have an {O10} coordination sphere arising from coordination to the equatorial 18-crown-6, a tetrabromocatecholate, and a nitrate ligand. The coordination geometries for both 2-Ln and 3-Ln are closest to a distorted sphenocorona according to continuous shape analysis (Table 2) performed with the Shape 2.1 software, although the 3-Ln series are closer to an ideal sphenocorona.[29] The compound 1-Dy has a coordination geometry closest to a distorted sphenocorona, with a distortion parameter very similar to that of 2-Dy (2.533 and 2.5459 respectively). The nearest intermolecular Ln⋯Ln distance also differs between the solvatomorphs. For 2-Ln, the intermolecular distance is 7.909 and 7.891 Å for 2-Tb and 2-Dy, respectively, which is very similar to the Dy⋯Dy distance of 7.877 Å found for 1-Dy. The intermolecular Ln⋯Ln distance in 3-Ln is slightly larger, 8.332 and 8.323 Å for 3-Tb and 3-Dy, respectively.
|

|
Physical characterisation
The isomorphous nature of compounds in the series 1-Ln and 1-LnD was confirmed by powder X-ray diffraction (PXRD) on bulk samples (Supplementary Fig. S2), confirming that deuteration does not change the unit cell. To confirm phase purity, the PXRD of 2-Ln and 3-Ln was also obtained. The PXRD of 2-Tb and 2-Dy was found to be in excellent agreement with that simulated from the single crystal structure of 2-Tb (Supplementary Fig. S3), while the PXRD of 3-Tb and 3-Dy was similarly found to agree with that simulated from the single crystal structure of 3-Tb (Supplementary Fig. S4).
The isostructural nature of the three series 1-LnD, 2-Ln, and 3-Ln was investigated with infrared (IR) spectroscopy. The Fourier transform IR (FTIR) spectra of 1-LnD are in agreement (Supplementary Fig. S5), as expected for an isostructural series. They differ from the previously reported 1-Ln due to the deuteration of both the 18-crown-6 ligand and the CH3CN solvate, which is evident in the decrease in intensity of the C–H stretches in the region ~2800–2950 cm−1, and the appearance of C–D stretches in the region 2100–2200 cm−1. There are still weak C–H stretches in the IR spectrum due to incomplete deuteration of the 18-crown-6 ligand. The IR spectra of 2-Ln (Supplementary Fig. S6) and 3-Ln (Supplementary Fig. S7) are again consistent within each family, and are consistent between 1-Ln, 2-Ln, and 3-Ln, with only minor differences. This suggests that the complexes remain isostructural between polymorphs, consistent with the structural analyses.
Thermogravimetric analysis was used to confirm the solvation for all compounds and is consistent with one CH3CN-d3 per complex for 1-LnD, one CH2Cl2 per complex for 2-Ln, and half a toluene per complex for 3-Ln (Supplementary Figs S8–10).
The particle sizes of as-synthesised samples 1-TbD and 1-DyD, as well as the ground samples 1-TbD-a and 1-DyD-a, were determined by light field microscopy (Supplementary Fig. S11, S12). The sample of 1-TbD used for magnetometry consisted of needles of approximate dimension 50–100 μm in length and 5 μm across; needles of 1-DyD were slightly larger in the range 100–150 μm in length and 5–10 μm across. Ground samples of 1-TbD and 1-DyD were small particles of ~2 μm in diameter.
Inelastic neutron scattering
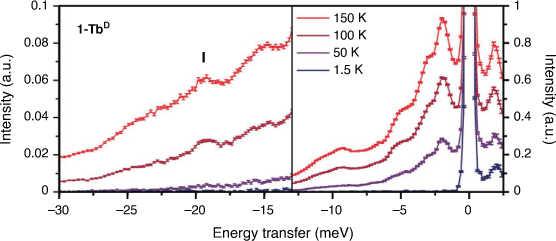
Inelastic neutron scattering spectra were obtained for large powder samples of 1-TbD and the diamagnetic 1-LaD analogue on the Pelican beamline at the Australian Centre for Neutron Scattering (ACNS), ANSTO. Deuterated samples were measured to reduce the intense incoherent scattering from the large amount of 1H in the hydrogenous samples, allowing observation of weaker magnetic and phononic features. The variable temperature INS spectra of 1-TbD (Fig. 2) are rich in peaks in the measured energy range. This is not unexpected – as a flexible molecular compound, one might expect a large number of possible lattice vibrations (phonons) in the energy range measured. Due to the geometry of the spectrometer, the maximum energy transfer that can be observed from a ground microstate up to a higher energy state is 13.5 meV (110 cm−1). From previously reported ab initio calculations on the hydrogenous analogue,[18] we expect to see no allowed transitions (ΔmJ = 0, ±1) within this energy range below 200 K, and as such have focused on the neutron energy gain side of the spectrum (negative energy transfer). Electronic structure calculations predicted an allowed transition of 21 meV (170 cm−1) from the first excited microstate to the ground microstate with thermal population.[18] The next lowest-lying electronic energy level lies at >40 meV (>325 cm−1), so one would not expect a significant thermal population of this state below room temperature. Careful examination of this region of the spectrum shows several peaks increasing in intensity with temperature. There is a potential CF transition in the 1-TbD compound at −19.2 meV (156 cm−1; I; Fig. 2), which has a peak width of 1.4 meV at 150 K, which is consistent with a resolution limited transition. There are several ways to identify magnetic excitations in an INS spectrum. An isomorphous diamagnetic analogue can be measured, which allows identification of phonon peaks. For this reason, we measured the diamagnetic La analogue, 1-LaD (Supplementary Fig. S13). However, the spectra of 1-TbD and 1-LaD differ in the whole energy range out to E = −30 meV (~240 cm−1), so differentiating vibrational modes and magnetic excitations in this manner was not straightforward.
|
The spatial dependence of a peak can also be used to determine the nature of a transition by analysis of the wavevector transfer (Q). A phononic peak will increase in intensity as a function of Q2, as observed for peaks at E = −9.3, –15, and –23 meV for 1-TbD (Fig. 3). The Q-dependence for a crystal field transition for a lanthanoid ion can be described using a dipole approximation of the magnetic form factor (F(Q))[30] – the intensity of a transition should fall off as a function of F2(Q).[31,32] For peak I (Fig. 2), the Q-dependence of the transition is not described well by either a CF-like transition or a phonon, but is well described by a linear combination of the two, suggesting a CF transition overlaid on top of a phononic background. It is difficult to assign this unambiguously as the Q-range of the instrument at this energy does not allow observation of the low Q region where the majority of the CF intensity would lie, however the observed Q-dependence is consistent with the assignment of I as a CF transition. Additionally, the Q-dependence of both the 1-LaD and 1-TbD spectra show no other magnetic transitions.
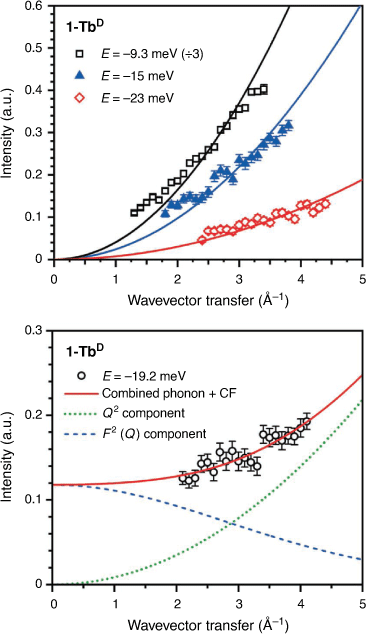
|
Magnetic peaks can also be assigned by identification of all the phononic peaks using a Bose-corrected spectrum.[24] As electrons are fermions, and phonons are bosons, the temperature dependence of CF peaks and phonon peaks should differ. To do this, the phonon generalised density of states (GDOS, g(ω)) has been calculated using a Bose-Einstein distribution for each of the temperatures and the two analogues, using Eqn 1:
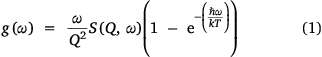
where S(Q, ω) is the scattering function in Q and energy dimensions.
The resultant phonon GDOS for 1-TbD are presented in Fig. 4. For a harmonic phonon with no spin-phonon coupling, the Bose corrected phonon GDOS at each temperature will overlay. As is evident, there are several deviations from this behaviour – in particular in the region near E = −19 meV, where there is a sharp feature in the phonon GDOS at 100 K which decreases in intensity with temperature, consistent with a CF transition.

|
A comparison of the Bose corrected spectra of 1-TbD with that of 1-LaD also shows a clear deviation at this energy (Fig. 4, right). The difference in phonon energies and relative intensities between the two analogues suggests that many of the modes in the low energy region are strongly rare-earth dependent, with the 1-TbD spectrum at 150 K exhibiting features at E = 11, 15, and 23 meV which have shifted in energy in the 1-LaD analogue, while features near E = 4 and 6 meV have shifted slightly between the analogues. The difference in ionic radius and mass between the two samples means that these strongly rare earth dependent lattice modes shift in energy significantly between La(III) and Tb(III). Additionally, several phonon modes in the 1-TbD Bose corrected spectra do not show the expected temperature dependence – in particular, in the region E = 9.3 meV, with smaller discrepancies at E = 15 and 23 meV. This could be due to strongly anharmonic phonon modes, and similar discrepancies are not observed in the phonon GDOS for 1-LaD (Supplementary Fig. S14). This anharmonicity may be due to spin-phonon coupling between the Tb(III) spin and these rare earth dependent phonons, which has been observed recently in the INS spectra of Co(II)-SMMs,[24] where the phonon mode coupled to the Co(II) spin is not scaled correctly by a Bose correction.
Altogether, the peak in the INS spectra of 1-TbD at E = −19.2 meV is consistent with a CF transition. This is in excellent agreement with the previously reported ab initio calculated CF splitting of 21 meV between the ground and first excited CF states and has allowed spectroscopic verification of the calculated splitting. This CF transition is at a high energy transfer in a sample with a strong phonon background, however, both the Q-dependence and Bose corrected spectra can be used to confirm the magnetic origin of the transition. The INS spectra of 1-TbD and 1-LaD exhibit strongly rare earth dependent phonon modes, and 1-TbD exhibits an unusual temperature dependence in several phonon modes. To further characterise the deuterated samples, as well as to probe how crystal packing might affect the slow magnetic relaxation through tuning of the phonon spectrum, we turned to magnetometric studies of 1-LnD, 2-Ln and 3-Ln.
Static magnetic properties
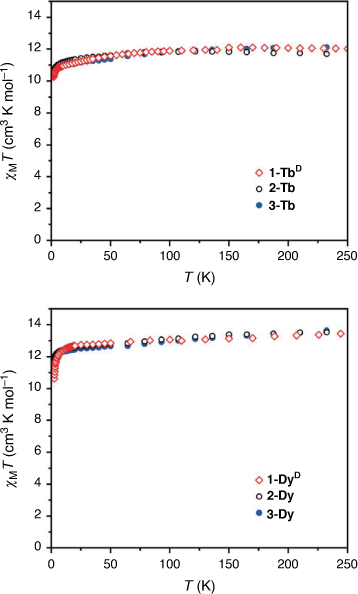
In order to check that the magnetic properties of the deuterated 1-LnD are the same as those of the hydrogenous analogues 1-Ln, static magnetic data were acquired for 1-TbD and 1-DyD (Fig. 5). The dc magnetic susceptibility temperature product profiles are consistent with that of the hydrogenous analogues, showing no change in the static magnetic properties with deuteration, as expected. This confirms that the CF splitting determined by INS for 1-TbD should remain unchanged for the hydrogenous analogue 1-Tb.
|
We then turned our attention to the characterisation of new solvatomorphs of both the Tb(III) and Dy(III) complexes. The magnetic properties of these compounds are strongly dependent on phonon effects, suggesting the possibility of tuning the properties by changing the lattice. The static magnetic properties of the solvated analogues 2-Ln and 3-Ln were measured (Fig. 5). For both 2-Tb and 3-Tb, the room temperature dc magnetic susceptibility temperature product values of 11.9 and 12.1 cm3 K mol−1, respectively, are consistent with the expected value for a Tb(III) ion (11.82 cm3 K mol−1), while there is a gradual decrease in χMT as the temperature is lowered. For 2-Dy and 3-Dy, the room temperature χMT values of 13.5 and 13.6 cm3 K mol−1 respectively; are consistent with the expected value for a Dy(III) ion (14.17 cm3 K mol−1) with similar overall profiles obtained for the two solvatomorphs.
Dynamic magnetic properties
Compound 1-TbD
As INS spectra were obtained for the deuterated compound 1-TbD, we wished to explore whether the dynamic magnetic properties changed upon deuteration of 1-Tb. The reported dynamic magnetic properties of 1-Tb are complicated, and the ac magnetic susceptibility could not be fit due to multiple overlapping relaxation processes.[18] In contrast, the deuterated 1-TbD analogue shows a clear frequency-dependent peak in the out-of-phase component of magnetic susceptibility (χM″) in an applied magnetic field (Supplementary Fig. S15). In lower applied fields there appears to be a weak feature at low frequency and low temperature; however, unlike in 1-Tb, this feature is very small. It is worth noting that the current measurements do not begin at as low a temperature, which may explain the lack of the more intense low frequency feature. An applied magnetic field of Bdc = 0.1 T was chosen to measure the ac magnetic susceptibility (Fig. 6, Supplementary Fig. S16).
The out-of-phase magnetic susceptibility, χM″, could be fitted with the Debye equation to give the relaxation rate with temperature (Fig. 7). The relaxation rate (τ−1) with temperature for the Tb(III) analogues was fit with Eqn 2:
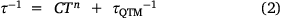
where C is the Raman relaxation parameter, n the Raman exponent, and τQTM−1 the rate of QTM. In an applied field of 0.1 T, the relaxation rate could be fit with only the Raman relaxation term in Eqn 2 – with C = 1064 ± 49 Kn s−1, and an exponent of n = 1.98 ± 0.02 (Table 3). An Orbach relaxation term was not included, as it gave an unreasonably small ΔE, compared to the smallest ΔE expected from the ground pseudo-doublet to the lowest energy excited pseudo-doublet of −19.2 meV as determined by INS. This is also consistent with the previously reported 1-Ln analogues, none of which could be fitted with an Orbach-like process.

|

|
The difference in the ac magnetic susceptibility data measured for 1-Tb and 1-TbD is intriguing – one wouldn’t expect deuteration to afford such a significant effect. We postulated that the variation may be due to a difference in particle size of the samples measured, as has been seen previously for phonon bottleneck relaxation in β-diketonate-vanadyl complexes.[33] We, therefore, measured the magnetic properties of a sample ground to an average particle diameter of 2 μm, 1-TbD-a, in contrast to the as synthesised 1-TbD with crystallites averaging 100 μm in length and 5 μm diameter, in the same conditions. In the well-ground sample, the low frequency feature is still apparent in low applied field (Supplementary Fig. S17). Fitting of the temperature dependent relaxation rates obtained from Debye fitting of the higher frequency feature in χM″ gave parameters of C = 1750 ± 49 Kn s−1, and n = 1.81 ± 0.02 (Fig. 6, 7, Supplementary Fig. S18). It should be noted that the differences between the ground and non-ground samples are relatively minor despite the difference in particle size, particularly considering the relatively fast relaxation in both analogues. A relaxation rate that varies with T2 is a hallmark of a spatial phonon bottleneck process, where the phonon mean free path is smaller than the dimensions of a crystallite.[34] This is consistent with a particle size dependence on the magnetic relaxation rate; however, the data are not conclusive due to the small temperature range measured and measurements on larger crystallites were not possible – we were unable to synthesise larger crystallites due to the rapid crystallisation and lack of solubility of the compound.
Compounds 2-Tb and 3-Tb
Following the magnetic measurements on 1-TbD, we measured the dynamic magnetic properties of the two hydrogenous solvatomorphs 2-Tb and 3-Tb. Neither 2-Tb nor 3-Tb have a peak in the out-of-phase magnetic susceptibility in an applied magnetic field of Bdc = 0 T. From scans of the ac magnetic susceptibility at 2 K in various applied fields, an optimum applied field of Bdc = 0.1 T was determined for both analogues (Supplementary Fig. S19, S21). For both compounds, the temperature dependent out-of-phase magnetic susceptibility (Fig. 6, Supplementary Fig. S20, S22) was fit to give the relaxation rate with temperature (Fig. 7).
The relaxation rate data for 2-Tb werefitted with a combination of the Raman relaxation term and the QTM term in Eqn 2, as shown in Fig. 7, giving C =2.05 ± 0.09 Kn s−1, n = 4.03 ± 0.02, and τQTM−1 = (4.93 ± 0.10) × 10−3 s−1. Fitting of the relaxation rate data for 3-Tb gave a best fit of C =27.8 ± 1.0 Kn s−1, n = 3.17 ± 0.02, and τQTM−1 = (1.26 ± 0.02) × 10−3 s−1 QTM. The faster τQTM−1 for 2-Tb than 3-Tb is consistent with a smaller Tb⋯Tb distance (7.9092 and 8.3317 Å, respectively), as small dipolar fields due to neighbouring spins can lead to QTM. Additionally, the coordination environment at the Tb(III) centre in 2-Tb is more distorted, and further from an ideal C2v symmetry, again consistent with faster QTM. This is consistent with previous studies which show that a small change in coordination geometry at a Ln(III) centre can drastically change the rate of QTM by changing the magnitude of the tunnel splitting.[35] The relaxation data for 1-TbD and 1-TbD-a show no QTM, which is perhaps explained by a more optimal applied field used for the measurement of those compounds.
The large difference in slow magnetic relaxation is of note for such structurally similar compounds. The effect different solvation has on the CF splitting of a Ln(III) ion has been spectroscopically observed previously for a [Tb(W5O18)2]9− complex, while studies of different magnetic relaxation in various polymorphs of Ln(III)-SMMs include the observation of cation dependent slow magnetic relaxation in bridged Dy2 dimers,[36] as well as a strong solvent dependence on the slow magnetic relaxation and magnetic hysteresis in [Er(W5O18)2]9−.[37] Slight deviations in coordination geometry have also been observed to affect the slow magnetic relaxation in Ln-SMM showing a Raman-like relaxation previously, for example in a family of substituted Er(trensal) (H3trensal = 2,2′,2′′-tris(salicylideneimino)triethylamine) compounds.[38] The difference in the Raman exponent n from ~2 to 4 between the three solvatomorphs is large – although whether this is due to the change in coordination geometry at the Tb(III) centre or to packing effects is not known. Particle size effects also cannot be ruled out, as the three solvatomorphs have distinctly different crystal shapes and dimensions.
Compound 1-DyD
Upon observing the effects of particle size on 1-TbD, we turned our attention to 1-DyD, to investigate whether particle size would have a similar effect on the phonon bottleneck process. As discussed, particle size has been observed to affect the phonon bottleneck in compounds with a T2 dependence on the relaxation rate.[33] The compound 1-Dy was observed to follow a phonon bottleneck-like relaxation process at low temperature with a T6 dependence, originating from a combination of the T2 dependence (arising from the specific heat of the spin system) and a T4 dependence (arising from the thermal conductivity between low and high frequency phonons).[18] This T6 dependence was observed in the relaxation rate and could be fit with Eqn 3:
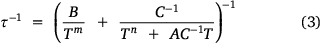
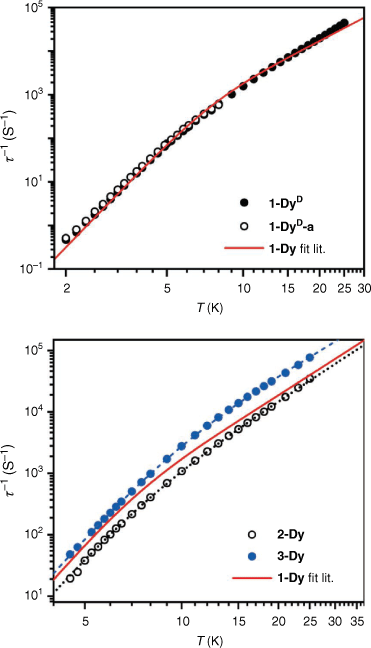
where B is the phonon bottleneck parameter, m the phonon bottleneck exponent, and A the direct relaxation parameter. Samples of both 1-DyD and the ground 1-DyD-a were measured in an applied field of 0.15 T (Supplementary Figs S23–S26). As can be observed in the plot of relaxation rate with temperature (Fig. 8), there is no change in relaxation rate between samples, and they overlay well with the fit from literature (Table 4), which incorporates a phonon bottleneck T6 term, a T3.4 term, and a direct relaxation process. This agreement is consistent with the assignment of the phonon bottleneck process in these compounds as a spectral phonon bottleneck since the lattice-bath relaxation is not the determining factor.[18,34] This is in stark contrast to the particle size dependence seen for 1-TbD and 1-TbD-a. As the agreement is so similar between the relaxation rates for 1-Dy, 1-DyD, and 1-DyD-a, we did not fit the experimental data for 1-DyD and 1-DyD-a.
|

|
Compounds 2-Dy and 3-Dy
We also measured the dynamic magnetic properties of the new solvatomorphs 2-Dy and 3-Dy. The ac magnetic susceptibility data for 2-Dy and 3-Dy were measured in an applied field of Bdc = 0.15 T, for comparison with published data on 1-Dy. Both analogues exhibit peaks in χM″ in the temperature range 4.5–25 K within the range of the instrument (Fig. 6, Supplementary Fig. S27, 28). The data were fit to the generalised Debye equation to determine the temperature dependence of the relaxation rate (Fig. 8). These data were fit using a combination of a fixed phonon-bottleneck like term, a Raman relaxation process, and a direct relaxation process (Eqn 3). As seen in Table 4, the phonon-bottleneck coefficient is fixed, while the Raman exponents are similar between the three analogues with values of 3.4, 3.39, and 3.09 for 1-Dy, 2-Dy, and 3-Dy respectively. They do instead differ significantly in the coefficients B and C. These coefficients depend on several factors – including the ratio of the specific heat capacity of the spin system and the specific heat capacity of the lattice. By modifying the lattice vibrational modes through different packing, the specific heat capacity of the lattice should change, which may account for the observed difference in behaviour. We are, however, unable to rule out that the small changes in intermolecular Dy⋯Dy distances and coordination geometry at the lanthanoid centre may also have impact on the slow magnetic relaxation, as discussed for 2-Tb and 3-Tb, although 1-Dy and 2-Dy are very similar. It should be notedthat the difference in relaxation rates between the Dy(III) compounds is much smaller than the large differences observed for the Tb(III) analogues.
Conclusions
Deuterated samples 1-LnD of the known SMM family 1-Ln were obtained using the deuterated ligand 18-crown-6-d24. Inelastic neutron scattering studies on the 1-TbD and 1-LaD analogues allowed identification of a CF transition for 1-TbD at a large energy transfer of E = −19.2 meV, through analysis of the Q-dependence of the transition and anomalies in the phonon generalised density of states. This is consistent with the CF splitting previously reported as determined by electronic structure calculations.[18] The INS spectra of both Tb(III) and La(III) analogues are rich in strongly rare earth dependent phonons. Additionally, anharmonic phonon modes were observed for 1-TbD from analysis of the Bose corrected g(ω). The reported anomalous phonon bottleneck T6 dependence in the slow magnetic relaxation for 1-Dy is a signature of anharmonic terms in the elastic potential, which is consistent with this observation.[17] The understanding of which phonon modes couple to spins, allowing magnetic relaxation, is important for accessing longer spin lifetimes. In particular, it has been suggested that improved SMM behaviour may be achieved with more rigid systems with fewer low energy phonon modes that afford fast relaxation.[39,40]
The magnetic properties of the deuterated compounds 1-TbD and 1-DyD were measured for two different particle sizes of the samples, with the observation that for 1-TbD, particle size influences the slow magnetic relaxation of Raman-like T~2 relaxation rate, while for 1-DyD, the slow magnetic relaxation in both the higher temperature Raman regime and lower temperature T6 phonon-bottleneck regime is unaffected by particle size, as expected for a spectral phonon bottleneck.[34]
New solvatomorphs of 1-Ln have also been synthesised, yielding a dichloromethane solvate 2-Ln, and a toluene solvate 3-Ln for Ln = Tb, Dy. Structurally the lanthanoid complex of all three solvatomorphs are very similar, with only slight differences in the coordination sphere of the Ln(III), but all three solvatomorphs crystallise in different space groups. For the Tb solvates 2-Tb and 3-Tb, there is a large difference in the magnetic relaxation rates as compared to 1-TbD, with a strong dependence of the Raman exponent on the polymorph. For the 2-Dy and 3-Dy solvatomorphs, small differences in the slow magnetic relaxation were observed, with the Raman and phonon-bottleneck parameters differing between analogues. These results demonstrate the importance of small changes in coordination geometry and changes in crystal packing for the slow magnetic relaxation of Ln-SMMs. These observations have implications for applications of Ln-SMMs on surfaces or in materials where the geometry of the complex can be altered significantly by the surface or when embedded in a matrix, potentially impairing the desired magnetic properties.
Experimental
Synthesis
All chemicals used were reagent grade or higher and used without further purification.
1,4,7,10,13,16-Hexaoxacyclooctadecane-d24 (18-crown-6-d24)
18-crown-6-d24 with an average 74% D was synthesised by the National Deuteration Facility (*unpublished result). 1H NMR (400 MHz, CDCl3) δ 3.62 (m, residual signal). 2H NMR (61.4 MHz, CDCl3) δ 3.65 (br s). 13C{1H} NMR (101 MHz, CDCl3) δ 70.03 (m). 13C{1H, 2H, d1 = 20 s} NMR (101 MHz, CDCl3) δ 69.95 (m), 70.34 (m), 70.72 (m). MS (ESI+): 1.9%, d23; 4.9%, d22; 6.9%, d21; 10.5%, d20; 14.0%, d19; 14.1%, d18; 14.7%, d17; 12.1%, d16; 9.7%, d15; 6.3%, d14; 4.9%, d13.
[Tb(18-crown-6-d24)(NO3)(Br4Cat)]·CH3CN-d3 (1-TbD)
A solution of stoichiometric amounts of 18-crown-6-d24 (118 mg, 0.420 mmol) and Tb(NO3)3·6H2O (190 mg, 0.420 mmol) in acetonitrile-d3 (8 mL) was refluxed with stirring for 30 min and allowed to cool to room temperature. One equivalent of tetrabromo-1,2-catechol (179 mg, 0.420 mmol) doubly deprotonated with triethylamine (117 µL, 0.840 mmol) in acetonitrile-d3 (4 mL) was added dropwise with no stirring. The product crystallised almost immediately, and was collected by vacuum filtration after 1 h, washed with chilled acetonitrile-d3 and dried, yielding yellow needle-like crystals. The overall deuteration of the compound was estimated to be 67%. Analysis calculated for H9D18C20N2O11Br4Tb: C: 24.81, H&D: 2.84, H: 0.94, D: 3.75, N: 2.89. Found: C: 24.70, H&D: 2.84, H: 0.99, D: 3.70, N: 2.79. Selected IR data (attenuated total reflectance (ATR), cm−1): 2913 (w), 2884 (w), 2200 (w), 2093 (w), 1466 (s), 1353 (m), 1292 (m), 1263 (m), 1243 (m), 1202 (w), 1022 (m),1016 (m), 995, (m), 925 (m), 814 (m), 725 (m), 617 (m), 567 (m).
[Dy(18-crown-6-d24)(NO3)(Br4Cat)]·CH3CN-d3 (1-DyD)
Compound 1-DyD was synthesised in an analogous manner to 1-TbD, using Dy(NO3)3·6H2O (192 mg, 0.420 mmol), and refluxing for 1 h. The product was obtained as yellow needles (75%). Analysis calculated for H9D18C20N2O11Br4Dy: C: 24.72, H&D: 2.83, H: 0.94, D: 3.73, N: 2.88. Found: C: 24.64, H&D: 2.82, H: 0.98, D: 3.67, N: 2.73.
[La(18-crown-6-d24)(NO3)(Br4Cat)]·CH3CN-d3 (1-LaD)
Compound 1-LaD was synthesised in an analogous manner to 1-TbD, using La(NO3)3·6H2O (182 mg, 0.420 mmol), and refluxing for 15 min. The product was obtained as yellow needles (56%).
[Dy(18-crown-6)(NO3)(Br4Cat)]·CH3CN (1-Dy)
Compound 1-Dy was synthesised as per the literature procedure,[18] with crystals suitable for single-crystal X-ray diffraction obtained directly from the reaction solution.
[Tb(18-crown-6)(NO3)(Br4Cat)]·CH2Cl2 (2-Tb)
A dichloromethane (5 mL) solution of 18-crown-6 (94 mg, 0.354 mmol) was added to Tb(NO3) ·6H2O (160 mg, 0.354 mmol) in 1:1 dichloromethane/methanol (10 mL) with stirring. The solution was heated with stirring at reflux for 1.5 h before cooling. A solution of Br4CatH2 (151 mg, 0.354 mmol) deprotonated with Et3N (99 μL, 0.708 mmol) in dichloromethane (5 mL) was added dropwise with no stirring, yielding a yellow solution. Crystals began forming shortly after, and the solution was left overnight to fully crystallise. The product was collected by vacuum filtration, washed with copious dichloromethane and air dried, yielding yellow rod-like crystals (288 mg, 82%). Crystals suitable for single-crystal X-ray diffraction were obtained directly from the reaction solution. Analysis calculated for H26C19NO11Br4Tb: C, 22.96; H, 2.64; N, 1.41. Found: C: 23.19, H: 2.63, N: 1.41. Selected IR data (ATR, cm−1): 2930 (w), 2924 (w), 1475 (m), 1453 (s), 1356 (m), 1296 (m), 1263 (m), 1243 (m), 1094 (m), 1074 (s), 1032 (m), 958 (s), 927 (m), 837 (m), 810 (w), 727 (s), 618 (w), 569 (w), 486 (m).
[Dy(18-crown-6)(NO3)(Br4Cat)]·CH2Cl2 (2-Dy)
The compound 2-Dy was synthesised in an analogous manner to 2-Tb, using Dy(NO3)3·6H2O (162 mg, 0.354 mmol), and refluxing for 1.5 h. The product was obtained as yellow rods (285 mg, 81%). Crystals suitable for single-crystal X-ray diffraction were obtained directly from the reaction solution. Analysis calculated for H26C19NO11Br4Dy: C, 22.88; H, 2.63; N, 1.40. Found: C: 23.11, H: 2.40, N: 1.30.
[Tb(18-crown-6)(NO3)(Br4Cat)]·0.5C7H8 (3-Tb)
A toluene (5 mL) solution of 18-crown-6 (94 mg, 0.354 mmol) was added to Tb(NO3) 6H2O (160 mg, 0.354 mmol) in 1:1 toluene/methanol (10 mL) with stirring. The solution was heated with stirring at reflux for 1.5 h before cooling. A solution of Br4CatH2 (150 mg, 0.354 mmol) deprotonated with Et3N (99 μL, 0.708 mmol) in toluene (5 mL) was added dropwise with no stirring, yielding a yellow solution. The solution was left overnight to fully crystallise. The product was collected by vacuum filtration, washed with copious toluene, then diethyl ether and air dried, yielding yellow block-like crystals (257 mg, 76%). Crystals suitable for single-crystal X-ray diffraction were obtained directly from the reaction solution. Analysis calculated for H28C21.5NO11Br4Tb: C, 27.04; H, 2.96; N, 1.47. Found: 27.25, H: 2.91, N: 1.41. Selected IR data (ATR, cm−1): 2938 (w), 2914 (w), 2877 (w), 1473 (m), 1447 (s), 1354 (m), 1311 (m), 1259 (m), 1241 (m), 1084 (s), 1069 (s), 1037 (m), 962 (m), 925 (m), 847 (w), 839 (m), 818 (w), 725 (m), 618 (w), 540 (w), 488 (m).
[Dy(18-crown-6)(NO3)(Br4Cat)]·0.5C7H8 (3-Dy)
The compound 3-Dy was synthesised in an analogous manner to 3-Tb, using Dy(NO3)3·6H2O (162 mg, 0.354 mmol), and refluxing for 1.5 h. The product was obtained as yellow rods (162 mg, 48%). Crystals suitable for single-crystal X-ray diffraction were obtained directly from the reaction solution. Analysis calculated for H28C21.5NO11Br4Dy: C: 26.94, H: 2.94, N: 1.46. Found: C: 27.04, H: 2.77, N: 1.30.
X-ray diffraction and structure solution
All X-ray diffraction patterns were obtained on an XtaLAB Synergy-S diffractometer from Rigaku Oxford Diffraction with a HyPix-6000HE detector, using Cu-Kα (λ = 1.5406 Å) radiation. All X-ray diffraction data were collected at 100 K.
Single crystal X-ray diffraction data were reduced using CrysalisPro[41] and corrected using a numerical absorption correction based on Gaussian integration over a multi-faceted crystal model. Crystals used for single crystal X-ray diffraction were transferred directly from solution to crystallographic oil to prevent solvent loss. All structures were solved with the SHELXT[42] structure solution program using Intrinsic Phasing and refined with the SHELXL[43] refinement package using Least Squares minimisation on all data, in Olex2.[44] All non-hydrogen atoms were refined with anisotropic displacement parameters, and all hydrogen atoms were placed at geometrical estimates and refined using the riding model.
Crystals of 1-Dy were highly twinned, and the data from the crystal chosen for single crystal X-ray diffraction was refined as a twin with three parts. The structure itself is highly disordered, with sections of the 18-crown-6 ligand, as well as the nitrate ligand, solved as two parts. Disordered sections of the 18-crown-6 ether ligand and nitrate ligand were refined to have similar anisotropic displacements as neighbouring atoms. The nitrate ligand was refined with bond distances fixed to the expected values for a nitrate anion and equivalent distances restrained to be the same between the two parts. The acetonitrile co-crystallised solvent is disordered and could not be modelled satisfactorily. A solvent mask was calculated and 62 electrons were found in a volume of 215 Å3 in 1 void per unit cell. This is consistent with the presence of one acetonitrile per asymmetric unit which accounts for 44 electrons per unit cell. Structures 2-Ln have a disordered 18-crown-6 ligand, and 2 carbon atoms were refined in two parts. The dichloromethane solvent molecule in 2-Ln may be disordered as one Cl atom has an elongated anisotropic displacement ellipsoid; however, refining the solvent molecule in two parts did not improve refinement indicators significantly, so the potential disorder was left untreated. The maximum residual electron density peak is near the dichloromethane and may be due to unresolved disorder. The components of the anisotropic displacement parameters in the direction of the bond of the dichloromethane were restrained to be equal. Structures 3-Ln have no disorder in the metal complex itself; but the toluene solvent molecule is disordered over two positions and was refined in two parts, using the FragmentDB tool with associated restraints.[45] For 3-Dy, the atoms of the toluene were constrained to have similar anisotropic displacement parameters as neighbouring atoms.
Samples for powder X-ray diffraction were lightly crushed and loaded into 3 mm borosilicate glass capillaries for measurement. A Gandolfi move for powders was used, with an exposure time of 60 s per frame, to 2θ = 70°. Powder X-ray diffraction data were simulated from single crystal X-ray structures using the software Mercury.[46]
Physical properties & characterisation
Fourier transform infrared spectra were obtained as attenuated total reflectance (ATR) on a Bruker Alpha FTIR spectrometer and normalised as absorbance spectra. Elemental analyses (CHN) and isotope analysis (H/D) were performed at the Campbell Microanalytical Laboratory, University of Otago. Thermogravimetric analyses were performed on a Mettler Toledo thermal analyser under an N2 atmosphere, with a ramp rate of 5°C per minute. Light field microscopy was obtained on a Nikon Eclipse LV-100 microscope.
Inelastic neutron scattering
Inelastic neutron scattering was measured on the Pelican cold neutron time-of-flight spectrometer at the Australian Centre for Neutron Scattering, at the Australian Nuclear Science and Technology Organisation.[47,48] Powder samples of ~2 g of the partially deuterated 1-TbD and 1-LaD were measured in an annular aluminium can with a 0.5 mm gap, chosen to give a 10% scatter and minimise multiple scattering events. The sample can was mounted in an Oxford Instruments CCR type cryostat with a secondary cooling circuit, with ~30 mbar of He exchange gas. A neutron wavelength of λ = 4.69 Å neutrons was used for all measurements. Both samples were measured for 8 h at 1.5, 50, 100, and 150 K, and 1-TbD was measured for 1 h at each of 200 and 250 K. The background due to the aluminium can was subtracted from all data except that used in calculating the GDOS plots, and the data were normalised to a vanadium standard, to correct for detector efficiencies. Data were then converted to S(Q,ω). All manipulations on the data were carried out using the Large Array Manipulation Program (LAMP).[49]
Magnetic measurements
Magnetic measurements were performed on a Quantum Design Physical Properties Measurement System (PPMS) with an AC Measurement System (ACMS) insert or a Quantum Design Magnetic Properties Measurement System (MPMS) instrument. Static (dc) magnetic susceptibility measurements were measured in an applied dc field of 0.1 T. Ferromagnetic checks were performed on all samples to confirm the absence of paramagnetic impurities. The powder samples were prepared in gelatine capsules and restrained in eicosane wax to prevent magnetic torquing. Static magnetic susceptibility measurements were corrected for the diamagnetism of the eicosane and gel cap, and the diamagnetic contribution from the sample using Pascal’s constants.
Data availability
Single crystal X-ray diffraction data are available in CIF format from the CCDC quoting deposition numbers 2124568–2124572. The data that support this study will be shared upon reasonable request to the corresponding author.
Conflicts of interest
The authors declare no conflicts of interest.
Declaration of funding
M. A. D. acknowledges support from an AINSE Post-Graduate Research Award and the Australian Government for a Research Training Program stipend. C. B., R. A. M., and K. S. M. thank the Australian Research Council for funding (DP170100034 and FT190100293). The authors would like to thank AINSE and ANSTO (P6363 & NDF6364) for access funding.
Supplementary material
Supplementary material included with this paper: crystallographic representations of 1-Dy, 2-Ln, and 3-Ln, powder X-ray diffraction data, FTIR spectra, and TGA of 1-LnD, 2-Ln, and 3-Ln, additional INS data for 1-TbD and 1-LaD, magnetic field dependence of the ac magnetic susceptibility and ac magnetic susceptibility plots. CIFs are available for CCDC #2124568–2124572. Supplementary material is available online.
Acknowledgements
The authors would like to thank Jack Heywood-Day for help with the light field microscopy, Moya Anne Hay for assistance with the X-ray crystallography and Elodie Rousset for helpful discussions. The National Deuteration Facility is partly funded by the National Collaborative Research Infrastructure Strategy (NCRIS) – an Australian Government initiative.
References
[1] A Saywell, G Magnano, CJ Satterley, LMA Perdigão, AJ Britton, N Taleb, M del Carmen Giménez-López, NR Champness, JN O’Shea, PH Beton, Nat Commun 2010, 1, 75.| Crossref | GoogleScholarGoogle Scholar | 20865804PubMed |
[2] M Mannini, F Bertani, C Tudisco, L Malavolti, L Poggini, K Misztal, D Menozzi, A Motta, E Otero, P Ohresser, P Sainctavit, GG Condorelli, E Dalcanale, R Sessoli, Nat Commun 2014, 5, 4582.
| Crossref | GoogleScholarGoogle Scholar | 25109254PubMed |
[3] S Marocchi, A Candini, D Klar, W Van den Heuvel, H Huang, F Troiani, V Corradini, R Biagi, V De Renzi, S Klyatskaya, K Kummer, NB Brookes, M Ruben, H Wende, U del Pennino, A Soncini, M Affronte, V Bellini, ACS Nano 2016, 10, 9353.
| Crossref | GoogleScholarGoogle Scholar | 27726335PubMed |
[4] G Serrano, L Poggini, M Briganti, AL Sorrentino, G Cucinotta, L Malavolti, B Cortigiani, E Otero, P Sainctavit, S Loth, F Parenti, A-L Barra, A Vindigni, A Cornia, F Totti, M Mannini, R Sessoli, Nat Mater 2020, 19, 546.
| Crossref | GoogleScholarGoogle Scholar | 32066930PubMed |
[5] M Atzori, S Benci, E Morra, L Tesi, M Chiesa, R Torre, L Sorace, R Sessoli, Inorg Chem 2018, 57, 731.
| Crossref | GoogleScholarGoogle Scholar | 29280628PubMed |
[6] M Shiddiq, D Komijani, Y Duan, A Gaita-Ariño, E Coronado, S Hill, Nature 2016, 531, 348.
| Crossref | GoogleScholarGoogle Scholar | 26983539PubMed |
[7] N Ishikawa, M Sugita, T Ishikawa, S-Y Koshihara, Y Kaizu, J Am Chem Soc 2003, 125, 8694.
| Crossref | GoogleScholarGoogle Scholar | 12862442PubMed |
[8] F Guo, BM Day, Y Chen, M-L Tong, A Mansikkamäki, RA Layfield, Science 2018, 362, 1400.
| Crossref | GoogleScholarGoogle Scholar | 30337456PubMed |
[9] P Zhang, L Zhang, J Tang, Dalton Trans 2015, 44, 3923.
| Crossref | GoogleScholarGoogle Scholar | 25641200PubMed |
[10] S-D Jiang, S-X Qin, Inorg Chem Front 2015, 2, 613.
| Crossref | GoogleScholarGoogle Scholar |
[11] SK Langley, DP Wielechowski, V Vieru, NF Chilton, B Moubaraki, LF Chibotaru, KS Murray, Chem Sci 2014, 5, 3246.
| Crossref | GoogleScholarGoogle Scholar |
[12] CA Gould, E Mu, V Vieru, LE Darago, K Chakarawet, MI Gonzalez, S Demir, JR Long, J Am Chem Soc 2020, 142, 21197.
| Crossref | GoogleScholarGoogle Scholar | 33322909PubMed |
[13] KR Meihaus, JD Rinehart, JR Long, Inorg Chem 2011, 50, 8484.
| Crossref | GoogleScholarGoogle Scholar | 21834501PubMed |
[14] F Habib, P Lin, J Long, I Korobkov, W Wernsdorfer, M Murugesu, J Am Chem Soc 2011, 133, 8830.
| Crossref | GoogleScholarGoogle Scholar | 21563820PubMed |
[15] J-L Liu, Y-C Chen, M-L Tong, Chem Soc Rev 2018, 47, 2431.
| Crossref | GoogleScholarGoogle Scholar | 29492482PubMed |
[16] MJ Giansiracusa, AK Kostopoulos, D Collison, REP Winpenny, NF Chilton, Chem Commun 2019, 55, 7025.
| Crossref | GoogleScholarGoogle Scholar |
[17] JH Van, Vleck, Phys Rev 1941, 59, 724.
| Crossref | GoogleScholarGoogle Scholar |
[18] E Rousset, M Piccardo, M-E Boulon, RW Gable, A Soncini, L Sorace, C Boskovic, Chem Eur J 2018, 24, 14768.
| Crossref | GoogleScholarGoogle Scholar | 29992641PubMed |
[19] MA Dunstan, RA Mole, C Boskovic, Eur J Inorg Chem 2019, 8, 1090.
| Crossref | GoogleScholarGoogle Scholar |
[20] M Vonci, MJ Giansiracusa, W Van den Heuvel, RW Gable, B Moubaraki, KS Murray, D Yu, RA Mole, A Soncini, C Boskovic, Inorg Chem 2017, 56, 378.
| Crossref | GoogleScholarGoogle Scholar | 27977150PubMed |
[21] R Marx, F Moro, M Dörfel, L Ungur, M Waters, SD Jiang, M Orlita, J Taylor, W Frey, LF Chibotaru, J van Slageren, Chem Sci 2014, 5, 3287.
| Crossref | GoogleScholarGoogle Scholar |
[22] DH Moseley, SE Stavretis, Z Zhu, M Guo, CM Brown, M Ozerov, Y Cheng, LL Daemen, R Richardson, G Knight, K Thirunavukkuarasu, AJ Ramirez-Cuesta, J Tang, Z-L Xue, Inorg Chem 2020, 59, 5218.
| Crossref | GoogleScholarGoogle Scholar | 32196322PubMed |
[23] BS Hudson, Vib Spectrosc 2006, 42, 25.
| Crossref | GoogleScholarGoogle Scholar |
[24] SE Stavretis, Y Cheng, LL Daemen, CM Brown, DH Moseley, E Bill, M Atanasov, AJ Ramirez-Cuesta, F Neese, Z-L Xue, Eur J Inorg Chem 2019, 8, 1119.
| Crossref | GoogleScholarGoogle Scholar |
[25] E Rousset, RW Gable, A Starikova, C Boskovic, Cryst Growth Des 2020, 20, 3396.
| Crossref | GoogleScholarGoogle Scholar |
[26] MA Dunstan, E Rousset, M-E Boulon, RW Gable, L Sorace, C Boskovic, Dalton Trans 2017, 46, 13756.
| Crossref | GoogleScholarGoogle Scholar | 28956877PubMed |
[27] WR Reed, MA Dunstan, RW Gable, W Phonsri, KS Murray, RA Mole, C Boskovic, Dalton Trans 2019, 48, 15635.
| Crossref | GoogleScholarGoogle Scholar | 31465054PubMed |
[28] MA Hay, C Boskovic, Chem Eur J 2021, 27, 3608.
| Crossref | GoogleScholarGoogle Scholar | 32965741PubMed |
[29] Llunell P, Casanova M, Cirera D, Bofill J, Alemany JM, Alvarez D, Pinsky S, Avnir M. SHAPE 2.1. Universitat de Barcelona and The Hebrew University of Jerusalem; 2003.
[30] Lovesey SW. Theory of Neutron Scattering from Condensed Matter: Vol. 2. Oxford: Clarendon Press; 1984.
[31] Anderson IS, Brown PJ, Carpenter JM, Lander G, Pynn R, Rowe JM, Schärpf O, Sears VF, Willis BTM. International Tables for Crystallography. International Union of Crystallography (IUCr); 2006. Vol. C, p. 430.
[32] EJ Lisher, JB Forsyth, Acta Crystallogr A 1971, 27, 545.
| Crossref | GoogleScholarGoogle Scholar |
[33] L Tesi, A Lunghi, M Atzori, E Lucaccini, L Sorace, F Totti, R Sessoli, Dalton Trans 2016, 45, 16635.
| Crossref | GoogleScholarGoogle Scholar | 27484897PubMed |
[34] AM Stoneham, Proc Phys Soc 1965, 86, 1163.
| Crossref | GoogleScholarGoogle Scholar |
[35] MA Sørensen, UB Hansen, M Perfetti, KS Pedersen, E Bartolomé, GG Simeoni, H Mutka, S Rols, M Jeong, I Zivkovic, M Retuerto, A Arauzo, J Bartolomé, S Piligkos, H Weihe, LH Doerrer, J van Slageren, HM Rønnow, K Lefmann, J Bendix, Nat Commun 2018, 9, 1292.
| Crossref | GoogleScholarGoogle Scholar | 29599433PubMed |
[36] S Liu, J Lu, X-L Li, Z Zhu, J Tang, Dalton Trans 2020, 49, 12372.
| Crossref | GoogleScholarGoogle Scholar | 32845258PubMed |
[37] J Flores Gonzalez, V Montigaud, V Dorcet, K Bernot, B Le Guennic, F Pointillart, O Cador, Chem Eur J 2021, 27, 10160.
| Crossref | GoogleScholarGoogle Scholar | 33998730PubMed |
[38] KS Pedersen, L Ungur, M Sigrist, A Sundt, M Schau-Magnussen, V Vieru, H Mutka, S Rols, H Weihe, O Waldmann, LF Chibotaru, J Bendix, J Dreiser, Chem Sci 2014, 5, 1650.
| Crossref | GoogleScholarGoogle Scholar |
[39] AL Blockmon, A Ullah, KD Hughey, Y Duan, KR O’Neal, M Ozerov, JJ Baldoví, J Aragó, A Gaita-Ariño, E Coronado, JL Musfeldt, Inorg Chem 2021, 60, 14096.
| Crossref | GoogleScholarGoogle Scholar | 34415149PubMed |
[40] A Lunghi, S Sanvito, Sci Adv 2019, 5, eaax7163.
| Crossref | GoogleScholarGoogle Scholar | 31598553PubMed |
[41] Agilent. CrysAlis PRO. Yarnton, Oxfordshire, England: Agilent Technologies Ltd; 2014.
[42] GM Sheldrick, Acta Crystallogr A 2015, 71, 3.
| Crossref | GoogleScholarGoogle Scholar |
[43] GM Sheldrick, Acta Crystallogr C 2015, 71, 3.
| Crossref | GoogleScholarGoogle Scholar |
[44] OV Dolomanov, LJ Bourhis, RJ Gildea, JAK Howard, H Puschmann, J Appl Crystallogr 2009, 42, 339.
| Crossref | GoogleScholarGoogle Scholar |
[45] D Kratzert, JJ Holstein, I Krossing, J Appl Crystallogr 2015, 48, 933.
| Crossref | GoogleScholarGoogle Scholar | 26089767PubMed |
[46] CF Macrae, I Sovago, SJ Cottrell, PTA Galek, P McCabe, E Pidcock, M Platings, GP Shields, JS Stevens, M Towler, PA Wood, J Appl Crystallogr 2020, 53, 226.
| Crossref | GoogleScholarGoogle Scholar | 32047413PubMed |
[47] D Yu, R Mole, T Noakes, S Kennedy, R Robinson, J Phys Soc Jpn 2013, 82, SA027.
| Crossref | GoogleScholarGoogle Scholar |
[48] D Yu, RA Mole, GJ Kearley, EPJ Web Conf 2015, 83, 03019.
| Crossref | GoogleScholarGoogle Scholar |
[49] D Richard, M Ferrand, GJ Kearley, J Neutron Res 1996, 4, 33.
| Crossref | GoogleScholarGoogle Scholar |



