Experimental Validation of Quantum Circuit Rules in Molecular Junctions*
Elena Gorenskaia A , Masnun Naher A , Lakshya Daukiya A B , Stephen A. Moggach A , David Costa Milan C , Andrea Vezzoli C , Colin J. Lambert D , Richard J. Nichols C , Thomas Becker E and Paul J. Low A F
A F
A School of Molecular Sciences, University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia.
B Present address: Department of Physics, Indian Institute of Technology Jodhpur, Jodhpur 342037, India.
C Department of Chemistry, University of Liverpool, Crown Street, Liverpool, L69 7ZD, UK.
D Department of Physics, Lancaster University, Lancaster LA1 4YB, UK.
E School of Molecular and Life Sciences, Curtin University, GPO Box U1987, Perth, WA 6845, Australia.
F Corresponding author. Email: paul.low@uwa.edu.au
Australian Journal of Chemistry 74(11) 806-818 https://doi.org/10.1071/CH21136
Submitted: 5 June 2021 Accepted: 22 July 2021 Published: 1 September 2021
Journal Compilation © CSIRO 2021 Open Access CC BY-NC-ND
Abstract
A series of diarylacetylene (tolane) derivatives functionalised at the 4- and 4′-positions by thiolate, thioether, or amine groups capable of serving as anchor groups to secure the molecules within a molecular junction have been prepared and characterised. The series of compounds have a general form X-B-X, Y-B-Y, and X-B-Y where X and Y represent anchor groups and B the molecular bridge. The single-molecule conductance values determined by the scanning tunnelling microscope break-junction method are found to be in excellent agreement with the predictions made on the basis of a recently proposed ‘molecular circuit law’, which states ‘the conductance 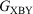 of an asymmetric molecule X-B-Y is the geometric mean
of an asymmetric molecule X-B-Y is the geometric mean 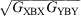 of the conductance of the two symmetric molecules derived from it,
of the conductance of the two symmetric molecules derived from it, 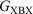 and
and 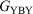 .’ The experimental verification of the circuit law, which holds for systems in which the constituent moieties X, B, and Y are weakly coupled and whose conductance takes place via off-resonance tunnelling, gives further confidence in the use of this relationship in the design of future compounds for use in molecular electronics research.
.’ The experimental verification of the circuit law, which holds for systems in which the constituent moieties X, B, and Y are weakly coupled and whose conductance takes place via off-resonance tunnelling, gives further confidence in the use of this relationship in the design of future compounds for use in molecular electronics research.
Keywords: molecular electronics, quantum interference, alkynes.
Introduction
Molecular electronics is a multi-disciplinary field of research broadly concerned with the electrical, magnetic, and chemical behaviour of one or more molecules electrically contacted between two macroscopic electrodes.[1,2] Given the experimental challenges in constructing an electrode | molecule | electrode experimental platform, or molecular junction,[3–5] many early studies in the field made use of charge transfer processes in donor–bridge–acceptor systems or intervalence charge transfer processes in M–bridge–M+ mixed-valence complexes as model systems to study intramolecular charge transfer.[6] The earliest true molecular junctions were constructed from Langmuir–Blodgett monolayers of fatty acids on aluminium substrates, top-contacted by a Hg drop or thermally evaporated lead or aluminium,[7] with the exponential decay of the junction conductance as a function of molecular length providing experimental evidence for the prominent role of tunnelling-based mechanisms of electron transport in these systems.
Beyond junctions based on ‘large area’ contacts to large numbers of molecules in well ordered monolayers,[8–11] the development of techniques for the formation of single-molecule junctions such as the scanning tunnelling microscope break junction (STM-BJ),[12] current–distance spectroscopy (I(s)),[13] and mechanically controlled break-junctions (MCBJ)[14] have become essential experimental tools through which to probe the electrical properties and physical structure of molecular junctions in unprecedented detail. Through such studies, molecules that integrate within a junction to give electrical responses that correspond to wires, rectifiers, and switches have been developed,[15,16] while the introduction of a third ‘gate’ electrode to the junction assembly has allowed the demonstration of a transistor-like response at the single-molecule level.[17] Molecular junctions are now also being recognised as tools through which to explore a wider range of processes beyond the mimicry of electronic components, including single-molecule reaction chemistry[18] and single-molecule electrochemistry.[19] The electrical and chemical properties of molecules within a junction are finding applications in areas such as molecular memory[20–22] and sensing,[23,24] while the use of paramagnetic molecular systems in combination with magnetic electrodes opens a suite of opportunities for spintronic applications.[25–30] Together, the use of molecular junctions to discover, develop, and exploit molecular properties and molecular materials science, have led to newly emerging fields such as molecular thermoelectric materials.[31]
The experimental study of molecular junctions and measurement of the electrical properties of single molecules and molecular ensembles has permitted exploration and verification of various theoretical models of junction behaviour. These simple models include structure–property relationships that illustrate the change in dominant conductance mechanism from coherent tunnelling to thermally activated hopping with increasing molecular length,[32,33] and correlations of molecular redox potential as a proxy for the tunnel barrier height with junction conductance.[34] More generally the electrical properties of a junction are a result of the integrated effects of the material composition and structure of the electrodes, the chemical and physical detail of the molecule–electrode contacts, the solvent or general environment in which the junction operates, and the molecular backbone. To this end, Landauer–Büttiker theory provides a detailed description of the junction that takes into account all of these features, and gives a more complete model that can be expressed within the electron transmission function T(E).[35] However, while a combination of DFT and non-equilibrium Greens functions can be used to compute T(E),[36] DFT methods cannot accurately predict the relative energies of the molecular orbital energies and the electrode Fermi levels, EF, which is critical to the prediction of molecular conductance, G. Thus, common practice in the field is to use the results of experimental measurements of molecular conductance to help determine the position of the Fermi level relative to transport resonances arising from, for example, the molecular HOMO and LUMO.
Coherent tunnelling dominates the charge transport mechanisms in many molecules of length up to ~3–5 nm, and so transport through an elementary molecular component of well defined chemical structure can be considered in terms of the scattering through three serially connected components: the left anchor group, X, the molecular backbone, B, and the right anchor group Y. It has been proposed that the off-resonance transport through such a molecular component can be described by several predictive numerical relationships.[37] For example, the single-molecule conductance of an asymmetrically contacted compound X-B-Y  can be expressed in terms of the conductance of the symmetrically contacted systems, X-B-X
can be expressed in terms of the conductance of the symmetrically contacted systems, X-B-X  and Y-B-Y
and Y-B-Y  (Eqn 1)
(Eqn 1)

In addition, numerical parameterisation of the molecular conductance is possible, which yields Eqn 2:

where  is the quantum of conductance, and
is the quantum of conductance, and  ,
,  ,
,  are parameters characterising the anchor and backbone sub-elements X, B, and Y respectively.[38] These circuit rules hold great promise for the prediction of trends in molecular conductance, in a manner that would be challenging for DFT calculations. While several anchor and bridge parameters have been derived, there are few combinations of experimental measurements of molecules X-B-X, Y-B-Y, and X-B-Y that allow direct verification of the above circuit rule.[38]
are parameters characterising the anchor and backbone sub-elements X, B, and Y respectively.[38] These circuit rules hold great promise for the prediction of trends in molecular conductance, in a manner that would be challenging for DFT calculations. While several anchor and bridge parameters have been derived, there are few combinations of experimental measurements of molecules X-B-X, Y-B-Y, and X-B-Y that allow direct verification of the above circuit rule.[38]
Here we describe the synthesis and characterisation of diphenylacetylene (tolane) compounds functionalised by different combinations of anchor groups. The molecular conductance of these compounds determined by STM-BJ methods, together with data from similarly functionalised 1,4-diphenylbuta-1,3-diyne and 1,4-bis(phenylethynyl)benzene compounds reported elsewhere,[35] verify the quantum circuit rules, and illustrate the predictive power of these relationships within the limits of the approximations used in their derivation.
Results and Discussion
The rigid, linear geometry and π-conjugated electronic structures of tolanes,[39] oligo(phenylethynyl)benzenes (OPE),[32] and polyynes,[40,41] coupled with the ease of synthesis and chemical compatibility with common anchor groups, makes such compounds exemplary systems through which to explore a wide range of fundamental properties of molecular junctions. In order to explore the quantum circuit rules expressed in Eqns 1 and 2,[38] and extend the library of anchor group parameters,  , tolane compounds 4,4’-functionalised by 3,3-dimethyl-2,3-dihydrobenzo[b]thiophene (DMBT), thiomethyl (SMe), thioacetate (SAc), and amine (NH2) groups were chosen. These structures complement similarly functionalised buta-1,3-diynes and 1,4-bis(phenylethynyl benzene) derivatives[35] that provide comparative data from molecules with the same anchor groups but different backbones (Chart 1).
, tolane compounds 4,4’-functionalised by 3,3-dimethyl-2,3-dihydrobenzo[b]thiophene (DMBT), thiomethyl (SMe), thioacetate (SAc), and amine (NH2) groups were chosen. These structures complement similarly functionalised buta-1,3-diynes and 1,4-bis(phenylethynyl benzene) derivatives[35] that provide comparative data from molecules with the same anchor groups but different backbones (Chart 1).

|
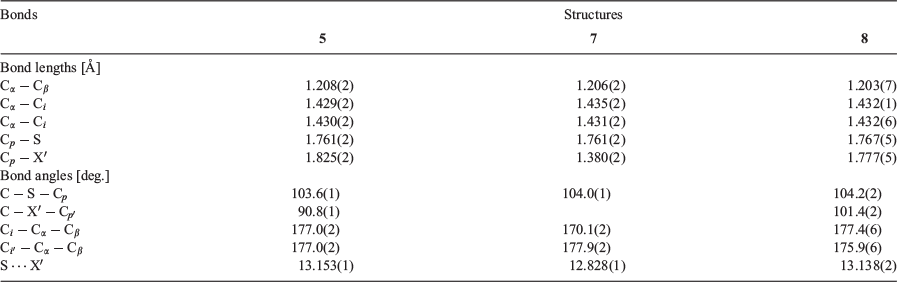
Compounds 1, 2, 3,[42] and 4[40] are readily prepared by Sonogashira cross-couplings of 5-ethynyl-3,3-dimethyl-2,3-dihydrobenzo[b]thiophene, 4-ethynyl thioanisole, 4-ethynyl benzenthioacetate, or 4-ethynylaniline with the appropriate aryl halide chosen from 5-bromo-3,3-dimethyl-2,3-dihydrobenzo[b]-thiophene, 4-iodothioanisole, 4-iodo-benzenethioacetate, or 4-iodoaniline in good to excellent yield. While the iodo-functionalised arenes were smoothly cross-coupled with PPh3-ligated palladium catalysts at room temperature, the conveniently prepared, but electron-rich, 5-bromo-3,3-dimethyl-2,3-dihydrobenzo[b]thiophene necessitated the use of the much more active JohnPhos ancillary ligand.[43] In addition to the usual array of 1H, 13C{1H} NMR and IR spectroscopic and high resolution mass spectrometric data which were used to fully characterise the compounds and are unremarkable for compounds of this type, the molecular structures of 1–3 were also determined by single crystal X-ray diffraction studies (Fig. 1, Table 1).

|

|
Single-molecule conductance measurements were carried out using the STM-BJ method. Briefly, a flame-annealed gold-on-glass substrate is sealed into an STM liquid cell before the introduction of the analyte as a 1 mM solution in mesitylene. A gold tip is driven ~2–3 nm into the substrate to create a fused metallic junction, and then the tip retracted at a rate of 5 nm s−1 while recording current–distance traces under –0.1 V bias.[44] The curves often show characteristic steps at the quantum of conductance,  , as the gold filament formed by the fusion of the tip and substrate thins to a single atom. As the last metallic contact breaks, the current undergoes a rapid decrease by several orders of magnitude. In many traces, additional features in the form of current plateaus near 10−3
, as the gold filament formed by the fusion of the tip and substrate thins to a single atom. As the last metallic contact breaks, the current undergoes a rapid decrease by several orders of magnitude. In many traces, additional features in the form of current plateaus near 10−3  are observed arising from the formation of a molecular junction. On continued tip retraction the molecular junction breaks and the current decays to the noise floor either abruptly, or via a series of shorter, lower conductance steps. These additional low conductance features of the current decay profiles are a result of dynamic reorganisation of the molecule within the junction and arise from different contact geometries and molecular configurations, including sliding of the molecule along the electrode surface. The individual plateau regions also exhibit a degree of variation from trace to trace due to thermal fluctuations, necessitating the collection of thousands of individual traces to obtain a statistically significant result.
are observed arising from the formation of a molecular junction. On continued tip retraction the molecular junction breaks and the current decays to the noise floor either abruptly, or via a series of shorter, lower conductance steps. These additional low conductance features of the current decay profiles are a result of dynamic reorganisation of the molecule within the junction and arise from different contact geometries and molecular configurations, including sliding of the molecule along the electrode surface. The individual plateau regions also exhibit a degree of variation from trace to trace due to thermal fluctuations, necessitating the collection of thousands of individual traces to obtain a statistically significant result.
The current–distance traces were analysed by binning the current data and plotted to give 1D current histograms. The peak around 1  corresponds to the single-atom gold contact in the junction, while the lower conductance features were fitted by Gaussian functions to give the most probable molecular conductance of the clearly apparent peaks (Fig. 2, Table 2).
corresponds to the single-atom gold contact in the junction, while the lower conductance features were fitted by Gaussian functions to give the most probable molecular conductance of the clearly apparent peaks (Fig. 2, Table 2).

|
In addition, composite plots of all the current–distance curves were used to generate two-dimensional (2D) conductance versus relative displacement histograms or heat maps (Fig. 2).
The break-off distances associated with the highest molecular conductance plateau, and allowing for the snap-back of the gold electrodes on rupture of the last Au-Au contact,[39] are somewhat shorter than the crystallographically determined molecular lengths. This indicates that, with the exception of bis-thiolate anchored 4,[40] the molecules are contacted in a tilted fashion within the junction, with contact angles at the substrate (α) in the range 40°–60° (Table 2).
Molecular conductance through tolanes such as 1–4 that are contacted within a molecular junction by electron-donating thiolate, thioether, and amine anchors is expected to be dominated by off-resonance tunnelling through the tail of the HOMO state. The molecular conductance in these cases is often well described by the Landauer–Büttiker model,[45,46] which for single channel conductance can be written as shown in Eqn 3:

where  is the transmission function which describes the probability of transport of an electron at the Fermi energy through the molecule. As noted in section 12.6 of ref. [46] in the weak coupling limit, the transmission function is proportional to the modulus squared of the Green’s function coupling the two ends of the molecule, which for a linear molecule can be written as a product of contributions from the individual moieties.
is the transmission function which describes the probability of transport of an electron at the Fermi energy through the molecule. As noted in section 12.6 of ref. [46] in the weak coupling limit, the transmission function is proportional to the modulus squared of the Green’s function coupling the two ends of the molecule, which for a linear molecule can be written as a product of contributions from the individual moieties.
The multi-parameter nature of electron transmission through a molecular junction helps to rationalise the relative molecular conductance values 3 < 2 < 4 ≈ 1, where the shorter junctions formed from compound 3, which might also be expected to offer the highest lying HOMO, is the least conductive member of the series. Clearly the molecular coupling terms mediated by the anchor groups is a significant factor in the overall molecular conductance, with the DMBT group giving particularly strong interactions with the electrodes.
The single molecule conductance data from 1–4 (Table 2) provide information to expand tests of the quantum circuit laws expressed in Eqns 1 and 2 beyond the original test set based on a large range of calculated conductance values and experimental data from 1,4-benzenedithiol, 1,4-benzenediamine, and 4-aminothiophenol.[38] The values of molecular conductance predicted by the quantum circuit rules are denoted here as  to distinguish them from the most probable conductance determined from the experimental conductance histograms, denoted
to distinguish them from the most probable conductance determined from the experimental conductance histograms, denoted  . Given the measured conductance values of the symmetrically contacted molecules 1 (
. Given the measured conductance values of the symmetrically contacted molecules 1 ( ), 2 (
), 2 ( ), 3 (
), 3 ( ), and 4 (
), and 4 ( ) it is possible to use the relationship in Eqn 1 to predict the conductance of asymmetric derivatives such as 5 (
) it is possible to use the relationship in Eqn 1 to predict the conductance of asymmetric derivatives such as 5 ( ), 6 (
), 6 ( ), 7 (
), 7 ( ), and 8 (
), and 8 ( ) (Chart 1, Table 2).
) (Chart 1, Table 2).
The parameterisation of molecular conductance in the form of Eqn 2 provides further exciting opportunities for designing molecular components for use in molecular electronics, should a sufficient range of terms to characterise a sufficiently wide range of anchors ( ,
,  , Table 2) and backbones (
, Table 2) and backbones ( , Table 3) be known. Although the anchor group parameters for the thioanisole and 3,3-dimethyl-2,3-dihydrobenzo[b]thiophene have not yet been determined, parameters have been determined for benzenethioate (
, Table 3) be known. Although the anchor group parameters for the thioanisole and 3,3-dimethyl-2,3-dihydrobenzo[b]thiophene have not yet been determined, parameters have been determined for benzenethioate ( ) and aniline contacts (
) and aniline contacts ( ), and for the ethynyl bridge (
), and for the ethynyl bridge ( ).[38] It is therefore also possible to use Eqn 2 to estimate the molecular conductance
).[38] It is therefore also possible to use Eqn 2 to estimate the molecular conductance  of, for example, the bis(amine) contacted compound 3
of, for example, the bis(amine) contacted compound 3

and the bis(thiolate) derived from the acyl-protected compound 4


|
These values are in excellent agreement with the experimentally determined values (3,  –3.2 ± 0.4; 4,
–3.2 ± 0.4; 4,  –2.8 ± 0.1) (Table 2).
–2.8 ± 0.1) (Table 2).
As noted above, the anchor group parameters for the 3,3-dimethyl-2,3-dihydrobenzo[b]thiophene ( ) and thioanisole (
) and thioanisole ( ) anchors have not been determined. However, the molecular conductance values of symmetrically structured molecules featuring either the DMBT (1, 9, 11) or thioanisole (2, 10, 12) anchor groups and molecular backbones with known backbone parameters (Table 4) have been reported here or elsewhere[35] (Chart 1, Table 2). The anchor parameters for these increasingly common contacting groups could therefore be obtained from the average solutions for
) anchors have not been determined. However, the molecular conductance values of symmetrically structured molecules featuring either the DMBT (1, 9, 11) or thioanisole (2, 10, 12) anchor groups and molecular backbones with known backbone parameters (Table 4) have been reported here or elsewhere[35] (Chart 1, Table 2). The anchor parameters for these increasingly common contacting groups could therefore be obtained from the average solutions for  from Eqn 2 using the experimental values of
from Eqn 2 using the experimental values of  from 1, 9, and 11 (
from 1, 9, and 11 ( ) or 2, 10, and 12 (
) or 2, 10, and 12 ( ) (Table 3).
) (Table 3).

|
Perhaps unsurprisingly, since the experimental data from 1 and 2 form part of the input used to calculate the anchor parameters for the DMBT and thioanisole moieties, Eqn 2 and the data in Tables 3 and 4 successfully estimate the conductance of these compounds, with excellent agreement between calculated ( ) and experimental (
) and experimental ( ) values (Table 2). With contact parameters for a range of anchor groups in hand (Table 3),
) values (Table 2). With contact parameters for a range of anchor groups in hand (Table 3),  for the proposed asymmetric compounds 5–8 can also be estimated from Eqn 2. Pleasingly, the
for the proposed asymmetric compounds 5–8 can also be estimated from Eqn 2. Pleasingly, the  values calculated for 5–8 in this manner with Eqn 2 are consistent with those obtained from Eqn 1 (Table 2).
values calculated for 5–8 in this manner with Eqn 2 are consistent with those obtained from Eqn 1 (Table 2).
The self-consistency of quantum circuit rules prompted further exploration of the relationships proposed and the synthesis and measurement of the asymmetric compounds 5–8. These compounds were also readily prepared via Sonogashira cross-coupling reactions, with the molecular structures of 5, 7, and 8 also being determined crystallographically (Fig. 3, Table 5). Each of these compounds was studied within molecular junctions using the STM-BJ technique as described above, giving current–distance traces with clear molecular conductance plateaus, leading to well defined peaks in the 1D current histograms and features in the 2D conductance–relative displacement maps (Fig. 4).

|
|
As noted above, from the conductance values determined experimentally for 1 and 2, Eqn 1 estimates the conductance of 5 to be  , which can now be shown to be in excellent agreement with the experimentally determined value of 1.0 ± 0.8 G0 (Table 2). Similarly, from Eqn 2 and the anchor and bridge parameters contained in Tables 3 and 4, the conductance of 5 is estimated to be
, which can now be shown to be in excellent agreement with the experimentally determined value of 1.0 ± 0.8 G0 (Table 2). Similarly, from Eqn 2 and the anchor and bridge parameters contained in Tables 3 and 4, the conductance of 5 is estimated to be  (i.e. also
(i.e. also  ). Similar high levels of agreement are also found in the molecular conductance values of the asymmetrically contacted compounds 6, 7, and 8 determined from single-molecule STM-BJ experiments, and the values estimated from Eqns 1 and 2 (Table 2). Together these results give considerable confidence in the use of the molecular circuit laws as predictive tools for use in the further study of the electrical properties of molecular junctions.
). Similar high levels of agreement are also found in the molecular conductance values of the asymmetrically contacted compounds 6, 7, and 8 determined from single-molecule STM-BJ experiments, and the values estimated from Eqns 1 and 2 (Table 2). Together these results give considerable confidence in the use of the molecular circuit laws as predictive tools for use in the further study of the electrical properties of molecular junctions.
Conclusions
A series of ‘molecular quantum circuit laws’ that have been developed for off-resonance tunnelling junctions treated as a series of weakly coupled scattering moieties, were previously verified largely by results from DFT calculations of junction conductance. Here we have tested the circuit laws using a small range of tolane compounds, symmetrically and asymmetrically functionalised by common anchoring groups. The circuit laws are found to hold true for these experimental data, giving great confidence in the potential for these relationships to be used in a predictive and design capability for future molecular-based electronic devices.
Experimental
General Conditions
All reactions were performed under an N2 atmosphere using standard Schlenk techniques unless noted otherwise. Reaction solvents were purified and dried by appropriate means before distillation and storage under nitrogen. No special precautions were taken to exclude air or moisture during work-up. The compounds 4-ethynylthioanisole, 5-ethynyl-3,3-dimethyl-2,3-dihydrobenzo[b]thiophene,[43] 4-ethynylaniline,[47] [PdCl2(PPh3)2],[48] and [Pd2(dba)3][49] were prepared by literature methods. All other materials were obtained from commercial suppliers and used as received.
NMR spectra were recorded in deuterated solvent solutions on Bruker Avance 500 MHz or 600 MHz spectrometers and referenced against residual protio-solvent resonances (CHCl3: 1H 7.26 ppm, 13C{1H} 77.16 ppm). Infrared spectra were recorded on an Agilent Technologies Cary 630 spectrometer using ATR sampling methods. High-resolution mass spectra were recorded using a Waters LCT Premier XE mass spectrometer using electrospray ionisation or atmospheric pressure chemical ionization with Leucine Enkephalin as reference.
Crystallography
Data were collected using an XtaLAB Synergy single source HyPix diffractometer operating at T 100 K. Data were measured using Cu Ka radiation. The diffraction pattern was indexed and the total number of runs and images was based on the strategy calculation from the program CrysAlisPro 1.171.41.103a. Data reduction, scaling, and absorption corrections were performed using CrysAlisPro (Rigaku, V1.171.41.103a, 2021).
The crystals were kept at a steady T 100 K during data collection. The structures were solved with the SHELXT 2018/2[50] solution program using dual methods and by using Olex2 1.3[51] as the graphical interface. The models were refined with SHELXL[52] using full matrix least-squares minimisation on F2. All crystallographic data have been deposited with the CCDC (2087332–2087337) and can be obtained free of charge via https://www.ccdc.cam.ac.uk/structures/ or from the Cambridge Crystallographic Data Centre, 12 Union Road, Cambridge CB2 1EZ, UK (fax +441223336033; email deposit@ccdc.cam.ac.uk). Crystal and refinement details are given in Table S1 (Supplementary Material).
Single-Molecule Conductance Characterisation
For the STM-BJ experiment, gold-on-glass substrates (Arrandee) were cleaned by immersion in a freshly prepared piranha solution (1 part of H2O2 (33 %) in 3 parts of H2SO4 (98 %) – CAUTION piranha solution is extremely corrosive) for 1–2 min and then rinsed with copious amounts of deionised water and dried under a nitrogen stream. A freshly cut gold wire of 99.99 % purity was used as the STM tip. A 1 mM solution of the target molecules in 1,3,5-trimethylbenzene (TMB, mesitylene) was used for analysis. For compound 8 the 1 mM TMB solution was also treated with small quantities of 1 M solution of tetra-n-butylammonium fluoride (TBAF) in tetrahydrofuran (THF) to assist in removing the protecting acyl group. The substrate surface was checked by STM imaging in solution before starting the conductance–distance measurements. The junctions form and break repeatedly between the sharp tip and the gold substrate by moving the tip into and away from the substrate at the rate of 5 nm s−1 (V bias –0.1 V). In the cases where the gold junction breaks without molecule(s) becoming trapped between electrodes while withdrawing the tip, the current–distance trace demonstrated only exponential decay. In contrast, if a target molecule(s) bridged the gap between electrodes, the conductive plateau-like features were observed. Typically, 2000 individual traces were recorded for each compound. All current–distance traces were plotted without selection, except in the case of compounds 3 and 8; for these compounds it was necessary to manually remove examples of exponential curves without molecular plateaus to improve signal to noise ratio and make the conductance peaks more prominent.
Synthetic Details
1,2-Bis(3,3-dimethyl-2,3-dihydrobenzo[b]thiophen-5-yl)ethyne (1)

A solution of 5-ethynyl-3,3-dimethyl-2,3-dihydrobenzo[b]thiophene (78 mg, 0.411 mmol) and 5-bromo-3,3-dimethyl-2,3-dihydrobenzo[b]thiophene (100 mg, 0.411 mmol) in dry and degassed NHiPr2 (20 mL) was treated with [Pd2(dba)3] (11 mg, 0.012 mmol), 2-biphenyl-di-tert-butylphosphine (JohnPhos, 8 mg, 0.025 mmol), and CuI (5 mg, 0.025 mmol) and the mixture allowed to stir at reflux temperature for 48 h. The solvent was removed under vacuum and the residue purified by column chromatography on silica using hexane giving the product as a white solid (95 mg, 66 %). Crystals suitable for X-ray diffraction were obtained from CH2Cl2/MeOH by slow diffusion. νmax (solid state, ATR)/cm−1 ν(C≡C) 2113. δH (CDCl3, 500 MHz) 7.28 (dd, J 8.0, 1.6, 2H, H3), 7.19 (d, J 1.4, 2H, H10), 7.14 (d, J 8.0, 2H, H3), 3.20 (s, 4H, H2), 1.39 (s, 12H, H8). δC (CDCl3, 126 MHz) 148.37 (C9), 141.43 (C5), 130.85 (C3), 125.91 (C10), 122.42 (C4), 119.41 (C2), 89.28 (C1), 47.46 (C6), 47.41 (C7), 27.50 (C8). m/z (ESI+) 350.1164; calcd. for C22H22S2 [M]+ 350.1163.

1,2-Bis(4-(methylthio)phenyl)ethyne (2)

A solution of 4-ethynylthioanisole (119 mg, 0.799 mmol) and 4-iodothioanisle (200 mg, 0.799 mmol) in dry and degassed NHiPr2 (20 mL) was treated with Pd(PPh3)2Cl2 (14 mg, 0.02 mmol) and CuI (4 mg, 0.02 mmol) and the mixture allowed to stir at room temperature for 20 h. The solvent was removed under vacuum and the residue purified by column chromatography on silica using hexane/CH2Cl2 (2:1) giving the product as a white solid (180 mg, 83 %). Crystals suitable for X-ray diffraction were obtained from CH2Cl2/n-pentane by slow diffusion. νmax (solid state, ATR)/cm−1 ν(C≡C) 2113. δH (CDCl3, 500 MHz) 7.42 (d, J 8.3, 4H, H3), 7.20 (d, J 8.3, 4H, H4), 2.50 (s, 3H, H6). δC (CDCl3, 126 MHz) 139.37 (C2), 131.95 (C3), 126.04 (C4), 119.74 (C5), 89.43 (C1), 15.56 (C6). m/z (ESI+) 270.0536; calcd. for C16H14S2 [M]+ 270.0537.

4,4’-(Ethyne-1,2-diyl)dianiline (3)

A solution of 4-ethynyaniline (59 mg, 0.502 mmol) and 4-iodoaniline (100 mg, 0.456 mmol) in dry and degassed NHiPr2 (20 mL) was treated with PdCl2(PPh3)2 (8 mg, 0.011 mmol) and CuI (2 mg, 0.01 mmol) and the mixture allowed to stir at room temperature for 20 h. The solvent was removed under vacuum and the residue purified by column chromatography on silica using hexane/CH2Cl2 (1:1) giving the product as an off-white solid (78 mg, 82 %). Crystals suitable for X-ray diffraction were obtained by slow evaporation of toluene. νmax (solid state, ATR)/cm−1 ν(C≡C) 2109, ν(N–H) 3464. δH (CDCl3, 500 MHz) 7.30 (d, J 8.6, 4H, H3), 6.62 (d, J 8.6, 4H, H4), 3.77 (s, 4H, H6). δC (CDCl3, 126 MHz) 146.27 (C2), 132.83 (C3), 114.93 (C4), 113.54 (C5), 87.89 (C1). m/z (ESI+) 209.1079; calcd. for C14H13N2 [M + H]+ 209.1079.

3,3-Dimethyl-5-((4-(methylthio)phenyl)ethynyl)-2,3-dihydrobenzo[b]thiophene (5)

A solution of 5-ethynyl-3,3-dimethyl-2,3-dihydrobenzo[b]thiophene (60 mg, 0.318 mmol) and 4-iodothioanisole (96 mg, 0.382 mmol) in dry and degassed NEt3 (20 mL) was treated with PdCl2(PPh3)2 (6 mg, 0.008 mmol) and CuI (2 mg, 0.01 mmol) and the mixture allowed to stir at room temperature for 20 h. The solvent was removed under vacuum and the residue purified by column chromatography on silica using hexane/CH2Cl2 (9:1) giving the product as a white crystal (90 mg, 90 %). Crystals suitable for X-ray diffraction were obtained from CH2Cl2/MeOH by slow diffusion. νmax (solid state, ATR)/cm−1 ν(C≡C) 2114. δH (CDCl3, 500 MHz) 7.42 (d, J 8.6, 2H, H4), 7.28 (dd, J 8.0, 1.6, 1H, H9), 7.22 – 7.18 (m, 3H, H3 and H16), 7.15 (d, J 8.0, 1H, H10), 3.20 (s, 2H, H12), 2.50 (s, 3H, H1), 1.39 (s, 6H, H14). δC (CDCl3, 126 MHz) 148.39 (9), 141.61 (11), 139.18 (5), 131.91 (4), 130.90 (9), 126.06 (3), 125.99 (16), 122.43 (10), 119.89 (2), 119.27 (8), 89.98 (6), 88.74 (7), 47.46 (12), 47.41 (13), 27.49 (14), 15.57 (1). m/z (ESI+) 311.0926; calcd. for C19H19S2 [M + H]+ 311.0928.

4-((3,3-Dimethyl-2,3-dihydrobenzo[b]thiophen-5-yl)ethynyl)aniline (6)

A solution of 5-ethynyl-3,3-dimethyl-2,3-dihydrobenzo[b]thiophene (60 mg, 0.318 mmol) and 4-iodothioanisole (84 mg, 0.382 mmol) in dry and degassed NEt3 (20 mL) was treated with PdCl2(PPh3)2 (6 mg, 0.008 mmol) and CuI (2 mg, 0.01 mmol) and the mixture allowed to stir at room temperature for 20 h. The solvent was removed under vacuum and the residue purified by column chromatography on silica using hexane/CH2Cl2 (1:1) followed by hexane/CH2Cl2 (1:6) giving the product as a yellow viscous oil (70 mg, 80 %). νmax (neat, ATR)/cm−1 ν(C≡C) 2194, ν(N–H) 3465. δH (CDCl3, 500 MHz) 7.32 (d, J 8.6, 2H, H4), 7.29 – 7.24 (m, 1H, H9), 7.17 (d, J 1.3, 1H, H16), 7.13 (d, J 8.0, 1H, H10), 6.63 (d, J 8.6, 2H, H3), 3.80 (s, 2H, H1), 3.19 (s, 2H, H12), 1.38 (s, 6H, H14). δC (CDCl3, 126 MHz) 148.27 (C3), 146.62 (C5), 140.81 (C11), 132.99 (C4), 130.71 (C9), 125.79 (C16), 122.36 (C10), 119.92 (C8), 114.91 (C3), 112.97 (C2), 89.56 (C7), 87.73 (C6), 76.84 (s), 47.46 (C12), 47.39 (C13) 27.48 (C1). m/z (ESI+) 280.1161; calcd. for C18H18NS [M + H]+ 280.1160.

4-((4-(Methylthio)phenyl)ethynyl)aniline (7)

A solution of 4-ethynylthioanisole (200 mg, 0.913 mmol) and 4-iodoaniline (164 mg, 1.105 mmol) in dry and degassed NHiPr2 (20 mL) was treated with PdCl2(PPh3)2 (36 mg, 0.023 mmol) and CuI (5 mg, 0.025 mmol) and the mixture allowed to stir at room temperature for 20 h. The solvent was removed under vacuum and the residue purified by column chromatography on silica using hexane/CHCl3 (1:1) giving the product as an off-white solid (198 mg, 62 %). Crystals suitable for X-ray diffraction were obtained from CH2Cl2/n-hexane by slow diffusion. νmax (solid state, ATR)/cm−1 ν(C≡C) 2199, ν(N–H) 3463. δH (CDCl3, 500 MHz) 7.40 (d, J 8.1, 2H, H4), 7.32 (d, J 8.2, 2H, H9), 7.19 (d, J 8.1, 2H, H3), 6.63 (d, J 8.2, 2H, H10), 3.81 (s, 2H, H1), 2.49 (s, 3H, H12). δC (CDCl3, 126 MHz) 146.73 (C8), 138.53 (C5), 133.05 (C9), 131.78 (C4), 126.15 (C3), 120.48 (C2), 114.90 (C10), 112.82 (C11), 90.33 (C6), 87.23 (C7), 15.68 (C1). m/z (ESI+) 240.0846; calcd. for C15H14NS [M + H]+ 240.0847.

S-(4-((4-(Methylthio)phenyl)ethynyl)phenyl) Ethanethioate (8)

A solution of 4-ethynylthioanisole (100 mg, 0.360 mmol) and S-(4-iodophenyl) ethanethioate (54 mg, 0.360 mmol) in dry and degassed NHiPr2 (20 mL) was treated with PdCl2(PPh3)2 (14 mg, 0.02 mmol) and CuI (4 mg, 0.02 mmol) and the mixture allowed to stir at room temperature for 20 h. The solvent was removed under vacuum and the residue purified by column chromatography on silica using hexane/CH2Cl2 (2:1) giving the product as an off-white solid (95 mg, 89 %). Crystals suitable for X-ray diffraction were obtained from CH2Cl2/n-hexane by slow diffusion. νmax (solid state, ATR)/cm−1 ν(C≡C) 2116. δH (CDCl3, 500 MHz) 7.54 (d, J 8.4, 2H, H9), 7.44 (d, J 8.5, 2H, H4), 7.39 (d, J 8.4, 2H, H10), 7.21 (d, J 8.5, 2H, H3), 2.50 (s, 3H, H1), 2.43 (s, 3H, H13). δC (CDCl3, 126 MHz) 193.63 (C12), 139.92 (C2), 134.36 (C10), 132.24 (C9), 132.09 (C4), 128.06 (C8), 125.99 (C3), 124.75 (C11), 119.28 (C5), 91.07 (C6), 88.88 (C7), 30.42 (C13), 15.49 (C1). m/z (ESI+) 298.0426; calcd. for C17H14OS2 [M]+ 298.0486.

Supplementary Material
Crystal structure and refinement details as well as plots of 1H and 13C{1H} NMR spectra are available on the Journal’s website.
Data Availability Statement
The data that support this study will be shared upon reasonable request to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Declaration of Funding
Funding was received from the Australian Research Council (DP190100073, DP109100074, LE1501000148, FT2001000243) and Forrest Research Foundation Engineering and Physical Sciences Research Council (UK).
Acknowledgements
This work has been supported by the research community through the agency of the Australian Research Council (DP19010073, DP19010074). The award of a LIEF grant (LE150100148) that has provided the STM facility for single molecule junction formation and study is most gratefully acknowledged. M.N. holds a Forrest Scholarship from the Forrest Research Foundation. S.A.M. holds an ARC Future Fellowship (FT2001000243). Further support for research carried out by the team from the UK Engineering and Physical Sciences Research Council is gratefully acknowledged.
On a more personal note, P.J.L. wishes to express his gratitude to the ensemble of students, collaborators, mentors, colleagues, and friends who have given their time, effort, talent, and insight to the research programs pursued in the group; without these people and their contributions, nothing could have been achieved.
References
[1] S. Marques-Gonzalez, P. J. Low, Aust. J. Chem. 2016, 69, 244.| Crossref | GoogleScholarGoogle Scholar |
[2] K. Wang, B. Q. Xu, Top. Curr. Chem. 2017, 375, 17.
| Crossref | GoogleScholarGoogle Scholar |
[3] D. Xiang, X. L. Wang, C. C. Jia, T. Lee, X. F. Guo, Chem. Rev. 2016, 116, 4318.
| Crossref | GoogleScholarGoogle Scholar | 26979510PubMed |
[4] R. L. McCreery, A. J. Bergren, Adv. Mater. 2009, 21, 4303.
| Crossref | GoogleScholarGoogle Scholar | 26042937PubMed |
[5] F. Chen, J. Hihath, Z. F. Huang, X. L. Li, N. J. Tao, Annu. Rev. Phys. Chem. 2007, 58, 535.
| Crossref | GoogleScholarGoogle Scholar | 17134372PubMed |
[6] J. P. Launay, Coord. Chem. Rev. 2013, 257, 1544.
| Crossref | GoogleScholarGoogle Scholar |
[7] B. Mann, H. Kuhn, J. Appl. Phys. 1971, 42, 4398.
| Crossref | GoogleScholarGoogle Scholar |
[8] E. Gorenskaia, K. L. Turner, S. Martin, P. Cea, P. J. Low, Nanoscale 2021, 13, 9055.
| Crossref | GoogleScholarGoogle Scholar | 34042128PubMed |
[9] L. Herrer, S. Martin, P. Cea, Appl. Sci. 2020, 10, 6064.
| Crossref | GoogleScholarGoogle Scholar |
[10] A. Vilan, D. Aswal, D. Cahen, Chem. Rev. 2017, 117, 4248.
| Crossref | GoogleScholarGoogle Scholar | 28177226PubMed |
[11] B. Branchi, F. C. Simeone, M. A. Rampi, Top. Curr. Chem. 2011, 313, 85.
| Crossref | GoogleScholarGoogle Scholar |
[12] B. Q. Xu, N. J. J. Tao, Science 2003, 301, 1221.
| Crossref | GoogleScholarGoogle Scholar |
[13] W. Haiss, H. van Zalinge, S. J. Higgins, D. Bethell, H. Hobenreich, D. J. Schiffrin, R. J. Nichols, J. Am. Chem. Soc. 2003, 125, 15294.
| Crossref | GoogleScholarGoogle Scholar | 14664565PubMed |
[14] L. Wang, L. Wang, L. Zhang, D. Xiang, Top. Curr. Chem. 2017, 375, 61.
| Crossref | GoogleScholarGoogle Scholar |
[15] P. T. Mathew, F. Z. Fang, Engineering 2018, 4, 760.
| Crossref | GoogleScholarGoogle Scholar |
[16] H. L. Chen, J. F. Stoddart, Nat. Rev. Mater. 2021,
| Crossref | GoogleScholarGoogle Scholar |
[17] H. M. Osorio, S. Catarelli, P. Cea, J. B. G. Gluyas, F. Hartl, S. J. Higgins, E. Leary, P. J. Low, S. Martin, R. J. Nichols, J. Tory, J. Ulstrup, A. Vezzoli, D. C. Milan, Q. Zeng, J. Am. Chem. Soc. 2015, 137, 14319.
| Crossref | GoogleScholarGoogle Scholar | 26488257PubMed |
[18] S. Ciampi, N. Darwish, H. M. Aitken, I. Diez-Perez, M. L. Coote, Chem. Soc. Rev. 2018, 47, 5146.
| Crossref | GoogleScholarGoogle Scholar | 29947390PubMed |
[19] R. J. Nichols, S. J. Higgins, Acc. Chem. Res. 2016, 49, 2640.
| Crossref | GoogleScholarGoogle Scholar | 27714992PubMed |
[20] K. Jiang, S. J. Pookpanratana, T. Ren, S. N. Natoli, B. A. Sperling, J. Robertson, C. A. Richter, S. Yu, Q. L. Li, Appl. Phys. Lett. 2019, 115, 162102.
| Crossref | GoogleScholarGoogle Scholar |
[21] S. Pookpanratana, H. Zhu, E. G. Bittle, S. N. Natoli, T. Ren, C. A. Richter, Q. Li, C. A. Hacker, J. Phys. Condens. Matter 2016, 28, 094009.
| Crossref | GoogleScholarGoogle Scholar | 26871549PubMed |
[22] V. Parkula, M. S. Maglione, S. Casalini, Q. M. Zhang, P. Greco, C. A. Bortolotti, C. Rovira, M. Mas-Torrent, F. Biscarini, Adv. Electron. Mater. 2019, 5, 1800875.
| Crossref | GoogleScholarGoogle Scholar |
[23] S. K. Saxena, U. M. Tefashe, M. Supur, R. L. McCreery, ACS Sens. 2021, 6, 513.
| Crossref | GoogleScholarGoogle Scholar | 33315386PubMed |
[24] C. P. Tao, C. C. Jiang, Y. H. Wang, J. F. Zheng, Y. Shao, X. S. Zhou, J. Phys. Chem. Lett. 2020, 11, 10023.
| Crossref | GoogleScholarGoogle Scholar | 33179941PubMed |
[25] E. Burzuri, A. Garcia-Fuente, V. Garcia-Suarez, K. S. Kumar, M. Ruben, J. Ferrer, H. S. J. van der Zant, Nanoscale 2018, 10, 7905.
| Crossref | GoogleScholarGoogle Scholar | 29682641PubMed |
[26] M. Ormaza, P. Abufager, B. Verlhac, N. Bachellier, M. L. Bocquet, N. Lorente, L. Limot, Nat. Commun. 2017, 8, 1974.
| Crossref | GoogleScholarGoogle Scholar | 29215014PubMed |
[27] S. Wagner, F. Kisslinger, S. Ballmann, F. Schramm, R. Chandrasekar, T. Bodenstein, O. Fuhr, D. Secker, K. Fink, M. Ruben, H. B. Weber, Nat. Nanotechnol. 2013, 8, 575.
| Crossref | GoogleScholarGoogle Scholar | 23851359PubMed |
[28] C. Herrmann, G. C. Solomon, M. A. Ratner, J. Am. Chem. Soc. 2010, 132, 3682.
| Crossref | GoogleScholarGoogle Scholar | 20192192PubMed |
[29] R. Liu, S. H. Ke, W. Yang, H. U. Baranger, J. Chem. Phys. 2007, 127, 141104.
| Crossref | GoogleScholarGoogle Scholar | 17994823PubMed |
[30] R. Liu, S. H. Ke, H. U. Baranger, W. T. Yang, Nano Lett. 2005, 5, 1959.
| Crossref | GoogleScholarGoogle Scholar | 16218717PubMed |
[31] K. Wang, E. Meyhofer, P. Reddy, Adv. Funct. Mater. 2020, 30, 1904534.
| Crossref | GoogleScholarGoogle Scholar |
[32] X. T. Zhao, C. C. Huang, M. Gulcur, A. S. Batsanov, M. Baghernejad, W. J. Hong, M. R. Bryce, T. Wandlowski, Chem. Mater. 2013, 25, 4340.
| Crossref | GoogleScholarGoogle Scholar |
[33] Q. Lu, C. Yao, X. H. Wang, F. S. Wang, J. Phys. Chem. C 2012, 116, 17853.
| Crossref | GoogleScholarGoogle Scholar |
[34] J. R. Quinn, F. W. Foss, L. Venkataraman, R. Breslow, J. Am. Chem. Soc. 2007, 129, 12376.
| Crossref | GoogleScholarGoogle Scholar | 17887757PubMed |
[35] M. Naher, D. C. Milan, O. A. Al-Owaedi, I. J. Planje, S. Bock, J. Hurtado-Gallego, P. Bastante, Z. M. Abd Dawood, L. Rincon-Garcia, G. Rubio-Bollinger, S. J. Higgins, N. Agrait, C. J. Lambert, R. J. Nichols, P. J. Low, J. Am. Chem. Soc. 2021, 143, 3817.
| Crossref | GoogleScholarGoogle Scholar | 33606524PubMed |
[36] J. Ferrer, C. J. Lambert, V. M. Garcia-Suarez, D. Z. Manrique, D. Visontai, L. Oroszlany, R. Rodriguez-Ferradas, I. Grace, S. W. D. Bailey, K. Gillemot, H. Sadeghi, L. A. Algharagholy, New J. Phys. 2014, 16, 093029.
| Crossref | GoogleScholarGoogle Scholar |
[37] C. J. Lambert, S. X. Liu, Chem. – Eur. J. 2018, 24, 4193.
| Crossref | GoogleScholarGoogle Scholar | 29120523PubMed |
[38] D. Z. Manrique, Q. Al-Galiby, W. J. Hong, C. J. Lambert, Nano Lett. 2016, 16, 1308.
| Crossref | GoogleScholarGoogle Scholar | 26784577PubMed |
[39] W. J. Hong, D. Z. Manrique, P. Moreno-Garcia, M. Gulcur, A. Mishchenko, C. J. Lambert, M. R. Bryce, T. Wandlowski, J. Am. Chem. Soc. 2012, 134, 2292.
| Crossref | GoogleScholarGoogle Scholar |
[40] P. Moreno-Garcia, M. Gulcur, D. Z. Manrique, T. Pope, W. J. Hong, V. Kaliginedi, C. C. Huang, A. S. Batsanov, M. R. Bryce, C. Lambert, T. Wandlowski, J. Am. Chem. Soc. 2013, 135, 12228.
| Crossref | GoogleScholarGoogle Scholar | 23875671PubMed |
[41] M. R. Bryce, J. Mater. Chem. C Mater. Opt. Electron. Devices 2021,
| Crossref | GoogleScholarGoogle Scholar |
[42] D. Nishimura, T. Oshikiri, Y. Takashima, A. Hashidzume, H. Yamaguchi, A. Harada, J. Org. Chem. 2008, 73, 2496.
| Crossref | GoogleScholarGoogle Scholar | 18336039PubMed |
[43] M. Naher, S. Bock, Z. M. Langtry, K. M. O’Malley, A. N. Sobolev, B. W. Skelton, M. Korb, P. J. Low, Organometallics 2020, 39, 4667.
| Crossref | GoogleScholarGoogle Scholar |
[44] M. S. Hybertsen, L. Venkataraman, Acc. Chem. Res. 2016, 49, 452.
| Crossref | GoogleScholarGoogle Scholar | 26938931PubMed |
[45] C. J. Lambert, Chem. Soc. Rev. 2015, 44, 875.
| Crossref | GoogleScholarGoogle Scholar | 25255961PubMed |
[46] C. J. Lambert, Quantum Transport in Nanostructures and Molecules: An Introduction to Molecular Electronics 2021 (IOP Publishing: Bristol, UK).
[47] A. K. Flatt, Y. X. Yao, F. Maya, J. M. Tour, J. Org. Chem. 2004, 69, 1752.
| Crossref | GoogleScholarGoogle Scholar | 14987042PubMed |
[48] N. Miyaura, A. Suzuki, Org. Synth. 1990, 68, 130.
| Crossref | GoogleScholarGoogle Scholar |
[49] S. S. Zalesskiy, V. P. Ananikov, A. J. Reay, I. J. S. Fairlamb, Inorg. Synth. 2018, 37, 183.
[50] G. M. Sheldrick, Acta Crystallogr. A 2015, 71, 3.
| Crossref | GoogleScholarGoogle Scholar |
[51] O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard, H. Puschmann, J. Appl. Cryst. 2009, 42, 339.
| Crossref | GoogleScholarGoogle Scholar |
[52] A. Thorn, G. M. Sheldrick, Acta Crystallogr. A 2008, 64, C221.
| Crossref | GoogleScholarGoogle Scholar |
* Paul Low was the recipient of the 2020 H. G. Smith Memorial Award of the RACI.



 ) versus electrode displacement curves, conductance histograms, and 2D conductance–relative displacement histograms (where the heat map colour ranges from zero counts (white) to high counts (deep blue)) from compounds 1–3.
) versus electrode displacement curves, conductance histograms, and 2D conductance–relative displacement histograms (where the heat map colour ranges from zero counts (white) to high counts (deep blue)) from compounds 1–3.

 ) versus electrode displacement curves, conductance histograms and 2D conductance–relative displacement histograms (where the heat map colour ranges from zero counts (white) to high counts (deep blue)) from compounds 5–8.
) versus electrode displacement curves, conductance histograms and 2D conductance–relative displacement histograms (where the heat map colour ranges from zero counts (white) to high counts (deep blue)) from compounds 5–8.
