Thermochemistry of Guanine Tautomers Re-Examined by Means of High-Level CCSD(T) Composite Ab Initio Methods*
Amir Karton A
A
A School of Molecular Sciences, The University of Western Australia, Perth, WA 6009, Australia. Email: amir.karton@uwa.edu.au
Australian Journal of Chemistry 72(8) 607-613 https://doi.org/10.1071/CH19276
Submitted: 17 June 2019 Accepted: 27 June 2019 Published: 18 July 2019
Abstract
We obtained accurate gas-phase tautomerization energies for a set of 14 guanine tautomers by means of high-level thermochemical procedures approximating the CCSD(T) energy at the complete basis set (CBS) limit. For the five low-lying tautomers, we use the computationally demanding W1-F12 composite method for obtaining the tautomerization energies. The relative W1-F12 tautomerization enthalpies at 298 K are: 0.00 (1), 2.37 (2), 2.63 (3), 4.03 (3′), and 14.31 (4) kJ mol−1. Thus, as many as four tautomers are found within a small energy window of less than 1.0 kcal mol−1 (1 kcal mol−1 = 4.184 kJ mol−1). We use these highly accurate W1-F12 tautomerization energies to evaluate the performance of a wide range of lower-level composite ab initio procedures. The Gn composite procedures (G4, G4(MP2), G4(MP2)-6X, G3, G3B3, G3(MP2), and G3(MP2)B3) predict that the enol tautomer (3) is more stable than the keto tautomer (2) by amounts ranging from 0.36 (G4) to 1.28 (G3(MP2)) kJ mol−1. We also find that an approximated CCSD(T)/CBS energy calculated as HF/jul-cc-pV{D,T}Z + CCSD/jul-cc-pVTZ + (T)/jul-cc-pVDZ results in a root-mean-square deviation (RMSD) of merely 0.11 kJ mol−1 relative to the W1-F12 reference values. We use this approximated CCSD(T)/CBS method to obtain the tautomerization energies of 14 guanine tautomers. The relative tautomerization enthalpies at 298 K are: 0.00 (1), 2.20 (2), 2.51 (3), 4.06 (3′), 14.30 (4), 25.65 (5), 43.78 (4′), 53.50 (6′), 61.58 (6), 77.37 (7), 82.52 (8′), 86.02 (9), 100.70 (10), and 121.01 (8) kJ mol−1. Using these tautomerization enthalpies, we evaluate the performance of standard and composite methods for the entire set of 14 guanine tautomers. The best-performing procedures emerge as (RMSDs are given in parentheses): G4(MP2)-6X (0.51), CCSD(T)+ΔMP2/CBS (0.52), and G4(MP2) (0.64 kJ mol−1). The worst performers are CCSD(T)/AVDZ (1.05), CBS-QB3 (1.24), and CBS-APNO (1.38 kJ mol−1).
Introduction
All DNA bases exist in several tautomeric forms and DNA tautomerization is an important chemical process that can alter base pairing. Over the past two decades, the gas-phase energetic and spectroscopic properties of the guanine tautomers have been extensively studied both experimentally and theoretically.[1–23] Nevertheless, as the most energetically stable guanine tautomers are separated by energy differences of only a few kilojoules per mole, it is of interest to use highly accurate ab initio methods for obtaining these energy separations. Hanus et al.[5] found that as many as four guanine tautomers lie within a narrow energy difference of ~5.5 kJ mol−1. In particular, they found that at the CCSD(T)/aug-cc-pVDZ level of theory, the energies of the keto and enol guanine tautomers are: 2.9 (2), 3.8 (3), and 5.5 (3′) kJ mol−1 relative to tautomer 1 (structures are shown in Fig. 1). In contrast, Plekan et al.[17] found that at the CCSD(T)/6–311+G** level of theory, the enol tautomer 3 is the second most stable tautomer after 1. In particular, they obtained energies of 0.9 (3), 1.2 (2), and 3.9 (3′) kJ mol−1 relative to tautomer 1. They also showed that the tautomer order remains the same when using the following additive basis-set correction: CCSD(T)/6–311+G** + CCSD/cc-pVTZ – CCSD/6–311+G**. In particular, they obtained energies of: 1.7 (3), 1.9 (2), and 3.4 (3′) kJ mol−1 relative to tautomer 1. Nevertheless, as these levels of theory are far from the CCSD(T)/CBS limit (coupled cluster with single, double, and quasiperturbative triple excitations at the complete basis set limit), it is of interest to obtain the energy separations closer to the CCSD(T)/CBS limit.
In the present work, we use the high-level composite W1-F12 protocol to determine the energy separation and ordering of the low-lying guanine tautomers. W1-F12 theory approximates the all-electron, relativistic CCSD(T)/CBS energy and has been found to produce thermochemical properties such as heats of formation and reaction energies with mean-absolute deviations (MADs) from highly accurate experimental or theoretical data below the threshold of chemical accuracy (i.e. with MADs below 1 kcal mol−1 (1 kcal mol−1 = 4.184 kJ mol−1)).[24–29] It should be noted, however, that because the low-lying guanine tautomers are chemically similar to each other, W1-F12 theory should yield even better performance for their relative energies owing to a high degree of error cancellation between reactants and products.[26,30–47] We find that at the all-electron, relativistic CCSD(T)/CBS limit, the four lowest-energy guanine tautomers are separated by less than 1 kcal mol−1. This work demonstrates that in order to reliably predict the order and energy separation between the low-lying guanine tautomers, highly accurate composite ab initio methods have to be used and that lower-level composite approaches may not be sufficiently accurate. For example, the considered Gn composite procedures (G4, G4(MP2), G4(MP2)-6X, G3, G3B3, G3(MP2), and G3(MP2)B3) predict that the enol tautomer (3) is more stable than the keto tautomer (2).
Computational Details
In order to obtain accurate energies for the guanine tautomers, calculations were carried out using the high-level ab initio W1-F12 thermochemical protocol. W1-F12 theory combines explicitly correlated F12 techniques[48] with basis-set extrapolations in order to approximate the all-electron, relativistic CCSD(T)/CBS energy. The computational details of W1-F12 theory have been specified elsewhere.[24] In short, the Hartree–Fock (HF) and valence CCSD-F12 correlation components are extrapolated from the VDZ-F12 and VTZ-F12 basis sets, where VnZ-F12 denotes the cc-pVnZ-F12 basis sets of Peterson et al.[49] The complementary auxiliary basis set (CABS) singles correction is included in the self-consistent field (SCF) energy.[50–52] An optimal extrapolation exponent of 3.38 was used in the CCSD-F12/cc-pV{D,T}Z-F12 extrapolation as recommended in reference [24]. The (T) valence correlation energy is obtained from the original W1 theory,[53] i.e. it is extrapolated from the jul-cc-pVDZ and jul-cc-pVTZ basis sets.[54–56] The diagonal, fixed-amplitude 3C(FIX) ansatz,[51,57–59] and the CCSD-F12b approximation are used in all of the explicitly correlated coupled cluster calculations.[52,60] The CCSD inner-shell contribution is calculated with the core-valence weighted correlation-consistent cc-pwCVTZ basis set of Peterson and Dunning,[61] while the (T) inner-shell contribution is calculated with the cc-pwCVTZ(no f) basis set (where cc-pwCVTZ(no f) indicates the cc-pwCVTZ basis set without the f functions). The scalar relativistic contribution (in the second-order Douglas–Kroll–Hess approximation)[62,63] is obtained as the difference between non-relativistic CCSD(T)/jul-cc-pVDZ and relativistic CCSD(T)/jul-cc-pVDZ-DK calculations.[64] The diagonal Born–Oppenheimer correction (DBOC) is calculated at the HF/cc-pVDZ level of theory using the CFOUR program suite.[65] The energy calculations involved in W1-F12 theory are carried out with the Molpro 2016.1 program.[66,67] The relativistic, all-electron, DBOC-inclusive W1-F12 CCSD(T)/CBS tautomerization energies are converted to tautomerization enthalpies at 298 K using zero-point vibrational energies (ZPVEs) and enthalpic corrections calculated at the B3LYP/jul-cc-pVTZ level of theory.[68–70] The harmonic ZPVEs were scaled as recommended in references [25] and [71].
In addition, the performance of more approximate Gaussian-n[72] and CBS-type[73] composite thermochemical procedures is assessed.[74,75] We consider the following composite procedures: G4,[76] G4(MP2),[77] G4(MP2)-6X,[78] G3,[79] G3(MP2),[80] G3B3,[81] G3(MP2)B3,[81] CBS-QB3,[82] and CBS-APNO.[83] The calculations for these composite methods were performed using the Gaussian 16 program suite.[84]
Results and Discussion
Overview of the Guanine Tautomerization Energies
Fig. 1 gives the relative enthalpies at 298 K for the guanine tautomers. The energies are calculated at the CCSD(T)/CBS level of theory, using the following formula HF/jul-cc-pV{D,T}Z + CCSD/jul-cc-pVTZ + (T)/jul-cc-pVDZ, which has been found to give excellent performance relative to W1-F12 theory (see below). For the enol tautomers, we have considered two possible conformers, one in which the O–H bond is pointing towards the pyrimidine ring (labelled n, Fig. 1) and the other in which the O–H bond is pointing towards the imidazole ring (labelled n′, Fig. 1). Inspection of the relative tautomerization energies in Fig. 1 reveals that the energy separations between the low-lying tautomers are spread over a narrow range; namely, the four most stable tautomers are found within a small energy window of less than 1.0 kcal mol−1. It is therefore clear that in order to reliably and accurately predict the order and energy separation between these tautomers, we have to use a high-level composite ab initio method such as W1-F12 theory. However, it should be noted that because tautomers 2 and 3 are separated by merely 0.3 kJ mol−1, the scaled ZPVE component of W1-F12 theory[24,25,37,71,85] may not be sufficiently accurate to unambiguously determine the energy separation between these two tautomers.
Basis Set Convergence of the HF, CCSD, and (T) Components of the Guanine Tautomerization Energies for the Five Energetically Low-Lying Tautomers
Table 1 gives an overview of the basis set convergence of the HF component of the guanine tautomerization energies relative to the HF/CBS limit from W1-F12 theory. As expected, the jul-cc-pVDZ basis set results in very large deviations from the CBS values, with deviations of up to 1.8 kJ mol−1. The jul-cc-pVTZ basis set performs well with deviations on the order of 0.1 kJ mol−1 and a maximum deviation of 0.2 kJ mol−1. The jul-cc-pV{D,T}Z basis set extrapolation results in deviations on the order of 0.05 kJ mol−1 and a maximum deviation of 0.08 kJ mol−1. The jul-cc-pVQZ basis set gives tautomerization energies that are practically identical to those at the HF/CBS values from W1-F12 theory (Table 1).

|
Similarly to the HF energy, calculating the CCSD correlation energy with the jul-cc-pVDZ basis set results in very large deviations of up to 1.8 kJ mol−1 from W1-F12 CBS limit values. The jul-cc-pVTZ basis set performs much better, with deviations on the order of 0.1 kJ mol−1. However, the jul-cc-pV{D,T}Z basis set extrapolation results in significantly larger deviations on the order of 0.8 kJ mol−1. Thus, the jul-cc-pVDZ basis set should not be used as a stand-alone basis set or in basis set extrapolations for the calculation of the the CCSD correlation component of the guanine tautomerization energies.
Calculating the (T) correlation energy with the jul-cc-pVDZ basis set results in fairly good performance, with deviations of 0.0–0.2 kJ mol−1 from W1-F12 CBS limit values.
Guanine Tautomerization Energies for the Energetically Low-Lying Tautomers from W1-F12 Theory
Table 2 gives the component breakdown of the W1-F12 tautomerization energies for the five energetically most stable guanine tautomers. The HF/CBS level of theory predicts the wrong order of the three most stable tautomers with relative energies of −0.34 (3), −0.20 (2), 0.00 (1), 2.77 (3′), and 16.31 (4) kJ mol−1. The CCSD/CBS level of theory gives the correct order of all tautomers with relative energies of 0.00 (1), 1.28 (2), 2.56 (3), 4.13 (3′), and 16.40 (4) kJ mol−1. The (T) correlation component affects the relative energies by significant amounts of up to 1.52 kJ mol−1. At the valence CCSD(T)/CBS level of theory, we obtain relative energies of 0.00 (1), 2.80 (2), 3.21 (3), 4.43 (3′), and 15.18 (4) kJ mol−1. The CCSD(T) core-valence correction still affects the relative energies by up to 0.17 kJ mol−1, whereas the scalar relativistic and DBOC corrections do not affect the tautomerization energies by a chemically significant amount; namely, they are ≤0.03 kJ mol−1.
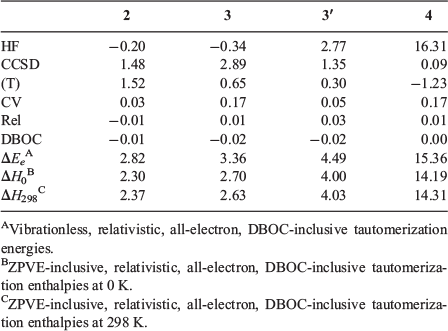
|
Evaluation of the Performance of Lower-Level Standard and Composite Ab Initio Procedures for the Five Most Stable Guanine Tautomers Relative to W1-F12 Reference Values
We proceed to evaluate the performance of computationally economical procedures for the relative energies of the guanine tautomers. Table 3 gives the root-mean-square deviations (RMSDs), MADs, and mean-signed deviations (MSDs) for several standard and composite ab initio procedures for the five most stable guanine tautomers relative to W1-F12 reference values. We note that as the four low-lying tautomers are separated by energy differences as small as 0.3 kJ mol−1, it is desirable to identify computationally economical methods with RMSDs below this threshold.
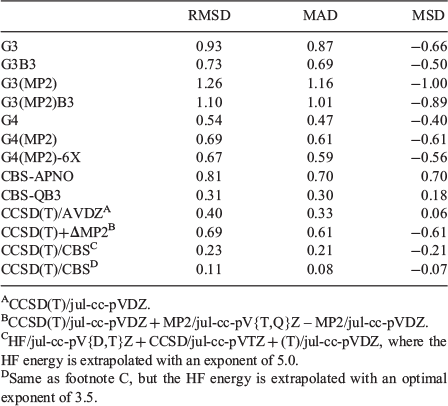
|
G3 theory, in which the geometries and ZPVEs are obtained at the MP2 and HF levels respectively, results in a large RMSD of 0.93 kJ mol−1. Using G3B3, in which the geometries and ZPVEs are obtained with B3LYP, results in a slightly lower RMSD of 0.73 kJ mol−1. In contrast, the more recent G4 theory results in better performance at a similar computational cost, with an RMSD of 0.54 kJ mol−1. Both G3(MP2) and G3(MP2)B3 result in relatively poor performance with RMSDs >1 kJ mol−1, whereas G4(MP2) and G4(MP2)-6X give essentially the same performance, with an RMSD of 0.7 kJ mol−1. We find that all the considered Gn procedures predict that the enol tautomer (3) is energetically more stable than the keto tautomer (2) by amounts ranging from 0.36 (G4) to 1.28 (G3(MP2)) kJ mol−1 (see Table S1 in the Supplementary Material for the tautomerization energies of the Gn-type methods).
Let us move to the CBS-type composite methods. CBS-QB3 results in excellent performance with an RMSD of 0.31 kJ mol−1. However, the older CBS-APNO method results in a significant deterioration of performance (RMSD = 0.81 kJ mol−1). Both CBS-QB3 and CBS-APNO predict the correct energy order of the low-lying tautomers.
A cost-effective approach for approximating the CCSD(T)/CBS energy is using an additivity-based scheme in which this energy is estimated from the CCSD(T)/jul-cc-pVDZ energy and an MP2-based basis-set correction (ΔMP2 = MP2/jul-cc-pV{T,Q}Z – MP2/jul-cc-pVDZ, where MP2/jul-cc-pV{T,Q}Z energy is extrapolated to the basis-set limit with an extrapolation exponent of 3).[86] This additivity scheme has been found to be an efficient way for approximating non-covalent interactions (e.g. hydrogen-bonding and dispersion interactions),[87–93] as well as reaction energies[45,94,95] at the CCSD(T)/CBS level. Nevertheless, this simple additivity scheme does not perform particularly well for the guanine tautomers, with an overall RMSD of 0.69 kJ mol−1. Furthermore, it should be noted that the CCSD(T)/jul-cc-pVDZ level of theory alone results in much better performance, with an RMSD of 0.40 kJ mol−1.
The results presented in the previous section indicate that a cost-effective approach to improve on the CCSD(T)/jul-cc-pVDZ result is to extrapolate the SCF energy from the jul-cc-pV{D,T}Z basis set pair and calculate the CCSD and (T) correlation energies with the jul-cc-pVTZ and jul-cc-pVDZ basis sets respectively. Using an extrapolation exponent of 5.0 in the SCF extrapolation results in an RMSD of 0.23 kJ mol−1. Thus, this approach outperforms all the composite and standard methods considered so far, including the CBS-QB3 method (Table 3). We note that using an optimal extrapolation exponent of α = 3.5 in the SCF extrapolation cuts this RMSD by ~50 % and gives an RMSD of 0.11 kJ mol−1. In the next section, we use this method to obtain reference values for evaluating the performance of approximated theoretical procedures for all the 14 guanine tautomers considered in this work (these reference values are given in Fig. 1).
Evaluation of the Performance of Standard and Composite Ab Initio Procedures for All Guanine Tautomers Relative to Approximated CCSD(T)/CBS Values
Table 4 gives the error statistics for several standard and composite ab initio procedures for the 14 guanine tautomers relative to approximated CCSD(T)/CBS reference values. The reference HF/jul-cc-pV{D,T}Z + CCSD/jul-cc-pVTZ + (T)/jul-cc-pVDZ values are given in Fig. 1 and the tautomerization energies for all methods are given in Table S1 (Supplementary Material). Before proceeding to a detailed discussion of the performance of the various methods, we note that with the composite methods that do not use B3LYP geometries, i.e. G3, G3(MP2), and CBS-APNO, we were unable to optimize the geometry of the highly energetic tautomer 8 (Fig. 1). Thus, in these cases, this tautomer is not included in the error statistics. Having said that, exclusion of one tautomer is not expected to drastically affect the overall error statistics in these cases.
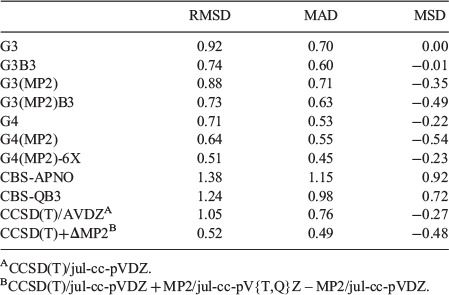
|
Inspection of the RMSDs obtained for the 14 guanine tautomers (Table 4) reveals that they are fairly similar to those obtained for the five most stable tautomers (Table 3). In particular, the RMSDs for G3, G3B3, and G4(MP2) remain practically unchanged, and the RMSDs for G4, G4(MP2)-6X, and CCSD(T)+ΔMP2 differ by less than 0.2 kJ mol−1 from each other. The largest changes between the two sets of RMSDs are observed for the CCSD(T)/jul-cc-pVDZ and CBS-QB3 methods, where the performance for the larger set deteriorates by 0.65 and 0.93 kJ mol−1, respectively. The methods that emerge as best performers for the entire set of tautomers are G4(MP2)-6X and CCSD(T)+ΔMP2 with nearly identical RMSDs of 0.51 and 0.52 kJ mol−1, respectively. Nevertheless, we note that the poorest performers (CCSD(T)/jul-cc-pVDZ, CBS-QB3, and CBS-APNO) still attain RMSDs of 1.05–1.38 kJ mol−1.
Conclusions
We obtained the gas-phase tautomerization energies at the W1-F12 level of theory for the five most stable guanine tautomers. We find that as many as four tautomers populate a small energetic window of less than 1.0 kcal mol−1. The W1-F12 relative enthalpies at 298 K for the five lowest-lying guanine tautomers are: 0.00 (1), 2.37 (2), 2.63 (3), 4.03 (3′), and 14.31 (4) kJ mol−1. We use these highly accurate W1-F12 tautomerization energies to benchmark the performance of a wide range of lower-level standard and composite ab initio procedures. The best performing procedures with RMSDs ≤0.5 kJ mol−1 are: 0.54 (G4), 0.40 (CCSD(T)/jul-cc-pVDZ), 0.31 (CBS-QB3), and 0.23 (approximately CCSD(T)/CBS) kJ mol−1. Here, approximated CCSD(T)/CBS is calculated via the additive formula HF/jul-cc-pV{D,T}Z + CCSD/jul-cc-pVTZ + (T)/jul-cc-pVDZ, where the HF energy is extrapolated with an exponent of 5.0. Using instead an effective extrapolation exponent of α = 3.5 in the SCF extrapolation results in an RMSD of merely 0.11 kJ mol−1. We use this approximate CCSD(T)/CBS method for calculating the tautomerization energies for all 14 tautomers. The resulting tautomerization energies are: 0.00 (1), 2.20 (2), 2.51 (3), 4.06 (3′), 14.30 (4), 25.65 (5), 43.78 (4′), 53.50 (6′), 61.58 (6), 77.37 (7), 82.52 (8′), 86.02 (9), 100.70 (10), and 121.01 (8, Fig. 1) kJ mol−1. Finally, we evaluate the performance of the standard and composite methods relative to these reference values. For the entire set of tautomers, the best performing procedures emerge as (RMSDs are given in parenthesis): G4(MP2)-6X (0.51), CCSD(T)+ΔMP2/CBS (0.52), and G4(MP2) (0.64 kJ mol−1).
Supplementary Material
Tautomerization energies for the 14 guanine tautomers calculated with the standard and composite CCSD(T) methods considered in this work (Table S1) and B3LYP/jul-cc-pVTZ optimized geometries for all guanine tautomers (Table S2) are available on the Journal’s website.
Conflicts of Interest
The author declares no conflicts of interest.
Acknowledgements
This research was undertaken with the assistance of resources from the National Computational Infrastructure (NCI), which is supported by the Australian Government. AK gratefully acknowledges the Royal Australian Chemical Institute (RACI) 2019 Physical Chemistry Division Lectureship and an Australian Research Council (ARC) Future Fellowship (Project no. FT170100373).
References
[1] E. Nir, C. Janzen, P. Imhof, K. Kleinermanns, M. S. de Vries, J. Chem. Phys. 2001, 115, 4604.| Crossref | GoogleScholarGoogle Scholar |
[2] F. Piuzzi, M. Mons, I. Dimicoli, B. Tardivel, Q. Zhao, Chem. Phys. 2001, 270, 205.
| Crossref | GoogleScholarGoogle Scholar |
[3] B. Mennucci, A. Toniolo, J. Tomasi, J. Phys. Chem. A 2001, 105, 7126.
| Crossref | GoogleScholarGoogle Scholar |
[4] M. Mons, I. Dimicoli, F. Piuzzi, B. Tardivel, M. Elhamine, J. Phys. Chem. A 2002, 106, 5088.
| Crossref | GoogleScholarGoogle Scholar |
[5] M. Hanus, F. Ryjacek, M. Kabelac, T. Kubar, T. V. Bogdan, S. A. Trygubenko, P. Hobza, J. Am. Chem. Soc. 2003, 125, 7678.
| Crossref | GoogleScholarGoogle Scholar | 12812509PubMed |
[6] M. Piacenza, S. Grimme, J. Comput. Chem. 2004, 25, 83.
| Crossref | GoogleScholarGoogle Scholar | 14634996PubMed |
[7] X. Yang, X. B. Wang, E. R. Vorpagel, L. S. Wang, Proc. Natl. Acad. Sci. USA 2004, 101, 17588.
| Crossref | GoogleScholarGoogle Scholar | 15591345PubMed |
[8] M. Haranczyk, M. Gutowski, J. Am. Chem. Soc. 2005, 127, 699.
| Crossref | GoogleScholarGoogle Scholar | 15643895PubMed |
[9] L. Gorb, A. Kaczmarek, A. Gorb, A. J. Sadlej, J. Leszczynski, J. Phys. Chem. B 2005, 109, 13770.
| Crossref | GoogleScholarGoogle Scholar | 16852725PubMed |
[10] M. K. Shukla, J. Leszczynski, J. Phys. Chem. A 2005, 109, 7775.
| Crossref | GoogleScholarGoogle Scholar | 16834154PubMed |
[11] G. K. Forde, A. E. Forde, G. Hill, A. Ford, A. Nazario, J. Leszczynski, J. Phys. Chem. B 2006, 110, 15564.
| Crossref | GoogleScholarGoogle Scholar | 16884280PubMed |
[12] M. K. Shukla, J. Leszczynski, Chem. Phys. Lett. 2006, 429, 261.
| Crossref | GoogleScholarGoogle Scholar |
[13] W. Liang, H. Li, X. Hu, S. Han, Chem. Phys. 2006, 328, 93.
| Crossref | GoogleScholarGoogle Scholar |
[14] D. B. Jones, F. Wang, D. A. Winkler, M. J. Brunger, Biophys. Chem. 2006, 121, 105.
| Crossref | GoogleScholarGoogle Scholar | 16464529PubMed |
[15] M. Y. Choi, R. E. Miller, J. Am. Chem. Soc. 2006, 128, 7320.
| Crossref | GoogleScholarGoogle Scholar | 16734487PubMed |
[16] K. Seefeld, R. Brause, T. Häber, K. Kleinermanns, J. Phys. Chem. A 2007, 111, 6217.
| Crossref | GoogleScholarGoogle Scholar | 17585845PubMed |
[17] O. Plekan, V. Feyer, R. Richter, M. Coreno, G. Vall-llosera, K. C. Prince, A. B. Trofimov, I. L. Zaytseva, T. E. Moskovskaya, E. V. Gromov, J. Schirmer, J. Phys. Chem. A 2009, 113, 9376.
| Crossref | GoogleScholarGoogle Scholar | 19634878PubMed |
[18] K. B. Bravaya, O. Kostko, S. Dolgikh, A. Landau, M. Ahmed, A. I. Krylov, J. Phys. Chem. A 2010, 114, 12305.
| Crossref | GoogleScholarGoogle Scholar | 21038927PubMed |
[19] Z. Yang, P. Duffy, Q. Zhu, M. Takahashi, F. Wang, J. Phys. At. Mol. Opt. Phys. 2015, 48, 205101.
| Crossref | GoogleScholarGoogle Scholar |
[20] W. Lu, J. Liu, Phys. Chem. Chem. Phys. 2016, 18, 32222.
| Crossref | GoogleScholarGoogle Scholar | 27849082PubMed |
[21] Y. Sun, W. Zhou, M. M. Moe, J. Liu, Phys. Chem. Chem. Phys. 2018, 20, 27510.
| Crossref | GoogleScholarGoogle Scholar | 30362479PubMed |
[22] A. Dang, Y. Liu, F. Turecek, J. Phys. Chem. A 2019, 123, 3272.
| Crossref | GoogleScholarGoogle Scholar | 30912657PubMed |
[23] A. A. Kroeger, A. Karton, J. Comput. Chem. 2019, 40, 630.
| Crossref | GoogleScholarGoogle Scholar | 30368841PubMed |
[24] A. Karton, J. M. L. Martin, J. Chem. Phys. 2012, 136, 124114.
| Crossref | GoogleScholarGoogle Scholar | 22612114PubMed |
[25] A. Karton, L.-J. Yu, M. K. Kesharwani, J. M. L. Martin, Theor. Chem. Acc. 2014, 133, 1483.
| Crossref | GoogleScholarGoogle Scholar |
[26] A. Karton, P. R. Schreiner, J. M. L. Martin, J. Comput. Chem. 2016, 37, 49.
| Crossref | GoogleScholarGoogle Scholar | 26096132PubMed |
[27] A. Karton, Wiley Interdiscip. Rev. Comput. Mol. Sci. 2016, 6, 292.
| Crossref | GoogleScholarGoogle Scholar |
[28] N. Sylvetsky, K. A. Peterson, A. Karton, J. M. L. Martin, J. Chem. Phys. 2016, 144, 214101.
| Crossref | GoogleScholarGoogle Scholar | 27276939PubMed |
[29] A. Karton, N. Sylvetsky, J. M. L. Martin, J. Comput. Chem. 2017, 38, 2063.
| Crossref | GoogleScholarGoogle Scholar | 28675494PubMed |
[30] E. I. Izgorodina, M. L. Coote, L. Radom, J. Phys. Chem. A 2005, 109, 7558.
| Crossref | GoogleScholarGoogle Scholar | 16834125PubMed |
[31] S. Grimme, Angew. Chem. Int. Ed. 2006, 45, 4460.
| Crossref | GoogleScholarGoogle Scholar |
[32] M. D. Wodrich, C. Corminboeuf, P. R. Schleyer, Org. Lett. 2006, 8, 3631.
| Crossref | GoogleScholarGoogle Scholar | 16898778PubMed |
[33] M. D. Wodrich, C. Corminboeuf, P. R. Schreiner, A. A. Fokin, P. R. Schleyer, Org. Lett. 2007, 9, 1851.
| Crossref | GoogleScholarGoogle Scholar | 17417862PubMed |
[34] P. R. Schreiner, Angew. Chem. Int. Ed. 2007, 46, 4217.
| Crossref | GoogleScholarGoogle Scholar |
[35] S. Grimme, M. Steinmetz, M. Korth, J. Org. Chem. 2007, 72, 2118.
| Crossref | GoogleScholarGoogle Scholar | 17286442PubMed |
[36] S. E. Wheeler, K. N. Houk, P. V. R. Schleyer, W. D. Allen, J. Am. Chem. Soc. 2009, 131, 2547.
| Crossref | GoogleScholarGoogle Scholar | 19182999PubMed |
[37] A. Karton, D. Gruzman, J. M. L. Martin, J. Phys. Chem. A 2009, 113, 8434.
| Crossref | GoogleScholarGoogle Scholar | 19569667PubMed |
[38] S. Grimme, Org. Lett. 2010, 12, 4670.
| Crossref | GoogleScholarGoogle Scholar | 20863101PubMed |
[39] R. O. Ramabhadran, K. Raghavachari, J. Chem. Theory Comput. 2011, 7, 2094.
| Crossref | GoogleScholarGoogle Scholar | 26606481PubMed |
[40] R. O. Ramabhadran, K. Raghavachari, J. Phys. Chem. A 2012, 116, 7531.
| Crossref | GoogleScholarGoogle Scholar | 22571375PubMed |
[41] R. J. O’Reilly, A. Karton, L. Radom, Int. J. Quantum Chem. 2012, 112, 1862.
| Crossref | GoogleScholarGoogle Scholar |
[42] A. Karton, J. M. L. Martin, Mol. Phys. 2012, 110, 2477.
| Crossref | GoogleScholarGoogle Scholar |
[43] M. D. Wodrich, C. Corminboeuf, S. E. Wheeler, J. Phys. Chem. A 2012, 116, 3436.
| Crossref | GoogleScholarGoogle Scholar | 22385306PubMed |
[44] S. E. Wheeler, Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 204.
| Crossref | GoogleScholarGoogle Scholar |
[45] L. J. Yu, A. Karton, Chem. Phys. 2014, 441, 166.
| Crossref | GoogleScholarGoogle Scholar |
[46] A. Karton, B. Chan, K. Raghavachari, L. Radom, J. Phys. Chem. A 2013, 117, 1834.
| Crossref | GoogleScholarGoogle Scholar | 23343032PubMed |
[47] A. Karton, J. Comput. Chem. 2017, 38, 370.
| Crossref | GoogleScholarGoogle Scholar | 27859494PubMed |
[48] C. Hättig, W. Klopper, A. Köhn, D. P. Tew, Chem. Rev. 2012, 112, 4.
| Crossref | GoogleScholarGoogle Scholar | 22206503PubMed |
[49] K. A. Peterson, T. B. Adler, H.-J. Werner, J. Chem. Phys. 2008, 128, 084102.
| Crossref | GoogleScholarGoogle Scholar | 18513018PubMed |
[50] J. Noga, S. Kedžuch, J. Šimunek, J. Chem. Phys. 2007, 127, 034106.
| Crossref | GoogleScholarGoogle Scholar | 17655430PubMed |
[51] G. Knizia, H.-J. Werner, J. Chem. Phys. 2008, 128, 154103.
| Crossref | GoogleScholarGoogle Scholar | 18433186PubMed |
[52] T. B. Adler, G. Knizia, H.-J. Werner, J. Chem. Phys. 2007, 127, 221106.
| Crossref | GoogleScholarGoogle Scholar | 18081383PubMed |
[53] J. M. L. Martin, G. Oliveira, J. Chem. Phys. 1999, 111, 1843.
| Crossref | GoogleScholarGoogle Scholar |
[54] T. H. Dunning, J. Chem. Phys. 1989, 90, 1007.
| Crossref | GoogleScholarGoogle Scholar |
[55] R. A. Kendall, T. H. Dunning, R. J. Harrison, J. Chem. Phys. 1992, 96, 6796.
| Crossref | GoogleScholarGoogle Scholar |
[56] E. Papajak, D. G. Truhlar, J. Chem. Theory Comput. 2011, 7, 10.
| Crossref | GoogleScholarGoogle Scholar | 26606214PubMed |
[57] S. Ten-no, J. Noga, Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 114.
| Crossref | GoogleScholarGoogle Scholar |
[58] S. Ten-no, Chem. Phys. Lett. 2004, 398, 56.
| Crossref | GoogleScholarGoogle Scholar |
[59] H.-J. Werner, T. B. Adler, F. R. Manby, J. Chem. Phys. 2007, 126, 164102.
| Crossref | GoogleScholarGoogle Scholar | 17552756PubMed |
[60] G. Knizia, T. B. Adler, H.-J. Werner, J. Chem. Phys. 2009, 130, 054104.
| Crossref | GoogleScholarGoogle Scholar | 19206956PubMed |
[61] K. A. Peterson, T. H. Dunning, J. Chem. Phys. 2002, 117, 10548.
| Crossref | GoogleScholarGoogle Scholar |
[62] M. Douglas, N. M. Kroll, Ann. Phys. 1974, 82, 89.
| Crossref | GoogleScholarGoogle Scholar |
[63] B. A. Hess, Phys. Rev. A 1986, 33, 3742.
| Crossref | GoogleScholarGoogle Scholar |
[64] W. A. de Jong, R. J. Harrison, D. A. Dixon, J. Chem. Phys. 2001, 114, 48.
| Crossref | GoogleScholarGoogle Scholar |
[65] J. F. Stanton, J. Gauss, M. E. Harding, P. G. Szalay, with contributions from A. A. Auer, R. J. Bartlett, U. Benedikt, C. Berger, D. E. Bernholdt, Y. J. Bomble, O. Christiansen, F. Engel, R. Faber, M. Heckert, O. Heun, M. Hilgenberg, C. Huber, T.-C. Jagau, D. Jonsson, J. Jusélius, T. Kirsch, K. Klein, W. J. Lauderdale, F. Lipparini, T. Metzroth, L. A. Mück, D. P. O’Neill, D. R. Price, E. Prochnow, C. Puzzarini, K. Ruud, F. Schiffmann, W. Schwalbach, C. Simmons, S. Stopkowicz, A. Tajti, J. Vázquez, F. Wang, J. D. Watts, CFOUR 2015. Available at: http://www.cfour.de
[66] H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, S. J. Bennie, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, S. J. R. Lee, Y. Liu, A. W. Lloyd, Q. Ma, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, T. F. Miller III, M. E. Mura, A. Nicklaß, D. P. O’Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, M. Wang, M. Welborn, MOLPRO 2016. Available at http://www.molpro.net
[67] H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schutz, Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 242.
| Crossref | GoogleScholarGoogle Scholar |
[68] C. Lee, W. Yang, R. G. Parr, Phys. Rev. B Condens. Matter 1988, 37, 785.
| Crossref | GoogleScholarGoogle Scholar | 9944570PubMed |
[69] A. D. Becke, J. Chem. Phys. 1993, 98, 5648.
| Crossref | GoogleScholarGoogle Scholar |
[70] P. J. Stephens, F. J. Devlin, C. F. Chabalowski, M. J. Frisch, J. Phys. Chem. 1994, 98, 11623.
| Crossref | GoogleScholarGoogle Scholar |
[71] M. K. Kesharwani, B. Brauer, J. M. L. Martin, J. Phys. Chem. A 2015, 119, 1701.
| Crossref | GoogleScholarGoogle Scholar | 25296165PubMed |
[72] L. A. Curtiss, P. C. Redfern, K. Raghavachari, Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 810.
| Crossref | GoogleScholarGoogle Scholar |
[73] J. A. Montgomery, M. J. Frisch, J. W. Ochterski, G. A. Petersson, J. Chem. Phys. 2000, 112, 6532.
| Crossref | GoogleScholarGoogle Scholar |
[74] K. A. Peterson, D. Feller, D. A. Dixon, Theor. Chem. Acc. 2012, 131, 1079.
| Crossref | GoogleScholarGoogle Scholar |
[75] T. Helgaker, W. Klopper, D. P. Tew, Mol. Phys. 2008, 106, 2107.
| Crossref | GoogleScholarGoogle Scholar |
[76] L. A. Curtiss, P. C. Redfern, K. Raghavachari, J. Chem. Phys. 2007, 126, 084108.
| Crossref | GoogleScholarGoogle Scholar | 17343441PubMed |
[77] L. A. Curtiss, P. C. Redfern, K. Raghavachari, J. Chem. Phys. 2007, 127, 124105.
| Crossref | GoogleScholarGoogle Scholar | 17902891PubMed |
[78] B. Chan, J. Deng, L. Radom, J. Chem. Theory Comput. 2011, 7, 112.
| Crossref | GoogleScholarGoogle Scholar | 26606224PubMed |
[79] L. A. Curtiss, K. Raghavachari, P. C. Redfern, V. Rassolov, J. A. Pople, J. Chem. Phys. 1998, 109, 7764.
| Crossref | GoogleScholarGoogle Scholar |
[80] L. A. Curtiss, P. C. Redfern, K. Raghavachari, V. Rassolov, J. A. Pople, J. Chem. Phys. 1999, 110, 4703.
| Crossref | GoogleScholarGoogle Scholar |
[81] A. G. Baboul, L. A. Curtiss, P. C. Redfern, K. Raghavachari, J. Chem. Phys. 1999, 110, 7650.
| Crossref | GoogleScholarGoogle Scholar |
[82] J. A. Montgomery, M. J. Frisch, J. W. Ochterski, G. A. Petersson, J. Chem. Phys. 1999, 110, 2822.
| Crossref | GoogleScholarGoogle Scholar |
[83] J. W. Ochterski, G. A. Petersson, J. A. Montgomery, J. Chem. Phys. 1996, 104, 2598.
| Crossref | GoogleScholarGoogle Scholar |
[84] M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, D. J. Fox, Gaussian 16, Revision A.01 2009 (Gaussian, Inc.: Wallingford, CT).
[85] B. Chan, L. Radom, J. Chem. Theory Comput. 2016, 12, 3774.
| Crossref | GoogleScholarGoogle Scholar | 27471908PubMed |
[86] A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper, H. Koch, J. Olsen, A. K. Wilson, Chem. Phys. Lett. 1998, 286, 243.
| Crossref | GoogleScholarGoogle Scholar |
[87] D. Manna, M. K. Kesharwani, N. Sylvetsky, J. M. L. Martin, J. Chem. Theory Comput. 2017, 13, 3136.
| Crossref | GoogleScholarGoogle Scholar | 28530805PubMed |
[88] B. Brauer, M. K. Kesharwani, S. Kozuch, J. M. L. Martin, Phys. Chem. Chem. Phys. 2016, 18, 20905.
| Crossref | GoogleScholarGoogle Scholar | 26950084PubMed |
[89] M. K. Kesharwani, A. Karton, J. M. L. Martin, J. Chem. Theory Comput. 2016, 12, 444.
| Crossref | GoogleScholarGoogle Scholar | 26653705PubMed |
[90] L. Goerigk, A. Karton, J. M. L. Martin, L. Radom, Phys. Chem. Chem. Phys. 2013, 15, 7028.
| Crossref | GoogleScholarGoogle Scholar | 23403537PubMed |
[91] D. G. Liakos, F. Neese, J. Phys. Chem. A 2012, 116, 4801.
| Crossref | GoogleScholarGoogle Scholar | 22489633PubMed |
[92] P. Jurečka, P. Hobza, Chem. Phys. Lett. 2002, 365, 89.
| Crossref | GoogleScholarGoogle Scholar |
[93] W. Klopper, H. P. Luthi, Mol. Phys. 1999, 96, 559.
| Crossref | GoogleScholarGoogle Scholar |
[94] J. Friedrich, J. Chem. Theory Comput. 2015, 11, 3596.
| Crossref | GoogleScholarGoogle Scholar | 26574443PubMed |
[95] L.-J. Yu, W. Wan, A. Karton, Chem. Phys. 2016, 480, 23.
| Crossref | GoogleScholarGoogle Scholar |
* Amir Karton is the recipient of the 2019 RACI Physical Chemistry Division Lectureship.



