Functional evaluation of height–diameter relationships and tree development in an Australian subtropical rainforest
Steven R. Howell A B , Guo-Zhang Michael Song A C , Kuo-Jung Chao D and David Doley
D and David Doley  A E *
A E *
A Department of Botany, The University of Queensland, Brisbane, Qld 4072, Australia.
B Present address: School of Earth and Environmental Sciences, The University of Queensland, Brisbane, Qld 4072, Australia.
C Present address: Department of Soil and Water Conservation, National Chung Hsing University, 145 Xingda Road, South District, Taichung City 402, Taiwan.
D International Master Program of Agriculture, National Chung Hsing University, 145 Xingda Road, South District, Taichung City 402, Taiwan.
E Present address: Centre for Mined Land Rehabilitation, Sustainable Minerals Institute, The University of Queensland, Brisbane, Qld 4072, Australia.
Australian Journal of Botany 70(2) 158-173 https://doi.org/10.1071/BT21049
Submitted: 17 April 2021 Accepted: 8 February 2022 Published: 5 March 2022
© 2022 The Author(s) (or their employer(s)). Published by CSIRO Publishing. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)
Abstract
Context: Allometric equations describing the relationships between tree height (H) and breast height diameter (D) should be both statistically efficient and biologically relevant.
Aims: To determine whether selected allometric equations can meet established criteria for both efficiency and relevance.
Methods: Nine equations were compared to define the H–D relationships of 1122 individuals and 18 species from an Australian subtropical rainforest.
Key results: Three-parameter asymptotic equations described initial slope (a), curvature (b), and asymptotic height (Ha). Each equation was evaluated for precision (root mean square error, RMSE) and bias in H estimates, and ease of interpretation of function parameters. For both individual species and all stems, a non-rectangular hyperbola (NRH) provided almost equally high precision and low bias as did the statistically most parsimonious generalised Michaelis–Menten function, plus linear parameter values easily relatable to tree structural and functional attributes. The value of NRH a increased linearly with wood density for canopy species, but not for understorey and subdominant species, whereas the value of NRH b decreased as Ha increased from understorey to canopy species.
Conclusions: Species within understorey, subdominant, and canopy structural groups shared similar ranges of parameter values within groups that reflect both intrinsic architectural and developmental patterns, and environmental limitations to Ha.
Implications: The NRH can be used to visualise both early and later tree development stages and differences among the growth patterns of species occupying different positions within a forest.
Keywords: allometric relationships, asymptotic tree height, canopy layers, convexity factor, non-rectangular hyperbola, proportionality factor, saplings, stem taper, understorey, tree architecture.
Introduction
Allometric relationships between total tree height (H) and stem diameter at breast height (1.3 m; D) have been applied to intersecting and potentially conflicting practical and explanatory objectives. First, the more accurate prediction of forest biomass (B) from inventories of D (Chave et al. 2005; Cook et al. 2005) has been sought by the incorporation of H (Williams et al. 2005; Feldpausch et al. 2012; Chave et al. 2014; Ledo et al. 2016; Martínez Cano et al. 2019b). Second, greater understanding has been sought of fundamental biological attributes of tree species that influence their ecological and evolutionary outcomes, particularly in structurally and floristically diverse rainforests (Kohyama et al. 2003; Banin et al. 2012; Forrester et al. 2017; Falster et al. 2018).
An effective allometric relationship should provide logical, biologically realistic, accurate, precise, parsimonious, and unbiased descriptions of the processes underlying tree and forest growth in different environments (Vanclay and Skovsgaard 1997; Cifuentes Jara et al. 2015). Model selection has been resolved most often in favour of statistical efficiency (Burnham and Anderson 2004; Ledo et al. 2016; Loubota Panzou et al. 2021b) over mechanistic interpretations of biological relevance (Hunt 1979).
Advanced statistical techniques (Aertsen et al. 2010; Cysneiros et al. 2021; Loubota Panzou et al. 2021a; Lu et al. 2021) have been used, especially on large, aggregated datasets, to describe multiple functional relationships across different environments and their effects on structure and growth of trees (Falster et al. 2018; Martínez Cano et al. 2019a). Following Hunt (1979), the present study seeks to complement this computational sophistication with an analysis of biological bases and ease of interpretation of allometric relationships that underpin tree growth models applied to different species in a single environment.
Categories of height–diameter relationships
Other than empirical solutions (Zeide 1993), three categories of biologically realistic allometric relationship have been applied to trees, including unbounded functions based on biophysical principles, and asymptotic functions based on growth rate and on process rate functions. Representative basic equations from each category are presented in Table 1.

|
Biophysical equations assume unrestricted proportionality in organ or organism construction, which can be related to the distribution of resources (Huxley 1924; Higham et al. 2021) and in trees to mechanical properties such as bending, shear and rupture strengths of wood (McMahon and Kronauer 1976; Niklas 2007). These proportions arise because wood strength is closely related to wood density (Kollmann 1968; Walton and Armstrong 1986; van Gelder et al. 2006), so trees with high wood strength have characteristically slender stem taper.
The most widely applied biophysical allometric relationship is the power equation, commonly expressed as a log–log relationship (Huxley 1924; Niklas 1995; Kooyman and Westoby 2009; Loubota Panzou et al. 2021a). The structural characteristics of tree saplings are reflected in the initial value of the allometric proportionality factor, a, which varies among species in a particular environment with wood density (van Gelder et al. 2006; Kooyman and Westoby 2009; Fournier et al. 2013; Francis et al. 2017), and among environments with different tree spacing (Hummel 2000; Vanclay 2009; del Río et al. 2019) or site resource availability (Vanclay and Henry 1988; Lines et al. 2012; Cysneiros et al. 2021), and by external stresses such as wind (Jacobs 1954; King 1986; Thomas et al. 2015). Changes in the H–D relationship with increasing organism size are described by the convexity factor, b, which appears as an exponent (Table 1, Eqn 2) and is related to species maximum dimensions, especially with the transition from early stage to late-stage successional species (Kohyama et al. 2003; Poorter et al. 2006; Martínez Cano et al. 2019a). Although it may describe accurately the early H–D relationships of tree stems (King 1990; Niklas 1995), the power equation does not incorporate the maximum or asymptotic height, Ha, and overestimates H at larger values of D (Ledo et al. 2016; Chenge 2021; Loubota Panzou et al. 2021b).
Growth rate functions are long-established and thoroughly reviewed (e.g. Evans 1972; Vrána et al. 2019). Most widely used equations (Table 1, Eqns 3–8) assume a sigmoidal pattern of plant growth (e.g. total height, H) as a negative exponential function of time, including a rate parameter, a, which describes the initial slope, an asymptote (e.g. maximum height, Ha) and usually a convexity factor, b, which describes the shape of the growth curve, both in its early acceleration and later deceleration as it approaches the asymptote (Tjørve and Tjørve 2010). These exponential parameters are not easy to interpret visually. For application to H–D allometry, D replaces time as the independent variable.
Process rate functions describe the rate of a reaction or process in relation to the availability of a resource, typically a substrate, that initially is entirely limiting but eventually becomes non-limiting, as described by the Michaelis–Menten equation (Table 1, Eqn 9). For application of this function to H–D allometry, D replaces resource availability as the independent variable, and Ha replaces maximum reaction rate; the proportionality factor is represented by k, the value of D at half-Ha (Canham et al. 1994). The convexity factor, b, introduced by Martínez Cano et al.(2019b) as an exponent of D, has the same meaning as for biophysical functions. This expression has been recognised as the generalised Michaelis–Menten (GMM) equation (Ledo et al. 2016; Martínez Cano et al. 2019a, 2019b; Loubota Panzou et al. 2021b).
The reaction kinetics of photosynthesis were described by Johnson and Thornley (1984) as a non-rectangular hyperbola (Table 1, Eqn 10), comprising the initial change in reaction rate with respect to light availability, a, the maximum reaction rate, and the convexity of the reaction rate curve, b, which varies from 0 to 1 as the maximum rate is approached and is interpreted as reflecting the transition from progressive to abrupt imposition of limiting conditions on the process (Prioul and Chartier 1977; Johnson and Thornley 1984; Thomas and Bazzaz 1999). This equation can also be applied to H–D allometry, adopting the terminology described above.
In principle, the initial course of H–D change in a tree may be assumed to be determined by resource distribution (Huxley 1924; Niklas 1995, 2007) and the mainstem, branching and foliation characteristics widely recognised as tree architecture (Hallé et al. 1978; Sterck et al. 2001; Poorter et al. 2006; Osunkoya et al. 2007; Iida et al. 2011; Loubota Panzou et al. 2018). This phase of tree development should be described accurately by all biophysical or process rate functions but not by growth rate functions that incorporate increasing stem slenderness in seedling and sapling tree growth stages (Tjørve and Tjørve 2010). Later changes in tree H–D relationships result in the attainment of a maximal H and D, characteristic for a species and its environment (Francis 1970; Thomas 1996; Floyd 2008) and should be described realistically and accurately by growth rate or process rate functions.
Most allometric equations in wide use, judged on their statistical attributes, have been based on biophysical or growth rate functions, although some recent analyses have favoured the GMM process rate function (Ledo et al. 2016; Martínez Cano et al. 2019b). Hunt (1979) argued that, when the objective is to understand patterns of plant growth, selective weight should also be given to biological relevance when it provides a clearer depiction of the factors influencing each allometric parameter, even if one or more statistical test is denied pre-eminence in model selection.
The following work explores the extent to which different categories of allometric equation satisfy the stated criteria for selection, taking account of both modelling objectives and the desire to incorporate relevant biological characteristics, such as stem strength and the elements of tree architecture. It also examines whether the non-rectangular hyperbola (NRH) might be applicable to the H–D allometry of species occupying different strata of an Australian subtropical rainforest.
Materials and methods
Study site
The study site was in the Main Range National Park, Queensland, Australia (28.23S, 152.42E, 1120 m asl), within the Gondwana Rainforests remnant basalt volcanic landscape of eastern Australia, covered by ferrosols up to 2 m deep (Debski et al. 2000). The average annual rainfall in the vicinity is approximately 1125 mm and cloud interception may contribute an additional 40% rainfall equivalent (Hutley et al. 1997). Mean annual temperature at the site is 14.5°C; summer daily mean maxima vary from 30°C to 35°C, and winter minima are close to 0°C within the forest (Hutley et al. 1997). The vegetation is designated as complex notophyll vine forest on Cainozoic igneous rocks, Regional Ecosystem 12.8.5 (Queensland Herbarium 2019).
Two plots, each 0.2075 ha, were established in 1962 in a portion of the then Gambubal State Forest. One plot, with an initial stand basal area of 67 m2 ha−1, was left unlogged, and one was subjected to typical Queensland Forestry Department timber harvesting practices that removed approximately 25 m2 ha−1 (Dale 1983). All trees with D greater than 10 cm were identified and D was measured periodically to monitor the regeneration of, first, commercial timber species, and later, all species (Dale 1983). Neither plot was subjected to any silvicultural treatment after 1962.
In 2003, each woody stem greater than 1.8 m tall was identified to species and its D was measured by callipers or girth tape, above buttresses if necessary. The accuracy of D measurement was established by checking current and recent values. Total height, to the uppermost location in the crown, was measured by height stick (up to 5 m) or by clinometer (over 5 m), verified through assessment of a sample of trees by two observers. Trees were excluded from analysis if the bole was broken, leaning by >10 degrees, or multi-stemmed.
The spacing and shading conditions for trees in the two plots were described respectively, by the number of stems surrounding and overtopping trees of a given size and indicated by frequency distributions for D and H in Supplementary Information and Supplementary Fig. S1. Because of the indistinguishable stand structures (Fig. S1) and H–D distributions for representative species (Fig. S2) at 40 years after disturbance, and their conformity to undisturbed forest structures (Coomes et al. 2003), the data for logged and unlogged plots were combined for further analysis.
Of the 1586 arborescent stems recorded, 401 were excluded because they belonged to understorey shrub species with a maximum height at the site (HmaxL) shorter than 10 m, and 57 because they were damaged or leaning. Six trees were excluded because their estimated heights appeared as extreme outliers (Zea-Camaño et al. 2020) from the H–D distributions for all tested equations. Analyses of the whole-sample data were based on 1122 tree stems.
Detailed species analyses were performed on 946 stems representing 18 species, with at least 18 stems being distributed among at least eight D classes (specified in Fig. S1) for each species, which was allocated to one of four published maximum height (HmaxP) classes (Supplementary Table S1). Of the stems included in the whole-sample estimates, 187 were excluded from species analyses, but were included in pooled data for HmaxP classes.
Evaluation of allometric relationships
The Microsoft Excel Solver (Excel) generalised reduced gradient (GRG) non-linear routine (Frontline Systems, Inc., Incline Village, Nevada, USA) was used to describe H–D relationships for the whole sample of 1122 tree stems, 18 selected species (Table S1) and all individuals in four height-class groups.
This routine maximised the regression coefficient of determination (R2) and minimised the root mean square error (RMSE) and mean bias by adjustment of the parameters a, b and Ha. Of the many allometric equations that have been developed, those listed in Table 1 were selected to provide the simplest basis for comparing categories of equations, using two or three fitted parameters, with no adjustments for local conditions. Linear and power regressions were applied to all trees <8 m tall as a basis for comparison with the initial proportionality parameter, a, in other equations. Three-parameter versions of the Weibull and generalised Michaelis–Menten (GMM) equations are presented as preliminary studies showed them to be more precise than are the two-parameter versions (cf. also Ledo et al. 2016). The GMM equation (Eqn 9) expresses the initial proportionality (slope) factor as a half-saturation constant, k. The reliability of these estimates was assessed by corresponding calculations on the whole sample conducted in R (R Core Team 2021), by using the modelr maximum-likelihood procedure (Wickham 2020) to optimise parameter values and their variance, and to minimise R2, RMSE, Akaike’s information criterion (AIC) and mean bias (Table S2).
Selected equations were applied to all trees ≥2 m tall from the whole sample, from all trees in four published species maximum height (HmaxP) classes (10–19 m, 20–29 m, 30–39 m, and 40+ m; Francis 1970; Floyd 2008), and from 18 selected species (Table S1). Data for six trees that were clearly outliers from sample distributions (Zea-Camaño et al. 2020) were excluded from analysis. Where a fitted relationship for an individual species (Ha-fitted) yielded unrealistic predictions of Ha, the mean H of the largest D class for the species at the site (HmaxL; Thomas 1996; Davies et al. 1998) was inserted as a fixed value (Ha-forced), and fitting was achieved by optimising a and b.
The explanatory value of a quantitative model is enhanced if it provides a reasonable depiction of responses of the system to changing conditions. For this purpose, attention is focused on the central statistics (chiefly parameter means) of an allometric relationship (Hunt 1979). The following three criteria from Vanclay and Skovsgaard (1997) are most applicable to single equations that describe H–D trajectories for both assemblages of trees within a single environment and for individual species with few measured individuals:
-
biological representation (adequate representation of the biological processes involved),
-
description of errors (attainment of specified accuracy requirements),
-
description of data (absence of bias in predictions throughout the likely range of application).
Quantitative values obtained in some tests could not be compared directly with qualitative assessments of utility in others. Biological representation was deemed to have been achieved if the parameters a, b and Ha could be described independently in a logical and easily interpreted way, if the assumptions underlying parameter determination were consistent with biophysical principles, and if predicted values (H, Ha) were consistently and reasonably close to observed data.
Results
Evaluation of allometric equations
Application of the Ha-fitted form of each allometric equation (Table 1) to the whole sample yielded estimates of parameters a, b, Ha, and the attributes R2, RMSE and mean bias (Table 2). Model precision was indicated by RMSE values, which for six of the equations were within 0.03 m of the lowest value (1.399 m for the GMM), including 1.409 m for the NRH (Table 2). The very close similarities between parameter and precision estimates using the R modelr package (Wickham 2020) and Excel procedures (Table S2) established the reliability of the latter for use in further analyses. Standard error estimates of parameter values determined by R (Table S2) were generally between 2% and 3% of respective means, but the differences were not consistent among equations. AIC values indicated that the GMM was clearly the most parsimonious model (Table S2).

|
Table 2 also shows the estimated maximum tree height, HmaxC (Ha + 1.3 m), and the estimated height (HD150) of the largest-diameter tree in the study (D = 149.6 cm, H = 36 m). Of the six best-fitting equations, the predicted HD150 from four functions (Mitscherlich, Pacala, Weibull and Richards) ranged between 33.2 and 34.0 m, being close to the HmaxC (Table 2). The Ha-fitted and Ha-forced versions of the GMM equation predicted HD150 of 35.2 and 35.4 m respectively, compared with 35.9 and 36.2 m for the equivalent NRH equations; predictions by these last two equations were close to the recorded tree height, but were 7–8 m less than respective HmaxC values.
The mean H–D trajectories for the whole sample, as described by nine allometric equations (Fig. 1a), indicated a close similarity among six equations for smaller trees, but divergence at values of D > 100 cm. The proximity of the GMM and NRH curves throughout their data ranges, their relatively low and similar RMSE values and their similar and limited biases throughout the data range (Fig. S3) suggested that either equation could provide an acceptably precise description of the whole-sample H–D relationship at the study site. Fig. 1b shows the distribution of data around the NRH mean H–D curve. Its accuracy and ease of application justified the use of the fitting routine, and the potential to visualise H–D trajectories for different species justified application of the NRH in the subsequent analyses of individual species and groups of species.
|
|
H–D relationships of individual species
Statistical analyses of selected Ha-fitted and, where applicable, Ha-forced versions of the nine non-linear H–D equations (cf. Table 1) for 18 species listed in Table S1 are presented in Table S3. The relative precision of Ha-fitted and Ha-forced solutions for the 18 species as determined by six equations was compared by differences between their RMSE values (Fig. S4a). For most species and most equations, Ha-forced equations were less precise than the Ha-fitted forms, but for GMM and NRH equations, the differences in RMSE were mostly less than 0.1 m.
There was considerable variation in the range of RMSE values determined by the nine Ha-forced equations for different species (Fig. S4b). No equation was consistently more precise than the others, although GMM and NRH were among the most precise for most species. Greater variation in RMSE values was associated with limited size ranges (Acronychia pubescens and Denhamia apetala) or, for Diploglottis australis, with RMSE values for both Ha-fitted and Ha-forced NRH that were much smaller than those for all other equations (Table S3).
The generally consistent RMSE values for each species suggest that valid interpretations may be made using either the Ha-fitted or Ha-forced forms of the selected equations. All subsequent analyses of the whole sample and the four height-class groups used Ha-fitted equations, but Ha-forced equations were adopted for individual species because they avoided many unrealistic estimates of Ha.
Initial H–D proportionality factor for species
The forms of most H–D regression equations involve exponential functions of the initial slope, a, (Table 1), so direct visual comparison of H–D slope values was restricted to the linear (<8 m tall), power, Pacala, GMM and NRH functions. Assuming that sapling stem allometry was determined by biophysical factors, the power equation applied to trees <8 m tall was used as the basis for comparison (Fig. 2). There was no correspondence between values of a (or for the GMM, k) determined by the power <8 m and other equations for trees with HmaxP of <30 m, and only weak associations in trees with HmaxP of 30+ m for all equations tested except the Ha-forced NRH (Fig. 2e). This suggests that comparisons of a among species at a given site, or within a species but among different conditions, may be attempted by using the NRH. The outlying species, Diploglottis australis (Fig. 2a, e), has a distinctive growth habit that was also expressed in other allometric parameters.
Variation in a was compared with a proxy for timber strength, namely published species wood density (Cause et al. 1989; Fig. 3). No equation indicated a close association for the two shorter HmaxP < 30 m classes. In contrast, linear relationships between a and wood density were found for the two taller HmaxP classes combined, positive for linear, power <8 m and NRH, and negative for GMM equations. Two outlying species in some analyses, Polyscias elegans and Diploglottis australis, with proportionally higher values of a (less rapid taper) than other species from their height-class groups, were also distinguished by their architectural characteristics.
|
|
Convexity factor and asymptotic height
For three-parameter growth-rate equations, b is an exponential value describing the abruptness of a sigmoid curve, which is difficult to interpret visually, but linear values are presented in the GMM and NRH equations. For understorey species (HmaxP 10–19 m), b estimated in Ha-forced regressions approached 2.0 in the GMM and 0.95 in the NRH (Fig. 4). The value of b decreased progressively and consistently in both the GMM and NRH for species in subdominant (HmaxP 20–29 m), co-dominant (HmaxP 30–39 m), and emergent (HmaxP 40+ m) classes (Fig. 4). These trends are taken to indicate that understorey trees mature in a uniform, low-stress environment, whereas canopy species experience progressive changes in their environment associated with light, spacing and wind. Two outlier species (Arytera divaricata and Cryptocarya obovata) lacked stems in the upper half of their published size ranges (Table S1).
One objective of fitting H–D regressions is to estimate Ha for local datasets. Two species for which most equations greatly overestimated Ha (Neolitsea australis and Orites excelsus) were notable for being the only ones for which a solution of the Ha-fitted NRH equation required a constraint of b > 0. Neither of these species showed evidence of having approached an asymptotic height. Realistic Ha-fitted estimates were not attained for Acronychia pubescens, and a solution of the Ha-fitted NRH equation required a constrain of b < 1 for four species (Arytera divaricata, Cryptocarya obovata, Daphnandra apetala and Zanthoxylum brachyacanthum), for which measured (DmaxL and HmaxL) values were much smaller than corresponding published (DmaxP and HmaxP) values (Table S1). Estimation of Ha for individual species clearly requires model-generating data from the full range of sizes, and larger samples than were available for some species in this study.
Aggregation into HmaxP classes
The H–D relationships described by Eqns 2–10 from Table 1 were applied to all individuals of all species belonging to four HmaxP classes (10–19 m, 20–29 m, 30–39 m, and 40+ m; extracted from Francis 1970; Boland et al. 2006; Floyd 2008), using the Ha-fitted form of each asymptotic equation (Table S4). The variation in accuracy, as assessed by its RMSE for each equation and each HmaxP class, is presented in Fig. S5.
The relative precision of allometric equations varied between HmaxP classes, but power, Gompertz and logistic equations resulted in consistently higher RMSEs than did the others. In contrast, RMSEs derived using the NRH differed by less than 3% from those obtained using the Mitscherlich, Pacala, Weibull, Richards or GMM equations for the three shorter HmaxP classes. This result was taken to indicate that the NRH could be used to describe H–D relationships of all HmaxP classes with acceptable precision.
Comparisons of NRH H–D trajectories for individual species and their HmaxP class means (Fig. 5) showed several features that assist in the interpretation of tree growth in these four structural classes (Table S4). For the understorey trees (HmaxP 10–19 m; Fig. 5a), the initial slopes of the H–D curve vary only slightly. Some DmaxL and HmaxL values (Table S1) indicate that some H–D trajectories (Fig. 5a) are incomplete (Acronychia pubescens), whereas in others (Denhamia celastroides), there is evidence of some increase in D after Ha is attained.
|
The HmaxP 20–29 m class (Fig. 5b) may be described as subdominant and is notable for the almost identical H–D trajectories for the four species, in both their initial slopes and convexities, despite showing a range of maximum sizes. The codominant HmaxP 30–39 m class (Fig. 5c) showed more variation in both the initial H–D slope and convexity as trees approach maturity. Diploglottis australis is notable for the higher slope (more gradual stem taper) than other species, although the convexity was not so distinctive. Extension of the class H–D curve well beyond the bounds of the four species shown was due to the inclusion in the HmaxP class data set of two individuals of Brachychiton acerifolium, one being the largest tree in the whole sample The emergent HmaxP 40+ m class showed more variation than others among initial slope, convexity, Dmax and Ha of the five species (Fig. 5d).
Because the HmaxP class mean curves for co-dominant (HmaxP 30–39 m) and emergent classes (HmaxP 40+ m) were very similar, these were combined into a canopy species group (HmaxP 30+ m) for a simpler structural comparison of the HmaxP class groups (Fig. 5e). The H–D curves for understorey (HmaxP 10–19 m) and subdominant (HmaxP 20–29 m) classes were sufficiently distinct, so as to warrant their separate classifications.
Discussion
Application of allometric models
Precision of H estimates for datasets, such as the RMSE (Huang et al. 1992; Zhang 1997; Williams et al. 2005; Qiu et al. 2021) has been used widely in the evaluation of allometric functions. Although the NRH was less precise than the GMM, it was much closer than all other tested equations (Table 2). Trends of bias in H–D predictions for D class means (Fig. S3) indicated a pattern of bias in the NRH that is very similar to that previously described for the GMM (Ledo et al. 2016; Martínez Cano et al. 2019a). Both equations have similar assessed utility for relating allometric parameters of datasets, except that the GMM initial proportionality factor cannot be visualised directly. For describing and comparing tree development for individual species (Fig. 5), the NRH was judged to be the better equation.
Where the developmental patterns of individual species are an important objective for investigation, explanations for plant attributes (e.g. tree height or crown width) may be sought in multivariate associations with functional attributes (Wright et al. 2007; Apgaua et al. 2015; Loubota Panzou et al. 2018). For individual species, more emphasis can be placed on the biological relevance of function parameters (Hunt 1979) and their utility in understanding the intrinsic factors underlying these developmental patterns.
Initial H–D proportionality factor
The average stand densities of trees overtopping regeneration <5 m tall (Fig. S1d) indicated that the environments in which small stems developed were at least equivalent to those in natural multi-species stands (Coomes et al. 2003; Ledo et al. 2016). It is suggested that the growing conditions within the Gambubal rainforest understorey did not prevent or exaggerate tree sway, but allowed direct interspecific comparison of the allometric parameter, a, as a basis for identifying critical functional attributes.
Under such conditions, the H–D ratio in sapling stems of different species is limited by the species’ intrinsic structural properties of the stem (King 1990; Morgan and Cannell 1994; Niklas et al. 2006) and related functional attributes (Poorter et al. 2006; Hérault et al. 2011; Martínez Cano et al. 2019a). If the power function for trees <8 m tall is a valid biophysical basis for comparison (Banin et al. 2012), the only function with a closely correlated and readily visualised form of a was the Ha-forced NRH for species with HmaxP of 30+ m (Fig. 2e). This association indicates the utility of the NRH for describing early development of canopy trees in this forest. Unlike the forest described by Martínez Cano et al.(2019a), both understorey and canopy species exhibited similar ranges of a (Fig. 2e). This may reflect less vertical environmental segregation within a subtropical as compared with an equatorial rainforest.
Wood density is closely associated with timber strength, stem allometry and tree stability (Falster and Westoby 2003; van Gelder et al. 2006; Fournier et al. 2013). Variations in a within the understorey (HmaxP 10–19 m) and subdominant (HmaxP 20–29 m) classes were not closely associated with wood density for the respective species, as was observed by Kooyman and Westoby (2009) for some species common to this study. In contrast, the closest positive linear relationships between these parameters occurred in canopy species (HmaxP 30+ m) when described by the linear (Fig. 3a) and power (Fig. 3b) equations for trees <8 m tall and by the NRH equation for all trees in this HmaxP class (Fig. 3d). This finding conforms to the observations of van Gelder et al. (2006) and Osunkoya et al. (2007) and gives credibility to the biophysical limitation of stem taper in these rainforest saplings (Niklas et al. 2006; Fournier et al. 2013). It also indicates the biological relevance of a determined by fitting the NRH to total data for a species.
Interspecific differences in initial stem taper can also be related to the architecture of each species (Claussen and Maycock 1995; Poorter et al. 2005, 2006; Duursma et al. 2010; Falster et al. 2018). The present analysis differs from some of these studies in that it relates to the initial stages of growth, and not to mature tree dimensions (Wang et al. 1998). Most species in the present study had simple or small compound leaves, carried on stems with slender primary growth, short internodes and, except in very low light conditions, a tendency to retain lateral branches (Floyd 2008). These species typically conform to Rauh’s architectural model, with monopodial rhythmic growth and tiers of branches that have indefinite growth potential (Hallé et al. 1978). As a result, height growth would be expected to accompany thickening of the stem, consistent with the number and physiological activity of lateral branches (Niklas 1995; Osunkoya et al. 2007: Falster et al. 2018; Loubota Panzou et al. 2018, 2021a).
In contrast, Polyscias elegans had an unusually high NRH Ha-forced a value for its wood density (Fig. 3d), but an overall H–D trajectory that was indistinguishable from other members of the HmaxP 20–29 m group (Fig. 5b). Polyscias elegans was notable for its large compound leaves carried on plagiotropic branches, and a very shallow crown, consistent with the Aubreville architectural model (Hallé et al. 1978), shade intolerance, and its occurrence in relatively high light environments and appearance soon after forest disturbance (Kariuki et al. 2006; Floyd 2008). A similar initial growth pattern was described for Polyscias australiana by Claussen and Maycock (1995), an early successional species from north Queensland rainforests.
Diploglottis australis, with the highest value of NRH Ha-forced a, 1.36 m cm−1 (Table S3, Panel 10B, Fig. 3d) possessed large compound pinnate leaves, commonly arranged oppositely or in pseudowhorls, separated by unusually long and robust internodes, consistent with the Aubreville architectural model (Hallé et al. 1978). These characteristics, with a high wood density (800 kg m−3), are suggested to impart stiffness that would increase height growth per unit of secondary xylem dry matter as compared with species having short and thin primary internodes. This pattern of height growth was maintained until trees were more than 20 m tall, making the H–D trajectory of D. australis distinctive among the HmaxP 30–39 m class (Fig. 5c).
Convexity factor and asymptotic height
For the species studied here, values of Ha-forced b for both GMM and NRH showed consistent and proportional patterns of decrease with an increasing HmaxL (Fig. 4). There was no clear difference between these two equations in the precision of these trends, and both were judged to reflect tree growth patterns.
The observed range of b for the NRH was about 0.7–0.95, and for the GMM it was about 0.8–1.9 (Fig. 4). Trees with low Ha usually have a small range of maximum stem diameter (Dmax), whereas trees that reach the upper canopy may continue to increase D for many years after they effectively reach Ha (Francis 1970; Thomas 1996, 2003; Floyd 2008; Banin et al. 2012).
The change in H–D trajectory for different HmaxP classes is very similar to that for photosynthesis in rainforest species from different strata (Thomas and Bazzaz 1999). It is suggested that species showing NRH b values close to 1.0 will reach Ha while growing in a constantly light-limited environment, with sufficient water, favourable temperatures, and limited wind, where the H–D relationship is determined principally by the intrinsic biophysical properties of the species, the static forces on the tree stem (King et al. 2009; Fournier et al. 2013) and stem hydraulic conductivity (Becker et al. 2000; Apgaua et al. 2015). Trees in these conditions would be expected to grow to their potential height, but lateral crown extension would be limited because of the high effective stand density (Vanclay 2009; Matos et al. 2015; Loubota Panzou et al. 2021a), so D would increase only very slowly with age after maturity. This pattern of growth is consistent with the application of the power equation to understorey species (Banin et al. 2012).
Once trees emerge from the forest understorey, a situation occurs that is analogous to the light response of photosynthetic rate, where multiple factors influence the rates of processes (Givnish 1988; Falster et al. 2018). The effective stand density decreases, intercepted radiation and atmospheric exposure increase, and the distance between neighbours may influence tree stem allometry (Wang et al. 1998; Poorter et al. 2005; Blanchard et al. 2016). These changes occur through a capacity for branch extension to continue, while crown depth increases through height growth (Poorter et al. 2006; Osunkoya et al. 2007; Loubota Panzou et al. 2021a), so that crown diameter and stem diameter increase in proportion (Henry and Aarssen 1999; Jucker et al. 2017), but varying with species’ architecture (Sterck et al. 2001; Bohlman and O’Brien 2006; Loubota Panzou et al. 2018; Xu et al. 2019) and strength properties of their wood (van Gelder et al. 2006; Fournier et al. 2013).
In addition, exposure to increased wind speeds would result in greater swaying of the stems, which tends to increase stem taper (Jacobs 1954; Mayer 1987; Meng et al. 2008) and may limit height growth through damage to the uppermost twigs and branches (McEwan et al. 2011; Fournier et al. 2013; Thomas et al. 2015) and result in mainstem breakage and overturning (Cremer et al. 1982; Niklas 2007).
Aggregation into structural groups
Amalgamations of data used to provide generalised descriptions of forest structure (Thomas 2003; Osunkoya et al. 2007; Iida et al. 2011; Banin et al. 2012; Martínez Cano et al. 2019a) or regional estimates of forest biomass (Djomo et al. 2010; Feldpausch et al. 2012; Chave et al. 2014; Jucker et al. 2017) are reflected in the analyses for species and HmaxP classes shown here.
Aggregation of species H–D curves into structural groups can help identify the similarities and differences between functional attributes of the constituent species and structural groups of species (Aiba and Kohyama 1997; Poorter et al. 2006; Falster et al. 2018; Martínez Cano et al. 2019a). The overall H–D patterns are more consistent in the two smaller HmaxP classes (<30 m) than in the two taller classes (>30 m; Fig. 5). This differentiation would be consistent with the increasing variability in environmental conditions surrounding the crowns of trees as they became taller (O’Brien et al. 1995; Poorter et al. 2003; Iida et al. 2011; Banin et al. 2012). Consistent with this proposition, there may be limited segregation of HmaxL values in many species from Malaysian lowland rainforests (King et al. 2009; Iida et al. 2011), but continental-scale differences in HmaxL (Banin et al. 2012) and crown dimensions (Loubota Panzou et al. 2021a) of tropical forests, possibly reflecting the lower frequency of storm events in Malaysia and Asia generally than in many other rainforest environments (de Gouvenain and Silander 2003).
The total sample NRH b value of about 0.24 (Table 2) is attributed to the fact that mature trees in the lower HmaxP classes are not distinguished from younger trees in the taller HmaxP classes (Falster and Westoby 2005; Thomas 2003).
Utility of the non-rectangular hyperbola
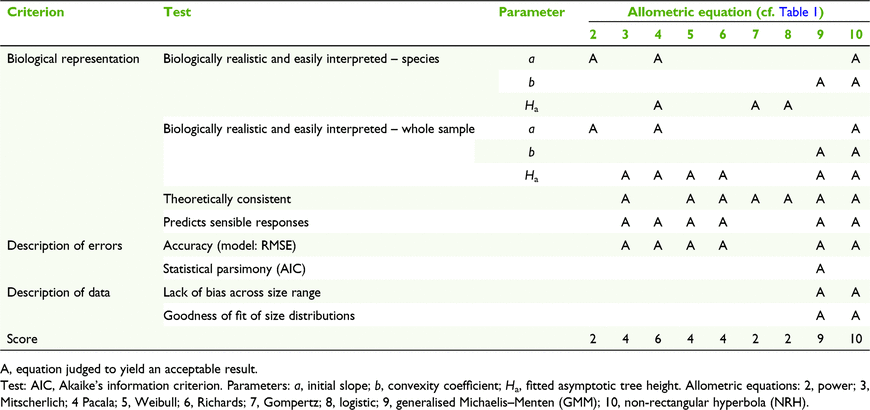
Vanclay and Skovsgaard (1997) identified six criteria for the assessment of forest growth models. Tests for the description of errors and description of data have been comprehensively reviewed elsewhere (Vanclay and Skovsgaard 1997; Ledo et al. 2016). Assessable criteria, as applied to nine allometric equations in this study, are shown in Table 3.
Parameter variance and statistical parsimony are the critical attributes for predictive modelling (Cifuentes Jara et al. 2015; Ledo et al. 2016, Loubota Panzou et al. 2021b), making the AIC value the determinant of model fitness. In this study, the GMM was the most efficient H–D allometric model for the whole sample (Tables 3, S2).
However, if the purpose of investigation is to visualise the components of species H–D trajectories, the NRH offers some advantages. The parameters of the NRH provide easily comprehended linear descriptions of three elements of tree growth in a specific environment, namely a, Ha and b. Application of the NRH across different environments would require modifications, as have been made to power (Lines et al. 2012; Zhao et al. 2021), logarithmic (Feldpausch et al. 2012; Chave et al. 2014; Cysneiros et al. 2021), Weibull and exponential (Banin et al. 2012; Mensah et al. 2018) models. An advantage of the NRH is that variations in environmental resource availability as reflected in forest type (Cysneiros et al. 2020), site quality (Vanclay 2009) and tree density (Vanclay 1992; Deng et al. 2019) may be identified and described quantitatively as factors independently altering a, b and Ha, and other dependent parameters, including crown dimensions and biomass.
Combination of the explanatory advantages of the NRH with statistical attributes that are equal or almost equal to those of several other widely used allometric equations, and especially the GMM (Table 3), suggests that the NRH can be used with confidence for both large datasets and for individual species, provided precautions are taken if the range of tree sizes is limited.
Conclusions
Although many allometric equations have been applied to describe H–D relationships for trees, and even though it is possible to estimate several tree dimensions and forest attributes remotely, value may be gained from understanding the development of individual species in complex vegetation associations such as rainforests. This analysis of individual species development depends on reliable identification and measurement of trees in the subcanopy zone of the forest as well as in the emergent canopy.
The non-rectangular hyperbola (NRH), although not as efficient as the generalised Michaelis–Menten (GMM) equation, is considered to provide a useful explanatory model for the development of tree height, H, in relation to stem diameter at breast height, D, over the complete range from saplings to mature trees. Application of the NRH to small samples of individual species may require the insertion of local maximum height, HmaxL, as asymptotic height, Ha, into the equation fitting routine; this value can best be obtained from measurement of a designated sample of trees. For more general application, the calculated maximum height, HmaxC, of a forest overstorey species may be related to climate and soil conditions. Advantages of this function are the accuracy and easy visualisation of realistic allometric relationships. The conceptual simplicity of the NRH allows testing of differences among forest environments through the comparison of numerical values for allometric parameters of individual species, especially where these differences are associated with climatic regime, site quality, tree spacing, and exposure to wind or to water deficits.
Supplementary material
Supplementary material is available online.
Data availability
Data are held by SRH and will be made available when a larger ongoing study has been completed.
Conflicts of interest
No conflicts of interest are declared.
Declaration of funding
This work was supported by the Australian Research Council (Grant No. A18931866), by in kind contributions from the Queensland Department of Forestry (latterly the Department of Environment and Science) and by staff and student research funds administered by the Department of Botany, The University of Queensland.
Acknowledgements
Material and professional assistance from the Queensland Department of Forestry (latterly the Department of Environment and Science) is gratefully acknowledged. The Department of Botany and the Centre for Mined Land Rehabilitation of The University of Queensland made their resources available. MF Olsen and WJF McDonald contributed critical species identifications and many student volunteers assisted in the field. We also gratefully acknowledge the valuable suggestions made by two anonymous reviewers on earlier versions of this paper.
References
Aertsen W, Kint V, van Orshoven J, Özkan K, Muys B (2010) Comparison and ranking of different modelling techniques for prediction of site index in Mediterranean mountain forests. Ecological Modelling 221, 1119–1130.| Comparison and ranking of different modelling techniques for prediction of site index in Mediterranean mountain forests.Crossref | GoogleScholarGoogle Scholar |
Aiba SI, Kohyama T (1997) Crown architecture and life-history traits of 14 tree species in a warm-temperate rain forest: significance of spatial heterogeneity. Journal of Ecology 85, 611–624.
| Crown architecture and life-history traits of 14 tree species in a warm-temperate rain forest: significance of spatial heterogeneity.Crossref | GoogleScholarGoogle Scholar |
Apgaua DMG, Ishida FY, Tng DYP, Laidlaw MJ, Santos RM, Rumman R, Eamus D, Holtum JAM, Laurance SGW (2015) Functional traits and water transport strategies in lowland tropical rainforest trees. PLoS ONE 10, e0130799
| Functional traits and water transport strategies in lowland tropical rainforest trees.Crossref | GoogleScholarGoogle Scholar |
Banin L, Feldpausch TR, Phillips OL, Baker TR, Lloyd J, Affum-Baffoe K, Arets EJMM, Berry NJ, Bradford M, Brienen RJW, Davies S, Drescher M, Higuchi N, Hilbert DW, Hladik A, Iida Y, Abu Salim K, Kassim AR, King DA, Lopez-Gonzalez G, Metcalfe D, Nilus R, Peh KS-H, Reitsma JM, Sonké B, Taedoumg H, Tan S, White L, Wöll H, Lewis SL (2012) What controls tropical forest architecture? Testing environmental, structural and floristic drivers. Global Ecology and Biogeography 21, 1179–1190.
| What controls tropical forest architecture? Testing environmental, structural and floristic drivers.Crossref | GoogleScholarGoogle Scholar |
Becker P, Meinzer FC, Wullschleger SD (2000) Hydraulic limitation of tree height: a critique. Functional Ecology 14, 4–11.
| Hydraulic limitation of tree height: a critique.Crossref | GoogleScholarGoogle Scholar |
Blanchard E, Birnbaum P, Ibanez T, Boutreux T, Antin C, Ploton P, Vincent G, Pouteau R, Vandrot H, Hequet V, Barbier N, Droissart V, Sonké B, Texier N, Kamdem NG, Zebaze D, Libalah M, Couteron P (2016) Contrasted allometries between stem diameter, crown area, and tree height in five tropical biogeographic areas. Trees 30, 1953–1968.
| Contrasted allometries between stem diameter, crown area, and tree height in five tropical biogeographic areas.Crossref | GoogleScholarGoogle Scholar |
Bohlman S, O’Brien S (2006) Allometry, adult stature and regeneration requirement of 65 tree species on Barro Colorado Island, Panama. Journal of Tropical Ecology 22, 123–136.
| Allometry, adult stature and regeneration requirement of 65 tree species on Barro Colorado Island, Panama.Crossref | GoogleScholarGoogle Scholar |
Boland DJ, Brooker MIH, Chippendale GM, Hall N, Hyland BPM, Johnston RD, Kleinig DA, McDonald MW, Turner JD (Eds) (2006) ‘Forest trees of Australia’, 5th edn. (CSIRO Publishing: Melbourne, Vic., Australia)
Burnham KP, Anderson DR (2004) ‘Model selection and multimodel inference: a practical information-theoretic approach’, 2nd edn. (Springer Verlag: New York, NY, USA)
Canham CD, Finzi AC, Pacala SW, Burbank DH (1994) Causes and consequences of resource heterogeneity in forests: interspecific variation in light transmission by canopy trees. Canadian Journal of Forest Research 24, 337–349.
| Causes and consequences of resource heterogeneity in forests: interspecific variation in light transmission by canopy trees.Crossref | GoogleScholarGoogle Scholar |
Cause ML, Rudder EJ, Kynaston WT (1989) ‘Queensland timbers: their nomenclature, density and lyctid susceptibility.’ Technical pamphlets 2. (Queensland Department of Agriculture and Fisheries: Brisbane, Qld, Australia)
Chave J, Andalo C, Brown S, Cairns MA, Chambers JQ, Eamus D, Fölster H, Fromard F, Higuchi N, Kira T, Lescure JP, Nelson BW, Ogawa H, Puig H, Riéra B, Yamakura T (2005) Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 145, 87–99.
| Tree allometry and improved estimation of carbon stocks and balance in tropical forests.Crossref | GoogleScholarGoogle Scholar | 15971085PubMed |
Chave J, Réjou-Méchain M, Burquez A, Chidumayo E, Colgan MS, Delitti WBC, Duque A, Eid T, Fearnside PM, Goodman RC, Henry M, Martinez-Yrizar A, Mugasha WA, Muller-Landau HC, Mencuccini M, Nelson BW, Ngomanda A, Nogueira EM, Ortiz-Malavassi E, Pelissier R, Ploton P, Ryan CM, Saldarriaga JG, Vielledent G (2014) Improved allometric models to estimate the aboveground biomass of tropical trees. Global Change Biology 20, 3177–3190.
| Improved allometric models to estimate the aboveground biomass of tropical trees.Crossref | GoogleScholarGoogle Scholar | 24817483PubMed |
Chenge IB (2021) Height–diameter relationship of trees in Omo strict nature forest reserve, Nigeria. Trees, Forests and People 3, 100051
| Height–diameter relationship of trees in Omo strict nature forest reserve, Nigeria.Crossref | GoogleScholarGoogle Scholar |
Cifuentes Jara MC, Henry M, Réjou-Méchain M, Wayson C, Zapata-Cuartas M, Piotto D, Guier FA, Lombis HC, López EC, Lara RC, Rojas KC (2015) Guidelines for documenting and reporting tree allometric equations. Annals of Forest Science 72, 763–768.
| Guidelines for documenting and reporting tree allometric equations.Crossref | GoogleScholarGoogle Scholar |
Claussen JW, Maycock CR (1995) Stem allometry in a north Queensland tropical rainforest. Biotropica 27, 421–426.
| Stem allometry in a north Queensland tropical rainforest.Crossref | GoogleScholarGoogle Scholar |
Cook GD, Liedloff AC, Eager RW, Chen X, Williams RJ, O’Grady AP, Hutley LB (2005) The estimation of carbon budgets of frequently burnt tree stands in savannas of northern Australia, using allometric analysis and isotopic discrimination. Australian Journal of Botany 53, 621–630.
| The estimation of carbon budgets of frequently burnt tree stands in savannas of northern Australia, using allometric analysis and isotopic discrimination.Crossref | GoogleScholarGoogle Scholar |
Coomes DA, Duncan RP, Allen RB, Truscott J (2003) Disturbances prevent stem size-density distributions in natural forests from following scaling relationships. Ecology Letters 6, 980–989.
| Disturbances prevent stem size-density distributions in natural forests from following scaling relationships.Crossref | GoogleScholarGoogle Scholar |
Cremer KW, Borough CJ, McKinnell FH, Carter PR (1982) Effects of stocking and thinning on wind damage in plantations. New Zealand Journal of Forest Science 12, 244–268.
Cysneiros VC, Pelissari AL, Gaui TD, Fiorentin LD, Carvalho DC, Silveira Filho TB, Machado SdA (2020) Modeling of tree height–diameter relationships in the Atlantic Forest: effect of forest type on tree allometry. Canadian Journal of Forest Research 50, 1289–1298.
| Modeling of tree height–diameter relationships in the Atlantic Forest: effect of forest type on tree allometry.Crossref | GoogleScholarGoogle Scholar |
Cysneiros VC, de Souza FC, Gaui TD, Pelissari AL, Orso GA, do Amaral Machado S, de Carvalho DC, Silveira-Filho TB (2021) Integrating climate, soil and stand structure into allometric models: an approach of site-effects on tree allometry in Atlantic Forest. Ecological Indicators 127, 107794
| Integrating climate, soil and stand structure into allometric models: an approach of site-effects on tree allometry in Atlantic Forest.Crossref | GoogleScholarGoogle Scholar |
Dale JA (1983) ‘Management studies in the escarpment rainforests of south east Queensland.’ Research Paper No. 14. (Queensland Department of Forestry: Brisbane, Qld, Australia)
Davies SJ, Palmiotto PA, Ashton PS, Lee HS, Lafrankie JV (1998) Comparative ecology of 11 sympatric species of Macaranga in Borneo: tree distribution in relation to horizontal and vertical resource heterogeneity. Journal of Ecology 86, 662–673.
| Comparative ecology of 11 sympatric species of Macaranga in Borneo: tree distribution in relation to horizontal and vertical resource heterogeneity.Crossref | GoogleScholarGoogle Scholar |
de Gouvenain RC, Silander JA (2003) Do tropical storm regimes influence the structure of tropical lowland rain forests? Biotropica 35, 166–180.
| Do tropical storm regimes influence the structure of tropical lowland rain forests?Crossref | GoogleScholarGoogle Scholar |
Debski I, Burslem DFRP, Lamb D (2000) Ecological processes maintaining differential tree species distributions in an Australian subtropical rain forest: implications for models of species coexistence. Journal of Tropical Ecology 16, 387–415.
| Ecological processes maintaining differential tree species distributions in an Australian subtropical rain forest: implications for models of species coexistence.Crossref | GoogleScholarGoogle Scholar |
del Río M, Bravo-Oviedo A, Ruiz-Peinado R, Condés S (2019) Tree allometry variation in response to intra-and inter-specific competitions. Trees 33, 121–138.
| Tree allometry variation in response to intra-and inter-specific competitions.Crossref | GoogleScholarGoogle Scholar |
Deng C, Zhang S, Lu Y, Froese RE, Ming A, Li Q (2019) Thinning effects on the tree height–diameter allometry of Masson pine (Pinus massoniana Lamb.). Forests 10, 1129
| Thinning effects on the tree height–diameter allometry of Masson pine (Pinus massoniana Lamb.).Crossref | GoogleScholarGoogle Scholar |
Djomo AN, Ibrahima A, Saborowski J, Gravenhorst G (2010) Allometric equations for biomass estimations in Cameroon and pan moist tropical equations including biomass data from Africa. Forest Ecology and Management 260, 1873–1885.
| Allometric equations for biomass estimations in Cameroon and pan moist tropical equations including biomass data from Africa.Crossref | GoogleScholarGoogle Scholar |
Duursma RA, Mäkelä A, Reid DEB, Jokela EJ, Porté AJ, Roberts SD (2010) Self-shading affects allometric scaling in trees. Functional Ecology 24, 723–730.
| Self-shading affects allometric scaling in trees.Crossref | GoogleScholarGoogle Scholar |
Evans GC (1972) ‘The quantitative analysis of plant growth,’ (Blackwell Scientific Publications: Oxford, UK)
Falster DS, Westoby M (2003) Plant height and evolutionary games. Trends in Ecology & Evolution 18, 337–343.
| Plant height and evolutionary games.Crossref | GoogleScholarGoogle Scholar |
Falster DS, Westoby M (2005) Alternative height strategies among 45 dicot rain forest species from tropical Queensland, Australia. Journal of Ecology 93, 521–535.
| Alternative height strategies among 45 dicot rain forest species from tropical Queensland, Australia.Crossref | GoogleScholarGoogle Scholar |
Falster DS, Duursma RA, FitzJohn RG (2018) How functional traits influence plant growth and shade tolerance across the life cycle. Proceedings of the National Academy of Sciences of the United States of America 115, E6789–E6798.
| How functional traits influence plant growth and shade tolerance across the life cycle.Crossref | GoogleScholarGoogle Scholar | 29959205PubMed |
Feldpausch TR, Lloyd J, Lewis SL, et al. (2012) Tree height integrated into pantropical forest biomass estimates. Biogeosciences 9, 3381–3403.
| Tree height integrated into pantropical forest biomass estimates.Crossref | GoogleScholarGoogle Scholar |
Floyd AG (2008) ‘Rainforest trees of mainland south-eastern Australia,’ (Terania Rainforest Publishing: Lismore, NSW, Australia)
Forrester DI, Benneter A, Bouriaud O, Bauhus J (2017) Diversity and competition influence tree allometric relationships: developing functions for mixed-species forests. Journal of Ecology 105, 761–774.
| Diversity and competition influence tree allometric relationships: developing functions for mixed-species forests.Crossref | GoogleScholarGoogle Scholar |
Fournier M, Dlouhá J, Jaouen G, Almeras T (2013) Integrative biomechanics for tree ecology: beyond wood density and strength. Journal of Experimental Botany 64, 4793–4815.
| Integrative biomechanics for tree ecology: beyond wood density and strength.Crossref | GoogleScholarGoogle Scholar | 24014867PubMed |
Francis WD (1970) ‘Australian rain-forest trees’, 3rd edn. (Australian Government Publishing Service: Canberra, ACT, Australia)
Francis EJ, Muller-Landau HC, Wright SJ, Visser MD, Iida Y, Fletcher C, Hubbell SP, Kassim AR (2017) Quantifying the role of wood density in explaining interspecific variation in growth of tropical trees. Global Ecology and Biogeography 26, 1078–1087.
| Quantifying the role of wood density in explaining interspecific variation in growth of tropical trees.Crossref | GoogleScholarGoogle Scholar |
Givnish TJ (1988) Adaptation to sun and shade: a whole-plant perspective. Australian Journal of Plant Physiology 15, 63–92.
| Adaptation to sun and shade: a whole-plant perspective.Crossref | GoogleScholarGoogle Scholar |
Hallé F, Oldeman RAA, Tomlinson PB (1978) ‘Tropical trees and forests: an architectural analysis’, (Springer-Verlag: Berlin, Germany)
Henry HAL, Aarssen LW (1999) The interpretation of stem diameter–height allometry in trees: biomechanical constraints, neighbour effects, or biased regressions? Ecology Letters 2, 89–97.
| The interpretation of stem diameter–height allometry in trees: biomechanical constraints, neighbour effects, or biased regressions?Crossref | GoogleScholarGoogle Scholar |
Hérault B, Bachelot B, Poorter L, Rossi V, Bongers F, Chave J, Paine CET, Wagner F, Baraloto C,
| Functional traits shape ontogenetic growth trajectories of rain forest tree species.Crossref | GoogleScholarGoogle Scholar |
Higham TE, Ferry LA, Schmitz L, Irschick DJ, Starko S, Anderson PS, Bergmann PJ, Jamniczky HA, Monteiro LR, Navon D, Messier J, Carrington E, Farina SC, Feilich KL, Hernandez LP, Johnson MA, Kawano SM, Law CJ, Longo SJ, Martin CH, Martone PT, Rico-Guevara A, Santana SE, Niklas KJ (2021) Linking ecomechanical models and functional traits to understand phenotypic diversity. Trends in Ecology & Evolution 36, 860–873.
| Linking ecomechanical models and functional traits to understand phenotypic diversity.Crossref | GoogleScholarGoogle Scholar |
Huang S, Titus SJ, Wiens DP (1992) Comparison of nonlinear height–diameter functions for major Alberta tree species. Canadian Journal of Forest Research 22, 1297–1304.
| Comparison of nonlinear height–diameter functions for major Alberta tree species.Crossref | GoogleScholarGoogle Scholar |
Hummel S (2000) Height, diameter and crown dimensions of Cordia alliodora associated with tree density. Forest Ecology and Management 127, 31–40.
| Height, diameter and crown dimensions of Cordia alliodora associated with tree density.Crossref | GoogleScholarGoogle Scholar |
Hunt R (1979) Plant growth analysis: the rationale behind the use of the fitted mathematical function. Annals of Botany 43, 245–249.
| Plant growth analysis: the rationale behind the use of the fitted mathematical function.Crossref | GoogleScholarGoogle Scholar |
Hutley LB, Doley D, Yates DJ, Boonsaner A (1997) Water balance of an Australian subtropical rainforest at altitude: the ecological and physiological significance of intercepted cloud and fog. Australian Journal of Botany 45, 311–329.
| Water balance of an Australian subtropical rainforest at altitude: the ecological and physiological significance of intercepted cloud and fog.Crossref | GoogleScholarGoogle Scholar |
Huxley JS (1924) Constant differential growth-ratios and their significance. Nature 114, 895–896.
| Constant differential growth-ratios and their significance.Crossref | GoogleScholarGoogle Scholar |
Iida Y, Kohyama TS, Kubo T, Kassim AR, Poorter L, Sterck F, Potts MD (2011) Tree architecture and life-history strategies across 200 co-occurring tropical tree species. Functional Ecology 25, 1260–1268.
| Tree architecture and life-history strategies across 200 co-occurring tropical tree species.Crossref | GoogleScholarGoogle Scholar |
Jacobs MR (1954) The effect of wind sway on the form and development of Pinus radiata D. Don. Australian Journal of Botany 2, 35–51.
| The effect of wind sway on the form and development of Pinus radiata D. Don.Crossref | GoogleScholarGoogle Scholar |
Johnson IR, Thornley JHM (1984) A model of instantaneous and daily canopy photosynthesis. Journal of Theoretical Biology 107, 531–545.
| A model of instantaneous and daily canopy photosynthesis.Crossref | GoogleScholarGoogle Scholar |
Jucker T, Caspersen J, Chave J, Antin C, Barbier N, Bongers F, et al. (2017) Allometric equations for integrating remote sensing imagery into forest monitoring programmes. Global Change Biology 23, 177–190.
| Allometric equations for integrating remote sensing imagery into forest monitoring programmes.Crossref | GoogleScholarGoogle Scholar | 27381364PubMed |
Kariuki M, Rolfe M, Smith RGB, Vanclay JK, Kooyman RM (2006) Diameter growth performance varies with species functional-group and habitat characteristics in subtropical rainforests. Forest Ecology and Management 225, 1–14.
| Diameter growth performance varies with species functional-group and habitat characteristics in subtropical rainforests.Crossref | GoogleScholarGoogle Scholar |
King DA (1986) Tree form, height growth, and susceptibility to wind damage in Acer saccharum. Ecology 67, 980–990.
| Tree form, height growth, and susceptibility to wind damage in Acer saccharum.Crossref | GoogleScholarGoogle Scholar |
King DA (1990) Allometry of saplings and understorey trees of a Panamanian forest. Functional Ecology 4, 27–32.
| Allometry of saplings and understorey trees of a Panamanian forest.Crossref | GoogleScholarGoogle Scholar |
King DA, Davies SJ, Tan S, Noor NSM (2009) Trees approach gravitational limits to height in tall lowland forests of Malaysia. Functional Ecology 23, 284–291.
| Trees approach gravitational limits to height in tall lowland forests of Malaysia.Crossref | GoogleScholarGoogle Scholar |
Kohyama T, Suzuki E, Partomihardjo T, Yamada T, Kubo T (2003) Tree species differentiation in growth, recruitment and allometry in relation to maximum height in a Bornean mixed dipterocarp forest. Journal of Ecology 91, 797–806.
| Tree species differentiation in growth, recruitment and allometry in relation to maximum height in a Bornean mixed dipterocarp forest.Crossref | GoogleScholarGoogle Scholar |
Kollmann FFP (1968) Mechanics and rheology of wood. In ‘Principles of wood science and technology’. (Eds FFP Kollmann, WA Cote) pp. 292–419. (Springer-Verlag: Berlin, Germany)
Kooyman RM, Westoby M (2009) Costs of height gain in rainforest saplings: main-stem scaling, functional traits and strategy variation across 75 species. Annals of Botany 104, 987–993.
| Costs of height gain in rainforest saplings: main-stem scaling, functional traits and strategy variation across 75 species.Crossref | GoogleScholarGoogle Scholar | 19635742PubMed |
Ledo A, Cornulier T, Illian JB, Iida Y, Kassim AR, Burslem DFRP (2016) Re-evaluation of individual diameter: height allometric models to improve biomass estimation of tropical trees. Ecological Applications 26, 2376–2382.
| Re-evaluation of individual diameter: height allometric models to improve biomass estimation of tropical trees.Crossref | GoogleScholarGoogle Scholar |
Lines ER, Zavala MA, Purves DW, Coomes DA (2012) Predictable changes in aboveground allometry of trees along gradients of temperature, aridity and competition. Global Ecology and Biogeography 21, 1017–1028.
| Predictable changes in aboveground allometry of trees along gradients of temperature, aridity and competition.Crossref | GoogleScholarGoogle Scholar |
Loubota Panzou GJ, Ligot G, Gourlet-Fleury S, Doucet JL, Forni E, Loumeto JJ, Fayolle A (2018) Architectural differences associated with functional traits among 45 coexisting tree species in Central Africa. Functional Ecology 32, 2583–2593.
| Architectural differences associated with functional traits among 45 coexisting tree species in Central Africa.Crossref | GoogleScholarGoogle Scholar |
Loubota Panzou GJ, Fayolle A, Jucker T, Phillips OL, Bohlman S, Banin LF, Lewis SL, Affum-Baffoe K, Alves LF, Antin C, Arets E (2021a) Pantropical variability in tree crown allometry. Global Ecology and Biogeography 30, 459–475.
| Pantropical variability in tree crown allometry.Crossref | GoogleScholarGoogle Scholar |
Loubota Panzou GJ, Bocko YE, Mavoungou AY, Loumeto JJ (2021b) Height–diameter allometry in African monodominant forest close to mixed forest. Journal of Tropical Ecology 37, 98–107.
| Height–diameter allometry in African monodominant forest close to mixed forest.Crossref | GoogleScholarGoogle Scholar |
Lu L, Chhin S, Zhang J, Zhang X (2021) Modelling tree height–diameter allometry of Chinese fir in relation to stand and climate variables through Bayesian model averaging approach. Silva Fennica 55, 10415
| Modelling tree height–diameter allometry of Chinese fir in relation to stand and climate variables through Bayesian model averaging approach.Crossref | GoogleScholarGoogle Scholar |
Martínez Cano I, Muller-Landau HC, Wright SJ, Bohlman SA, Pacala SW (2019a) Tropical tree height and crown allometries for the Barro Colorado Nature Monument, Panama: a comparison of alternative hierarchical models incorporating interspecific variation in relation to life history traits. Biogeosciences 16, 847–862.
| Tropical tree height and crown allometries for the Barro Colorado Nature Monument, Panama: a comparison of alternative hierarchical models incorporating interspecific variation in relation to life history traits.Crossref | GoogleScholarGoogle Scholar |
Martínez Cano I, Shevliakova E, Malyshev S, Wright SJ, Detto M, Pacala SW, Muller-Landau HC (2019b) Allometric constraints and competition enable the simulation of size structure and carbon fluxes in a dynamic vegetation model of tropical forests (LM3PPA-TV). Global Change Biology 26, 4478–4494.
| Allometric constraints and competition enable the simulation of size structure and carbon fluxes in a dynamic vegetation model of tropical forests (LM3PPA-TV).Crossref | GoogleScholarGoogle Scholar |
Matos FA, Daniel O, Serra AP, Heid DM, Matos do Nascimento J, Nogueira IM, Ensinas SC, Altomar PH, do Amaral Conrad V, Potrich DC, Martinez MA (2015) Effects of intra-specific tree competition on dendrometric parameters of Peltophorum dubium. Australian Journal of Crop Science 9, 1003–1009.
Mayer H (1987) Wind-induced tree sways. Trees 1, 195–206.
| Wind-induced tree sways.Crossref | GoogleScholarGoogle Scholar |
McEwan RW, Lin Y-C, Sun I-F, Hsieh C-F, Su S-H, Chang L-W, Song G-ZM, Wang H-H, Hwong J-L, Lin K-C, Yang K-C, Chiang J-M (2011) Topographic and biotic regulation of aboveground carbon storage in subtropical broad-leaved forests of Taiwan. Forest Ecology and Management 262, 1817–1825.
| Topographic and biotic regulation of aboveground carbon storage in subtropical broad-leaved forests of Taiwan.Crossref | GoogleScholarGoogle Scholar |
McMahon TA, Kronauer RE (1976) Tree structures: deducing the principle of mechanical design. Journal of Theoretical Biology 59, 443–466.
| Tree structures: deducing the principle of mechanical design.Crossref | GoogleScholarGoogle Scholar | 957700PubMed |
Meng SX, Huang S, Lieffers VJ, Nunifu T, Yang Y (2008) Wind speed and crown class influence the height–diameter relationship of lodgepole pine: nonlinear mixed effects modeling. Forest Ecology and Management 256, 570–577.
| Wind speed and crown class influence the height–diameter relationship of lodgepole pine: nonlinear mixed effects modeling.Crossref | GoogleScholarGoogle Scholar |
Mensah S, Pienaara OL, Kunnekea A, du Toita B, Seydackd A, Uhle E, Pretzsche H, Seiferta T (2018) Height–diameter allometry in South Africa’s indigenous high forests: assessing generic models performance and function forms. Forest Ecology and Management 410, 1–11.
| Height–diameter allometry in South Africa’s indigenous high forests: assessing generic models performance and function forms.Crossref | GoogleScholarGoogle Scholar |
Meyer HA (1940) A mathematical expression for height curves. Journal of Forestry 38, 415–420.
| A mathematical expression for height curves.Crossref | GoogleScholarGoogle Scholar |
Morgan J, Cannell MGR (1994) Shape of tree stems: a re-examination of the uniform stress hypothesis. Tree Physiology 14, 49–62.
| Shape of tree stems: a re-examination of the uniform stress hypothesis.Crossref | GoogleScholarGoogle Scholar | 14967633PubMed |
Niklas KJ (1995) Size-dependent allometry of tree height, diameter and trunk-taper. Annals of Botany 75, 217–227.
| Size-dependent allometry of tree height, diameter and trunk-taper.Crossref | GoogleScholarGoogle Scholar |
Niklas KJ (2007) Maximum plant height and the biophysical factors that limit it. Tree Physiology 27, 433–440.
| Maximum plant height and the biophysical factors that limit it.Crossref | GoogleScholarGoogle Scholar | 17241985PubMed |
Niklas KJ, Spatz H-C, Vincent J (2006) Plant biomechanics: an overview and prospectus. American Journal of Botany 93, 1369–1378.
| Plant biomechanics: an overview and prospectus.Crossref | GoogleScholarGoogle Scholar | 21642084PubMed |
O’Brien ST, Hubbell SP, Spiro P, Condit R, Foster RB (1995) Diameter, height, crown, and age relationship in eight neotropical tree species. Ecology 76, 1926–1939.
| Diameter, height, crown, and age relationship in eight neotropical tree species.Crossref | GoogleScholarGoogle Scholar |
Osunkoya OO, Omar-Ali K, Amit N, Dayan J, Daud DS, Sheng TK (2007) Comparative height-crown allometry and mechanical design in 22 tree species of Kuala Belalong rainforest, Brunei, Borneo. American Journal of Botany 94, 1951–1962.
| Comparative height-crown allometry and mechanical design in 22 tree species of Kuala Belalong rainforest, Brunei, Borneo.Crossref | GoogleScholarGoogle Scholar | 21636390PubMed |
Pacala SW, Canham CD, Silander JA (1993) Forest models defined by field measurements: I. The design of a northeastern forest simulator. Canadian Journal of Forest Research 23, 1980–1988.
| Forest models defined by field measurements: I. The design of a northeastern forest simulator.Crossref | GoogleScholarGoogle Scholar |
Poorter L, Bongers F, Sterck FJ, Wöll H (2003) Architecture of 53 rain forest tree species differing in adult stature and shade tolerance. Ecology 84, 602–608.
| Architecture of 53 rain forest tree species differing in adult stature and shade tolerance.Crossref | GoogleScholarGoogle Scholar |
Poorter L, Bongers F, Sterck FJ, Wöll H (2005) Beyond the regeneration phase: differentiation of height-light trajectories among tropical tree species. Journal of Ecology 93, 256–267.
| Beyond the regeneration phase: differentiation of height-light trajectories among tropical tree species.Crossref | GoogleScholarGoogle Scholar |
Poorter L, Bongers L, Bongers F (2006) Architecture of 54 moist-forest tree species: traits, trade-offs, and functional groups. Ecology 87, 1289–1301.
| Architecture of 54 moist-forest tree species: traits, trade-offs, and functional groups.Crossref | GoogleScholarGoogle Scholar | 16761607PubMed |
Prioul JL, Chartier P (1977) Partitioning of transfer and carboxylation components of intracellular resistance to photosynthetic CO2 fixation: a critical analysis of the methods used. Annals of Botany 41, 789–800.
| Partitioning of transfer and carboxylation components of intracellular resistance to photosynthetic CO2 fixation: a critical analysis of the methods used.Crossref | GoogleScholarGoogle Scholar |
Qiu H, Liu S, Zhang Y, Li J (2021) Variation in height–diameter allometry of ponderosa pine along competition, climate, and species diversity gradients in the western United States. Forest Ecology and Management 497, 119477
| Variation in height–diameter allometry of ponderosa pine along competition, climate, and species diversity gradients in the western United States.Crossref | GoogleScholarGoogle Scholar |
Queensland Herbarium (2019) Regional ecosystem description database (REDD). Version 11.1. April 2019 (DES: Brisbane, Qld, Australia). Available at https://www.qld.gov.au/environment/plants-animals/plants/ecosystems/descriptions
R Core Team (2021) ‘R: a language and environment for statistical computing’, (R Foundation for Statistical Computing: Vienna, Austria) Available at https://www.R-project.org/. [Verified 1 October 2021]
Richards FJ (1959) A flexible growth function for empirical use. Journal of Experimental Botany 10, 290–301.
| A flexible growth function for empirical use.Crossref | GoogleScholarGoogle Scholar |
Sterck FJ, Bongers F, Newbery DM (2001) Tree architecture in a Bornean lowland rain forest: intraspecific and interspecific patterns. Plant Ecology 153, 279–292.
| Tree architecture in a Bornean lowland rain forest: intraspecific and interspecific patterns.Crossref | GoogleScholarGoogle Scholar |
Thomas SC (1996) Asymptotic height as a predictor of growth and allometric characteristics in Malaysian rain forest trees. American Journal of Botany 83, 556–566.
| Asymptotic height as a predictor of growth and allometric characteristics in Malaysian rain forest trees.Crossref | GoogleScholarGoogle Scholar |
Thomas SC (2003) Comparative biology of tropical trees: a perspective from Pasoh. In ‘Pasoh: ecology of a lowland rain forest in Southeast Asia’. (Eds T Okuda, N Manokaran, Y Matsumoto, K Niiyama) pp. 171–194. (Springer: Tokyo, Japan)
Thomas SC, Bazzaz FA (1999) Asymptotic height as a predictor of photosynthetic characteristics in Malaysian rain forest trees. Ecology 80, 1607–1622.
| Asymptotic height as a predictor of photosynthetic characteristics in Malaysian rain forest trees.Crossref | GoogleScholarGoogle Scholar |
Thomas SC, Martin AR, Mycroft EE (2015) Tropical trees in a wind-exposed island ecosystem: height–diameter allometry and size at onset of maturity. Journal of Ecology 103, 594–605.
| Tropical trees in a wind-exposed island ecosystem: height–diameter allometry and size at onset of maturity.Crossref | GoogleScholarGoogle Scholar |
Tjørve E, Tjørve KMC (2010) A unified approach to the Richards-model family for use in growth analyses: why we need only two model forms. Journal of Theoretical Biology 267, 417–425.
| A unified approach to the Richards-model family for use in growth analyses: why we need only two model forms.Crossref | GoogleScholarGoogle Scholar | 20831877PubMed |
Vanclay JK (1992) Assessing site productivity in tropical moist forests: a review. Forest Ecology and Management 54, 257–287.
| Assessing site productivity in tropical moist forests: a review.Crossref | GoogleScholarGoogle Scholar |
Vanclay JK (2009) Tree diameter, height and stocking in even-aged forests. Annals of Forest Science 66, 702
| Tree diameter, height and stocking in even-aged forests.Crossref | GoogleScholarGoogle Scholar |
Vanclay JK, Henry NB (1988) Assessing site productivity of indigenous cypress pine forest in southern Queensland. Commonwealth Forestry Review 67, 53–64.
Vanclay JK, Skovsgaard JP (1997) Evaluating forest growth models. Ecological Modelling 98, 1–12.
| Evaluating forest growth models.Crossref | GoogleScholarGoogle Scholar |
van Gelder HA, Poorter L, Sterck FJ (2006) Wood mechanics, allometry, and life-history variation in a tropical rain forest tree community. New Phytologist 171, 367–378.
| Wood mechanics, allometry, and life-history variation in a tropical rain forest tree community.Crossref | GoogleScholarGoogle Scholar |
Vrána J, Remeš V, Matysioková B, Tjørve KMC, Tjørve E (2019) Choosing the right sigmoid growth function using the unified-models approach. Ibis 161, 13–26.
| Choosing the right sigmoid growth function using the unified-models approach.Crossref | GoogleScholarGoogle Scholar |
Walton DR, Armstrong JP (1986) Taxonomic and gross anatomical influences on specific gravity-mechanical property relationships. Wood and Fiber Science 18, 413–420.
Wang Y, Titus SJ, LeMay VM (1998) Relationships between tree slenderness coefficients and tree or stand characteristics for major species in boreal mixedwood forests. Canadian Journal of Forest Research 28, 1171–1183.
| Relationships between tree slenderness coefficients and tree or stand characteristics for major species in boreal mixedwood forests.Crossref | GoogleScholarGoogle Scholar |
Wickham H (2020) modelr: Modelling functions that work with the Pipe. R package version 0.1.8. Available at https://CRAN.R-project.org/package=modelr. [Verified 1 October 2021]
Williams RJ, Zerihun A, Montagu KD, Hoffman M, Hutley LB, Chen X (2005) Allometry for estimating aboveground tree biomass in tropical and subtropical eucalypt woodlands: towards general predictive equations. Australian Journal of Botany 53, 607–619.
| Allometry for estimating aboveground tree biomass in tropical and subtropical eucalypt woodlands: towards general predictive equations.Crossref | GoogleScholarGoogle Scholar |
Winsor CP (1932) The Gompertz curve as a growth curve. Proceedings of the National Academy of Sciences of the United States of America 18, 1–8.
| The Gompertz curve as a growth curve.Crossref | GoogleScholarGoogle Scholar | 16577417PubMed |
Wright IJ, Ackerly DD, Bongers F, Harms KE, Ibarra-Manriquez G, Martinez-Ramos M, Mazer SJ, Muller-Landau HC, Paz H, Pitman NC, Poorter L, Silman MR, Vriesendorp CF, Webb CO, Westoby M, Wright SJ (2007) Relationships among ecologically important dimensions of plant trait variation in seven Neotropical forests. Annals of Botany 99, 1003–1015.
| Relationships among ecologically important dimensions of plant trait variation in seven Neotropical forests.Crossref | GoogleScholarGoogle Scholar | 16595553PubMed |
Xu Y, Iida Y, Huang H, Shi Z, Franklin SB, Luo Y, Bao D, Qiao X, Lu Z, Jiang M (2019) Linkages between tree architectural designs and life-history strategies in a subtropical montane moist forest. Forest Ecology and Management 438, 1–9.
| Linkages between tree architectural designs and life-history strategies in a subtropical montane moist forest.Crossref | GoogleScholarGoogle Scholar |
Yang RC, Kozak A, Smith JHG (1978) The potential of Weibull-type functions as flexible growth curves. Canadian Journal of Forest Research 8, 424–431.
| The potential of Weibull-type functions as flexible growth curves.Crossref | GoogleScholarGoogle Scholar |
Zea-Camaño JD, Soto JR, Arce JE, Pelissari AL, Behling A, Orso GA, Guachambala MS, Eisfeld RDL (2020) Improving the modeling of the height–diameter relationship of tree species with high growth variability: robust regression analysis of Ochroma pyramidale (balsa-tree). Forests 11, 313
| Improving the modeling of the height–diameter relationship of tree species with high growth variability: robust regression analysis of Ochroma pyramidale (balsa-tree).Crossref | GoogleScholarGoogle Scholar |
Zeide B (1993) Analysis of growth equations. Forest Science 39, 594–616.
| Analysis of growth equations.Crossref | GoogleScholarGoogle Scholar |
Zhang L (1997) Cross-validation of non-linear growth functions for modelling tree height–diameter relationships. Annals of Botany 79, 251–257.
| Cross-validation of non-linear growth functions for modelling tree height–diameter relationships.Crossref | GoogleScholarGoogle Scholar |
Zhao M, Tian S, Zhu Y, Li Z, Zeng S, Liu S (2021) Allometric relationships, functional differentiations, and scaling of growth rates across 151 tree species in China. Ecosphere 12, e03522
| Allometric relationships, functional differentiations, and scaling of growth rates across 151 tree species in China.Crossref | GoogleScholarGoogle Scholar |
Appendix 1. Symbols and abbreviations
Symbol Definition a Proportionality factor (initial slope) of allometric function (m cm−1) b Convexity factor of allometric function D Diameter of individual tree at breast height (DBH, 1.3 m from ground) (cm) DmaxL Maximum value of D for a species at the study site (cm) DmaxP Maximum value of D for a species from published records (cm) GMM Generalised Michaelis–Menten equation H Height of individual tree (measured or calculated) (m) Ha Asymptotic value of tree height calculated by equation (m) Ha-fitted Allometric equation parameters all derived by fitted regression Ha-forced Allometric equation parameters derived by fitted regression after setting Ha as HmaxL HD150 Calculated value of H for D = 150 cm (m) HmaxC Calculated maximum tree height for species or larger datasets (Ha + 1.3 m) (m) HmaxL Maximum measured tree height for a species from study site (m) HmaxP Maximum value of H for a species from published records (m) k Proportionality factor of Michaelis–Menten equation (D at half-Ha, cm) NRHs Non-rectangular hyperbola equation


