The economic optimum mob size at lambing for triplet-bearing Maternal and Merino ewes across southern Australia
John M. Young A * , Paul R. Kenyon B , Lyndon J. Kubeil C , Andrew N. Thompson
A * , Paul R. Kenyon B , Lyndon J. Kubeil C , Andrew N. Thompson  D , Jason Trompf E and Amy Lockwood
D , Jason Trompf E and Amy Lockwood  D F
D F
A
B
C
D
E
F Present address:
Abstract
Lambing triplet-bearing ewes in smaller mobs significantly increases lamb survival.
This paper reports economic analysis to assess the optimum mob size for triplet-bearing ewes during lambing.
The analyses considered scenarios for Merino and non-Merino (Maternal) flocks where producers subdivided lambing paddocks using permanent fencing or where ewes were re-allocated within existing paddocks on the basis of pregnancy status.
The optimum mob sizes for triplet-bearing ewes during lambing were affected by ewe breed, stocking rate, lamb price and the target return-on-investment if subdividing paddocks. The optimum mob size for triplet-bearing Maternal and Merino ewes was between 27% and 40% of the optimum for twin-bearing ewes and this was similar for scenarios where paddocks were subdivided, or where ewes were re-allocated within existing paddocks. At the standard lamb price of AUD$7/kg carcass weight, the economic return from adjusting the relative mob size of triplet-bearing ewes was AUD$2.05 per multiple-bearing or AUD$14.20 per triplet-bearing Maternal ewe and AUD$0.54 per multiple-bearing ewe or AUD$5.70 per triplet-bearing Merino ewe.
Overall, these analyses demonstrated that reducing mob size at lambing can be a profitable strategy for improving survival of triplet-born lambs, depending on the current size of lambing mobs.
As reported previously for single- and twin-bearing ewes, it is difficult to provide generic recommendations to producers for the optimum mob size of triplet-bearing ewes at lambing because optimum mob size was dependent on several enterprise-specific factors.
Keywords: lamb survival, lambing paddock, marking rate, multiple-bearing, non-Merino, permanent fencing, reallocation, subdivision.
Introduction
Lamb-marking rates increased from about 81% to 92%, or by about 1% per annum, between 2006 and 2016 in Australia (Kubeil 2017). This resulted from widespread adoption of practices to improve ewe nutrition before joining and during pregnancy (Trompf et al. 2011; Thompson et al. 2020), improved management during lambing (Lockwood et al. 2020a, 2020b) and increased use of sires with higher breeding values for the number of lambs conceived and weaned. In addition, there has been significant displacement of Merino sheep by more fecund maternal ewe types (Trompf et al. 2018). These increases in fecundity are associated with an increase in the proportion of multiple-bearing ewes, including those carrying triplets (Amer et al. 1999), which can result in higher rates of mortality of both ewes and lambs (Kenyon et al. 2019). High mortality of triplet-bearing ewes and their lambs limits productivity and represents an animal-welfare concern.
Industry consultation in Australia showed that the potential impact of the mob size of ewes during lambing on the survival of triplet-born lambs was an important research priority (Thompson et al. 2023). Past survey data collected from sheep producers in south-eastern Australia found that the survival of single- and twin-born lambs in relation to mob size was linear and increased by 1.4% and 3.5% when mob size at lambing was reduced by 100 ewes (Lockwood et al. 2020b). This was verified by experimental data collected from 70 on-farm research sites across Australia which found that reducing mob size at lambing by 100 twin-bearing ewes increased the survival of their lambs by 1.9%, regardless of ewe breed and stocking rate at lambing (Lockwood et al. 2020a). Similarly, data collected from 15 on-farm research sites found that reducing mob size at lambing by 100 twin-bearing Merino ewes increased the survival of their lambs by 2.5% when ewes lambed at stocking rates of less than four ewes per hectare (Lockwood et al. 2020a). The effect of mob size on the survival of Merino and non-Merino (Maternal) triplet-bearing ewes was recently examined, where it was found that reducing mob size by 10 triplet-bearing ewes increased the survival of their lambs by 1.5% (Lockwood et al. 2023). When expressed per 100 ewes, this effect is over seven times the effect for twins and over 10 times the effect for singles. Higher mob sizes at lambing are understood to increase the risk of mismothering and ewe–lamb separations, owing to a greater number of lambs being born in the mob per day (Winfield 1970; Cloete 1992). Triplet-born lambs are poorer at identifying their dam than are twin-born lambs (Pollard 1992). Triplet-bearing ewes also display limited bleating when separated from one of their lambs, and are less likely to approach and reunite with the lamb (Pollard 1992). Similarly, Cloete (1992) found that the risk of ewe–lamb separation was greater for triplets and twins than for singles, and increased with a greater density of lambed ewes. Therefore, it is not surprising that the effect of mob size at lambing on lamb survival is greatest for triplets.
Economic analysis has been conducted to assess the optimum mob size at lambing for single- and twin-bearing ewes (Lockwood et al. 2020c). This analysis demonstrated that no generic recommendations could be made because optimum mob size was dependent on several enterprise-specific factors, including breed, ewe pregnancy status, existing paddock shape, the target return on investment if subdividing paddocks and whether paddocks are subdivided with permanent or temporary fencing. However, the optimum mob size for twin-bearing ewes was smaller than for single-bearing ewes by approximately 55% for Merino ewes and 62% for Maternal ewes (Lockwood et al. 2020c). Therefore, it was concluded that smaller mobs at lambing should be prioritised for twin-bearing ewes over single-bearing ewes. This paper reports economic analysis to assess the optimum mob size for triplet-bearing ewes, which has not previously been undertaken.
Methods
The analyses in this paper evaluated (i) the optimum mob size at lambing for triplet-bearing ewes if producers subdivide the lambing paddocks, and compared this to the optimum mob size for twin-bearing ewes, and (ii) the relative mob size at lambing for twin- and triplet-bearing ewes if paddocks are not subdivided and the ewes are just reallocated in the existing paddocks. The analyses were based on the average change in lamb survival from studies using singles, twins and triplets, which found the relationship between mob size and lamb survival to be linear between the range in those mob sizes examined (Hancock et al. 2019; Lockwood et al. 2020a, 2020b, 2023). The averages presented in Table 1 were used in the calculation of profitability. There was no evidence from these studies that the response to mob size at lambing differed between Merino and Maternal ewes.
| Source | Data | Singles | Twins | Triplets | Breed/s evaluated | |
|---|---|---|---|---|---|---|
| Lockwood et al. (2020b) | Survey data from producers in south-eastern Australia | +1.4% | +3.5% | – | Merino and Maternal | |
| Hancock et al. (2019) | Survey data from producers across southern Australia | +0.3% | +1.1% | – | Merino and Maternal | |
| Lockwood et al. (2020a) | On-farm research sites across southern Australia (Experiment 1) | – | +1.9 | – | Merino and Maternal | |
| Lockwood et al. (2020a) | On-farm research sites across southern Australia (Experiment 2) | – | +2.5 | – | Merino | |
| Lockwood et al. (2023) | On-farm research sites across southern Australia | – | – | +15.1% | Merino and Maternal | |
| Average | +0.85% | +2.25% | +15.1% |
Calculation of profitability
The calculations followed a similar process as outlined in Lockwood et al. (2020c), except that the effect of paddock size on pasture utilisation was not included. Pasture utilisation was deemed less important for this analysis, which was focussing on comparing optimum mob size at lambing for twin- versus triplet-bearing ewes.
The value of an extra triplet-born lamb surviving was calculated using the Australian Farm Optimisation model (AFO). The AFO model employed in this analysis was a refined version of Model of an Integrated Dryland Agricultural System (MIDAS), a linear programming model with a dual focus on the economics and biology of farming systems (e.g. Pannell 1995). For a comprehensive overview of the AFO refer to Young et al. (2024) or visit https://australian-farm-optimising-model.readthedocs.io/en/latest/index.html. The value of an extra lamb was net of the costs associated with feeding the extra lactating ewes, feeding the lamb through to the time of sale and the cost of husbandry of the extra lambs. It accounted for the change in birth-type–rear-type of the triplet-born lambs, which affects weaning weight and lifetime wool production of the lamb born and raised in larger litters. It also accounted for the lower weight at weaning of the ewes that are lactating with triplets and the lower wool production of lactating ewes. The genotypes evaluated were a medium-wool Merino with a standard reference weight of 60 kg and a maternal composite genotype with a standard reference weight of 70 kg. Sale age and weight was selected to maximise profit and varied by genotype and birth-type–rear-type. Three meat price scenarios were evaluated; lamb at AUD$6/kg, AUD$7/kg and AUD$8/kg dressed weight (Table 2). Previous analysis by Young et al. (2014) showed that wool price did not alter the value of an extra lamb, so wool price was not included in the analysis.
The cost of subdividing paddocks could vary greatly depending on the individual farm layout, including the shape of paddocks and location of water points. The cost would also depend on whether permanent or temporary fencing was used and whether watering points were required in the new paddocks. This analysis has considered only permanent fencing. Previous analysis has shown that the economic optimum mob size was much smaller if temporary fencing was used (Lockwood et al. 2020c).
In this analysis, it was assumed that existing paddocks were square, as square paddocks are the most expensive to subdivide because they require the longest dividing fences for any given area. A long and narrow paddock is cheaper to subdivide, depending on the location and requirement for water. By using square paddocks with the existing water point in the corner, the values calculated for profitability of subdividing will be a conservative estimate of the value that farmers would achieve.
The analysis quantified the costs of subdividing paddocks associated with the cost of materials and labour for fencing and provision of water, including pipe to move the water and a trough, and maintenance of the water trough (Table 3). The life spans of the fence and watering points were assumed to be 15 years. The size of the paddock was calculated from the size of the mob, the stocking rate of the ewes at lambing and the dry sheep equivalent (DSE) rating of the ewes, being 1.8 DSE/head for twin-bearing ewes and 2.1 DSE/head for triplet-bearing ewes. A lower stocking rate meant a larger paddock and therefore a higher cost of subdivision. It was assumed that the water point was in the corner of the paddock and that pipe was required to get half-way across the paddock to the newly installed fence that was down the middle of the paddock.
An investment analysis calculated the benefits and costs of halving paddock size. Subdividing existing paddocks is the relevant decision for producers because this will generate a greater return on investment than does removing all existing fences and refencing the whole farm. As an individual paddock analysis, it was independent of region and initial flock size but was affected by stocking rate and mob size.
The net present value of the annual income associated with increased lamb survival, the annual maintenance costs and the capital costs associated with paddock subdivision was calculated with the discount rate at the target return-on-investment. Different scenarios were evaluated with varying stocking rates and varying initial paddock size for a given flock size. The analysis calculates the mob size for which subdividing the paddock in half has equal net present value to not subdividing (on the basis of the economic theory that profit is maximised when marginal cost = marginal revenue). As such, the optimum mob size and paddock size were a range and if the current paddock size was within or below the range then it was not profitable to subdivide the paddock. If the paddock size was larger than the upper end of the range, then subdividing the paddock would increase profit and achieve the target return on investment or greater. To simplify the presentation of the results, the optimum mob size has been graphed as the lower value of the optimum range. Thus, subdivision was not profitable if it generated a mob size smaller than the analysis result. Where a return on investment is presented, it was the return achieved if a paddock was subdivided to the specified size.
This analysis was conducted as a single-year analysis of just the value of the extra lambs surviving because there are no capital costs and no maintenance costs because there is no subdivision of paddocks. The change in survival of twin- and triplet-born lambs was calculated on the basis of reducing mob size for triplet-bearing ewes and increasing mob size for twin-bearing ewes. Previous analysis of singles and twins (Lockwood et al. 2020c) showed that the proportion of singles versus twins in the flock altered the value of reallocating ewes to paddocks on the basis of litter size but had little effect on the most profitable relative mob sizes, so a sensitivity on the proportion of twins and triplets was not examined in this analysis. The analysis was conducted for a mob of Maternal ewes scanning 170% and Merino ewes scanning 150%, with an initial mob size at lambing for an unscanned flock of 100 ewes. The change in the value of the lambs surviving was calculated when the relative mob size of triplet-bearing ewes versus twin-bearing ewes was adjusted in the range from both equal through to the triplet-bearing ewes being 15% of the twin-bearing ewes. The mob size when both were equal was 70 Merino ewes per mob and 80 Maternal ewes per mob. The higher initial mob size for the Maternal flock reflects the greater number of multiple-bearing ewes owing to the higher scanning percentage.
Results
Optimum mob size when subdividing paddocks
Several factors affected the optimum mob size and paddock size. The optimum varied with the target return-on-investment, ewe stocking rate, breed and lamb price. The optimum mob size for triplet-bearing ewes varied between 18 and 23 for Maternal ewes and between 27 and 34 for Merino ewes for the scenarios tested (Table 4). These mob sizes, which reflect the greater response in lamb survival for triplets than for twins were, on average, 29% of the optimum mob size for twin-bearing Maternal ewes and approximately 37% of the optimum mob size for twin-bearing Merino ewes. The optimum mob size was higher for flocks with a low stocking rate and for Merino ewes than for Maternal ewes. The optimum paddock size varied from 2 ha up to 34 ha.
| Item | Stocking rate (DSE/ha) | Maternal | Merino | |||||
|---|---|---|---|---|---|---|---|---|
| Single | Twin | Triplet | Single | Twin | Triplet | |||
| Optimum mob size (number of ewes) | 2.1 | 206 | 84 | 23 | 262 | 100 | 34 | |
| 4.2 | 188 | 75 | 21 | 238 | 88 | 32 | ||
| 8.4 | 173 | 67 | 20 | 216 | 79 | 29 | ||
| 14.7 | 163 | 62 | 19 | 202 | 74 | 28 | ||
| 21.0 | 158 | 60 | 18 | 194 | 71 | 27 | ||
| Optimum paddock size (ha) | 2.1 | 167 | 82 | 27 | 187 | 86 | 34 | |
| 4.2 | 76 | 36 | 12 | 85 | 38 | 16 | ||
| 8.4 | 35 | 16 | 6 | 39 | 17 | 7 | ||
| 14.7 | 19 | 9 | 3 | 21 | 9 | 4 | ||
| 21.0 | 13 | 6 | 2 | 14 | 6 | 3 | ||
The data represent a scenario when paddocks are subdivided with permanent fencing, the meat price was AUD$7/kg for lamb and the target return-on-investment was 5%. The values presented are the lower value of the optimum range of mob size and paddock size.
Factors influencing optimum mob size and paddock size
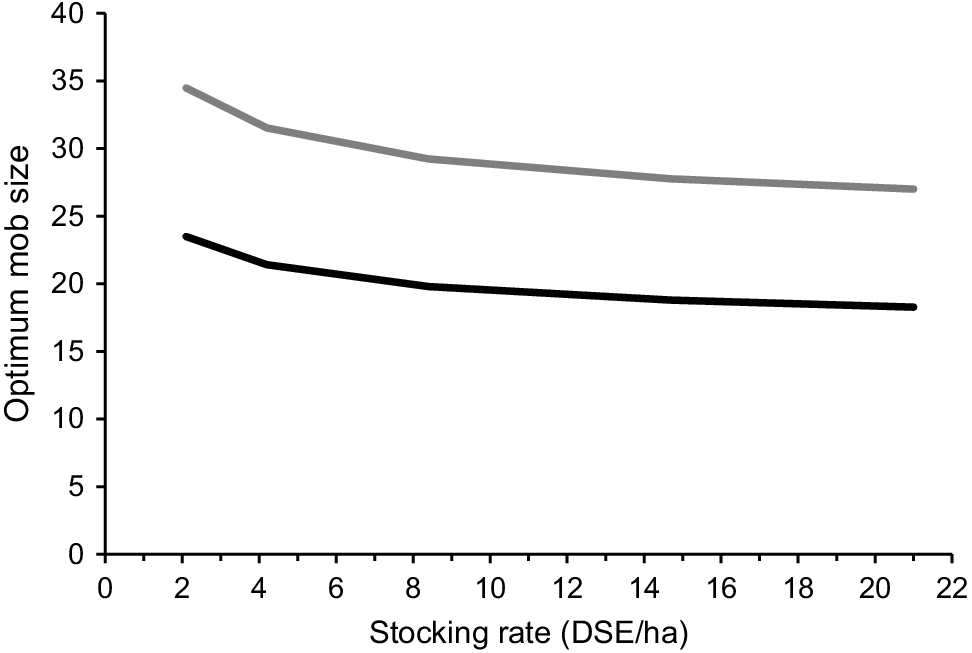
The optimum mob size was larger for flocks run at lower stocking rates; however, the impact was small (Fig. 1). There was a smaller than 12% change in the optimum mob size for triplet-bearing ewes from a 10-fold change in stocking rate and a similarly small change in the optimum relative to twin-bearing ewes.
The economic optimum mob size (n ewes) for triplet-bearing Maternal (black) and Merino (grey) ewes, with a varying stocking rate, a lamb price of AUD$7/kg carcass weight and target return-on-investment of 5%.
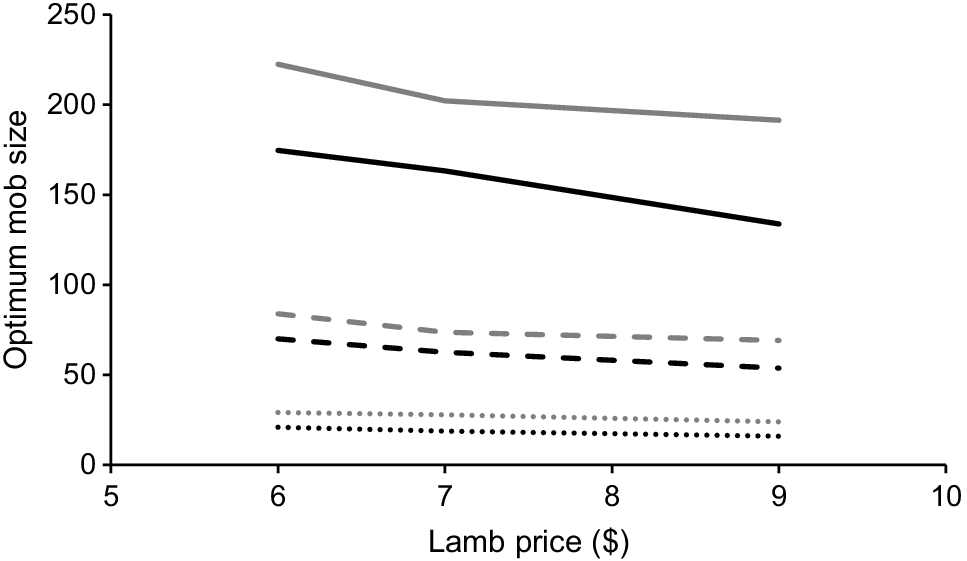
Higher meat prices reduce the optimum mob size through the extra value of the extra lambs surviving. However, the percentage reduction in the optimum mob size for single-, twin- and triplet-bearing ewes was similar when prices vary (Fig. 2).
Impact of varying lamb price on the optimum mob size (n ewes) at lambing for single-bearing (solid line), twin-bearing (dashed line) and triplet-bearing (dotted line) Maternal (black) and Merino (grey) ewes, when paddocks were subdivided using permanent fencing and stocking rate was 14.7 DSE/ha.
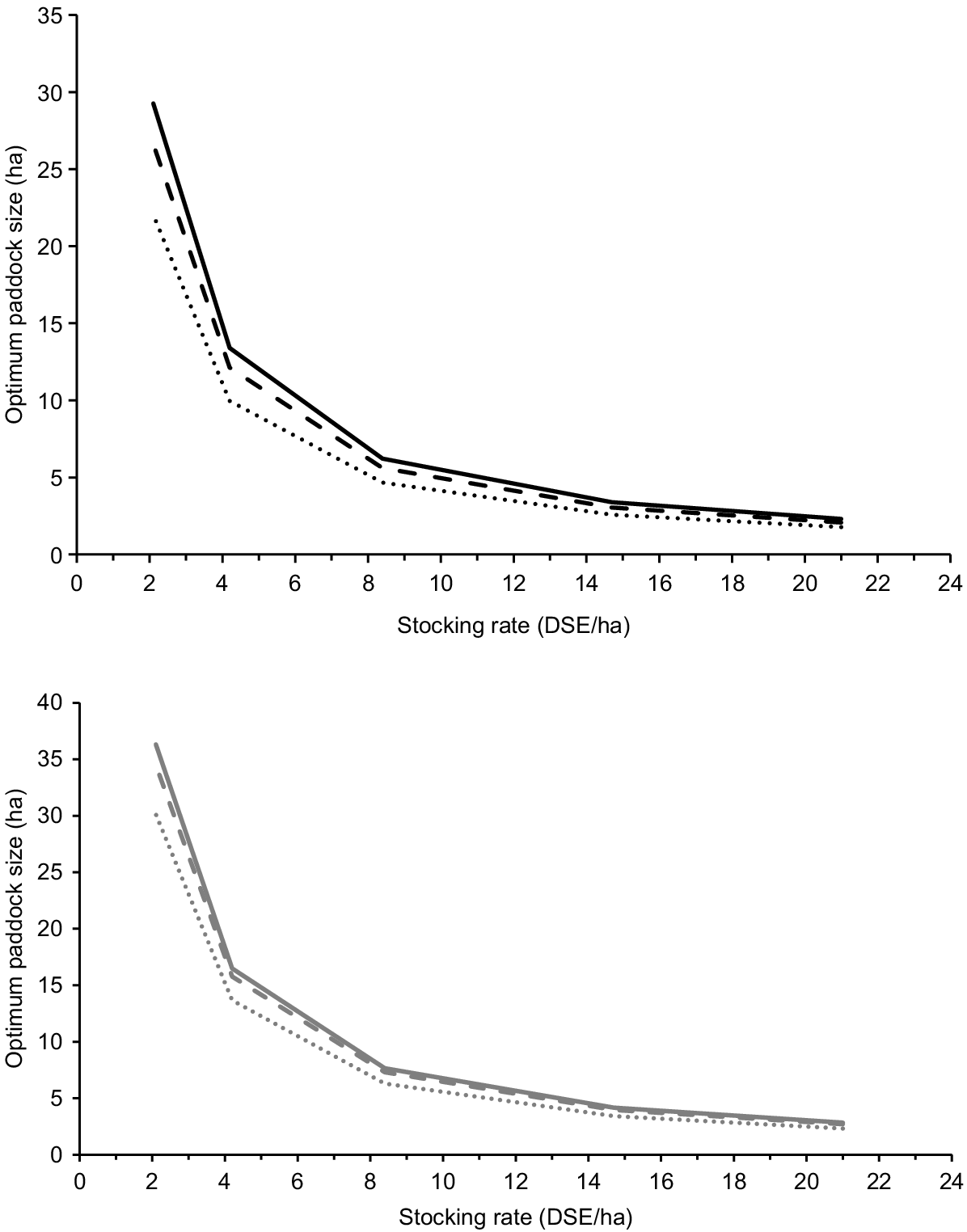
Optimum paddock size (ha) equals optimum mob size (DSE), divided by the stocking rate (DSE/ha), and therefore reduces more with an increasing stocking rate than does the optimum mob size (Fig. 3). As mentioned in the Methods section, the lower value of the optimum range in paddock size was reported in Fig. 3 and Table 4. When lamb price was AUD$7/kg, paddocks were subdivided using permanent fencing and the target return-on-investment was 5%, the optimum paddock size for triplet-bearing Maternal ewes was between 27 and 54 ha at 2.1 DSE/ha and reduced to between 2 and 4 ha at 21.0 DSE/ha.
Optimum paddock size (ha) at lambing for triplet-bearing Maternal (black, top graph) and Merino (grey, bottom graph) ewes for a range of stocking rates at lamb prices of AUD$6/kg (solid line), AUD$7/kg (dashed line) and AUD$8/kg carcass weight (dotted line) when paddocks were subdivided using permanent fencing and the target return-on-investment was 5%.
Relative mob size using existing paddocks
The optimum relative mob size for triplet- versus twin-bearing ewes if they are being allocated to existing paddocks was for the mob size of triplet-bearing ewes 30–40% of that for the twin-bearing ewes (Fig. 4). This compares with the relative mob size of twin-bearing ewes being 40–45% of that for single-bearing ewes, indicating that the optimum ratio of triplet- to single-bearing ewes was 12–18%.
Impact of varying relative mob size (triplet mob size/twin mob size) on the value of extra lambs surviving per multiple-bearing ewe for Maternal (black) and Merino (grey) flocks with lamb price of AUD$7/kg, and a scanning percentage of 170% for Maternal ewes and 150% for Merino ewes.
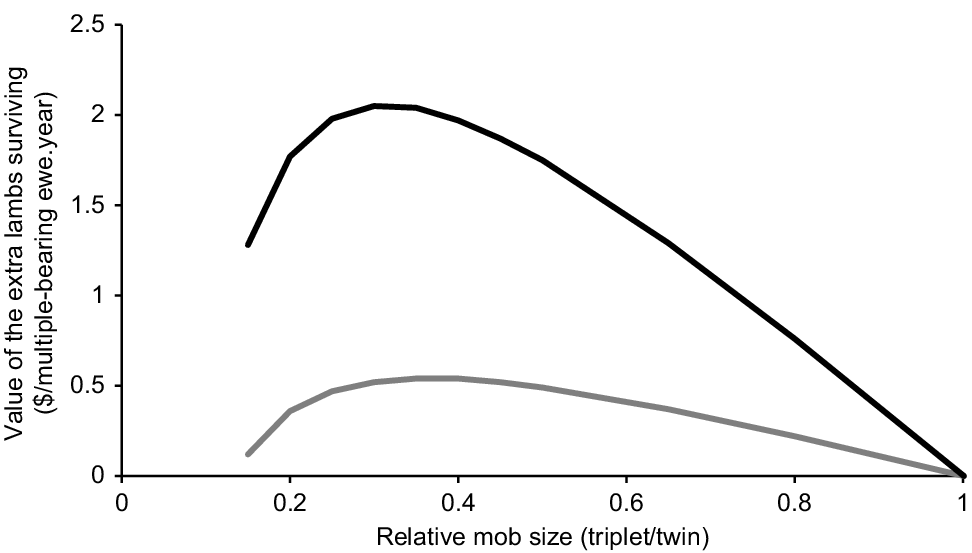
The benefit gained from differential allocation was AUD$2.05 per multiple-bearing Maternal ewe and AUD$0.54 per multiple-bearing Merino ewe (Fig. 4). This equates to AUD$14.20 per triplet-bearing Maternal ewe and AUD$5.70 per triplet-bearing Merino ewe at the assumed scanning percentage. These values were estimated for a Maternal flock that had an initial mob size for multiple-bearing ewes of 80 ewes and a Merino flock with 70 multiple-bearing ewes. The value for optimal allocation increased if the existing mob size was larger and vice versa. The final optimum mob sizes were 100 twin-bearing and 30 triplet-bearing ewes for the Maternal flock and 90 twin-bearing and 33 triplet-bearing ewes for the Merino flock.
Discussion
This analysis showed that the effects of mob size on the survival of triplet-born lambs justify reducing the mob size of triplet-bearing ewes compared with twin-bearing ewes either by subdivision of existing paddocks utilising permanent fencing or by allocating more of the existing paddocks to triplet-bearing ewes at the expense of the single- and twin-bearing ewes. The rule of thumb for the optimum mob size for triplet-bearing ewes was 30–40% the optimum mob size for twin-bearing ewes. Focusing on relative mob size for each litter size maximises profit rather than, for example, achieving the target for triplet-bearing ewes, while having twin-bearing ewes at double the target size. However, this rule of thumb does not account for costs incurred in other enterprises associated with smaller paddocks, for example, affecting seeding, spraying and harvesting in the crop enterprise. Therefore, on broadacre mixed livestock-cropping farms, practical issues may reduce or negate the financial benefits of permanent subdivision fencing. Previous research has shown that subdividing paddocks with temporary fencing is cost effective (Lockwood et al. 2020c) and this may be an option to achieve the benefits of subdivision without affecting other enterprises; however, there is a requirement for extra labour for erecting and dismantling the fences.
Survey data from producers in Australia highlighted variation in the perceived optimum mob size for triplet-bearing ewes. On average, the optimum mob size recommended by the producers was 52 triplet-bearing ewes. However, recommendations ranged from 10 to 150 triplet-bearing ewes. These same producers recommended optimum mob sizes for twin-bearing ewes ranging from 50 to 250 ewes, with an average of 134 ewes (Thompson et al. 2023). The on-farm research reported by Lockwood et al. (2023) that investigated the relationship between mob size at lambing and survival of triplet-born lambs involved mob sizes ranging from 10 to 139 ewes, which was very similar to the range recommended by producers in the survey study. The results from our economic analysis showed that the optimum mob sizes for triplet-bearing ewes is typically less than the optimum mob sizes recommended by producers, at less than 40 ewes within the price range examined. However, optimum mob sizes are greater if producers are targeting a higher return-on-investment and this may explain some of the difference.
The return-on-investment achieved from subdividing by an individual farmer is dependent on the factors included in this analysis, genotype, stocking rate, existing mob size and prices. However, there are also several landscape and logistical factors including the existing and resulting paddock shape, access to water, availability of shelter and access to laneways as discussed by Lockwood et al. (2020c) and interaction with other enterprises as previously discussed. These are complicated calculations to perform and, hence, a decision-support tool that captures these factors and enables producers to identify the most practical and profitable options for their enterprise could be useful.
Prioritising smaller mobs and paddocks to triplet-bearing ewes increased profit because the survival of their lambs was more sensitive to mob size at lambing than was that of twin- and single-born lambs. However, only 3% of flocks in Australia are scanned for triplet-bearing ewes (Trompf et al. 2018), with about a third of Australian sheep producers scanning for single- and multiple-bearing ewes (Kubeil 2017; Howard and Beattie 2018). The indication from this analysis was that identifying triplet-bearing ewes at pregnancy scanning, costing an extra AUD$0.40/ewe scanned, was justified purely from the benefits of differential paddock allocation at lambing to reduce mob size if the proportion of triplet-bearing ewes was greater than 3% for Maternal ewes or 7% for Merino ewes, on the basis of the identified benefit of AUD$14.20 per triplet-bearing Maternal ewe and AUD$5.90 per triplet-bearing Merino ewe. These proportions of triplet-bearing ewes would be expected from scanning percentages of greater than 125% and 160%. Our economic analysis determined that the ability to reduce mob size for triplet-bearing ewes represented, on average, 70% of the benefit of scanning ewes to identify triplets, with the remaining benefit from differential management of ewe nutrition to optimise ewe condition score during pregnancy (J.M. Young, unpubl. data).
Adjusting the relative mob size of triplet- and twin-bearing ewes within existing paddocks to improve lamb survival is an option only where ewes have been pregnancy scanned to identify the number of fetuses. Reallocating ewes within existing paddocks requires no capital investment and is therefore a strategy that can be implemented immediately. The total economic gains from reallocating ewes within existing paddocks are generally much lower when compared with those achieved from paddock subdivision. However, this can be a strategy to improve lamb survival where producers are not interested in paddock subdivision.
Conclusions
This analysis has demonstrated that producers could prioritise smaller mob sizes at lambing for triplet-bearing ewes over twin-bearing ewes to improve lamb survival and overall farm profitability. The economic optimum mob size for triplet-bearing ewes was approximately 35% that for twin-bearing ewes, regardless of whether that is achieved by subdividing paddocks or differential allocation of ewes to existing paddocks. The analysis has indicated that identifying triplet-bearing ewes was justified purely from the benefits of differential paddock allocation at lambing to reduce mob size if the proportion of triplet-bearing ewes was greater than 3% for Maternal ewes or 7% for Merino ewes. Therefore, producers who are pregnancy scanning their ewes for triplets can optimise lamb survival and profitability by identifying and implementing the optimum mob size for their enterprise.
Data availability
The data that support this study will be shared upon reasonable request to the corresponding author.
Declaration of funding
This research was funded by Meat & Livestock Australia (Grant number: L.LSM.0013).
References
Amer PR, McEwan JC, Dodds KG, Davis GH (1999) Economic values for ewe prolificacy and lamb survival in New Zealand sheep. Livestock Production Science 58, 75-90.
| Crossref | Google Scholar |
Cloete SWP (1992) Observations on litter size, parturition and maternal behaviour in relation to lamb mortality in fecund Dormer and South African Mutton Merino ewes. South African Journal of Animal Science 22, 214-222.
| Google Scholar |
Hancock S, Lockwood A, Trompf J, Kubeil L (2019) Improving lamb survival by optimising lambing density and mob size. Australian Wool Innovation, Sydney, NSW, Australia. Available at https://www.wool.com/globalassets/wool/sheep/reproduction/lambing/lambing-density-and-mob-size-final-report.pdf
Kenyon PR, Roca Fraga FJ, Blumer S, Thompson AN (2019) Triplet lambs and their dams – a review of current knowledge and management systems. New Zealand Journal of Agricultural Research 62, 399-437.
| Crossref | Google Scholar |
Kubeil L (2017) Informing future sheep extension strategies to improve reproduction and related welfare outcomes. Meat & Livestock Australia, Sydney, NSW, Australia. Available at https://www.mla.com.au/contentassets/218ddb9d5f85496a87b491655ae44e08/e.rep.1404_final_report.pdf
Lockwood A, Trompf J, Kubeil L, Thompson A, Refshauge G, Kearney G, Hancock S (2020a) Decreasing the mob size but not stocking rate of ewes at lambing increases the survival of twin lambs born on farms across southern Australia. Animal Production Science 60, 1949-1958.
| Crossref | Google Scholar |
Lockwood AL, Hancock SN, Trompf JP, Kubeil LJ, Ferguson MB, Kearney GA, Thompson AN (2020b) Data from commercial sheep producers shows that lambing ewes in larger mobs and at higher stocking rates reduces the survival of their lambs. New Zealand Journal of Agricultural Research 63, 246-259.
| Crossref | Google Scholar |
Lockwood A, Trompf J, Hancock S, Kubeil L, Thompson A, Young J (2020c) Factors influencing the optimum mob size of ewes at lambing and the economic benefit of lambing ewes in smaller mobs to increase lamb survival across southern Australia. Agricultural Systems 184, 102916.
| Crossref | Google Scholar |
Lockwood A, Allington T, Blumer SE, Boshoff J, Clarke BE, Hancock SN, Kearney GA, Kenyon PR, Krog J, Kubeil LJ, Refshauge G, Trompf JP, Thompson AN (2023) Decreasing mob size at lambing increases the survival of triplet lambs born on farms across southern Australia. Animals 13, 1936.
| Crossref | Google Scholar |
Pannell DJ (1995) Economic aspects of legume management and legume research in dryland farming systems of southern Australia. Agricultural Systems 49, 217-236.
| Crossref | Google Scholar |
Pollard JC (1992) Effects of litter size on the vocal behaviour of ewes. Applied Animal Behaviour Science 34, 75-84.
| Crossref | Google Scholar |
Thompson AN, Gordon DJ, Hamill B, King E, Scott M, Trompf J (2020) Impacts of the lifetime ewe management program on the Australian sheep industry. Animal Production Science 61, i-cxcvii.
| Google Scholar |
Thompson AN, Allington T, Blumer S, Cameron J, Kearney G, Kubeil L, Lockwood A, Trompf J, Winslow E, Kenyon P (2023) Reproductive performance of triplet-bearing ewes on commercial farms and research priorities identified by sheep producers to improve the survival of triplet-bearing ewes and their lambs. Animals 13, 1258.
| Crossref | Google Scholar |
Trompf JP, Gordon DJ, Behrendt R, Curnow M, Kildey LC, Thompson AN (2011) Participation in Lifetime Ewe Management results in changes in stocking rate, ewe management and reproductive performance on commercial farms. Animal Production Science 51, 866-872.
| Crossref | Google Scholar |
Winfield CG (1970) The effect of stocking intensity at lambing on lamb survival and ewe and lamb behaviour. Proceedings of the Australian Society of Animal Production 8, 291-296.
| Google Scholar |
Young JM, Trompf J, Thompson AN (2014) The critical control points for increasing reproductive performance can be used to inform research priorities. Animal Production Science 54, 645-655.
| Crossref | Google Scholar |
Young M, Young J, Kingwell RS, Vercoe PE (2024) Identifying high-value tactical livestock decisions on a mixed enterprise farm in a variable environment. Animal Production Science 64, AN23407.
| Crossref | Google Scholar |


