Global beef cattle methane emissions: yield prediction by cluster and meta-analyses
D. J. Cottle A B and R. J. Eckard AA Faculty of Veterinary and Agricultural Science, The University of Melbourne, Vic. 3010, Australia.
B Corresponding author. Email: david.cottle@unimelb.edu.au
Animal Production Science 58(12) 2167-2177 https://doi.org/10.1071/AN17832
Submitted: 23 November 2017 Accepted: 9 March 2018 Published: 25 May 2018
Journal Compilation © CSIRO 2018 Open Access CC BY-NC-ND
Abstract
Methane yield values (MY; g methane/kg dry-matter intake) in beef cattle reported in the global literature (expanded MitiGate database of methane-mitigation studies) were analysed by cluster and meta-analyses. The Ward and k means cluster analyses included accounting for the categorical effects of methane measurement method, cattle breed type, country or region of study, age and sex of cattle, and proportion of grain in the diet and the standardised continuous variables of number of animals, liveweight and MY. After removal of data from outlier studies, meta-analyses were conducted on subsets of data to produce prediction equations for MY. Removing outliers with absolute studentised residual values of >1, followed by meta-analysis of data accounting for categorical effects, is recommended as a method for predicting MY. The large differences among some countries in MY values were significant but difficult to interpret. On the basis of the datasets available, a single, global MY or percentage of gross energy in feed converted to methane (Ym) value is not appropriate for use in Intergovernmental Panel on Climate Change (IPCC) greenhouse accounting methods around the world. Therefore, ideally country-specific MY values should be used in each country’s accounts (i.e. an IPCC Tier 2 or 3 approach) from data generated within that country.
Additional keywords: greenhouse accounting, methane yield, outliers.
Introduction
Robust estimates of daily methane production (MP, g) and methane yield (MY, MP/kg daily dry-matter intake (DMI)) are needed for the calculation of methane emissions for national greenhouse gas (GHG) inventory reporting (UNFCCC 2015). Veneman et al. (2016) recently described their online database (MitiGate) of MY metadata collated from international sheep and cattle methane-mitigation studies. They suggested that the database could be continually updated with new MP and MY data by research workers. MitiGate currently contains data from 412 sheep, beef and dairy cattle publications. The eight largest published beef MY datasets with all data needed for meta-analyses are from Herd et al. (2014), Richmond et al. (2015), Rooke et al. (2014), McGinn et al. (2009), Eugène et al. (2011), Fitzsimons et al. (2013), Boadi et al. (2004) and Velazco et al. (2014). Most of these datasets were missing from the MitiGate database at the time of our study, but were included in the meta-analysis presented in the current paper.
Escobar-Bahamondes et al. (2017) recently evaluated MP prediction equations from five studies (Ellis et al. 2007, 2009; Yan et al. 2009; Ricci et al. 2013; Moraes et al. 2014). Only Ricci et al. (2013) and Yan et al. (2009) are included in MitiGate and they are not beef cattle studies. Escobar-Bahamondes et al. (2017) noted that the data from Ellis et al. (2009); Yan et al. (2009) and Ricci et al. (2013) that they used were not available in the published literature.
No guidance is given on the MitiGate website for the choice of data to analyse. Within some subsets of data, the results of particular studies can become outliers and should, therefore, be excluded. There are different approaches available to determine outliers. Ungerfeld et al. (2007) identified outliers by removing data one by one, using an absolute studentised residual value over 2 standard deviations, or a leverage value over 2k/n (where k = number of independent variables and n = number of studies) or Cook’s distance over 90%. Boval et al. (2015) removed outliers that were greater than an absolute value of 3 of normalised residuals. Escobar-Bahamondes et al. (2016) identified and excluded outliers by using Mahalanobis distance calculated from various dietary components, liveweight (LW), DMI and MP.
Diaz et al. (2013) used a cluster analysis approach to allow the formation of groups of results of similar studies before conducting a meta-analysis of genetic parameters. The k-means approach to clustering is an iterative fitting process to form a user-specified number of clusters. The k-means method first selects a set of n points called cluster seeds, as a first estimate of the means of the clusters. Each observation is assigned to the nearest seed to form a set of temporary clusters. The seeds are then replaced by the cluster means, the points are reassigned, and the process continues until no further changes occur in the clusters. The k-means approach is a special case of a general approach called the expectation maximisation algorithm (JMP 2015). With smaller data tables (<200 studies), the results can be highly sensitive to the order of the observations in the data table. k-means clustering supports only numeric values (treats values as continuous) and ignores categorical (nominal and ordinal) variables.
Recently Charmley et al. (2016) conducted a meta-analysis of MP and DMI data from Australian, forage-fed, beef-cattle methane-chamber studies to develop a universal MP prediction equation for use in Australian GHG accounting. If one relationship could be recommended for all forage-fed beef cattle in Australia, then could a global equation with country or region and dietary correction effects (if needed) be developed? The Global Rumen Census project reported that global solutions to reduce methane emissions from ruminant animals should be feasible, because the microbes causing the emissions are similar around the world (Henderson et al. 2015).
Our study has expanded the MitiGate database and conducted cluster analyses and meta-analyses of MY. The aim was to explore the potential and associated uncertainty with using a global MY equation for use in Tier 1 IPCC default GHG accounting methods around the world when there is a lack of country-specific data.
Materials and methods
Data
The metadata and MY values for only control treatments from beef experiments in the MitiGate database (Veneman et al. 2016) were downloaded into an Excel spreadsheet and data were screened and corrected for transcription errors, such as control cattle being recorded as treated groups from some papers and vice versa. Data were added from non-included, available papers to expand the currently available database. Rows of data were then excluded from further analyses, if any metadata (i.e. effects in the fitted models) were not recorded in the study (see Tables S1 and S2, available as Supplementary material for this paper). Some studies provided multiple (control) MY values. Cluster analyses are best conducted with only a small number of levels of each categorical variable, so measurement methods, breeds, diets and countries were each amalgamated into three to five groupings or levels, as described below.
Cluster-analysis methods
Dummy variables were coded for categorical effects, as follows:
-
d_measure: chamber 0, sulfur hexafluoride tracer (SF6) 1, Greenfeed emission monitoring units (GEM) 2, (measure = MP measurement method used);
-
d_breed: British 0, European 1, Tropical 2, Crossbred 3, Unknown 4 (breed = cattle type);
-
d_country: Australia 0, Americas 1, Europe 2, Other 3 (country = continent);
-
d_sex: calves, 0, steers/bulls 1, heifers 2, cows 3 (sex = age and sex);
-
d_diet: no grain (roughage) 0, 1–50% grain 1, 50–75% grain 2, >75% grain 3 (diet = % grain).
Quantitative variables (number of animals, LW and MY) were standardised to a scale of 0–1 for all records, by using the formula z = (X – minimum) / (maximum – minimum).
The data were also analysed using two-way Ward’s hierarchical cluster analyses (JMP 2015) with all dummy and standardised variables. Also the Ward’s analysis was conducted for individual countries with no d_country dummy variable. The data were also analysed using k-means cluster analyses and principal components with two or three clusters with and without the inclusion of the categorical variables. k means tend to produce equal-sized clusters, while the expectation–maximisation algorithm benefits from the normal distribution present in the dataset. However, when the normal mixture k-means option was run, with outliers that do not fall into any of the normal clusters automatically excluded to a fourth cluster, the three clusters overlapped more. Different clusters of studies were generated each time the data were re-analysed due to the random selection of initial cluster centres. The cluster number allocated to each study was calculated from the formula ((z_N – cluster mean) / cluster standard deviation)2.
Meta-analysis
The studies had their least-square means (LSMs) of MY and standard errors of these LSMs (s.e.m.), or reported variance parameters such as standard deviation, residual mean square or standard error of differences (that could be used to calculate the s.e.m.), collated in a dataset. Where an estimate of MY s.e.m. was not given in a study, the relative s.e. (rse) was set equal to s.e./mean, then for a ratio of means (MY = mean MP : mean DMI), rse (of MY) was calculated as square root [rse(MP)2 + rse(DMI)2], where MY s.e.m. was equal to MY × MY rse. Results from bulls and heifers in the study of Herd et al. (2014) could be separated by having access to the raw data. When MP results were reported in litres of methane, a conversion factor of 0.716 (specific gravity at standard temperature and pressure) was used to calculate grams of methane.
The meta-analyses were conducted using a least-square residual maximum-likelihood (REML) model in the statistical package JMP, following the methods of Sauvant et al. (2008). In brief, the LSM observations were weighted by the inverse of the squares of their standard errors, i.e. the reciprocals of the s.e.m. However, when such weights are used, the resulting measures of model errors (such as, for example, standard error, standard error of predictions) are no longer expressed in the original scale of the data. To maintain the expressions of dispersion in the original scale of the measurements, the approach of St-Pierre (2001) of dividing each weight by the mean of all weights, and using the resulting values as weighting factors in the analysis, was used. Under this procedure, the average weight used is algebraically equal to 1.0, thus resulting in expressions of dispersion that are in the same scale as the original data. The study effect was considered random because it represents, in essence, the sum of many effects on the dependent variable, MY. Statistical theory indicates that these effects would be close to Gaussian (normal), thus being much better estimated if treated as random effects (Sauvant et al. 2008). The root mean-square errors (RMSE) of the REML models serve to aggregate the residuals (observed–predicted) into a single measure of the precision of the model prediction. The weighting factors were calculated on the basis of the studies allocated to each of the clusters included in any analysis, so they varied when different clusters or combinations of clusters were analysed.
The categorical effects included in the REML models were subsets of those used in the cluster analyses and are shown in prediction Eqns 1–4 in the Results section. The data were too sparse to enable model solutions to be found when interaction effects among diet, breed or country were included in any models. Adding more categorical effects, such as, for example, conserved versus fresh forage, would also likely have resulted in solution singularity problems.
Results
Cluster analyses
Ward’s hiercharchial clusters (2-way) for all studies are shown in Fig. 1.

|
In order of importance, the categorical effects that best separate clusters of studies are those that result in the greatest distance between clusters, namely breed, measurement method, sex, diet and country (Table 1). Studies that join closer to the left of the cluster diagram are less disparate in MY values. Studies that join in the last clustering (1 cluster) were the most disparate (Beauchemin and McGinn 2005; Herd et al. 2014). Groups of studies to be collated for a meta-analysis could be those that cluster together earlier or those studies in the same path of the constellation plots. As there were numerous paths in these plots, the hierarchial clustering method was rejected as a data-filtering method. The k-means clustering technique was used instead to generate two large clusters and a third small cluster, and meta-analyses were conducted on these two large clusters separately or with all data combined.

|
The Ward’s hiercharchial and k-means cluster means from the various analyses are shown in Table 2. k-mean cluster values (1, 2 and 3) were assigned to each study from the k-means cluster without categorical variables analysis.
Clusters are shown in Fig. 2 and these clusters were meta-analysed separately or with all clusters included. On average, studies in the third cluster (3) were slightly smaller studies with lighter cattle with lower MY values than were studies in the second cluster (2). Cluster 1 was solely the male and female results in the large study of Herd et al. (2014) and was the last cluster (7) in the Ward’s hiercharchial analysis.
All-clusters model
The REML model for all included data (51 papers, 138 MY estimates), with studies fit as a random effect, had a prediction Eqn 1 for MY, as follows:

Equation 1 had R2 = 0.65 and RMSE = 3.95. No effects or LSM differences were significant (P < 0.05), including the random effect of studies. The LSM of MY values for all data are shown in Table 3. The LSM for an effect is equal to its effect size in the model plus the overall intercept (20.34) in predictive Eqn 1.

|
The MY values from beef cattle studies conducted in Brazil, Switzerland, Australia and Canada had (non-significantly; P > 0.05) lower LSM, while the LSM values from studies in Ireland, France, the United Kingdom, New Zealand, and India were (not significantly; P > 0.05) higher. Data screening removed all beef MY studies from USA, Denmark and Japan (Table S2). Studies with beef cattle conducted in Ireland had the highest MY value (29.31 g/kg DMI), while studies with cattle in Canada had the lowest (14.60 g/kg DMI). Interactions of country with diet or breed fixed effects could not be included in the models due to the sparsity of data.
When d_country (amalgamation of countries into continents) was fitted as an effect instead of country, then the d_diet and d_country effects became significant (P < 0.05) but the goodness of fit of the model (as measured by R2 and RMSE) slightly decreased. Higher-roughage diets (d_diet = 0, 1) had significantly (P < 0.05) higher MY values than did higher-grain diets and European studies had significantly (P < 0.05) higher MY values than did those from North and South America (Canada and Brazil).
Cluster 2 (larger studies, heavier cattle) model
The REML model for Cluster 2 studies, with studies fit as a random effect, had a prediction Eqn 2 for MY, as follows:

Equation 2 had R2 = 0.90 and RMSE = 1.20. No effects were significant (P < 0.05) with LSMs shown in Table 4.

|
Cluster 3 (smaller studies, lighter cattle) model
The REML model for Cluster 3 results, with studies fit as a random effect, had a prediction Eqn 3 for MY, as follows:
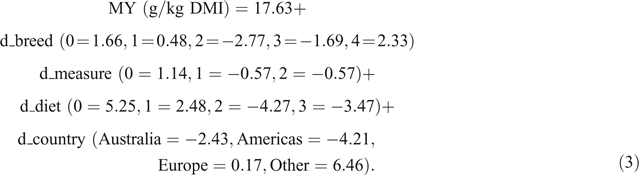
Equation 3 had R2 = 0.53 and RMSE = 4.91. The LSMs were not significantly different (Table 5).

|
There were no consistent trends for the effects of measurement method, breed, diet or continent when comparing the LSM results or prediction equations from Clusters 2 and 3. Cluster 1, which consisted only of data from Herd et al. (2014) had a LSM value for MY of 22.96 g/kg DMI.
Outliers
The mean studentised residual value from the all-in model was 0.089 ± 1.267, with quartiles of –0.110, and a value range from –9.380 to 9.319. There were only three rows of data from 138 rows with absolute studentised residual (ASR) values for MY greater than or equal to 1.96 from the all-in analysis. These MY values were from trials reported by Beauchemin and McGinn (2005) and Boadi et al. (2004). When the threshold for outlier exclusion was reduced to an ASR value of 1.0 (which includes 66% of the normal distribution), seven data rows were excluded. With an ASR value of 0.9, nine data rows were excluded and, with an ASR value of 0.8, 13 data rows were excluded.
All-clusters model excluding outliers
Data with seven outlier rows removed (ASR threshold value = 1.0) were chosen for further analyses. The excluded rows of data were from Beauchemin and McGinn (2005), Boadi et al. (2004), Boland et al. (2013), McCaughey et al. (1999) and Velazco et al. (2016). The REML model, with studies fit as a random effect, had a prediction Eqn 4 for MY, as follows:

Equation 4 had R2 = 0.90, RMSE = 1.20, which was, as expected, a much improved fit compared with the all-clusters model with no outliers removed. Significant differences in MY LSM are shown in Table 6.

|
One example of using predictive Eqn 4, which can be compared with the prediction equation of Charmley et al. (2016), is for British cattle breeds, measured in chambers, on a roughage diet in Australia. In this case, the MY value solves to 21.85 + 0.77 – 0.61 + 3.76 – 3.37 = 22.40 ± 1.20 g methane/kg DMI.
The changes in predicted MY value with changes in measurement method, breed, diet or country are given by the size of the fixed-effect categorical values. For example, MY measured with a GreenFeed Emissions Monitoring system (d_measure = 2) rather than a chamber (d_measure = 0) was predicted to be 1.77 – 0.77 = 1.0 g methane/kg DMI higher. However, this does not suggest or prove that one measurement method gives more accurate values for the true MY than does another, but the effect-level difference allows a correction to be made for methane-measurement method.
Discussion
Country and other effects
Overall differences among countries were not significant, but some individual countries were significantly different from each other in the MY value. The country effect is an unknown mixture of the inherent MY value of animals from each country, independent of the other fitted effects, and the skills and expertise of the technicians and scientists deploying specific equipment used in measuring animals in each country. These effects could be interpreted more clearly only if representative samples of animals from different countries were transported to a common centre for measurement or scientists from different countries measured exactly the same animals using the same methods. None of these situations is likely to happen due to their cost and impracticality. Data were too sparse to study the interactions of country with any other effects causing singularities in any model. There is no evidence in the literature for significant interactions between country and breed or country and diet type for MY.
Henderson et al. (2015) suggested that rumen methanogens in cattle around the world have similar genetics, which could suggest that MY may be similar everywhere. No strong associations were found between the most abundant rumen bacteria and archaea (~3% of microbes that are mostly autotrophic methanogens). However, Wallace et al. (2015) reported that the abundance of archaeal genes in ruminal digesta correlated strongly with differing methane emissions from individual animals. Lower emissions were accompanied by higher Succinovibrionaceae abundance and changes in acetate and hydrogen production leading to less methanogenesis. Large numbers of predicted protein sequences, nearly all unknown, differed between high- and low-methane-emitting cattle.
Different species of rumen biota, while a major factor affecting rumen methanogenesis, are not the only factor (Eckard et al. 2010; Cottle et al. 2011). Other factors include level and variation of DMI, type of carbohydrate in the diet, feed digestibility and processing, addition of additives such as lipids or ionophores to the diet, as well as manipulations of the ruminal microflora. Efficiency of feed use depends on the type of animal, the type or quality and quantity of feed and environmental conditions (Cottle and Pitchford 2014). Country variation in MY value may be due to effects not included in the model, such as, for example, conserved versus fresh forage, and proportion of legume. However, adding additional effects to a model when data are sparse often has the problem that model solutions are not obtained.
National accounts based on IPCC (2006) use the percentage of gross energy (GE) in feed converted to methane (Ym) to calculate methane production. The values of Ym and MY respectively predict the percentage of feed energy and feed dry weight converted to methane energy and dry weight. It is proposed that it is problematic to have a universal MY or Ym value for use in all countries for national accounting, given the significance and size of some of the fixed effects found in this meta-analysis, including specific countries. However, prediction Eqn 4 could be used, for example, for different countries and diets to provide a MY (or Ym) value to be used in the national accounts of various countries.
The IPCC Tier 1 guidelines for national GHG inventories (IPCC 2006) use the same methane-conversion factor (Ym) of 6.5% for grazing beef cattle and 3% for feedlot cattle in all major beef regions. Methane production of beef cattle in IPCC-based national inventories, using Tier 1, 2 or 3 approaches, is calculated using IPCC (2006) eqn 10.21, as follows:
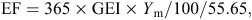
where
EF = emission factor, kg methane/head.year (MP = EF/365),
GEI = gross energy intake, MJ/head/day,
Ym = percentage of gross energy in feed converted to methane,
55.65 (MJ/kg methane) = the energy content of methane.
IPCC (2006) recommends that either Tier 2 or Tier 3 approaches are used for beef cattle. This is where regional, national and global estimates of enteric methane generation rely on small-scale determinations of GEI, Ym and the influence of feed and animal properties on GEI and Ym. The GEI values depend on the assumed DMI level and diet quality for different classes of animals. Default feed intakes (kg/day) and energy intakes (MJ/day) for beef-stock classes and regions are listed in IPPC Volume 4 Appendix B, based on the report of Gibbs and Johnson (1994). These different intake levels lead to the different default Tier 1 values for EF (or MP) listed for the various regions (IPCC 2006). These values for North America, western Europe, eastern Europe, Oceania, Latin America, Asia, Africa, Middle East and Indian subcontinent are 14.5, 15.6, 15.9, 16.4, 15.3, 12.9, 8.5 and 7.4 g methane/day respectively.
From our review of the national inventories of the major beef-producing nations, the value of Ym for grazing cattle has not been modified from the Tier 1 value of 6.5%; for example, the USA inventory (US EPA 2017) still uses the Ym value of 6.5% recommended by Johnson (2002). The value of MY (g methane/kg DMI) = GE content of DM × Ym / 100 / 55.65. As the GE content of pasture and grain is typically 18.45 MJ/kg DM (Cottle et al. 2011), the Tier 1 MY value = 21.5, assuming Ym = 6.5% for pasture, and MY = 9.9 for grain, assuming Ym = 3%, for all countries. Thus, universal values for Ym, and hence MY, appear to be used to estimate beef MP in most national inventories.
Other methane meta-analyses
Most published methane related meta-analyses have been focussed on mitigation strategies rather than estimating MY values in control, non-mitigated animals. Examples of meta-analyses focussed on mitigation strategies include Ungerfeld et al. (2007), Beauchemin et al. (2008), Eugène et al. (2008), Grainger and Beauchemin (2011), Jayanegara et al. (2011), Patra (2013), Hristov et al. (2013a) and the more recent papers by Veneman et al. (2016) and Escobar-Bahamondes et al. (2017).
Ramin and Huhtanen (2013) estimated beef cattle MY as 21.9 g/kg DMI from their meta-analysis of five beef papers (Kirkpatrick et al. 1997; Kurihara et al. 1999; Beauchemin and McGinn 2005, 2006; Beauchemin et al. 2007). Our predicted MY value from the data that excluded outliers, which interestingly included some of the papers analysed by Ramin and Huhtanen (2013), was 22.4 g/kg DMI for British cattle breeds, measured in chambers, on a roughage diet in Australia. This estimate from many more studies is very similar to their estimate from Canadian, Australian and Irish studies. Ramin and Huhtanen (2013) may have fit too many dietary fixed effects (organic matter digestibility, neutral detergent fibre, non-fibre carbohydrates and ether extract) to their MY models for the relative small number of beef studies they analysed.
Ricci et al. (2013) reported a meta-analysis of 38 beef studies where MP, DMI, type of enterprise, diet type, physiological stage, MP measurement technique, intake restriction and methane-mitigation treatment were used as classificatory factors. A series of equations for different physiological stages and diet types based on DMI or GE intake explained 96% of the variation in observed MP outputs. Hristov et al. (2013a, 2013b) also demonstrated a simple relationship between MP and DMI (MP (g/day) = 19.14 × DMI + 2.54) in a meta-analysis of dairy data. Similarly, Dijkstra et al. (2011) reported that MY for dairy cows in The Netherlands was 23.1 g MP/kg DMI, suggesting a linear relationship between MP and DMI, with an intercept of zero.
Most national inventories predict MP from its linear, not curvilinear, relationship with predicted DMI. This has the implicit assumption that the MY value is constant for all DMI values if there is no intercept in the MP/DMI equation (e.g. Bannink et al. 2011; Charmley et al. 2016). If there is an intercept in the MP/DMI equation (e.g. Hristov et al. 2013a, 2013b), then the MY–DMI relationship is slightly curvilinear. Appuhamy et al. (2016) found that MP in dairy cows could be predicted successfully if DMI could be estimated accurately. However, they found that the best methane-prediction model for North American lactating dairy-cow studies (modified from Nielsen et al. 2013) was different than the best model for European, Australian and New Zealand studies (Yan et al. 2000).
Charmley et al. (2016) analysed a total of 1034 individual animal records of MP to re-assess the relationship between MP and DMI. Data were restricted to trials conducted in the past 10 years using respiration chambers, with cattle fed forage-based diets (forage >70%). Results from diets considered to inhibit methanogenesis were omitted from the dataset. Records were from beef cattle fed temperate forages (680 records) and beef cattle fed tropical forages (133 records). Relationships were very similar for both forages and a single relationship for MP on a DMI basis was proposed for the purposes of Australian national inventory. This relationship was as follows: MP (g/day) = 20.7 (±0.28) × DMI (kg/day; R2 = 0.92, P < 0.001), i.e. MY = 20.7. The prediction of MY value for Australian beef cattle on non-grain diets measured in chambers in Eqn 4, derived from an analysis of global MY data, was 21.85 + 0.77 + d_breed (0, 1, 2, average of 0.35) + 3.76 – 3.37 = 23.4. This is 2.7 g/kg DMI higher than the MY value of Charmley et al. (2016).
Charmley et al. (2016) noted that MP and DMI variances increase as MP and DMI levels increase while their coefficient of variance remain steady. They also analysed Australian MY data (i.e. the data formed by the ratio MP : DMI) directly. This reduced variance heterogeneity, but not completely. It also simplified the fixed-effects model to one without DMI, as Charmley et al. (2016) noted a perceived difficulty of dealing with DMI on both sides of the model equation for MP. However, they still argued that analysing MP in terms of DMI was conceptually the simplest.
For the classes of beef cattle used, Charmley et al. (2016) found that MY ranged from 19.6 ± 0.49 to 21.5 ± 0.45 g/kg DMI, which is close but lower than our Australian predicted values, as noted above, and previously published values. Charmley et al. (2016) noted that Irish beef data suggested a higher MY value of ~25 g/kg DMI (Yan et al. 2009), while our Eqn 4 fixed-effect value for Ireland was 8.7, compared with –3.4 for Australia. Thus, our prediction of the difference between Australia and Ireland in MY value from our higher number of studies was a larger difference of 12.04 g/kg DMI. Their analysis included Australian trials with growing beef cattle fed diets containing 0–70% concentrate. This discrepancy between Irish and Australian data may be attributed to the predominance of extensively fermented grass silages in many of the Irish studies. Dairy research from the United Kingdom (Hammond et al. 2014) supports Irish research (Yan et al. 2000), showing that MY is higher for ensiled forages than fresh pasture. We included relative amount of grain in the diet (d_diet) as a fixed categorical effect, but other dietary effects, such as fresh versus ensiled pasture, were not included for reasons given previously.
Use of the MitiGate database
The MitiGate database potentially provides a very useful global resource for collation of results from ruminant methane studies. However, control versus mitigation-treatment data from MitiGate need to be accurately transcribed from the original publications. Some control (non-mitigated) MY values were listed as the mitigated treatment values and vice versa, so data need to be checked. Some large beef methane-study results have not been uploaded yet. About 50% of the 326 beef cattle methane-related papers in MitiGate reported methane production in units of either grams or litres of methane per kilogram DMI. The other publications (in decreasing frequency) used a variety of methane units, including %GEI, L/day, g/day, g/kg organic matter intake, mol/mol glucose equivalent, MJ/day, MJ/100 MJ GE, MJ/kg BW, MJ/MJ GE, KJ/BW0.75, mcal/100 mcal, mcal/day, mL/min, mmol/L, %gas, g/h, g/kg LW.day, g/MJ ME, kcal/day and L/kg BW0.75. Some publication authors have used different methane units in their own different studies. Some of these units are not easy to convert to g MP/kg DMI and consistency would be helpful when collating MP or MY results. We suggest g MP/kg DMI as an emerging standard and, thus, the preferred MY unit. MitiGate does not include DMI data, so it is not possible to calculate MP from the MitiGate MY values.
The meta-analyses of selected subsets from the MitiGate database in regard to mitigation effects are based on the metaphor method using R as described by Viechtbauer (2010), which is based on the ratio of the mean MY value of control and treated animals. If particular mitigation options are being compared the user could download all data for those options, with no guidance given on outlier study removal. The metaphor method, while valid, differs from the methods of Sauvant et al. (2008), which are the basis of many published meta-analyses in ruminant nutrition.
The current classification of methane-mitigation options in MitiGate does not include management options, such as faster growth to sale weight of stock or younger age structures, which are probably the most cost-effective mitigation options available (Eckard et al. 2010; Cottle et al. 2011; Cottle and Eckard 2014; Mazzetto et al. 2015). It could, therefore, be useful to add these management options in MitiGate by adding studies that have MY values for control versus modified management systems.
Conclusions
Our main aim was to explore the potential and associated uncertainty with using a standard MY estimate for use in Tier 1 IPCC default GHG accounting methods around the world. We conclude that the differences in MY values from beef-cattle studies with different methane-measurement methods, breeds and diets in different countries are such that a universal MY value cannot be recommended at this stage. A more accurate approach would be to use a predictive equation, such as our Eqn 4, derived from country-specific data to provide Ym or MY values in national accounting methods that also take account of different breeds and diets. Such equations can be regularly updated in meta-analyses as more data become available.
Conflicts of interest
The authors declare no conflicts of interest.
Acknowledgements
We thank Dr Robert Herd, NSWDPI, for supplying raw data from NSWDPI trial work, and Dr Ed Charmley, CSIRO, for providing an advance copy of his 2016 paper and reading our manuscript.
References
Appuhamy JADRN, France J, Kebreab E (2016) Models for predicting enteric methane emissions from dairy cows in North America, Europe, and Australia and New Zealand. Global Change Biology 22, 3039–3056.| Models for predicting enteric methane emissions from dairy cows in North America, Europe, and Australia and New Zealand.Crossref | GoogleScholarGoogle Scholar |
Bannink A, van Schijndel MW, Dijkstra J (2011) A model of enteric fermentation in dairy cows to estimate methane emission for the Dutch National Inventory Report using the IPCC Tier 3 approach. Animal Feed Science and Technology 166–167, 603–618.
| A model of enteric fermentation in dairy cows to estimate methane emission for the Dutch National Inventory Report using the IPCC Tier 3 approach.Crossref | GoogleScholarGoogle Scholar |
Beauchemin KA, McGinn SM (2005) Methane emissions from feedlot cattle fed barley or corn diets. Journal of Animal Science 83, 653–661.
| Methane emissions from feedlot cattle fed barley or corn diets.Crossref | GoogleScholarGoogle Scholar |
Beauchemin KA, McGinn SM (2006) Methane emissions from beef cattle: effects of fumaric acid, essential oil, and canola oil. Journal of Animal Science 84, 1489–1496.
| Methane emissions from beef cattle: effects of fumaric acid, essential oil, and canola oil.Crossref | GoogleScholarGoogle Scholar |
Beauchemin KA, McGinn SM, Petit HV (2007) Methane abatement strategies for cattle: lipid supplementation of diets. Canadian Journal of Animal Science 87, 431–440.
| Methane abatement strategies for cattle: lipid supplementation of diets.Crossref | GoogleScholarGoogle Scholar |
Beauchemin KA, Kreuzer M, O’Mara F, McAllister T (2008) Nutritional management for enteric methane abatement: a review. Australian Journal of Experimental Agriculture 48, 21–27.
| Nutritional management for enteric methane abatement: a review.Crossref | GoogleScholarGoogle Scholar |
Boadi DA, Wittenberg KM, Scott SL, Burton D, Buckley K, Small JA, Ominski KH (2004) Effect of low and high forage diet on enteric and manure pack greenhouse gas emissions from a feedlot. Canadian Journal of Animal Science 84, 445–453.
| Effect of low and high forage diet on enteric and manure pack greenhouse gas emissions from a feedlot.Crossref | GoogleScholarGoogle Scholar |
Boland TM, Quinlan C, Pierce KM, Lynch MB, Kelly AK, Purcell PJ (2013) The effect of pasture pre-grazing herbage mass on methane emissions, ruminal fermentation, and average daily gain of grazing beef heifers. Journal of Animal Science 91, 3867–3874.
| The effect of pasture pre-grazing herbage mass on methane emissions, ruminal fermentation, and average daily gain of grazing beef heifers.Crossref | GoogleScholarGoogle Scholar | .
Boval M, Edouard N, Sauvant D (2015) A meta-analysis of nutrient intake, feed efficiency and performance in cattle grazing on tropical grasslands. Animal 9, 973–982.
| A meta-analysis of nutrient intake, feed efficiency and performance in cattle grazing on tropical grasslands.Crossref | GoogleScholarGoogle Scholar |
Charmley E, Williams SRO, Moate PJ, Hegarty RS, Herd RM, Oddy VH, Reyenga P, Staunton KM, Anderson A, Hannah MC (2016) A universal equation to predict methane production of forage-fed cattle in Australia. Animal Production Science 56, 169–180.
| A universal equation to predict methane production of forage-fed cattle in Australia.Crossref | GoogleScholarGoogle Scholar |
Cottle DJ, Eckard R (2014) Modelling the reduction in enteric methane from voluntary intake versus controlled individual animal intake of lipid or nitrate supplements. Animal Production Science 54, 2121–2131.
| Modelling the reduction in enteric methane from voluntary intake versus controlled individual animal intake of lipid or nitrate supplements.Crossref | GoogleScholarGoogle Scholar |
Cottle DJ, Pitchford W (2014) Production efficiency. In ‘Beef production and trade’. (Eds D Cottle, L Kahn) pp. 421–458. (CSIRO Publishing: Melbourne)
Cottle DJ, Nolan J, Vand Wiedemann SG (2011) Ruminant enteric methane mitigation: a review. Animal Production Science 51, 491–514.
| Ruminant enteric methane mitigation: a review.Crossref | GoogleScholarGoogle Scholar |
Diaz ID, Crews DH, Enns RM (2013) Cluster and meta-analyses of genetic parameters for feed intake traits in growing beef cattle. Journal of Animal Breeding and Genetics 131, 217–226.
| Cluster and meta-analyses of genetic parameters for feed intake traits in growing beef cattle.Crossref | GoogleScholarGoogle Scholar |
Eckard RJ, Grainger C, de Klein CAM (2010) Options for the abatement of methane and nitrous oxide from ruminant production: a review. Livestock Science 130, 47–56.
| Options for the abatement of methane and nitrous oxide from ruminant production: a review.Crossref | GoogleScholarGoogle Scholar |
Ellis JL, Kebreab E, Odongo NE, McBride BW, Okine EK, France J (2007) Prediction of methane production from dairy and beef cattle. Journal of Dairy Science 90, 3456–3466.
| Prediction of methane production from dairy and beef cattle.Crossref | GoogleScholarGoogle Scholar |
Ellis JL, Kebreab E, Odongo NE, Beauchemin K, McGinn S, Nkrumah JD, Moore SS, Christopherson R, Murdoch GK, McBride BW, Okine EK, France J (2009) Modeling methane production from beef cattle using linear and nonlinear approaches. Journal of Animal Science 87, 1334–1345.
| Modeling methane production from beef cattle using linear and nonlinear approaches.Crossref | GoogleScholarGoogle Scholar |
Escobar-Bahamondes P, Oba M, Beauchemin KA (2016) Universally applicable methane prediction equations for beef cattle fed high- or low-forage diets. Canadian Journal of Animal Science 97, 83–94.
| Universally applicable methane prediction equations for beef cattle fed high- or low-forage diets.Crossref | GoogleScholarGoogle Scholar |
Escobar-Bahamondes P, Oba M, Beauchemin KA (2017) An evaluation of the accuracy and precision of methane prediction equations for beef cattle fed high-forage and high-grain diets. Animal 11, 68–77.
| An evaluation of the accuracy and precision of methane prediction equations for beef cattle fed high-forage and high-grain diets.Crossref | GoogleScholarGoogle Scholar |
Eugène M, Massé D, Chiquette J, Benchaar C (2008) Meta-analysis on the effects of lipid supplementation on methane production in lactating dairy cows. Canadian Journal of Animal Science 88, 331–337.
| Meta-analysis on the effects of lipid supplementation on methane production in lactating dairy cows.Crossref | GoogleScholarGoogle Scholar |
Eugène M, Martin C, Mialon MM, Krauss D, Renand G, Doreau M (2011) Dietary linseed and starch supplementation decreases methane production of fattening bulls. Animal Feed Science and Technology 166–167, 330–337.
| Dietary linseed and starch supplementation decreases methane production of fattening bulls.Crossref | GoogleScholarGoogle Scholar |
Fitzsimons C, Kenny DA, Deighton MH, Fahey A, McGee M (2013) Methane emissions, body composition, and rumen fermentation traits of beef heifers differing in residual feed intake. Journal of Animal Science 91, 5789–5800.
| Methane emissions, body composition, and rumen fermentation traits of beef heifers differing in residual feed intake.Crossref | GoogleScholarGoogle Scholar |
Gibbs MJ, Johnson DE (1994) Methane emissions from the digestive process of livestock. In ‘International anthropogenic methane emissions: estimates for 1990’. Rep. EPA 230-R-93-010. (US Environmental Protection Agency: Washington, DC)
Grainger C, Beauchemin KA (2011) Can enteric methane emissions from ruminants be lowered without lowering their production? Animal Feed Science and Technology 166–167, 308–320.
| Can enteric methane emissions from ruminants be lowered without lowering their production?Crossref | GoogleScholarGoogle Scholar |
Hammond KJ, Humphries DJ, Westbury DB, Thompson A, Crompton LA, Kirton P, Green C, Reynolds CK (2014) The inclusion of forage mixtures in the diet of growing dairy heifers: impacts on digestion, energy utilization, and methane emissions. Agriculture, Ecosystems & Environment 197, 88–95.
| The inclusion of forage mixtures in the diet of growing dairy heifers: impacts on digestion, energy utilization, and methane emissions.Crossref | GoogleScholarGoogle Scholar |
Henderson G, Cox F, Ganesh S, Jonker A, Young W, Global Rumen Census Collaborators Janssen PH (2015) Rumen microbial community composition varies with diet and host, but a core microbiome is found across a wide geographical range. Scientific Reports 5, 14567
| Rumen microbial community composition varies with diet and host, but a core microbiome is found across a wide geographical range.Crossref | GoogleScholarGoogle Scholar |
Herd RM, Arthur PF, Donoghue KA, Bird SH, Bird-Gardiner T, Hegarty RS (2014) Measures of methane production and their phenotypic relationships with dry matter intake, growth, and body composition traits in beef cattle. Journal of Animal Science 92, 5267–5274.
| Measures of methane production and their phenotypic relationships with dry matter intake, growth, and body composition traits in beef cattle.Crossref | GoogleScholarGoogle Scholar |
Hristov AN, Oh J, Firkins JL, Dijkstra J, Kebreab E, Waghorn G, Makkar HPS, Adesogan AT, Yang W, Lee C, Gerber PJ, Henderson B, Tricarico JM (2013a) Mitigation of methane and nitrous oxide emissions from animal operations: I. A review of enteric methane mitigation options. Journal of Animal Science 91, 5045–5069.
| Mitigation of methane and nitrous oxide emissions from animal operations: I. A review of enteric methane mitigation options.Crossref | GoogleScholarGoogle Scholar |
Hristov AN, Ott T, Tricarico J, Rotz A, Waghorn G, Adesogan A, Dijkstra J, Montes F, Oh J, Kebreab E, Oosting SJ, Gerber PJ, Henderson B, Makkar HPS, Firkins JL (2013b) Mitigation of methane and nitrous oxide emissions from animal operations: III. A review of animal management mitigation options. Journal of Animal Science 91, 5095–5113.
| Mitigation of methane and nitrous oxide emissions from animal operations: III. A review of animal management mitigation options.Crossref | GoogleScholarGoogle Scholar |
Intergovernmental Panel on Climate Change (2006) ‘2006 IPCC guidelines for national greenhouse gas inventories. Vol. 4. Agriculture, forestry and other land use.’ Available at http://www.ipcc-nggip.iges.or.jp/public/2006gl/ [Verified 13 April 2017]
Jayanegara A, Leiber F, Kreuzer M (2011) Meta‐analysis of the relationship between dietary tannin level and methane formation in ruminants from in vivo and in vitro experiments. Journal of Animal Physiology and Animal Nutrition 96, 365–375.
| Meta‐analysis of the relationship between dietary tannin level and methane formation in ruminants from in vivo and in vitro experiments.Crossref | GoogleScholarGoogle Scholar |
JMP (2015) ‘Cluster analysis.’ Available at http://www.jmp.com/support/help/Cluster_Analysis.shtml [Verified 22 October 2015]
Johnson D (2002) Personal communication. Don Johnson, Colorado State University, Fort Collins, and ICF 28 International, cited by US Environmental Protection Agency (2017). Inventory of U.S. Greenhouse Gas Emissions and Sinks 1990–2015. ANNEX 3 Methodological Descriptions for Additional Source or Sink Categories. Section 3.1. Methodology for estimating emissions of CH4, N2O, and indirect greenhouse gases from stationary combustion. pp. A131–A138. Available at https://www.epa.gov/sites/production/files/2017-2/documents/2017_annex_3-_part_a.pdf [Verified 28 April 2018]
Kirkpatrick DE, Steen RWJ, Unsworth EF (1997) The effect of differing forage: concentrate ratio and restricting feed intake on the energy and nitrogen utilization by beef cattle. Livestock Production Science 51, 151–164.
| The effect of differing forage: concentrate ratio and restricting feed intake on the energy and nitrogen utilization by beef cattle.Crossref | GoogleScholarGoogle Scholar |
Kurihara M, Magner T, Hunter RA, McCrabb GJ (1999) Methane production and energy partition of cattle in the tropics. British Journal of Nutrition 81, 227–234.
Mazzetto AM, Feigl BJ, Schils RLM, Cerri CEP, Cerri CC (2015) Improved pasture and herd management to reduce greenhouse gas emissions from a Brazilian beef production system Livestock Science 175, 101–112.
| Improved pasture and herd management to reduce greenhouse gas emissions from a Brazilian beef production systemCrossref | GoogleScholarGoogle Scholar |
McCaughey WP, Wittenberg K, Corrigan D (1999) Impact of pasture type on methane production by lactating beef cows. Canadian Journal of Animal Science 79, 221–226.
| Impact of pasture type on methane production by lactating beef cows.Crossref | GoogleScholarGoogle Scholar |
McGinn SM, Chung Y-H, Beauchemin KA, Iwaasa AD, Grainger C (2009) Use of corn distillers’ dried grains to reduce enteric methane loss from beef cattle. Canadian Journal of Animal Science 89, 409–413.
| Use of corn distillers’ dried grains to reduce enteric methane loss from beef cattle.Crossref | GoogleScholarGoogle Scholar |
Moraes LE, Strathe AB, Fadel JG, Casper DP, Kebreab E (2014) Prediction of enteric methane emissions from cattle. Global Change Biology 20, 2140–2148.
| Prediction of enteric methane emissions from cattle.Crossref | GoogleScholarGoogle Scholar |
Nielsen NI, Volden H, Akerlind M, Brask M, Hellwing ALF, Storlein T, Bertilsson J (2013) A prediction equation for enteric methane emission from dairy cows for use in NorFor. Acta Agriculturae Scand Section A 63, 126–130.
Patra AK (2013) The effect of dietary fats on methane emissions, and its other effects on digestibility, rumen fermentation and lactation performance in cattle: a meta-analysis. Livestock Science 155, 244–254.
| The effect of dietary fats on methane emissions, and its other effects on digestibility, rumen fermentation and lactation performance in cattle: a meta-analysis.Crossref | GoogleScholarGoogle Scholar |
Ramin M, Huhtanen P (2013) Development of equations for predicting methane emissions from ruminants. Journal of Dairy Science 96, 2476–2493.
| Development of equations for predicting methane emissions from ruminants.Crossref | GoogleScholarGoogle Scholar |
Ricci P, Rooke JA, Nevison I, Waterhouse A (2013) Methane emissions from beef and dairy cattle: quantifying the effect of physiological stage and diet characteristics. Journal of Animal Science 91, 5379–5389.
| Methane emissions from beef and dairy cattle: quantifying the effect of physiological stage and diet characteristics.Crossref | GoogleScholarGoogle Scholar |
Richmond S, Wylie ARG, Laidlaw AS, Lively FO (2015) Methane emissions from beef cattle grazing on semi-natural upland and improved lowland grasslands. Animal 9, 130–137.
| Methane emissions from beef cattle grazing on semi-natural upland and improved lowland grasslands.Crossref | GoogleScholarGoogle Scholar |
Rooke JA, Wallace RJ, Duthie C-A, McKain N, Motta de Souza S, Hyslop JJ, Ross DW, Waterhouse T, Roehe R (2014) Hydrogen and methane emissions from beef cattle and their rumen microbial community vary with diet, time after feeding and genotype. British Journal of Nutrition 112, 398–407.
| Hydrogen and methane emissions from beef cattle and their rumen microbial community vary with diet, time after feeding and genotype.Crossref | GoogleScholarGoogle Scholar |
Sauvant D, Schmidely P, Daudin JJ, St-Pierre NR (2008) Meta-analyses of experimental data in animal nutrition. Animal 2, 1203–1214.
| Meta-analyses of experimental data in animal nutrition.Crossref | GoogleScholarGoogle Scholar |
St-Pierre NR (2001) Invited review: integrating quantitative findings from multiple studies using mixed model methodology. Journal of Dairy Science 84, 741–755.
| Invited review: integrating quantitative findings from multiple studies using mixed model methodology.Crossref | GoogleScholarGoogle Scholar |
UNFCCC (2015) ‘National reports.’ Available at http://unfccc.int/national_reports/items/1408.php [Verified 9 October 2015]
Ungerfeld EM, Kohn RA, Wallace RJ, Newbold CJ (2007) A meta-analysis of fumarate effects on methane production in ruminal batch cultures. Journal of Animal Science 85, 2556–2563.
| A meta-analysis of fumarate effects on methane production in ruminal batch cultures.Crossref | GoogleScholarGoogle Scholar |
U.S. Environmental Protection Agency (2017) ‘DRAFT Inventory of US greenhouse gas emissions and sinks: 1990–2015.’ Available at https://www.epa.gov/sites/production/files/2017-02/documents/2017_complete_report.pdf [Verified 13 April 2017]
Velazco J, Cottle DJ, Hegarty R (2014) Methane emissions and feeding behaviour of feedlot cattle supplemented with nitrate or urea. Animal Production Science 54, 1737–1740.
| Methane emissions and feeding behaviour of feedlot cattle supplemented with nitrate or urea.Crossref | GoogleScholarGoogle Scholar |
Velazco JI, Mayer DG, Zimmerman S, Hegarty RS (2016) Use of short-term breath measures to estimate daily methane production by cattle. Animal 10, 25–33.
| Use of short-term breath measures to estimate daily methane production by cattle.Crossref | GoogleScholarGoogle Scholar |
Veneman JB, Saetnan ER, Clare A, Newbold CJ (2016) MitiGate; an online meta-analysis database for quantification of mitigation strategies for enteric methane emissions. The Science of the Total Environment 572, 1166–1174.
| MitiGate; an online meta-analysis database for quantification of mitigation strategies for enteric methane emissions.Crossref | GoogleScholarGoogle Scholar |
Viechtbauer W (2010) Conducting meta-analyses in R with the metaphor package. Journal of Statistical Software 36, 1–48.
| Conducting meta-analyses in R with the metaphor package.Crossref | GoogleScholarGoogle Scholar |
Wallace RJ, Rooke JA, McKain N, Duthie C-A, Hyslop JJ, Ross DW, Waterhouse A, Watson M, Roehe R (2015) The rumen microbial metagenome associated with high methane production in cattle. BMC Genomics 16, 839
| The rumen microbial metagenome associated with high methane production in cattle.Crossref | GoogleScholarGoogle Scholar |
Yan T, Agnew RE, Gordon FJ, Porter MG (2000) Prediction of methane energy output in dairy and beef cattle offered grass silage-based diets. Livestock Production Science 64, 253–263.
| Prediction of methane energy output in dairy and beef cattle offered grass silage-based diets.Crossref | GoogleScholarGoogle Scholar |
Yan T, Porter MG, Mayne CS (2009) Prediction of methane emission from beef cattle using data measured in indirect open-circuit respiration chambers. Animal 3, 1455–1462.
| Prediction of methane emission from beef cattle using data measured in indirect open-circuit respiration chambers.Crossref | GoogleScholarGoogle Scholar |




