Improving accuracy and stability of genetic predictions for dairy cow survival
M. Khansefid A B * , J. E. Pryce
A B * , J. E. Pryce  A B , S. Shahinfar
A B , S. Shahinfar  A , M. Axford
A , M. Axford  A B C , M. E. Goddard
A B C , M. E. Goddard  A D and M. Haile-Mariam
A D and M. Haile-Mariam  A B
A B
A Agriculture Victoria Research, AgriBio, Centre for AgriBioscience, 5 Ring Road, Bundoora, Vic. 3083, Australia.
B School of Applied Systems Biology, La Trobe University, Bundoora, Vic. 3083, Australia.
C DataGene Ltd, 5 Ring Road, Bundoora, Vic. 3083, Australia.
D Faculty of Veterinary and Agricultural Sciences, The University of Melbourne, Parkville, Vic. 3010, Australia.
Animal Production Science 63(11) 1031-1042 https://doi.org/10.1071/AN23018
Submitted: 11 January 2023 Accepted: 28 March 2023 Published: 17 April 2023
© 2023 The Author(s) (or their employer(s)). Published by CSIRO Publishing. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)
Abstract
Context: Cow survival is an important trait for dairy farm profitability and animal welfare, yet it is difficult to improve because of its complexity arising, in part, from varied reasons for culling and delay in getting actual culling data, which leads to low accuracy and instability of genetic predictions.
Aims: To explore the benefits of partitioning the cow survival trait into ‘early survival’ (survival coded as a binary trait from the first to the second lactation) and ‘late survival’ (survival from the second to later lactations) on genetic predictions in addition to predictors of culling decisions.
Methods: The raw phenotypic survival records for 1 619 542 Holstein and 331 996 Jersey cows were used in our study. All cows within each herd were allocated to either a reference or validation set. The accuracy and stability of genetic predictions were compared across lactations in the validation set. Further, we estimated the phenotypic and genetic correlation between overall, early or late cow survival and production, type, workability, and fertility traits using bivariate sire models.
Key results: The heritability of overall survival in Jerseys (0.069 ± 0.003) was higher than in Holsteins (0.044 ± 0.001). The heritability of early survival was higher than that of late survival in Holstein (0.039 ± 0.002 vs 0.036 ± 0.001) and Jersey (0.080 ± 0.006 vs 0.053 ± 0.003). The genetic correlation between early and late survival was high in both breeds (0.770 ± 0.017 in Holstein and 0.772 ± 0.028 in Jersey). Adding survival information up to the sixth lactation had a large effect on genetic predictions of overall and late survival, whereas the predictions of early survival remained the same across lactations. Milk and protein yields, somatic cell score, fertility and temperament were highly correlated with early survival in Holstein and Jersey. However, the genetic correlations between production, type or workability traits and late survival were generally weaker than those and early survival.
Conclusions: Early and late survival should be considered as different traits in genetic evaluations, because they are associated with different culling decisions.
Implications: Partitioning cow survival into early and late survival and analysing them as two correlated traits could improve the accuracy and the stability of estimated breeding values compared with analysing overall survival as a single trait.
Keywords: calving interval, cow survival rate, longevity, milk traits, prediction accuracy, prediction stability, type traits, workability traits.
Introduction
In addition to welfare and direct economic benefits, improving longevity or cow survival reduces replacement costs, medicine and treatment expenses (veterinary costs) and methane emissions (Sewalem et al. 2006; Pritchard et al. 2013; Zhang et al. 2019). Although survival has a high relative weight or percentage emphasis (~8%) in Australia’s national selection index, namely, the balanced performance index (BPI), this weight was almost doubled (~13%) in the sustainability index (SI) launched nationally in Australia in 2022 (DataGene 2022a). The aim of the SI is to reduce methane emission intensity, which is achieved through increasing the relative emphasis on feed saved and survival traits compared with BPI (Pryce et al. 2015; Richardson et al. 2022).
Longevity in dairy cows is often defined as productive life (number of days the cows are in milk in their whole life or up to 84 months of age) or number of completed lactations (Hu et al. 2021). The latter definition for cow survival seems to be more suitable for countries with predominantly seasonal pasture-based dairy production system because the exact cow exit time from herds and the underlying culling reason are often not recorded precisely. Consequently, calving events are used to identify completed lactations, more specifically survival up to the nine calving events is used in genetic evaluations in Australia (Madgwick and Goddard 1989).
The reasons for culling a cow from the first to the second lactation are often different from the factors influencing survival of cows in later lactations. Further, the economic benefits of improving survival rate is highest in the first lactation (Holtsmark et al. 2009). We anticipated that culling reasons in the first lactation could be associated with milk production (voluntary culling) and workability traits. Whereas in later lactations, poor fertility and high somatic cell score could be the major underlying reason for removing cows from herds (involuntary culling; Workie et al. 2021).
Actual cow survival cannot be recorded before the end of productive life. Survival can also be considered as success or failure of a cow to reach a certain age or life event such as calving. These binary codes associated with different numbers of calving events could be analysed as a single or correlated traits using linear or threshold models (Holtsmark et al. 2009). Yet, for the first successful survival binary score, cows need to have two calving events. Therefore, predictor traits are often used in many countries, such as conformation traits that are used either to predict cow survival indirectly, or improve the accuracy of genetic predictions (Forabosco et al. 2009; Khansefid et al. 2021). It is reasonable to take censored survival data into account, especially for young cows, by using appropriate methods, such as proportional-hazards models (Forabosco et al. 2009; Sasaki 2013). Considering censored data in a multi-trait model with binary survival codes and predictor traits has been reported to have no or limited benefits, and could increase the complexity of the model significantly (Holtsmark et al. 2009).
In the present study, we analysed the binary cow survival codes in Holstein and Jersey to (1) explore the cow survival rate across lactations, (2) estimate the genetic correlation between ‘early survival’ (survival from the first to the second lactation) and ‘late survival’ (survival from the second to the eighth lactation), (3) estimate the phenotypic and genetic correlations between overall, early or late survival and production, conformation, workability and fertility traits, and (4) estimate the accuracy, bias and stability of genetic predictions for overall, early and late survival across lactations.
Materials and methods
Data
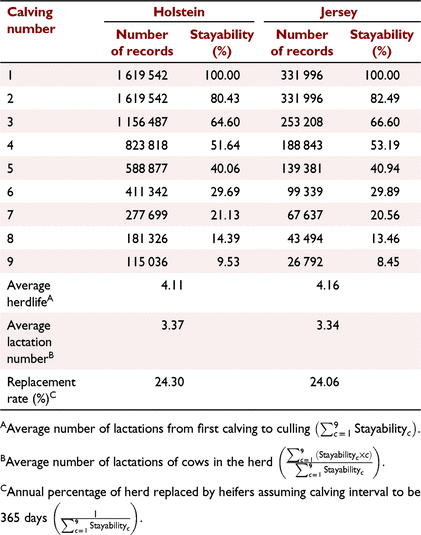
We used the data provided by DataGene Pty Ltd (Melbourne, Australia) and Holstein Australia (Melbourne, Australia) in our study. Pure Holstein and Jersey cows were identified according to DataGene four-character breed codes. Cows were excluded from the analyses where their sires were unknown, or they belonged to a contemporary group (herd–year–season) in their first calving with fewer than five cows. The final dataset contained raw survival data for 1 619 542 Holstein cows (5 174 127 records) and 331 996 Jersey cows (1 150 690 records). The year of first calving for almost all these cows was between 1980 and 2020. The cow survival records (1 = survived to the next lactation, 0 = failed to survive to the next lactation) consisted of survival records up to the eighth lactation.
By using the above data, first, we calculated the stayability of the cows across nine calving events (i.e. eight lactations), as well as average herdlife, average number of lactations and replacement rate in Holstein and Jersey cows (Table 1). We defined stayability as the probability of cows surviving to a specific number of calvings. We partitioned survival or ‘overall survival’ to ‘early survival’ (survival from the first to the second lactation) and ‘late survival’ (survival from the second to later lactations), because the traits associated with culling decisions could be different in the first and subsequent lactations.
|
For the cows that had survival data, we extracted their first-lactation production (12 traits), conformation (25 linear- and 5 composite-type traits), body condition score (BCS), workability (3 traits), and fertility (first calving interval) records from the DataGene Database (DataGene 2022b).
The predicted ‘305-day’ milk, fat, protein and lactose yields were obtained from DataGene. Additionally, the adjusted test-day deviation records (‘Test-day’) were predicted using ASReml (Gilmour et al. 2022). The ‘Test-day’ record for each cow (i.e. effect of Cowl) was calculated as follows:
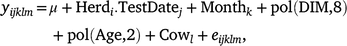
where, yijklm is the test-day record (milk, fat, protein, lactose yields and percentages or somatic cell score) in the first lactation; μ is the effect of overall mean; Herdi.TestDatej is the effect of the ith herd at the jth test date; Monthk is the effect of the kth calving month; pol(DIM,8) and pol(Age,2) are the regression coefficients of legendre polynomials of order 1–8 for days in milk (DIM) and of order 1–2 for age at calving in months; Cowl ~ N(0, Iσ2c) and eijklm ~ N(0, Iσ2e) are the random effect of the lth cow and the random residual term respectively.
The pedigree information was also provided by DataGene and used to perform genetic analyses. Using ASReml (Gilmour et al. 2022), we pruned the pedigree and extracted breed-specific pedigree files that contained the relatives of the cows with survival records back to 20 and 19 generations in Holstein and Jersey respectively.
Heritability of cow survival
The variance components and heritability (h2) of overall, early and late survival in Holstein and Jersey were estimated by univariate sire models by using ASReml (Gilmour et al. 2022), as follows:
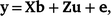
where, y is the vector of cow survival data (for Lactation 1–8 in overall survival, for Lactation 1 in early survival, and for Lactation 2–8 in late lactation); b is the vector of fixed effects (mean and herd–year–season, as well as parity number for overall and late survival); u ~ N(0, Aσ2u) contains the predicted transmitting abilities (PTAs) of sires and A is the numerator relationship matrix; e ~ N(0, Iσ2e) contains random residual effects and I is the identity matrix; X and Z are design matrices relating the phenotypes to the fixed and random effects respectively.
Genetic correlation between early and late survival
Using ASReml (Gilmour et al. 2022), we estimated genetic correlation between early and late survival within Holstein and Jersey, by a bivariate sire model, as follows:
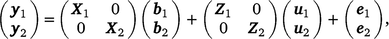
where, y1 and y2 contain the early and late survival records respectively; b1, u1 and e1 are the vectors of fixed effects (mean and herd–year–season), PTAs of sires and residual effects for early survival respectively; b2, u2 and e2 are the vectors of fixed effects (mean, herd–year–season and parity number), PTAs of sires and residual effects for late survival respectively; and X1, Z1, X2 and Z2 are design matrices. The genetic effects were driven from ~ N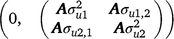 . As a cow needs to survive to the second lactation to have a late survival record, the random residual covariance between early and late survival was set to zero. Therefore, the residual effects were driven from ~ N
. As a cow needs to survive to the second lactation to have a late survival record, the random residual covariance between early and late survival was set to zero. Therefore, the residual effects were driven from ~ N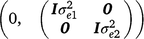 .
.
Accuracy and stability of genetic predictions for cow survival
The cow survival dataset was divided into two groups with almost the same number of cows. Based on the herds the cows calved for the first time, cows within the same herds were all allocated to either the first group (reference set), or the second group (validation set). We explored the effect of including survival records up to different number of lactations in the reference set on the genetic predictions for overall, early and late survival in the validation set. To have a fair comparison between predictions in different models, we used the variance components estimated when survival records for all lactations were included in the model. Further, to reduce the runtime, especially for the larger analyses (Holstein bivariate models), we ran animal models by solving the mixed-model equations with preconditioned conjugate gradient (PCG) method (Tsuruta et al. 2001) implemented in ASReml (Gilmour et al. 2022).
We calculated the accuracy and bias of estimated breeding values (EBVs) for the cows in the validation set and their sires. The accuracy of EBVs was calculated according to the reduction in error sum of squares (or alternatively error variance) due to fitting cow or sire EBVs in the model.
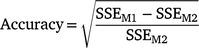
where, SSEM1 and SSEM2 are the error sum of squares for Models M1 and M2 respectively. M1 contains the fixed effects as well as linear effect of EBVs and is used to regress the survival phenotypes (overall, early or late survival) on EBVs of either cows in the validation set or their sires, whereas M2 contains only the fixed effects. M2 is the model often used to adjust phenotypes for the fixed effects. Therefore, the calculated prediction accuracy in this formula is in fact the correlation coefficient between survival EBVs and phenotypes adjusted for fixed effects.
The prediction bias was defined as the regression coefficient of phenotypes on EBVs (bSurvival,EBV) in M1. Consequently, when cow survival phenotypes were regressed on their own EBVs and their sires EBVs, bSurvival,EBV should be close to 1 and 0.5 respectively.
Correlation between overall, early and late survival and other traits
Using a univariate sire model, we estimated the variance components and h2 for first-lactation milk production, milk components and somatic cell score (305-day and Test-day), conformation traits, BCS, workability traits, and first calving interval in Holstein and Jersey. The model was like the univariate sire model used to estimate h2 for survival. However, the fixed effects in the model were different and included the overall mean for all traits; herd–year–season, month of calving, age at calving for calving interval and 305-day milk traits; herd–year–season for test-day milk traits; and herd–year–classifier, age and DIM at classification date for BCS, conformation and workability traits.
Using the variance components from the univariate models as starting values, we ran bivariate sire models to calculate the phenotypic and genetic correlations between overall, early or late survival and the traits measured in first lactation, described in the previous paragraph. We estimated residual covariance between survival and all traits except for the calving interval between first and second calving, which was set to zero, because of the necessity to survive to the second calving to have a calving-interval record. Hence, we reported only the genetic correlation between survival and first calving interval.
Results
Cow survival
The cow survival rate of Australian cows in herds is shown in Table 1. The survival of Holstein and Jersey cows across lactations was very similar to each other during 1980–2020. However, in the first few lactations, the survival rate of Jersey cows was slightly higher than that of Holstein cows. In both breeds, the proportion of cows surviving to the next lactation declined with age. For instance, about 80% of Holstein cows survived from the first to second lactation, but this rate was reduced to 65% in the eighth lactation. Consequently, only 9.53% and 8.45% of Holstein and Jersey cows had more than nine calvings respectively (i.e. eight or more completed lactations). As a result of reduction in survival rate by age, the average number of lactations of cows in herds was less than average herdlife.
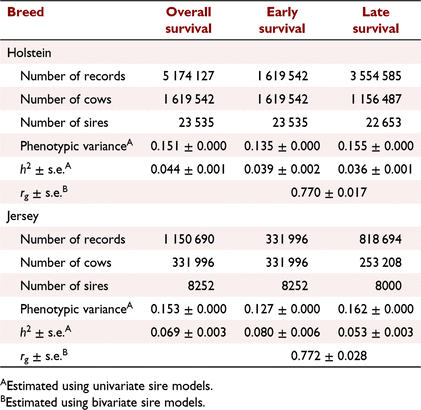
The estimated h2 for overall, early and late survival as well as genetic correlation between early and late survival are shown in Table 2. The h2 ± s.e. of overall survival in Jersey (0.069 ± 0.003) was higher than that in Holstein (0.044 ± 0.001). The h2 of early survival was higher than that of late survival in Holstein (0.039 ± 0.002 vs 0.036 ± 0.001), and in Jersey (0.080 ± 0.006 vs 0.053 ± 0.003). The genetic correlation between early and late survival was high in Holstein (0.770 ± 0.017) and Jersey (0.772 ± 0.028).
|
Accuracy, bias and stability of genetic predictions for cow survival
Prediction accuracy and bias of EBVs for overall, early and late survival are shown for Holstein sires and cows in Figs 1, 2, and for Jersey sires and cows in Figs 3, 4, respectively. The overall, early and late survival phenotypes of the cows in the validation set were regressed on their own EBVs, or on EBV of their sires for overall, early and late survival. In these figures, the columns are highlighted with red lines where the phenotypes and the EBVs are associated with the same trait (e.g. survival phenotypes and EBVs are for early survival). Although the early survival phenotypes remained the same across lactations, the bivariate models used to estimate EBVs for early and late survival could include different number of lactations for late survival. Further, using genetic correlation between early and late survival in bivariate models, we could estimate late survival EBVs when we only had survival phenotypes for the first lactation.
The accuracy of EBVs was generally low in both Holsteins and Jerseys. However, the highest accuracy and lowest bias of predictions were achieved when the phenotypes and the EBVs were associated with the same trait. As we expected, early survival was the most stable prediction across lactations (i.e. the accuracy and bias of EBVs did not change by adding survival records of subsequent lactations to the prediction model). For overall survival and late survival, the genetic predictions became stable after the sixth lactation.
Correlation between cow survival and other traits
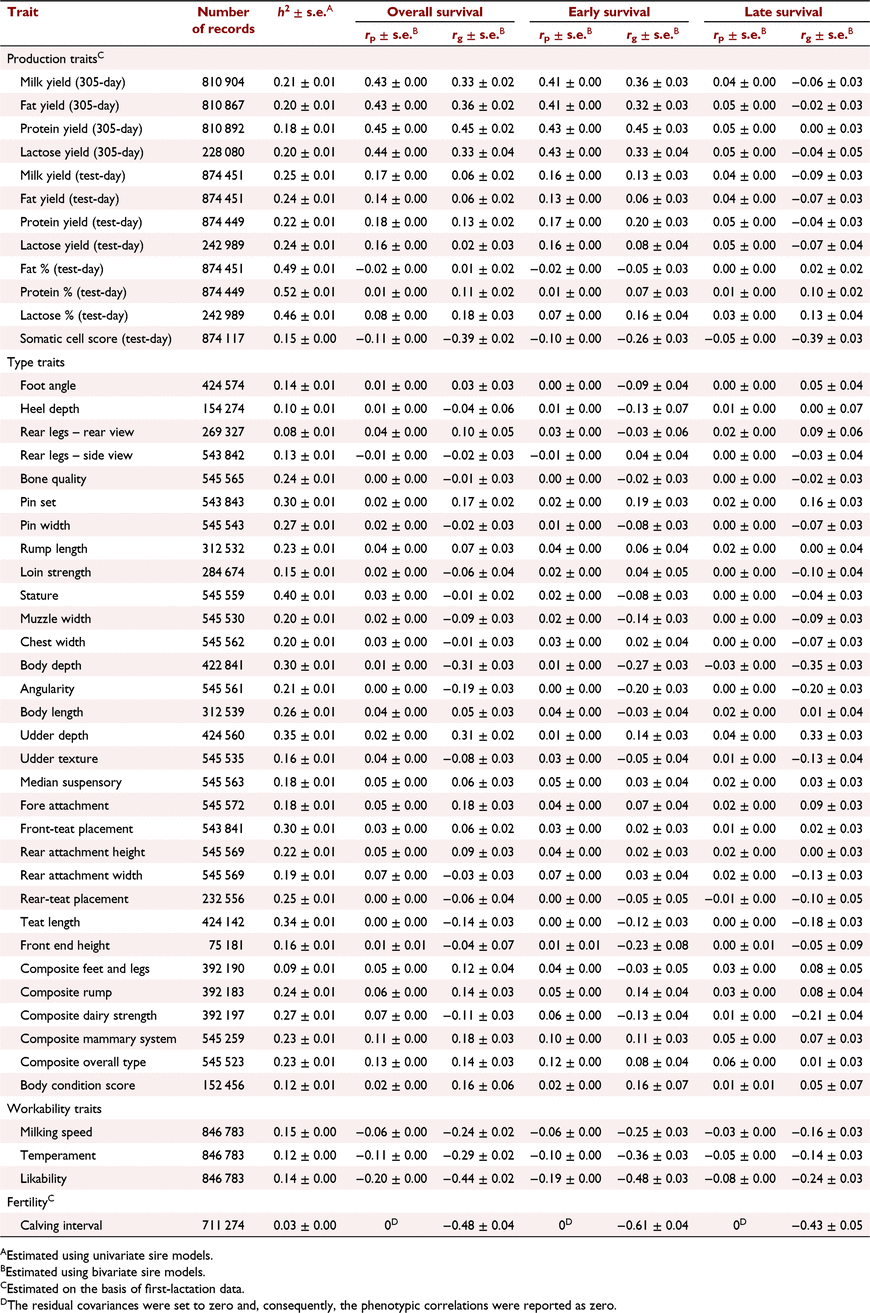
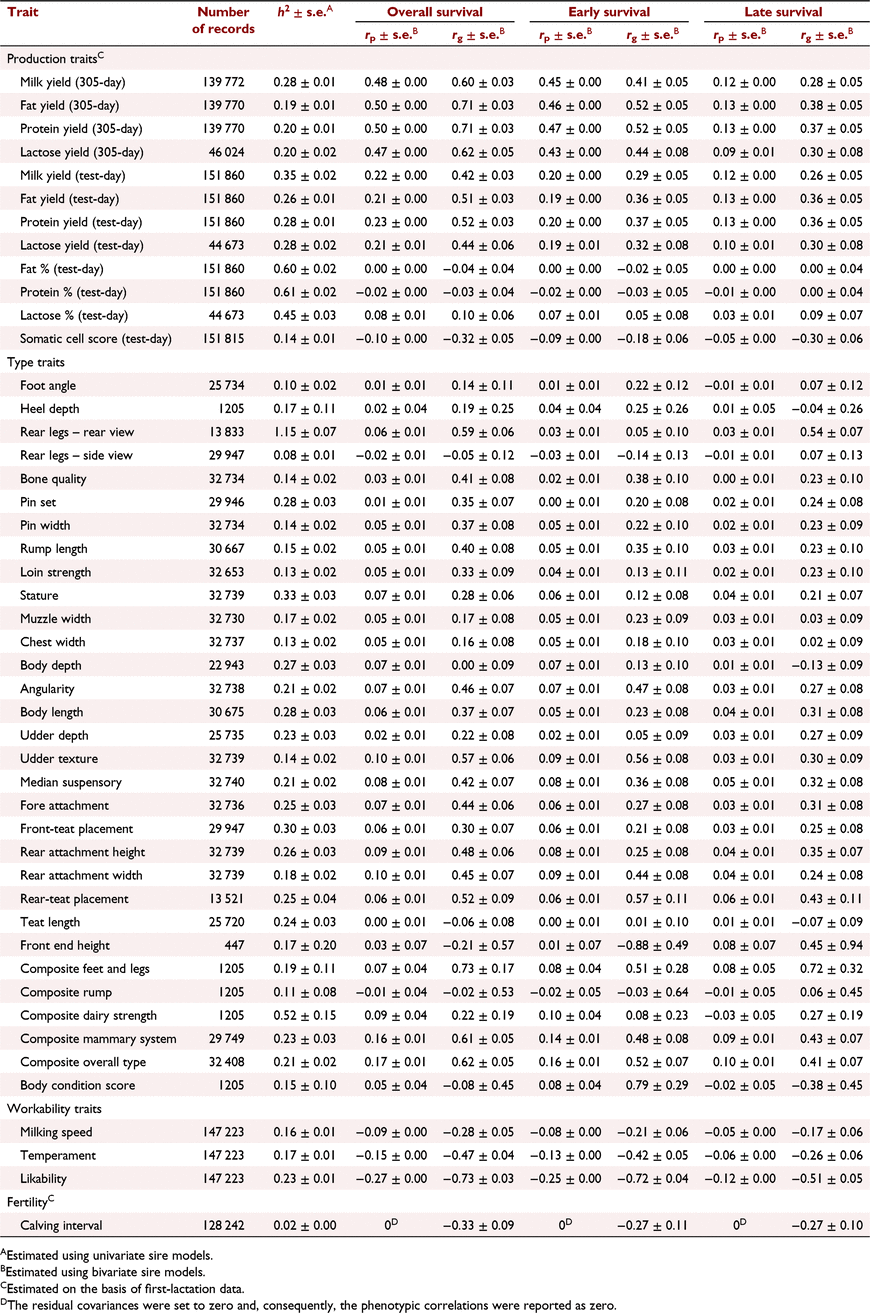
The h2 of some commonly recorded phenotypes and their phenotypic and genetic correlations with overall, early and late survival are shown in Table 3 for Holstein and in Table 4 for Jersey. Generally, the phenotypic correlations between cow survival and other traits were lower than the genetic correlations.
The genetic correlations between milk production traits in the first lactation and early survival were higher than their correlation with late survival. In Holsteins, overall and early survival were highly correlated with 305-day milk production traits. However, there was a weak correlation between late survival and 305-day milk traits, and also survival and test-day milk traits. In Jerseys, there was a high genetic correlation between overall, early or late survival and milk production traits. In Holstein 305-day protein yield (0.45 ± 0.02) and in Jersey 305-day protein and fat yields (both 0.71 ± 0.03) had the highest genetic correlation with overall survival. The genetic correlation between somatic cell count and late survival was stronger than that with early survival in Holstein (−0.39 ± 0.03 vs −0.26 ± 0.03) and Jersey (−0.30 ± 0.06 vs −0.18 ± 0.06).
The genetic correlation between conformation traits and survival were often low in Holstein. In Jersey, the correlations were higher but were associated with large standard errors. However, pin set had low to moderate genetic correlation with overall survival in Holstein (0.17 ± 0.02) and Jersey (0.35 ± 0.07). Body depth (−0.31 ± 0.03), angularity (−0.19 ± 0.03) and udder depth (0.31 ± 0.02) in Holstein, and angularity (0.46 ± 0.07) and the type traits associated with body size (stature and body length) or milk production such as udder depth (0.22 ± 0.08) in Jersey, were genetically correlated with overall survival. There was a positive genetic correlation between survival and overall type, as well as composite mammary system in Holstein and Jersey.
The genetic correlation between workability traits and survival was strong in Holstein and Jersey. The correlations between workability traits and early survival were stronger than those between workability traits and late survival. Likeability had the highest correlation with early survival in Holstein (−0.48 ± 0.03) and Jersey (−0.72 ± 0.04). The most and least desirable cows by farmers were scored one and five for likeability respectively. Similarly, low scores are associated with placid temperament and very fast milking speed. Hence, we expected negative correlation between workability traits and cow survival.
Fertility (first calving interval) was highly correlated with early, late and overall survival in Holstein and Jersey. The genetic correlation between early survival and fertility was much higher in Holstein (−0.61 ± 0.04) than in Jersey (−0.27 ± 0.11).
Discussion
Survival of a cow depends on its ability to live (avoid death) and perform well (avoid being culled). Cow survival rate gradually declined with lactation number in both Holstein and Jersey. This is in line with previously reported cow survival rates in the USA (Nieuwhof et al. 1989), New Zealand (Harris 1989), and Norway (Holtsmark et al. 2009) and highlighted the importance of including the effect of parity in genetic evaluations for survival. The average number of lactations for cows remaining in the herd was ~4.1 in our study. This is still high despite the reduction in number of dairy cows in Australia, especially since 2000 (DataGene 2022c).
The h2 of early survival was larger than that of late survival. This could be due to higher h2 of the traits underlying culling decisions in early survival (milk production traits and likeability) than in late survival (fertility and somatic cell score). The h2 estimates for overall, early and late survival were very similar to the reported h2 for cow survival in Australian Holsteins by Haile-Mariam et al. (2003) (0.02) and Haile-Mariam and Pryce (2015) (0.03–0.07). Generally, the h2 estimates for survival analysed as binary scores with a linear model were low in different breeds and across different countries (Sasaki 2013). However, the relative emphasis of survival is large in BPI (Byrne et al. 2016) and is almost doubled in the SI due to its relationship with lowering methane emissions (Richardson et al. 2022). Hence, improving the accuracy of genetic predictions could lead to greater genetic gain for survival, which has a large economic as well as environmental impact.
Holtsmark et al. (2009) reported the genetic correlation between survival in the first and second (0.85 ± 0.02), second and third (0.93 ± 0.02), and first and third (0.66 ± 0.03) lactations. They concluded that survival in the first lactation could be considered as a different trait from survival in later lactations. In our study, the lowest genetic correlation was observed between survival in the first and survival in the second lactation. However, we reported the genetic correlation only between survival in the first lactation (i.e. early survival) and survival in the later lactations (i.e. late survival) in our paper. The genetic correlation between early and late survival was high, but lower than one. Therefore, a multi-trait model could be a suitable method for analysing these two correlated traits.
In the present study, there was a strong positive correlation between early survival and milk production traits, and there was a strong correlation between late survival and fertility and somatic cell score. Therefore, farmers are more likely to cull cows for low production in their first lactation, while fertility and health traits influence survival of the cows in subsequent lactations. These results were in line with the findings of Workie et al. (2021). We could assume that early survival is a better predictor for voluntary culling and late survival is a better predictor for involuntary culling. In Holsteins, late survival is almost independent of milk production and could be considered to be similar to functional survival (Weigel et al. 2003; Holtsmark et al. 2009). However, milk production appears to still be important for culling decisions in later lactations in Jerseys. The moderate to large genetic correlation between survival and type traits represents deliberate culling for small size and poor type in Jerseys as well. The genetic correlations between late survival and milk production traits as well as some type traits are different between Jersey and Holstein, probably because the reasons for culling cows or their relative importance, especially in multiparous cows, are different across breeds. For instance, milk production has a high impact on culling decisions in Jersey, whereas in Holstein fertility is of higher importance.
Although we used only the first-lactation milk records and calving interval to calculate correlations between production or fertility and survival, this does not appear to have contributed to the higher correlation between production traits and early survival than that between production traits and late survival. For instance, the genetic correlation between first-lactation somatic cell scores and late survival was even higher than that between first-lactation somatic cell scores and early survival. Generally, the correlation between most of the conformation traits, such as mammary system, or pin set and survival could be associated with their effect on either production or reproduction traits (Zavadilová et al. 2011). Workability traits were also strongly correlated with survival, which could be associated with their moderate to high correlation with production traits and also their direct effect on culling decisions.
The phenotypic and genetic correlations between overall survival and production or conformation traits were similar, but not exactly the same as those previously reported by Khansefid et al. (2021). In the present study, we used raw binary survival scores instead of survival trait deviations. We also kept all survival records back to 1980, which are currently used in national cow survival evaluations by DataGene. We assumed that survival was a same trait across four decades. This could be a debatable assumption as the reasons for culling cows could have changed across years to meet the needs of a changing business environment in the dairy industry. Haile-Mariam and Pryce (2015) and Workie et al. (2021) reported that the h2 of survival and the culling probabilities due to different reasons changed across years. To be able to still use the historical survival data in genetic evaluations, survival across certain year intervals could be potentially analysed as different traits in a multi-trait model. However, the practicality of such a model for routine national genetic evaluations and its impacts on prediction accuracy and bias is yet to be investigated.
The prediction accuracy in the validation set was low for overall survival (univariate model), and early and late survival (bivariate model). Further, the predictions were slightly biased, which could be associated with inaccurate estimation of variance components, as we assumed that survival was a same trait across four decades. However, according to Haile-Mariam and Pryce (2015), survival changes genetically over time. Considering survival in the first lactation as a separate trait in the model resulted in a more accurate and stable genetic prediction across lactations. Further, this could reduce the prediction bias for early survival compared with analysing survival in the first lactation by using a univariate model. The reduction in prediction bias for early survival in bivariate models could be due to using accurate variance components for early survival instead of estimated variance components for overall survival. The reduction in prediction bias for late survival was less obvious, especially in Jerseys, probably because the variance components for late survival (survival in lactations two to eight) were closer to those estimated for overall survival (survival in lactation one to eight). Due to using appropriate variance components and the same definition for survival in the validation set, each of the overall, early and late survival phenotypes was predicted the best (highest accuracy and lowest bias), with the EBVs being associated with the same trait. There was little change in the accuracy of predictions from adding data from the seventh and eighth lactations, perhaps because only a small proportion of cows record survival to the seventh and eighth lactations.
The EBVs for early and late survival can be combined and presented as a single trait to the industry. Further, different predictor traits for early and late survival could be incorporated to calculate survival index. As early survival was highly correlated with milk and protein yields, double counting should be avoided in selection indices when recalculating the economic weights, or simply reducing the economic weights for production traits according to the genetic correlation between milk traits and early survival.
Conclusions
The genetic correlation between survival in the first lactation and later lactations was high, but still different from one. Genetic correlations between other traits and survival were different for early and late survival, probably due to different reasons for culling in first lactation and in later lactations. Therefore, partitioning survival to early and late survival and analysing them as two correlated traits could be an easy and practical method to indirectly incorporate the culling reasons into genetic evaluations of cow survival. In a bivariate model, the genetic predictions for early survival were stable and less biased than those for overall survival, and, for late survival, inclusion of more than six lactations had no benefit on the accuracy or bias of the EBVs.
Data availability
The data that support this study were obtained from DataGene and Holstein Australia by permission/licence. Data will be shared upon reasonable request to the corresponding author with permission from DataGene and Holstein Australia.
Conflicts of interest
The authors declare no conflicts of interest.
Declaration of funding
This research did not receive any specific funding.
Acknowledgements
The authors acknowledge DataGene and Holstein Australia for providing the data for our research. We also appreciate financial support from DairyBio, a joint venture of Dairy Australia, The Gardiner Foundation, and Agriculture Victoria (Melbourne, Australia).
References
Byrne TJ, Santos BFS, Amer PR, Martin-Collado D, Pryce JE, Axford M (2016) New breeding objectives and selection indices for the Australian dairy industry. Journal of Dairy Science 99, 8146–8167.| New breeding objectives and selection indices for the Australian dairy industry.Crossref | GoogleScholarGoogle Scholar |
DataGene (2022a) Sustainability index – technote 29. Available at https://datagene.com.au/sites/default/files/Upload%20Files/Technote%2029%20Sustainability%20Index.pdf [Accessed 1 December 2022]
DataGene (2022b) Data interchange formats effective from November 2022. Available at https://datagene.com.au/sites/default/files/Upload%20Files/dif2022v1.0.pdf [Accessed 25 November 2022]
DataGene (2022c) Australian national herd recording statistics. Available at https://datagene.com.au/sites/default/files/Upload%20Files/National%20Statistics%2020202021_0.xls [Accessed 10 December 2022]
Forabosco F, Jakobsen JH, Fikse WF (2009) International genetic evaluation for direct longevity in dairy bulls. Journal of Dairy Science 92, 2338–2347.
| International genetic evaluation for direct longevity in dairy bulls.Crossref | GoogleScholarGoogle Scholar |
Gilmour AR, Gogel BJ, Cullis BR, Welham SJ, Thompson R (2022) ASReml user guide release 4.2 structural specification. VSN International, Hemel Hempstead, UK. Available at www.vsni.co.uk
Haile-Mariam M, Pryce JE (2015) Variances and correlations of milk production, fertility, longevity, and type traits over time in Australian Holstein cattle. Journal of Dairy Science 98, 7364–7379.
| Variances and correlations of milk production, fertility, longevity, and type traits over time in Australian Holstein cattle.Crossref | GoogleScholarGoogle Scholar |
Haile-Mariam M, Bowman PJ, Goddard ME (2003) Genetic and environmental relationship among calving interval, survival, persistency of milk yield and somatic cell count in dairy cattle. Livestock Production Science 80, 189–200.
| Genetic and environmental relationship among calving interval, survival, persistency of milk yield and somatic cell count in dairy cattle.Crossref | GoogleScholarGoogle Scholar |
Harris BL (1989) New Zealand dairy cow removal reasons and survival rate. New Zealand Journal of Agricultural Research 32, 355–358.
| New Zealand dairy cow removal reasons and survival rate.Crossref | GoogleScholarGoogle Scholar |
Holtsmark M, Heringstad B, Ødegård J (2009) Predictive abilities of different statistical models for analysis of survival data in dairy cattle. Journal of Dairy Science 92, 5730–5738.
| Predictive abilities of different statistical models for analysis of survival data in dairy cattle.Crossref | GoogleScholarGoogle Scholar |
Hu H, Mu T, Ma Y, Wang X, Ma Y (2021) Analysis of longevity traits in holstein cattle: a review. Frontiers in Genetics 12, 695543
| Analysis of longevity traits in holstein cattle: a review.Crossref | GoogleScholarGoogle Scholar |
Khansefid M, Haile-Mariam M, Pryce JE (2021) Improving the accuracy of predictions for cow survival by multivariate evaluation model. Animal Production Science 61, 1828–1836.
| Improving the accuracy of predictions for cow survival by multivariate evaluation model.Crossref | GoogleScholarGoogle Scholar |
Madgwick PA, Goddard ME (1989) Genetic and phenotypic parameters of longevity in Australian dairy cattle. Journal of Dairy Science 72, 2624–2632.
| Genetic and phenotypic parameters of longevity in Australian dairy cattle.Crossref | GoogleScholarGoogle Scholar |
Nieuwhof GJ, Norman HD, Dickinson FN (1989) Phenotypic trends in herdlife of dairy cows in the United States. Journal of Dairy Science 72, 726–736.
| Phenotypic trends in herdlife of dairy cows in the United States.Crossref | GoogleScholarGoogle Scholar |
Pritchard T, Coffey M, Mrode R, Wall E (2013) Understanding the genetics of survival in dairy cows. Journal of Dairy Science 96, 3296–3309.
| Understanding the genetics of survival in dairy cows.Crossref | GoogleScholarGoogle Scholar |
Pryce JE, Gonzalez-Recio O, Nieuwhof G, Wales WJ, Coffey MP, Hayes BJ, Goddard ME (2015) Hot topic: definition and implementation of a breeding value for feed efficiency in dairy cows. Journal of Dairy Science 98, 7340–7350.
| Hot topic: definition and implementation of a breeding value for feed efficiency in dairy cows.Crossref | GoogleScholarGoogle Scholar |
Richardson CM, Amer PR, Quinton C, Crowley J, Hely FS, van den Berg I, Pryce JE (2022) Reducing greenhouse gas emissions through genetic selection in the Australian dairy industry. Journal of Dairy Science 105, 4272–4288.
| Reducing greenhouse gas emissions through genetic selection in the Australian dairy industry.Crossref | GoogleScholarGoogle Scholar |
Sasaki O (2013) Estimation of genetic parameters for longevity traits in dairy cattle: a review with focus on the characteristics of analytical models. Animal Science Journal 84, 449–460.
| Estimation of genetic parameters for longevity traits in dairy cattle: a review with focus on the characteristics of analytical models.Crossref | GoogleScholarGoogle Scholar |
Sewalem A, Miglior F, Kistemaker GJ, Van Doormaal BJ (2006) Analysis of the relationship between somatic cell score and functional longevity in Canadian Dairy Cattle. Journal of Dairy Science 89, 3609–3614.
| Analysis of the relationship between somatic cell score and functional longevity in Canadian Dairy Cattle.Crossref | GoogleScholarGoogle Scholar |
Tsuruta S, Misztal I, Strandén I (2001) Use of the preconditioned conjugate gradient algorithm as a generic solver for mixed-model equations in animal breeding applications. Journal of Animal Science 79, 1166–1172.
| Use of the preconditioned conjugate gradient algorithm as a generic solver for mixed-model equations in animal breeding applications.Crossref | GoogleScholarGoogle Scholar |
Weigel KA, Palmer RW, Caraviello DZ (2003) Investigation of factors affecting voluntary and involuntary culling in expanding dairy herds in Wisconsin using survival analysis. Journal of Dairy Science 86, 1482–1486.
| Investigation of factors affecting voluntary and involuntary culling in expanding dairy herds in Wisconsin using survival analysis.Crossref | GoogleScholarGoogle Scholar |
Workie ZW, Gibson JP, van der Werf JHJ (2021) Analysis of culling reasons and age at culling in Australian dairy cattle. Animal Production Science 61, 680–689.
| Analysis of culling reasons and age at culling in Australian dairy cattle.Crossref | GoogleScholarGoogle Scholar |
Zavadilová L, Němcová E, Štípková M (2011) Effect of type traits on functional longevity of Czech Holstein cows estimated from a Cox proportional hazards model. Journal of Dairy Science 94, 4090–4099.
| Effect of type traits on functional longevity of Czech Holstein cows estimated from a Cox proportional hazards model.Crossref | GoogleScholarGoogle Scholar |
Zhang X, Amer PR, Jenkins GM, Sise JA, Santos B, Quinton C (2019) Prediction of effects of dairy selection indexes on methane emissions. Journal of Dairy Science 102, 11153–11168.
| Prediction of effects of dairy selection indexes on methane emissions.Crossref | GoogleScholarGoogle Scholar |