Quantification of behavioural variation among sheep grazing on pasture using accelerometer sensors
F. Almasi A * , H. Nguyen B C , D. Heydarian D , R. Sohi
A * , H. Nguyen B C , D. Heydarian D , R. Sohi  D , S. Nikbin A , C. J. Jenvey
D , S. Nikbin A , C. J. Jenvey  A , E. Halliwell A , E. N. Ponnampalam
A , E. Halliwell A , E. N. Ponnampalam  E , A. Desai F , M. Jois
E , A. Desai F , M. Jois  D and M. J. Stear
D and M. J. Stear  A
A
A Department of Animal, Plant and Soil Sciences, La Trobe University, Vic. 3083, Australia.
B Department of Mathematics and Statistics, La Trobe University, Bundoora, Vic. 3083, Australia.
C School of Mathematics and Physics, University of Queensland, St. Lucia, QLD 7072, Australia.
D Department of Physiology, Anatomy and Microbiology, La Trobe University, Vic. 3083, Australia.
E Animal Production Sciences, Agriculture Victoria Research, Department of Jobs, Precincts and Regions, Bundoora, Vic. 3083, Australia.
F Centre for Technology Infusion, La Trobe University, Melbourne, Vic. 3083, Australia.
Animal Production Science 62(15) 1527-1538 https://doi.org/10.1071/AN21464
Submitted: 7 September 2021 Accepted: 5 May 2022 Published: 22 July 2022
© 2022 The Author(s) (or their employer(s)). Published by CSIRO Publishing. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)
Abstract
Context: Monitoring the behaviour of animals can provide early warning signs of disease or indicate loss of appetite. Also, an understanding of the variation in behaviours among animals and their distributions is essential for meaningful statistical inference. Therefore, quantifying the variation of behaviours is of both biological and statistical interest.
Aim: The objectives of this study were to determine the distributions and quantify the variation among animals with respect to the times spent grazing, ruminating, idling, walking, and licking.
Methods: The activities of 147 (male = 67, female = 80) Merino lambs at 10–11 months of age on a commercial farm in Edenhope, Victoria, Australia were recorded for 26 days, using ActiGraph accelerometer sensors attached to the left side of the sheep’s muzzle. The male and female sheep were kept in separate paddocks. A Support Vector Machine algorithm was used to differentiate sheep behaviour into six categories: grazing, ruminating, idling, walking, licking, and other activities. The distributions of behaviours were analysed using energy statistics-based tests and Generalised Additive Models for Location, Scale, and Shape (GAMLSS). Different distributions were compared using Akaike Information Criterion (AIC) values.
Key results: Among the distributions that were considered, we found that times spent ruminating in both male and female sheep populations as well as idling in male sheep were best described by the skew exponential type 2 distribution. Grazing, walking and licking behaviours were best described by the Box–Cox t distribution. The distribution of time spent grazing was symmetrical and unimodal in males, and adequately modelled by a normal distribution, but the distribution in females had a prominent left skew. Also, we found that females typically grazed for a longer time than males. However, males spent more time ruminating than grazing.
Conclusions: The time spent by the animal in each activity varied during the day. Within each population, the variation among animals in the time spent grazing was best described by a Box–Cox t distribution.
Implications: This study has enhanced our understanding of grazing behaviour and will facilitate more appropriate analyses of the causes of variation among animals in grazing behaviour.
Keywords: accelerometer sensors, behavioural data, distribution modelling, grazing behaviour, Merino, rumination behaviour, sheep, Support Vector Machine.
Introduction
Monitoring the behaviours of grazing animals is important for detecting early signs of disease or stress and allows corrective measures to be undertaken, to both improve the health and wellbeing of animals and to increase productivity (Krohn and Munksgaard 1993; Frost et al. 1997; Bikker et al. 2014). However, in an extensive farming system, monitoring large numbers of animals can be very difficult. Traditional methods such as physical observation (directly or with cameras) are impractical in an extensive system, because they are time consuming and labour intensive. Recently, sensor technology has been used to monitor feeding behaviours of livestock (mainly cattle and sheep), although most experiments have investigated only small numbers of animals for short periods of time (Hejcmanová et al. 2009; Alvarenga et al. 2016; Burgunder et al. 2018; Ikurior et al. 2020). The accuracy, sensitivity, specificity and precision of tri-axial accelerometers and their predictive ability regarding the grazing behaviours of sheep was evaluated by Alvarenga et al. (2016). They found that the accuracy of predicted grazing, lying, running, standing, and walking behaviours was over 80% with measurements for three time epochs: 3, 5, and 10 s.
The variation in rumination times in dairy cows was investigated by Byskov et al. (2015) and it was found that 32% of the variation was because of variation in feed intake of the different diets, while 48% of the variation was because of variation among individuals. Variation in rumination time among individuals was confirmed in a separate study (Andreen et al. 2020). Gastrointestinal nematode infection reduced the total activity levels of young sheep (Ikurior et al. 2020). They found that the activity of an animal might be affected even at low to moderate gastrointestinal nematode infection. Therefore, variation in activity among individuals is of biological interest because it underlies variation in productivity and disease susceptibility, but it has not yet been well quantified.
Quantifying the variation in activities among grazing animals is also of statistical interest because appropriate analyses require knowledge of the distributions of measurements. Inappropriate analyses can give misleading inferences and unreliable conclusions. For instance, assuming a Gaussian distribution when the data are not normally distributed can adversely affect Type I error and statistical power (Lehmann and Romano 2005). Data often exhibit excess kurtosis and skewness (Blanca et al. 2013). Therefore, the objectives of this study were to determine the distributions of grazing behaviours in sheep and to quantify the variation among animals on a commercial farm to facilitate future use of digital monitoring in improving stock management.
Materials and methods
Animal management
All the experimental procedures were approved by the Animal Ethics Committee, La Trobe University, Victoria, Australia (AEC number 19-037).
The study was conducted on a commercial farm (36°55′56.6″S 141°13′53.9″E) at Edenhope, Victoria, Australia. The temperature during this study varied from 0.6 to 21.6°C with an average of 11°C. The mean daily precipitation, from 4 to 29 May 2020, was 2.1 mm. All of the sensors were attached on 2 May 2020 to all animals. Each day ran from 00:00:00 to 23:59:59 hours.
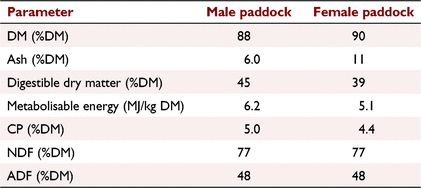
This study was conducted on 191 10–11-month-old Merino sheep. The average liveweight of animals at the start of the experiment was 45.8 kg ± 14 kg (mean ± s.d.) and was 46.6 kg ± 15 kg at the end of the study. Male and female sheep grazed on two different paddocks of sizes 16 and 30 ha, respectively. The pasture height was not measured during this study because of the large variation in sward height throughout each of the study paddocks. There were several species on both paddocks, predominantly Phalaris, barley grass, cape weed and clover. The composition of pasture was analysed in early April by Livestock Logic (60 Portland Road, Hamilton, Vic. 3300) using Near Infrared Reflectance Spectroscopy (NIR) technique (Table 1). Also, the pasture availability was assessed by the farmer 3 weeks prior to starting the study. The pasture availability on female and male paddocks was 1500 kg/ha and 2000 kg/ha, respectively.
|
Accelerometer sensors
ActiGraph (wGT3X-BT; ActiGraph, LLC, Pensacola, FL) sensors with a weight of 19 g and dimensions of 4.6 cm by 3.3 cm by 1.5 cm were embedded into halters (The Farmers Mailbox, Whittlesea, Victoria 3757 Australia) and positioned at the left side of the muzzle (Fig. 1). The orientation of all sensors was the same for all animals to simplify analysis. The sensors were equipped with 4GB storage memory, which can store the data for up to 180 days. The accelerometer sensors recorded data in three axes: X, Y, and Z. Once the sensors were fully charged, they were initialised through the ActiLife software (ver. 6.13.4) at 30 Hz, to record the movements of the animals 30 times per second. All of the sensors were set to start recording from 00:00:00 on 4 May 2020 and secured onto each sheep halter. The activities of sheep were recorded by accelerometer sensors from 4 to 29 May 2020 (26 days). All sensors recorded activities for the first 6 days but because of battery life only 66 sensors were able to record data for the full 26 days (Table 2). The data from the sensors were available for 147 animals (male = 67, female = 80), because some sensors fell off the animals during the study and some of them did not record the necessary information. The rams were yarded on 16 and 21 May, 11:00–14:00 hours and 08:00–11:00 hours, respectively. The data for these times were removed from the analysis.
|
|
|
|
Algorithms
The data were downloaded using the ActiLife software, then converted to CSV batch format. The CSV files were converted to MAT format, using MATLAB software (ver. R2019b). Classifier algorithms developed at the Centre for Technology Infusion (CTI), La Trobe University, using Support Vector Machine (SVM) procedures, were used to process the motion sensor data (Sohi et al. 2021).
For our data, SVM was a good classifier as data were not linearly separable. The SVM models to classify accelerometer data streams into animal behaviour data were developed using human-verified (labelled data) that was collected from previous commercial farm studies (Sohi et al. 2021). The placement and orientation of sensors attached to the sheep were the same as the validation study Sohi et al. (2021). In order to improve the accuracy of classification a number of features from the data were evaluated to determine which were the most useful in discriminating between the models. In addition to custom variables, for instance total magnitude (across X, Y and Z axis), a range of features of motion sensor data were considered such as mean, standard deviation, kurtosis, power signal, peak-to-peak amplitude, autocorrelation, principal component analysis (PCA), and spectral analysis. The percentage of time that the sensor information agreed with the video recordings ranged from 90 to 96% for grazing, rumination, idle and walking but for licking was only 81%.
Statistical analyses
All statistical procedures were implemented in R (R Core Team 2020). The data were summarised by transformation to minutes of each behaviour per hour and then condensed to minutes of each behaviour per day for further analysis. Energy statistics were applied to test whether all the patterns of behaviour were the same across all animals and to test the normality of each distribution (Székely and Rizzo 2004, 2005). The procedure was carried out using the energy package (Rizzo and Szekely 2019). The test uses the Euclidean distances between sample elements. The statistic is given by
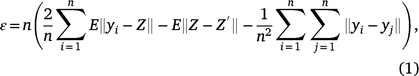
where yi, …, yn is the standardised sample, Z, Z′ are independent, identically distributed standard d-variate normal, n is the number of observations, and ||. || is the Euclidean norm. This test statistic is known to be consistent against all fixed alternatives, which means that as n increases to infinity, ε approaches 0 if and only if the data are normally distributed. If ε tends to a non-zero value, then the data are not normally distributed. The energy package implements bootstrap tests using energy statistics and the functions mvnorm.etest and eqdist.etest were used to evaluate the normality and equality of distributions, respectively.
The best-fitting distributions were determined using the gamlss and histdist functions in the gamlss package (Rigby and Stasinopoulos 2005). All of the graphs were drawn using the ggplot2 (Wickham 2016) and gamlss packages. Several continuous distributions were compared to find the best description of grazing behaviour per day. These included the beta, exponential, exponential Gaussian, gamma, generalised gamma, logistic, inverse Gaussian, power exponential, skew exponential power (SEP) types 1, 2, 3 and 4, skew t types, Box–Cox t distribution, and Weibull distributions. The Akaike Information Criterion,
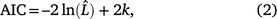
was used to rank the fitted distributions, where k is the number of estimated parameters and 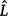 is the maximum value of the likelihood function for the model. A smaller AIC implies a better fit (Akaike 1974; Korner-Nievergelt et al. 2015). The mean ± s.e.m. of each behaviour were estimated through Generalised Additive Models for Location, Scale, and Shape (GAMLSS) models based on the best fit for that behaviour.
is the maximum value of the likelihood function for the model. A smaller AIC implies a better fit (Akaike 1974; Korner-Nievergelt et al. 2015). The mean ± s.e.m. of each behaviour were estimated through Generalised Additive Models for Location, Scale, and Shape (GAMLSS) models based on the best fit for that behaviour.
Model selection refers to the process of evaluating the best model for the observed data. One of the most popular methods to compare multiple distributions is AIC. In the current study, AIC values were used to determine the best-fitting models for all behaviours. However, BIC (Bayesian Information Criterion) is a better choice when the true model is included within the model space; whereas, selecting models based on the AIC is more effective in predicting the model (Bandyopadhyay et al. 2011). The AIC is computed from a model’s maximum likelihood estimate and measures the distance between a candidate model and a true model (Claeskens and Hjort 2008).
Skew exponential power type 2 distribution
The skew exponential power type 2 distribution was first defined by Azzalini (1986) and then further developed by DiCiccio and Monti (2004). Skew exponential power type 2 distributions have a heavy tail and skewness and include the normal distribution as a special case. This model is defined by
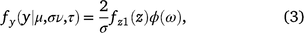
for −∞ < y < +∞, where −∞ < μ < +∞, σ > 0, −∞ < ν < +∞, τ > 0, and where z = (y − μ)/σ and ω = sign(z)|z|τ/2ν√2/τ, and fZ1 is the probability density function of Z1 ∼ PE2 (0, τ1/τ, τ), and Φ(ω) is the cumulative density function of a standard normal variable evaluated at ω.
Box–Cox t distribution
The Box–Cox t distribution is a family of distributions generated by a Box–Cox power transformation. The Box–Cox power transformation was introduced by Box and Cox (1964) to normalise data. The power transformation is
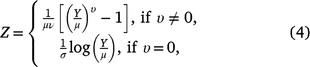
where 0 < Y < ∞, μ > 0, σ> 0, and −∞ < υ < ∞, and the random variable Z is assumed to follow a truncated t distribution. The Box–Cox t distribution has four parameters μ, σ, υ and τ which can be interpreted as median, scale (centile-based coefficient of variation), skewness and kurtosis, respectively (Rigby and Stasinopoulos 2006).
Results
The mean times spent grazing and ruminating, walking, idling, licking and other activities for both male and female sheep each day during the study period are shown in Fig. 2. For all activities, there was no consistent trend over time. The mean ± s.e. time spent grazing by male sheep was 215 ± 2.3 min/day while for ruminating it was 464 ± 3.0 min/day. Female sheep grazed 563 ± 2.0 min/day on average and spent on average 399 ± 2.0 min/day ruminating. The time spent licking varied for both male and female sheep but on average males spent more time licking than females (24 ± 0.3 vs 14.8 ± 0.2 min/day).
|
|
The mean times each animal spent in each activity for each hour of the day is shown in Fig. 3. The time spent grazing in each hour for female sheep varied from a few minutes in the hours before dawn to a maximum of 48 min/h in the late afternoon. The maximum time spent grazing by male sheep was 30 min in the late afternoon.
The proportion of each hour spent ruminating varied between 5 and 30 min/h in female sheep whereas male sheep spent as much as 20 min/h in the morning after sunrise. The maximum time spent ruminating occurred when grazing was lowest, and the minimum time was when grazing was highest (Fig. 3a, b). The time spent idling varied from just under 10 to just around 40 min/h. Time spent idling was lowest at the peak of grazing in both male and female sheep, but idling was at its highest just after peak grazing time. Time spent walking varied between just over 0 to around 10 min/h (Fig. 3c, d). Licking varied between just over 0 and around 4 min/h. Time spent in other activities varied from around 1 to just under 4 min/h (Fig. 3e, f).
The amount of time spent grazing, ruminating, idling, walking and licking varied among individuals and the distribution did not follow a Gaussian distribution (P < 0.05). The calculated energy statistic for all behaviours is shown in Table 3.
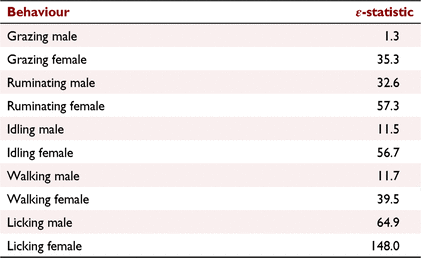
|
The distributions of grazing behaviour of male and female lambs on a daily basis are illustrated in Figs 4 and 5 (the illustration of other behaviours is provided in supplementary materials). There was substantial variation among individuals in the time spent grazing each day. The best-fitting distribution of all behaviours for both males and females is shown in Fig. 6. The Box–Cox t distribution was the best fit for all behaviours except ruminating in both males and females and idling in males which were best described by the skew exponential type 2 distribution (Table 4). However, the AIC value for the skew exponential type 2 distribution and the Box–Cox t distribution for idling behaviour in males were very similar (20 368 vs 20 369).
|
|
|
|

|
The distributions of behaviour among individuals on an hourly basis are indicated in Fig. 7 for male sheep and Fig. 8 for female sheep. There was considerable variation among individuals during daylight, however, the variation was smaller for male sheep except in h 15, 16 and 17.
Discussion
This current study has used sensors to classify on-farm sheep behaviour into six categories and quantified the variations in these behaviours among sheep grazing on pasture. Sheep spent most time grazing, ruminating and idling, while licking, walking and other behaviours occupied less time. The times spent grazing varied among animals. In this study, differences were found among the genders in the times spent grazing, with females grazing longer than males. However, the male and female sheep were grazed on two different paddocks and thus gender differences cannot be reliably disentangled from potential paddock effects in this study. Within each sex, the variation among animals were best described by the Box–Cox t distribution for all behaviours, with the exception of ruminating in males and females and idling in males, which were best described by the skew exponential type 2 distribution, when time spent per day was analysed.
On average, females grazed longer than males. This was initially surprising because males grow faster than females. However, the time spent grazing is also influenced by the nutritive characteristics and length of grass and this is likely to vary between paddocks (Hodgson 1981). The grazing time might also be influenced by the bite size (Poppi 2011). Females might require more time to achieve their daily nutrient requirements (Ruckstuhl 1998). Also, male sheep spent more time ruminating than grazing. Wang et al. (2018) showed that bighorn sheep spent more time ruminating than grazing and females ruminated less and grazed more than males. In dairy cows, a negative correlation between eating time and rumination has been reported which means cows that spent less time eating spent longer ruminating (Dado and Allen 1994). Perhaps males swallowed a larger proportion of grass per bite containing more fibrous stem materials that requires more time to break down (ruminate) while females selecting tender leaves and shoots with small bites would spend a longer time grazing, which then required less time to ruminate. However, further research is necessary to examine the difference between sexes in bite size and bite depth, in relation to sward height and the botanical composition of the herbage. Particularly, as our male and female sheep were grazed on separate paddocks, differences between the paddocks could have contributed to the differences observed between the two populations.
Grazing behaviour varied among animals each day (Figs 4 and 5). Most females grazed between 08:00 and 10:00 hours in the morning and 14:00 and 17:00 hours in the afternoon. The time spent grazing in females was greater in daylight. Gregorini (2012) reported the major grazing events happen during early morning and late afternoon. The duration of the grazing events can be longer in short days, while short grazing events occur at night. Our results were consistent with findings from that research. The time spent feeding can be affected by many factors, including the health of the animal (Palmer et al. 2012), pasture availability (Pérez-Prieto and Delagarde 2013), weather conditions (Redbo et al. 2001) or selection of herbage by sheep. The animals in our study showed no signs of disease, but like all grazing animals, they were exposed to nematodes (Stear et al. 2007). A study in New Zealand has indicated that behaviour is influenced by subclinical nematode infection (Ikurior et al. 2020).
The distributions of variation among animals are of considerable biological interest. For example, the distribution of nematodes in grazing sheep follows a negative binomial distribution (Stear et al. 1997). The observed variation is a result of variation in larval intake, resistance to infection and the counting process (Bishop and Stear 1997). Variation in larval intake will be a consequence of variation in feeding behaviour as well as variation in the distribution of larvae on pasture. Quantifying the variation in grazing behaviour is an essential step towards a detailed understanding of parasitic infection. There is considerable interest in building models of nematode infection and disease (Learmount et al. 2006; Laurenson et al. 2011; Prada Jiménez de Cisneros et al. 2014; Garnier et al. 2016) and a better understanding of variation in grazing behaviour will help the development of mechanistic models under realistic farm conditions to improve health and wellbeing as well as animal productivity. Determining the best-fitting distribution is important to implement the appropriate statistical analysis. Using an appropriate distribution for analysis provides more accurate estimates of parameters and reliable values. There is little value in experiments which provide inaccurate estimates of parameters and draw incorrect inferences from the data.
We believe that there are benefits in a multivariate model of the behavioural data, such as the quantification of the correlation between variables, and the potential relationships between rates of behaviours occurring. However, these analyses would require significant amounts of further analysis that goes beyond the intended scope of the paper. We believe that such an exploration, along with other more complex modelling and inference is better suited for a separate manuscript.
Conclusions
In conclusion, variation in behaviours among grazing sheep was quantified with the use of sensors. Sheep spent most of their time grazing, ruminating and idling with smaller amounts of time spent walking, licking and in other behaviours. The times spent by an animal in each activity varied during the day. Males and females were kept on separate paddocks and there were differences between the populations in the time spent grazing. Within each sex, the variation among animals in the time spent grazing was best described by a Box–Cox t distribution. This study has improved our understanding of variation in grazing behaviour among sheep and will facilitate more appropriate analyses of the causes of this variation.
Supplementary material
Supplementary material is available online.
Data availability
All data are available upon request.
Conflicts of interest
Markandeya Jois is an Associate Editor of Animal Production Science but was blinded from the peer-review process for this paper.
Declaration of funding
This research received no specific grant from any funding agency, commercial or not-for-profit organisation.
Acknowledgements
We would like to thank Australian Wool Innovation (AWI) for lending us ActiGraph sensors. We also thank the Kealy family who allowed us to use the animals on their farm and provided support and assistance.
References
Akaike H (1974) A new look at the statistical model identification. IEEE Transactions on Automatic Control 19, 716–723.| A new look at the statistical model identification.Crossref | GoogleScholarGoogle Scholar |
Alvarenga FAP, Borges I, Palkovič L, Rodina J, Oddy VH, Dobos RC (2016) Using a three-axis accelerometer to identify and classify sheep behaviour at pasture. Applied Animal Behaviour Science 181, 91–99.
| Using a three-axis accelerometer to identify and classify sheep behaviour at pasture.Crossref | GoogleScholarGoogle Scholar |
Andreen DM, Haan MM, Dechow CD, Harvatine KJ (2020)) Relationships between milk fat and rumination time recorded by commercial rumination sensing systems. Journal of Dairy Science 103, 8094–8104.
| Relationships between milk fat and rumination time recorded by commercial rumination sensing systems.Crossref | GoogleScholarGoogle Scholar |
Azzalini A (1986) Further results on a class of distributions which includes the normal ones. Statistica 46, 199–208.
| Further results on a class of distributions which includes the normal ones.Crossref | GoogleScholarGoogle Scholar |
Bandyopadhyay PS, Forster MR, Gabbay DM (Eds) (2011) ‘Philosophy of statistics: handbook of the philosophy of science.’ 1st edn. (Elsevier: Amsterdam)
Bikker JP, van Laar H, Rump P, Doorenbos J, van Meurs K, Griffioen GM, Dijkstra J (2014) Technical note: Evaluation of an ear-attached movement sensor to record cow feeding behavior and activity. Journal of Dairy Science 97, 2974–2979.
| Technical note: Evaluation of an ear-attached movement sensor to record cow feeding behavior and activity.Crossref | GoogleScholarGoogle Scholar |
Bishop SC, Stear MJ (1997) Modelling responses to selection for resistance to gastro-intestinal parasites in sheep. Animal Science 64, 469–478.
| Modelling responses to selection for resistance to gastro-intestinal parasites in sheep.Crossref | GoogleScholarGoogle Scholar |
Blanca MJ, Arnau J, López-Montiel D, Bono R, Bendayan R (2013) Skewness and kurtosis in real data samples. Methodology 9, 78–84.
| Skewness and kurtosis in real data samples.Crossref | GoogleScholarGoogle Scholar |
Box GEP, Cox DR (1964)) An analysis of transformations. Journal of the Royal Statistical Society: Series B (Methodological) 26, 211–243.
| An analysis of transformations.Crossref | GoogleScholarGoogle Scholar |
Burgunder J, Petrželková KJ, Modrý D, Kato A, MacIntosh AJJ (2018)) Fractal measures in activity patterns: do gastrointestinal parasites affect the complexity of sheep behaviour? Applied Animal Behaviour Science 205, 44–53.
| Fractal measures in activity patterns: do gastrointestinal parasites affect the complexity of sheep behaviour?Crossref | GoogleScholarGoogle Scholar |
Byskov MV, Nadeau E, Johansson BEO, Nørgaard P (2015) Variations in automatically recorded rumination time as explained by variations in intake of dietary fractions and milk production, and between-cow variation. Journal of Dairy Science 98, 3926–3937.
| Variations in automatically recorded rumination time as explained by variations in intake of dietary fractions and milk production, and between-cow variation.Crossref | GoogleScholarGoogle Scholar |
Claeskens G, Hjort NL (2008) ‘Model selection and model averaging.’ (Cambridge University Press)
Dado RG, Allen MS (1994) Variation in and relationships among feeding, chewing, and drinking variables for lactating dairy cows. Journal of Dairy Science 77, 132–144.
| Variation in and relationships among feeding, chewing, and drinking variables for lactating dairy cows.Crossref | GoogleScholarGoogle Scholar |
DiCiccio TJ, Monti AC (2004) Inferential aspects of the skew exponential power distribution. Journal of the American Statistical Association 99, 439–450.
| Inferential aspects of the skew exponential power distribution.Crossref | GoogleScholarGoogle Scholar |
Frost AR, Schofield CP, Beaulah SA, Mottram TT, Lines JA, Wathes CM (1997) A review of livestock monitoring and the need for integrated systems. Computers and Electronics in Agriculture 17, 139–159.
| A review of livestock monitoring and the need for integrated systems.Crossref | GoogleScholarGoogle Scholar |
Garnier R, Grenfell BT, Nisbet AJ, Matthews JB, Graham AL (2016) Integrating immune mechanisms to model nematode worm burden: an example in sheep. Parasitology 143, 894–904.
| Integrating immune mechanisms to model nematode worm burden: an example in sheep.Crossref | GoogleScholarGoogle Scholar |
Gregorini P (2012) Diurnal grazing pattern: its physiological basis and strategic management. Animal Production Science 52, 416–430.
| Diurnal grazing pattern: its physiological basis and strategic management.Crossref | GoogleScholarGoogle Scholar |
Hejcmanová P, Stejskalová M, Pavlů V, Hejcman M. (2009)) Behavioural patterns of heifers under intensive and extensive continuous grazing on species-rich pasture in the Czech Republic. Applied Animal Behaviour Science 117, 137–143.
| Behavioural patterns of heifers under intensive and extensive continuous grazing on species-rich pasture in the Czech Republic.Crossref | GoogleScholarGoogle Scholar |
Hodgson J (1981) Variations in the surface characteristics of the sward and the short-term rate of herbage intake by calves and lambs. Grass and Forage Science 36, 49–57.
| Variations in the surface characteristics of the sward and the short-term rate of herbage intake by calves and lambs.Crossref | GoogleScholarGoogle Scholar |
Ikurior SJ, Pomroy WE, Scott I, Corner-Thomas R, Marquetoux N, Leu ST (2020) Gastrointestinal nematode infection affects overall activity in young sheep monitored with tri-axial accelerometers. Veterinary Parasitology 283, 109188
| Gastrointestinal nematode infection affects overall activity in young sheep monitored with tri-axial accelerometers.Crossref | GoogleScholarGoogle Scholar |
Korner-Nievergelt F, Von Felten S, Roth T, Almasi B, Guélat J, Korner-Nievergelt P (2015) ‘Bayesian data analysis in ecology using linear models with R, Bugs, and Stan.’ (Elsevier/AP, Academic Press is an imprint of Elsevier: Amsterdam; Boston)
Krohn CC, Munksgaard L (1993) Behaviour of dairy cows kept in extensive (loose housing/pasture) or intensive (tie stall) environments II. Lying and lying-down behaviour. Applied Animal Behaviour Science 37, 1–16.
| Behaviour of dairy cows kept in extensive (loose housing/pasture) or intensive (tie stall) environments II. Lying and lying-down behaviour.Crossref | GoogleScholarGoogle Scholar |
Laurenson YCSM, Bishop SC, Kyriazakis I (2011) In silico exploration of the mechanisms that underlie parasite-induced anorexia in sheep. British Journal of Nutrition 106, 1023–1039.
| In silico exploration of the mechanisms that underlie parasite-induced anorexia in sheep.Crossref | GoogleScholarGoogle Scholar |
Learmount J, Taylor MA, Smith G, Morgan C (2006) A computer model to simulate control of parasitic gastroenteritis in sheep on UK farms. Veterinary Parasitology 142, 312–329.
| A computer model to simulate control of parasitic gastroenteritis in sheep on UK farms.Crossref | GoogleScholarGoogle Scholar |
Lehmann EL, Romano J (2005) Basic large sample theory. In ‘Testing statistical hypotheses’. Springer Texts in Statistics. pp. 419–481. (Springer New York: New York, NY)
| Crossref |
Palmer MA, Law R, O’Connell NE (2012) Relationships between lameness and feeding behaviour in cubicle-housed Holstein–Friesian dairy cows. Applied Animal Behaviour Science 140, 121–127.
| Relationships between lameness and feeding behaviour in cubicle-housed Holstein–Friesian dairy cows.Crossref | GoogleScholarGoogle Scholar |
Pérez-Prieto LA, Delagarde R (2013) Meta-analysis of the effect of pasture allowance on pasture intake, milk production, and grazing behavior of dairy cows grazing temperate grasslands. Journal of Dairy Science 96, 6671–6689.
| Meta-analysis of the effect of pasture allowance on pasture intake, milk production, and grazing behavior of dairy cows grazing temperate grasslands.Crossref | GoogleScholarGoogle Scholar |
Poppi DP (2011) Nutritional constraints for grazing animals and the importance of selective grazing behaviour. In ‘Grassland productivity and ecosystem services’. (Eds G Lemaire, J Hodgson, A Chabbi) pp. 19–26. (CABI: Wallingford)
| Crossref |
Prada Jiménez de Cisneros J, Stear MJ, Mair C, Singleton D, Stefan T, Stear A, Marion G, Matthews L (2014) An explicit immunogenetic model of gastrointestinal nematode infection in sheep. Journal of the Royal Society Interface 11, 20140416
| An explicit immunogenetic model of gastrointestinal nematode infection in sheep.Crossref | GoogleScholarGoogle Scholar |
R Core Team (2020) R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. Available at https://www.R-project.org
Redbo I, Ehrlemark A, Redbo-Torstensson P (2001) Behavioural responses to climatic demands of dairy heifers housed outdoors. Canadian Journal of Animal Science 81, 9–15.
| Behavioural responses to climatic demands of dairy heifers housed outdoors.Crossref | GoogleScholarGoogle Scholar |
Rigby RA, Stasinopoulos DM (2005) Generalized additive models for location, scale and shape. Journal of the Royal Statistical Society: Series C (Applied Statistics) 54, 507–554.
| Generalized additive models for location, scale and shape.Crossref | GoogleScholarGoogle Scholar |
Rigby RA, Stasinopoulos DM (2006) Using the Box-Cox t distribution in GAMLSS to model skewness and kurtosis. Statistical Modelling 6, 209–229.
| Using the Box-Cox t distribution in GAMLSS to model skewness and kurtosis.Crossref | GoogleScholarGoogle Scholar |
Rizzo M, Szekely GJ (2019) energy: E-statistics: multivariate inference via the energy of data. R package version 1.7-7. Available at https://CRAN.R-project.org/package=energy
Ruckstuhl KE (1998) Foraging behaviour and sexual segregation in bighorn sheep. Animal Behaviour 56, 99–106.
| Foraging behaviour and sexual segregation in bighorn sheep.Crossref | GoogleScholarGoogle Scholar |
Sohi R, Almasi F, Nguyen H, Carroll A, Tromph J, Weerasinghe M, Bervan A, Godoy BI, Ahmed A, Stear MJ, Desai A, Jois M (2021) Determination of ewe behaviour around lambing time and prediction of parturition seven days prior to lambing by smart technology in an extensive farming system. Publication in Progress in Animal Production Science Journal
Stear MJ, Bairden K, Duncan JL, Holmes PH, McKellar QA, Park M, Strain S, Murray M, Bishop SC, Gettinby G (1997) How hosts control worms. Nature 389, 27–27.
| How hosts control worms.Crossref | GoogleScholarGoogle Scholar |
Stear MJ, Doligalska M, Donskow-Schmelter K (2007) Alternatives to anthelmintics for the control of nematodes in livestock. Parasitology 134, 139–151.
| Alternatives to anthelmintics for the control of nematodes in livestock.Crossref | GoogleScholarGoogle Scholar |
Székely GJ, Rizzo ML (2004) Testing for equal distributions in high dimension. InterStat 5, 1249–1272.
Székely GJ, Rizzo ML (2005) A new test for multivariate normality. Journal of Multivariate Analysis 93, 58–80.
| A new test for multivariate normality.Crossref | GoogleScholarGoogle Scholar |
Wang M, Alves J, Tucker M, Yang W, Ruckstuhl KE (2018) Effects of intrinsic and extrinsic factors on ruminating, grazing, and bedding time in bighorn sheep (Ovis canadensis). PLoS ONE 13, e0206664
| Effects of intrinsic and extrinsic factors on ruminating, grazing, and bedding time in bighorn sheep (Ovis canadensis).Crossref | GoogleScholarGoogle Scholar |
Wickham H (2016) ‘ggplot2: elegant graphics for data analysis.’ 2nd edn. 2016. Use R!. (Springer International Publishing: Imprint: Springer: Cham)
| Crossref |


