Assessing the role played by meteorological conditions on the interannual variability of fire activity in four subregions of Iberia
Sílvia A. Nunes A * , Carlos C. DaCamara
A * , Carlos C. DaCamara  A , José M. C. Pereira
A , José M. C. Pereira  B and Ricardo M. Trigo
B and Ricardo M. Trigo  A
A
A Instituto Dom Luiz (IDL), Faculdade de Ciências, Universidade de Lisboa, 1749-016, Lisbon, Portugal.
B Centro de Estudos Florestais, Instituto Superior de Agronomia, Universidade de Lisboa, 1349-017, Lisbon, Portugal.
Abstract
The Iberian Peninsula is recurrently affected by severe wildfires resulting from an interplay of human activities, landscape features and atmospheric conditions.
The role played by atmospheric conditions on wildfire activity in 2001–2020 is assessed in four pyroregions of the Iberian Peninsula.
Wildfire activity is characterised by Fire Radiative Power (FRP) and meteorological danger is rated by the Fire Weather Index (FWI). The distribution of log10FRP in each pyroregion consists of a truncated lognormal central body with Generalised Pareto distributions as tails, and the model is improved using FWI as covariate. Synthetic time series of total annual FRP are generated using the models with and without FWI as covariate, and compared against observed FRP.
Pyroregions NW, N, SW and E present increases of 1, 5, 6 and 7% in interannual explained variance of FRP when progressing from the model without to that with FWI as covariate.
The models developed characterise the role of meteorological conditions on fire activity in the Iberian Peninsula, and are especially valuable when comparing expected impacts for different scenarios of climate change.
The largest effects of atmospheric conditions on fire activity are in regions of the IP where the strongest impact of climate change is expected.
Keywords: fire activity, Fire Radiative Power (FRP), Fire Weather Index (FWI), Iberian Peninsula, meteorological conditions, Moderate Resolution Imaging Spectroradiometer (MODIS), two generalised Pareto tail lognormal body distribution, wildfires.
Introduction
The Iberian Peninsula is recurrently affected by severe wildfires that relate to an increase in fuel availability due to land abandonment and the expansion of forest and shrubland areas (Pausas and Vallejo 1999; Lloret et al. 2002), as well as to an increase in the occurrence of prolonged droughts and in the number of days with extreme fire weather associated with climate change (Pereira et al. 2005, 2013; Trigo et al. 2006; Carvalho et al. 2011; Sousa et al. 2015; Pérez-Sánchez et al. 2019; Turco et al. 2019).
The tragic years 2003, 2005 and 2017 in Portugal are worth pointing out. The Iberian Peninsula was struck by a severe heat wave in August 2003 and by two severe heatwaves in 2017 (the first in mid-June and the second in the second week of July), and 2005 and 2017 were affected by two severe droughts, that of 2005 being the most severe in recent times (García-Herrera et al. 2007). Several studies have underlined the critical role played by different meteorological variables, including temperature, humidity and wind on the occurrence of extreme years of fire activity both at shorter (e.g. summer heat waves) and longer (e.g. prolonged droughts) time scales (Ruffault et al. 2020).
The fact that the entire Mediterranean basin, and the Iberian Peninsula in particular, is considered a hotspot of climate change (Cramer et al. 2018) calls for the need to pay particular attention to the role played by fire weather on wildfire activity. Accordingly, the aim of the present work is to assess the impact of meteorological conditions on the interannual variability of fire activity in four pyroregions of the Iberian Peninsula (Trigo et al. 2016).
Wildfire activity is quantified here by released Fire Radiative Power (FRP), as measured by the Moderate Resolution Imaging Spectroradiometer (MODIS) on board Terra and Aqua satellites (Giglio et al. 2020). Meteorological conditions are characterised by means of the Fire Weather Index (FWI), an indicator of meteorological fire danger that is part of the Canadian Forest Fire Weather Index System (Stocks et al. 1989). FWI combines in a single number the effects of air temperature, air humidity, surface wind and lack of rainfall on fire potential spread rate and fuel consumption (van Wagner 1987), making it appropriate to be related to FRP. However, because fire activity results from a complex interplay of climate, vegetation cover, topography and human activity (Bowman et al. 2020; Pereira et al. 2022), relationships between FRP and FWI have a regional character. As such relationships are not deterministic, their nature has to be uncovered using a probabilistic approach. Following a methodology previously set up to develop operational models to forecast meteorological fire danger (DaCamara et al. 2014a; Pinto et al. 2018, 2020), for each pyroregion, a statistical model is adjusted to the distribution of the logarithm of FRP, and the model is then improved by incorporating FWI as a covariate of the model.
For each pyroregion, the statistical distribution of the logarithm of FRP as obtained from the first model reflects the influence of static factors (during the study period), such as regional climate, vegetation cover and topography; in turn, the statistical distribution that incorporates FWI as a covariate reflects both the influences of static factors and meteorological conditions prevailing in each FRP observation. The role played by meteorological conditions may therefore be assessed by comparing the statistical behaviour of time series randomly generated by the two adjusted models (i.e. with and without FWI as covariate). Accordingly, the models are used to synthetically generate two sets of 100 time series of total annual FRP, and the role played by prevailing fire weather is assessed by comparing the two sets against each other and against the time series of annual FRP derived from observations of the MODIS instrument.
Data and methods
Study area
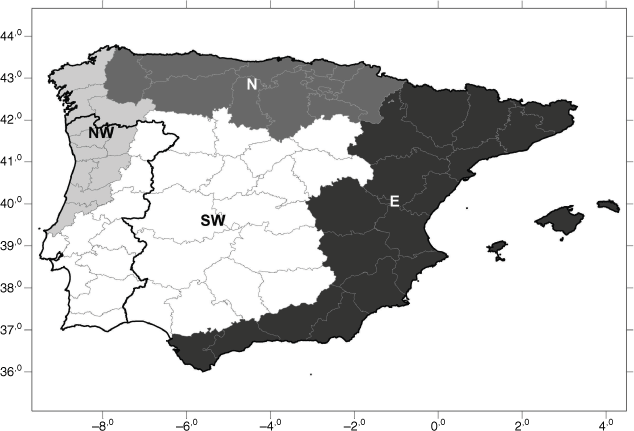
The study area comprises four pyroregions in the Iberia Peninsula as identified by Trigo et al. (2016) based on a cluster analysis of monthly burned area (Fig. 1); the Northwestern (NW) region, with an area of 46 563 km2, encompasses the relatively low lands of the north-western half of Portugal and the northwestmost provinces of Spain, the Northern (N) region, with an area of 86 619 km2 covers the Cantabrian mountainous areas of northern Spain, the Southwestern (SW) region, with an area of 267 474 km2, spans the southern lowlands and inland Portugal and expands into central and southwest Spain over Meseta Central, and the Eastern (E) region, with an area of 189 429 km2, includes the Ibérico and Penibético mountain ranges, and forms a band along the Mediterranean eastern and southern coasts of Spain. As shown by Trigo et al. (2016), each pyroregion presents a distinctive interannual variability and an annual cycle of burned area that is consistent with its topography, climate conditions and vegetation dynamics. The spatial distributions of the pyroregions are also in close agreement with the regionalisation proposed by Rasilla et al. (2010) to study wildfire risk and wildfire occurrence in continental Spain. The four pyroregions are therefore appropriate to develop regional models relating FRP and FWI.
The four pyroregions of the Iberian Peninsula: Northwestern (NW), Northern (N), Southwestern (SW) and Eastern (E). The border between Portugal and Spain is represented by the thick solid line and fine grey lines delimit the Administrative Regions of the two countries. Adapted from Trigo et al. (2016).
Datasets
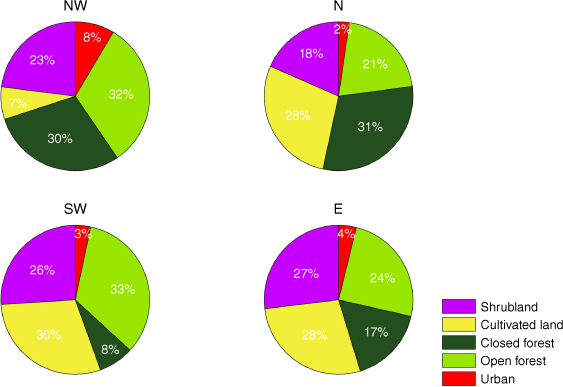
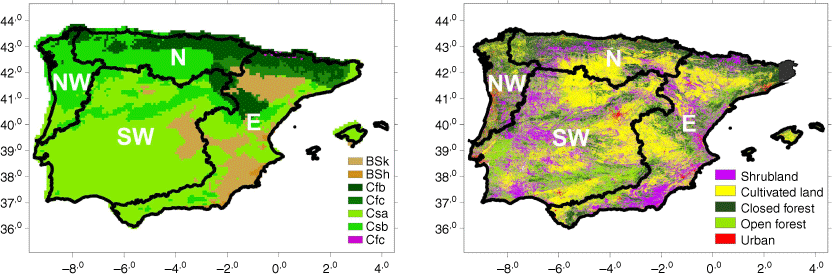
Information about climate types (Fig. 2, left panel) was extracted from the updated classification by Köppen–Geiger (Kottek et al. 2006). Information about land cover was obtained from the Copernicus Global Land Service (Version 3), and relates to the period 2015–2019 (Buchhorn et al. 2020). Data are provided at 100-m resolution and consist of 23 discrete classes of vegetation cover that were regrouped into five main types, namely shrubland, cultivated land, closed forest, open forest and urban (Fig. 2, right panel).
Distribution of Köppen–Geiger climate types as described by Kottek et al. (2006) (left panel) and land cover (right panel) on the Iberian Peninsula. The four pyroregions are delimited by thick black lines.
Information about radiative power released by wildfires was obtained from the MODIS Collection 6 Active Fire Product (Giglio et al. 2020). Data are provided at 0.25° × 0.25° resolution and consist of location, date and time, and FRP estimates and respective confidence for hotspots, identified as active vegetation fires, as detected by the MODIS instrument over the Iberian Peninsula for the period 2001–2020. As FRP is a physical quantity that measures combustion rate, it is also a good proxy of fire intensity (Wooster et al. 2005). FRP estimates by the MODIS instrument are known to depend on viewing geometry because the sensitivity of the radiometer decreases with increasing viewing zenith angle; however, when applied to large regions, results from MODIS are strongly correlated with those obtained with more recent instruments that do not have that limitation, such as the Visible Infrared Imaging Radiometer Suite (VIIRS) currently flying on the Suomi NPP and NOAA-20 satellite missions (Li et al. 2018). Vegetation fire hotspots, here referred to as hotspot events, were distributed among the four pyroregions according to the location of the hotspots, and percentiles 10, 25, 50, 75 and 90 of associated FRP were computed for each subset. Hotspot events of each pyroregion were stratified into the following six classes of fire intensity according to the values of FRP: below percentile 10, between percentiles 10 and 25, between percentiles 25 and 50, between percentiles 50 and 75, between percentiles 75 and 90, and above percentile 90.
Information about meteorological fire danger for the same period consists of daily values at a nominal 12:00 hours local time (noon) of FWI, an index that solely depends on weather information, namely temperature, relative humidity, wind speed and cumulative precipitation. FWI was initially developed to represent frontal fire intensity in the Canadian forest landscape (Van Wagner 1987), a feature that makes it appropriate to relate FRP with fire weather conditions. When calibrated, FWI is known to be a suitable measure of meteorological fire danger for a variety of ecosystems, namely those of Mediterranean Europe (DaCamara et al. 2014a; Pinto et al. 2018). Data are supplied at 0.25° × 0.25° resolution by the Copernicus Emergency Management Service for the European Forest Fire Information System (EFFIS) as obtained using weather forecast from historical simulations provided by European Centre for Medium‐Range Weather Forecasts (ECMWF) ERA5 reanalysis (Vitolo et al. 2020). A value of FWI was attributed to each hotspot event according to the location and day of the hotspot.
Base model
Using the ‘peaks over-threshold’ (POT) approach (Pickands 1975), Pinto et al. (2018) showed that exceedances (i.e. values above a sufficiently high threshold) of the logarithm of daily radiative energy released by wildfires over Mediterranean Europe follow a Generalised Pareto (GP) distribution. They further showed that the model is significantly improved when FWI is integrated as a covariate of scale parameters of GP distributions. However, the approach in the present study requires having a distribution that deals with the whole range of values of FRP at a time. Following DaCamara et al. (2022), we consider a model, hereafter referred to as the base model, that consists of a doubly truncated lognormal central body with a reversed GP lower tail and a GP upper tail.
For a generic random variable X, the cumulative density function (cdf), F, of the two generalised Pareto tail lognormal body distribution is:
where a, b, and c are normalising constants, x1 and xu are positive transition points, κl and σl are the shape and the scale parameters of the reversed GP lower tail, λb and σb are the location and scale parameters of the doubly truncated lognormal central body, and κu and σu are the shape and the scale parameters of the GP upper tail. When κl < 0, the distribution has a finite left point xLF = xl + σl/κl, and a finite right point xUF = xu − σu/κu when κu < 0.
Given an independent and identically distributed (i.i.d.) sample of observed data, x = (x1, x2, …, xn), the eight parameters (κl, σl, xl, λb, σb, κu, σu, xu) of F in Eqn 1 are obtained by maximising the log-likelihood function, log L(κl, σl, xl, λb, σb, κu, σu, xu|x). More details about the distribution and the fitting procedure are provided in DaCamara et al. (2022).
The A2 test (Anderson and Darling 1952) is then used to evaluate the goodness of fit. The probability of exceedance of the value of A2 obtained for the sample is estimated by computing A2 for 1000 data samples randomly generated from the fitted distribution, and in the case , the null hypothesis that the sample follows the distribution is rejected at the 5% significance level. Model validation is finally performed by analysing a Q–Q plot of empirical quantiles of the sample versus corresponding estimates using F−1.
Model with covariate
The base model is then improved by introducing a new variable y as a covariate in each one of the eight parameters of F using the following relations:
iv where pairs (m, b) for each parameter are again estimated by maximum likelihood from the original i.i.d. sample x and associated values of covariate y, using as first guesses for each parameter m = 0 and b equal to the estimate obtained for the base model. It may be noted that the exponential dependence of all parameters but λb preserves the negative sign of shape parameters κl and κu and the positive sign of the remaining ones. In the case of the location parameter λb, a linear relationship is used posing no restrictions in the domain.
Performances of the base model and the model with covariate are compared by computing the Bayes Factor (Nagin 2005) as well as by applying Vuong’s closeness test (Vuong 1989). Given two models, say Model 0 and Model 1, the Bayes Factor, B01, that measures the posterior odds that model 0 is the correct model given the data is approximated as , where BIC0 and BIC1 are the Bayesian Information Criterion scores (Amaral Turkman et al. 2019) for Model 0 and Model 1, respectively. It may be noted that BIC is defined as −2log(L) + klog(n), i.e. the lower the BIC score, the better the model, the negative contribution of the goodness of fit (rated by the likelihood logL) being penalised by the size n of the sample together with the number k of parameters of the model (k0 = 8 and k1 = 16 for the base model and the model with covariate, respectively). According to Jeffreys’ scale of evidence for Bayes Factors, there is strong evidence for Model 1 when (and strong evidence for Model 0 when B01 > 10). Details may be found in Nagin (2005).
Vuong’s test is based on the statistic , where SLR10 and VLR10 are respectively the sum and the variance of the individual log-likelihood ratio between Models 1 and 0, and is a correction term (which takes into account the number of parameters of the models and the size of the sample). V is N(0,1) distributed and e.g. at the 5% significance level, Model 1 is better when V > 1.96 and Model 0 is better when V < −1.96.
Synthetic time series
For each pyroregion, we fitted the base model given by Eqn 1 to the sample of the logarithm of FRP (i.e. x = log10FRP) of all hotspot events recorded during the period 2001–2020. Then, we fitted the model with covariate given by Eqns 1 and 2 to the sample of the logarithm of FRP using FWI as covariate (i.e. x = log10FRP and y = FWI), as obtained by associating with each hotspot event of the sample the respective daily value of FWI at the respective time and location.
Distribution F given by Eqn 1 can be inverted, i.e. values x of random variable X may be obtained associated with values of probability P according to:
where F−1 is the inverse of F. Samples of values of X with size n may therefore be generated from distribution F by inversion, i.e. by applying Eqn 3 to a set of n randomly generated values of P as obtained from a uniform distribution between 0 and 1 (Wilks 2020).
Accordingly, for each pyroregion, a set of ny synthetic values of log10FRP was generated for each year of the study period (where ny is the number of hotspot events recorded in year y) from distribution F with parameters previously obtained from the base model fit. An annual value of FRP was then computed by adding the ny synthetic values of FRP. This procedure allows generation of a synthetic time series of annual values of FRP covering the study period, which reflects the role played by static factors that are captured by the base model, namely regional climate, vegetation and topography. A time series of synthetic annual values of FRP reflecting both the roles played by static factors and by meteorological conditions prevailing in hotspot events may be obtained in a similar way from the model with FWI, i.e. by using the set of values of FWI associated with the hotspot events and relationships (Eqn 2) to prescribe the parameters of distribution for each hotspot event. By repeating the described series of steps for each pyroregion, a set of 100 synthetic time series of annual values of FRP was generated using the base model, and a second set of 100 synthetic time series of annual values of FRP was also generated, this time using the model with FWI as covariate.
Results
Characterisation of pyroregions
The four pyroregions of the Iberian Peninsula are characterised by different distributions of land cover (Figs 2, right panel, and 3) that reflect to a large extent the dominant Köppen–Geiger climate types (Fig. 2, left panel). Forests cover more than half the surface of the wetter regions NW and N, whereas shrubland and cultivated land dominate the drier regions SW and E. Representing 62% of the land cover, closed and open forests are almost evenly distributed in region NW, characterised for its most part by a Csb Mediterranean type of climate, with mild winters and dry and hot summers. Open forest and cultivated land represent 63% of land cover in region SW, mostly characterised by a Csa Mediterranean type of climate, with dry and very hot summers. Closed forest and cultivated land cover 59% of region N, which is characterised by a Csb Mediterranean climate in its southern part and, forming a strip along the northern coast, by oceanic climate, with wet and cold winters followed by humid summers, mostly of Cfb climate type with warm summers and a small patch of Cfc type with colder summers over the more mountainous areas. Finally, shrubland and cultivated land represent 66% of land cover of region E, which is a strip of Csa type with patches of Atlantic Cfb and Cfc climate and of cold semiarid climate (Bsk) covering the mountainous areas of the north and becoming cold continental (Dfc) at the highest points; large patches of semiarid Bsk type (and some small areas of hot semiarid Bsh type near the coast) are found in southeastern Spain, with very sparse vegetation and bare soils. The proportion of shrubland is approximately the same in regions SW and E and is lowest in region N. Cultivated land dominates over shrubland in all regions but NW, where it only represents 7% of the land cover. Large areas of region SW are covered by sparse vegetation with a peak of activity in spring and by rainfed crops that mature in late spring and early summer (Trigo et al. 2016).
During the study period 2001–2020, a total of 141 652 hotspots were recorded by the MODIS instrument over the Iberian Peninsula, the two pyroregions with Mediterranean-type climate contributing to three quarters of the total, almost evenly distributed between region NW with 53 591 hotspots (38% of the total) and 52 896 hotspots (37%) in region SW. Region N accounts for 19 437 hotspots (14%), and region E for the remaining 15 728 hotspots (11%).
The median annual cycle of hotspot density of region NW shows a pronounced maximum in August (reaching 78 hotspots/10 000 km2) and a secondary maximum in March (Fig. 4, first row); hotspot density is very small from November to January and the month of August has outstandingly large interannual variability. Region SW shows an absolute maximum hotspot density in August (16 hotspots/10 000 km2) and two secondary maxima, one in October with a magnitude close to that of August and another, much smaller, in March; there is a contrast in variability along the year, the months of June to November showing much larger interannual variability than the remaining 6 months. Region N shows two well-defined periods of fire activity, both in the median and the interannual variability of hotspot density, the first extending from February to April and the second from August to October (with a peak in September). Region E has a less pronounced median annual cycle of hotspot density than the other regions and, as in region SW, there are three peaks, in March, July and October.
Annual cycles and interannual variability of monthly hotspot density (first row), monthly mean FRP per hotspot (second row) and monthly mean FWI (third row) in 2001–2020 for regions NW (first column), N (second column), SW (third column) and E (fourth column). Circles with dots indicate the median and black bars extend down to percentile 25 and up to percentile 75. For each parameter, note the different scales used for the pyroregions.
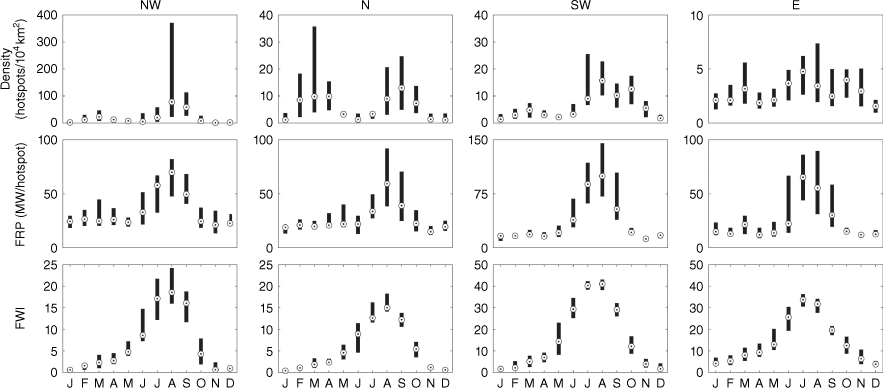
The annual cycles of monthly mean FRP per hotspot (Fig. 4, second row) display a well-defined maximum in August for all pyroregions and it is worth noting that the values reached in July and August in region SW are substantially larger than in the other regions. The annual cycle of FWI (Fig. 4, third row) has the highest values in July and August in all pyroregions, but there is a sharp contrast between regions SW and E versus regions NW and N, the magnitude of the peaks in the former two regions being approximately twice those in the latter two.
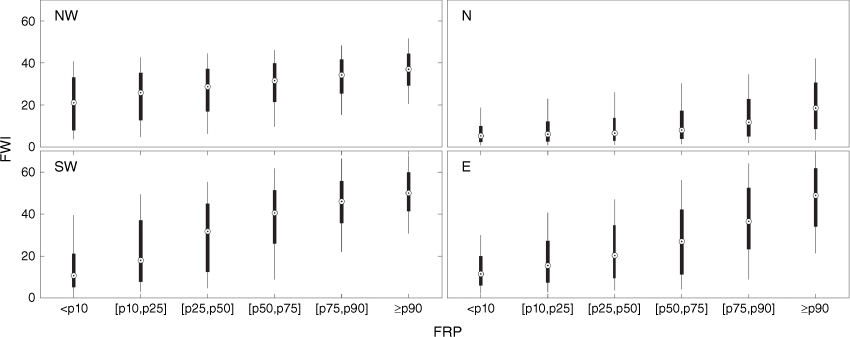
For all pyroregions, there is a systematic displacement of the distributions of FWI associated with each class of fire intensity when going from classes of low to high fire intensity towards higher values of FWI (Fig. 5). In each pyroregion, fires of higher FRP tend, therefore, to be associated with higher values of FWI, i.e. with higher meteorological fire danger.
Box plots of FWI associated with hotspots belonging to six classes of released FRP for regions NW (upper left panel), N (upper right panel), SW (lower left panel), and E (lower right panel). Circles with dots indicate the median of the FWI, thick whiskers extend down to percentile 25 and up to percentile 75, and thin whiskers down to percentile 10 and up to percentile 90. The six classes of FRP are below percentile 10 of FRP of the considered region, between percentiles 10 and 25, between percentiles 25 and 50, between percentiles 50 and 75, between percentiles 75 and 90, and above percentile 90.
Statistical models
Maximum likelihood estimates obtained for the parameters of the base models of log10FRP for the four pyroregions are presented in Table 1. Shape parameters κl and κu of the tails of all base models have values of approximately −0.2, and because they are negative, all distributions have bounded support. The scale parameters σu are 4–6 times larger than the corresponding scale parameters σl, meaning that, for all base models, the upper tails of the distributions are heavier than the lower tails. Unlike the scale parameters of the lower tail of the distributions, σl that have close values (~0.1) in all pyroregions, there are differences among the scale parameters σu of the upper tails, with region E having the highest value and region N the lowest. Table 1 also presents the results of the A2 tests for all regions, with for all samples indicating that the null hypothesis that the sample follows the distributions fitted cannot be rejected at the 5% level.
| Region | Support | Lower tail | Central body | Upper tail | Sample size | A2 test | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| xLF | xl | xu | xUF | κl | σl | λb | σb | κu | σu | n | |||
| NW | 0.24 | 0.84 | 1.74 | 3.88 | −0.19 | 0.11 | 0.50 | 0.43 | −0.20 | 0.43 | 53 591 | 0.23 | |
| N | 0.25 | 0.65 | 2.35 | 3.83 | −0.19 | 0.08 | 0.22 | 0.34 | −0.20 | 0.29 | 19 437 | 0.47 | |
| SW | 0.20 | 0.74 | 1.75 | 4.21 | −0.19 | 0.10 | 0.34 | 0.55 | −0.20 | 0.50 | 52 896 | 0.48 | |
| E | 0.22 | 0.74 | 1.12 | 4.09 | −0.23 | 0.12 | −0.08 | 0.25 | −0.23 | 0.68 | 15 728 | 0.21 | |
Each pyroregion has a characteristic cdf curve of log10FRP (Fig. 6). Regions NW and SW have the highest values of probability of exceedance of log10FRP, the former region for values below ~2.1 and the latter for values above this threshold. A similar behaviour is displayed by regions E and N regarding lowest values of probability of exceedance, the former region for values of log10FRP below ~1.6 and the latter for values above this threshold.
Cdf curves and Q–Q plots (insets) of fitted statistical models of log10FRP (in MW) for regions NW (red), N (green) SW (blue), and E (magenta). Both axes of Q–Q plots are in log10FRP, the 1:1 lines delimit the central body and the upper and lower tails of the distributions, and the small coloured dots represent the hotspot events of the sample. For each pyroregion, the number of events and respective fraction (in brackets) of the sample in the central body and in the lower and upper tails of the distribution are indicated next to the 1:1 line of the respective Q–Q plot.
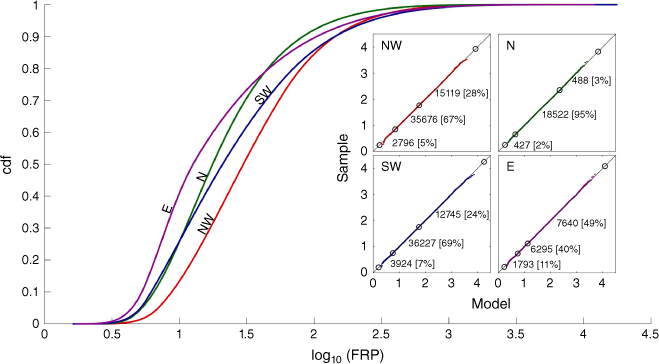
For all pyroregions, goodness of fit of the distributions to the respective samples is confirmed when examining the Q–Q plot of the empirical quantiles for the datasets versus the estimated quantiles of the base models, with almost all points lying along the 1:1 lines (Fig. 6). Regarding the characteristics of the support of the distribution, there are similarities between regions NW and SW, with the central body containing the large majority of events of the sample (67% for NW and 69% for SW), followed by the upper tail (28% for NW and 24% for SW) and by a lower tail with a small fraction of events (5% for NW and 7% for SW). For region N, the vast majority of events (95%) concentrates in the central body and the remaining ones are distributed almost evenly in the tails (3% in the upper tail and 2% in the lower). Region E has very distinct characteristics, with almost half of the sample (49%) belonging to the upper tail, the central body containing most of the remaining events (40%) and the other small portion (11%) belonging to the lower tail.
Maximum likelihood estimates obtained for the parameters of the models of log10FRP with FWI as covariate are presented in Table 2 for the four pyroregions. Transition point xl increases with FWI in all regions but E whereas transition point xu decreases with FWI in all regions but NW. All parameters of the central body and upper tail increase with FWI in regions N and SW, whereas all parameters but λb decrease with FWI in region NW. In region E, λb and σu increase with FWI, whereas σb and κu decrease. Regarding the lower tail, σl decreases with FWI in all regions, whereas κl increases with FWI in all regions but NW.
| Region | Support | Lower body | Central body | Upper body | Bayes factor | Vuong’s statistic | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| xl | xu | κl | σl | λb | σb | κu | σu | B01 | V | |||
| NW | m | 0.00090 | 0.011 | 0.0067 | −0.010 | 0.0013 | −0.0070 | 0.0090 | −0.00030 | 0 | 35 | |
| b | −0.30 | 0.22 | −2.21 | −2.33 | 0.49 | −0.69 | −1.96 | −0.94 | ||||
| N | m | 0.0055 | −0.00050 | −0.012 | −0.0078 | 0.011 | 0.0085 | −0.0074 | 0.00030 | 0 | 20 | |
| b | −0.63 | 0.85 | −1.85 | −2.91 | 0.11 | −1.21 | −2.26 | −1.33 | ||||
| SW | m | 0.0034 | −0.0039 | −0.0088 | −0.0022 | 0.012 | 0.0016 | −0.019 | 0.0063 | 0 | 63 | |
| b | −0.50 | 1.02 | −1.94 | −2.72 | −0.10 | −1.05 | −0.74 | −1.30 | ||||
| E | m | −0.0093 | −0.0076 | −0.021 | −0.026 | 0.0027 | −0.010 | 0.018 | 0.021 | 0 | 31 | |
| b | −0.47 | 0.38 | −5.97 | −2.70 | −0.11 | −1.11 | −1.97 | −1.10 | ||||
Values of m and b in bold indicate that the parameter increases with increasing FWI.
As also shown in Table 2, for all pyroregions, values of the Bayes Factors B01 are lower than , meaning that, according to Jeffreys’ scale of evidence, when the model with covariate FWI is compared with the base model, there is strong evidence in favour of the model with covariate. This perception is further confirmed through the values of Vuong’s statistic, V, that are all larger than 1.96, meaning that, at the 5% significance level, the model with covariate FWI is better than the base model.
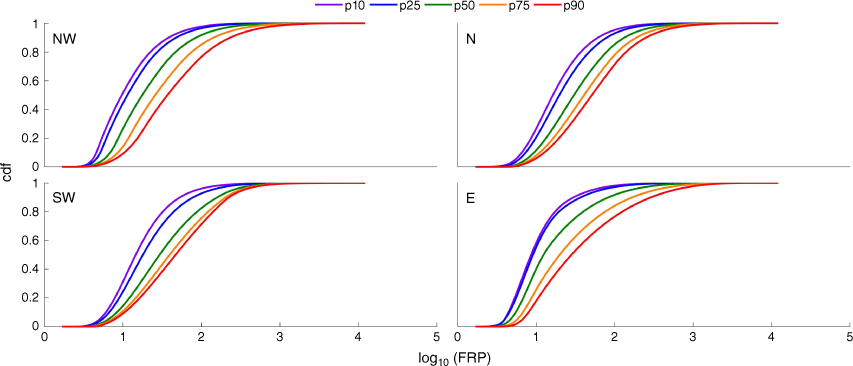
The overall effect of FWI on the distributions of log10FRP is illustrated in Fig. 7, which shows, for each pyroregion, the cdf curves for chosen values of FWI, namely percentiles 10, 20, 50, 75 of the set of values associated with the hotspots of the sample. For all pyroregions, there is a clear right displacement of the cdf curves with increasing FWI, which reflects substantial increases in probability of exceedance of a given threshold of log10FRP.
Sensitivity to FWI of cdf curves of fitted statistical models of log10FRP (in MW) with FWI as covariate for regions NW (upper left panel), N (upper right panel), SW (lower left panel) and E (lower right panel). Colours of each curve identify the prescribed value of FWI, respectively percentiles 10 (purple), 25 (blue), 50 (green), 75 (orange) and 90 (red) of the respective samples.
Synthetic time series
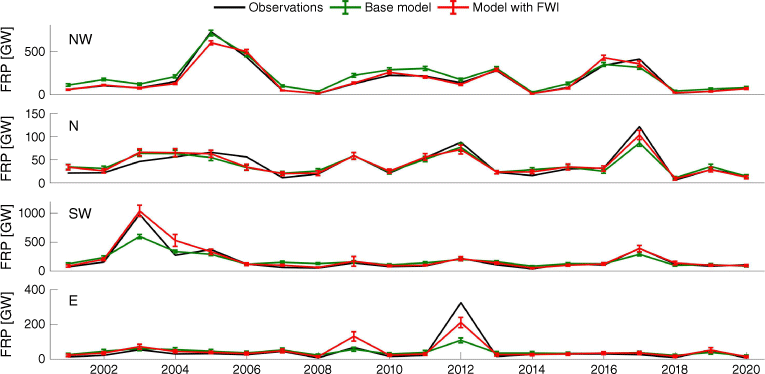
Fig. 8 presents, for each pyroregion, the time series of annual FRP as derived from observations from the MODIS instrument (black curves) and the two time series obtained by averaging the two sets of 100 annual values of FRP as derived from the base model (green curve) and the model with FWI as covariate (red curve). The interannual variability of the time series generated by the base model is just due to the interannual variability of hotspots observed by the MODIS instrument, and it is worth noting that some years with large (small) values of total FRP tend to be underestimated (overestimated). The underestimation is conspicuous in 2017 for pyroregions NW and N, in 2003 for pyroregion SW, and in 2012 for pyroregion E, whereas overestimation is clear in 2007 and 2008 for pyroregion SW. In the case of the time series generated by the model with FWI, improved behaviour is observed that is particularly noticeable for years with large values of total FRP. Overall, synthetic values obtained from the model with FWI are much closer to observed values than synthetic values generated by the base model, where meteorological conditions are not taken into account.
Time series, for regions NW, N, SW, and E (top to bottom panels) of annual values of observed (black curves) and of mean values of the set of synthetically generated annual values of FRP using the base models (green curves) and the models with FWI as covariate (red curves). The error bars in the synthetic time series delimit the mean plus/minus one standard deviation.
A quantitative assessment is provided in Table 3, which presents the mean and standard deviation of the time series of annual FRP derived from MODIS observations and of the annual FRP synthetically generated by the base models and the models with FWI. Results indicate that the synthetic time series generated by both models are unbiased, the only exception being pyroregion E, where the time series generated by the model with FWI displays a mean value 12% larger than the mean of the time series of observed FRP. Considerable differences do, however, occur with the values of standard deviation, for which time series of synthetically generated FRP present considerably lower values than the corresponding time series of observed FRP. However, time series generated using the model with FWI systematically display larger variability than the corresponding ones obtained with the base model. For instance, there is an 11% increase (from 21 to 24 GW) for pyroregion N, a 17% increase (from 143 to 167 GW) for pyroregion NW, a 48% increase (from 121 to 179 GW) for pyroregion SW and a 230% increase (from 20 to 46 GW) for pyroregion E.
| NW | N | SW | E | |||
|---|---|---|---|---|---|---|
| Mean (GW) | Observed | 179 | 40 | 185 | 43 | |
| Base model | 180 | 40 | 184 | 42 | ||
| Model with FWI | 179 | 40 | 186 | 47 | ||
| Standard deviation (GW) | Observed | 181 | 29 | 211 | 68 | |
| Base model | 143 | 21 | 121 | 20 | ||
| Model with FWI | 167 | 24 | 179 | 46 | ||
| Variance explained (%) | Base model | 95 | 84 | 90 | 79 | |
| Model with FWI | 96 | 89 | 96 | 86 | ||
Table 3 also presents, for each pyroregion, the explained variance accounted for by the synthetic series when they are used to simulate interannual variability. Explained variance was estimated by squaring the linear correlation of the time series of annual observed FRP with the corresponding synthetic time series generated by the base model and the model with FWI. For all pyroregions, there is an increase in explained variance when shifting from synthetic values of annual FRP generated by the base models to those by the models with FWI. Region NW shows a modest increase of 1% in explained variance (95–96%), but the other three regions show larger increases, respectively of 5% (84–89%) in region N, 6% (90–96%) in region SW and 7% (79–86%) in region E.
Discussion
Fire activity in the four pyroregions of the Iberian Peninsula results from the interplay of climate types, lansdscape features and human activities (Costa et al. 2011). Regions NW and SW, with Mediterranean climate and with 55 and 59% of the area covered by open forest and shrubland, respectively, rank first and second in the median value of hotspot density in August, when FWI is maximum; however, in the case of region NW, which has a very small fraction of cultivated land (7%), the maximum reached in August (78 hotspots/10 000 km2) is almost five times larger than that in region SW (16 hotspots/10 000 km2). In turn, region SW, with hotter summers, presents much larger median values of mean FRP per hotspot and FWI (93 MW/hotspot and 41) than region NW (70 MW/hotspot and 19). Because fuel availability is limited by the aridity of the environment (Pausas and Fernández-Muñoz 2012), region E, although with very hot and dry summers and a median value of FWI of 32 in August, presents the smallest median value of hotspot density in August (9 hotspots/10 000 km2), and is also the region with the smallest median value of mean FRP per hotspot (55 MW/hotspot) in August. Finally, region N, with a wetter oceanic climate and the smallest proportion of open forest and shrubland (39%), presents median values of FWI for July, August and September (respectively 13, 15 and 12) that are the lowest among the regions for the respective months. July presents the lowest median values of hotspot density and median FRP per hotspot among the four regions whereas August and September rank third for both parameters. The annual cycles of number of hotspots also show secondary peaks in March for all regions, that of region E being quite prominent and, in the case of region N, the peak extends to the contiguous months of February and April and is similar in amplitude to the summer one. Secondary peaks in number of hotspots are also identifiable in October in regions SW and E, and in September in region N. However, the peaks in March and October are associated with rather low average values of FRP. A large fraction of such hotspots corresponds to vegetation fires related to agricultural and pastoral practices, including forest operations to remove crop residues, rejuvenate pastures and burn residues (Casau et al. 2022). When associated with fire weather, these practices are a major cause of large rural fires (DaCamara et al. 2014b).
The distributions of log10FRP of the base models for the four pyroregions reflect the characteristics of respective fire activity. Region SW has the widest support (from 0.20 to 4.21), whereas region N has the narrowest (0.25–3.83). The shape parameters of the lower and upper tails have similar values (with κl ⋍ −0.2) for all pyroregions, and the same happens with the scale parameter of the lower tails (σl ⋍ 0.1). This is to be expected because fires with low FRP have a weak dependence on static factors (regional climate, vegetation cover and topography). However, the same does not happen with the scale parameters of the upper tails, region E, with the highest proportion (27%) of shrubland, presenting the highest value (σu = 0.68) and therefore the heaviest tail, and region N, with the lowest proportion (18%) and the highest of closed forest (31%) presenting the smallest value (σu = 0.29) and therefore the lightest tail.
When vegetation fires of each pyroregion are stratified into classes of FRP, the distribution of FWI associated with the classes indicates that fires with higher release of FRP tend to be associated with higher values of FWI. This suggests improvement of the base model of each pyroregion by incorporating FWI as a covariate of all parameters of the respective distribution. For all pyroregions, the cdf curves of the models with FWI show a systematic displacement towards larger values of log10FRP with increasing FWI that indicates an increase in probability of exceedance of fire intensity with increasing meteorological fire danger.
The strong dependence of the distributions of log10FRP on FWI makes of the models with FWI an appropriate tool to assess the impact of meteorological conditions on the interannual variability of fire activity. Results obtained by generating synthetic series of annual totals of FRP for each pyroregion using the base model and the model with FWI, and then comparing their temporal variability with that of corresponding time series obtained from observed FRP point out the crucial role of meteorological fire danger in years of very high and very low fire activity. This translates into values of standard deviation of the time series generated with the model with FWI that are larger than those of the synthetic time series produced by the base model and closer to those of time series from observations. When compared against the latter, synthetic time series generated with the models with FWI also present larger values of explained variance than those generated with the base models, where meteorological conditions are not taken into consideration.
Conclusions
The results obtained clearly indicate the importance of atmospheric conditions as drivers of interannual variability in fire activity, measured by annual FRP values. This is especially true in pyroregions SW and E, where climate change is expected to have a pronounced impact in terms of the main climatic drivers of fires in these regions, namely an increase in frequency both of drought events and of days with extreme fire weather (Sousa et al. 2015).
It is worth pointing out that the assessment performed in this work is likely to be conservative, given that time series of annual FRP were estimated by randomly generating values for all hotspots identified by the MODIS instrument for each year of the study period. The interannual variability of total number of hotspots was therefore the same for both statistical models (with and without FWI as covariate); as the number of hotspots strongly depends on the number of large vegetation fire events, which in turn depends on fire weather conditions, the interannual variability of synthetically generated time series of FRP was very likely overestimated when using the base model (without FWI as covariate), leading to an inflated interannual variability of FRP. Circumventing this problem would imply modelling the interannual variability of hotspots (with and without FWI as covariate), a task that is beyond the purpose of the present work.
The approach proposed in this study can provide valuable information about fire activity in the Iberian Peninsula both for present and future climate conditions. An example of application for present climate is currently being proposed by some of us in a project funded by the Portuguese Environment Agency through Pre-defined Project-2 National Roadmap for Adaptation XXI (PDP-2); in this context, we are evaluating the effect of different policies of ignition limitation by generating and comparing two sets of synthetic samples of FRP as obtained from the statistical model, first by using observed values of FWI associated with ignitions from historical records and then using the same observed values of FWI but deprived of a fraction of large values of FWI according to a given policy of ignition limitation. The rationale stems from the fact that most fires are human-made, and authorities may be able to enforce policies during extreme fire risk days, thus decreasing the number of ignitions on those occasions. In a similar fashion, the approach developed can be used to assess the effect of changes in fire weather by generating and comparing two synthetic samples of FRP as obtained using simulated values of FWI by climate models, first with historic radiative forcing and then with forcing according to a given future climate scenario.
Data availability
Köppen-Geiger climate classification data are available at: http://koeppen-geiger.vu-wien.ac.at/present.htm; land cover data are available at: https://lcviewer.vito.be/download; MODIS fire/hotspot information was downloaded from: https://firms.modaps.eosdis.nasa.gov/download/; and FWI historical data were downloaded from: https://cds.climate.copernicus.eu/cdsapp#!/dataset/cems-fire-historical?tab=form.
Acknowledgements
This work was supported by EEA-Financial Mechanism 2014–2021 and the Portuguese Environment Agency through Pre-defined Project-2 National Roadmap for Adaptation XXI (PDP-2), by the Portuguese Fundação para a Ciência e a Tecnologia (FCT) IP/MCTES through national funds (PIDDAC) – IDL (UIDB/50019/2020), Centro de Estudos Florestais (CEF) (UIDB/00239/2020). Sílvia A. Nunes was supported by EUMETSAT Satellite Application Facility on Land Surface Analysis (LSA SAF) through a PhD scholarship. Carlos C. DaCamara was supported by the project ‘Compound extremes in Mediterranean temperature, wind and wildfires’.
References
Anderson TW, Darling DA (1952) Asymptotic theory of certain ‘goodness of fit’ criteria based on stochastic processes. The Annals of Mathematical Statistics 23, 193-212.
| Crossref | Google Scholar |
Bowman DM, Kolden CA, Abatzoglou JT, Johnston FH, van der Werf GR, Flannigan M (2020) Vegetation Fires in the Anthropocene. Nature Reviews Earth & Environment 1(10), 500-515.
| Crossref | Google Scholar |
Buchhorn M, Lesiv M, Tsendbazar N-E, Herold M, Bertels L, Smets B (2020) Copernicus Global Land Cover Layers—Collection 2. Remote Sensing 12, 1044.
| Crossref | Google Scholar |
Carvalho AC, Carvalho A, Martins H, Marques C, Rocha A, Borrego C, Viegas DX, Miranda AI (2011) Fire weather risk assessment under climate change using a dynamical downscaling approach. Environmental Modelling & Software 26(9), 1123-1133.
| Crossref | Google Scholar |
Casau M, Dias MF, Teixeira L, Matias JCO, Nunes LJR (2022) Reducing Rural Fire Risk through the Development of a Sustainable Supply Chain Model for Residual Agroforestry Biomass Supported in a Web Platform: A Case Study in Portugal Central Region with the Project BioAgroFloRes. Fire 5, 61.
| Crossref | Google Scholar |
Costa L, Thonicke K, Poulter B, Badeck F-W (2011) Sensitivity of Portuguese forest fires to climatic, human, and landscape variables: subnational differences between fire drivers in extreme fire years and decadal averages. Regional Environmental Change 11, 543-551.
| Crossref | Google Scholar |
Cramer W, Guiot J, Fader M, Garrabou J, Gattuso J-P, Iglesias A, Lange MA, Lionello P, Llasat MC, Paz S, Peñuelas J, Snoussi M, Toreti A, Tsimplis MN, Xoplaki E (2018) Climate change and interconnected risks to sustainable development in the Mediterranean. Nature Climate Change 8, 972-980.
| Crossref | Google Scholar |
DaCamara CC, Calado TJ, Ermida SL, Trigo IF, Amraoui M, Turkman KF (2014a) Calibration of the Fire Weather Index over Mediterranean Europe based on fire activity retrieved from MSG satellite imagery. International Journal of Wildland Fire 23, 945-958.
| Crossref | Google Scholar |
DaCamara CC, Trigo RM, Nascimento ML (2014b) Characterizing the secondary peak of Iberian fires in March. In ‘Advances in Forest Fire Research’. (Ed. DX Viegas) pp. 1671–1682. (Imprensa da Universidade de Coimbra: Coimbra, Portugal) 10.14195/978-989-26-0884-6_184
DaCamara CC, Libonati R, Nunes SA, de Zea Bermudez P, Pereira JMC (2022) Modeling fire radiative power released by vegetation fires at the global scale using a two generalized Pareto tail lognormal body distribution. SSRN Electronic Journal
| Crossref | Google Scholar |
García-Herrera R, Hernández E, Barriopedro D, Paredes D, Trigo RM, Trigo IF, Mendes MA (2007) The outstanding 2004/05 drought in the Iberian Peninsula: associated atmospheric circulation. Journal of Hydrometeorology 8, 483-498.
| Crossref | Google Scholar |
Giglio L, Schroeder W, Hall JV, Justice CO (2020) MODIS Collection 6 Active Fire Product User’s Guide. Available at https://modis-fire.umd.edu/files/MODIS_C6_Fire_User_Guide_C.pdf [verified 26 June 2022]
Kottek M, Grieser J, Beck C, Rudolf B, Rubel F (2006) WorldMap of the Köppen-Geiger climate classification updated. Meteorologische Zeitschrift 15, 259-263.
| Crossref | Google Scholar |
Li F, Zhang X, Kondragunta S, Csiszar I (2018) Comparison of Fire Radiative Power estimates from VIIRS and MODIS observations. Journal of Geophysical Research: Atmospheres 123, 4545-4563.
| Crossref | Google Scholar |
Lloret F, Calvo E, Pons X, Díaz-Delgado R (2002) Wildfires and landscape patterns in the Eastern Iberian Peninsula. Landscape Ecology 17, 745-759.
| Crossref | Google Scholar |
Pausas JG, Fernández-Muñoz S (2012) Fire regime changes in the Western Mediterranean Basin: from fuel-limited to drought-driven fire regime. Climatic Change 110, 215-226.
| Crossref | Google Scholar |
Pausas JG, Vallejo R (1999) The role of fire in European Mediterranean ecosystems. In ‘Remote Sensing of Large Wildfires in the European Mediterranean Basin’. (Ed. E Chuvieco) pp. 3–16. (Springer-Verlag: Berlin) 10.1007/978-3-642-60164-4_2
Pereira M, Calado TJ, DaCamara CC, Calheiros T (2013) Effects of regional climate change on rural fires in Portugal. Climate Research 57(3), 187-200.
| Crossref | Google Scholar |
Pereira MG, Trigo RM, DaCamara CC, Pereira JMC, Leite SM (2005) Synoptic patterns associated with large summer forest fires in Portugal. Agricultural and Forest Meteorology 129, 11-25.
| Crossref | Google Scholar |
Pereira JMC, Oom D, Silva PC, Benali A (2022) Wild, Tamed, and Domesticated: Three Fire Macroregimes for Global Pyrogeography in the Anthropocene. Ecological Applications 32(6), e2588.
| Crossref | Google Scholar |
Pérez-Sánchez J, Jimeno-Sáez P, Senent-Aparicio J, Díaz-Palmero JM, Cabezas-Cerezo JdD (2019) Evolution of burned area in forest fires under climate change conditions in southern Spain using ANN. Applied Sciences 9(19), 4155.
| Crossref | Google Scholar |
Pickands III J (1975) Statistical inference using extreme order statistics. The Annals of Statistics 3, 119-131.
| Crossref | Google Scholar |
Pinto MM, DaCamara CC, Trigo IF, Trigo RM, Turkman KF (2018) Fire danger rating over Mediterranean Europe based on Fire Radiative Power derived from Meteosat. Natural Hazards and Earth System Sciences 18, 515-529.
| Crossref | Google Scholar |
Pinto MM, DaCamara CC, Hurduc A, Trigo RM, Trigo IF (2020) Enhancing the fire weather index with atmospheric instability information. Environmental Research Letters 15, 0940b7.
| Crossref | Google Scholar |
Rasilla DF, García-Codron JC, Carracedo V, Diego C (2010) Circulation patterns, wildfire risk and wildfire occurrence at continental Spain. Physics and Chemistry of the Earth, Parts A/B/C 35, 553-560.
| Crossref | Google Scholar |
Ruffault J, Curt T, Moron V, Trigo RM, Mouillot F, Koutsias N, Pimont F, Martin-StPaul N, Barbero R, Dupuy J-L, Russo A, Belhadj-Khedher C (2020) Increased likelihood of heat-induced large wildfires in the Mediterranean Basin. Scientific Reports 10, 13790.
| Crossref | Google Scholar |
Sousa PM, Trigo RM, Pereira MG, Bedia J, Gutiérrez JM (2015) Different approaches to model future burnt area in the Iberian Peninsula. Agricultural and Forest Meteorology 202, 11-25.
| Crossref | Google Scholar |
Stocks BJ, Lawson BD, Alexander ME, Van Wagner CE, McAlpine RS, Lynham TJ, Dubé DE (1989) The Canadian Forest Fire Danger Rating System: an overview. The Forestry Chronicle 65(6), 450-457.
| Crossref | Google Scholar |
Trigo RM, Pereira JMC, Pereira MG, Mota B, Calado TJ, DaCamara CC, Santo FE (2006) Atmospheric conditions associated with the exceptional fire season of 2003 in Portugal. International Journal of Climatology 26(13), 1741-1757.
| Crossref | Google Scholar |
Trigo RM, Sousa PM, Pereira MG, Rasilla D, Gouveia CM (2016) Modelling wildfire activity in Iberia with different atmospheric circulation weather types. International Journal of Climatology 36(7), 2761-2778.
| Crossref | Google Scholar |
Turco M, Jerez S, Augusto S, Tarín-Carrasco P, Ratola N, Jiménez-Guerrero P, Trigo RM (2019) Climate drivers of the 2017 devastating fires in Portugal. Scientific Reports 9, 13886.
| Crossref | Google Scholar |
Vitolo C, Di Giuseppe F, Barnard C, Coughlan R, San-Miguel-Ayanz J, Libertá G, Krzeminski B (2020) ERA5-based global meteorological wildfire danger maps. Scientific Data 7, 216.
| Crossref | Google Scholar |
Vuong QH (1989) Likelihood Ratio Tests for Model Selection and Non-Nested Hypotheses. Econometrica 57, 307-333.
| Crossref | Google Scholar |
Wilks DS (2020) ‘Statistical Methods in the Atmospheric Sciences’, 4th edn. (Elsevier) 10.1016/C2017-0-03921-6
Wooster MJ, Roberts G, Perry GLW, Kaufman YJ (2005) Retrieval of biomass combustion rates and totals from Fire Radiative Power observations: FRP derivation and calibration relationships between biomass consumption and fire radiative energy release. Journal of Geophysical Research 110, D24311.
| Crossref | Google Scholar |