Physics-based modelling for mapping firebrand flux and heat load on structures in the wildland–urban interface
Amila Wickramasinghe A , Nazmul Khan
A , Nazmul Khan  A , Alexander Filkov
A , Alexander Filkov  B and Khalid Moinuddin A *
B and Khalid Moinuddin A *
A
B
Abstract
This study investigates firebrand and heat flux exposures of structures in the wildland–urban interface (WUI). Australian Building Standard AS3959 defines Bushfire Attack Levels (BALs) based on radiant heat flux exposure of properties at the WUI. Despite the fact that firebrands are one of the main causes of house losses in the WUI, firebrand attack levels on houses are still not quantified owing to inherent difficulties.
We aimed to quantify firebrand flux on houses for three Fire Danger Indices (FDIs).
Three wildfires with varying fireline intensities were modelled to mimic wildfire exposure at FDIs of 100, 80 and 50. The current model was improved by adding the effects of fuel moisture content (FMC), vegetation and wind speed to estimate firebrand generation rates in different vegetation species for various fire severities, and these rates were used to simulate firebrand attack on structures. The firebrand and radiative heat fluxes on the structures were calculated to develop correlations to quantify firebrand attack.
A logarithmic relationship between firebrand flux and radiative heat flux was found.
The findings are beneficial in quantifying firebrand flux on houses for different vegetation fires to improve building construction requirements and mitigate the vulnerability of structures at the WUI.
Keywords: Australian Standard AS3959, bushfire attack level, firebrands, firebrand flux, physics-based modelling, radiative heat flux, radiant heat, wildland fire.
Introduction
Firebrands generated from burning vegetation are a potential threat to people and structures in the wildland–urban interface (WUI) owing to the unpredictable nature of spotting (the phenomenon of ignition of new fires by burning particles like wood chips, bark, twigs, leaves, or seeds ahead of a main fire front). This phenomenon becomes more severe with the magnitude of the wildfire and structural ignition becomes harder to control. The hazards from wildfire on structures in the WUI can be classified as direct flame contact, radiant heat, firebrand attack and a combination of two or all of these (Blanchi et al. 2006). Post-fire investigations reveal more than 50% of houses destroyed by wildfires are from firebrands and two thirds of these are ignited directly or indirectly by firebrands (Maranghides and Mell 2011). Leonard et al. (2004) claim that firebrands caused the ignition of over 90% of houses in Australia during a number of wildfire events. Firebrands may accumulate in particular locations of residential structures such as gutters, roofs, decks and corners or may penetrate through vulnerable openings such as windows, vents and gables, eventually triggering structural ignitions (Leonard 2009; Manzello et al. 2011, 2020; Whittaker et al. 2017). Hence, quantifying firebrand attacks and selecting building materials capable of withstanding ignitions by firebrands are required.
Numerous standards and guidelines are used in different jurisdictions for constructing buildings to mitigate wildfire and firebrand attack. Some of these standards provide protocols to follow for minimising the danger of firebrands landing on structures and secondary ignition. The FireSmart guide book (Alberta Government 2013; Intini et al. 2020) provides guidance to Canadian provinces to define three buffer zones (<10, 10−30, >30 m) for the degree of vegetation close to buildings. The guidebook states the roof is the most vulnerable component of a building owing to landing glowing and flaming firebrands. The importance of selecting proper construction materials for exterior siding, vents and other openings to avoid firebrand ignition is also described. The US National Fire Protection Association standards (NFPA 1141–1144) includes provisions regarding hazard definition, WUI fire prevention, suppression, protection and mitigation. The generalised US codes are further made more specific for the fire weather conditions of jurisdictions, including some of the California Fire Code (California Standard 2016) and the Colorado WUI Hazards Assessment Methodology (Edel 2002).
The Fire Emergency New Zealand Act (New Zealand Governement 2017) and the New Zealand Building Code (Department of Building and Housing 2012) provide guidelines to ensure the safety of rural homes. The forest code of France (Francaise 2017; Intini et al. 2020) sets up plans to reduce wildfire risk in vulnerable areas and plans for preventing fires by vegetation clearing in fire-prone regions. The fire code in Italy (Bovio et al. 2001) applies to country-level WUI fires and defines regional planning activities and danger zones for structures against wildfires and interface fires. The International Wildland–Urban Interface Code (International Code Council 2022) proposes firebrand and wildfire safety provisions for properties in the WUI and aligns with other international building standards.
In Australia, Australian Standard AS3959:2018 (Weir 2018) is used to define construction requirements in wildfire-prone areas. The Bushfire Attack Level (BAL) of AS3959 measures the severity of a building’s potential exposure to firebrand attack, radiant heat and direct flame contact using increases of radiant heat flux (kW m−2) (Weir 2018). BAL describes the safe distance between the building and the edge of vegetation expressed quantitatively as radiant heat. AS3959 also provides construction guidelines to prevent firebrand attack. In general, the effect of firebrands generated in proximity to the main fire front and its attack is generalised in all the above-mentioned codes.
Quantifying firebrand attack is necessary to improve the quality of the standards as firebrands are the main cause of house ignition during wildfires. In this study, we mainly focus on Australian Standard AS3959:2018. However, the methodology can be applied to any code.
The intensities of wildfires that occur in different jurisdictions and regions of Australia are expressed by the Fire Danger Index (FDI) in AS3959. The numerical value of FDI varies with environmental conditions, as shown by Eqn 1 (Noble et al. 1980):
where D, Drought Factor; Rh, relative humidity (%); T, ambient temperature T (°C) and U10, wind speed (km h−1) at 10 m elevation in open land.
Compared with the DF and temperature, wind speed changes in a shorter time, resulting in rapid changes in FDI. Also, increasing wind speed results in a higher number of firebrands generated, according to Bahrani (2020). Experiments of Adusumilli et al. (2021), Hudson et al. (2020) and Manzello et al. (2007) showed that a lower Fuel Moisture Content (FMC) also causes a higher number of firebrands. The Rh also affects the FMC according to Eqn 2 (Cruz et al. 2014), which is an empirical correlation widely used by Australian fire agencies:
where T is the air temperature (°C). Eqn 2 is widely used by Australian fire agencies to calculate FMC (Cruz et al. 2014). Further, Adusumilli et al. (2021), Hudson et al. (2020) and Manzello et al. (2007) revealed the number of firebrands generated depends on the burning fuel species. Therefore, calculating the firebrand generation rate by accounting for fuel species, wind speed and FMC is important to apply in any realistic firebrand modelling study.
Firebrand modelling and dynamics have been extensively studied over the past few decades. These models can be categorised into mathematical, empirical and computational fluid dynamics (CFD) models according to the degree of complexity, availability of input data and computational power. The empirical models of Tarifa et al. (1965), Albini (1979) and Woycheese and Pagni (1999) explained the effect of firebrand shape, size and terminal velocity on spotting distance and the influence of the convective column on the critical height attained during flight. The empirical model of Ellis (2000) combined aerodynamic and combustion behaviours of firebrands to estimate spotting distance. Koo et al. (2010) developed a physics-based model for the transport of cylindrical and disk-shaped firebrands. They showed the spotting distance of firebrands generated from a crown fire is larger than that originating from a surface fire. Wadhwani et al. (2022) validated short-range firebrand transport using the physics-based model Fire Dynamics Simulator (FDS) and Wadhwani et al. (2019) examined the dispersion of firebrands inside an idealised forest. They found the streamwise distribution of firebrands qualitatively similar to field measurements and observations of Eucalyptus and pine vegetation fires (Gould et al. 2008; Thomas et al. 2017; Storey et al. 2020). Wickramasinghe et al. (2022) reproduced the single tree burning experimental results of Manzello et al. (2007) using physics-based modelling. They also numerically estimated the firebrand generation rate using the experimental data from a single tree burning conducted by Manzello et al. (2007) and a management-scale forest fire test conducted by Thomas et al. (2017) using an inverse analysis process. In these simulations, they reproduced experimental firebrand collection using a trial and error method while maintaining the environmental (wind speed, temperature, relative humidity) and fuel (fuel density, FMC, tree height and dimensions of vegetation particles) conditions of the laboratory and field experiments. It was found that the firebrand generation rate was 4.18 pieces (pcs) MW−1 s−1 for a pitch pine forest fire (correlated with fire intensity). In the present work, firebrand generation data calculated from Wickramasinghe et al. (2022) are used as simulation inputs.
In this study, we seek to address a significant gap in building codes, standards and guidelines, which currently do not provide a means to quantify firebrand attacks on houses under various wildfire conditions. Our objective is to establish a correlation between wildfire intensity, firebrand attack and radiative heat flux, making this study the first of its kind to bridge this knowledge gap. To achieve this, we conducted a series of physics-based simulations exploring the potential correlation between the firebrand landing flux on structures and the corresponding received radiative heat flux. Our simulations encompassed a range of fire intensity levels, specifically FDI 100, 80 and 50, along with different distances of a house from a static fire front. With these simulations, we aim to fill the knowledge gap and provide valuable information for the development of comprehensive recommendations and standards for the characterisation of a firebrand attack.
Methodology
The simulations were conducted using a physics-based model in FDS, which is an open-source fire modelling tool of the National Institute of Standards and Technology (NIST), USA (McGrattan et al. 2005). FDS uses the multiphase modelling technique, with fluid turbulence modelled by Large Eddy Simulation (LES), while firebrands are introduced into the domain using a Lagrangian particle-based transport scheme (McGrattan et al. 2013). The FDS 6.6.0 version used in the present study comes with Deardorff’s viscosity model (McDermott et al. 2008) as the default transport coefficient. It solves governing conservation equations for buoyant flow, combustion rate, energy and species transport in a low Mach number approximation. The concepts of mass, momentum and energy conservation are applied to sub-divided smaller volumes (rectilinear cells or control volumes) to obtain time-dependent, three-dimensional solutions (McGrattan et al. 2013). The flaming laboratory-scale firebrand landing distribution (~10 m travel distance) simulation using FDS was validated by Wadhwani et al. (2022) against experimental data obtained from a firebrand generator. Wadhwani (2019) showed the distributions of firebrands in the downwind direction were qualitatively similar to the field study in Project Vesta (Gould et al. 2008) for short-range firebrands. Hence, it can be considered that the FDS model is suitable for short-range firebrand simulation. As per Wadhwani et al. (2022), we modified the FDS source code to include the Haider and Levenspiel (1989) drag model accounting for the sphericity of particles.
Model set-up
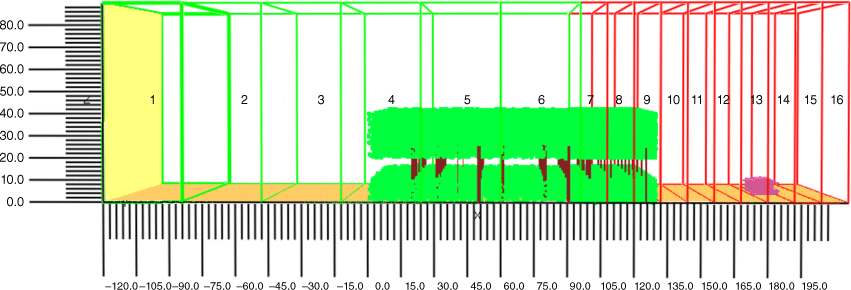
The simulation domain size was chosen as 336 × 100 × 90 m with a 1.5 m grid size in the wind developing region and 0.75 m grid size in the volume where fireline, firebrand generation and landing occur. These grid sizes were determined both graphically and using the grid convergence index (GCI) according to the grid sensitivity analysis by Wickramasinghe et al. (2022). Both time-averaged wind velocity and temperature were used in the grid sensitivity analysis for 0.5, 0.75 and 1.5 m grid sizes. It was found that GCIs for time-averaged velocity are 16% for 0.5 m/0.75 m grids and 32% for 0.75 m/1.0 m grids. These values are 19% and 27% for time-averaged temperature. Therefore, a 0.75 m grid size was chosen for conducting the simulations in the current study for reasonable accuracy of results and lower computational cost. The inlet of the domain is set at X = −120 m and the forest starts at X = 0 m, providing sufficient space to develop the wind field. The end of the forest is at X = 130 m. The domain was divided into 16 meshes, as shown in Fig. 1. All these mesh segments are set along the X direction as slices parallel to the Y-axis. The height of each mesh segment is 90 m.
Mesh segmentation of the forest simulation. Green meshes are discretised into 1.5 m cubic grids and red meshes are divided into 0.75 m grids. The width of the green and red segments is 100 m (scale is in metres). The model house is shown in pink and the forest is illustrated in green (leaves) and brown (trunks).
The side boundaries, with an area of 336 × 90 m, were defined as ‘MIRROR’ boundary conditions (free slip) to represent the extending nature of the fireline and forest to avoid any edge effects. The top and the outlet boundaries were set with ‘OPEN’ boundary conditions to allow free wind flow and firebrand movement. The inlet boundary is set by the wind while the bottom boundary represents the ground surface.
The dimensions and shapes of vegetation particles, FMC, thermo-physical properties (density, thermal conductivity, specific heat) and mass per volume (MPV) are important input parameters to model a forest in FDS. Table 1 presents the input parameters for Eucalypt forest that we used for the respective simulations taken from the literature. The MPV for understorey (0.25 kg m−3) and canopy (0.05 kg m−3) were calculated according to the forest fuel load given in AS3959 (Weir 2018). The vegetation particles were randomly distributed in a volume of 130 × 100 × 40 m with an average forest height of 40 m. The vegetation height was taken as the average forest height given in AS3959 (Weir 2018) to be relevant to Australian jurisdictions. Researchers can follow our methodology to conduct research for their jurisdiction with a chosen forest height. There are two vegetation layers from 0 to 10 m and 20 to 40 m for the understorey and the canopy within this volume (Weir 2018). The trunks of the Eucalyptus trees were represented by 25 m high and 0.75 m diameter non-burning (INERT) obstacles.
| Parameter | Pine needles | Moisture | |
|---|---|---|---|
| Thermal conductivity (W m−1 K−1) | 0.31 (Hays 1975) | 2.0 (Khan et al. 2019) | |
| Specific heat (kJ kg−1 K−1) | 2.760 (Aston 1985) | 4.184 (Khan et al. 2019) | |
| Density (kg m−3) | 650 (Wadhwani 2019) | 1000 (Khan et al. 2019) | |
| FMC (%) | 3.84 (Cruz et al. 2015) | – | |
| MPV (kg m−3) | 0.05 (canopy) and 0.25 (understorey) | – |
In this study, we focused on FDIs 100, 80 and 50 to represent a variety of fire intensity conditions. To obtain the selected FDIs, we varied the wind speed while keeping the DF, relative humidity and temperature constant, as per Eqn 1. The reason for selecting wind speed as the controlling parameter is its sensitivity to FDI and the rate of change compared with other parameters. We selected the annual maximum mean temperature of 39°C in Australia according to the Bureau of Meteorology (Australia Bureau of Meteorology 2022) as the ambient temperature. The DF indicates the degree of absence of moisture in the duff and upper soil layer on a scale from 1 to 10 (CSGNetwork 2022). In this case, we considered the worst-case scenario for starting a fire based on a DF of 10, which indicates complete dryness of the fuel surface. The relative humidity was taken as 25% from a psychrometric chart, ensuring the possibility of the existence of an extreme day according to the chosen ambient temperature. The climatological records from the Australian Bureau of Meteorology suggest that there is potential occurrence of simultaneous conditions featuring 25% relative humidity (Australia Bureau of Meteorology 2006) and a maximum temperature of 39°C (Australia Bureau of Meteorology 2022) in specific geographic areas. Based on these data, FDIs of 100, 80 and 50 were obtained for open land wind speeds of 70 km h−1 (19.44 m s−1), 60 km h−1 (16.67 m s−1) and 40 km h−1 (11.11 m s−1) respectively. The FMC of both canopy and subcanopy was calculated as 3.84% with an Rh of 25% and T of 39°C according to Eqn 2 (Cruz et al. 2014).
Wind flow development
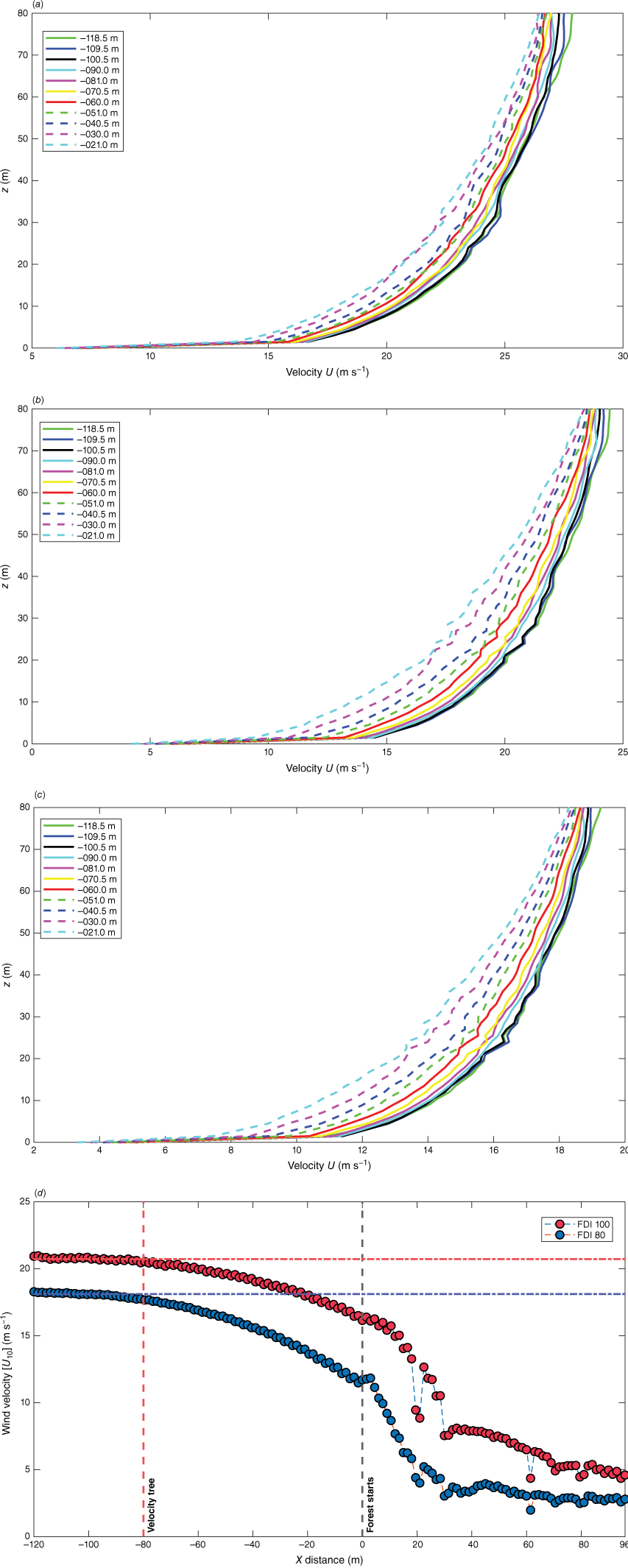
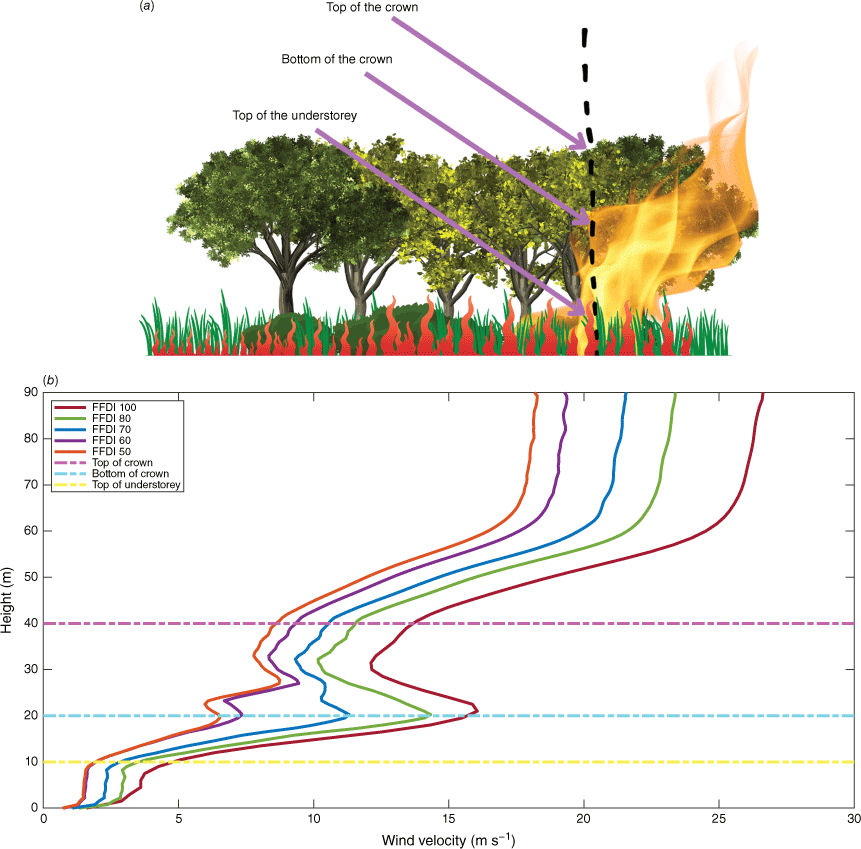
A wall of wind approach (McGrattan et al. 2005) was applied by setting up the atmospheric profile. The length scale and the number of eddies at the inlet were calculated and added to the model according to Jarrin et al. (2006). In this case, the eddy length scale is calculated as three times the cell length of the inlet domain (3 × 1.5 m) and the number of eddies (~450) is calculated by dividing the area of the inlet domain by the square of the length scale ((102 × 90 m/(4.5 m))2. When the wind blows over the ground, its speed decreases with distance owing to surface roughness. Therefore, to obtain the desired wind speed on the open land, we need to apply a slightly higher wind speed at the domain inlet. Hence, a few trials were carried out with several initial wind speeds (20.7, 18.2 and 14.3 m s−1) at the domain inlet to obtain the intended average U10 wind speeds on the open land (X = −80 m) to match the FDIs. The spin-up time was 5 × DTT (Domain Travel Time) to obtain the developed wind fields without the fire having started, as proposed by Moinuddin et al. (2018) in precursor simulations. The well-developed wind field was applied in the following simulations to establish the desired wind speed in a shorter time. These wind profiles are presented in Fig. 2a–c at a few locations on the open land. The locations from X = −120 to 0 m (i.e. X = −109.5, −100.5, −90.0, −81.0 m, etc.) were chosen with an ~10 m gap to each to cover the entire open land area. These wind profiles help to determine the steady state wind speed in this region.
Developed wind field at X = −80 m and other locations in open land with ~10 m gap for: (a) FDI 100; (b) FDI 80; (c) FDI 50. Z is the vertical height in metres; and (d) is the velocity reduction when the wind enters the forest region at FDIs 100 (red dots) and 80 (blue dots). The velocity tree is the set of devices included in the simulation to capture the wind velocity at X= −80 m and along the vertical direction.
House designs
Australian Standard AS3959 describes construction requirements for each building component, such as roofs, gutters, sub-floor, decks, windows and doors, to avoid firebrand attack. Therefore, we designed two houses (single-storey and double-storey) following the technical drawings of standard house designs proposed by the Australian Government Guide to Environmentally Sustainable Homes (Australian Government 2020). Fig. 3 shows the iso-views of the houses designed by SOLIDWORKS to import into the FDS simulations and the respective designs proposed by the Australian government.
Iso-views of the modelled (a) single-storey, (b) double-storey houses and their respective designs (c), and (d) proposed by the Australian Government. Heat flux devices are located at the deck (violet), front wall (red), side wall (blue), door and windows (green), and gutter (yellow), as shown in (a) and (b).
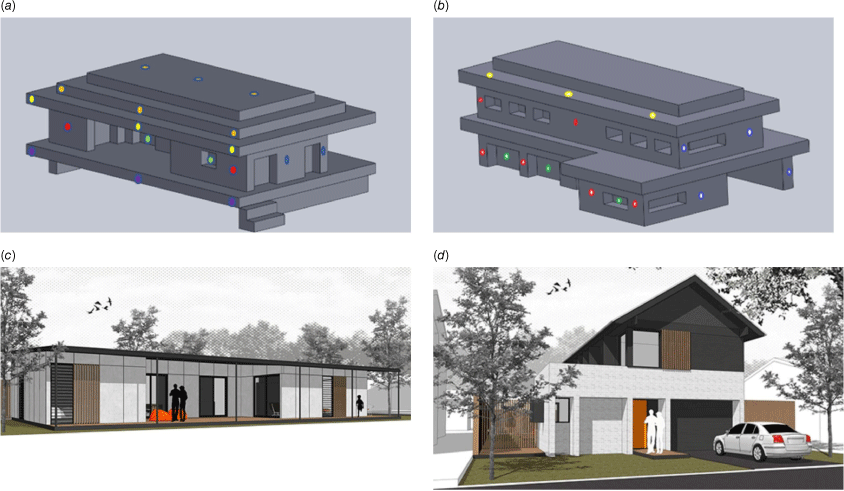
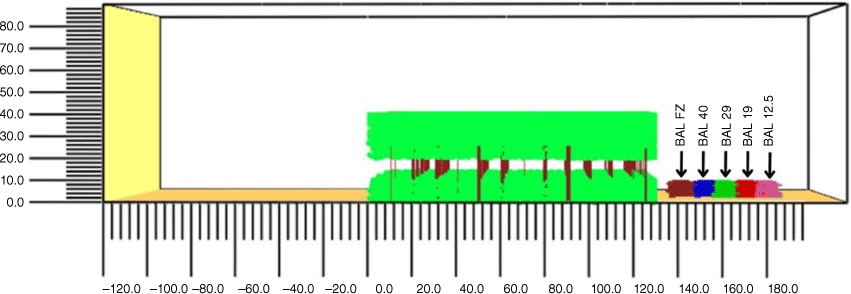
We did not consider the ignition of the houses at this stage and decided to represent housing components by non-burning obstacles with the relevant dimensions. The location of the house (distance from the edge of the vegetation) was maintained according to the BALs presented in Table 2. Here, we positioned the frontmost location of the house (gutter and the deck), as shown in Fig. 4, at the mid-value of each distance range except for BAL 12.5. In AS3959, the acceptable distance for constructing houses from the vegetation at BAL 12.5 is given as 48–100, 42–100, 32–100 m for FDIs 100, 80 and 50 respectively. Therefore, we maintained the distance between the modelled house and the vegetation as 50 m while fulfilling the above requirement to reduce the length of the simulation domain.
Heat and firebrand flux
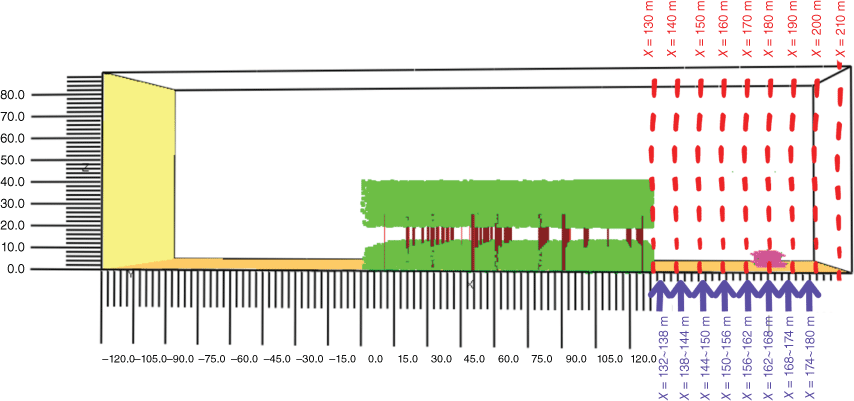
The measurement point devices in FDS were set up at strategic locations (roof, gutter, window, steps, understorey, deck, etc.) to capture the radiative heat flux and firebrands landing on the houses. As mentioned earlier, these locations are considered as openings and vulnerable to spread fire according to AS3959. Laboratory-scale experiments of Manzello et al. (2011) and Suzuki and Manzello (2020, 2021) also underscore the importance of concentrating on these vulnerable strategic locations to prevent firebrand attacks. Fig. 3 illustrates the location (not to scale) of the heat flux devices. The cuboid firebrand flux devices were positioned at strategic locations such as roof, gutter, deck, window and door corners. These devices have a bottom surface area that is the same as the area covered by the strategic locations and a thickness of one grid cell. The firebrand flux devices record the mass of each size of firebrand landing on the device volume. Firebrand mass accumulates in the cuboid collector and the number of collected firebrands is calculated by dividing the mass accumulated by the individual firebrand’s mass. The firebrand flux is calculated by dividing the collected number of firebrands by the area of the device and the time duration of collection. The maximum and average radiative heat fluxes on the houses are calculated during the fire time with the data recorded in the FDS device output file. The firebrand distribution in the downwind direction was also investigated by setting devices as vertical and horizontal planes as illustrated in Fig. 5. These devices measure the quantity of ‘PARTICLE FLUX’ using an area integral technique through the defined area of the plane and facilitate understanding of the risk areas where a large number of firebrands land.
A sketch of firebrand mass flux devices to identify firebrand distribution in the downwind direction. The vertical devices (red) with an area of 90 × 100 m measure the mass of firebrands passing through a unit area of each plane and the horizontal devices (purple) with an area of 6 × 100 m measure the mass of firebrands landing on each sector of the ground (scale is in metres).
Firebrand data
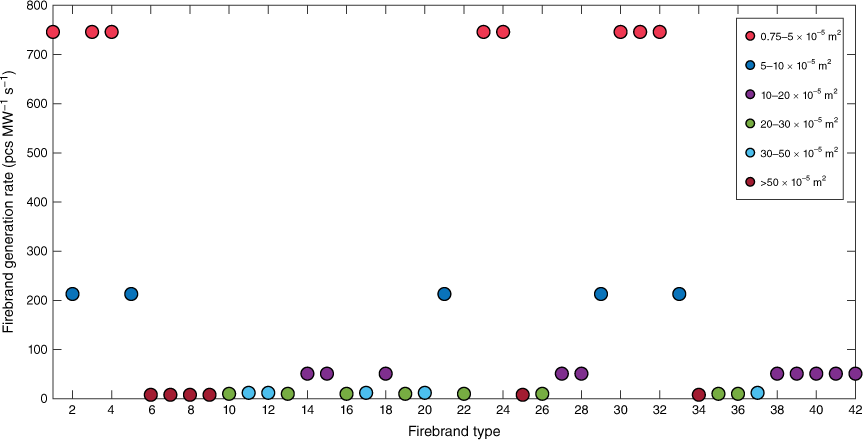
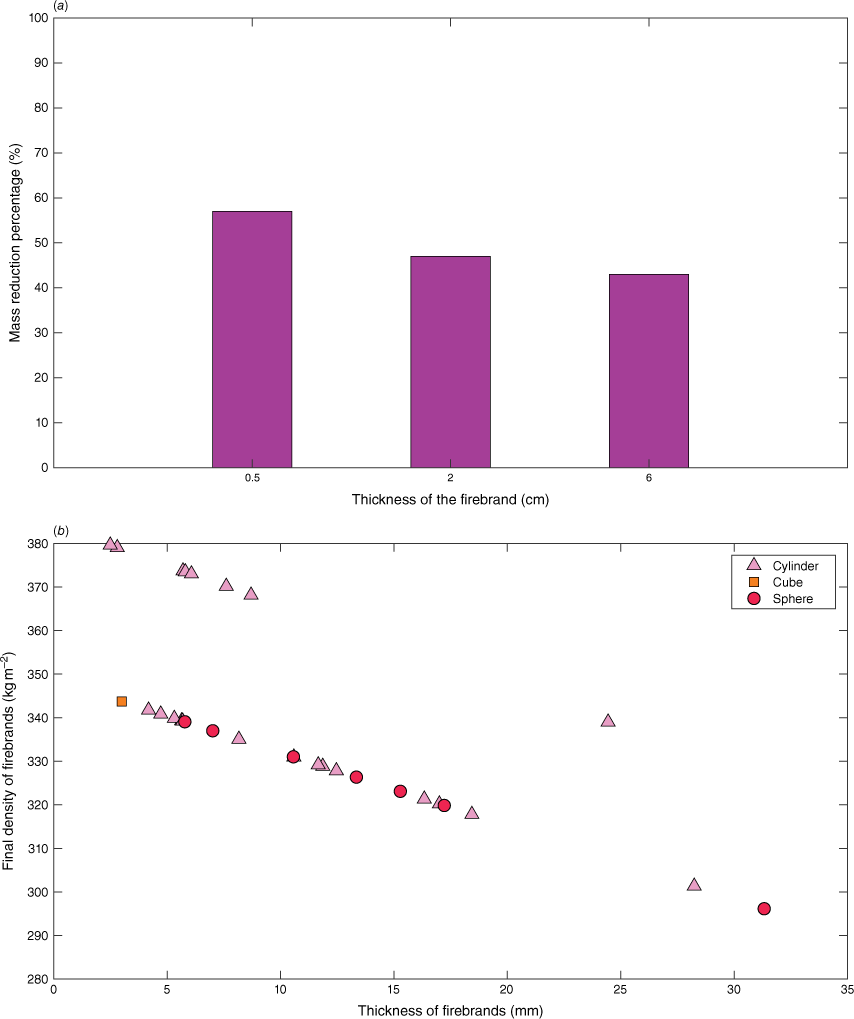
The firebrand data (shape, size, composition) were taken from Thomas et al. (2017). There were 42 sizes of firebrands used as inputs to the FDS model while varying their generation numbers based on the composition of firebrands collected, as shown in Fig. 6. Most of these firebrands are fragments of bark (81%), and the rest are twigs (9.5%) and needles (9.5%). Out of these, 55% are cylinders, 32.5% cubic and 17.5% are sphere-shaped firebrands. The thermo-physical data of the firebrands were taken from the literature (Hays 1975; Aston 1985; Wadhwani 2019) to match Eucalyptus fuel, as presented in Table 3. A density of 650 kg m−3 was used for Eucalyptus wood (Wadhwani 2019). The density variations of the firebrands were approximated by accounting for moisture evaporation, pyrolysis and combustion that occur during flight based on the findings of Menzemer (2021). In this approximation, we consider the initial temperature of the firebrands (900°C) based on the flame temperature of simulations as firebrand generation happens in the forest volume where the trees are engulfed by flame. As per Fig. 7a, we estimated the density reduction percentage and calculated the density of the landing firebrands, which varied from 355 to 467 kg m−3 depending on their thickness. We also assumed the shape and the size of firebrands remained the same during flight regardless of combustion and pyrolysis, as Menzemer (2021) showed that combustion and pyrolysis occur in the first few seconds after release from the vegetation. The estimated density distribution of these firebrands is presented in Fig. 7b and was used as input in the simulation to differentiate between the characteristics of the cylinder, sphere and cube firebrands generated.
Firebrand generation rates for each firebrand type (42) according to size distribution in terms of projected area (m2).
| Parameter | Canopy woody fuels | Live needles | |
|---|---|---|---|
| Conductivity (W m−1 K−1) | 0.38 (Aston 1985) | 2.802 (Hays 1975) | |
| Specific heat (kJ kg−1 K−1) | 0.36 (Aston 1985) | 2.607 (Aston 1985) | |
| Element density (kg m−3) | 590 (Wadhwani 2019) | 650 (Wadhwani 2019) |
(a) Firebrand density reduction percentage at 900°C initial temperature for different thickness classes; (b) estimated density of firebrands considering pyrolysis and combustion according to Menzemer (2021).
Firebrand generation rate estimation for vegetation species, wind and FMC
We considered firebrand collection data of species such as ponderosa pine, western juniper, loblolly pine and Leyland cypress from the experimental studies of Hudson et al. (2020) and Bahrani (2020) to approximate firebrand generation for Eucalyptus. We compared the average tree height, shape of the canopy and the orientation of tree leaves of these species with Eucalyptus to identify vegetation from the same family using photographs and databases (World Agroforestry 2023; International Botanic Gardens Conservation 2023) of numerous vegetation species. Owing to the scarcity of data, we considered tree species from the same family produce similar numbers of firebrands under the same wind and fuel moisture conditions. Out of the species used to find the effect of wind speed on firebrand generation by Bahrani (2020), loblolly pine is the species that matches Eucalyptus most closely. As per the experiment of Hudson et al. (2020), western juniper is the closest species to Eucalyptus to approximate firebrand generation rates for different FMCs. Using these experimental data, we derived mathematical relationships to understand the effect of wind and FMC on firebrand generation. However, the firebrand generation numbers of these experiments were not correlated with fire intensity. We needed a base value to find firebrand generation rates correlated with fire intensity using the mathematical relationships derived for firebrand generation against wind speed and FMC. Therefore, we used the firebrand generation rate of 4.18 pcs MW−1 s−1 (Wickramasinghe et al. 2022) determined for pitch pine at 31% FMC and with 2 m s−1 average wind speed as the base information for estimating the firebrand generation rate for Eucalyptus.
The experiment of Bahrani (2020) shows higher firebrand production with increasing wind speed. Based on these experimental data, we obtained the mathematical relationships (Eqns 3 and 4) for the number of generated firebrands with wind speed for FDIs 100, 80 and 50:
where fbgeneration is the number of firebrands generated and Uwind is the wind speed at the burning vegetation. As the wind enters the forest region, it is deflected owing to the drag force exerted by the vegetation. Therefore, the wind speed obtained on the open land decreases and we need to find the speed at the fireline to estimate firebrand generation to match the experimental procedure of Bahrani (2020). Fig. 8 is a sketch of the locations where wind velocities were measured in our simulations to average them and use them in the estimation of firebrand generation rate against wind speed. The average wind velocities at the fireline for FDI 100, 80 and 50 were found to be 10.38, 8.88 and 5.48 m s−1 for open land wind speeds of 19.44, 16.67 and 11.11 m s−1, respectively. All these open land wind speeds were calculated according to Eqn 1, where wind velocity (U10) was adjusted to obtain the FDIs of 100, 80 and 50. The wind-specified firebrand generation ratio, which is the number of firebrands produced at the average wind velocity at the fireline compared with the number of firebrands produced at the reference wind speed (2 m s−1), was calculated, as shown in Table 4.
(a) The locations (top of the crown, bottom of the crown and top of the understorey) where wind velocity is measured in the forest. (b) Wind profiles for different FDIs at the fireline. There are some deflection points due to the vegetation drag force in canopy and understorey regions.
| Similar vegetation | Firebrand generation rate (pcs MW−1 s−1) | Wind speed (m s−1) | Number of firebrands | Generation ratio relative to 2 m s−1 | |
|---|---|---|---|---|---|
| Loblolly pine Eucalyptus | 4.18 (pitch pine at 2 m s−1) | 2.00 (reference) | 298 | (298/298) = 1.00 | |
| 5.48 (FDI 50) | 454 | (454/298) = 1.52 | |||
| 8.88 (FDI 80) | 575 | (575/298) = 1.93 | |||
| 10.38 (FDI 100) | 575 | (575/298) = 1.93 |
According to the relationship of Hudson et al. (2020) between the number of firebrands produced and FMC, fbgeneration was mathematically derived as shown in Eqn 5:
where FMC is the dry basis fuel moisture content. From this, the FMC-specified firebrand generation ratio of Eucalyptus, which is the number of firebrands produced at a certain FMC compared with the number of firebrands produced at a reference FMC (31%), was estimated and is shown in Table 5.
| Similar vegetations | Firebrand generation rate (pcs MW−1 s−1) | FMC (%) | Number of firebrands | Generation ratio to 3.84% FMC | |
|---|---|---|---|---|---|
| Ponderosa pine Eucalyptus | 4.18 (pitch pine at 31%) | 31 (reference) | 393 | (393/393) = 1.00 | |
| 3.84 (all FDIs) | 520 | (520/393) = 1.33 |
Although numerous researchers have experimentally explored the effects of firebrand generation solely for wind speeds, fuel moisture and vegetation, a comprehensive experiment incorporating all these effects for a vegetation species such as Eucalyptus is still lacking. However, it is possible to include all these relevant parameters in the simulation, which represents the physics of the wildfire. In the novelty of this work, we introduced calculated individual firebrand generation ratios to account for the combined influence of these factors. Therefore, final firebrand generation rates were approximated by multiplication of the quantified individual generation ratios of species, wind and FMC with the reference firebrand generation rate of pitch pine. Hence, the firebrand generation rates of forest vegetation were found to be 8.43, 10.68 and 10.68 pcs MW−1 s−1 for FDI 50, 80 and 100.
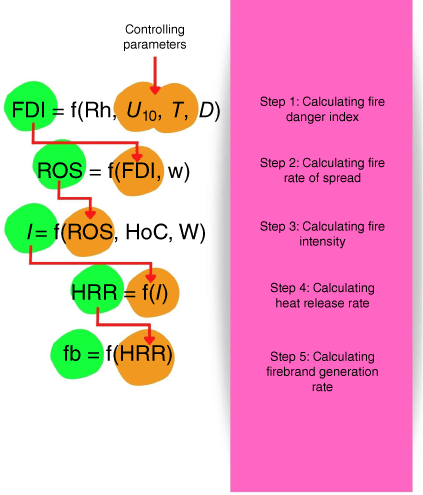
Firebrand input rate
From the firebrand generation rates (pcs MW−1 s−1), we calculated the firebrand input rate (pcs s−1) to use as simulation input based on the total heat release rate (HRR) (MW) of the fire. The process of estimating firebrand input rate is presented in Fig. 9; it is initiated with the FDI at Step 1 according to Eqn 1. The rate of spread (ROS) of the fire was calculated in the second step as per Noble et al. (1980):
where w is the surface fuel load (t ha−1) of the forest. Modelling coupled pyrolysis and combustion reactions of vegetation material (leaves, twigs, trunks) is a computationally expensive complex task that needs accurate thermo-physical properties of non-homogeneous vegetation materials under different environmental and fuel conditions as well as huge computational resources. Hence, it is noteworthy that we prescribed the forest fire using the pyrolysis rate (reflecting fireline intensities) to represent the burning forest. The intensity I of the fireline (MW m−1) was calculated according to Eqn 7 (Step 3) as per Byram (1959) to apply in the fourth step:
where W is the total fuel load (t ha−1) and HoC is the heat of combustion, which is taken as 18 600 kJ kg−1 from AS3959 (Weir 2018). Fire intensities were calculated for extreme weather conditions corresponding to FDI 50, 80 and 100 according to Eqns 6 and 7. In the fifth step, the total HRR (MW) is calculated by:
where L is the fireline length (100 m). The firebrand input rate FI (pcs s−1) is calculated with Eqn 9:
where FGR (pcs MW−1 s−1) is the final firebrand generation rate found in 'Firebrand generation rate estimation' section for the selected FDIs.
The process for estimating the firebrand input rate to use in the numerical simulation. The controlling parameter is the U10 wind velocity on open land to obtain different Fire Danger Indices (FDIs); w and W are the surface and total fuel load of vegetation.
The fireline depth is a product of ROS and the residence time (37 s) (Wotton et al. 2012) and was used to calculate the fireline area at each fire event. The HRR per unit area of 1759 kW m−2 (HRRPUA) was calculated by dividing the total HRR by the area of the fireline, which was also used as an input parameter. Although we used instant ROS (in Eqn 6) to calculate the fire intensity, the fireline is set as a stationary line close to the edge of the forest and does not spread further. We defined the total HRR in FDS with the calculated value from Eqn 8 to ensure the simulation replicated the behaviour of the fire described in Australian Standard AS3959. The final firebrand input rates were calculated and are presented with ROS, I and HRR in Table 6 for the FDIs.
| FDI | ROS (km h−1) | I (kW m−1) | HRR (MW) | FI (pcs s−1) | |
|---|---|---|---|---|---|
| 50 | 1.493 | 27 002 | 2700 | 22 766 | |
| 80 | 2.384 | 43 117 | 4312 | 46 057 | |
| 100 | 3.013 | 54 485 | 5449 | 58 199 |
The theoretical radiative flux exposure of the house was calculated based on the detailed method presented in Appendix B of AS3959 (Weir 2018). The firefront location was also adjusted (tuned) to match the theoretical radiative heat flux as described in detail in 'Sensitivity analysis' section. After setting up the models following the fire weather conditions given in AS3959, a total of 30 simulations were conducted with the three FDIs and five different BALs to calculate the firebrand and heat fluxes on the two different house designs. We compared the radiative heat flux received by the houses in FDS simulations with the values calculated according to the procedure given in AS3959. When these radiative heat flux matched reasonably, we could assume the simulations represented the quantified radiative heat flux on houses in AS3959.
Results and discussion
Wind effect
Fig. 10 presents some snapshots taken from Smokeview, the visualisation software of FDS, illustrating some major events of a simulation. The vector format of the developed wind field including eddies is shown in Fig. 10a. The wind has been deflected at the top of the canopy owing to vegetation drag. The speed of the flow through the vegetation is decreasing as it proceeds into the forest. Fig. 10b shows the fire at the edge of the forest. The flow at the volume over the fireline becomes highly turbulent, creating a convective column because of the heat provided by the fire. However, this fire column leans towards the house because of the force of the wind flow. The incline of the flame varies with the FDI corresponding to the wind speed and the intensity of fire.
Smokeview representation of streamlines from the simulation of Forest fire at FDI 100 and BAL 12.5 with (a) developed wind flow, (b) buoyancy from forest fire, (c) firebrand generation, transport and landing on the modelled house. The distance between the house and the forest edge is maintained at 50 m according to the BAL.
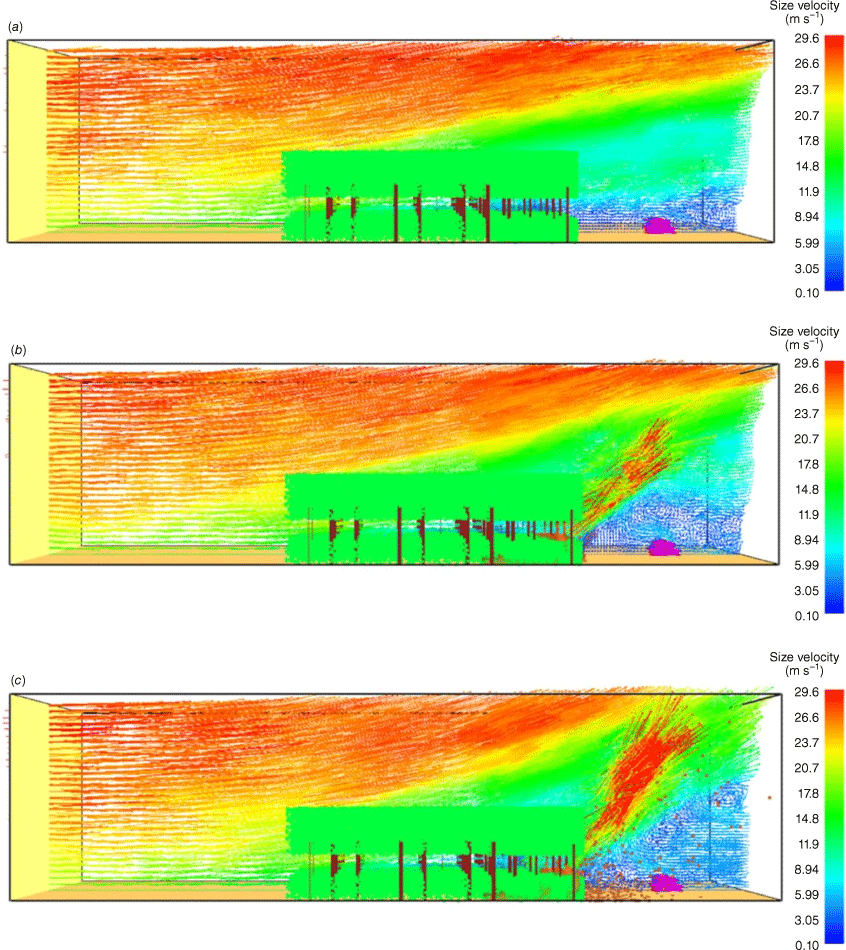
Firebrand generation and landing downwind are shown in Fig. 10c. Many of these particles follow the path of fire-induced buoyancy and rise above the understorey layer of the forest. Some firebrands are highly influenced by the upwards flow and do not move away from the convective column until reaching the top of the domain. When the horizontal wind field becomes the dominant force acting on them, some firebrands leave the convective column, following parabolic trajectories. These firebrands land on the ground or the house depending on the instant resultant forces exerted. The mass, size, shape and flow dynamics determine the firebrand paths and their spotting distance.
Sensitivity analysis
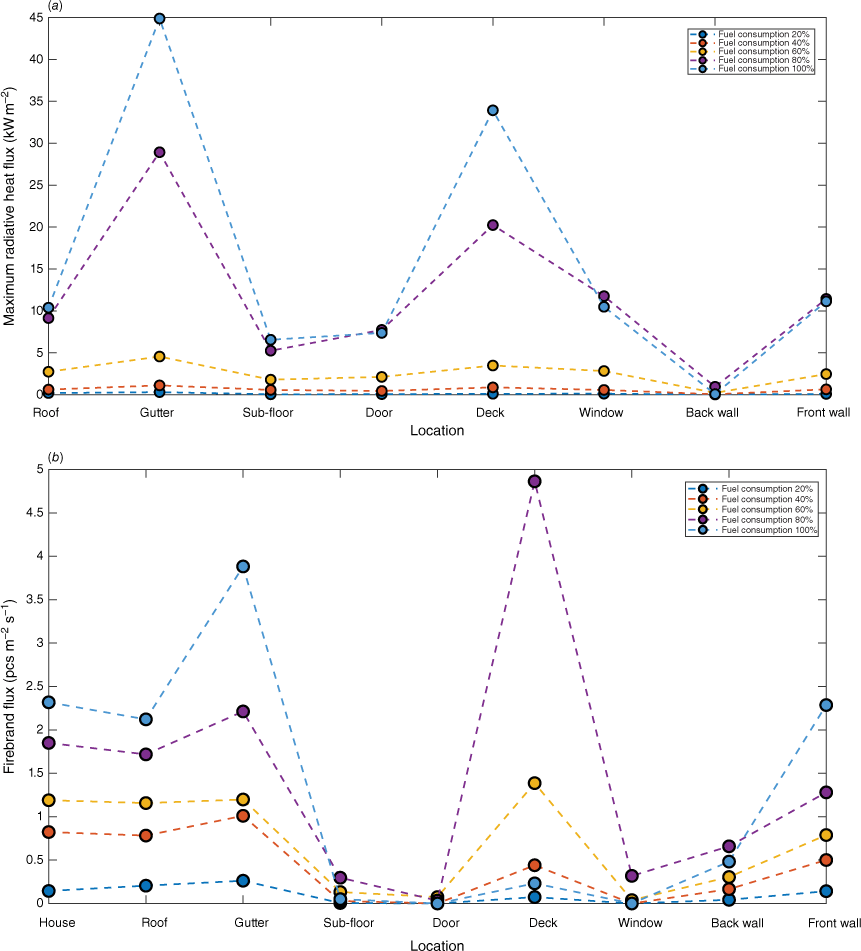
We carried out a sensitivity analysis to understand the effect of forest fuel consumption and fireline location on total radiative heat flux (sum of convective and radiative heat fluxes) and firebrand flux on the single-storey house. Fig. 11 shows the variations of radiative heat and firebrand fluxes at strategic locations of the house for FDI 100 and BAL 29 for demonstration purposes. We maintained canopy and understorey fuel consumption of 20, 40, 60, 80 and 100%. HRR varies according to the fuel load as per Eqns 6, 7 and 8, affecting both radiative heat and firebrand flux. According to Fig. 11a, b, all firebrand and radiative heat fluxes decrease with lower fuel consumption. The highest radiative heat and firebrand fluxes are observed when 100% of the fuel is consumed. These values are significantly higher than for the lower fuel-consuming events. For example, the maximum radiative heat flux on the house when 100% fuel is consumed is greater than 35, 89, 97, 99% compared with fuel consumptions of 80, 60, 40, 20%. This value is 20, 48, 64, 94% for the total firebrand flux on the house. The gaps between the adjacent radiative heat flux values increase, showing the danger increases with higher fuel consumption. This result is consistent with conventional knowledge that management-scale burns help reduce the fuel load in forests and mitigate the danger from firebrand and radiative heat fluxes on houses in the WUI.
Effect on fuel consumption for (a) radiative heat flux, and (b) firebrand flux on the single-storey house. These cases relate to FDI 100 and BAL 29.
The effect of fireline location was examined by positioning the fire front inside the forest at a distance of 0, 5, 8, 10 and 12 m to the edge of the forest. In this process, we aimed to obtain a comparable radiative heat flux for the BALs given in AS3959 and obtain a realistic flame that engulfed the top of the canopy and the lower edge of the forest where firebrands are produced. As the first step, we positioned the model house at BAL 40 (to represent the upper range of the BAL spectrum) and observed the radiative heat flux for the above locations of the fireline. As presented in Fig. 12a, the radiative heat flux was significantly higher for all FDIs when the fire front was aligned with the forest edge (0 m gap). Increasing the gap results in a decreasing radiative heat flux. When this gap is 10 m, the radiative heat flux is reasonable in comparison with the BAL values given in AS3959. However, increasing the gap further results in decreasing radiative heat flux.
Maximum radiative heat flux on the single-storey house (a) for different gaps between the forest edge and fire front in BAL 40, and(b) for 10 m gap between the forest edge and the fire front in BALs 12.5 to 40 for different FDIs.
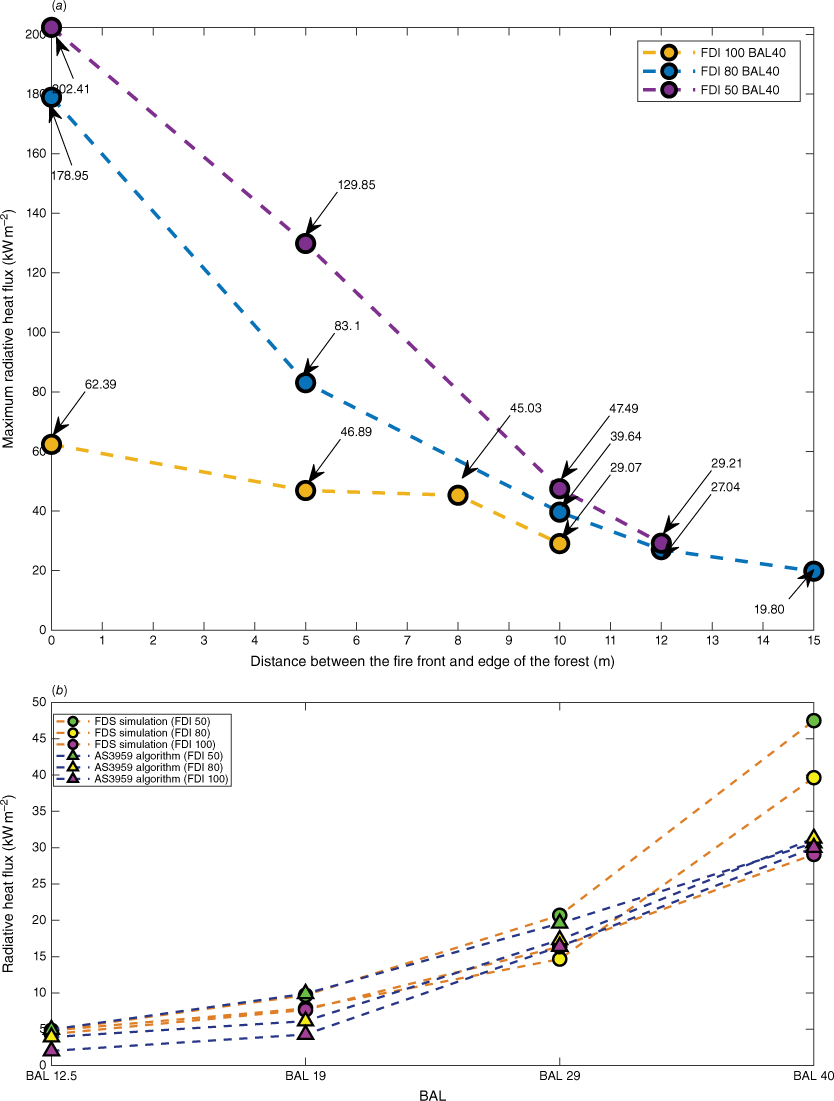
The effect of fireline location was further investigated for other BALs (BAL 12.5 to BAL 40) and FDIs maintaining a gap of 10 m between the fire front and the forest edge. As shown in Fig. 12b–d, the radiative heat flux values obtained for each BAL are comparable with the values given in AS3959 for FDI 100, 80 and 50. From this sensitivity analysis, we chose the distance between the fire front and the forest edge as 10 m to obtain the desired radiative heat flux given in the BALs in AS3959.
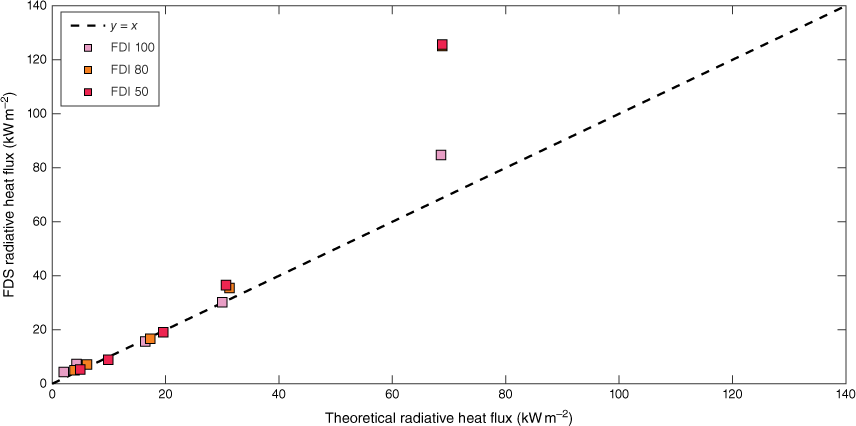
The theoretical and FDS radiative heat fluxes are compared in Fig. 13. When they match, the values should lie on y = x. As per Fig. 13, most of the comparison points are close to y = x, implying the fire behaviour of the simulations reasonably represents the fire behaviour theoretically expressed in AS3959. However, there is a notable deviation at the highest radiative heat flux that relates to BAL FZ. In this case, the distance between the house and the forest is the shortest and the flame is almost in contact with the house. Owing to the complexity of fire behaviour and heat transfer to the house, the divergence of FDS radiative heat flux is coherent at BAL FZ. Compared with theoretical radiative heat flux, there is an underprediction of simulated radiative heat flux for all the values of FDIs 80 and 50 but a slight overprediction for BALs 12.5 and 19 of FDI 100.
Firebrand flux on the houses and distribution in downwind
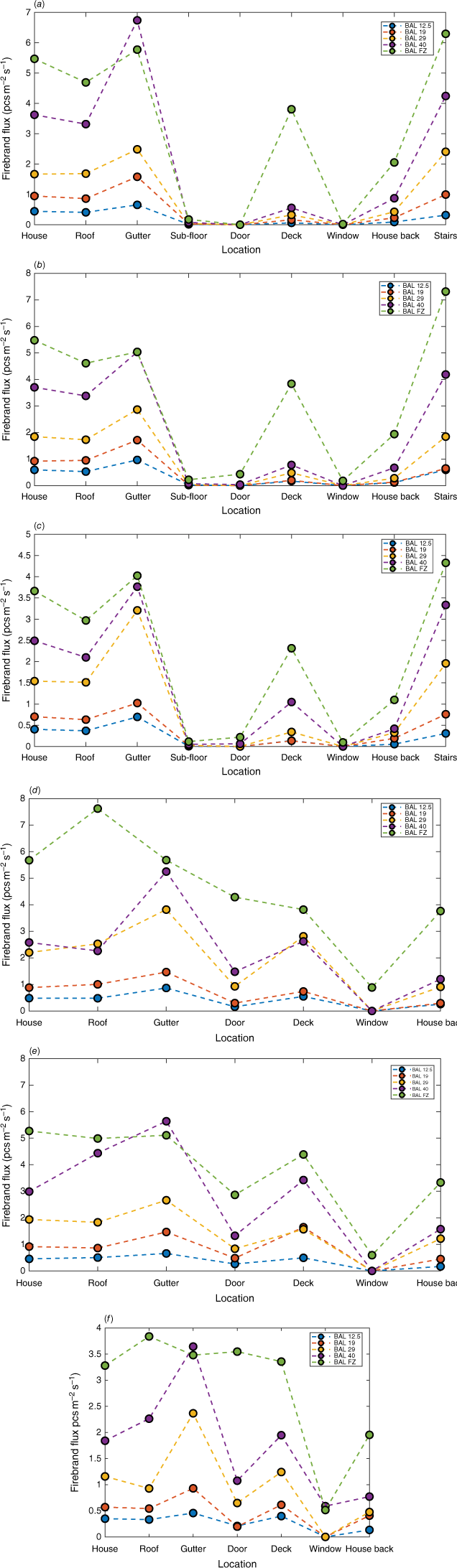
Fig. 14 shows the location-specific total firebrand flux on both house designs for FDIs 100, 80 and 50. It shows the gutter, roof, stairs and deck are the places where most firebrands landed. The locations that are not directly exposed to the wind flow such as doors and windows, receive comparatively a lower firebrand flux. Although it is not directly exposed to the wind, the back of the house receives a considerable number of firebrands owing to the recirculation zone created behind the house, as shown in Fig. 10. The firebrands accumulate close to the back wall of the house following the streamlines of the created vortices. The streamlines and firebrand movement following the circulation near the house location are presented as enlarged images in Supplementary material 1. The video of the forest fire simulation cases for FDI 100, 80 and 50 and BAL 29 are also presented in Supplementary material 2 for clarity. The ignition probability becomes high upon the accumulation number of firebrands on the landing location of the house (Manzello et al. 2006; Suzuki and Manzello 2020, 2021). Therefore, some housing components (roof, gutter, etc.) are more vulnerable than others and need to have special construction requirements, such as material selection, to overcome ignition from accumulated firebrands.
(a–c) Firebrand flux at different locations of the single-storey house and (d–f) double-storey house for Forest in FDI 100 (a) and (d), FDI 80 (b) and (e), FDI 50 (c) and (f) at different BALs. The x-axis shows the total firebrand flux on the complete house during the fire.
The experimental study of investigated firebrand accumulation close to the walls and corners of a model house placed in a wind tunnel facility at the Insurance Institute for Business and Home Safety (IBHS), USA. The high and medium wind speeds (17.4 and 10.3 m s−1) applied in their experiment are close to the relevant wind speeds for FDI 80 and 50, and the distance between the firebrand feeder and the house is close to the BAL FZ in our simulations. Therefore, we converted our simulation results of firebrand number flux (pcs m−2 s−1) on the deck area of the single-storey house into firebrand mass flux (kg m−2 s−1) by multiplying by the individual particle masses as it is the most comparable location with experimental firebrand accumulation near the front wall of the house. The average experimental firebrand accumulation at the wall at high and medium wind speed is 0.2 and 0.073 g mm−2 s−1, respectively. However, these are 0.0047 and 0.0027 g mm−2 s−1 for comparable high and medium wind speeds in the simulations. These variations between the experiment and the simulations may be due to the differences in firebrand generation/injection rates, firebrand characteristics and designs of the houses and not maintaining an actual fire for lofting firebrands in the wind tunnel facility. For example, in the experiment, the firebrand feeding rate (by an auger feeder) was controlled based on visual inspection whereas the simulations maintained constant firebrand generation rates for each FDI. However, both simulation and experiment show that high wind speeds result in a greater accumulation of firebrands. The majority of the firebrands accumulate immediately adjacent to the wall in the simulation and the experiment, and both show a greater vulnerability in corner areas. Furthermore, the wind tunnel experiment of Nguyen and Kaye (2021) shows similar results to our simulation for rooftop firebrand accumulation hotspots. In this experiment, many firebrands were retained at internal corners (around dormers) making those places hotspots depending on the flow characteristics around the building.
The firebrand fluxes decreased with decreasing BAL and FDI. In other words, firebrand attack decreases when the house is located far from the fire and the fire intensity is low. The difference in firebrand flux of adjacent BALs (i.e. BAL 19 and BAL 29, BAL 29 and BAL 40, etc.) also increases when the house is located closer to the vegetation. This suggests the firebrand attack becomes significantly higher when the house is built near vegetation.
The average total firebrand mass distribution through vertical planes and horizontal sections in the downwind direction is presented in Fig. 15. The total firebrand mass flux (kg s−1) is the sum of each firebrand type’s mass flux. Dividing the mass flux of the individual firebrand type by the weight of a single firebrand of that type and the area of the plane that firebrands pass through or land on gives the firebrand number flux (pcs m−2 s−1). Therefore, an increasing total firebrand mass flux indicates an increase of total firebrand number flux (pcs m−2 s−1) and vice versa.
Firebrand distribution (a) through vertical planes, and (b) on the horizontal sections in the downwind direction for FDI 100, 80 and 50. The front location of the house at BAL 29 for each FDI is presented in (a) for demonstration purposes. (The forest edge is at X = 130 m. The section 132–138 m is equal to a distance of 2–10 m from the edge of the forest. Similarly, 138–144 m is equal to a distance of 10–16 m and so on.)
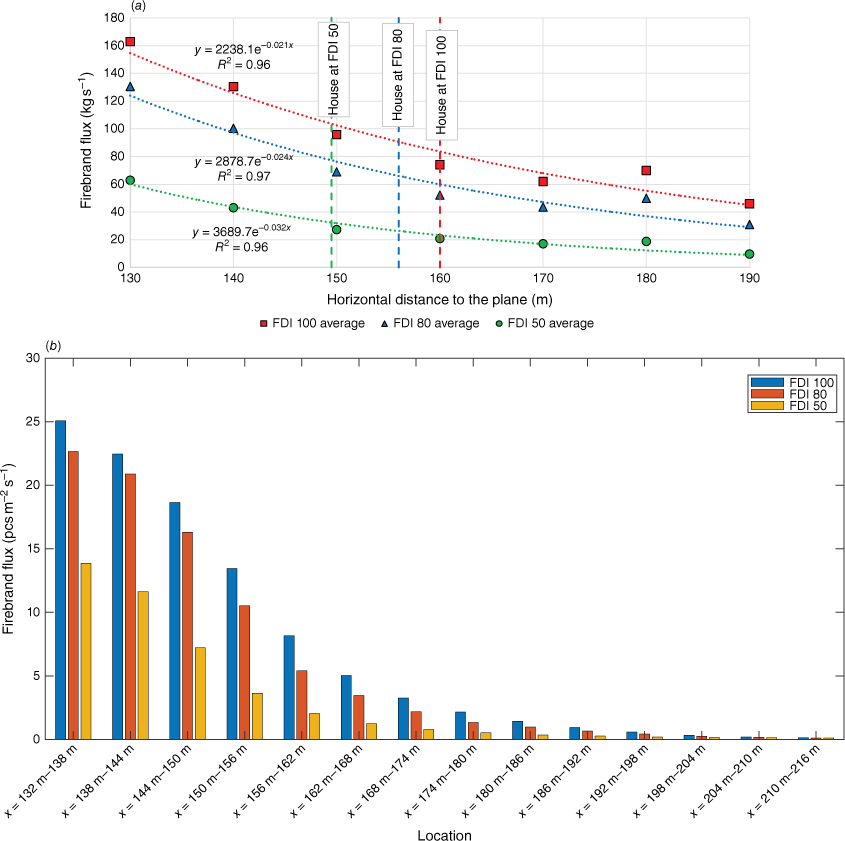
According to Fig. 15a, there is an exponential relationship for the total firebrand mass flux through the vertical planes in the downwind direction, with an agreement R2 ≥ 0.96. The highest total firebrand mass flux is at the plane aligned with the forest edge and it decreases with distance. This total firebrand mass flux decreases with decrease in FDI. The histograms in Fig. 15b show the total firebrand mass flux on the horizontal sections in the downwind direction. Similarly to the particle mass distribution through vertical planes, the highest total firebrand mass landing flux is obtained for FDI 100 followed by FDIs 80 and 50. The pattern of firebrand flux vs distance is similar to the particle distribution of an idealised forest fire by Wadhwani (2019) and the firebrand distribution experiment conducted in a Eucalyptus forest under project Vesta (Gould et al. 2008).
Correlation between firebrand flux and radiative heat flux
We used the maximum radiative heat flux and the total firebrand flux on the houses to develop a mathematical correlation. There is no significant difference in total firebrand flux between FDI 100 and 80 compared with FDI 50. Therefore, we decided to consider FDI 100 and 80 together as ‘high FDI’ and FDI 50 as ‘low FDI’. According to Fig. 16, the firebrand flux on both house designs shows a logarithmic relationship with radiative heat flux, with an R2 over 0.95 for both high and low FDIs. The high FDI curve is located over the low FDI, implying a higher firebrand risk for the same radiative heat flux at higher FDIs. The results show that the firebrand risk is minimum (i.e. BAL 12.5) when the house is situated far from the fire and there is no large difference in the firebrand flux between the high and low FDIs. This difference becomes huge with higher BALs, such as BAL FZ where the house is much closer to the fire.
The correlation of the firebrand flux and the radiative heat flux (a) single-storey houses, and (b) double-storey houses for forest vegetation at high and low FDI.
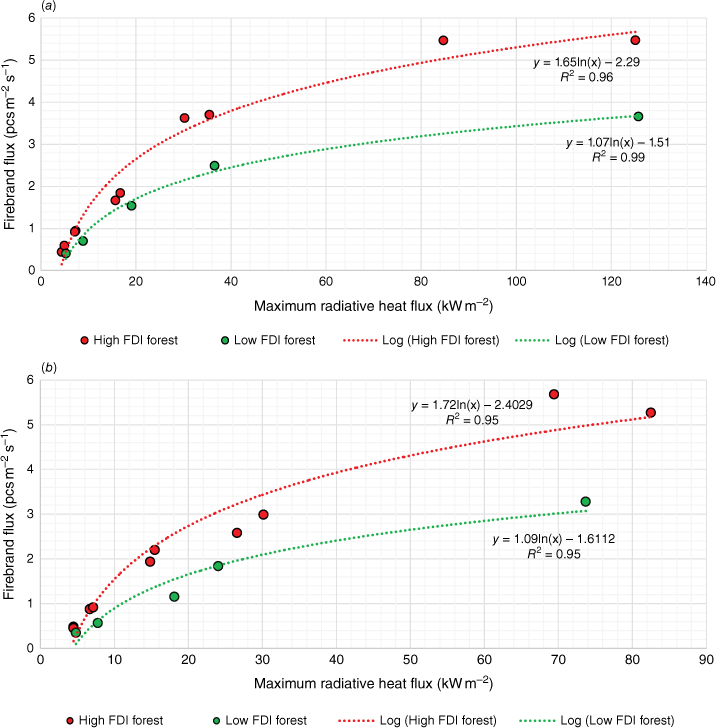
We can use the mathematical correlations developed to estimate the firebrand flux for a known maximum radiative heat flux on a house. For instance, when the maximum radiative heat flux is 25 kW m−2, the firebrand flux on the single-storey house for low and high FDIs will be 1.93 and 3.02 pcs m−2 s−1 respectively. This is 1.89 and 3.13 pcs m−2 s−1 for the double-storey house. Furthermore, when the maximum radiative heat fluxes are 4 kW m−2 for high FDI and 4.1 kW m−2 for low FDI, there is virtually no firebrand flux on the single-storey house. The ignition time for some construction materials decreases rapidly with increasing radiative heat flux (e.g. 20 s at 45 kW m−2 and 10 s at 55 kW m−2 for timber; Weir 2018). Therefore, having additional protection for construction materials that are closer to vegetation is encouraged to withstand longer radiative heat exposure. Furthermore, higher firebrand flux increases the ignition risk of building materials (Manzello et al. 2006; Suzuki and Manzello 2020, 2021). Hence, the selection of proper building materials that are capable of enduring firebrand attacks in particular locations will enhance the resilience of houses. The findings may assist building regulators in improving the construction requirements not solely concerning radiative heat, but also in regard to firebrand flux. Maintaining a suitable distance between a house and vegetation plays an important role when setting up construction standards and policies to mitigate heat flux and firebrand attack.
Conclusion
A series of physics-based simulations were conducted to quantify the firebrand and radiative heat fluxes on two different house patterns. The radiative heat flux exposure of houses was consistent with the theoretical values of Australian Standard AS3959 as expressed by BALs. The sensitivity analysis showed that the highest radiative heat flux was received by the house from maximum fuel consumption. The fireline location was also adjusted to match the theoretical radiative heat flux and it was found that a distance of 10 m from the forest edge was suitable. The gutters, roofs and decks received a higher number of firebrands and radiative heat flux compared with doors and windows, which are not directly exposed to the fire and wind flow. An exponential relationship was found for firebrand mass flux with radiative heat flux. The highest firebrand landing flux occurred close to the vegetation edge and it decreased rapidly with distance. The firebrand flux and radiative heat flux exposure of the houses was found to follow a logarithmic (R2 ≥ 0.95) trend. In this work, we approximated firebrand generation for Eucalypt trees from similar vegetation species owing to a scarcity of data. Conducting experimental work to identify firebrand generation from the dominant fuel species in each vegetation classification in different environmental conditions is recommended to improve the fidelity of models. The quantification of firebrand flux will be useful to develop building construction requirements to mitigate house ignitions by firebrand attack and improve Australian Standard AS3959 to better counter wildfire risk on structures at the WUI.
Nomenclature
| BAL | Bushfire Attack Level |
| CFD | Computational Fluid Dynamics |
| D | Drought Factor |
| FDI | Fire Danger Index |
| FDS | Fire Dynamics Simulator |
| FGR | Firebrand generation rate, pcs MW−1 s−1 |
| FI | Firebrand input rate, pcs s−1 |
| FMC | Fuel Moisture Content, (%) |
| GCI | Grid convergence index, (%) |
| HoC | Heat of combustion, kJ kg−1 |
| HRR | Heat release rate, MW |
| HRRPUA | Heat release rate per unit area, kW m−2 |
| I | Fire intensity, kW |
| L | Fireline length, m |
| LES | Large Eddy Simulation |
| MPV | Mass per volume, kg m−3 |
| NFPA | National Fire Protection Association Standards |
| Rh | Relative humidity, (%) |
| ROS | Rate of spread of fire, km h−1, m s−1 |
| T | Ambient temperature, °C |
| U10 | Wind speed at 10 m elevations, km h−1, m s−1 |
| w | Surface fuel load, t ha−1 |
| W | Total fuel load, t ha−1 |
| WUI | Wildland–urban interface |
Acknowledgements
We would like to acknowledge the scholarship provided to the first named author by Victoria University under the auspices of Bushfire and Natural Hazard Cooperative Research Centre. The authors thank David Blunk and Hudson Tyler (Oregon State University, USA) and Babak Bahrani (The University of North Carolina, USA) for providing data on the firebrand collection.
References
Adusumilli S, Hudson T, Gardner N, Blunck DL (2021) Quantifying production of hot firebrands using a fire-resistant fabric. International Journal of Wildland Fire 30(2), 154-159.
| Crossref | Google Scholar |
Aston A (1985) Heat storage in a young eucalypt forest. Agricultural and Forest Meteorology 35(1–4), 281-297.
| Crossref | Google Scholar |
Australia Bureau of Meteorology (2006) ‘Average 9 am and 3 pm relative humidity. Commonwealth of Australia 2023.’ (Bureau of Meteorology) Available at http://www.bom.gov.au/climate/maps/averages/relative-humidity/?maptype=15&period=dec [verified 16 September 2023]
Australia Bureau of Meteorology (2022) ‘Australia in March 2022. Areal average temperatures.’ (Bureau of Meteorology Australia) Available at http://www.bom.gov.au/climate/current/annual/aus/ [verified 16 September 2023]
Australian Government (2020) Your Home. Australia’s Guide to Environmentally Sustainable Homes. Available at https://www.yourhome.gov.au/house-designs [verified 16 September 2023]
Blanchi R, Leonard JE, Leicester RH (2006) Lessons learnt from post-bushfire surveys at the urban interface in Australia. Forest Ecology and Management 234(1), S139.
| Crossref | Google Scholar |
Byram GM (1959) Combustion of forest fuels. In ‘Firest fire: control and use’. pp. 61–89. (McGraw-Hill) Available at: https://cir.nii.ac.jp/crid/1572543024897550080
California Standard (2016) Califonia Fire Code. Ch. 49: Requirements for wildland–urban interface fire areas. Available at https://up.codes/viewer/california/ca-fire-code-2016/chapter/49/requirements-for-wildland-urban-interface-fire-areas#49 [verified 16 September 2023]
CSGNetwork (2022) ‘Drought Factor Calculator.’ (Palm Springs, CA) Available at http://www.csgnetwork.com/droughtindxcalc.html [verified 16 September 2023]
Department of Building and Housing (2012) ‘Extract from the New Zealand Building Code: Clauses C1–C6 Protection from Fire, Clause A3 Building Importance Levels.’ (New Zealand Government) Available at https://www.building.govt.nz/assets/Uploads/building-code-compliance/c-protection-from-fire/asvm/c1-c6-protection-from-fire-a3.pdf [verified on 16 September 2023]
Francaise R (2017) Code forestier. (Legifrance) Available at https://www.legifrance.gouv.fr/codes/id/LEGITEXT000025244092/ [verified 16 September 2023] [In French]
Haider A, Levenspiel O (1989) Drag coefficient and terminal velocity of spherical and non-spherical particles. Powder technology 58(1), 63-70.
| Crossref | Google Scholar |
Hays RL (1975) The thermal conductivity of leaves. Planta 125(3), 281-287.
| Crossref | Google Scholar | PubMed |
Hudson TR, Bray RB, Blunck DL, Page W, Butler B (2020) Effects of fuel morphology on ember generation characteristics at the tree scale. International Journal of Wildland Fire 29(11), 1042-1051.
| Crossref | Google Scholar |
International Botanic Gardens Conservation (2023) GlobalTreeSearch. Available at https://www.bgci.org/resources/bgci-databases/globaltreesearch/ [verified 16 September 2023]
International Code Council (2022) International Wildland–Urban Interface Code (IWUIC). Availble at https://codes.iccsafe.org/content/IWUIC2015/preface [verified 16 September 2023]
Intini P, Ronchi E, Gwynne S, Bénichou N (2020) Guidance on design and construction of the built environment against wildland–urban interface fire hazard: a review. Fire Technology 56(5), 1853-1883.
| Crossref | Google Scholar |
Jarrin N, Benhamadouche S, Laurence D, Prosser R (2006) A synthetic eddy-method for generating inflow conditions for large-eddy simulations. International Journal of Heat and Fluid Flow 27(4), 585-593.
| Crossref | Google Scholar |
Khan N, Sutherland D, Wadhwani R, Moinuddin K (2019) Physics-based simulation of heat load on structures for improving construction standards for bushfire-prone areas. Frontiers in Mechanical Engineering 5, 35.
| Crossref | Google Scholar |
Koo E, Pagni PJ, Weise DR, Woycheese JP (2010) Firebrands and spotting ignition in large-scale fires. International Journal of Wildland Fire 19(7), 818-843.
| Crossref | Google Scholar |
Manzello SL, Cleary TG, Shields JR, Yang JC (2006) On the ignition of fuel beds by firebrands. Fire and Materials 30(1), 77-87.
| Crossref | Google Scholar |
Manzello SL, Maranghides A, Mell WE (2007) Firebrand generation from burning vegetation. International Journal of Wildland Fire 16(4), 458-462.
| Crossref | Google Scholar |
Manzello SL, Park SH, Suzuki S, Shields JR, Hayashi Y (2011) Experimental investigation of structure vulnerabilities to firebrand showers. Fire Safety Journal 46(8), 568-578.
| Crossref | Google Scholar |
Manzello SL, Suzuki S, Gollner MJ, Fernandez-Pello AC (2020) Role of firebrand combustion in large outdoor fire spread. Progress in Energy and Combustion Science 76, 100801.
| Crossref | Google Scholar | PubMed |
Maranghides A, Mell W (2011) A case study of a community affected by the Witch and Guejito wildland fires. Fire Technology 47(2), 379-420.
| Crossref | Google Scholar |
Moinuddin KAM, Sutherland D, Mell W (2018) Simulation study of grass fire using a physics-based model: striving towards numerical rigour and the effect of grass height on the rate of spread. International Journal of Wildland Fire 27(12), 800-814.
| Crossref | Google Scholar |
New Zealand Government (2017) ‘Fire and Emergency New Zealand Act 2017.’ (New Zealand) Available at https://www.legislation.govt.nz/act/public/2017/0017/46.0/DLM6678607.html
Nguyen D, Kaye NB (2021) Experimental investigation of rooftop hotspots during wildfire ember storms. Fire Safety Journal 125, 103445.
| Crossref | Google Scholar |
Noble IR, Gill AM, Bary GAV (1980) McArthur’s fire‐danger meters expressed as equations. Austral Ecology 5(2), 201-203.
| Crossref | Google Scholar |
Quarles SL, Standohar-Alfano C, Hedayati F, Gorham DJ (2023) Factors influencing ember accumulation near a building. International Journal of Wildland Fire 32(3), 380-387.
| Crossref | Google Scholar |
Storey MA, Price OF, Bradstock RA, Sharples JJ (2020) Analysis of variation in distance, number, and distribution of spotting in southeast Australian wildfires. Fire 3(2), 10.
| Crossref | Google Scholar |
Suzuki S, Manzello SL (2020) Role of accumulation for ignition of fuel beds by firebrands. Applications in Energy Combustion Science 1–4, 100002.
| Crossref | Google Scholar |
Suzuki S, Manzello SLJS (2021) Ignition vulnerabilities of combustibles around houses to firebrand showers: further comparison of experiments. Sustainability 13(4), 2136.
| Crossref | Google Scholar | PubMed |
Tarifa CS, del Notario PP, Moreno FG (1965) On the flight paths and lifetimes of burning particles of wood. Symposium (International) on Combustion 10, 1021-1037.
| Crossref | Google Scholar |
Thomas JC, Mueller EV, Santamaria S, Gallagher M, El Houssami M, Filkov A, Clark K, Skowronski N, Hadden RM, Mell W, Simeoni A (2017) Investigation of firebrand generation from an experimental fire: development of a reliable data collection methodology. Fire Safety Journal 91, 864-871.
| Crossref | Google Scholar |
Wadhwani R, Sutherland D, Ooi A, Moinuddin K (2022) Firebrand transport from a novel firebrand generator: numerical simulation of laboratory experiments. International Journal of Wildland Fire 31(6), 634-648.
| Crossref | Google Scholar |
Whittaker J, Blanchi R, Haynes K, Leonard J, Opie K (2017) Experiences of sheltering during the Black Saturday bushfires: implications for policy and research. International Journal of Disaster Risk Reduction 23, 119-127.
| Crossref | Google Scholar |
Wickramasinghe A, Khan N, Moinuddin K (2022) Determining firebrand generation rate using physics-based modelling from experimental studies through inverse analysis. Fire 5(1), 6.
| Crossref | Google Scholar |
World Agroforestry (2023) Global Tree Knowledge Platform. Available at https://worldagroforestry.org/tree-knowledge/type-of-resource/tree-databases [verified 16 September 2023]
Wotton BM, Gould JS, McCaw WL, Cheney NP, Taylor SW (2012) Flame temperature and residence time of fires in dry eucalypt forest. International Journal of Wildland Fire 21(3), 270-281.
| Crossref | Google Scholar |