The development of fire-induced damage functions for forest recreation activity in Alberta, Canada
Michael Rausch A , Peter C. Boxall A D and Arunas P. Verbyla B CA Department of Rural Economy, University of Alberta, Edmonton, AB, T6G 2H1, Canada.
B School of Agriculture, Food and Wine, The University of Adelaide, SA 5005, Australia.
C CSIRO Mathematical and Information Sciences, Urrbrae, SA 5064, Australia.
D Corresponding author. Email: peter.boxall@ualberta.ca
International Journal of Wildland Fire 19(1) 63-74 https://doi.org/10.1071/WF08137
Submitted: 2 August 2008 Accepted: 8 May 2009 Published: 5 February 2010
Abstract
This study develops an intertemporal fire damage function for forest recreation activity in the eastern slopes region of the Canadian Rocky Mountains. The methodology employed combined revealed-stated preference data in which the behavioral response variable was annual camping trip frequencies. Photographs were used to portray changes in stand ages and related changes in trip frequencies. The data were analysed using negative binomial count data models. Unlike previous studies employing similar methods, a random effects specification was used to develop trip demand parameters. The results suggest that fires initially decrease annual trips from ~2.56 to 1.0 after the burn. As the stand ages, the effect of the fire decreases until ~12 years after the fire when the trip frequencies recover to about their previous ‘old-growth’ levels. This function is different from others described in the literature for similar mountain ecosystems in North America.
Acknowledgements
Funding for this project was provided by the Sustainable Forest Management Network of the Canadian National Centres of Excellence at the University of Alberta. The authors also thank Vic Adamowicz, Rick Pelletier and Uldis Silins for valuable advice and assistance.
Boxall PC , Englin J (2008) Fire and recreation values in fire-prone forests: Exploring an intertemporal amenity function using pooled RP-SP data. Journal of Agricultural and Resource Economics 33, 19–33.
Englin J , Cameron TA (1996) Augmenting travel cost models with contingent behavior data; Poisson regression analyses with individual panel data. Environmental and Resource Economics 7, 133–147.
| Crossref | GoogleScholarGoogle Scholar |
Loomis JB, González-Cabán A , Englin J (2001) Testing for differential effects of forest fires on hiking and mountain biking demand and benefits. Journal of Agricultural and Resource Economics 26, 508–522.
Shaw D (1988) On-site samples’ regression; problems of non-negative integers, truncation, and endogenous stratification. Journal of Econometrics 37, 211–223.
| Crossref | GoogleScholarGoogle Scholar |
Yen ST , Adamowicz WL (1993) Statistical properties of welfare measures from count-data models of recreation demand. Review of Agricultural Economics 15, 203–215.
| Crossref | GoogleScholarGoogle Scholar | suggests that the relationship between forest age, as mitigated by fire and recreation is not straightforward.
B Note that this approach ignores the role of substitutes by considering a region or network of recreation areas as the single site. Accounting for substitutes requires significant information from recreationists as well as alternate econometric modelling frameworks. Generally, substitution effects will be important if economic welfare measurement is a goal in the analysis.
C Random campers are people who camp in undesignated areas on forested public lands and are not subject to camping fees or regulations. Also known as ‘bush’ campers, random campers believe in right of access and many experts believe that random campers are the most common forest recreation users in Alberta’s eastern slopes region.
D Including long distance travellers significantly alters the parameters of recreation demand models. These travellers typically have multiple destinations, which, if included, biases the travel cost variable and overestimates resulting economic values (Englin et al. 2001). People have numerous stopping points and activities planned when undertaking long journeys; most local campers take shorter trips whose primary objective was to camp at the place they were contacted.
E The total number of camping days was not recorded, but rather the number of trips taken. As Morey and Breffle (2003, p. 3) explain, ‘Not modeling the total number of…days simplifies data collection and modeling while still generating policy-relevant results that are often easier to defend than the results of models that explain and predict both participation and site choice’.
F This involves calculating λj using the Poisson coefficients, and then regressing ((vj – λj)2 – vj)(λj)–1 against δ1λj and δ2λj2. Statistically significant δ parameters from these regressions suggest that overdispersion exists and that a Poisson model would be unsuitable for the data.
G The random camping value is comparable to most other recreation demand studies, but the regular camper result is high with the exception of Englin et al.’s (2001) total of CA$398 per trip for Wyoming recreationists. The difference among per trip values across studies could be due to differences in either or both of the type of recreation (camping as opposed to trail-based activities) or the region studied (Alberta, as opposed to various American states). However, the most likely reason for the discrepancy in values is the length of time required for the activity examined – the average duration for a trip in this Alberta study was 5.26 days compared with single-day outings for most of the other studies. Establishing ‘per day’ consumer surplus values yields a regular camper value of CA$78.76 per day and CA$30.46 per day for random campers.
Appendix
The hierarchical model that underlies RENEGBIN is as follows:
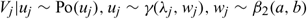
where β2(a, b) indicates the β distribution of the second-kind. Thus, the density function for wj is given by:
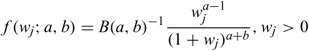
where B(a, b) is the β function:
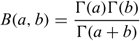
Note that in the RENEGBIN model, the dependence on λj and hence on xj is via the shape parameter of the gamma distribution. The distribution of Vj is given by.
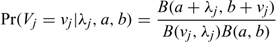
The mean and variance of the RENEGBIN model are given by (using conditional expectations and variances):
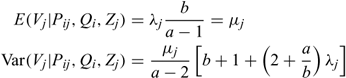
The moments of the RENEGBIN and NEGBIN are quite similar. The additional level of random effects in RENEGBIN, however, introduces further flexibility in the conditional variance. One proviso is that a >2.


