A 229-year dendroclimatic-inferred record of forest fire activity for the Boreal Shield of Canada
Martin P. Girardin A C F , Yves Bergeron B , Jacques C. Tardif C , Sylvie Gauthier A , Mike D. Flannigan D and Manfred Mudelsee EA Natural Resources Canada, Canadian Forest Service, Laurentian Forestry Centre, 1055 du PEPS, PO Box 10380, Stn. Sainte-Foy, QC G1V 4C7, Canada.
B Groupe de recherche en écologie forestière inter-universitaire (GREFI), Université du Quebec à Montréal, CP 8888, Succ. Centre-Ville, Montréal, QC H3C 3P8, Canada.
C Center for Forest Interdisciplinary Research (C-FIR), University of Winnipeg, 515 Avenue Portage, Winnipeg, MB R3B 2E9, Canada.
D Natural Resources Canada, Canadian Forest Service, Great Lakes Forestry Centre, 1219 Queen Street-East, Sault Ste. Marie, ON P6A 2E5, Canada.
E Institute of Meteorology, University of Leipzig, Stephanstrasse 3, 04103 Leipzig, Germany, and Climate Risk Analysis, Wasserweg 2, 06114 Halle, Germany.
F Corresponding author. Email: martin.girardin@rncan.gc.ca
International Journal of Wildland Fire 15(3) 375-388 https://doi.org/10.1071/WF05065
Submitted: 14 June 2005 Accepted: 21 December 2005 Published: 5 September 2006
Abstract
Six independent tree-ring reconstructions of summer drought were calibrated against instrumental fire data to develop a 229-year dendroclimatic-inferred record of fire activity (annual area burned and fire occurrence) on the Boreal Shield, Canada. As a means of validating the statistical reconstructions of the fire activity, a comparison was made with a stand age distribution derived from a regional time-since-last-fire map for an area located at the transition between the mixedwood and coniferous boreal forests of south-western Quebec. Calibration statistics indicated that 31% of the area burned variance and 45% of the fire occurrence variance could be accounted for by the six drought reconstructions. The verification statistics indicated a tendency for the statistical reconstructions of the fire activity to reproduce with confidence both high and relatively low frequency variations in fire. Episodes of succeeding years with important fire activity were estimated for 1789–1796, 1820–1823, 1837–1841, 1862–1866, 1906–1912, 1919–1922, 1933–1938, and 1974–1977. Also estimated were periods of reduced forest fire activity, particularly in the occurrence rate of extreme fire years, from c. 1850 to 1900 and again during the second half of the 20th century. Correlation analysis between the statistical reconstruction of the area burned and the stand age distribution suggested that both proxies shared similar information on the fire activity. Correlation maps, however, indicated that variability in the statistical reconstructions was not necessarily representative of fire activity in all regions of the Boreal Shield.
Amiro BD, Logan KA, Wotton BM, Flannigan DM, Todd JB, Stocks BJ , Martell DL (2004) Fire weather index system components for large fires in the Canadian boreal forest. International Journal of Wildland Fire 13, 391–400.
| Crossref | GoogleScholarGoogle Scholar |
Cook ER, Briffa KR , Jones PD (1994) Spatial regression methods in dendroclimatology: a review and comparison of two techniques. International Journal of Climatology 14, 379–402.
DesRochers A , Gagnon R (1997) Is ring count at ground level a good estimation of black spruce age? Canadian Journal of Forest Research 27, 1263–1267.
| Crossref | GoogleScholarGoogle Scholar |
Flannigan MD , Harrington JB (1988) A study of the relation of meteorological variables to monthly provincial area burned by wildfire in Canada (1953–80). Journal of Applied Meteorology 27, 441–452.
| Crossref | GoogleScholarGoogle Scholar |
Fox JF (1989) Bias in estimating forest disturbance rates and tree life-times. Ecology 70, 1267–1272.
| Crossref |
Hofgaard A, Tardif J , Bergeron Y (1999) Dendroclimatic response of Picea mariana and Pinus banksiana along a latitudinal gradient in the eastern Canadian boreal forest. Canadian Journal of Forest Research 29, 1333–1346.
| Crossref | GoogleScholarGoogle Scholar |
Johnson EA , Gutsell SL (1994) Fire frequency models, methods and interpretations. Advances in Ecological Research 25, 239–287.
Luterbacher J, Xoplaki E, Dietrich D, Rickli R, Jacobeit J, Beck C, Gyalistras D, Schmutz C , Wanner H (2002) Reconstruction of sea level pressure fields over the Eastern North Atlantic and Europe back to 1500. Climate Dynamics 18, 545–561.
Mudelsee M (2003) Estimating Pearson’s correlation coefficient with bootstrap confidence interval from serially dependent time series. Mathematical Geology 35, 651–665.
| Crossref | GoogleScholarGoogle Scholar |
Skinner WR, Stocks BJ, Martell DL, Bonsal B , Shabbar A (1999) The association between circulation anomalies in the mid-troposphere and the area burned by wildland fire in Canada. Theoretical and Applied Climatology 63, 89–105.
| Crossref | GoogleScholarGoogle Scholar |
Tardif J, Conciatori F , Bergeron Y (2002) Comparative analysis of the climatic response of seven boreal tree species from north-western Québec, Canada. Tree-Ring Research 57, 25–37.
Veillette JJ (1994) Evolution and paleohydrology of glacial lakes Barlow and Ojibway. Quaternary Science Reviews 13, 945–971.
| Crossref | GoogleScholarGoogle Scholar |
Zhang X, Vincent L, Hogg WD , Niitsoo A (2000) Temperature and precipitation trends in Canada during the 20th century. Atmosphere and Ocean 38, 395–429.
is the ratio of the total squared error obtained with the regression estimates and the total squared error obtained using the dependent period mean as the only estimate. This average becomes a standard against which the regression estimation is compared. If the reconstruction does a better job than the average of the dependant period, then the total error of the regression estimate is less, the ratio is less than one, and the RE is positive.
The PM test calculates the products of the deviations and collects the positive and negative products in two separate groups based on their sign. The values of the products in each group are summed, and the means computed. The difference between the absolute values of the two means M+ − M− can be tested for significance using the t statistics:
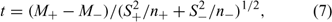
where n+ and n− are the number of positive and negative products and S+2 and S−2 are the corresponding variance.


