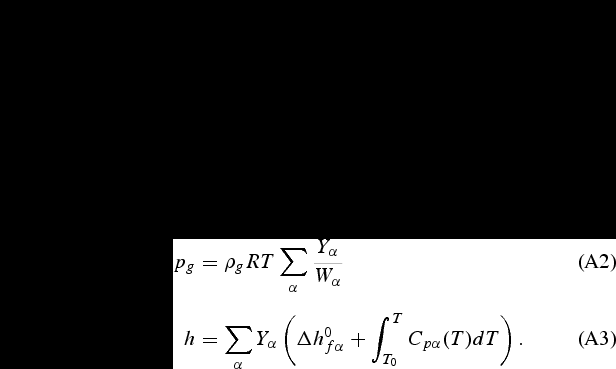Fire spread across pine needle fuel beds: characterization of temperature and velocity distributions within the fire plume
Thierry Marcelli A C , Paul A. Santoni A , Albert Simeoni A , Eric Leoni A and Bernard Porterie BA SPE, Université de Corse, UMR CNRS 6134, ERT FEUX, Campus Grossetti, B.P. 52, 20250 Corte, France.
B IUSTI–UMR CNRS 6595, ERT FEUX, Technopôle de Château-Gombert 5, Rue Enrico Fermi, 13453 Marseille Cedex 13, France.
C Corresponding author. Telephone: +33 4 95 45 01 61; email: marcelli@univ-corse.fr
International Journal of Wildland Fire 13(1) 37-48 https://doi.org/10.1071/WF02065
Submitted: 11 December 2002 Accepted: 27 May 2003 Published: 8 April 2004
Abstract
The aim of this article is twofold. First, it concerns the improvement of knowledge on the fundamental physical mechanisms that control the propagation of forest fires. To proceed, an experimental apparatus was designed to study, in laboratory conditions, the flame of a fire spreading across a pine needle fuel bed. Characterization of temperature was managed by using a reconstruction method based on a double thermocouple probe technique developed recently. The vertical gas velocity distribution was derived from the previous reconstructed signals by measuring the transit time of a thermal fluctuation between two points of the flow. Second, the experimental data were used for the testing of a physical two-phase model of forest fire behavior in which the decomposition of solid fuel constituting a forest fuel bed as well as the multiple interactions with the gas phase are represented.
Bellemare LO, Porterie B , Loraud JC (2001) On the prediction of firebreak efficiency. Combustion Science and Technology 163, 131–176.

Chow WK , Cheung YL (1997) Comparison of the algorithms PISO and SIMPLER for solving pressure-velocity linked equations in simulating compartment fire. Numerical Heat Transf er Part A: Applications 31, 87–112.

Cox G (1977) Gas velocity measurement in fires by the cross-correlation of random thermal fluctuations—a comparison with conventional techniques. Combustion and Flame 28, 155–163.
| Crossref | GoogleScholarGoogle Scholar |

Cox G , Chitty R (1985) Some source-dependent effects of unbounded fires. Combustion and Flame 60, 219–232.
| Crossref | GoogleScholarGoogle Scholar |

Dupuy JL, Maréchal J, Bouvier L , Loïs N (1998) Measurement of temperatures and radiant fluxes during static fires in a porous fuel. Proceedings of the III International Conference on Forest Fire Research, Vol I 14th Conference on Fire and Forest Meteorology, Luso.
Fletcher CAJ (1988) Computational techniques for fluid dynamics. In
Grishin AM (1978) Mathematical modelling of forest fires. Numerical Methods in Continuum Mechanics 9, 30–56.

Grishin AM (1997) Mathematical modeling of forest fires and new methods of fighting them (Publishing House of the Tomsk State University: Tomsk)
Kennedy IM, Kollmann W , Chen JY (1990) A model for soot formation in a laminar diffusion flame. Combustion and Flame 81, 73–85.
| Crossref | GoogleScholarGoogle Scholar |

Larini M, Giroux F, Porterie B , Loraud JC (1998) A multiphase formulation for fire propagation in heterogeneous combustible media. International Journal of Heat and Mass Transfer 41, 881–897.
| Crossref | GoogleScholarGoogle Scholar |

Leonard BP , Mokhtari S (1990) Beyond first-order upwinding: the ultrasharp alternative for non-oscillatory steady-state simulation of convection. International Journal for Numerical Methods in Engineering 30, 729–766.

Leonard BP (1991) The ultimate conservative difference scheme applied to unsteady one-dimensional advection. Computer Methods in Applied Mechanics and Engineering 88, 17–74.
| Crossref | GoogleScholarGoogle Scholar |

Leonard BP , Drummond JE (1995) Why you should not use hybrid, power-law or related exponential schemes for convective modelling. There are much better alternatives. International Journal for Numerical Methods in Engineering 20, 421–442.

McCaffrey BJ (1979) Purely buoyant diffusion flame: Some experimental results. In
Mcenally CS, Köylü ÜÖ, Pfefferle LD , Rosner DE (1997) Soot volume fraction and temperature measurements in laminar nonpremixed flames using thermocouples. Combustion and Flame 109, 701–720.
| Crossref | GoogleScholarGoogle Scholar |

Olim M, Igra O, Mond M , Ben-Dor G (1990) Numerical investigation of the flow field behind a shock wave propagating into a carbon-oxygen suspension. Physics of Fluids 2(8), 1393–1403.
| Crossref | GoogleScholarGoogle Scholar |

Patankar SV (1980) Numerical heat transfer and fluid flow (Hemisphere Publishing Corporation: New York)
Porterie B, Morvan D, Loraud JC , Larini M (2000) Firespread through fuel beds: Modeling of wind-aided fires and induced hydrodynamics. Physics of Fluids 12, 1762–1781.
| Crossref | GoogleScholarGoogle Scholar |

Santoni PA, Marcelli T , Leoni E (2002) Measurement of fluctuating temperatures in a continuous flame spreading across a fuel bed using a double thermocouple probe. Combustion and Flame 131, 47–58.
| Crossref | GoogleScholarGoogle Scholar |

Séro-Guillaume O , Margerit J (2002a) Modelling forest fires. Part I: A complete set of equations derived by extended irreversible thermodynamics. International Journal of Heat and Mass Transfer 45(8), 1705–1722.
| Crossref |

Séro-Guillaume O , Margerit J (2002b) Modelling forest fires. Part II: Reduction to two-dimensional models and simulation of propagation. International Journal of Heat and Mass Transfer 45(8), 1723–1737.
| Crossref |

Tagawa M , Ohta Y (1997) Two-thermocouple probe for fluctuating temperature measurement in combustion—rational estimation of mean and fluctuating time constants. Combustion and Flame 109, 549–560.
| Crossref | GoogleScholarGoogle Scholar |

Vachon M, Cambray P, Maciaszek T , Bellet JV (1986) Temperature and velocity fluctuation measurements in a diffusion flame with large buoyancy effects. Combustion Science and Technology 48, 223–240.

Weber RO (1991) Modelling fire spread through fuel beds. Progress in Energy and Combustion Science 17, 67–82.
| Crossref | GoogleScholarGoogle Scholar |

Yakhot V , Orzag S (1986) Renormalization group analysis of turbulence. Journal of Scientific Computing 1, 3–52.

Zukoski EE (1995) Properties of fire plume, combustion fundamentals of fire (Academic Press: San Diego)
Appendix: Model equations
The general form of the transport equations of the gas phase is the following:
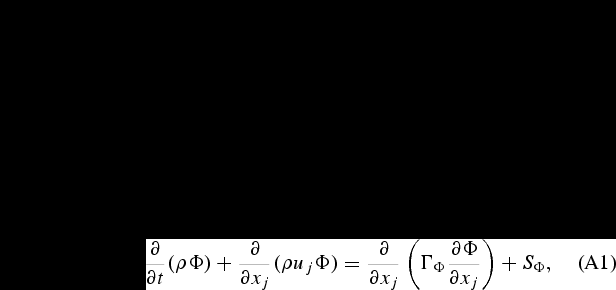
where  is any transported property (species mass fraction, momentum through two velocity components, turbulent kinetic energy, rate of dissipation of turbulent kinetic energy, soot volume fraction or energy by means of the enthalpy);
is any transported property (species mass fraction, momentum through two velocity components, turbulent kinetic energy, rate of dissipation of turbulent kinetic energy, soot volume fraction or energy by means of the enthalpy);  and
and  are the diffusion exchange coefficient and source/sink terms for
are the diffusion exchange coefficient and source/sink terms for  . They are summarized as follows:
. They are summarized as follows:

The three source terms in the transport equation of soot account for the thermophoresis, formation, and oxidation processes, respectively, and ρs = 1800 kg/m3 is the soot density. The terms Fi, Sh, SYα, and  are the drag force, the chemical sources of enthalpy and species as a consequence of thermal degradation of the fuel material, and the chemical source of species as a consequence of homogeneous reactions.
are the drag force, the chemical sources of enthalpy and species as a consequence of thermal degradation of the fuel material, and the chemical source of species as a consequence of homogeneous reactions.
The shear and buoyancy turbulent production/destruction terms P and W can be expressed by
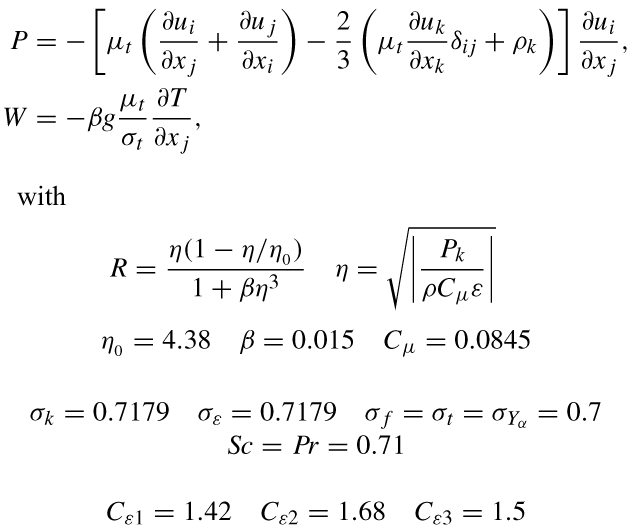
Equations of state
The gas is assumed to be a mixture of perfect gases and, including the chemical energy in the mixture static enthalpy, the equations of state will take the form